Temperature Effect on the Compressive Behavior and Constitutive Model of Plain Hardened Concrete
Abstract
:1. Introduction
2. Problem Formulation
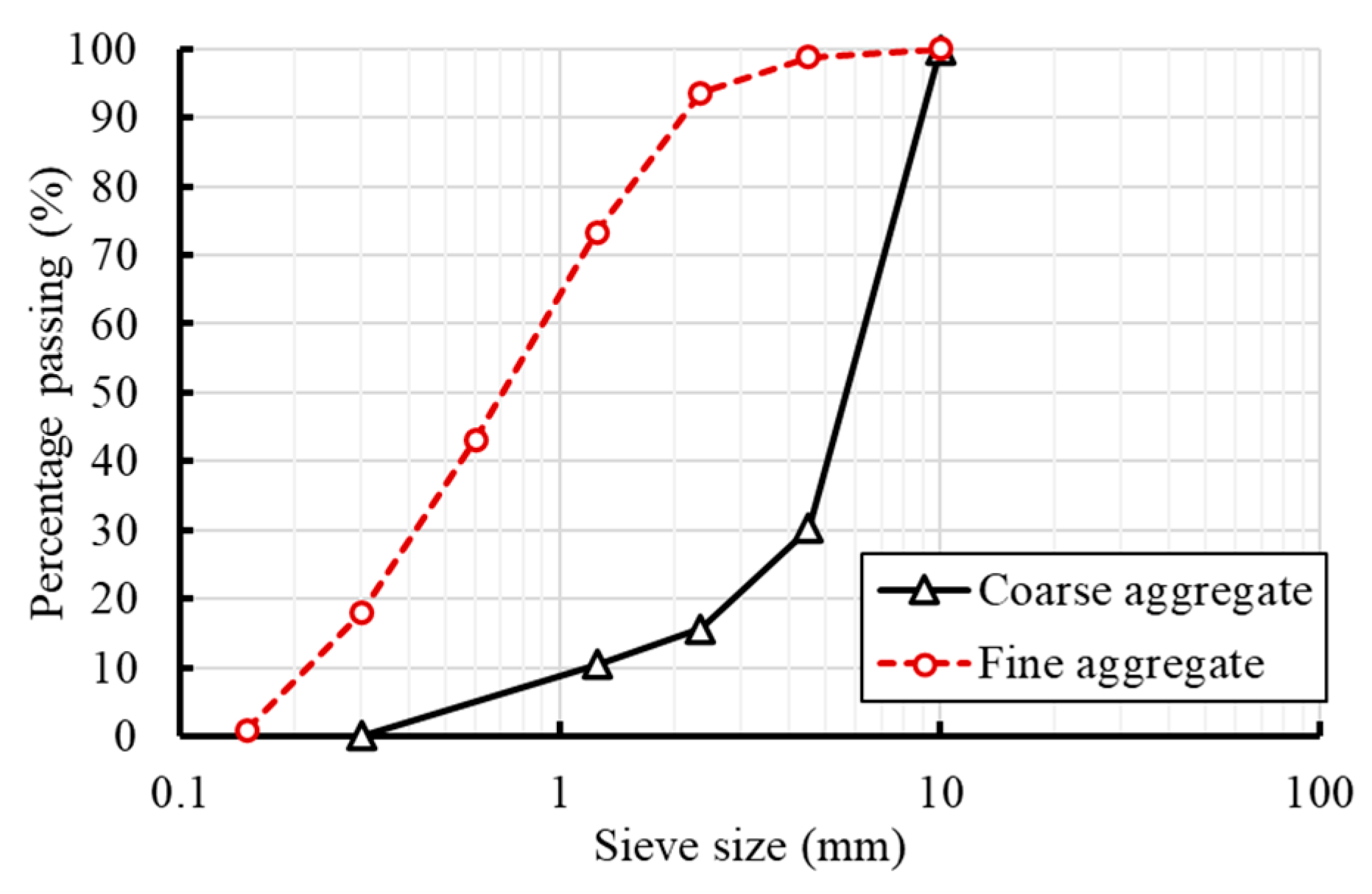
2.1. Materials
2.2. Mixing, Fabrication, and Curing of Specimens
2.3. Detection of The Temperature Effect on the Mechanical Properties of Concrete
3. Test Results and Discussion
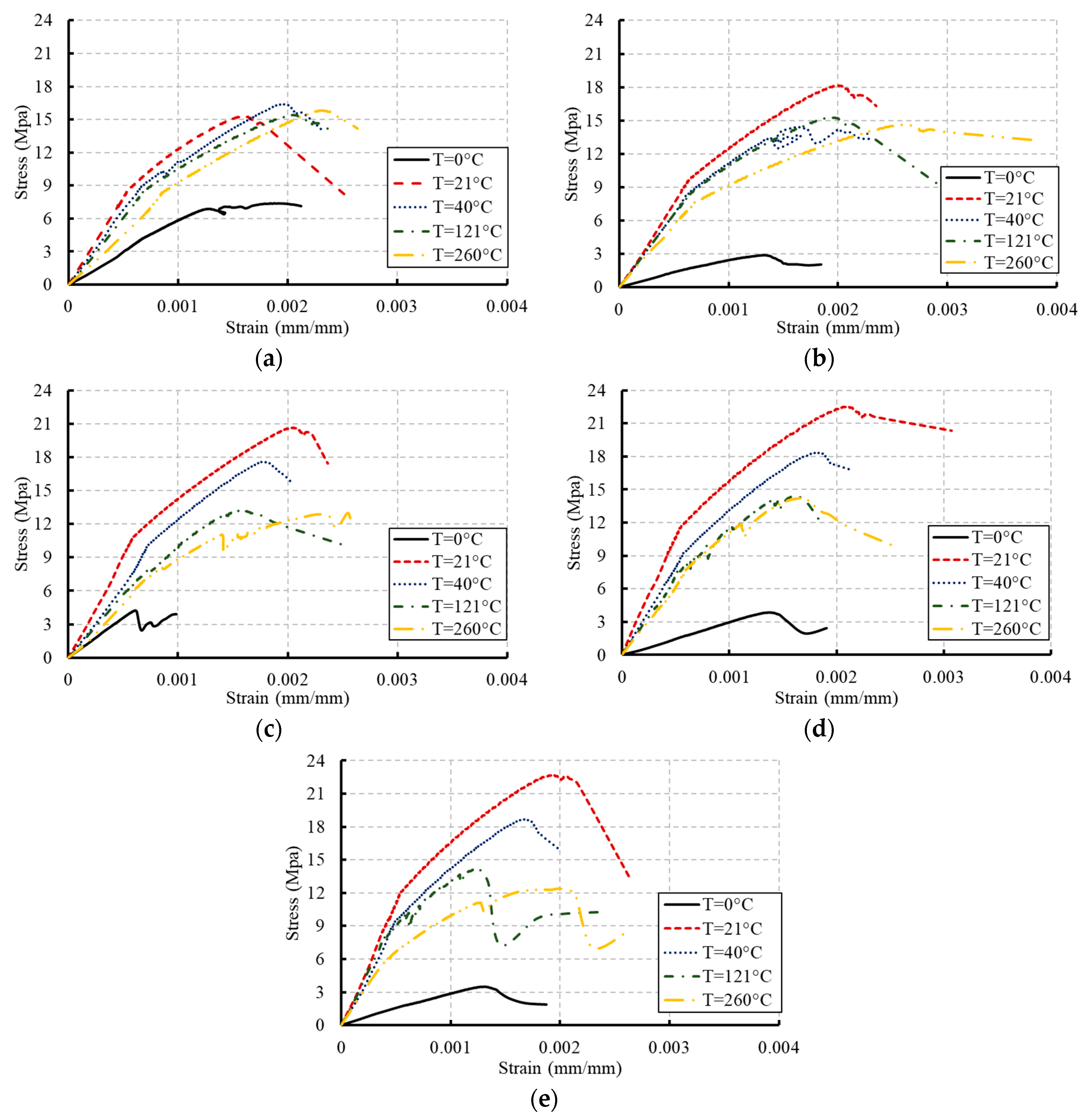
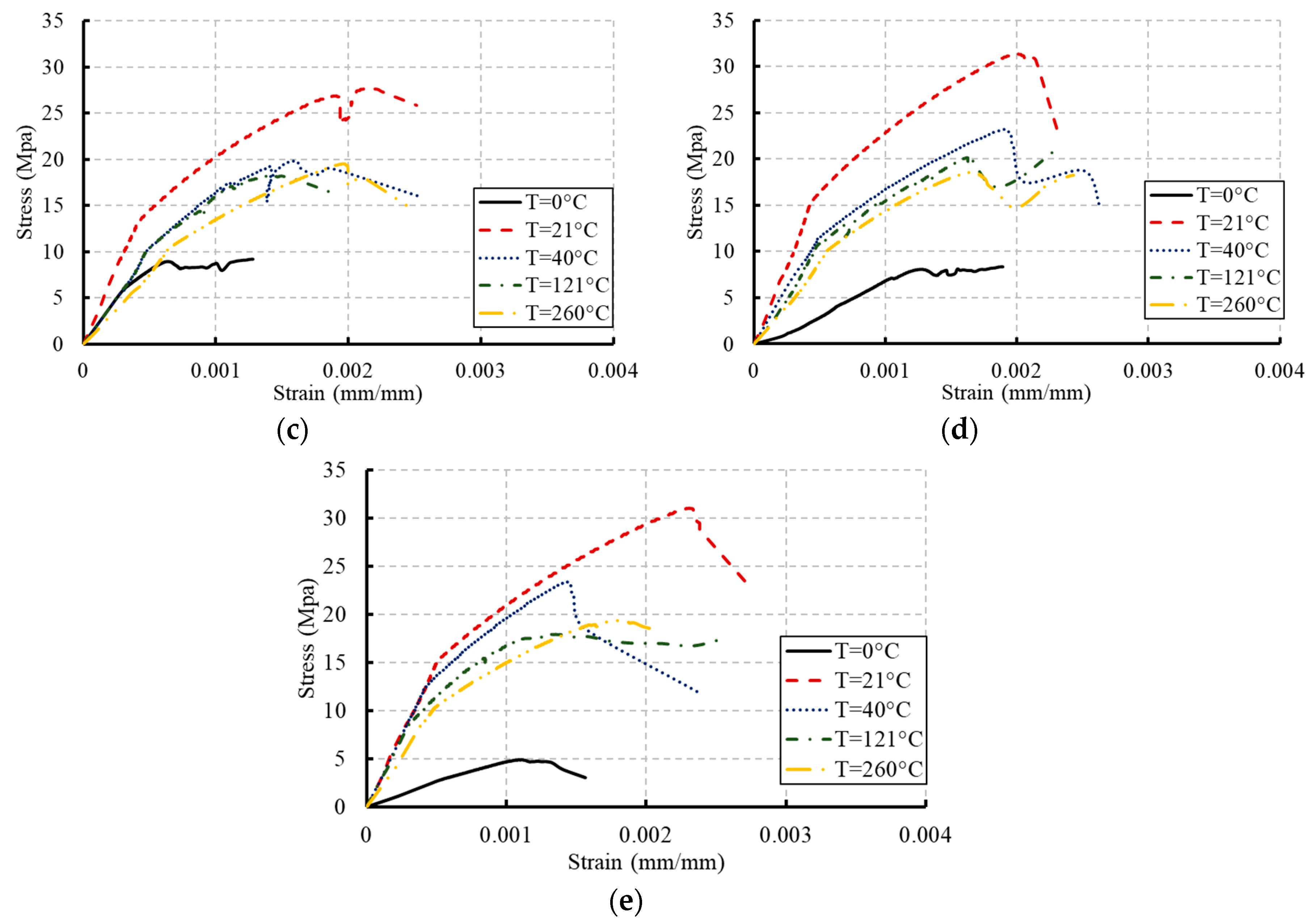
3.1. Stress–Strain Relationships
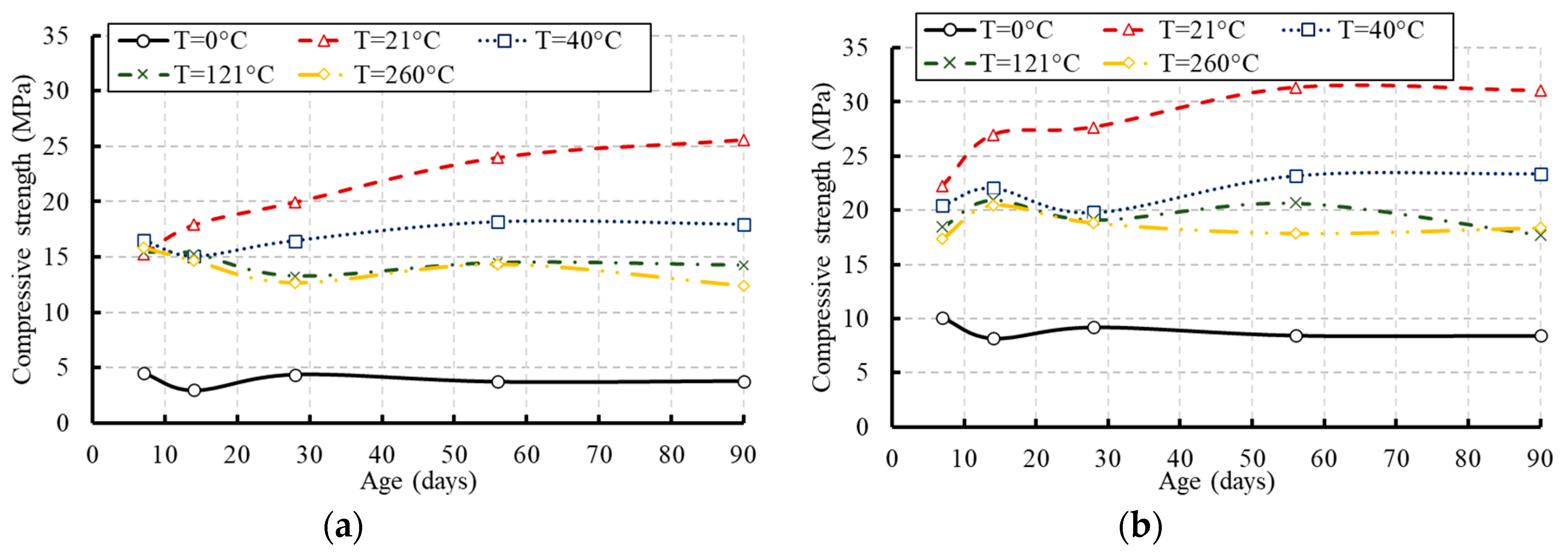
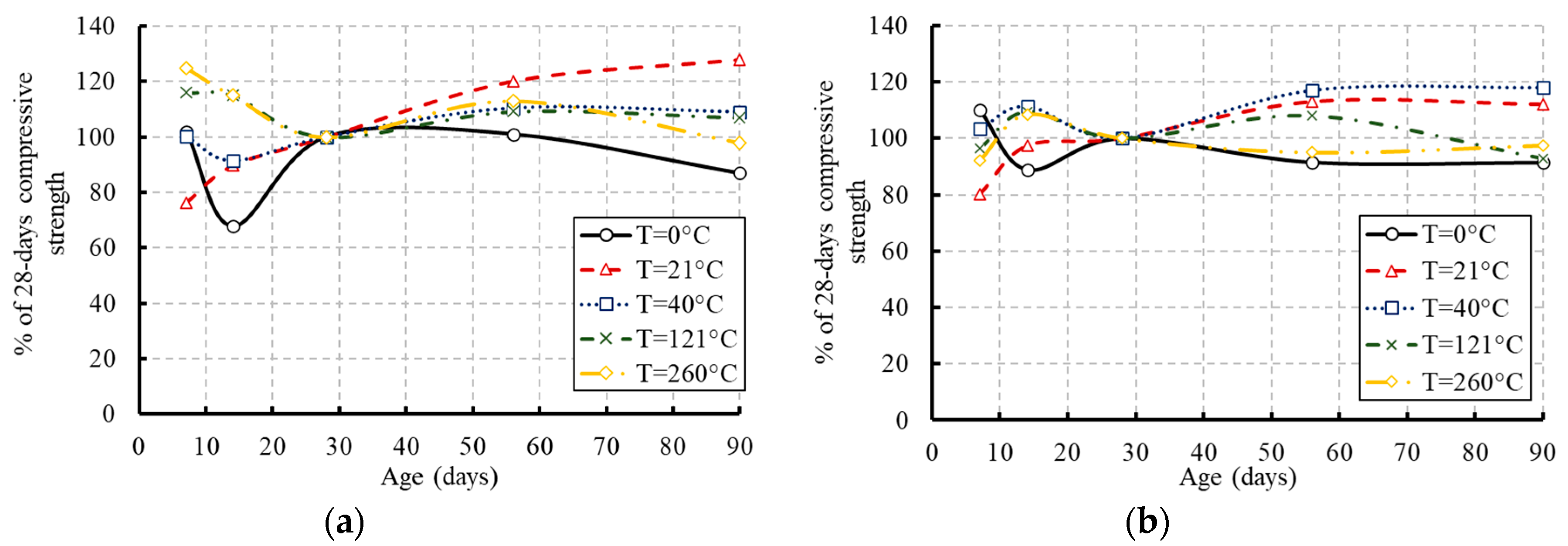
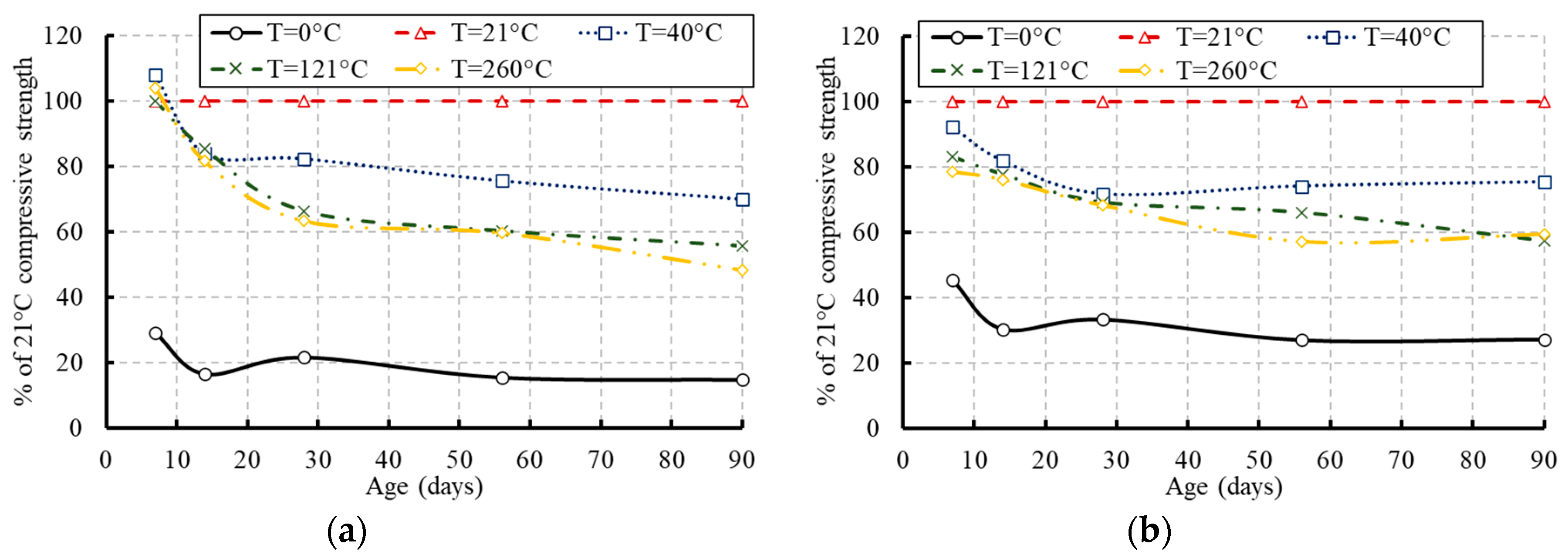
3.2. Compressive Strength
3.3. Ultimate Strain Corresponding to the Compressive Strength
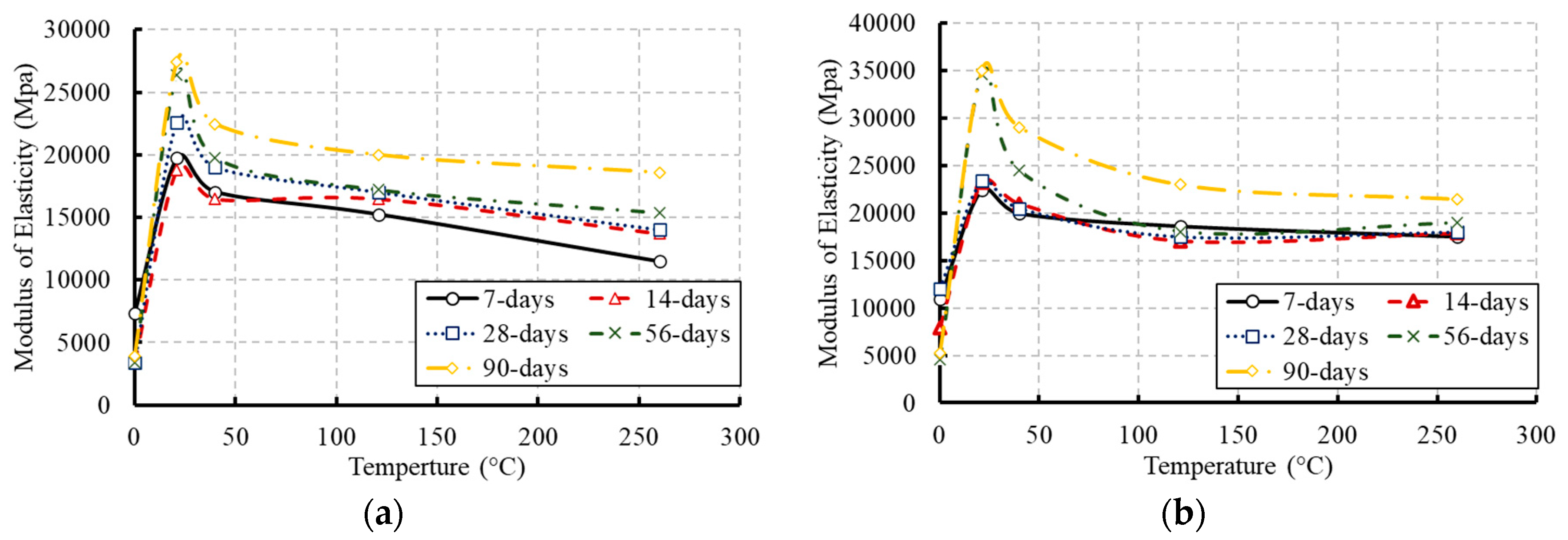
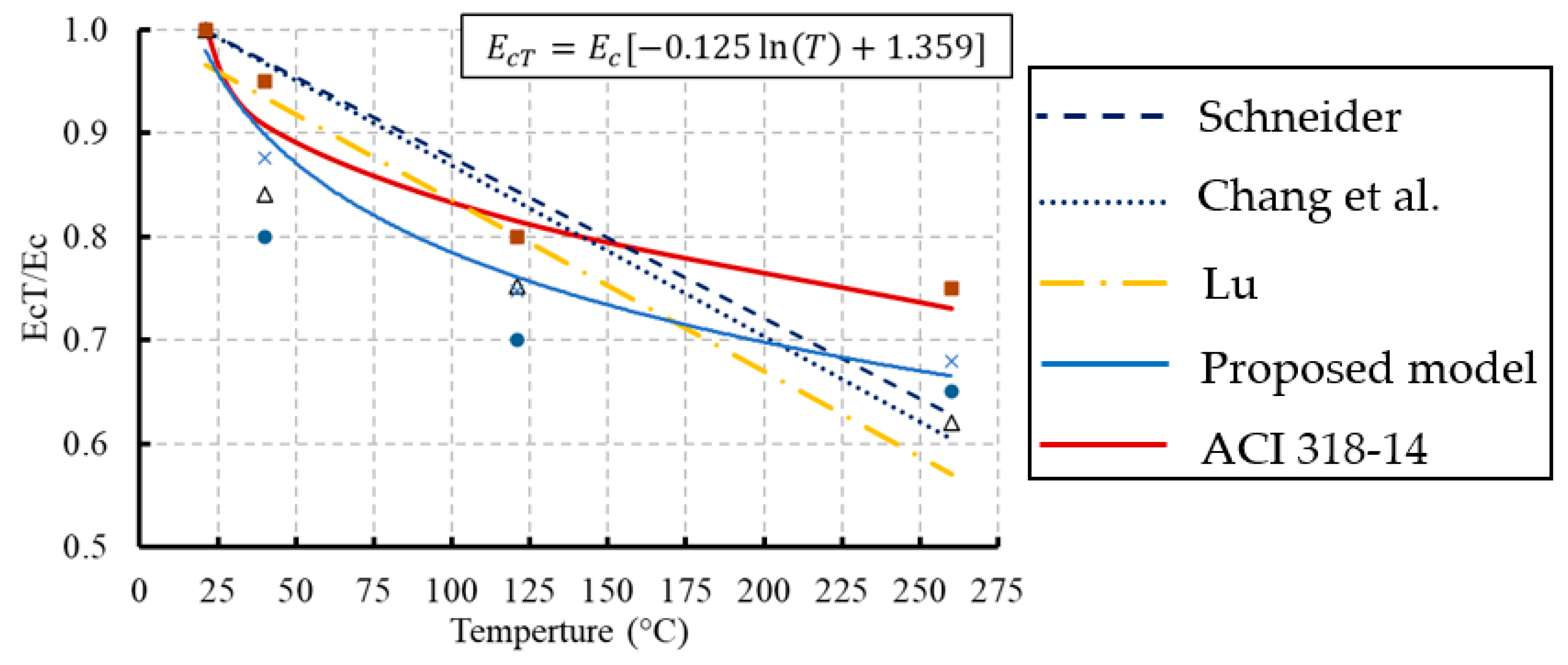
3.4. Modulus of Elasticity
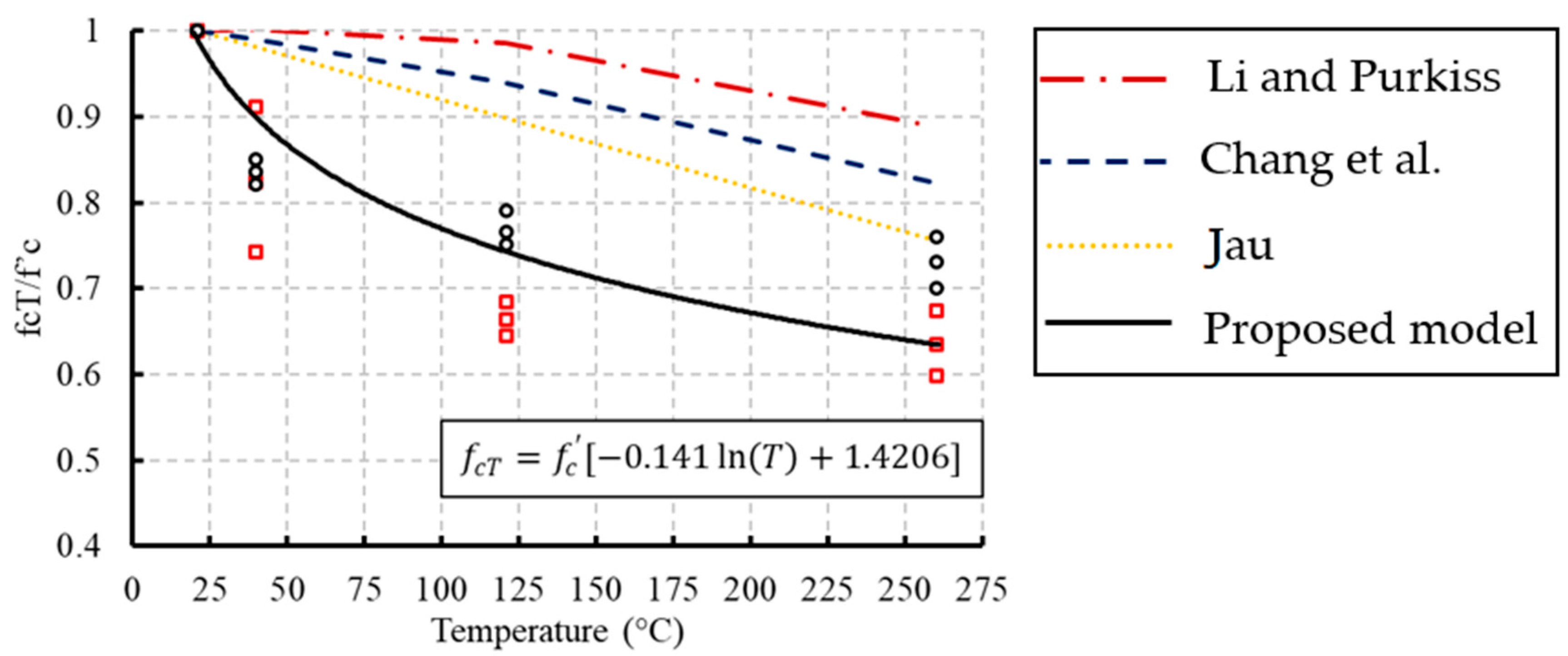
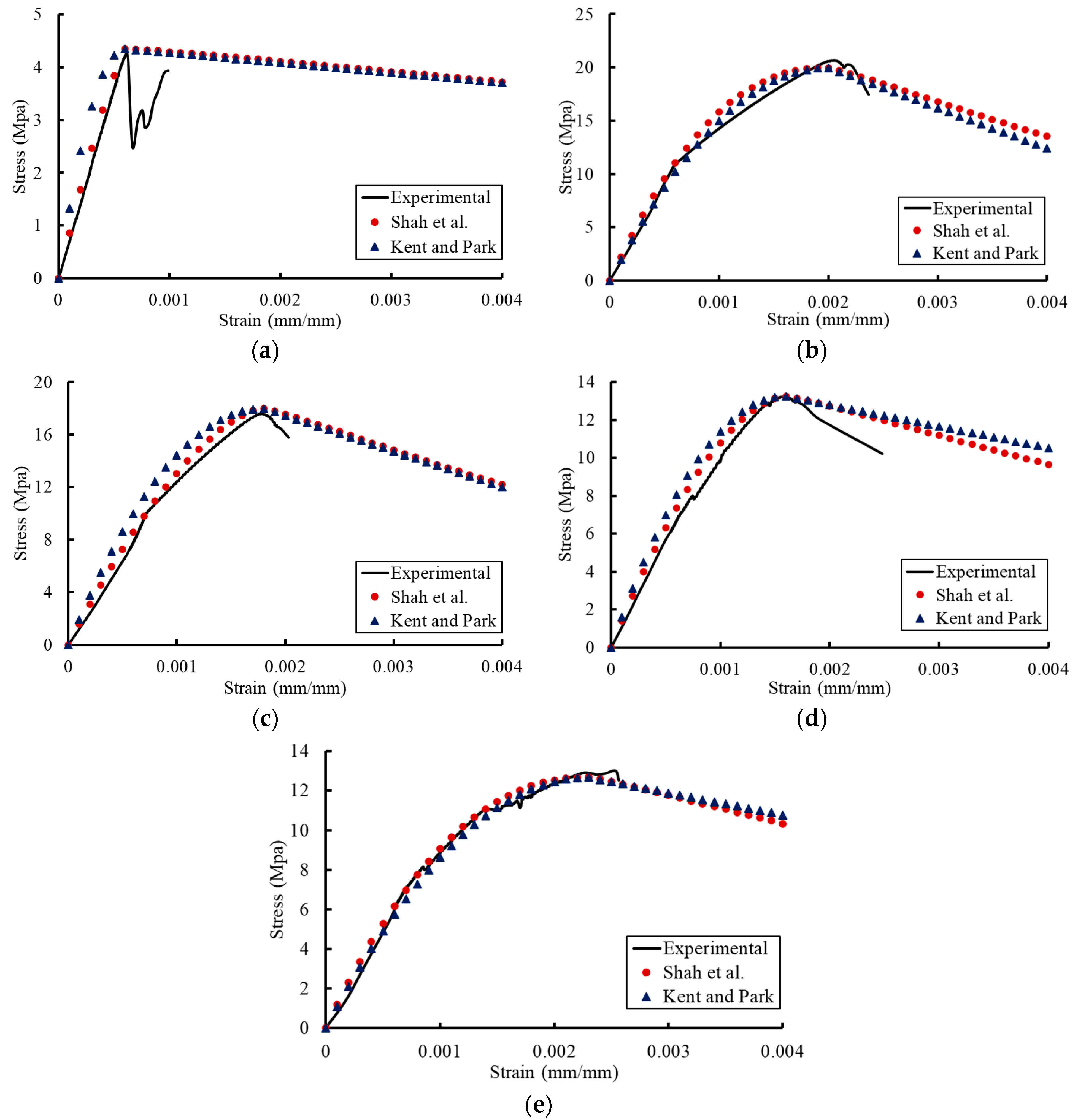
4. Previous Constitutive Models for the Stress–Strain Relationships
5. Conclusions
- The previous constitutive models for stress–strain relationships of concrete at normal temperatures can be used to capture these relationships under the effect of temperature by using the compressive strength, ultimate strain, and modulus of elasticity affected by temperature and developed in this study.
- The effect of temperature on the modulus of elasticity of concrete can be considered in the ACI 318-14 equation by using the compressive strength affected by temperature.
- The increasing rate of slopes of the linear portions of the stress–strain relationships of concrete decreased through the concrete age as the temperature increased. This behavior indicated a reduction in the stiffness of concrete. However, dramatic reductions were monitored in the case of freezing.
- The exposure to different temperature conditions altered the mode of failure of the tested specimens. A well-formed cone without vertical splitting was the mode of failure observed for the concrete cylinders at 21 °C and 40 °C. Columnar vertical cracking was the mode of failure observed at a temperature of 121 °C. Side fractures at the top or bottom of the concrete cylinders were the mode of failure noticed for the specimens at the highest temperature (260 °C).
- Based on the experimental data and the newly proposed model, concrete lost 10–20% of its original compressive strength when heated to 100 °C and 30–40% at 260 °C.
- The compressive strength of the frozen specimens remained at low levels over their ages. No significant strength was earned as the concrete aged. Keeping the concrete cylinders frozen at an early age could be very harmful and caused more damage to the concrete strength. Therefore, it is particularly important to protect concrete from freezing at an early age if possible, to complete the hydration process and gain most of the strength.
- Most of the compressive strength was gained at the early age of concrete due to the exposure to elevated temperature. However, reductions in the strength occurred at later ages.
- The specimens exposed to the moderate temperature of 21 °C achieved only 75% of their 28-day compressive strength at the early age of concrete and further strength was achieved as the concrete age increased.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Walter, H.P. Factors influencing concrete strength. J. Am. Concr. Inst. (ACI) 1951, 47, 417–432. [Google Scholar]
- Burg, R.G. The Influence of Casting and Curing Temperature on the Properties of Fresh and Hardened Concrete; Research and Development Bulletin RD113; Portland Cement Association: Skokie, IL, USA, 1996. [Google Scholar]
- Shetty, M.S. Concrete Technology: Theory and Practice; S. Chand & Co.: New Delhi, India, 2009. [Google Scholar]
- ASTM International. ASTM C387/C387M-17, Standard Specification for Packaged, Dry, Combined Materials for Concrete and High Strength Mortar; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar] [CrossRef]
- Goncalves, M.C.; Margarido, F. Materials for Construction and Civil Engineering; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Shen, J.; Xu, Q. Effect of elevated temperatures on compressive strength of concrete. J. Constr. Build. Mater. 2019, 229, 116846. [Google Scholar] [CrossRef]
- Husain, A.; Ahmad, J.; Mujeeb, A.; Ahmed, R. Effects of temperature on concrete. Int. J. Adv. Res. Sci. Eng. 2016, 5, 33–42. [Google Scholar]
- Araldi, P.; Balestra, C.E.T.; Savaris, G. Influence of multiple methods and curing temperatures on the concrete compressive strength. J. Eng. Proj. Prod. Manag. 2019, 9, 66–73. [Google Scholar] [CrossRef] [Green Version]
- Ortiz, J.; Aguado, A.; Agulló, L.; García, T. Influence of environmental temperatures on the concrete compressive strength: Simulation of hot and cold weather conditions. J. Cem. Concr. Res. 2005, 35, 1970–1979. [Google Scholar] [CrossRef] [Green Version]
- Kodur, V. Properties of concrete at elevated temperatures. ISRN Civ. Eng. 2014, 468510. [Google Scholar] [CrossRef]
- Shang, X.; Lu, Z. Impact of high temperature on the compressive strength of ECC. Adv. Mater. Sci. Eng. 2014, 919078. [Google Scholar] [CrossRef] [Green Version]
- Knaack, A.M.; Kurama, Y.C.; Kirkner, D.J. Stress-Strain Properties of Concrete at Elevated Temperatures. Structural Engineering Research Report; Report #NDSE-09-01; University of Notre Dame: Notre Dame, Indiana, 2009. [Google Scholar]
- Bastami, M.; Aslani, F.; Omran, M.E. High-temperature mechanical properties of concrete. Int. J. Civ. Eng. 2010, 8, 337–351. [Google Scholar]
- Gardner, N.J. Effect of temperature on the early-age properties of Type I, Type II, and Type III/fly ash concretes with temperature. J. Mater. (ACI) 1990, 87, 68–78. [Google Scholar]
- Singh, S.B.; Munjal, P.; Thammishetti, N. Role of water/cement ratio on strength development of cement mortar. J. Build. Eng. 2015, 4, 94–100. [Google Scholar] [CrossRef]
- Holan, J.; Novák, J.; Štefan, R. Air-entrainment as an alternative to polypropylene fibers and its effect on the compressive strength of concrete at high temperatures. IOP Conf. Ser. Mater. Sci. Eng. 2019, 596, 12032. [Google Scholar] [CrossRef]
- Hognestad, E. Concrete stress distribution in ultimate strength design. J. Am. Concr. Inst. (ACI) 1955, 52, 455–479. [Google Scholar]
- Rüsch, H. Research toward a general flexural theory for structural concrete. J. Am. Concr. Inst. (ACI) 1960, 57, 1–28. [Google Scholar]
- Guo, Z.H. The Strength and Deformation of Concrete (Experimental Basis and Constitutive Relationship); Tsinghua University Press: Beijing, China, 1997. [Google Scholar]
- Guan, X.; Niu, D.T.; Wang, J.B. Study of the freeze-thaw damage constitutive model of concrete based on WEIBULL’s strength theory. J. Appl. Mech. Mater. 2014, 584–586, 1322–1327. [Google Scholar] [CrossRef]
- Youssef, M.A.; Moftah, M. General stress-strain relationship for concrete at elevated temperatures. J. Eng. Struct. 2007, 29, 2618–2634. [Google Scholar] [CrossRef]
- ASTM C31/C31M-19a, Standard Practice for Making and Curing Concrete Test Specimens in the Field; ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- ASTM C150/C150M-20, Standard Specification for Portland Cement; ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- ASTM C39/C39M-20, Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- Gujel, D.A.; Kazmierczak, C.S.; Masuero, J.R. Stress-strain curve of concretes with recycled concrete aggregates: Analysis of the NBR 8522 methodology. Rev. IBRACON Estrut. Mater. 2017, 10, 547–567. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.F.; Wong, Y.L.; Poon, C.S.; Tang, C.A. Stress-strain behaviour of high-strength concrete at elevated temperatures. J. Concr. Res. 2005, 57, 535–544. [Google Scholar] [CrossRef]
- Korhonen, C. Effect of High Doses of Chemical Admixtures on the Freeze-Thaw Durability of Portland Cement Concrete; Technical Report ERDC/CRREL TR-02-5; US Army Corps of Engineers, Engineer Research and Development Center: Vicksburg, MS, USA, 2002. [Google Scholar]
- Le, Q.X.; Dao, V.T.N.; Torero, J.L.; Maluk, C.; Bisby, L. Effects of temperature and temperature gradient on concrete performance at elevated temperatures. J. Adv. Struct. Eng. 2018, 21, 1223–1233. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Jiao, W.; Sha, A.; Gao, J.; Han, Z.; Xu, W. Portland cement hydration behavior at low temperatures: Views from calculation and experimental study. Adv. Mater. Sci. Eng. 2017, 3927106. [Google Scholar] [CrossRef] [Green Version]
- Deschner, F.; Lothenbach, B.; Winnefeld, F.; Neubauer, J. Effect of temperature on the hydration of Portland cement blended with siliceous fly ash. J. Cem. Concr. Res. 2013, 52, 169–181; [Google Scholar] [CrossRef]
- Li, L.; Purkiss, J.A. Stress-strain constitutive equations of concrete material at elevated temperatures. J. Fire Saf. 2005, 40, 669–686. [Google Scholar] [CrossRef]
- Jau, W.C.; Chang, C.H. Study of Fired Concrete Strengthened with Confinement. Master’s Thesis, National Chiao Tung University, Hsinchu, Taiwan, 2001. [Google Scholar]
- Chang, Y.F.; Chen, Y.H.; Sheu, M.S.; Yao, G.C. Residual stress-strain relationship for concrete after exposure to high temperatures. J. Cem. Concr. Res. 2006, 36, 1999–2005. [Google Scholar] [CrossRef]
- Bazant, P.; Chern, J.C. Stress-induced thermal and shrinkage strains in concrete. J. Eng. Mech. 1987, 113, 1493–1511. [Google Scholar] [CrossRef] [Green Version]
- Lie, T.T. Structural Fire Protection; American Society of Civil Engineers: New York, NY, USA, 1992. [Google Scholar]
- Cruz, C.R. Elastic properties of concrete at high temperatures. J. PCA Res. Dev. Lab. 1966, 8, 37–45. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete: (ACI 318-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Schneider, U. Concrete at high temperatures—A general review. J. Fire Saf. 1988, 13, 55–68. [Google Scholar] [CrossRef]
- Xiao, J.; Konig, G. Study on concrete at high temperature in China—An overview. J. Fire Saf. 2004, 39, 89–103. [Google Scholar] [CrossRef]
- Shah, S.P.; Fafitis, A.; Arnold, R. Cyclic loading of spirally reinforced concrete. J. Struc. Eng. 1983, 109, 1695–1710. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Flexural members with confined concrete. J. Struct. Div. Proc. Am. Soc. Civ. Eng. 1971, 97, 1969–1990. [Google Scholar]









| Concrete Grade | Design Strength (MPa) | Aggregate Size * (mm) | Slump (mm) | W/C | Gravel (kg/m3) | Sand (kg/m3) | Portland Cement (kg/m3) | Fly Ash (kg/m3) |
|---|---|---|---|---|---|---|---|---|
| C20 | 20 | 10 | 127.20 | 0.55 | 1067.9 | 830.6 | 334.6 | 30 |
| C27 | 27 | 10 | 82.55 | 0.45 | 1067.9 | 830.6 | 334.6 | 30 |
| Constituent | % by Weight * |
|---|---|
| Lime (CaO) | 65.00 |
| Silica (SiO2) | 21.00 |
| Alumina (Al2O3) | 5.60 |
| Iron Oxide (Fe2O3) | 3.80 |
| Magnesia (MgO) | 2.10 |
| Sulphur Trioxide (SO3) | 2.22 |
| Loss of Ignition | 0.65 |
| Lime saturation factor | 0.90 |
| Time | Temperature | 0 °C | 21 °C | 40 °C | 121 °C | 260 °C |
|---|---|---|---|---|---|---|
| 7-day | C20 | 4.47 | 15.27 | 16.49 | 15.42 | 15.83 |
| C27 | 10.08 | 22.21 | 20.46 | 18.44 | 17.40 | |
| 14-day | C20 | 2.97 | 17.93 | 15.05 | 15.29 | 14.64 |
| C27 | 8.17 | 26.96 | 22.06 | 20.95 | 20.47 | |
| 28-day | C20 | 4.35 | 19.98 | 16.45 | 13.25 | 12.67 |
| C27 | 9.19 | 27.68 | 19.81 | 19.12 | 18.85 | |
| 56-day | C20 | 3.73 | 24.01 | 18.16 | 14.47 | 14.33 |
| C27 | 8.43 | 31.34 | 23.19 | 20.66 | 17.89 | |
| 90-day | C20 | 3.79 | 25.61 | 17.93 | 14.24 | 12.40 |
| C27 | 8.41 | 31.03 | 23.37 | 17.74 | 18.40 |
| Reference | Compressive Strength Models |
|---|---|
| Li and Purkiss [31] | |
| Jau [32] | |
| Chang et al. [33] |
| Reference | Ultimate Strain Models |
|---|---|
| Bazant and Chern [34] | |
| Lie [35] | |
| Kodur et al. [10] |
| Time | Temperature | 0 °C | 21 °C | 40 °C | 121 °C | 260 °C |
|---|---|---|---|---|---|---|
| 7-day | C20 | 7319.28 | 19,762.05 | 17,036.25 | 15,236.05 | 11,474.74 |
| C27 | 11,821.12 | 22,456.88 | 20,249.47 | 18,639.21 | 17,542.78 | |
| 14-day | C20 | 3433.34 | 18,821.00 | 16,468.38 | 16,468.38 | 13,701.69 |
| C27 | 7904.82 | 23,249.47 | 19,762.05 | 17,067.23 | 17,884.21 | |
| 28-day | C20 | 3426.62 | 22,585.20 | 19,937.14 | 17,242.92 | 14,161.26 |
| C27 | 12,000.25 | 23,400.65 | 20,500.1 | 17,500.02 | 18,201.58 | |
| 56-day | C20 | 3423.95 | 26,349.40 | 19,762.05 | 17,207.77 | 15,370.48 |
| C27 | 4526.056 | 34,670.26 | 24,467.30 | 18,068.16 | 19,077.6 | |
| 90-day | C20 | 3952.41 | 27,447.29 | 22,456.88 | 20,702.56 | 18,599.58 |
| C27 | 5269.88 | 35,000.31 | 29,061.84 | 23,231.5 | 21,480.49 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Zohairy, A.; Hammontree, H.; Oh, E.; Moler, P. Temperature Effect on the Compressive Behavior and Constitutive Model of Plain Hardened Concrete. Materials 2020, 13, 2801. https://doi.org/10.3390/ma13122801
El-Zohairy A, Hammontree H, Oh E, Moler P. Temperature Effect on the Compressive Behavior and Constitutive Model of Plain Hardened Concrete. Materials. 2020; 13(12):2801. https://doi.org/10.3390/ma13122801
Chicago/Turabian StyleEl-Zohairy, Ayman, Hunter Hammontree, Eddie Oh, and Perry Moler. 2020. "Temperature Effect on the Compressive Behavior and Constitutive Model of Plain Hardened Concrete" Materials 13, no. 12: 2801. https://doi.org/10.3390/ma13122801
APA StyleEl-Zohairy, A., Hammontree, H., Oh, E., & Moler, P. (2020). Temperature Effect on the Compressive Behavior and Constitutive Model of Plain Hardened Concrete. Materials, 13(12), 2801. https://doi.org/10.3390/ma13122801






