Refined Calibration Model for Improving the Orientation Precision of Electron Backscatter Diffraction Maps
Abstract
1. Introduction
2. Experimental and Theoretical Details
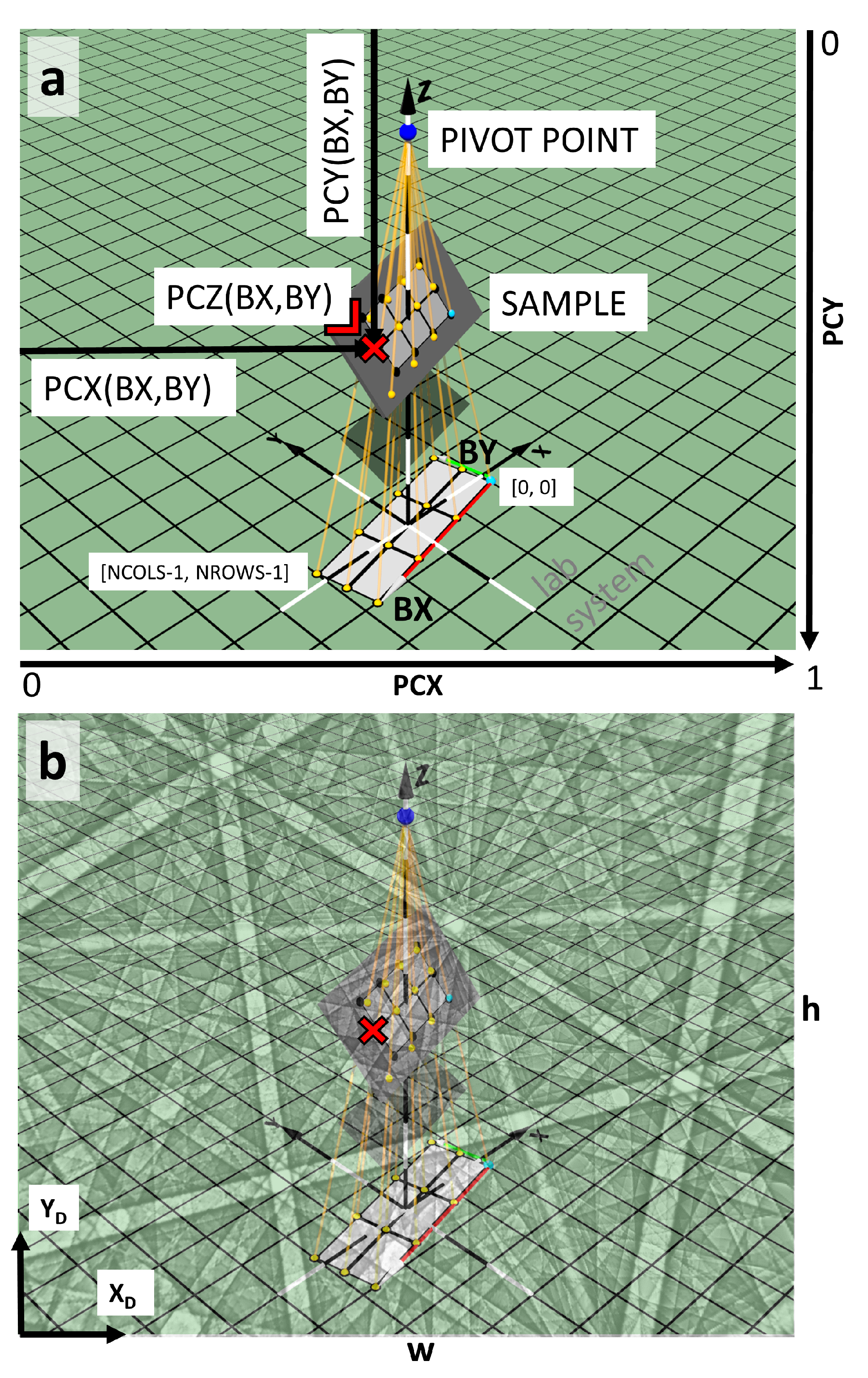
2.1. Relationships between SEM Imaging Parameters and Projection Center
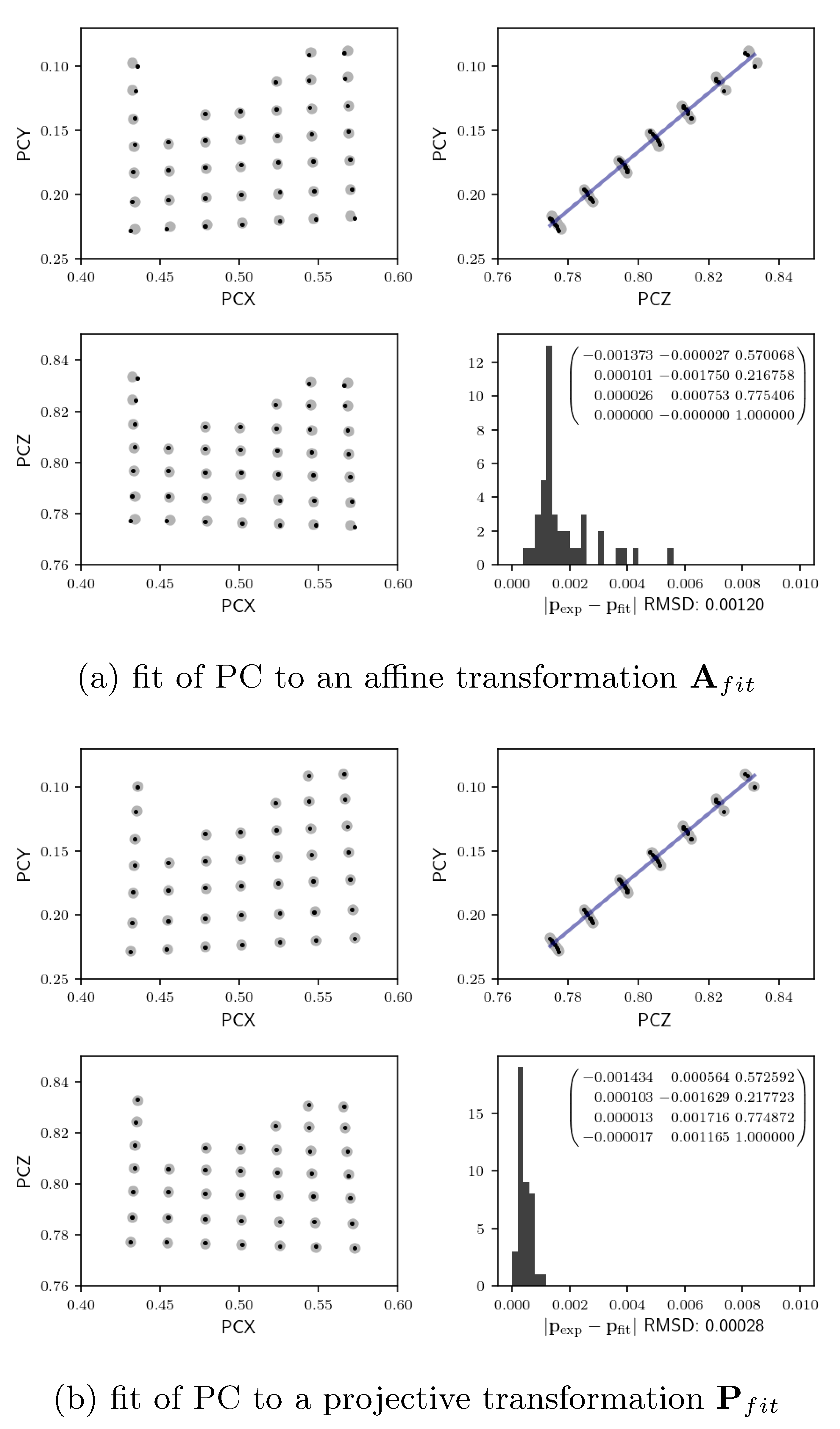
2.2. Projective Transformation Model
2.3. Kikuchi Pattern Matching for Projection Center Calibration
2.4. EBSD Measurements
3. Results
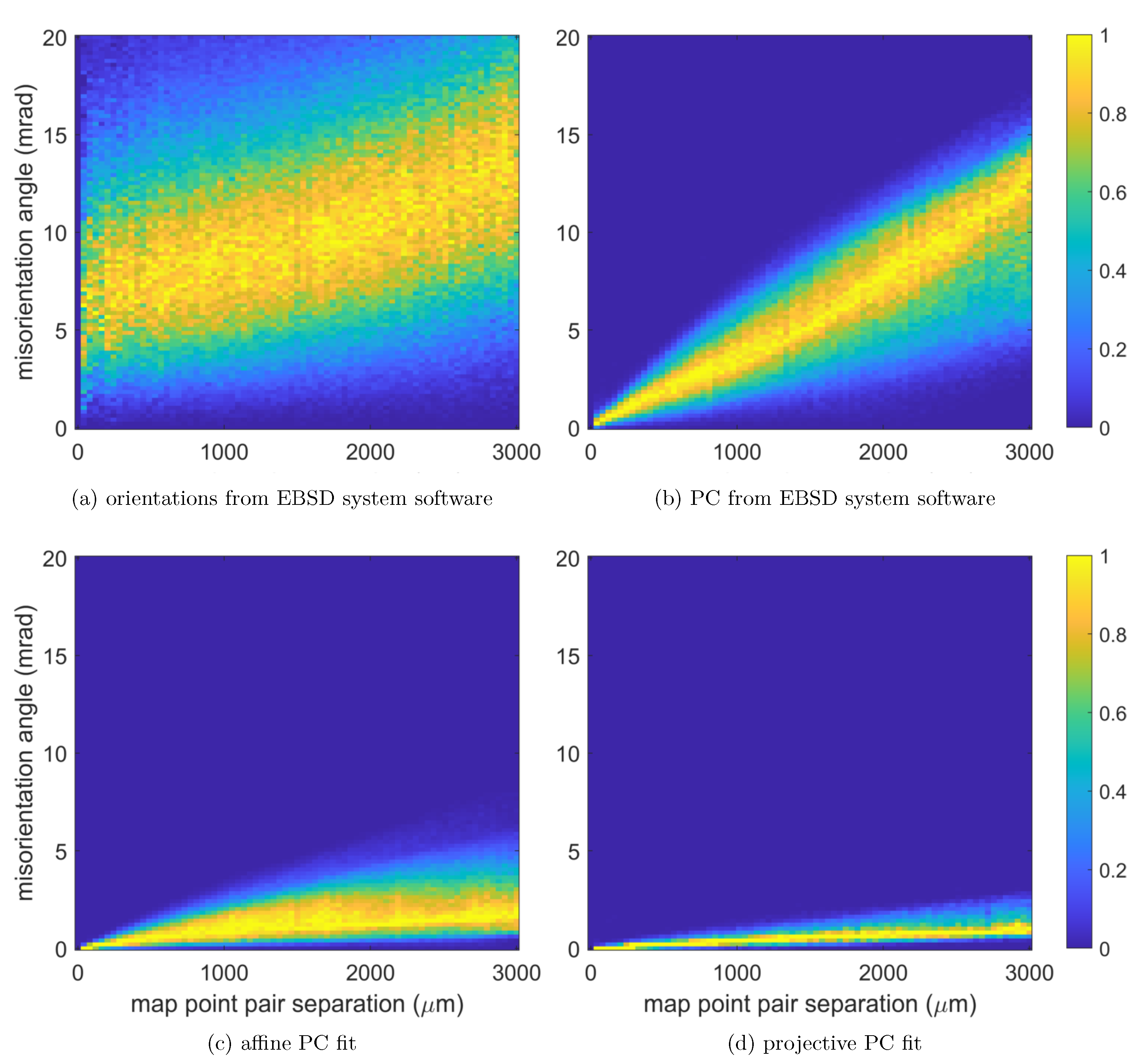
3.1. Projection Center Calibration
3.2. Orientation Analysis
3.2.1. Local Orientation Precision
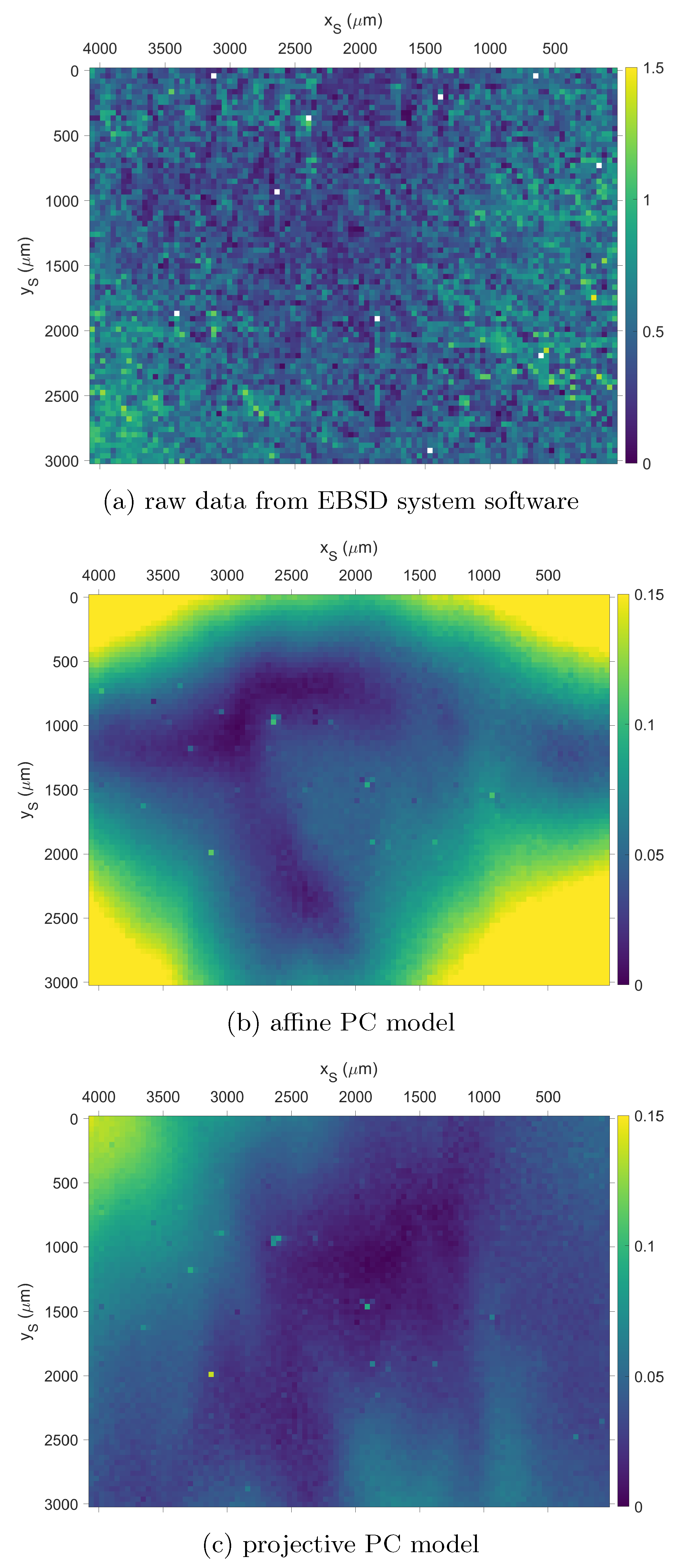
3.2.2. Global Orientation Precision
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwartz, A.J.; Kumar, M.; Adams, B.L. (Eds.) Electron Backscatter Diffraction in Materials Science; Kluwer Academic/Plenum Publications: New York, NY, USA, 2000. [Google Scholar]
- Engler, O.; Randle, V. Introduction to Texture Analysis: Macrotexture, Microtexture, and Orientation Mapping, 2nd ed.; CRC Press: Boston, MA, USA, 2009. [Google Scholar]
- Palache, C. The Gnomonic Projection. Am. Mineral. 1920, 5, 67–80. [Google Scholar]
- Britton, T.; Jiang, J.; Guo, Y.; Vilalta-Clemente, A.; Wallis, D.; Hansen, L.; Winkelmann, A.; Wilkinson, A. Tutorial: Crystal orientations and EBSD—Or which way is up? Mater. Charact. 2016, 117, 113–126. [Google Scholar] [CrossRef]
- Venables, J.A.; Bin-Jaya, R. Accurate microcrystallography using electron back-scattering patterns. Philos. Mag. 1977, 35, 1317–1332. [Google Scholar] [CrossRef]
- Biggin, S.; Dingley, D.J. A general method for locating the X-ray source point in Kossel diffraction. J. Appl. Crystallogr. 1977, 10, 376–385. [Google Scholar] [CrossRef]
- Dingley, D.J.; Longden, M.; Weinbren, J.; Alderman, J. Online Analysis of Electron Back Scatter Diffraction Patterns. 1. Texture Analysis of Zone Refined Polysilicon. Scanning Microsc. 1987, 1, 451–456. [Google Scholar]
- Baba-Kishi, K.Z. Measurement of crystal parameters on backscatter Kikuchi diffraction patterns. Scanning 1998, 20, 117–127. [Google Scholar] [CrossRef]
- Krieger Lassen, N.C.; Bilde-Sørensen, J.B. Calibration of an electron back-scattering pattern set-up. J. Microsc. 1993, 170, 125–129. [Google Scholar] [CrossRef]
- Krieger Lassen, N.C. Source point calibration from an arbitrary electron backscattering pattern. J. Microsc. 1999, 195, 204–211. [Google Scholar] [CrossRef]
- Carpenter, D.A.; Pugh, J.L.; Richardson, G.D.; Mooney, L.R. Determination of pattern centre in EBSD using the moving-screen technique. J. Microsc. 2007, 227, 246–247. [Google Scholar] [CrossRef] [PubMed]
- Nolze, G. Image distortions in SEM and their influences on EBSD measurements. Ultramicroscopy 2007, 107, 172–183. [Google Scholar] [CrossRef] [PubMed]
- Britton, T.B.; Maurice, C.; Fortunier, R.; Driver, J.H.; Day, A.P.; Meaden, G.; Dingley, D.J.; Mingard, K.; Wilkinson, A.J. Factors affecting the accuracy of high resolution electron backscatter diffraction when using simulated patterns. Ultramicroscopy 2010, 110, 1443–1453. [Google Scholar] [CrossRef] [PubMed]
- Maurice, C.; Dzieciol, K.; Fortunier, R. A method for accurate localisation of EBSD pattern centres. Ultramicroscopy 2011, 111, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Mingard, K.; Day, A.; Maurice, C.; Quested, P. Towards high accuracy calibration of electron backscatter diffraction systems. Ultramicroscopy 2011, 111, 320–329. [Google Scholar] [CrossRef] [PubMed]
- Basinger, J.; Fullwood, D.; Kacher, J.; Adams, B. Pattern center determination in electron backscatter diffraction microscopy. Microsc. Microanal. 2011, 17, 330–340. [Google Scholar] [CrossRef]
- Alkorta, J. Limits of simulation based high resolution EBSD. Ultramicroscopy 2013, 131, 33–38. [Google Scholar] [CrossRef]
- Ram, F.; Zaefferer, S.; Raabe, D. Kikuchi bandlet method for the accurate deconvolution and localization of Kikuchi bands in Kikuchi diffraction patterns. J. Appl. Cryst. 2014, 47, 264–275. [Google Scholar] [CrossRef]
- Vespucci, S.; Naresh-Kumar, G.; Trager-Cowan, C.; Mingard, K.P.; Maneuski, D.; O’Shea, V.; Winkelmann, A. Diffractive triangulation of radiative point sources. Appl. Phys. Lett. 2017, 110, 124103. [Google Scholar] [CrossRef]
- Friedrich, T.; Bochmann, A.; Dinger, J.; Teichert, S. Application of the pattern matching approach for EBSD calibration and orientation mapping, utilising dynamical EBSP simulations. Ultramicroscopy 2018, 184, 44–51. [Google Scholar] [CrossRef]
- Pang, E.L.; Larsen, P.M.; Schuh, C.A. Global optimization for accurate determination of EBSD pattern centers. Ultramicroscopy 2020, 209, 112876. [Google Scholar] [CrossRef]
- Lafond, C.; Douillard, T.; Cazottes, S.; Steyer, P.; Langlois, C. Electron CHanneling ORientation Determination (eCHORD): An original approach to crystalline orientation mapping. Ultramicroscopy 2018, 186, 146–149. [Google Scholar] [CrossRef]
- Lafond, C.; Douillard, T.; Cazottes, S.; Graef, M.D.; Steyer, P.; Langlois, C. Towards large scale orientation mapping using the eCHORD method. Ultramicroscopy 2020, 208, 112854. [Google Scholar] [CrossRef] [PubMed]
- Nolze, G.; Winkelmann, A. Exploring structural similarities between crystal phases using EBSD pattern comparison. Cryst. Res. Technol. 2014, 49, 490–501. [Google Scholar] [CrossRef]
- Winkelmann, A.; Nolze, G. Point-group sensitive orientation mapping of non-centrosymmetric crystals. Appl. Phys. Lett. 2015, 106, 072101. [Google Scholar] [CrossRef]
- Chen, Y.H.; Park, S.U.; Wei, D.; Newstadt, G.; Jackson, M.A.; Simmons, J.P.; De Graef, M.; Hero, A.O. A Dictionary Approach to Electron Backscatter Diffraction Indexing. Microsc. Microanal. 2015, 21, 739–752. [Google Scholar] [CrossRef]
- Hielscher, R.; Bartel, F.; Britton, T.B. Gazing at crystal balls: Electron backscatter diffraction pattern analysis and cross correlation on the sphere. Ultramicroscopy 2019, 207, 112836. [Google Scholar] [CrossRef]
- Winkelmann, A.; Jablon, B.M.; Tong, V.S.; Trager-Cowan, C.; Mingard, K.P. Improving EBSD precision by orientation refinement with full pattern matching. J. Microsc. 2020, 277, 79–92. [Google Scholar] [CrossRef]
- Tilli, M.; Motooka, T.; Airaksinen, V.M.; Franssila, S.; Paulasto-Kröckel, M.; Lindroos, V. (Eds.) Handbook of Silicon Based MEMS Materials and Technologies; Elsevier: Norwich, UK, 2015. [Google Scholar] [CrossRef]
- McLean, M.J.; Osborn, W.A. In-situ elastic strain mapping during micromechanical testing using EBSD. Ultramicroscopy 2018, 185, 21–26. [Google Scholar] [CrossRef]
- Prior, D.J.; Mariani, E.; Wheeler, J. EBSD in the Earth Sciences: Applications, Common Practice, and Challenges. In Electron Backscatter Diffraction in Materials Science; Springer: Boston, MA, USA, 2009; pp. 345–360. [Google Scholar] [CrossRef]
- Wallis, D.; Hansen, L.N.; Britton, T.B.; Wilkinson, A.J. High-Angular Resolution Electron Backscatter Diffraction as a New Tool for Mapping Lattice Distortion in Geological Minerals. J. Geophys. Res. Solid Earth 2019, 124, 6337–6358. [Google Scholar] [CrossRef]
- Humphreys, F.J. Grain and subgrain characterisation by electron backscatter diffraction. J. Mater. Sci. 2001, 36, 3833–3854. [Google Scholar] [CrossRef]
- Glez, J.C.; Driver, J. Orientation distribution analysis in deformed grains. J. Appl. Crystallogr. 2001, 34, 280–288. [Google Scholar] [CrossRef]
- Pantleon, W. Retrieving orientation correlations in deformation structures from orientation maps. Mater. Sci. Technol. 2005, 21, 1392–1396. [Google Scholar] [CrossRef]
- Nowell, M.M.; Wright, S.I. Thoughts on Standards Materials and Analytical Routines for Electron Backscatter Diffraction (EBSD). Microsc. Microanal. 2017, 23, 510–511. [Google Scholar] [CrossRef][Green Version]
- Reimer, L. Scanning Electron Microscopy—Physics of Image Formation and Microanalysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Winkelmann, A.; Nolze, G.; Vespucci, S.; Naresh-Kumar, G.; Trager-Cowan, C.; Vilalta-Clemente, A.; Wilkinson, A.J.; Vos, M. Diffraction effects and inelastic electron transport in angle-resolved microscopic imaging applications. J. Microsc. 2017, 267, 330–346. [Google Scholar] [CrossRef] [PubMed]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Oliphant, T.E. A Guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006; Volume 1. [Google Scholar]
- Zhang, Z. Estimating Projective Transformation Matrix (Collineation, Homography); Technical Report MSR-TR-2010-63; Microsoft Research: Redmond, WA, USA, 2010. [Google Scholar]
- Nolze, G.; Jürgens, M.; Olbricht, J.; Winkelmann, A. Improving the precision of orientation measurements from technical materials via EBSD pattern matching. Acta Mater. 2018, 159, 408–415. [Google Scholar] [CrossRef]
- Kirkland, E.J. Advanced Computing in Electron Microscopy; Springer Science + Business Media: Berlin, Germany; New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z. Equivalence of digital image correlation criteria for pattern matching. Appl. Opt. 2010, 49, 5501. [Google Scholar] [CrossRef]
- Woodford, O.J. Using Normalized Cross Correlation in Least Squares Optimizations. arXiv 2018, arXiv:1810.04320. [Google Scholar]
- Winkelmann, A. xcdskd: Tools and Methods for Kikuchi Diffraction. 2018. Available online: https://github.com/wiai/xcdskd (accessed on 26 May 2020).
- Winkelmann, A.; Britton, T.B.; Nolze, G. Constraints on the effective electron energy spectrum in backscatter Kikuchi diffraction. Phys. Rev. B 2019, 99, 064115. [Google Scholar] [CrossRef]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. 2020. Available online: https://github.com/stevengj/nlopt (accessed on 26 May 2020).
- Bachmann, F.; Hielscher, R.; Jupp, P.E.; Pantleon, W.; Schaeben, H.; Wegert, E. Inferential statistics of electron backscatter diffraction data from within individual crystalline grains. J. Appl. Crystallogr. 2010, 43, 1338–1355. [Google Scholar] [CrossRef]
- Wright, S.I.; Nowell, M.M.; Field, D.P. A review of strain analysis using electron backscatter diffraction. Microsc. Microanal. 2011, 17, 316–329. [Google Scholar] [CrossRef]
- MTEX. Kernel Average Misorientation (KAM). 2020. Available online: https://github.com/mtex-toolbox/mtex (accessed on 26 May 2020).
- Wright, S.; Nowell, M.; Basinger, J. Precision of EBSD based Orientation Measurements. Microsc. Microanal. 2011, 17, 406–407. [Google Scholar] [CrossRef]
- Wright, S.I.; Basinger, J.A.; Nowell, M.M. Angular Precision of Automated Electron Backscatter Diffraction Measurements. Mater. Sci. Forum 2011, 702–703, 548–553. [Google Scholar] [CrossRef]
- Thomsen, K.; Schmidt, N.H.; Bewick, A.; Larsen, K.; Goulden, J. Improving the Accuracy of Orientation Measurements using EBSD. Microsc. Microanal. 2013, 19, 724–725. [Google Scholar] [CrossRef]
- Nicolay, A.; Franchet, J.M.; Cormier, J.; Mansour, H.; Graef, M.D.; Seret, A.; Bozzolo, N. Discrimination of dynamically and post-dynamically recrystallized grains based on EBSD data: Application to Inconel 718. J. Microsc. 2018, 273, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Barton, N.R.; Dawson, P.R. On the spatial arrangement of lattice orientations in hot-rolled multiphase titanium. Model. Simul. Mater. Sci. Eng. 2001, 9, 433–463. [Google Scholar] [CrossRef]
- Quey, R.; Driver, J.; Dawson, P. Intra-grain orientation distributions in hot-deformed aluminium: Orientation dependence and relation to deformation mechanisms. J. Mech. Phys. Solids 2015, 84, 506–527. [Google Scholar] [CrossRef]
- Morawiec, A. Orientations and Rotations; Springer: Berlin, Germany, 2004. [Google Scholar] [CrossRef]
- Albou, A.; Driver, J.H.; Maurice, C. Microband evolution during large plastic strains of stable {110}〈112〉 Al and Al–Mn crystals. Acta Mater. 2010, 58, 3022–3034. [Google Scholar] [CrossRef]
- Seret, A.; Moussa, C.; Bernacki, M.; Signorelli, J.; Bozzolo, N. Estimation of geometrically necessary dislocation density from filtered EBSD data by a local linear adaptation of smoothing splines. J. Appl. Crystallogr. 2019, 52, 548–563. [Google Scholar] [CrossRef]
- Morawiec, A. A method of precise misorientation determination. J. Appl. Crystallogr. 2003, 36, 1319–1323. [Google Scholar] [CrossRef]
- Kainuma, Y. The theory of Kikuchi patterns. Acta Cryst. 1955, 8, 247. [Google Scholar] [CrossRef]
- Michael, J.R.; Eades, J.A. Use of reciprocal lattice layer spacing in electron backscatter diffraction pattern analysis. Ultramicroscopy 2000, 81, 67–81. [Google Scholar] [CrossRef]
- Winkelmann, A. Dynamical effects of anisotropic inelastic scattering in electron backscatter diffraction. Ultramicroscopy 2008, 108, 1546–1550. [Google Scholar] [CrossRef] [PubMed]
- Bingham, M.A.; Nordman, D.J.; Vardeman, S.B. Finite-sample investigation of likelihood and Bayes inference for the symmetric von Mises-Fisher distribution. Comput. Stat. Data Anal. 2010, 54, 1317–1327. [Google Scholar] [CrossRef]
- Shi, Q.; Roux, S.; Latourte, F.; Hild, F.; Loisnard, D.; Brynaert, N. On the use of SEM correlative tools for in situ mechanical tests. Ultramicroscopy 2018, 184, 71–87. [Google Scholar] [CrossRef] [PubMed]
- Ernould, C.; Beausir, B.; Fundenberger, J.J.; Taupin, V.; Bouzy, E. Global DIC approach guided by a cross-correlation based initial guess for HR-EBSD and on-axis HR-TKD. Acta Mater. 2020, 191, 131–148. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision; Springer: London, UK, 2011. [Google Scholar] [CrossRef]

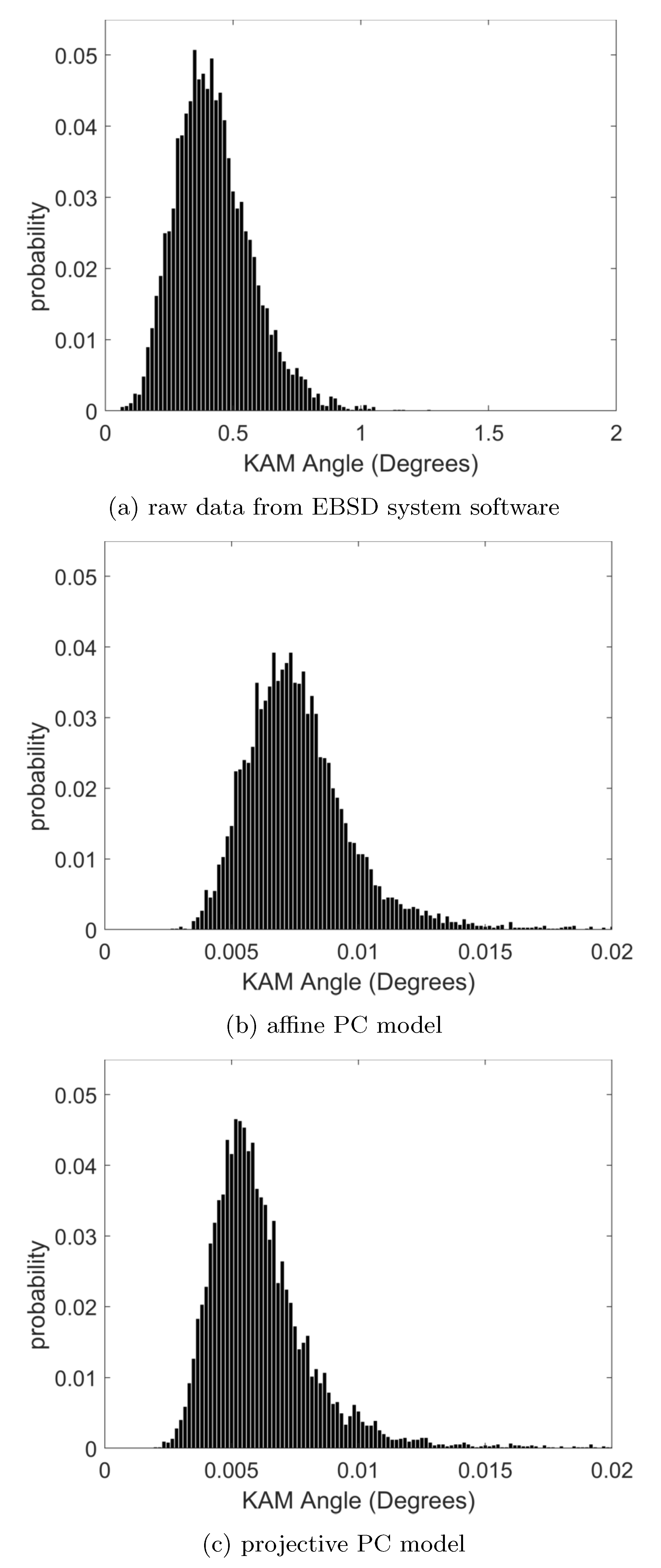

| Orientation Data | KAM Median | KAM 95th Percentile |
|---|---|---|
| Esprit 1.94 | 0.4100 | 0.690 |
| Affine PC | 0.0074 | 0.011 |
| Projective PC | 0.0058 | 0.010 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winkelmann, A.; Nolze, G.; Cios, G.; Tokarski, T.; Bała, P. Refined Calibration Model for Improving the Orientation Precision of Electron Backscatter Diffraction Maps. Materials 2020, 13, 2816. https://doi.org/10.3390/ma13122816
Winkelmann A, Nolze G, Cios G, Tokarski T, Bała P. Refined Calibration Model for Improving the Orientation Precision of Electron Backscatter Diffraction Maps. Materials. 2020; 13(12):2816. https://doi.org/10.3390/ma13122816
Chicago/Turabian StyleWinkelmann, Aimo, Gert Nolze, Grzegorz Cios, Tomasz Tokarski, and Piotr Bała. 2020. "Refined Calibration Model for Improving the Orientation Precision of Electron Backscatter Diffraction Maps" Materials 13, no. 12: 2816. https://doi.org/10.3390/ma13122816
APA StyleWinkelmann, A., Nolze, G., Cios, G., Tokarski, T., & Bała, P. (2020). Refined Calibration Model for Improving the Orientation Precision of Electron Backscatter Diffraction Maps. Materials, 13(12), 2816. https://doi.org/10.3390/ma13122816





