Structure Dependence of Poisson’s Ratio in Cesium Silicate and Borate Glasses
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Characterization
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Sehgal, J.; Ito, S. Brittleness of glass. J. Non Cryst. Solids 1999, 253, 126–132. [Google Scholar] [CrossRef]
- Wondraczek, L.; Mauro, J.C.; Eckert, J.; Kühn, U.; Horbach, J.; Deubener, J.; Rouxel, T. Towards ultrastrong glasses. Adv. Mater. 2011, 23, 4578–4586. [Google Scholar] [CrossRef] [PubMed]
- Rouxel, T.; Yoshida, S. The fracture toughness of inorganic glasses. J. Am. Ceram. Soc. 2017, 100, 4374–4396. [Google Scholar] [CrossRef]
- Bertoldi, M.; Sglavo, V.M. Soda–borosilicate glass: Normal or anomalous behavior under Vickers indentation? J. Non Cryst. Solids 2004, 344, 51–59. [Google Scholar] [CrossRef]
- Rouxel, T.; Ji, H.; Hammouda, T.; Moréac, A. Poisson’s ratio and the densification of glass under high pressure. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Vella-Zarb, L.; Grima, J.N. Negative linear compressibility and auxeticity in boron arsenate. Annalen der Physik 2020, 532, 1900550. [Google Scholar] [CrossRef]
- Rouxel, T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 2007, 90, 3019–3039. [Google Scholar] [CrossRef]
- Deschamps, T.; Margueritat, J.; Martinet, C.; Mermet, A.; Champagnon, B. Elastic moduli of permanently densified silica glasses. Sci. Rep. 2014, 4, 7193. [Google Scholar] [CrossRef] [Green Version]
- Lewandowski, J.J.; Wang, W.H.; Greer, A.L. Intrinsic plasticity or brittleness of metallic glasses. Philos. Mag. Lett. 2005, 85, 77–87. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–838. [Google Scholar] [CrossRef] [PubMed]
- Østergaard, M.B.; Hansen, S.R.; Januchta, K.; To, T.; Rzoska, S.J.; Bockowski, M.; Bauchy, M.; Smedskjaer, M.M. Revisiting the dependence of poisson’s ratio on liquid fragility and atomic packing density in oxide glasses. Materials (Basel) 2019, 12, 2439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Januchta, K.; Bauchy, M.; Youngman, R.E.; Rzoska, S.J.; Bockowski, M.; Smedskjaer, M.M. Modifier field strength effects on densification behavior and mechanical properties of alkali aluminoborate glasses. Phys. Rev. Mater. 2017, 1, 063603. [Google Scholar] [CrossRef]
- Wilkinson, C.J.; Zheng, Q.; Huang, L.; Mauro, J.C. Topological constraint model for the elasticity of glass-forming systems. J. Non-Cryst. Solids X 2019, 2, 100019. [Google Scholar] [CrossRef]
- Smedskjaer, M.M.; Mauro, J.C.; Yue, Y. Prediction of glass hardness using temperature-dependent constraint theory. Phys. Rev. Lett. 2010, 105, 115503. [Google Scholar] [CrossRef] [PubMed]
- Smedskjaer, M.M.; Mauro, J.C.; Sen, S.; Yue, Y. Quantitative design of glassy materials using temperature-dependent constraint theory. Chem. Mater. 2010, 22, 5358–5365. [Google Scholar] [CrossRef]
- Makishima, A.; Mackenzie, J.D. Calculation of bulk modulus, shear modulus, and Poisson’s ratio of glass. J. Non Cryst. Solids 1975, 17, 147–157. [Google Scholar] [CrossRef]
- Pedone, A.; Malavasi, G.; Cormack, A.N.; Segre, U.; Menziani, M.C. Insight into elastic properties of binary alkali silicate glasses; Prediction and interpretation through atomistic simulation techniques. Chem. Mater. 2007, 19, 3144–3154. [Google Scholar] [CrossRef]
- Novikov, V.N.; Sokolov, A.P. Poisson’s ratio and the fragility of glass-forming liquids. Nature 2004, 431, 961–963. [Google Scholar] [CrossRef]
- Sidebottom, D.L. Fragility of network-forming glasses: A universal dependence on the topological connectivity. Phys. Rev. E 2015, 92, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Yannopoulos, S.N.; Johari, G.P. Glass behaviour: Poisson’s ratio and liquid’s fragility. Nature 2006, 442, E7–E8. [Google Scholar] [CrossRef]
- Kodama, M.; Kojima, S. Velocity of sound in and elastic properties of alkali metal borate glasses. Phys. Chem. Glas. Eur. J. Glas. Sci. Technol. B 2014, 55, 1–12. [Google Scholar] [CrossRef]
- Dupree, R.; Holland, D.; Williams, D.S. The structure of binary alkali silicate glasses. J. Non Cryst. Solids 1986, 81, 185–200. [Google Scholar] [CrossRef]
- Maekawa, H.; Maekawa, T.; Kawamura, K.; Yokokawa, T. The structural groups of alkali silicate glasses determined from 29Si MAS-NMR. J. Non Cryst. Solids 1991, 127, 53–64. [Google Scholar] [CrossRef]
- Du, J.; Corrales, L.R. First sharp diffraction peak in silicate glasses: Structure and scattering length dependence. Phys. Rev. B 2005, 72, 092201. [Google Scholar] [CrossRef]
- Feller, S.A.; Dell, W.J.; Bray, P.J. 10B NMR studies of lithium borate glasses. J. Non Cryst. Solids 1982, 51, 21–30. [Google Scholar] [CrossRef]
- Bray, P.J.; Feller, S.A.; Jellison, G.E.; Yun, Y.H. B10 NMR studies of the structure of borate glasses. J. Non Cryst. Solids 1980, 38, 93–98. [Google Scholar] [CrossRef]
- Konijnendijk, W.L.; Stevels, J.M. The structure of borate glasses studied by raman scattering. J. Non Cryst. Solids 1975, 18, 307–331. [Google Scholar] [CrossRef]
- Dietzel, A. The cation field strengths and their relation to devitrifying processes, to compound formation and to the melting points of silicates. Z. Elektrochem. Angew. Phys. Chemie 1942, 48, 9–23. [Google Scholar]
- Frederiksen, K.F.; Januchta, K.; Mascaraque, N.; Youngman, R.E.; Bauchy, M.; Rzoska, S.J.; Bockowski, M.; Smedskjaer, M.M. structural compromise between high hardness and crack resistance in aluminoborate Glasses. J. Phys. Chem. B 2018, 122, 6287–6295. [Google Scholar] [CrossRef]
- Tiegel, M.; Hosseinabadi, R.; Kuhn, S.; Herrmann, A.; Rüssel, C. Young’s modulus, Vickers hardness and indentation fracture toughness of alumino silicate glasses. Ceram. Int. 2015, 41, 7267–7275. [Google Scholar] [CrossRef]
- Burkhard, D.J.M. Elastic properties of alkali silicate glasses with iron oxide: Relation to glass structure. Solid State Commun. 1997, 101, 903–907. [Google Scholar] [CrossRef]
- Yiannopoulos, Y.D.; Chryssikos, G.D.; Kamitsos, E.I. Structure and properties of alkaline earth borate glasses. Phys. Chem. Glas. 2001, 42, 164–172. [Google Scholar]
- Berkemeier, F.; Voss, S. Molar volume, glass-transition temperature, and ionic conductivity of Na- and Rb-borate glasses in comparison with mixed Na-Rb borate glasses. J. Non Cryst. Solids 2005, 351, 3816–3825. [Google Scholar] [CrossRef]
- Rouse, G.B.; Kamitsos, E.I.; Risen, W.M. Brillouin spectra of mixed alkali glasses: xCs2O(1-x)Na2O5SiO2. J. Non Cryst. Solids 1981, 45, 257–269. [Google Scholar] [CrossRef]
- Royle, M.; MacKenzie, J.; Taylor, J.; Sharma, M.; Feller, S. Densities, glass transition temperatures, and structural models resulting from extremely modified caesium and rubidium borate glasses. J. Non Cryst. Solids 1994, 177, 242–248. [Google Scholar] [CrossRef]
- Yue, Y. Characteristic temperatures of enthalpy relaxation in glass. J. Non Cryst. Solids 2008, 354, 1112–1118. [Google Scholar] [CrossRef]
- Zheng, Q.; Mauro, J.C.; Yue, Y. Reconciling calorimetric and kinetic fragilities of glass-forming liquids. J. Non Cryst. Solids 2017, 456, 95–100. [Google Scholar] [CrossRef]
- Bødker, M.S.; Sørensen, S.S.; Mauro, J.C.; Smedskjaer, M.M. Predicting composition-structure relations in alkali borosilicate glasses using statistical mechanics. Front. Mater. 2019, 6, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zhong, J.; Bray, P.J. Change in boron coordination in alkali borate glasses, and mixed alkali effects, as elucidated by NMR. J. Non Cryst. Solids 1989, 111, 67–76. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chaleogenides. Acta Crystallogr. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Nascimento, M.L.F.; Do Nascimento, E.; Watanabe, S. Test of Anderson-Stuart model and the “universal” conductivity in rubidium and cesium silicate glasses. Braz. J. Phys. 2005, 35, 626–631. [Google Scholar] [CrossRef]
- Kodama, M.; Nakashima, N.; Matsushita, T. Velocity of Sound in and Elastic Properties of Cs2O-B2O3 glasses. Jpn. J. Appl. Phys. 1993, 32, 2227. [Google Scholar] [CrossRef]
- Sidebottom, D.L.; Tran, T.D.; Schnell, S.E. Building up a weaker network: The effect of intermediate range glass structure on liquid fragility. J. Non Cryst. Solids 2014, 402, 16–20. [Google Scholar] [CrossRef]
- Ferreira Nascimento, M.L.; Aparicio, C. Viscosity of strong and fragile glass-forming liquids investigated by means of principal component analysis. J. Phys. Chem. Solids 2007, 68, 104–110. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, J.; Mohr, R. Rayleigh and Brillouin Scattering in K2O-SiO2 Glasses. J. Am. Ceram. Soc. 1973, 56, 510–514. [Google Scholar] [CrossRef]
- Martin, S.W.; Angell, C.A. Glass formation and transition temperatures in sodium and lithium borate and aluminoborate melts up to 72 mol.% alkali. J. Non Cryst. Solids 1984, 66, 429–442. [Google Scholar] [CrossRef]
- Shartsis, L.; Capps, W.; Spinner, S. Density and expansivity of Alkali Borates and Density. J. Am. Ceram. Soc. 1953, 36, 35–43. [Google Scholar] [CrossRef]
- Carini, G.; Carini, G.; D’Angelo, G.; Tripodo, G.; Bartolotta, A.; Salvato, G. Ultrasonic relaxations, anharmonicity, and fragility in lithium borate glasses. Phys. Rev. B Condens. Matter 2005, 72, 1–10. [Google Scholar] [CrossRef]
- Shaw, R.R.; Uhlmann, D.R. Effect of phase separation on the properties of simple glasses II. Elastic properties. J. Non Cryst. Solids 1971, 5, 237–263. [Google Scholar] [CrossRef]
- Januchta, K.; To, T.; Bødker, M.S.; Rouxel, T.; Smedskjaer, M.M. Elasticity, hardness, and fracture toughness of sodium aluminoborosilicate glasses. J. Am. Ceram. Soc. 2019, 102, 4520–4537. [Google Scholar] [CrossRef]
- Soga, N.; Yamanaka, H.; Hisamoto, C.; Kunugi, M. Elastic properties and structure of alkaline-earth silicate glasses. J. Non Cryst. Solids 1976, 22, 67–76. [Google Scholar] [CrossRef]
- Hermansen, C.; Matsuoka, J.; Yoshida, S.; Yamazaki, H.; Kato, Y.; Yue, Y. Densification and plastic deformation under microindentation in silicate glasses and the relation to hardness and crack resistance. J. Non Cryst. Solids 2013, 364, 40–43. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, S.; Sanglebœuf, J.C.; Rouxel, T. Quantitative evaluation of indentation-induced densification in glass. J. Mater. Res. 2005, 20, 3404–3412. [Google Scholar] [CrossRef]
- Limbach, R.; Rodrigues, B.P.; Möncke, D.; Wondraczek, L. Elasticity, deformation and fracture of mixed fluoride-phosphate glasses. J. Non Cryst. Solids 2015, 430, 99–107. [Google Scholar] [CrossRef]
- Winterstein-Beckmann, A.; Möncke, D.; Palles, D.; Kamitsos, E.I.; Wondraczek, L. A Raman-spectroscopic study of indentation-induced structural changes in technical alkali-borosilicate glasses with varying silicate network connectivity. J. Non Cryst. Solids 2014, 405, 196–206. [Google Scholar] [CrossRef]
- Pönitzsch, A.; Nofz, M.; Wondraczek, L.; Deubener, J. Bulk elastic properties, hardness and fatigue of calcium aluminosilicate glasses in the intermediate-silica range. J. Non Cryst. Solids 2016, 434, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Kjeldsen, J.; Smedskjaer, M.M.; Mauro, J.C.; Yue, Y. On the origin of the mixed alkali effect on indentation in silicate glasses. J. Non Cryst. Solids 2014, 406, 22–26. [Google Scholar] [CrossRef]
- Kodama, M.; Matsushita, T.; Kojima, S. Velocity of sound in and elastic properties of Li2O–B2O3 glasses. Jpn. J. Appl. Phys. 1995, 34, 2570–2574. [Google Scholar] [CrossRef]
- Sanditov, D.S.; Mashanov, A.A.; Sanditov, B.D.; Mantatov, V.V. Fragility and anharmonicity of lattice vibrations of glass-forming systems. Glas. Phys. Chem. 2008, 34, 389–393. [Google Scholar] [CrossRef]
- Hassan, A.K.; Börjesson, L.; Torell, L.M. Relaxations in Complex Systems the boson peak in glass formers of increasing fragility. J. Non Cryst. Solids 1994, 172, 154–160. [Google Scholar] [CrossRef]
- Griebenow, K.; Bragatto, C.B.; Kamitsos, E.I.; Wondraczek, L. Mixed-modifier effect in alkaline earth metaphosphate glasses. J. Non Cryst. Solids 2018, 481, 447–456. [Google Scholar] [CrossRef]
- Matori, K.A.; Zaid, M.H.M.; Quah, H.J.; Aziz, S.H.A.; Wahab, Z.A.; Ghazali, M.S.M. Studying the Effect of ZnO on Physical and Elastic Properties of (ZnO)x(P2O5)1−x Glasses Using Nondestructive Ultrasonic Method. Adv. Mater. Sci. Eng. 2015, 2015, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Striepe, S.; Deubener, J. Effect of lithium-to-magnesium ratio in metaphosphate glasses on crack-tip condensation and sub-critical crack growth. J. Non Cryst. Solids 2013, 375, 47–54. [Google Scholar] [CrossRef]
- Ashizuka, M.; Ishida, E.; Uto, S.; Bradt, R.C. Fracture toughness and surface energies of binary CaO- and MgO-phosphate glasses. J. Non Cryst. Solids 1988, 104, 316–322. [Google Scholar] [CrossRef]
- Bødker, M.S.; Mauro, J.C.; Youngman, R.E.; Smedskjaer, M.M. Statistical mechanical modeling of borate glass structure and topology: Prediction of superstructural units and glass transition temperature. J. Phys. Chem. B 2019, 123, 1206–1213. [Google Scholar] [CrossRef]
- Toplis, M.J.; Kohn, S.C.; Smith, M.E.; Poplett, I.J.F. Fivefold-coordinated aluminum in tectosilicate glasses observed by triple quantum MAS NMR. Am. Mineral. 2000, 85, 1556–1560. [Google Scholar] [CrossRef]
- Stebbins, J.F.; Xu, Z. NMR evidence for excess non-bridging oxygen in an aluminosilicate glass. Nature 1997, 390, 60–62. [Google Scholar] [CrossRef]
- Konijnendijk, W.L.; Stevels, J.M. The structure of borosilicate glasses studied by Raman scattering. J. Non Cryst. Solids 1976, 20, 193–224. [Google Scholar] [CrossRef]
- Mascaraque, N.; Bauchy, M.; Smedskjaer, M.M. Correlating the network topology of oxide glasses with their chemical durability. J. Phys. Chem. B 2017, 121, 1139–1147. [Google Scholar] [CrossRef]
- Gupta, P.K.; Mauro, J.C. Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature- dependent constraints. J. Chem. Phys. 2009, 130, 094503. [Google Scholar] [CrossRef]
- Smedskjaer, M.M.; Mauro, J.C.; Youngman, R.E.; Hogue, C.L.; Potuzak, M.; Yue, Y. Topological principles of borosilicate glass chemistry. J. Phys. Chem. B 2011, 115, 12930–12946. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C. Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys. J. Non Cryst. Solids 1979, 34, 153–181. [Google Scholar] [CrossRef]
- Phillips, J.C.; Thorpe, M.F. Constraint theory, vector percolation and glass formation. Solid State Commun. 1985, 53, 699–702. [Google Scholar] [CrossRef]
- Mauro, J.C. Topological constraint theory of glass. Am. Ceram. Soc. Bull. 2011, 90, 31–37. [Google Scholar]
- Micoulaut, M. Constrained interactions, rigidity, adaptative networks, and their role for the description of silicates. Am. Mineral. 2008, 93, 1732–1748. [Google Scholar] [CrossRef]
- Smedskjaer, M.M. Topological model for boroaluminosilicate glass hardness. Front. Mater. 2014, 1, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Takeda, W.; Wilkinson, C.J.; Feller, S.A.; Mauro, J.C. Journal of non-crystalline solids: X Topological constraint model of high lithium content borate glasses. J. Non-Cryst. Solids X 2019, 3, 100028. [Google Scholar] [CrossRef]
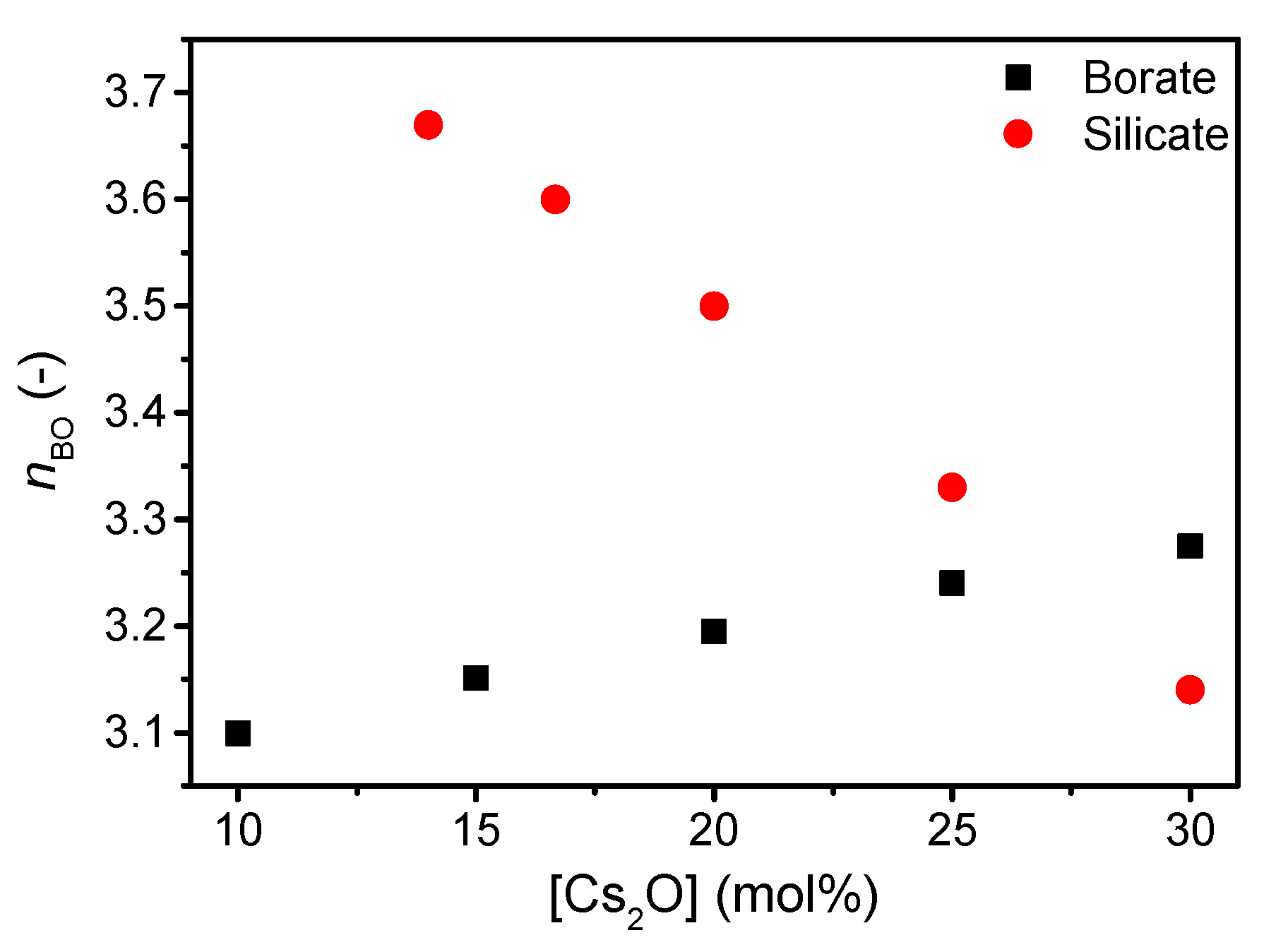
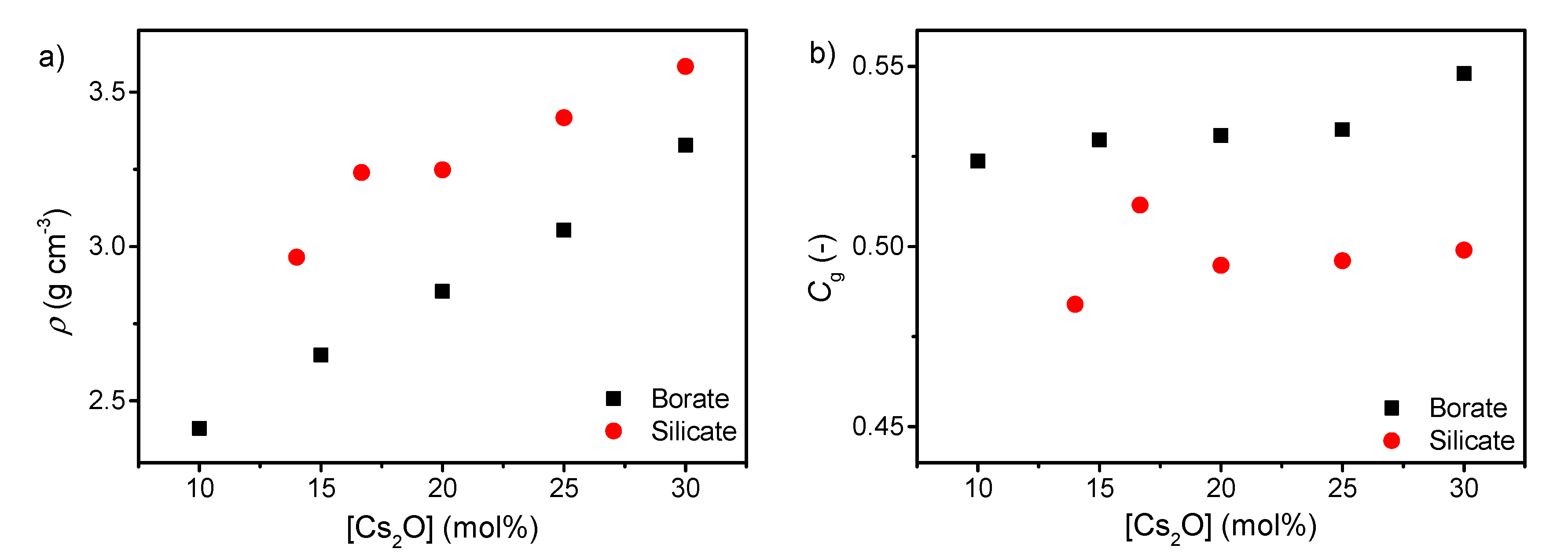
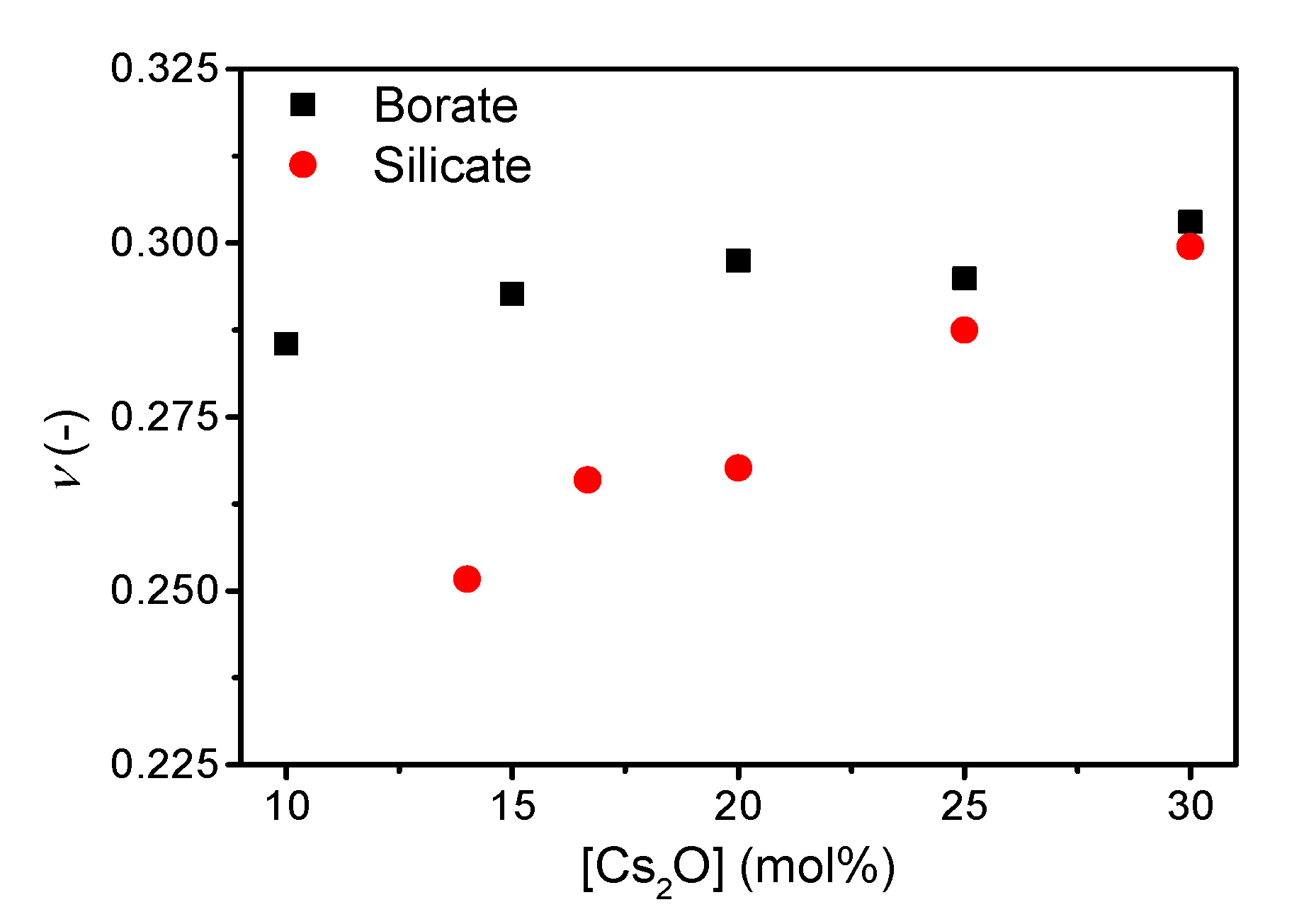
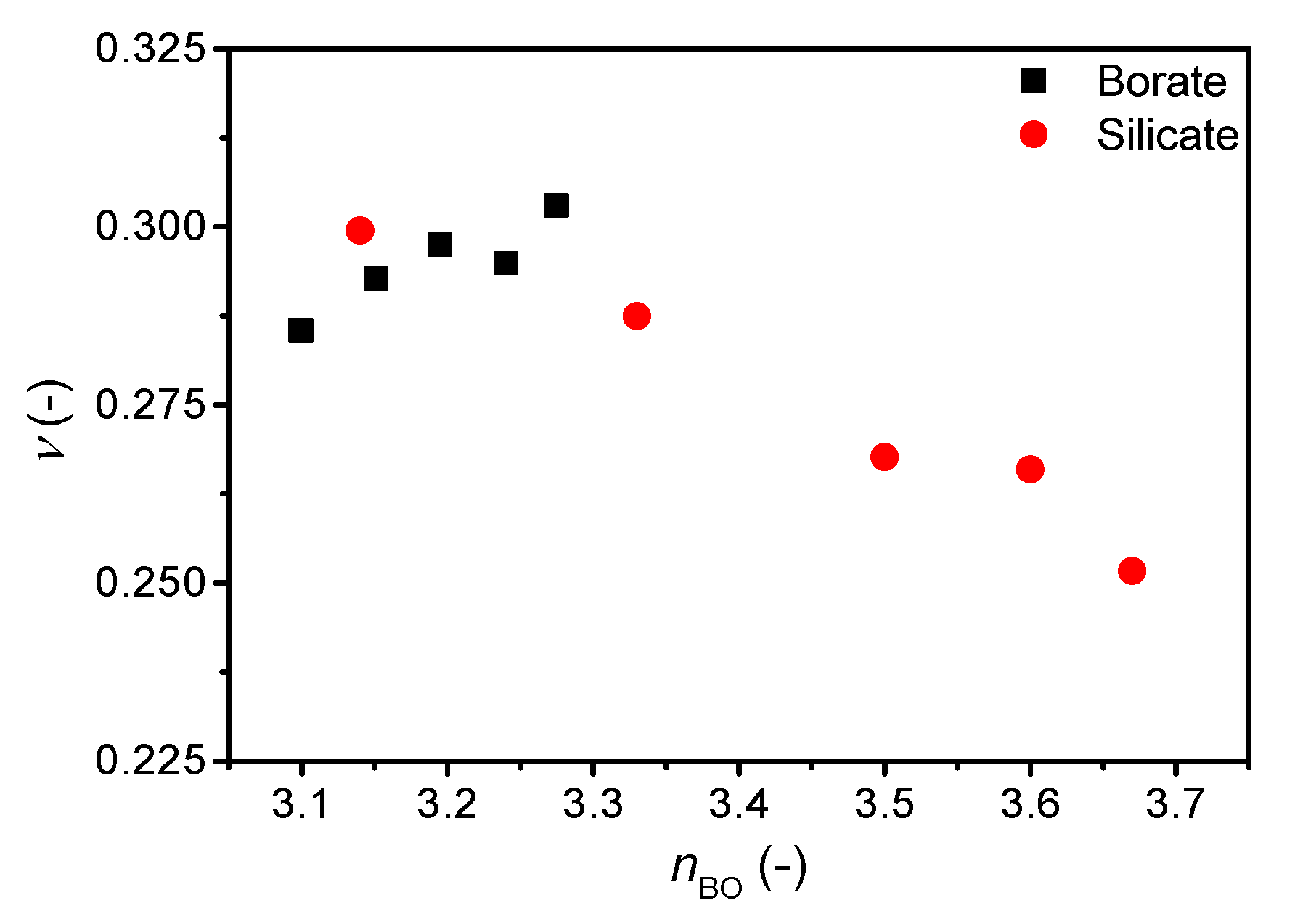
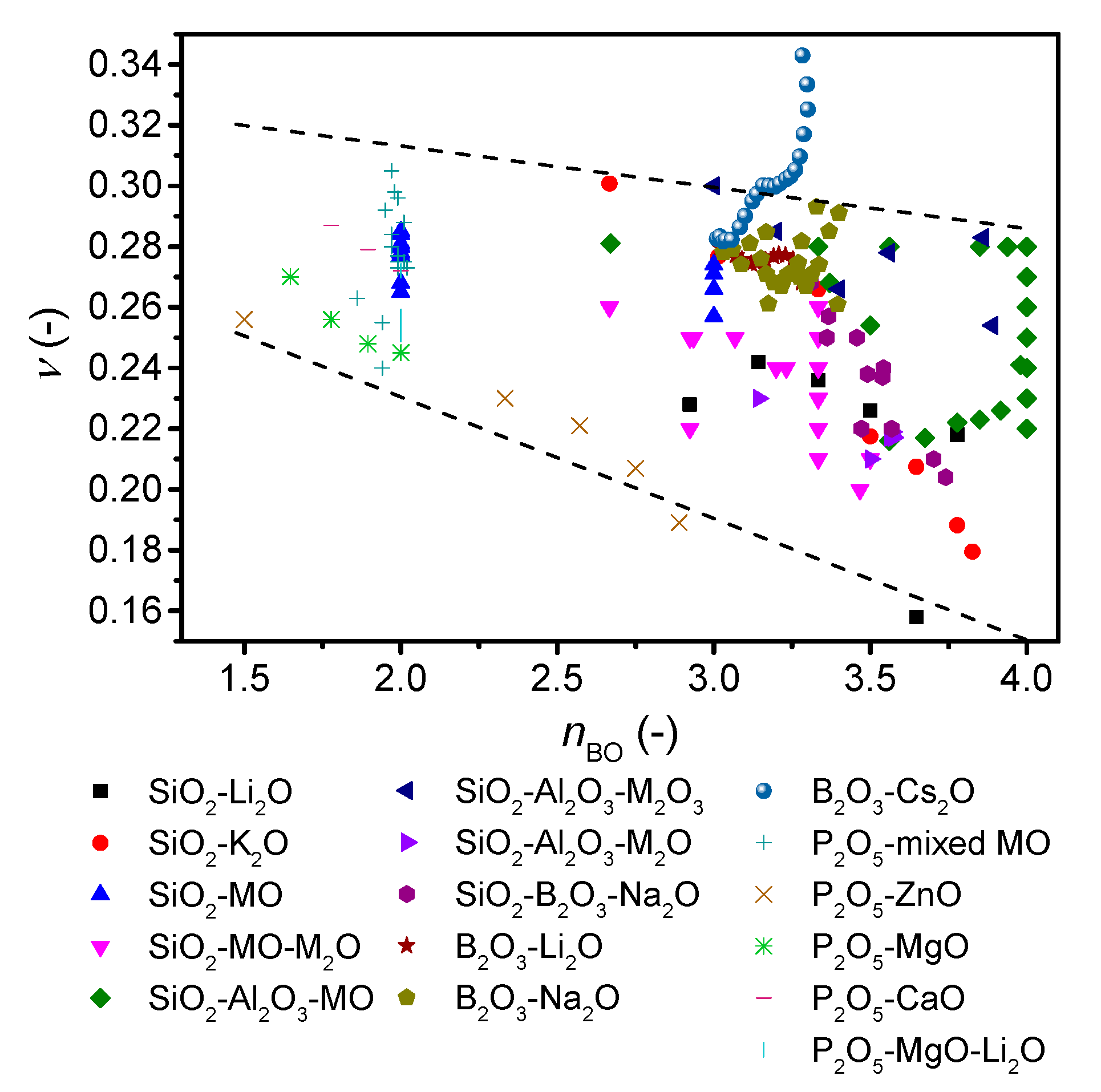
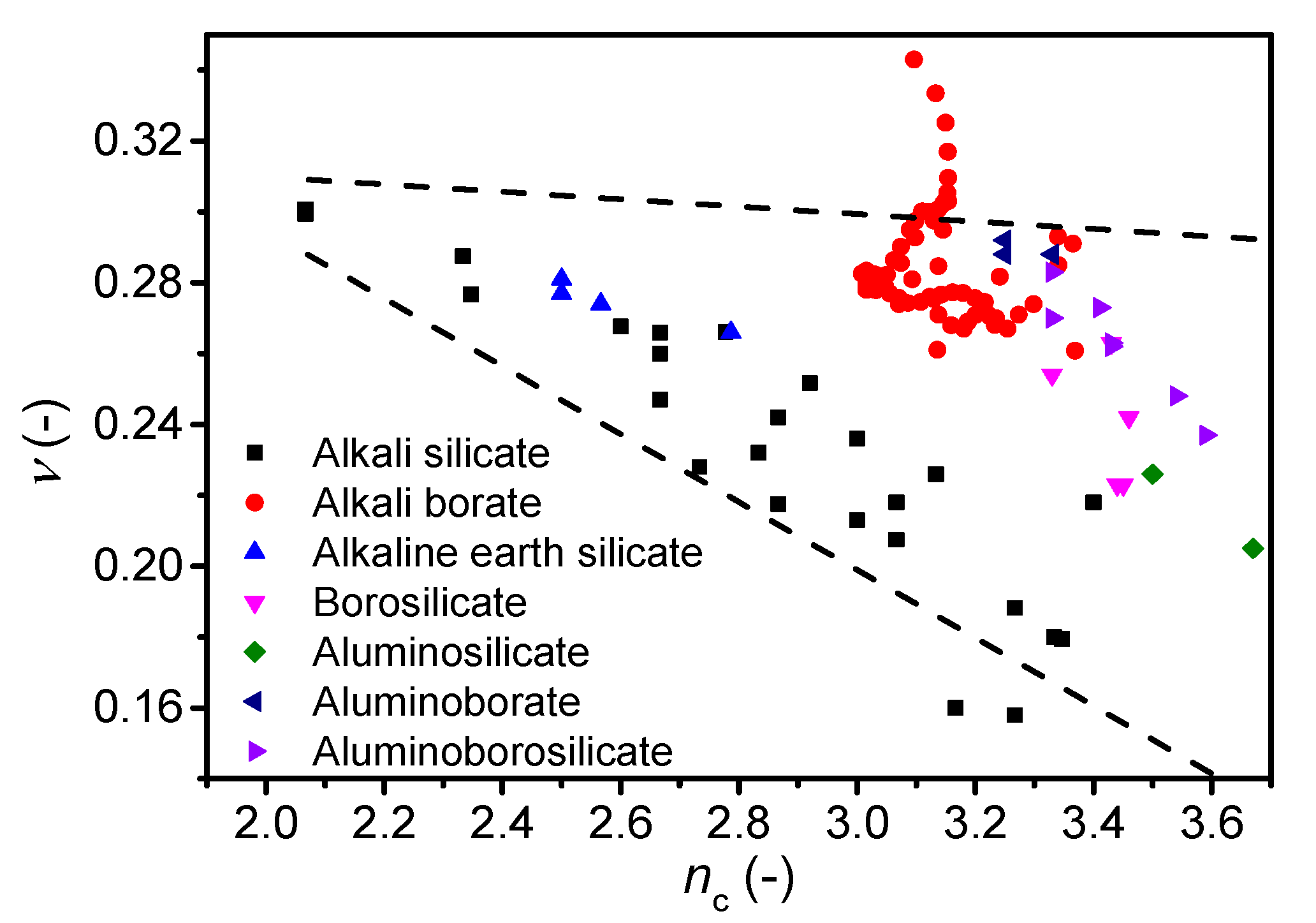
| Sample ID | Nominal Composition (mol%) | Tg (°C) | M (-) | ρ (g cm−3) | Cg (-) | E (GPa) | G (GPa) | ν (-) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | B2O3 | Cs2O | ||||||||
| Si86 | 86 | - | 14 | 555 | 20 | 2.97 | 0.484 | 44 | 18 | 0.25 |
| Si83 | 83.3 | - | 16.7 | 549 | 30 | 3.24 | 0.512 | 40 | 16 | 0.27 |
| Si80 | 80 | - | 20 | 539 | 30 | 3.25 | 0.495 | 38 | 15 | 0.27 |
| Si75 | 75 | - | 25 | 530 | 37 | 3.42 | 0.496 | 33 | 13 | 0.29 |
| Si70 | 70 | - | 30 | 490 | 47 | 3.58 | 0.499 | 31 | 12 | 0.30 |
| B90 | - | 90 | 10 | 319 | 25 | 2.41 | 0.524 | 25 | 10 | 0.29 |
| B85 | - | 85 | 15 | 343 | 30 | 2.65 | 0.530 | 26 | 10 | 0.29 |
| B80 | - | 80 | 20 | 376 | 32 | 2.85 | 0.531 | 25 | 10 | 0.30 |
| B75 | - | 75 | 25 | 416 | 47 | 3.05 | 0.532 | 30 | 11 | 0.30 |
| B70 | - | 70 | 30 | 403 | 49 | 3.33 | 0.548 | 31 | 18 | 0.30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Østergaard, M.B.; Bødker, M.S.; Smedskjaer, M.M. Structure Dependence of Poisson’s Ratio in Cesium Silicate and Borate Glasses. Materials 2020, 13, 2837. https://doi.org/10.3390/ma13122837
Østergaard MB, Bødker MS, Smedskjaer MM. Structure Dependence of Poisson’s Ratio in Cesium Silicate and Borate Glasses. Materials. 2020; 13(12):2837. https://doi.org/10.3390/ma13122837
Chicago/Turabian StyleØstergaard, Martin B., Mikkel S. Bødker, and Morten M. Smedskjaer. 2020. "Structure Dependence of Poisson’s Ratio in Cesium Silicate and Borate Glasses" Materials 13, no. 12: 2837. https://doi.org/10.3390/ma13122837
APA StyleØstergaard, M. B., Bødker, M. S., & Smedskjaer, M. M. (2020). Structure Dependence of Poisson’s Ratio in Cesium Silicate and Borate Glasses. Materials, 13(12), 2837. https://doi.org/10.3390/ma13122837






