Identification of Stress States in Compressed Masonry Walls Using a Non-Destructive Technique (NDT)
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Propagation of Ultrasonic Waves in Linear-Elastic Material
2.2. Propagation of Ultrasonic Waves in Porous Material
- different dimensions and properties of components—matrix grains,
- different models (systems) of arrangement and connections of individual grains—they can have a direct contact or are connected with binder of other properties. In the case of chemically bonded materials, the binder changes its properties during the transformation from liquid to solid state.
- internal frictions in the medium—δr,
- thermal effects—δT,
- Rayleigh scattering δR.
- dimensions of the matrix grains,
- thermal properties of components,
- elastic properties of components, and their density.
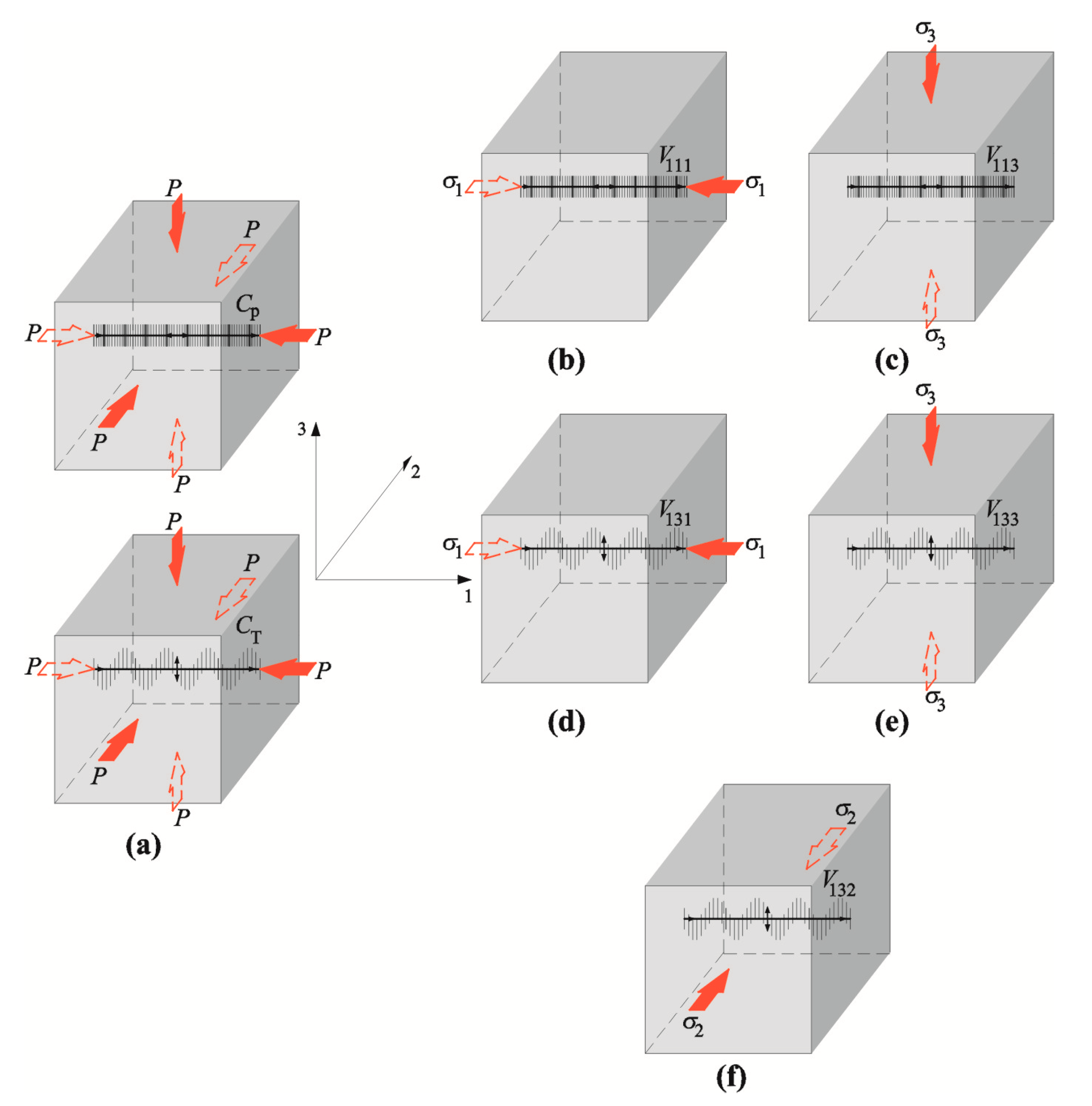
3. Stress Measurements Using an Ultrasonic Technique
4. Test Program and Results
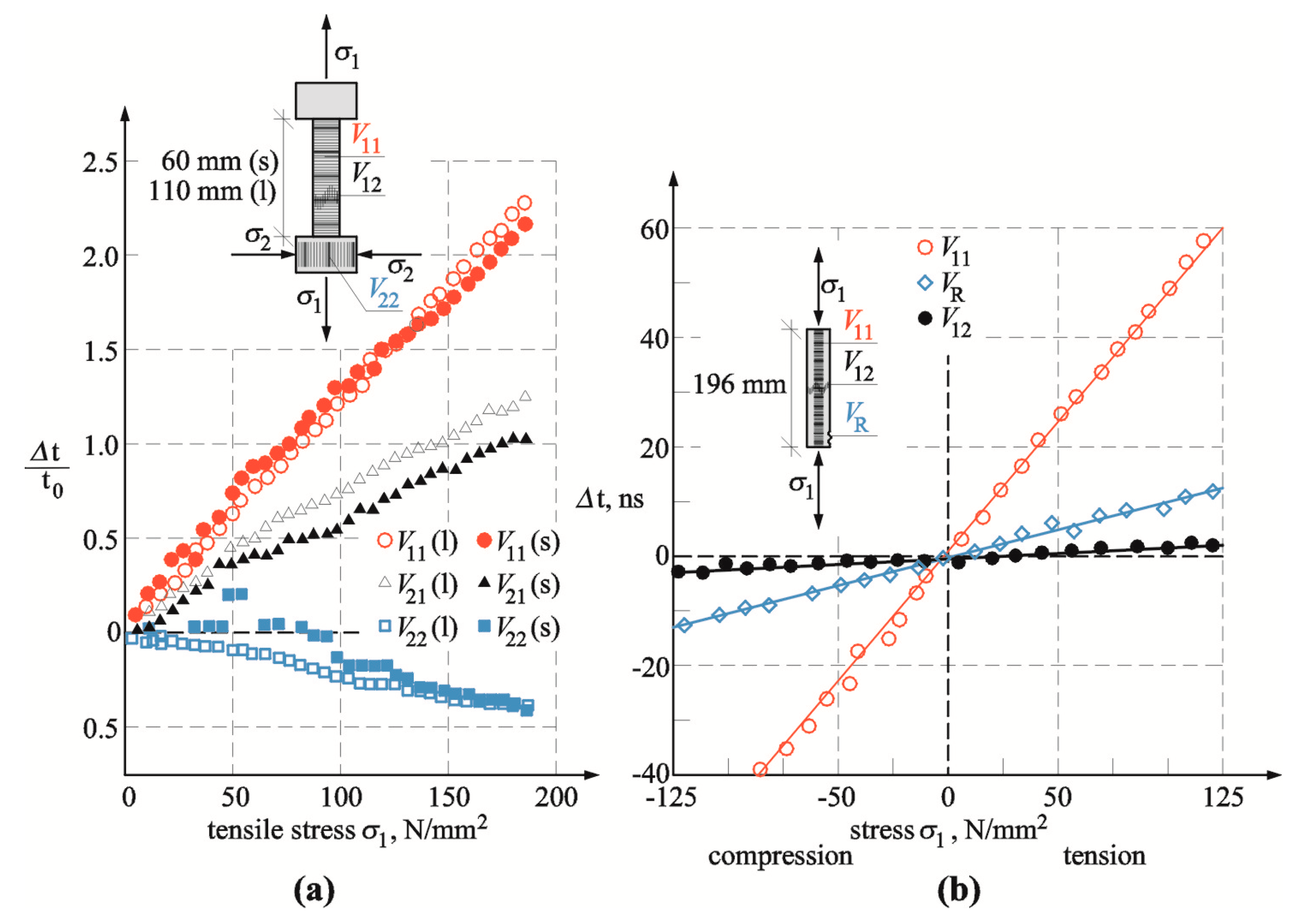
4.1. Stage I—Determination of Acoustoelastic Constant
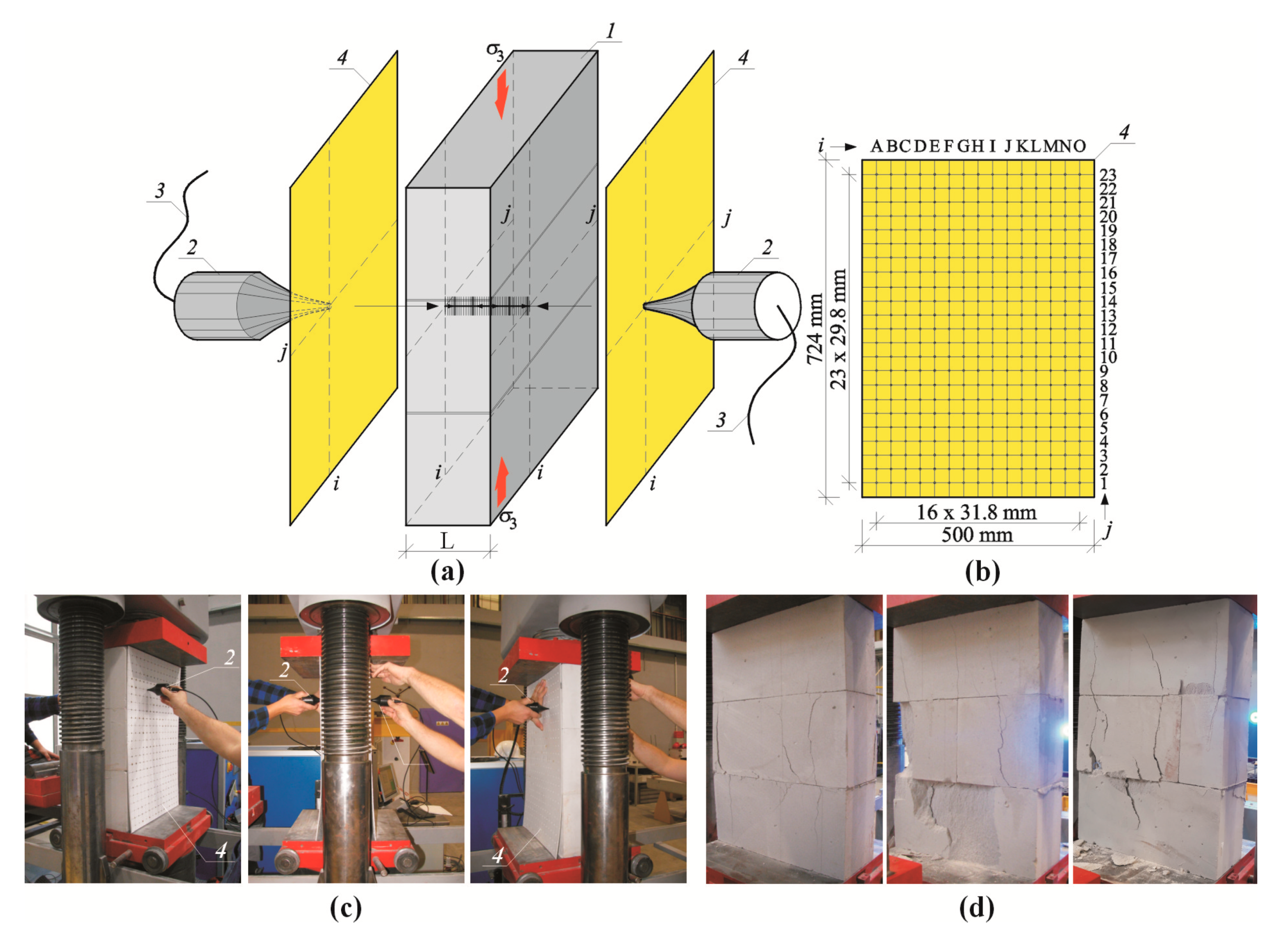
4.2. Stage II—Test Results for Small Masonry Models
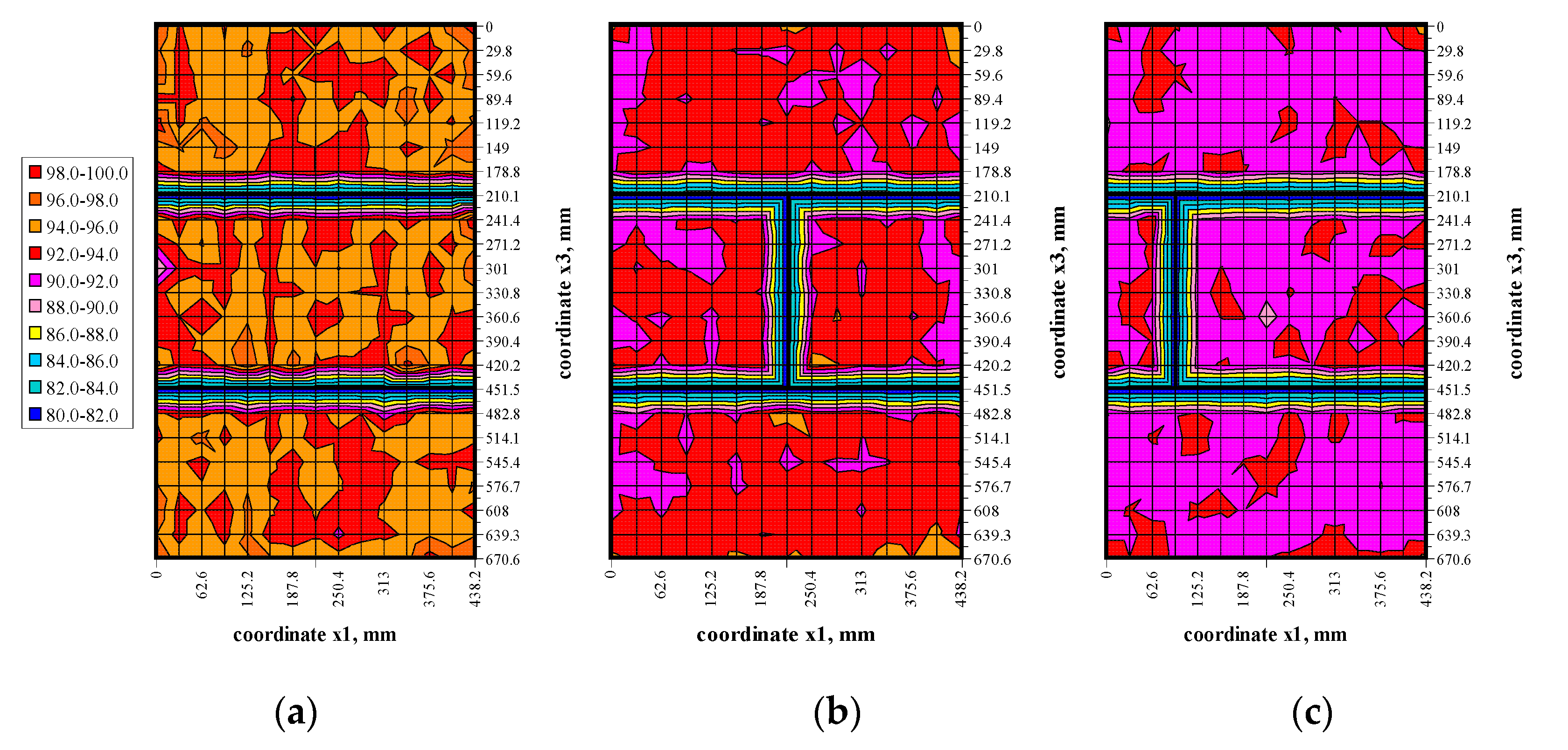
5. Analysis of Test Results
Statistical Estimation of Stress in Walls
6. Conclusions
- (a)
- the acoustoelastic method (AE) can be used to determine stress in autoclaved aerated concrete,
- (b)
- correlations were obtained that bind the value of acoustoelastic coefficient β113 as a function of density and moisture content in AAC,
- (c)
- the effect of scattering of the ultrasonic wave in medium can be neglected when the coefficient β113 is applied,
- (d)
- rather precise values of mean stress in the wall were determined on the basis of measured velocity of ultrasonic wave propagation at a high number of measuring points,
- (e)
- reduced number of measuring points resulted in a significant underestimation of mean stress,
- (f)
- determination of the quantile equal to 95% for passing time of the ultrasonic wave was used to estimate stress in the wall with the underestimation of the order of 12–18%, which can be considered as satisfactory.
Funding
Acknowledgments
Conflicts of Interest
References
- Auld, B.A. Acoustic Fields and Waves in Solid; John Wiley and Sons: Hoboken, NJ, USA, 1973. [Google Scholar]
- Bayer, R.T.; Letcher, S.V. Phisical Ultarsonics; Academic Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Malhotra, V.M.; Carino, N.J. Handbook on Nondestructive Testing of Concrete; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Huan, H.; Liu, L.; Mandelis, A.; Peng, C.; Chen, X.; Zhan, J. Mechanical strength evaluation of elastic materials by multiphysical nondestructive methods: A review. Appl. Sci. 2020, 10, 1588. [Google Scholar] [CrossRef] [Green Version]
- Hola, J.; Schabowicz, K. State-of-the-art non-destructive methods for diagnostic testing of building structures—Anticipated development trends. Arch. Civ. Mech. Eng. 2010, 10, 5–18. [Google Scholar] [CrossRef]
- Breysse, D. Nondestructive evaluation of concrete strength: An historical review and a new perspective by combining NDT methods. Constr. Build. Mater. 2012, 33, 139–163. [Google Scholar] [CrossRef]
- Forde, M.C. International practice using NDE for the inspection of concrete and masonry arch bridges. Bridge Struct. 2010, 6, 25–34. [Google Scholar] [CrossRef]
- Cotic, P.; Jaglicic, Z.; Niederleithinger, E.; Effner, U.; Kruschwitz, S.; Trela, C.; Bosiljkov, V. Effect of moisture on the reliability of void detection in brickwork masonry using radar, ultrasonic and complex resistivity tomography. Mater. Struct. 2013, 46, 1723–1735. [Google Scholar] [CrossRef]
- de Nicolo, B.; Piaga, C.; Popescu, V.; Concu, G. Non-invasive acoustic measurements for faults detecting in building materials and structures. Appl. Meas. Syst. 2012, 259–292. [Google Scholar] [CrossRef]
- Khan, F.; Rajaram, S.; Vanniamparambil, P.A.; Bolhassani, M.; Hamid, A.; Kontsos, A.; Bartoli, I. Multi-sensing NDT for damage assessment of concrete masonry walls. Struct. Control. Health Monit. 2015, 22, 449–462. [Google Scholar] [CrossRef]
- Homann, M. Porenbeton Handbuch. Planen und Bauen Mit System, 6th ed.; Auflage: Hannover, Germany, 2008. [Google Scholar]
- Jasiński, R.; Drobiec, Ł.; Mazur, W. Validation of selected non-destructive methods for determining the compressive strength of masonry units made of autoclaved aerated concrete. Materials 2019, 12, 389. [Google Scholar] [CrossRef] [Green Version]
- Jasiński, R. Determination of AAC masonry compressive strength by semi destructive method. Nondestruct Test Diagn. 2018, 3, 81–85. [Google Scholar] [CrossRef] [Green Version]
- Benson, R.W.; Raelson, V.J. Acoustoelasticity. Prod. Eng. 1959, 20, 565–569. [Google Scholar]
- Lurie, A.I. Nonlinear Theory of Elasticity; Elsevier: Amsterdam, The Netherlads, 1991; ISBN 978-0444567710. [Google Scholar]
- Biot, M.A. Theory of propagation of elastic waves in fluid-saturated porous solid. J. Acoust. Soc. Am. 1958, 28, 168–191. [Google Scholar] [CrossRef]
- Biot, M.A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Plona, T.J. Observation of a second bulk compression wave in a porous medium at ultrasonic frequencies. Appl. Phys. Lett. 1980, 36, 259–261. [Google Scholar] [CrossRef] [Green Version]
- Berryman, J.G. Confirmation of Biot’s theory. Appl. Phys. Lett. 1980, 37, 382. [Google Scholar] [CrossRef]
- Soczkiewicz, E.; Chivers, R.C. Propagation and scattering of acoustic waves in a turbulent medium. J. Sound Vib. 2001, 241, 197–205. [Google Scholar] [CrossRef]
- Soczkiewicz, E. Aplication of quantum field theory methods in studies of ultrasonic wave propagation in random media. Ultrason. Methods Eval. Inhomogeneous Mater. 1978, 126, 163–173. [Google Scholar]
- Edelman, I. On the existence of low-frequency surface waves in a porous medium. Comptes Rendus Mécanique 2004, 332, 43–49. [Google Scholar] [CrossRef]
- Edelman, I. Bifurcation of the biot slow wave in a porous medium. J. Acoust. Soc. Am. 2002, 114, 90–97. [Google Scholar] [CrossRef]
- Boutin, C.; Royer, P.; Aurialt, J.L. Acoustic absorbtion of porous surcacing with dual porosity. Int. J. Solid Struct. 1998, 35, 4709–4737. [Google Scholar] [CrossRef] [Green Version]
- Mozhaev, V.G.; Weihnacht, M. Subsonic leaky rayleigh waves at liqud-solid interfaces. Ultrasononics 2002, 40, 927–933. [Google Scholar] [CrossRef]
- Biot, M.A. The influence of initial stress on elastic waves. J. Appl. Phys. 1940, 11, 522–530. [Google Scholar] [CrossRef]
- Huges, D.S.; Kelly, J.L. Second order elastic deformation of solids. Phys. Rev. 1953, 92, 1145–1149. [Google Scholar] [CrossRef]
- Bergman, R.H.; Shahbender, R.A. Effect of statically applied stresses on the velocity of propagation of ultrasonic waves. J. Appl. Phys. 1958, 29, 1736–1738. [Google Scholar] [CrossRef]
- Tokuoka, T.; Saito, M. Elastic wave propagations and acoustical birefringence in stressed crystals. J. Acoust. Soc. Am. 1968, 45, 1241–1246. [Google Scholar] [CrossRef]
- Husson, D.; Kino, G.S. A perturbation theory for acoustoelastic effects. J. Appl. Phys. 1982, 53, 7250–7258. [Google Scholar] [CrossRef]
- Nikitina, N.Y.; Ostrovsky, L.A. An ultrasonic method for measuring stresses in engineering materials. Ultrasonics 1998, 35, 605–610. [Google Scholar] [CrossRef]
- Dorfi, H.R.; Busby, H.R.; Janssen, M. Ultrasonic stress measurements based on the generalized acoustic ratio technique. Int. J. Solids Struct. 1996, 33, 1157–1174. [Google Scholar] [CrossRef]
- Man, C.; Lu, W.Y. Towards an acoustoelastic theory for measurement of residual stress. J. Elast. 1987, 17, 159–182. [Google Scholar] [CrossRef]
- Murnagham, F.D. Finite Deformation of an Elastic Solid; Wiley Publishing: Hoboken, NJ, USA, 1951. [Google Scholar]
- Murnaghan, F.D. Finite deformations of an elastic solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Tylczyński, Z.; Mróz, B. The influence of uniaxial stress on ultrasonic wave propagation in ferroelastic (NH4)4LiH3(SO4)4. Solid State Commun. 1997, 101, 653–656. [Google Scholar] [CrossRef]
- Takahashi, S.; Motegi, R. Measurement of third-order elastic constants and applications to loaded structural materials. Springer Plus 2015, 4, 325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, S. Measurement of third-order elastic constants and stress dependent coefficients for steels. Mech. Adv. Mater. Mod. Process. 2018, 4. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, S. Stress Measurement Method and its Apparatus. U.S. Patent 7299138, 10 December 2007. [Google Scholar]
- Deputat, J. Properties and Use of the Elastoacoustic Phenomenon to Measure Self-Stress; Institute of Fundamental Technological Research Polish Academy of Sciences: Warsaw, Poland, 1987. (In Polish) [Google Scholar]
- Egle, D.M.; Bray, D.E. Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 1976, 60, 741–744. [Google Scholar] [CrossRef]
- British Standards Institution. EN 771-4:2011 Specification for Masonry Units—Part 4: Autoclaved Aerated Concrete Masonry Units; British Standards Institution: London, UK, 2011. [Google Scholar]
- CEN. PN-EN 1996-1-1:2010+A1:2013-05P. Eurocode 6: Design of Masonry Structures. Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures; Europeand Commettee for Standardization: Brusselles, Belgium, 2005. (In Polish) [Google Scholar]
- Bartlett, F.M.; Macgregor, J.G. Effect of moisture condition on concrete core strengths. ACI Mater. J. 1993, 91, 227–236. [Google Scholar]
- Suprenant, B.A.; Schuller, M.P. Nondestructive Evaluation & Testing of Masonry Structures; Hanley Wood Inc.: Washinton, DC, USA, 1994; ISBN 978-0924659577. [Google Scholar]
- McCann, D.M.; Forde, M.C. Review of NDT methods in the assessment of concrete and masonry structures. NDT E Int. 2001, 34, 71–84. [Google Scholar] [CrossRef]
- Haach, V.G.; Ramirez, F.C. Qualitative assessment of concrete by ultrasound tomography. Constr. Build. Mater. 2016, 119, 61–70. [Google Scholar] [CrossRef]
- Zielińska, M.; Rucka, M. Non-destructive assessment of masonry pillars using ultrasonic tomography. Materials 2018, 11, 2543. [Google Scholar] [CrossRef] [Green Version]
- EN 1015-11:2001/A1:2007. Methods of Test for Mortar for Masonry. Part 11: Determination of Flexural and Compressive Strength of Hardened Mortar; European Committee for Standardization: Brussels, Belgium, 1999. [Google Scholar]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A.; Peters, W.H. Application of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Lord, J.D. Digital Image Correlation (DIC), Modern Stress and Strain Analysis. A State of the Art Guide to Measurement Techniques, BSSM; Evans, J.E., Dulie-Barton, J.M., Burguete, R.L., Eds.; Eureka Magazine: Cambridge, UK, 2009; pp. 14–15. [Google Scholar]
- Frankovský, P.; Virgala, I.; Hudák, P.; Kostka, J. The use of the digital image correlation in a strain analysis. Int. J. Appl. Mech. Eng. 2013, 4, 1283–1292. [Google Scholar] [CrossRef] [Green Version]
- Volk, W. Applied Statistics for Engineers; Literary Licensing LLC: Whitefish, MT, USA, 2013. [Google Scholar]











| No. | Nominal Class of Density kg/m3 | Density Range of AAC, kg/m3 | No. of Specimens (Cores φ59 × 120 mm) | Mean Density ρ0, kg/m3 (C.O.V) acc. to [12] | Mean Modulus of Elasticity, E, N/mm2 (C.O.V) | Mean Poisson’s Ratio ν, (C.O.V) |
|---|---|---|---|---|---|---|
| 1 | 400 | 375–446 | 6 | 397 (6%) | 1516 (9.6%) | 0.19 (7.9%) |
| 2 | 500 | 462–532 | 6 | 492 (3%) | 2039 (8.9%) | 0.21 (8.7%) |
| 3 | 600 | 562–619 | 6 | 599 (2%) | 2886 (10.5%) | 0.20 (8.5%) |
| 4 | 700 | 655–725 | 6 | 674 (3%) | 4778 (10.1%) | 0.19 (9.2%) |
| No. | Mean Density ρ (Nominal Class of Density) kg/m3 | Mean Compressive Stress σ3, N/mm2 | Mean Relative Compressive Stress σ3/σ3max | Mean Path Length L, mm | Mean Passing Time of Wave T, µs | Mean Ultrasound Velocity cp = L/t, m/s | Standard Deviation, s, m/s | COV, % |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 397 (400) | 0 | 0 | 100.2 | 53.5 | obscp0 = 1875 | 1.02 | 1.9% |
| 2 | 0.75 | 0.27 | 55.7 | 1801 | 1.78 | 3.2% | ||
| 3 | 1.33 | 0.48 | 57.3 | 1750 | 0.56 | 1.0% | ||
| 4 | 2.08 | 0.75 | 60.4 | 1660 | 0.13 | 0.2% | ||
| 5 | 2.58 | 0.93 | 60.9 | 1647 | 1.19 | 2.0% | ||
| 6 | 492 (500) | 0 | 0 | 100.3 | 53.0 | obscp0 = 1893 | 0.62 | 1.2% |
| 7 | 0.83 | 0.24 | 54.3 | 1849 | 1.04 | 1.9% | ||
| 8 | 1.66 | 0.48 | 57.1 | 1756 | 0.54 | 1.0% | ||
| 9 | 2.59 | 0.75 | 58.2 | 1724 | 1.55 | 2.7% | ||
| 10 | 3.33 | 0.96 | 59.3 | 1691 | 1.23 | 2.1% | ||
| 11 | 599 (600) | 0 | 0 | 100.4 | 49.5 | obscp0 = 2031 | 1.32 | 2.7% |
| 12 | 1.25 | 0.24 | 51.7 | 1942 | 1.79 | 3.5% | ||
| 13 | 2.58 | 0.50 | 52.9 | 1898 | 1.32 | 2.5% | ||
| 14 | 3.92 | 0.75 | 54.6 | 1841 | 1.75 | 3.2% | ||
| 15 | 5.00 | 0.96 | 53.9 | 1866 | 2.40 | 4.5% | ||
| 16 | 674 (700) | 0 | 0 | 100.2 | 45.1 | obscp0 = 2225 | 1.56 | 3.5% |
| 17 | 2.00 | 0.24 | 46.5 | 2159 | 2.34 | 5.0% | ||
| 18 | 4.17 | 0.50 | 47.5 | 2114 | 2.08 | 4.4% | ||
| 19 | 6.17 | 0.74 | 48.3 | 2075 | 1.72 | 3.6% | ||
| 20 | 8.17 | 0.98 | 48.6 | 2064 | 1.71 | 3.5% |
| No. | Series | Model | Mean Density ρ0, kg/m3 | Moisture Content w, % | Maximum Moisture Content (39) w, % | Compressive Stress Inducing Cracks σ3cr, N/mm2 | Maximum Compressive Stress σ3max, N/mm2 | ||
|---|---|---|---|---|---|---|---|---|---|
| of Model | Mean (COV) | of Model | Mean (COV) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | I | I-1 * | 594 | 6.0% | 60.9% | 2.93 | 2.89 (1.1%) | 2.97 | 3.01 (1.3%) |
| 2 | I-2 | 589 | 4.5% | 61.6% | 2.87 | 3.04 | |||
| 3 | I-3 | 592 | 5.1% | 61.2% | 2.88 | 3.01 | |||
| 4 | II | II-1 * | 588 | 6.0% | 61.7% | 3.00 | 2.95 (2.8%) | 3.00 | 2.96 (2.6%) |
| 5 | II-2 | 597 | 4.9% | 60.6% | 2.85 | 2.87 | |||
| 6 | II-3 | 593 | 6.0% | 61.1% | 2.99 | 3.01 | |||
| 7 | III | III-1 * | 594 | 5.1% | 60.9% | 2.97 | 2.90 (3.3%) | 2.99 | 2.97 (1.9%) |
| 8 | III-2 | 587 | 5.5% | 61.8% | 2.79 | 2.90 | |||
| 9 | III-3 | 590 | 5.4% | 61.4% | 2.95 | 3.01 | |||
| Model | Number of Measuring Points in Each Step of Loading n | Passing Time of Ultrasonic Wave Under Various Levels of Loading tp, μs (COV) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||||||
| tpmin | tpmax | tpmv | tpmin | tpmax | tpmv | tpmin | tpmax | tpmv | tpmin | tpmax | tpmv | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| I-1 | 315 | 86 | 94.2 | 90.8 (1.4%) | 86.7 | 98.8 | 92.2 (1.3%) | 90.5 | 99.2 | 93.9 (1.4%) | 87.7 | 99.9 | 94.4 (1.4%) |
| II-1 | 308 | 82.2 | 92.9 | 89.2 (1.6%) | 86.3 | 94.4 | 90.6 (1.2%) | 89.0 | 97.4 | 92.2 (1.1%) | 90.2 | 96.4 | 92.5 (1.1%) |
| III-1 | 308 | 85 | 92.9 | 88.8 (1.4%) | 87.1 | 93.5 | 90.2 (1.2%) | 88.8 | 95.1 | 91.6 (0.9%) | 90.1 | 95.4 | 92.1 (0.9%) |
| Model | Number of Measuring Points n | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β113 mm2/N (38) | N/mm2 (36) | β113 mm2/N (38) | N/mm2 (36) | β113 mm2/N (38) | N/mm2 (36) | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 315 | −0.0154 | −0.0215 | 0.715 | −0.0310 | −0.0224 | 1.437 | −0.0388 | −0.0215 | 1.800 |
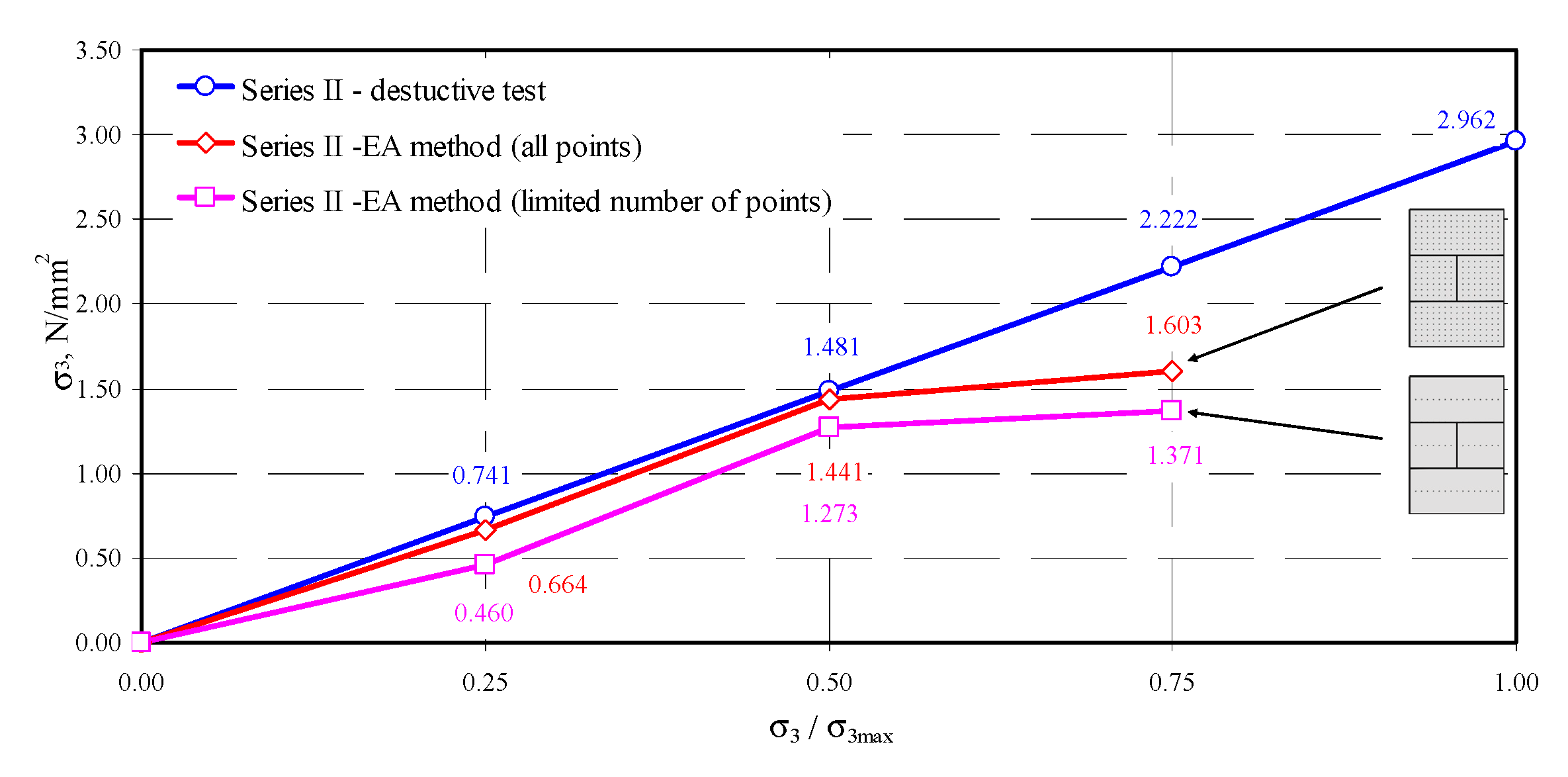
| II-1 | 308 | −0.0149 | −0.0215 | 0.664 | −0.0322 | −0.0224 | 1.441 | −0.0359 | −0.0215 | 1.603 |
| III-1 | 308 | −0.0150 | −0.0215 | 0.696 | −0.0306 | −0.0224 | 1.419 | −0.0360 | −0.0215 | 1.672 |
| Model | Number of Measuring Points n | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β113 mm2/N (38) | N/mm2 (36) | β113 mm2/N (38) | N/mm2 (36) | β113 mm2/N (38) | N/mm2 (36) | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 45 | −0.0113 | −0.0215 | 0.526 | −0.0255 | −0.0215 | 1.183 | −0.0326 | −0.0215 | 1.512 |
| II-1 | 44 | −0.0103 | −0.0224 | 0.460 | −0.0285 | −0.0224 | 1.273 | −0.0307 | −0.0224 | 1.371 |
| III-1 | 44 | −0.0117 | −0.0215 | 0.545 | −0.0263 | −0.0215 | 1.223 | −0.0314 | −0.0215 | 1.459 |
| Model | Number of Measuring Points n | u1−α/2 | 0.25σ3max | 0.50σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
N/mm2 | σ3obs N/mm2 | N/mm2 | σ3obs N/mm2 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 45 | 1.645 | 92.6 | 0.656 | 0.752 | 1.15 | 93.9 | 1.329 | 1.503 | 1.13 |
| II-1 | 44 | 90.8 | 0.595 | 0.741 | 1.24 | 92.4 | 1.37 | 1.481 | 1.08 | |
| III-1 | 44 | 90.3 | 0.640 | 0.742 | 1.16 | 91.7 | 1.302 | 1.485 | 1.14 | |
| on average: | 1.18 | on average: | 1.12 | |||||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiński, R. Identification of Stress States in Compressed Masonry Walls Using a Non-Destructive Technique (NDT). Materials 2020, 13, 2852. https://doi.org/10.3390/ma13122852
Jasiński R. Identification of Stress States in Compressed Masonry Walls Using a Non-Destructive Technique (NDT). Materials. 2020; 13(12):2852. https://doi.org/10.3390/ma13122852
Chicago/Turabian StyleJasiński, Radosław. 2020. "Identification of Stress States in Compressed Masonry Walls Using a Non-Destructive Technique (NDT)" Materials 13, no. 12: 2852. https://doi.org/10.3390/ma13122852
APA StyleJasiński, R. (2020). Identification of Stress States in Compressed Masonry Walls Using a Non-Destructive Technique (NDT). Materials, 13(12), 2852. https://doi.org/10.3390/ma13122852





