Estimation of Viscosity and Yield Stress of Cement Grouts at True Ground Temperatures Based on the Flow Spread Test
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Investigation
2.1.1. Materials
2.1.2. Proportioning and Mixing
2.1.3. Flow Spread Test
2.1.4. Viscosity Measurement
2.2. Modelling of Water Viscosity
2.3. Estimation of Viscosity and Yield Stress
2.3.1. Estimation of Viscosity
2.3.2. Prediction of Yield Stress
3. Results and Discussion
3.1. Evolution of Packing Density
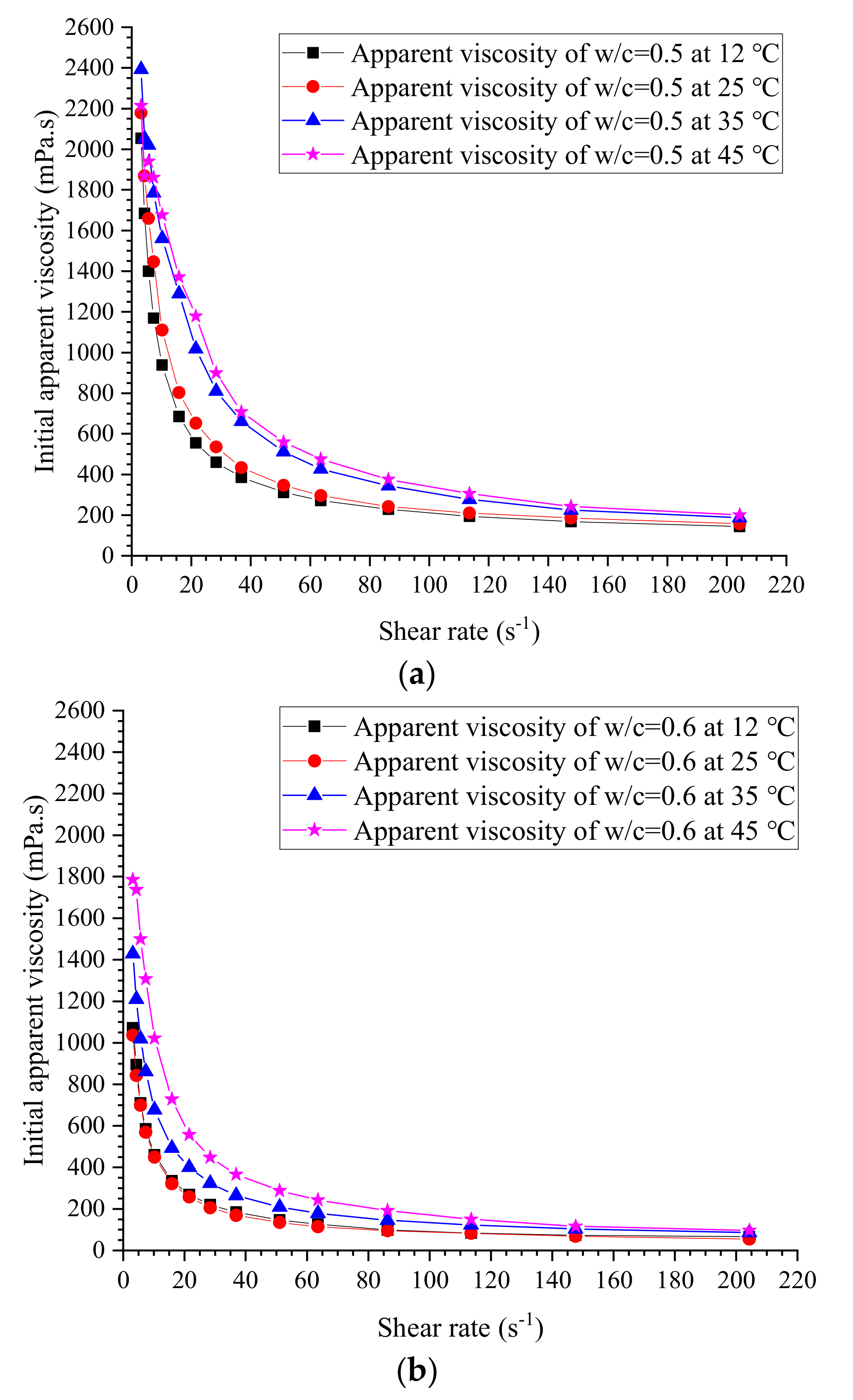
3.2. Measured Viscosity and Yield Stress
3.3. Temperature Dependence of Water Viscosity
3.4. Prediction of Viscosity at True Ground Temperature
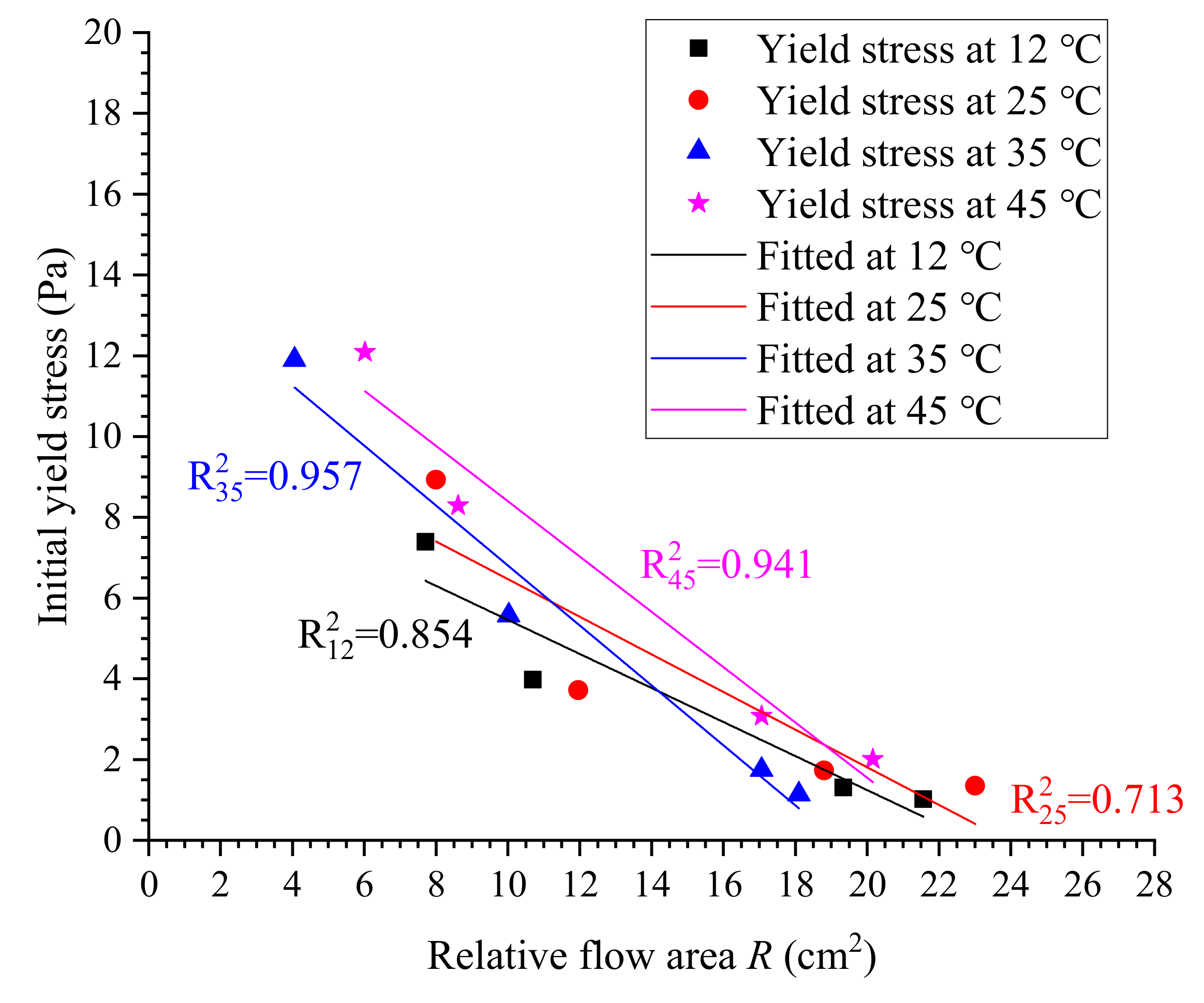
3.5. Estimation of Yield Stress
4. Conclusions
- (1)
- The packing density of cement, determined by flow spread test, was temperature dependent. It generally decreases with increasing temperature. Hence, the effect of temperature on packing density should be taken into account in related issues. The temperature dependence of packing density was found to be linear in this work.
- (2)
- The initial viscosity and yield stress of thick grouts (w/c ≤ 0.8) were prone to be improved by elevated temperature. The rheology of thick cement grouts should be focused on more in deep rock grouting.
- (3)
- If the fluctuation of water viscosity at different temperatures was not taken into account, the relative viscosity of cement grout mixtures was considerably underestimated at higher temperatures, resulting in unreasonable understanding of the viscosity of cement grouts at true ground temperatures.
- (4)
- Based on Liu’s model and the flow spread test, a temperature-based model for estimating the initial viscosity of cement grout was successfully developed. In the proposed prediction model, the effects of elevated temperature on both water viscosity and the packing density of cement were properly taken into account. The developed method for predicting the viscosity of cement grouts produced sufficient accuracy at the engineering level, which will facilitate field technicians to readily control the viscosity of cement grouts at true ground temperatures in deep rock grouting.
- (5)
- The yield stress of cement grouts cannot be predicted using the Lapasin model due to the absence of plastic behavior of cement grouts. In contrast, it was linearly correlated to the results of the flow spread test, i.e., the relative flow area. In addition, it was also found that the dependence of the yield stress of cement grouts on the relative spread area is in the strongly exponential law in form of with the highest reliability for the estimation of yield stress of the investigated cement grouts.
Author Contributions
Funding
Data Availability
Conflicts of Interest
References
- Håkansson, U.; Hässler, L.; Stille, H. Rheological properties of microfine cement grouts. Tunn. Undergr. Space Technol. 1992, 7, 453–458. [Google Scholar] [CrossRef]
- Gustafson, G.; Claesson, J.; Fransson, Å. Steering Parameters for Rock Grouting. J. Appl. Math. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Nonveiller, E. Grouting Theory and Practice; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Kazemian, S.; Prasad, A.; Huat, B.B. Rheological Behavior of Grout in Context of Newtonian and non-Newtonian Fluids. Electron. J Geotech. Eng. (EJGE) 2010, 15, 1103–1115. [Google Scholar]
- Shamu, T.J.; Håkansson, U. Rheology of cement grouts: On the critical shear rate and no-slip regime in the Couette geometry. Cem. Concr. Res. 2019, 123, 105769. [Google Scholar] [CrossRef]
- Rahman, M.; Wiklund, J.; Kotzé, R.; Håkansson, U. Yield stress of cement grouts. Tunn. Undergr. Space Technol. 2017, 61, 50–60. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, C.; Zhou, X.; Gao, G.; Feng, X. Full-scale physical modelling of fissure grouting in deep underground rocks. Tunn. Undergr. Space Technol. 2019, 89, 249–261. [Google Scholar] [CrossRef]
- Le Roy, R.; Roussel, N. The marsh cone as a viscometer: Theoretical analysis and practical limits. Mater. Struct. 2005, 38, 25–30. [Google Scholar] [CrossRef]
- Kamalakannan, S.; Thirunavukkarasu, R.; Pillai, R.G.; Santhanam, M. Factors affecting the performance characteristics of cementitious grouts for post-tensioning applications. Constr. Build. Mater. 2018, 180, 681–691. [Google Scholar] [CrossRef]
- He, S.; Lai, J.; Wang, L.; Wang, K. A literature review on properties and applications of grouts for shield tunnel. Constr. Build. Mater. 2020, 239, 117782. [Google Scholar] [CrossRef]
- Mirza, J.; Mirza, M.; Roy, V.; Saleh, K. Basic rheological and mechanical properties of high-volume fly ash grouts. Constr. Build. Mater. 2002, 16, 353–363. [Google Scholar] [CrossRef]
- Widmann, R. International society for rock mechanics commission on rock grouting. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1996, 33, 803–847. [Google Scholar] [CrossRef]
- Lombardi, G.; Don, U.D. Grout slurries—Thick or thin? In Issues in Dam Grouting, Proceedings of the Session Sponsored by the Geotechnical Engineering, Division of the American Society of Civil Engineers in Conjunction with the ASCE, Detroit, MI, USA, 23 October 1985; ASCE: Denver, CO, USA, 1985; pp. 156–164. [Google Scholar]
- Verfel, J. Rock Grouting and Diaphragm Wall Construction; Elsevier Science: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Houlsby, A.C. Construction and Design of Cement Grouting: A Guide to Grouting in Rock Foundations; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Khayat, K.; Yahia, A. Effect of Welan Gum-High-Range Water Reducer Combinations on Rheology of Cement Grout. ACI Mater. J. 1997, 94, 365–372. [Google Scholar]
- Azadi, M.; Taghichian, A.; Taheri, A. Optimization of cement-based grouts using chemical additives. J. Rock Mech. Geotech. Eng. 2017, 9, 623–637. [Google Scholar] [CrossRef]
- Bras, A.; Gião, R.; Lúcio, V.; Chastre, C. Development of an injectable grout for concrete repair and strengthening. Cem. Concr. Compos. 2013, 37, 185–195. [Google Scholar] [CrossRef] [Green Version]
- Mirza, J.; Saleh, K.; Langevin, M.-A.; Mirza, S.; Bhutta, M.A.R.; Tahir, M. Properties of microfine cement grouts at 4 °C, 10 °C and 20 °C. Constr. Build. Mater. 2013, 47, 1145–1153. [Google Scholar] [CrossRef]
- Bohloli, B.; Morgan, E.K.; Grøv, E.; Skjølsvold, O.; Hognestad, H.O. Strength and filtration stability of cement grouts at room and true tunnelling temperatures. Tunn. Undergr. Space Technol. 2018, 71, 193–200. [Google Scholar] [CrossRef]
- He, L.; Hu, S.; Huang, S.; Yang, W.; Wang, J.; Yuan, Y.; Yang, S. Heat flow study at the Chinese Continental Scientific Drilling site: Borehole temperature, thermal conductivity, and radiogenic heat production. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- He, M.; Qian, Q. The Basis of Deep Rock Mechanics; China Science Publishing & Media Ltd.: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Mooney, M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 1951, 6, 162–170. [Google Scholar] [CrossRef]
- Krieger, I.M. A Mechanism for Non-Newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Chong, J.S.; Christiansen, E.B.; Baer, A.D. Rheology of concentrated suspensions. J. Appl. Polym. Sci. 1971, 15, 2007–2021. [Google Scholar] [CrossRef]
- Dabak, T.; Yucel, O. Shear viscosity behavior of highly concentrated suspensions at low and high shear-rates. Rheol. Acta 1986, 25, 527–533. [Google Scholar] [CrossRef]
- Liu, D.-M. Particle packing and rheological property of highly-concentrated ceramic suspensions: φm determination and viscosity prediction. J. Mater. Sci. 2000, 35, 5503–5507. [Google Scholar] [CrossRef]
- Aboulayt, A.; Jaafri, R.; Samouh, H.; El Idrissi, A.C.; Rozière, E.; Moussa, R.; Loukili, A. Stability of a new geopolymer grout: Rheological and mechanical performances of metakaolin-fly ash binary mixtures. Constr. Build. Mater. 2018, 181, 420–436. [Google Scholar] [CrossRef]
- Wong, H.H.C.; Kwan, A.K.H. Packing density of cementitious materials: Part 1—Measurement using a wet packing method. Mater. Struct. 2007, 41, 689–701. [Google Scholar] [CrossRef]
- Koutný, O.; Kratochvíl, J.; Švec, J.; Bednárek, J. Modelling of Packing Density for Particle Composites Design. Procedia Eng. 2016, 151, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Domone, P.; Hsi-Wen, C. Testing of binders for high performance concrete. Cem. Concr. Res. 1997, 27, 1141–1147. [Google Scholar] [CrossRef]
- GB2175. Common Portland Cement; Standards Press of China: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Gupta, S.V. Viscometry for Liquids; Springer: Basel Switzerland, 2014. [Google Scholar]
- Lowry, B.A.; Rice, S.A.; Gray, P. On the Kinetic Theory of Dense Fluids XVII. The Shear Viscosity. J. Chem. Phys. 1964, 40, 3673–3683. [Google Scholar] [CrossRef]
- Fang, H.; Ni, K.; Wu, J.; Li, J.; Huang, L.; Reible, D. The effects of hydrogen bonding on the shear viscosity of liquid water. Int. J. Sediment Res. 2019, 34, 8–13. [Google Scholar] [CrossRef]
- Romagnoli, M.; Leonelli, C.; Kamse, E.; Gualtieri, M.L. Rheology of geopolymer by DOE approach. Constr. Build. Mater. 2012, 36, 251–258. [Google Scholar] [CrossRef]
- Senapati, P.K.; Panda, D.; Parida, A. Predicting Viscosity of Limestone–Water Slurry. J. Miner. Mater. Charact. Eng. 2009, 8, 203–221. [Google Scholar] [CrossRef]
- Lapasin, R.; Grassi, M.; Pricl, S. Rheological modeling of fractal and dense suspensions. Chem. Eng. J. Biochem. Eng. J. 1996, 64, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Zupancic, A.; Lapasin, R.; Kristoffersson, A. Influence of particle concentration on rheological properties of aqueous α-Al2O3 suspensions. J. Eur. Ceram. Soc. 1998, 18, 467–477. [Google Scholar] [CrossRef]
- Xiao, F.; Zhao, Z.; Chen, H. A simplified model for predicting grout flow in fracture channels. Tunn. Undergr. Space Technol. 2017, 70, 11–18. [Google Scholar] [CrossRef]
- Huang, B.; Lu, G.; Liu, P. Cementing technology for slim hole drilling: Part I. Drill. Fluid Completion Fluid 1999, 16, 35–41. (In Chinese) [Google Scholar]
- Baltazar, L.G.; Henriques, F.; Jorne, F.; Cidade, M. Combined effect of superplasticizer, silica fume and temperature in the performance of natural hydraulic lime grouts. Constr. Build. Mater. 2014, 50, 584–597. [Google Scholar] [CrossRef]
- Korosi, A.; Fabuss, B.M. Viscosity of liquid water from 25 to 150 degree. measurements in pressurized glass capillary viscometer. Anal. Chem. 1968, 40, 157–162. [Google Scholar] [CrossRef]
- Ma, S.; Yuan, Y. Theoretical calculation of the coefficient of viscosity of water by non-equilibrium statistical mechanics of simple liquid. Chin. J. Oceanol. Limnol. 1994, 12, 30–41. [Google Scholar]
- ASTM, A. Standard Test Method for Arrhenius Kinetic Constants for Thermally Unstable Materials; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Justnes, H.; Vikan, H. Viscosity of cement slurries as a function of solids content. Annu. Trans. Nord. Rheol. Soc. 2005, 13, 75–82. [Google Scholar]



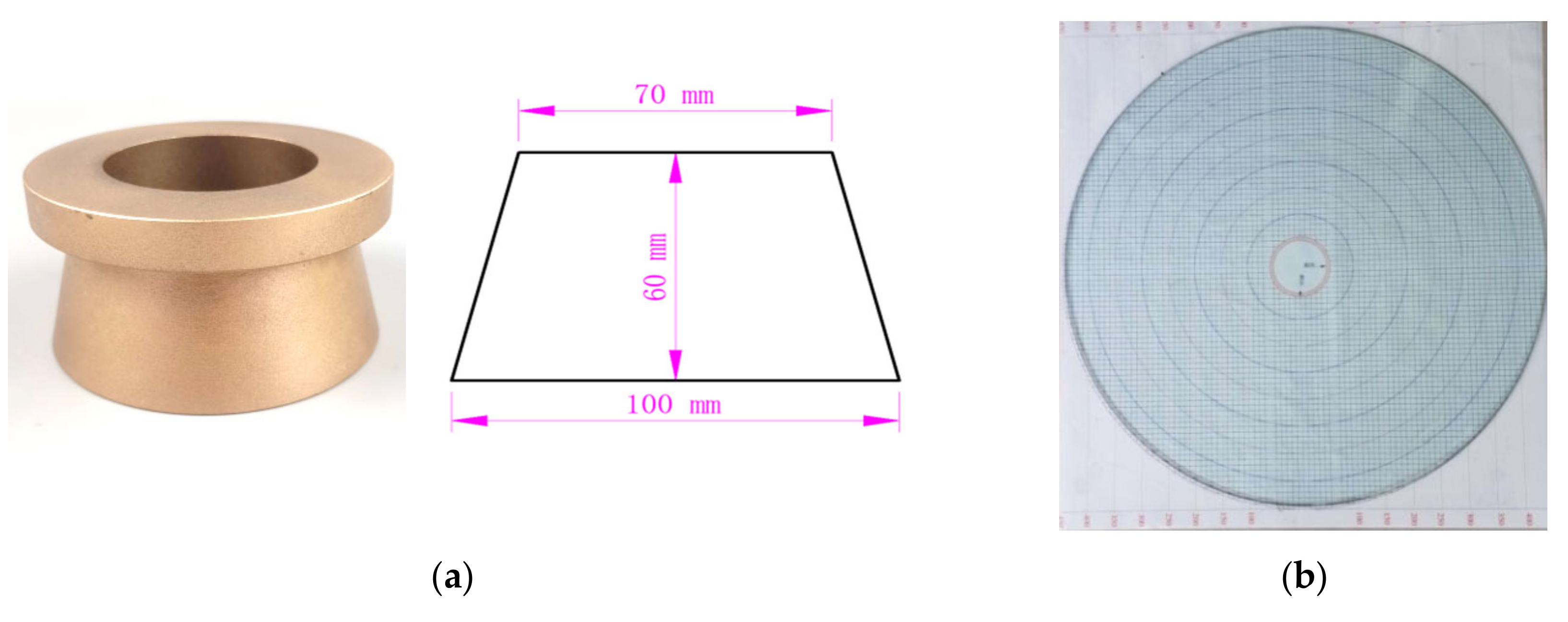














| Chemical Properties | Physical Properties | ||
|---|---|---|---|
| Chemical Composition | Amount (wt.%) | Item | Value |
| CaO | 62.47 | Specific gravity (g/cm3) | 3.11 |
| SiO2 | 20.39 | Blaine fineness (m2/kg) | 387 |
| Al2O3 | 6.23 | Mean grain size D50 (µm) | 19.908 |
| Fe2O3 | 2.87 | Maximum grain size D100 (µm) | 81 |
| MgO | 1.86 | Compressive strength at 3 days (MPa) | 25.8 |
| SO3 | 2.95 | Compressive strength at 28 days (MPa) | 49.5 |
| K2O | 0.64 | ||
| Na2O | 0.25 | ||
| TiO2 | 0.39 | ||
| L.O.I. | 1.95 | ||
| No. | Ratio of Water to Cement (w/c) | Dosage of NaCl (wt.% of Cement) | Dosage of TEA (wt.% of Cement) |
|---|---|---|---|
| 1 | 0.50 | 0.5% | 0.05% |
| 2 | 0.60 | 0.5% | 0.05% |
| 3 | 0.75 | 0.5% | 0.05% |
| 4 | 0.80 | 0.5% | 0.05% |
| 5 | 1.00 | 0.5% | 0.05% |
| 6 | 1.20 | 0.5% | 0.05% |
| 7 | 1.50 | 0.5% | 0.05% |
| Models | Year | Equation |
|---|---|---|
| Mooney’s equation | 1951 | |
| K–D equation | 1959 | |
| Chong et al.’s model | 1971 | |
| Dabak and Yucel’s model | 1986 | |
| Liu’s model | 2000 |
| Temperature | R2 | |
|---|---|---|
| 12 °C | 0.56 | 0.917 |
| 25 °C | 0.54 | 0.916 |
| 35 °C | 0.82 | 0.953 |
| 45 °C | 0.98 | 0.969 |
| Temperature | |
|---|---|
| 12 °C | 0.641 |
| 25 °C | 0.649 |
| 35 °C | 0.549 |
| 45 °C | 0.505 |
| Ratio (w/c) | Ratio of Water to Solid (Vwater/Vpowder) | Volume Fraction of Solid | Temperature (°C) | Measured Viscosity (mPa·s) |
|---|---|---|---|---|
| 0.5 | 1.52 | 0.396 | 12 | 144.44 |
| 25 | 157.22 | |||
| 35 | 187.78 | |||
| 45 | 200.56 | |||
| 0.6 | 1.83 | 0.3534 | 12 | 66.39 |
| 25 | 55.00 | |||
| 35 | 86.11 | |||
| 45 | 96.11 | |||
| 0.75 | 2.29 | 0.3042 | 12 | 19.3 |
| 25 | 15.3 | |||
| 35 | 22.6 | |||
| 45 | 24.7 | |||
| 0.8 | 2.44 | 0.2907 | 12 | 12.0 |
| 25 | 11.8 | |||
| 35 | 11.4 | |||
| 45 | 14.7 | |||
| 1.0 | 3.05 | 0.247 | 12 | 4.2 |
| 25 | 4.65 | |||
| 35 | 6.9 | |||
| 45 | 9.1 | |||
| 1.2 | 3.66 | 0.215 | 12 | 4.75 |
| 25 | 3.5 | |||
| 35 | 3.6 | |||
| 45 | 2.4 | |||
| 1.5 | 4.58 | 0.179 | 12 | 3.15 |
| 25 | 2.4 | |||
| 35 | 2.6 | |||
| 45 | 1.5 |
| Ratio (w/c) | Ratio of Water to Solid (Vwater/Vpowder) | Volume Fraction of Solid | Temperature (°C) | Measured Yield Stress (Pa) |
|---|---|---|---|---|
| 0.5 | 1.52 | 0.396 | 12 | 7.39 |
| 25 | 8.93 | |||
| 35 | 11.9 | |||
| 45 | 12.09 | |||
| 0.6 | 1.83 | 0.3534 | 12 | 3.98 |
| 25 | 3.72 | |||
| 35 | 5.57 | |||
| 45 | 8.29 | |||
| 0.75 | 2.2875 | 0.3042 | 12 | 1.31 |
| 25 | 1.73 | |||
| 35 | 1.75 | |||
| 45 | 3.08 | |||
| 0.8 | 2.44 | 0.2907 | 12 | 1.02 |
| 25 | 1.35 | |||
| 35 | 1.14 | |||
| 45 | 2.01 |
| Temperature (°C/K) | Experiment Value (mPa·s) | Temperature (°C/K) | Experiment Value (mPa·s) | ||
|---|---|---|---|---|---|
| 0 | 273 | 1.794 | 60 | 333 | 0.47 |
| 10 | 283 | 1.31 | 70 | 343 | 0.407 |
| 20 | 293 | 1.009 | 80 | 353 | 0.357 |
| 30 | 303 | 0.8 | 90 | 363 | 0.317 |
| 40 | 313 | 0.654 | 100 | 373 | 0.284 |
| 50 | 323 | 0.549 | |||
| Temperature (°C) | a | n |
|---|---|---|
| 12 | 1.791 | 5.761 |
| 25 | 1.913 | 7.056 |
| 35 | 1.718 | 4.146 |
| 45 | 1.342 | 3.025 |
| Temperature (°C) | Experimental (mPa·s) | Calculated (mPa·s) | Deviation |
|---|---|---|---|
| 12 | 19.3 | 23.4 | +21.5% |
| 25 | 15.3 | 17.6 | +15.3% |
| 35 | 22.6 | 27.1 | +20.6% |
| 45 | 24.7 | 32.1 | +30.8% |
| Temperature (°C) | Equations | Correlation Coefficient |
|---|---|---|
| 12 | 0.854 | |
| 25 | 0.713 | |
| 35 | 0.957 | |
| 45 | 0.941 |
| Temperature (°C) | Equations | Correlation Coefficient |
|---|---|---|
| 12 | 0.946 | |
| 25 | 0.953 | |
| 35 | 0.991 | |
| 45 | 0.997 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Miao, Y.; Wu, H.; Yuan, X.; Liu, C. Estimation of Viscosity and Yield Stress of Cement Grouts at True Ground Temperatures Based on the Flow Spread Test. Materials 2020, 13, 2939. https://doi.org/10.3390/ma13132939
Xu Z, Miao Y, Wu H, Yuan X, Liu C. Estimation of Viscosity and Yield Stress of Cement Grouts at True Ground Temperatures Based on the Flow Spread Test. Materials. 2020; 13(13):2939. https://doi.org/10.3390/ma13132939
Chicago/Turabian StyleXu, Zhipeng, Yichen Miao, Haikuan Wu, Xun Yuan, and Changwu Liu. 2020. "Estimation of Viscosity and Yield Stress of Cement Grouts at True Ground Temperatures Based on the Flow Spread Test" Materials 13, no. 13: 2939. https://doi.org/10.3390/ma13132939




