Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation
Abstract
:1. Introduction
2. Material and Experiment
2.1. Materials Specifications
2.2. Indentation and Fatigue Testing
2.3. Numerical Models
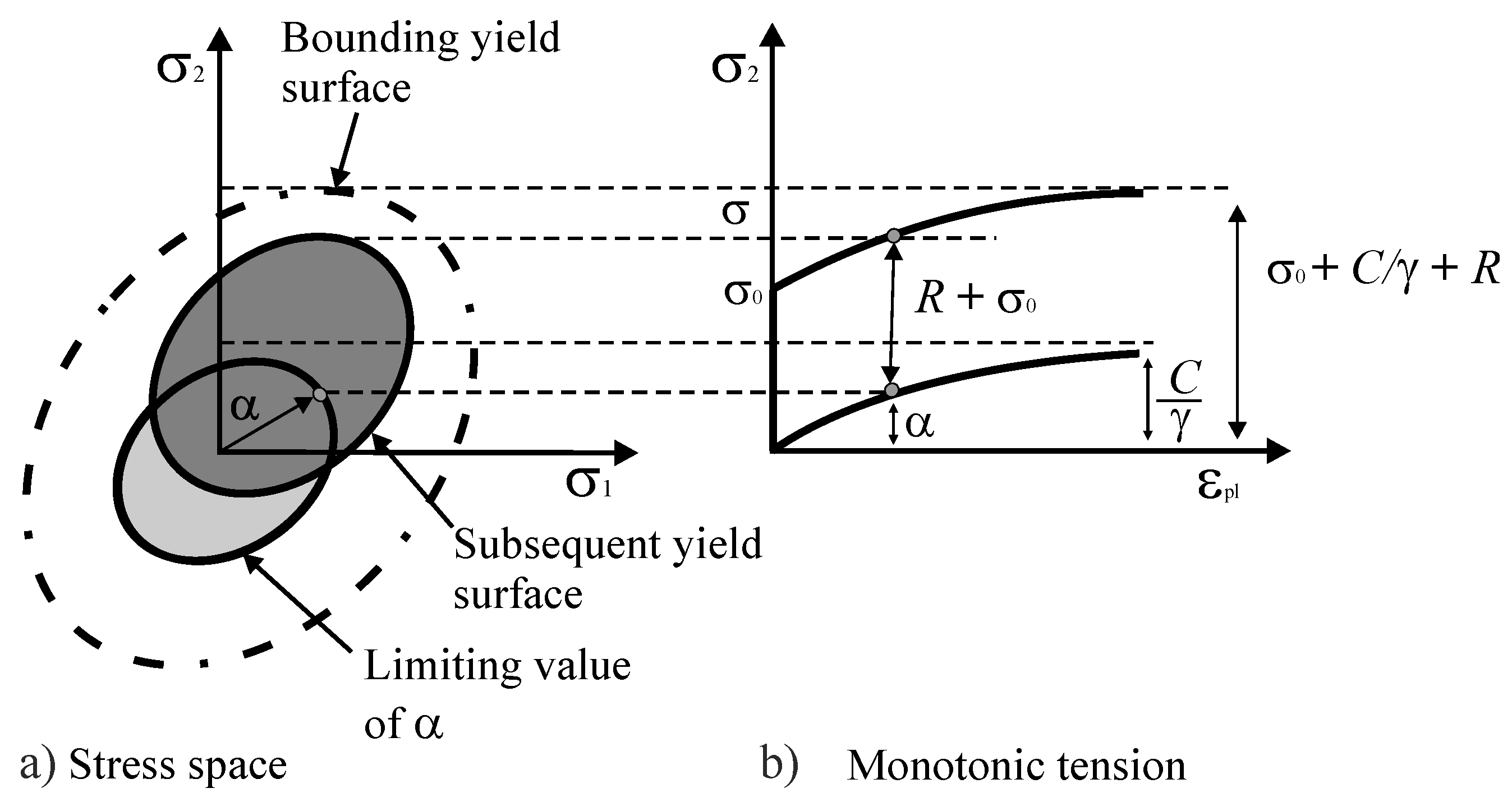
2.4. Material Model
3. Inverse Parameter Identification
4. Results and Discussion
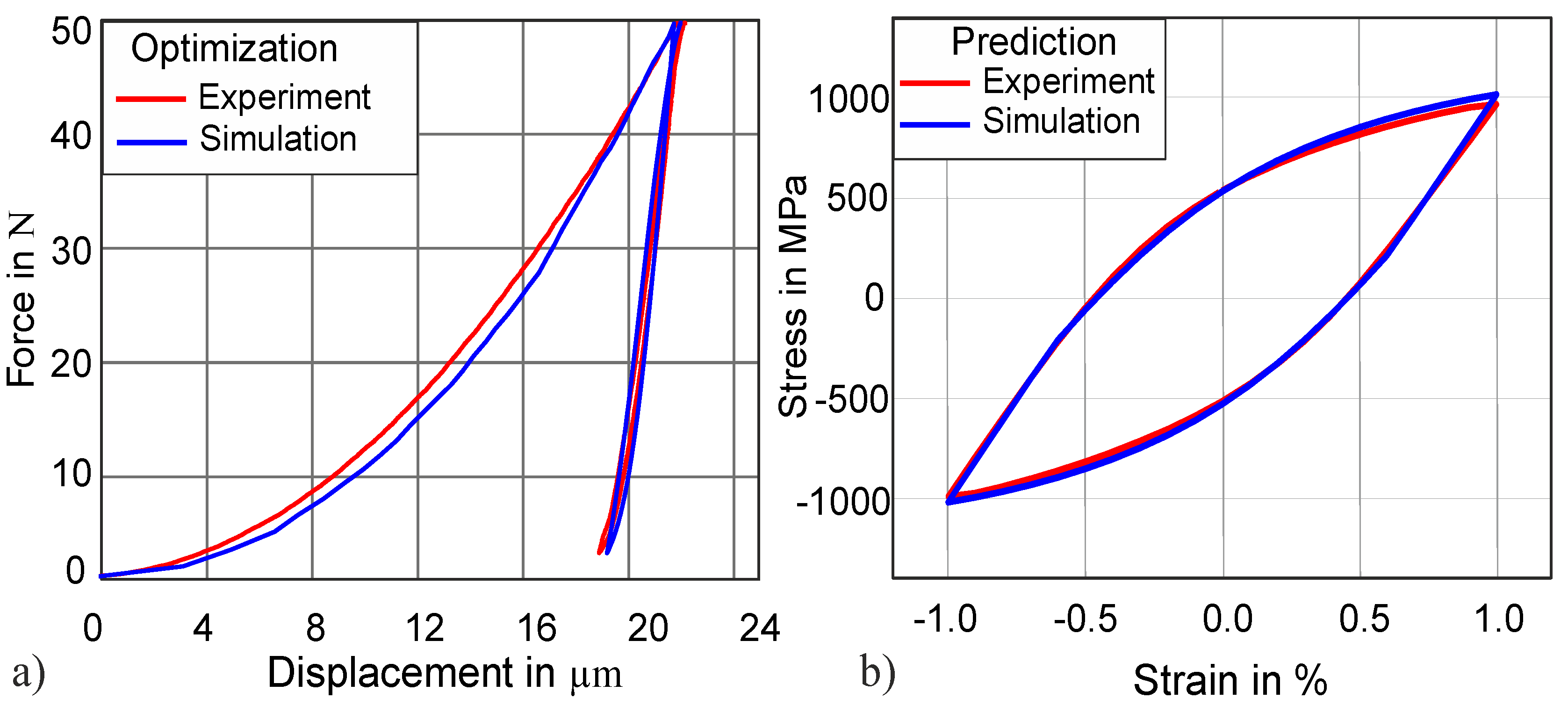
4.1. Method Development
4.2. Validation
4.3. Transferability of the Method
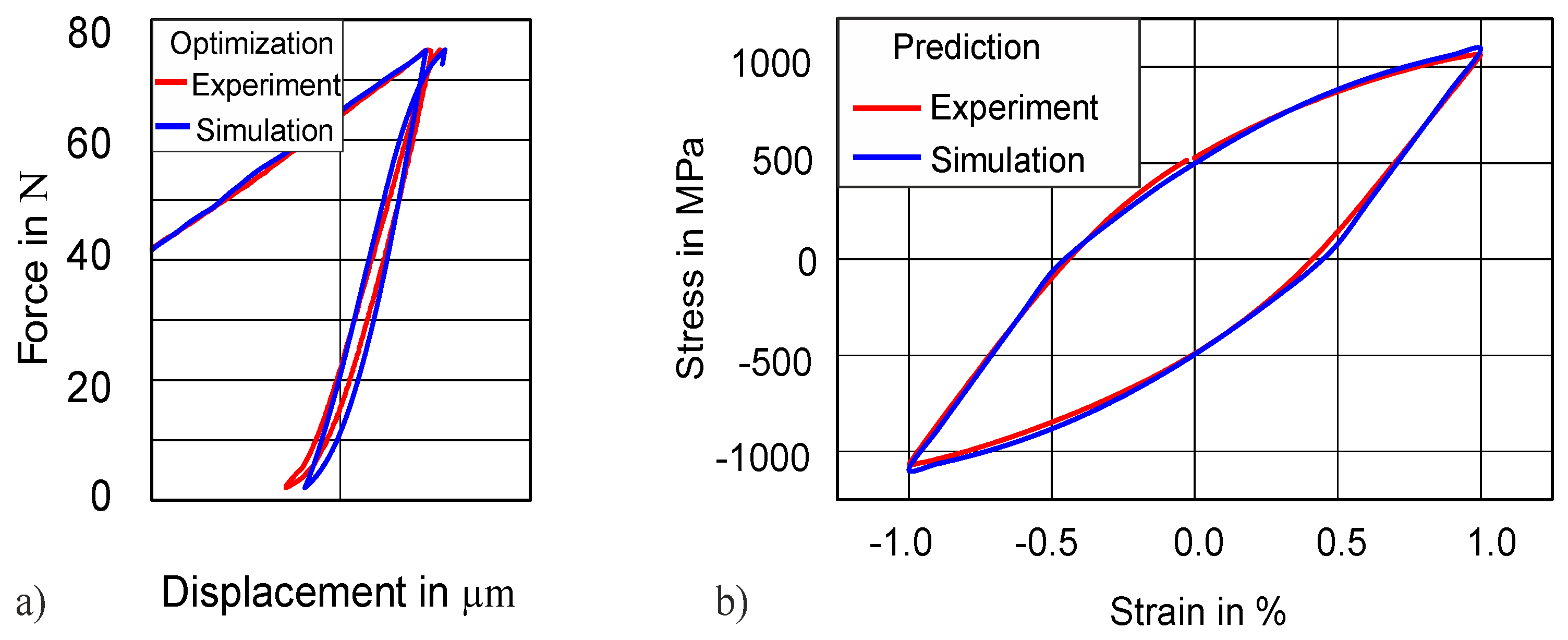
4.3.1. Transferability to Higher Force Amplitude (75 N)
4.3.2. Transferability to Higher Hardness (47 HRC)
4.3.3. Transferability for Other Material (Cu)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huber, N.; Tsakmakis, C. Determination of constitutive properties from spherical indentation data using neural networks. Part I: The case of pure kinematic hardening in plasticity laws. J. Mech. Phys. Solids 1999, 47, 1569–1588. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties from spherical indentation data using neural networks. Part II: Plasticity with nonlinear isotropic and kinematic hardening. J. Mech. Phys. Solids 1999, 47, 1589–1607. [Google Scholar] [CrossRef]
- Wymysłowski, A.; Dowhań, Ł. Application of nanoindentation technique for investigation of elasto-plastic properties of the selected thin film materials. Microelectron. Reliab. 2013, 53, 443–451. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Hyung-Yil, L. Ball Indenter Utilizing Fea Solutions for Property Evaluation. WO2003010515A1, 2002. Available online: https://patents.google.com/patent/WO2003010515A1 (accessed on 10 July 2020).
- Suresch, A.; Alcala, S.; Giannakopoulos, J. Depth Sensing Indentation and Methodology for Mechanical Property Measurements. WO1997039333A2, 1996. Available online: https://patents.google.com/patent/WO1997039333A2 (accessed on 10 July 2020).
- Suresh, T.A.; Dao, S.; Chollacoop, M.; Van, N.; Venkatesh, K.V. Systems and Methods for Estimation and Analysis of Mechanical Property Data. WO2002073162A2, 2002. Available online: https://patents.google.com/patent/WO2002073162A2 (accessed on 10 July 2020).
- Fontanari, V.; Beghini, M.; Bertini, L. Method and Apparatus for Determining Mechanical Features of a Material with Comparison to Reference Database. WO2006013450A2, 2004. Available online: https://patents.google.com/patent/WO2006013450A2/en (accessed on July 10 2020).
- Schmaling, B.; Hartmaier, A. Method for Testing Material, particularly for Hardness Testing, Involves Producing Impression in to Be Tested Material in Experimental Manner with Test Body with Known Geometry and with Known Test Load. DE102011115519A1, 2011. Available online: https://patents.google.com/patent/DE102011115519A1/de (accessed on 10 July 2020).
- Broitman, E. Indentation Hardness Measurements at Macro-, Micro-, and Nanoscale: A Critical Overview. Tribol. Lett. 2017, 65, 23. [Google Scholar] [CrossRef] [Green Version]
- Strzelecki, P. Analytical Method for Determining Fatigue Properties of Materials and Construction Elements in High Cycle Life; Uniwersytet Technologiczno-Przyrodniczy w Bydgoszczy: Bydgoszcz, Poland, 2014. [Google Scholar]
- Murakami, Y. Effects of small defects and nonmetallic inclusions on the fatigue strength of metals. JMSE Int. J. 1989, 32, 167–180. [Google Scholar] [CrossRef] [Green Version]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Developing a full range S-N curve and estimating cumulative fatigue damage of steel elements. Comput. Mater. Sci. 2015, 96, 96–101. [Google Scholar] [CrossRef]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Full range S-N curves for fatigue life evaluation of steels using hardness measurements. Int. J. Fatigue 2016, 82, 325–331. [Google Scholar] [CrossRef]
- Strzelecki, P.; Tomaszewski, T. Analytical models of the S-N curve based on the hardness of the material. Procedia Struct. Integr. 2017, 5, 832–839. [Google Scholar] [CrossRef]
- Lyamkin, V.; Starke, P.; Boller, C. Cyclic indentation as an alternative to classic fatigue evaluation. In Proceedings of the 7th International Symposium on Aircraft Materialsno, Compiegne, France, 24–26 April 2018. [Google Scholar]
- Faisal, N.H.; Prathuru, A.K.; Goel, S.; Ahmed, R.; Droubi, M.G.; Beake, B.D.; Fu, Y.Q. Cyclic Nanoindentation and Nano-Impact Fatigue Mechanisms of Functionally Graded TiN/TiNi Film. Shape Mem. Superelasticity 2017, 3, 149–167. [Google Scholar] [CrossRef] [Green Version]
- Haghshenas, M.; Klassen, R.J.; Liu, S.F. Depth-sensing cyclic nanoindentation of tantalum. Int. J. Refract. Met. Hard Mater. 2017, 66, 144–149. [Google Scholar] [CrossRef]
- Prakash, R.V. Evaluation of fatigue damage in materials using indentation testing and infrared thermography. Trans. Indian Inst. Met. 2010, 63, 173–179. [Google Scholar] [CrossRef]
- Prakash, R.V. Study of Fatigue Properties of Materials through Cyclic Automated Ball Indentation and Cyclic Small Punch Test Methods. Key Eng. Mater. 2017, 734, 273–284. [Google Scholar] [CrossRef]
- Xu, B.X.; Yue, Z.F.; Chen, X. Numerical investigation of indentation fatigue on polycrystalline copper. J. Mater. Res. 2009, 24, 1007–1015. [Google Scholar] [CrossRef]
- Schäfer, B.; Song, X.; Sonnweber-Ribic, P.; Hassan, H.U.; Hartmaier, A. Micromechanical Modelling of the Cyclic Deformation Behavior of Martensitic SAE 4150—A Comparison of Different Kinematic Hardening Models. Metals (Basel) 2019, 9, 368. [Google Scholar] [CrossRef] [Green Version]
- Kramer, H.S.; Starke, P.; Klein, M.; Eifler, D. Cyclic hardness test PHYBALCHT - Short-time procedure to evaluate fatigue properties of metallic materials. Int. J. Fatigue 2014, 63, 78–84. [Google Scholar] [CrossRef]
- DIN EN ISO 6507-2. Metallic Materials—Vickers Hardness Test—Part 2: Verification and Calibration of Testing Machines; NSAI: Dublin, Ireland, 2005. [Google Scholar]
- Mises, R.V. Mechanik der festen Körper im plastisch- deformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1913, 1913, 582–592. [Google Scholar]
- Srnec Nova, J.; Benasciutti, D.; De Bona, F.; Stanojević, A.; De Luca, A.; Raffaglio, Y. Estimation of Material Parameters in Nonlinear Hardening Plasticity Models and Strain Life Curves for CuAg Alloy. IOP Conf. Ser. Mater. Sci. Eng. 2016, 119, 12020. [Google Scholar] [CrossRef]
- Chaboche, J.L.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Frederick, C.O.; Armstrong, P.J. A mathematical representation of the multiaxial Bauschinger effect. Mater. High Temp. 2007, 24, 1–26. [Google Scholar] [CrossRef]
- Sajjad, H.M.; Hanke, S.; Güler, S.; ul Hassan, H.; Fischer, A.; Hartmaier, A. Modelling cyclic behaviour of martensitic steel with J2 plasticity and crystal plasticity. Materials 2019, 12, 1767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- About LS-OPT—DYNAmore GmbH. Available online: https://www.dynamore.de/de/produkte/opt/ls-opt (accessed on 26 April 2020).
- Chaparro, B.M.; Thuillier, S.; Menezes, L.F.; Manach, P.Y.; Fernandes, J.V. Material parameters identification: Gradient-based, genetic and hybrid optimization algorithms. Comput. Mater. Sci. 2008, 44, 339–346. [Google Scholar] [CrossRef] [Green Version]










| Symbol | Value |
|---|---|
| C1 (MPa) | 262,197 |
| γ1 | 373 |
| C2 (MPa) | 4714 |
| γ2 | 0.25 |
| Q (MPa) | −575 |
| b | 262 |
| Symbol | Value |
|---|---|
| C1 (MPa) | 257,503 |
| γ1 | 354 |
| C2 (MPa) | 3663 |
| γ2 | 0.2837 |
| Q (MPa) | −611 |
| b | 163 |
| Symbol | Value |
|---|---|
| C1 (MPa) | 337,885 |
| γ1 | 374 |
| C2 (MPa) | 6681 |
| γ2 | 2.3 |
| Q (MPa) | −724 |
| b | 273 |
| Symbol. | Value |
|---|---|
| C1 (MPa) | 154,790 |
| γ1 | 2,257 |
| C2 (MPa) | 11,586 |
| γ2 | 82 |
| Q (MPa) | −12 |
| b | 47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajjad, H.M.; ul Hassan, H.; Kuntz, M.; Schäfer, B.J.; Sonnweber-Ribic, P.; Hartmaier, A. Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation. Materials 2020, 13, 3126. https://doi.org/10.3390/ma13143126
Sajjad HM, ul Hassan H, Kuntz M, Schäfer BJ, Sonnweber-Ribic P, Hartmaier A. Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation. Materials. 2020; 13(14):3126. https://doi.org/10.3390/ma13143126
Chicago/Turabian StyleSajjad, Hafiz Muhammad, Hamad ul Hassan, Matthias Kuntz, Benjamin J. Schäfer, Petra Sonnweber-Ribic, and Alexander Hartmaier. 2020. "Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation" Materials 13, no. 14: 3126. https://doi.org/10.3390/ma13143126
APA StyleSajjad, H. M., ul Hassan, H., Kuntz, M., Schäfer, B. J., Sonnweber-Ribic, P., & Hartmaier, A. (2020). Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation. Materials, 13(14), 3126. https://doi.org/10.3390/ma13143126









