Rigid Finite Element Method in Modeling Composite Steel-Polymer Concrete Machine Tool Frames
Abstract
:1. Introduction
2. Materials and Methods
2.1. Steel-Polymer Concrete Frame
2.2. Static Tests of Polymer Concrete
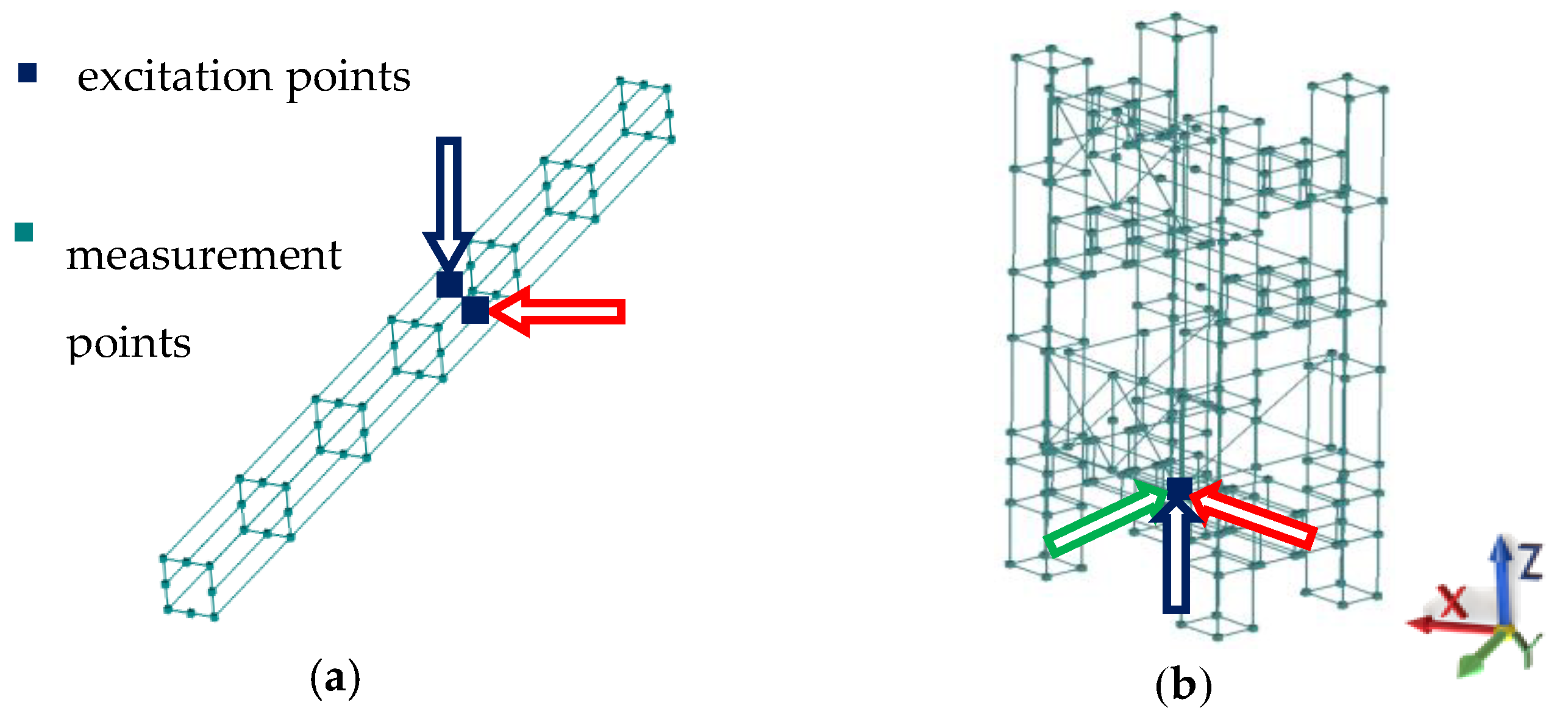
2.3. Dynamic Experimental Tests of the Basic Structural Component and Frame
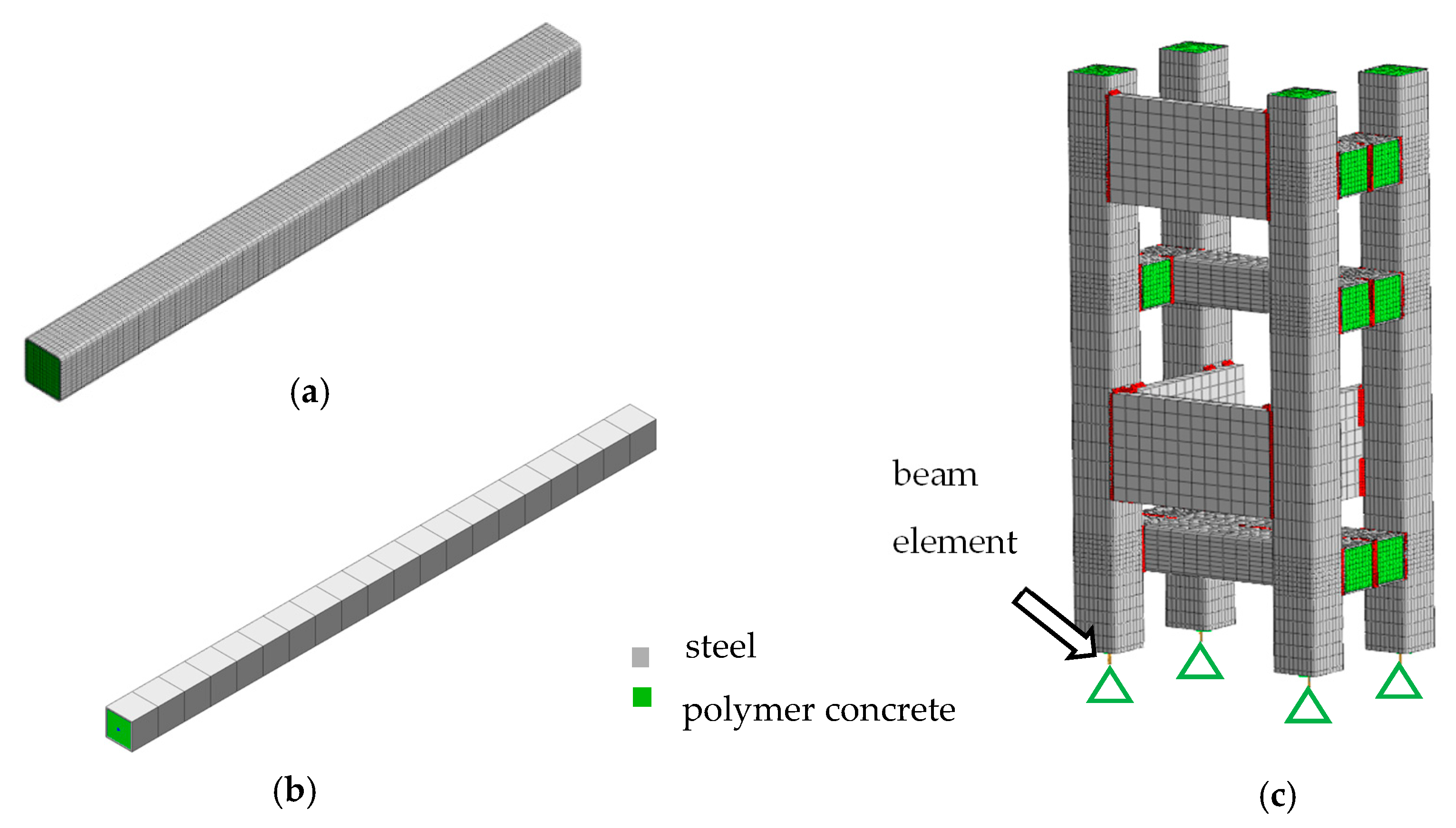
2.4. Finite Element Modeling
3. Rigid Finite Element Modeling
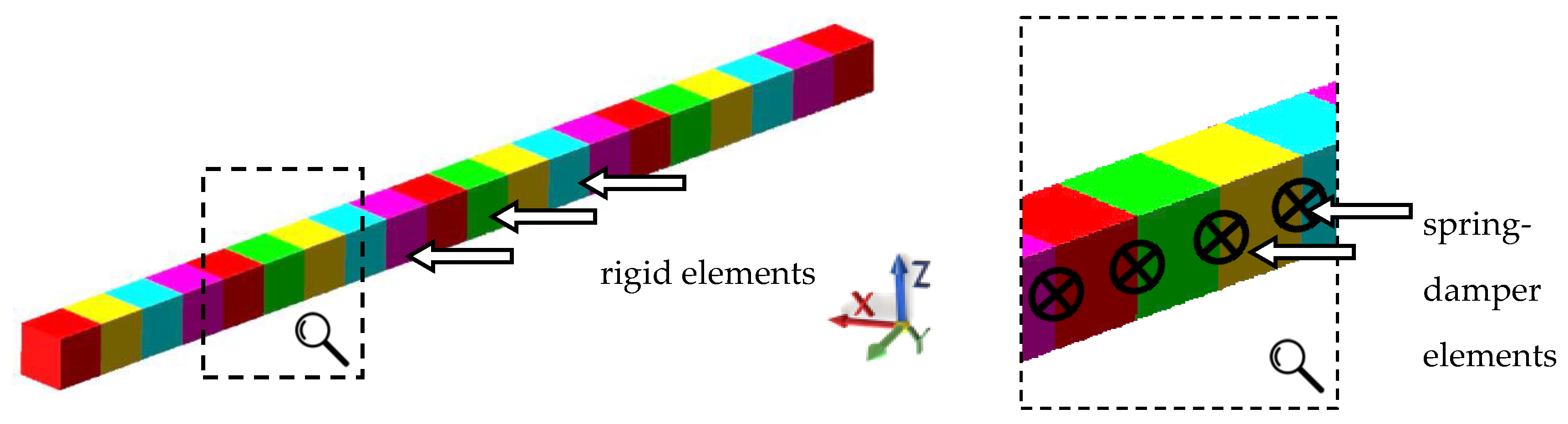
3.1. Rigid Finite Element Model of the Basic Structural Component
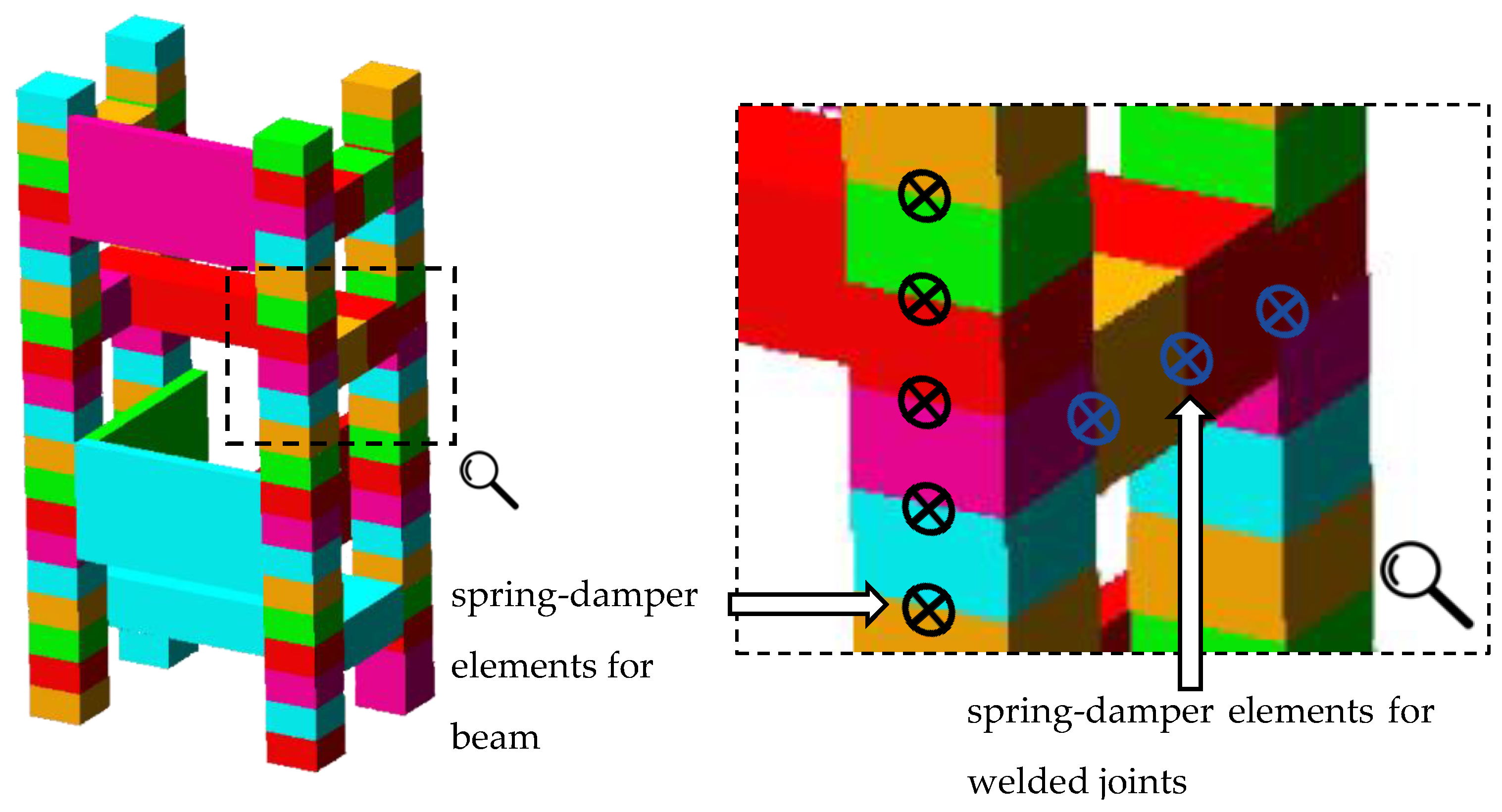
3.2. Rigid Finite Element Model of the Steel-Polymer Concrete Body
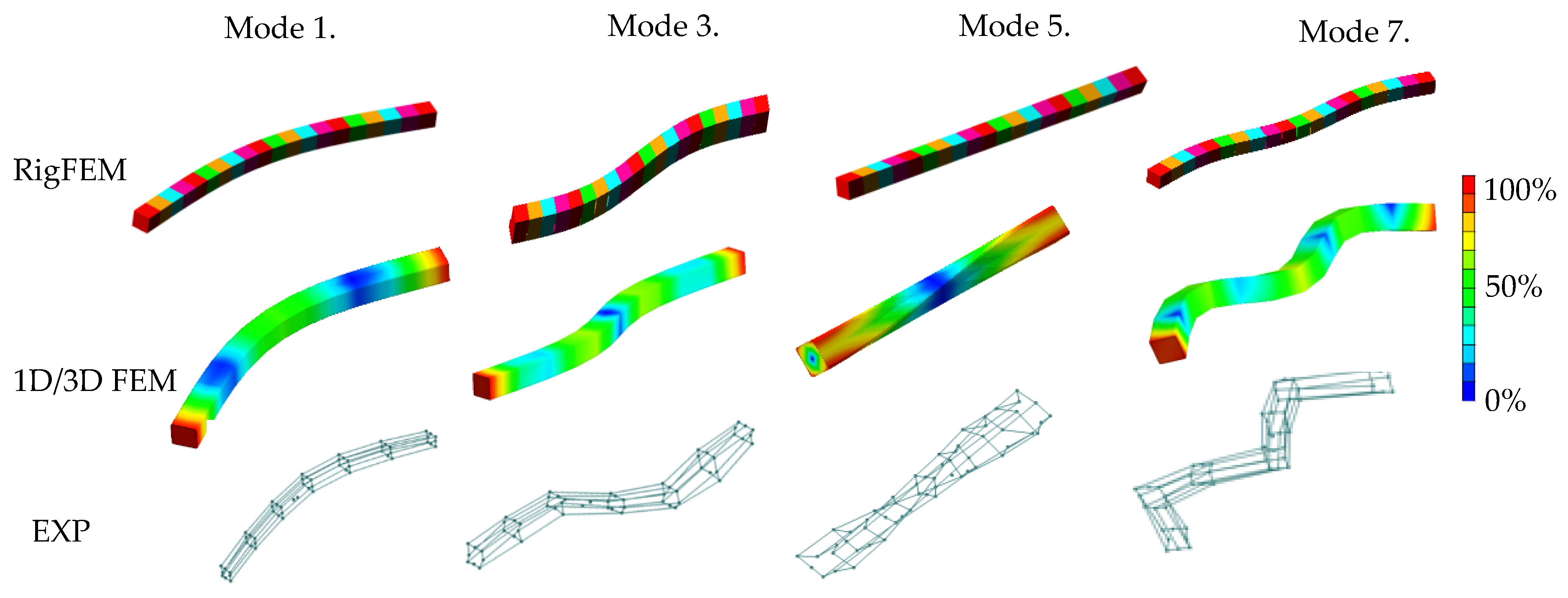
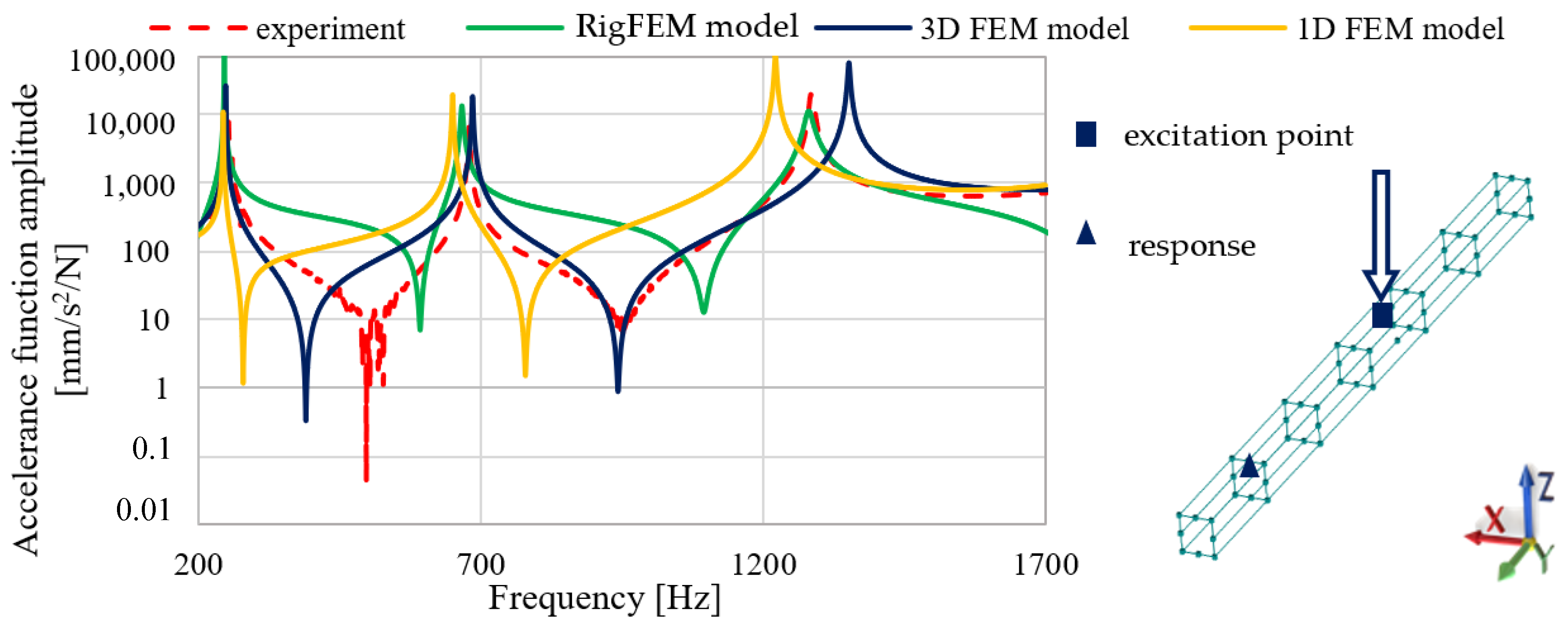
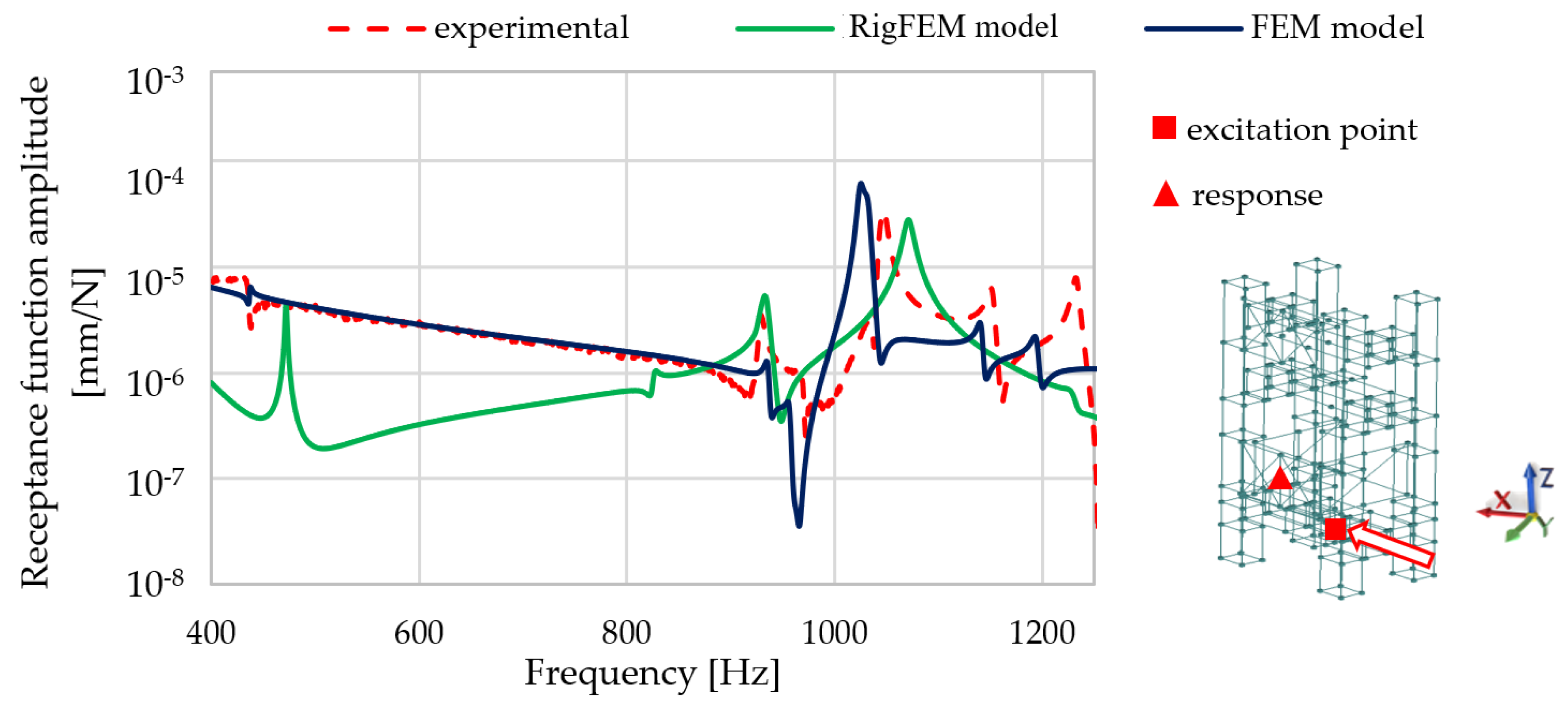
3.3. Comparison of the Results of Model Calculations of the Basic Structural Component with the Results of the Experimental Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chybowska, D.; Chybowski, L. A Review of TRIZ Tools for Forecasting the Evolution of Technical Systems. Manag. Syst. Prod. Eng. 2019, 27, 174–182. [Google Scholar] [CrossRef] [Green Version]
- Jasiewicz, M.; Miądlicki, K. Implementation of an algorithm to prevent chatter vibration in a CNC system. Materials 2019, 12, 3193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Powałka, B.; Okulik, T. Influence of application of special casting compound on dynamic characteristics of the guideway system. J. Mach. Eng. 2010, 10, 71–81. [Google Scholar]
- Kim, M.; Kim, J.; Lee, M.; Lee, S.-K. Surface finish improvement using a damping-alloy sleeve-insert tool holder in the end milling process. Int. J. Adv. Manuf. Technol. 2020, 106, 2433–2449. [Google Scholar] [CrossRef]
- Chodnicki, M.; Kaliński, K.J.; Galewski, M.A. Vibration surveillance during milling flexible details with the use of active optimal control. J. Low Freq. Noise Vib. Act. Control 2013, 32, 145–155. [Google Scholar] [CrossRef]
- Kaliński, K.J.; Galewski, M.A. A modified method of vibration surveillance by using the optimal control at energy performance index. Mech. Syst. Signal Process. 2015, 58, 41–52. [Google Scholar] [CrossRef]
- Hernandez-Vazquez, J.-M.; Garitaonandia, I.; Fernandes, M.H.; Muñoa, J.; de Lacalle, L.N.L. A consistent procedure using response surface methodology to identify stiffness properties of connections in machine tools. Materials 2018, 11, 1220. [Google Scholar] [CrossRef] [Green Version]
- Mahendrakumar, N.; Thyla, P.R.; Mohanram, P.V.; Raja Kumaran, C.; Jayachandresh, J. Study on static and dynamic characteristics of nettle–polyester composite micro lathe bed. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 141–155. [Google Scholar] [CrossRef]
- Möhring, H.-C. Composites in production machines. Procedia CIRP 2017, 66, 2–9. [Google Scholar] [CrossRef]
- Möhring, H.-C.; Brecher, C.; Abele, E.; Fleischer, J.; Bleicher, F. Materials in machine tool structures. CIRP Ann. 2015, 64, 725–748. [Google Scholar]
- Murugan, S.; Thyla, P.R. Mechanical and dynamic properties of alternate materials for machine tool structures: A review. J. Reinf. Plast. Compos. 2018, 37, 1456–1467. [Google Scholar] [CrossRef]
- Rangasamy, S.; Loganathan, K.; Natesan, A. Experimental investigation and numerical analysis of the dynamic characteristics of a laminated hybrid composite bed. Polym. Compos. 2017, 38, 20–26. [Google Scholar] [CrossRef]
- Cortés, F.; Castillo, G. Comparison between the dynamical properties of polymer concrete and grey cast iron for machine tool applications. Mater. Des. 2007, 28, 1461–1466. [Google Scholar] [CrossRef]
- Aggogeri, F.; Borboni, A.; Merlo, A.; Pellegrini, N.; Ricatto, R. Vibration damping analysis of lightweight structures in machine tools. Materials 2017, 10, 297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Do Suh, J. Thermal characteristics of composite sandwich structures for machine tool moving body applications. Compos. Struct. 2004, 66, 429–438. [Google Scholar] [CrossRef]
- Do Suh, J.; Kim, H.S.; Kim, J.M. Design and manufacture of composite high speed machine tool structures. Compos. Sci. Technol. 2004, 64, 1523–1530. [Google Scholar]
- Hwang, H.Y.; Lee, H.G. Clamping effects on the dynamic characteristics of composite machine tool structures. Compos. Struct. 2004, 66, 399–407. [Google Scholar] [CrossRef]
- Kim, D.I.; Jung, S.C.; Lee, J.E.; Chang, S.H. Parametric study on design of composite–foam–resin concrete sandwich structures for precision machine tool structures. Compos. Struct. 2006, 75, 408–414. [Google Scholar] [CrossRef]
- Kroll, L.; Blau, P.; Wabner, M.; Frieß, U.; Eulitz, J.; Klärner, M. Lightweight components for energy-efficient machine tools. CIRP J. Manuf. Sci. Technol. 2011, 4, 148–160. [Google Scholar] [CrossRef]
- Kulisek, V.; Janota, M.; Ruzicka, M.; Vrba, P. Application of fibre composites in a spindle ram design. J. Mach. Eng. 2013, 13, 7–23. [Google Scholar]
- Suh, J.D.; Lee, D.G.; Kegg, R. Composite machine tool structures for high speed milling machines. CIRP Ann. 2002, 51, 285–288. [Google Scholar] [CrossRef]
- Gao, X.; Qin, Z.; Guo, Y.; Wang, M.; Zan, T. Adaptive Method to Reduce Thermal Deformation of Ball Screws Based on Carbon Fiber Reinforced Plastics. Materials 2019, 12, 3113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suh, J.D.; Lee, D.G. Design and manufacture of hybrid polymer concrete bed for high-speed CNC milling machine. Int. J. Mech. Mater. Des. 2008, 4, 113–121. [Google Scholar] [CrossRef]
- Sonawane, H.; Subramanian, T. Improved Dynamic Characteristics for Machine Tools Structure Using Filler Materials. Procedia CIRP 2017, 58, 399–404. [Google Scholar] [CrossRef]
- Cho, S.-K.; Kim, H.-J.; Chang, S.-H. The application of polymer composites to the table-top machine tool components for higher stiffness and reduced weight. Compos. Struct. 2011, 93, 492–501. [Google Scholar] [CrossRef]
- Venugopal, P.R.; Kalayarasan, M.; Thyla, P.R.; Mohanram, P.V.; Nataraj, M.; Mohanraj, S.; Sonawane, H. Structural investigation of steel-reinforced epoxy granite machine tool column by finite element analysis. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 2267–2279. [Google Scholar] [CrossRef]
- Venugopal, P.R.; Dhanabal, P.; Thyla, P.R.; Mohanraj, S.; Nataraj, M.; Ramu, M.; Sonawane, H. Design and analysis of epoxy granite vertical machining centre base for improved static and dynamic characteristics. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 481–495. [Google Scholar] [CrossRef]
- Mahendrakumar, N.; Thyla, P.R.; Mohanram, P.V.; Ramu, M.; Prabhu Raja, V.; Raja Kumaran, C.; Manojkumar, K.N.; Siddarth, A. Enhancement of Static and Dynamic Characteristics on Micro-lathe Bed by the Use of Alternate Form Design and Composite Materials. In Proceedings of the Advances in Simulation, Product Design and Development, Chennai, India, 13–15 December 2018; Shunmugam, M.S., Kanthababu, M., Eds.; Springer: Singapore, 2020; pp. 611–621. [Google Scholar]
- Wittbrodt, E.; Adamiec-Wójcik, I.; Wojciech, S. Dynamics of Flexible Multibody Systems: Rigid Finite Element Method; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 3-540-32352-X. [Google Scholar]
- Kono, D.; Lorenzer, T.; Weikert, S.; Wegener, K. Evaluation of modelling approaches for machine tool design. Precis. Eng. 2010, 34, 399–407. [Google Scholar] [CrossRef] [Green Version]
- Zaeh, M.; Siedl, D. A new method for simulation of machining performance by integrating finite element and multi-body simulation for machine tools. CIRP Ann. 2007, 56, 383–386. [Google Scholar] [CrossRef]
- Dunaj, P.; Berczyński, S.; Chodźko, M.; Niesterowicz, B. Finite Element Modeling of the Dynamic Properties of Composite Steel–Polymer Concrete Beams. Materials 2020, 13, 1630. [Google Scholar] [CrossRef] [Green Version]
- Peeters, B.; Van der Auweraer, H.; Guillaume, P.; Leuridan, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Dunaj, P.; Berczyński, S.; Chodźko, M. Method of modeling steel-polymer concrete frames for machine tools. Compos. Struct. 2020, 242, 112197. [Google Scholar] [CrossRef]
- Midas, I.T. User’s Manual of Midas NFX; MIDAS IT: Seongnam, Korea, 2011. [Google Scholar]
- Nozdrzykowski, K.; Chybowski, L.; Dorobczyński, L. Model-based estimation of the reaction forces in an elastic system supporting large-size crankshafts during measurements of their geometric quantities. Measurement 2020, 155, 107543. [Google Scholar] [CrossRef]
- Adamiec-Wójcik, I.; Drąg, Ł.; Metelski, M.; Nadratowski, K.; Wojciech, S. A 3D model for static and dynamic analysis of an offshore knuckle boom crane. Appl. Math. Model. 2019, 66, 256–274. [Google Scholar] [CrossRef]
- Adamiec-Wójcik, I.; Drąg, Ł.; Wojciech, S. A new approach to the rigid finite element method in modeling spatial slender systems. Int. J. Struct. Stab. Dyn. 2018, 18, 1850017. [Google Scholar] [CrossRef]
- Neumark, S. Concept of Complex Stiffness Applied to Problems of Oscillations with Viscous and Hysteretic Damping; HM Stationery Office: London, UK, 1962. [Google Scholar]
- Holanda, S.A.; Silva, A.A.; de Araújo, C.J.; de Aquino, A.S. Study of the complex stiffness of a vibratory mechanical system with shape memory alloy coil spring actuator. Shock Vib. 2014, 2014, 162781. [Google Scholar] [CrossRef] [Green Version]
- Adams, M. ADAMS User’s Manual; MacNeal-Schwendler Inc.: Oakdale, IA, USA, 2001. [Google Scholar]
- Niesterowicz, B.; Dunaj, P.; Berczyński, S. Timoshenko beam model for vibration analysis of composite steel-polymer concrete box beams. J. Theor. Appl. Mech. 2020, 58, 799–810. [Google Scholar] [CrossRef]
- Dunaj, P.; Dolata, M.; Berczyński, S. Model Order Reduction Adapted to Steel Beams Filled with a Composite Material. In Proceedings of the International Conference on Information Systems Architecture and Technology, Nysa, Poland, 16–18 September 2018; Springer: Cham, Switzerland, 2018; pp. 3–13. [Google Scholar]
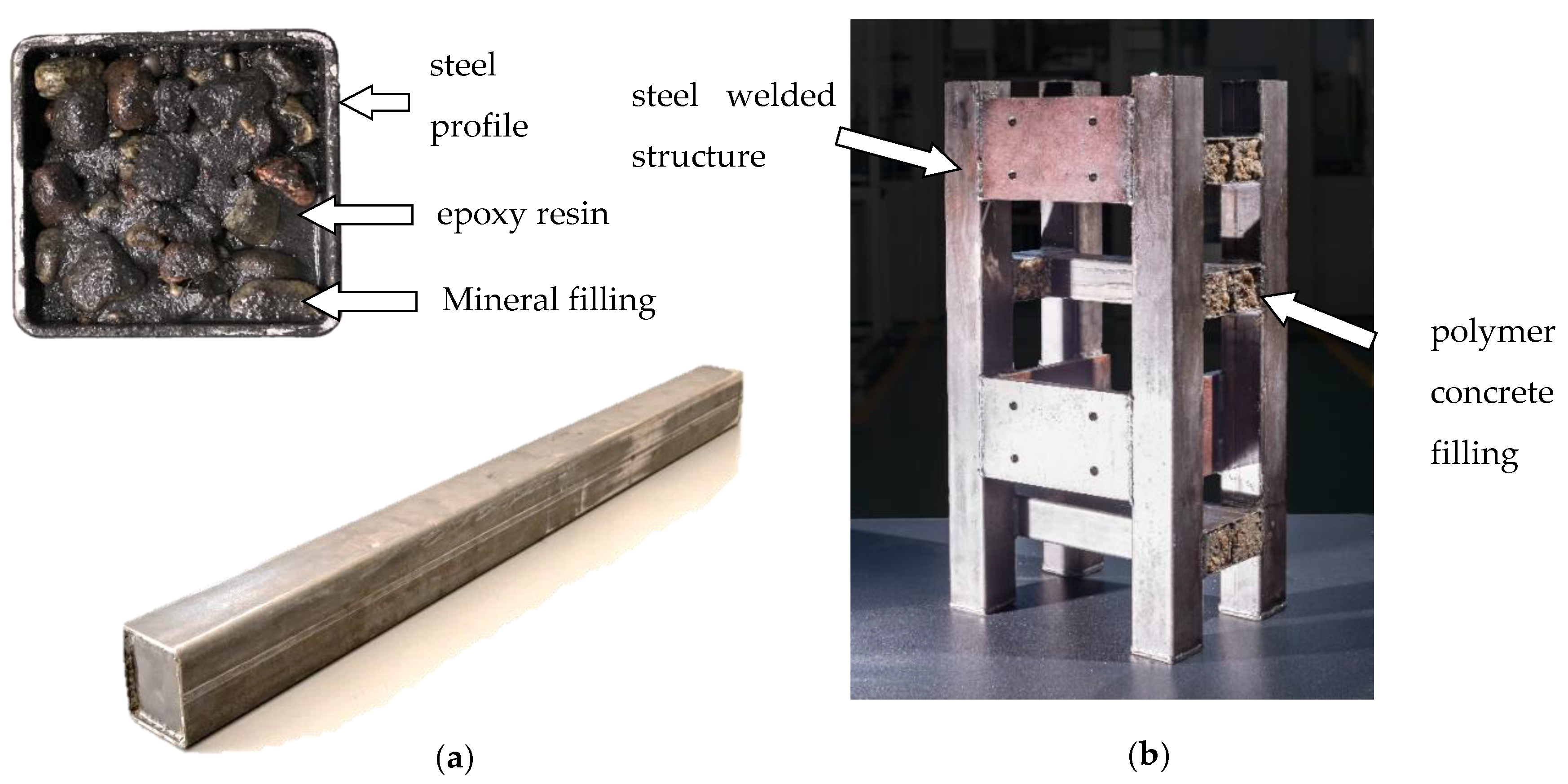

| Component | Epoxy Resin | Ash | Fine Fraction (0.25–2 mm) | Medium Fraction (2–10 mm) | Coarse Fraction (8–16 mm) |
|---|---|---|---|---|---|
| Percentage share of component weight | 15% | 1% | 19% | 15% | 50% |
| Parameter | Steel | Polymer Concrete |
|---|---|---|
| Young’s modulus E | 210 ± 5 GPa | 16.8 ± 0.2 GPa |
| Poisson’s ratio ν | 0.28 ± 0.03 | 0.20 ± 0.05 |
| Density ρ | 7487 ± 35 kg/m3 | 2118 ± 6 kg/m3 |
| Parameter | Value |
|---|---|
| Sampling rate | 4096 Hz |
| Frequency resolution | 0.5 Hz |
| Signal acquisition time | 2 s |
| Frequency response function estimator | H1 |
| Number of averages | 10 |
| Scaling of the frequency response function | global |
| Parameter | Steel | Polymer Concrete |
|---|---|---|
| Loss factor | 0.00220 ± 0.00005 | - |
| Equivalent loss factor | 0.00480 ± 0.00024 | |
| Mode Number | Experimental Results | RigFEM Results | Relative Error δRigFEM | 3D FEM Results | Relative Error δ3D-FEM | 1D FEM Results | Relative Error δ1D-FEM |
|---|---|---|---|---|---|---|---|
| 1 | 247 Hz | 244 Hz | ~1% | 248 Hz | <1% | 243 Hz | <2% |
| 2 | 251 Hz | 245 Hz | ~2% | 248 Hz | ~1% | 243 Hz | <2% |
| 3 | 676 Hz | 664 Hz | ~2% | 685 Hz | ~1% | 650 Hz | ~4% |
| 4 | 678 Hz | 665 Hz | ~2% | 685Hz | ~1% | 650 Hz | <4% |
| 5 | 1276 Hz | 1224 Hz | ~4% | 1241 Hz | <3% | 1184 Hz | ~7% |
| 6 | 1282 Hz | 1275 Hz | <1% | 1326 Hz | ~3% | 1223 Hz | <5 |
| 7 | 1282 Hz | 1275 Hz | <1% | 1326 Hz | ~3% | 1223 Hz | <5 |
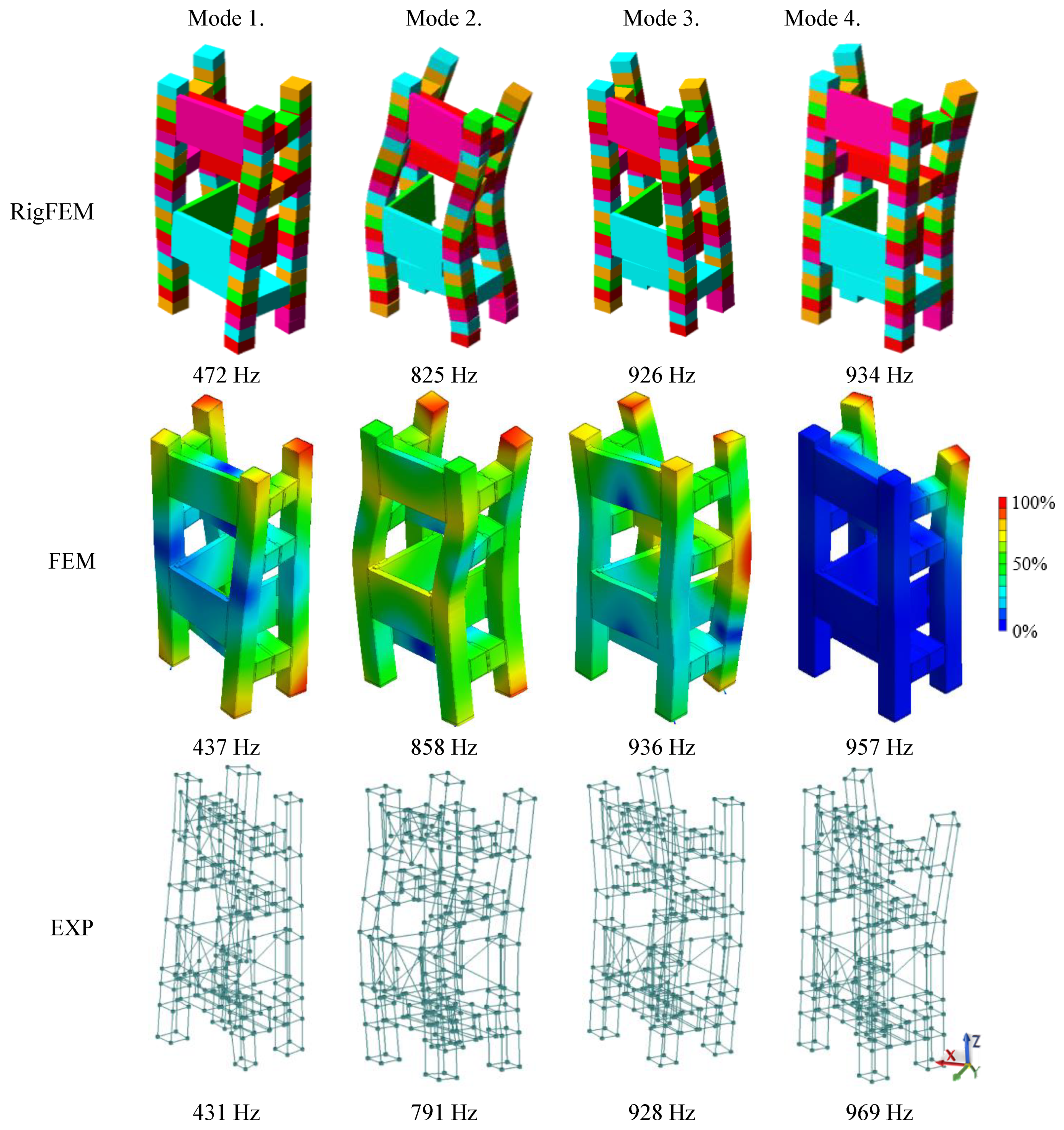
| Mode Number | Experimental Results | RigFEM Results | Relative Error δRigFEM | FEM Results | Relative Error δFEM |
|---|---|---|---|---|---|
| 1 | 431 Hz | 472 Hz | ~9% | 437 Hz | <1% |
| 2 | 791 Hz | 825 Hz | ~4% | 858 Hz | <9% |
| 3 | 928 Hz | 926 Hz | <1% | 936 Hz | <1% |
| 4 | 969 Hz | 934 HZ | ~4% | 957 Hz | ~1% |
| 5 | 1041 Hz | 1070 Hz | <3% | 1032 Hz | <1% |
| 6 | 1151 Hz | 1230 Hz | <7% | 1141 Hz | <1% |
| 7 | 1232 Hz | 1372 Hz | ~11% | 1195 Hz | ~3% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunaj, P.; Marchelek, K.; Berczyński, S.; Mizrak, B. Rigid Finite Element Method in Modeling Composite Steel-Polymer Concrete Machine Tool Frames. Materials 2020, 13, 3151. https://doi.org/10.3390/ma13143151
Dunaj P, Marchelek K, Berczyński S, Mizrak B. Rigid Finite Element Method in Modeling Composite Steel-Polymer Concrete Machine Tool Frames. Materials. 2020; 13(14):3151. https://doi.org/10.3390/ma13143151
Chicago/Turabian StyleDunaj, Paweł, Krzysztof Marchelek, Stefan Berczyński, and Berkay Mizrak. 2020. "Rigid Finite Element Method in Modeling Composite Steel-Polymer Concrete Machine Tool Frames" Materials 13, no. 14: 3151. https://doi.org/10.3390/ma13143151
APA StyleDunaj, P., Marchelek, K., Berczyński, S., & Mizrak, B. (2020). Rigid Finite Element Method in Modeling Composite Steel-Polymer Concrete Machine Tool Frames. Materials, 13(14), 3151. https://doi.org/10.3390/ma13143151






