Research on the Reasonable Grouting Strength of Rock-Like Samples in Different Strengths
Abstract
:1. Introduction
2. Samples Preparation and Experiment Schemes
2.1. Design and Preparation of the Structural Plane of Samples
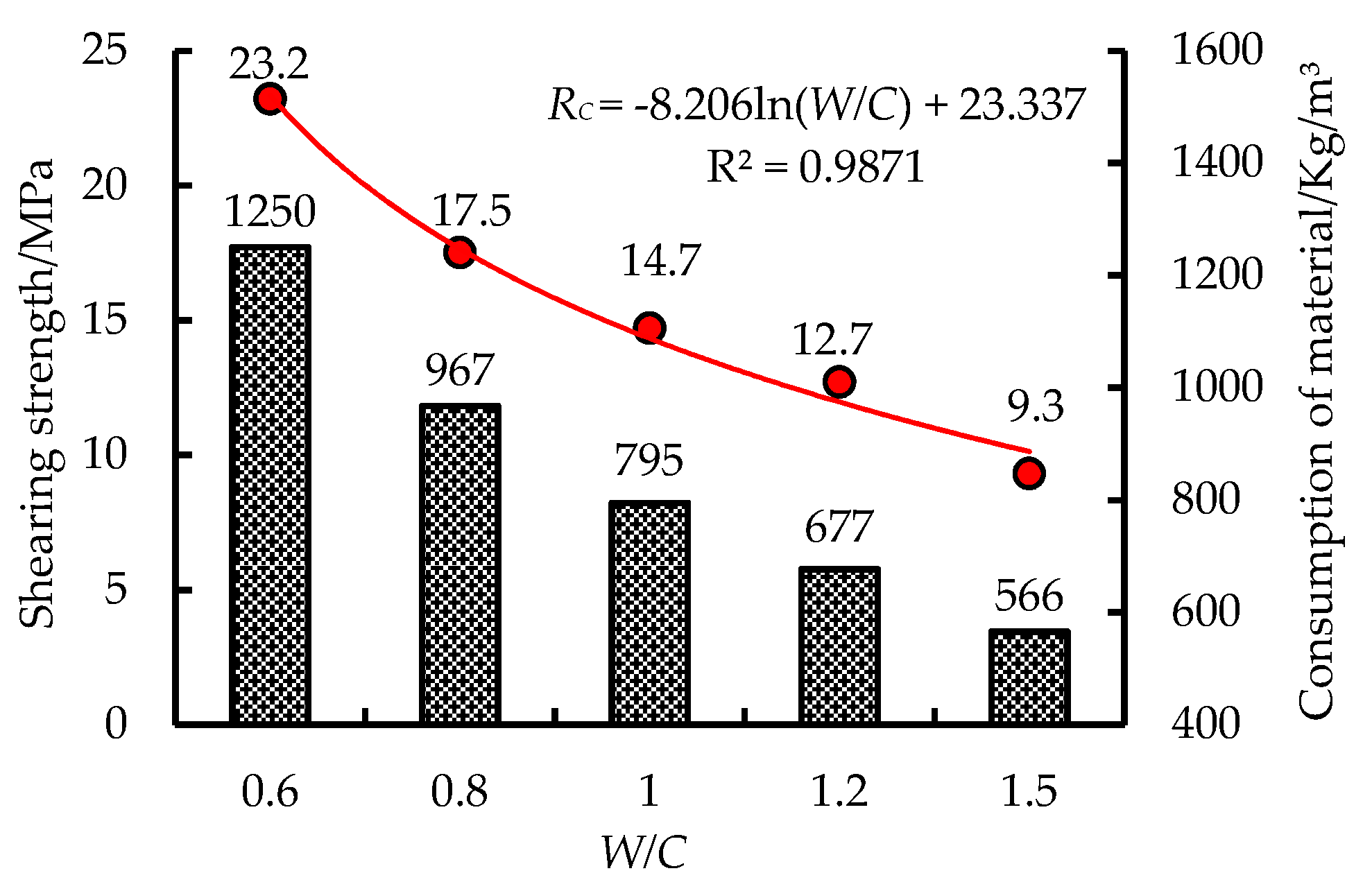
2.2. Inorganic Double Liquid Grouting Material
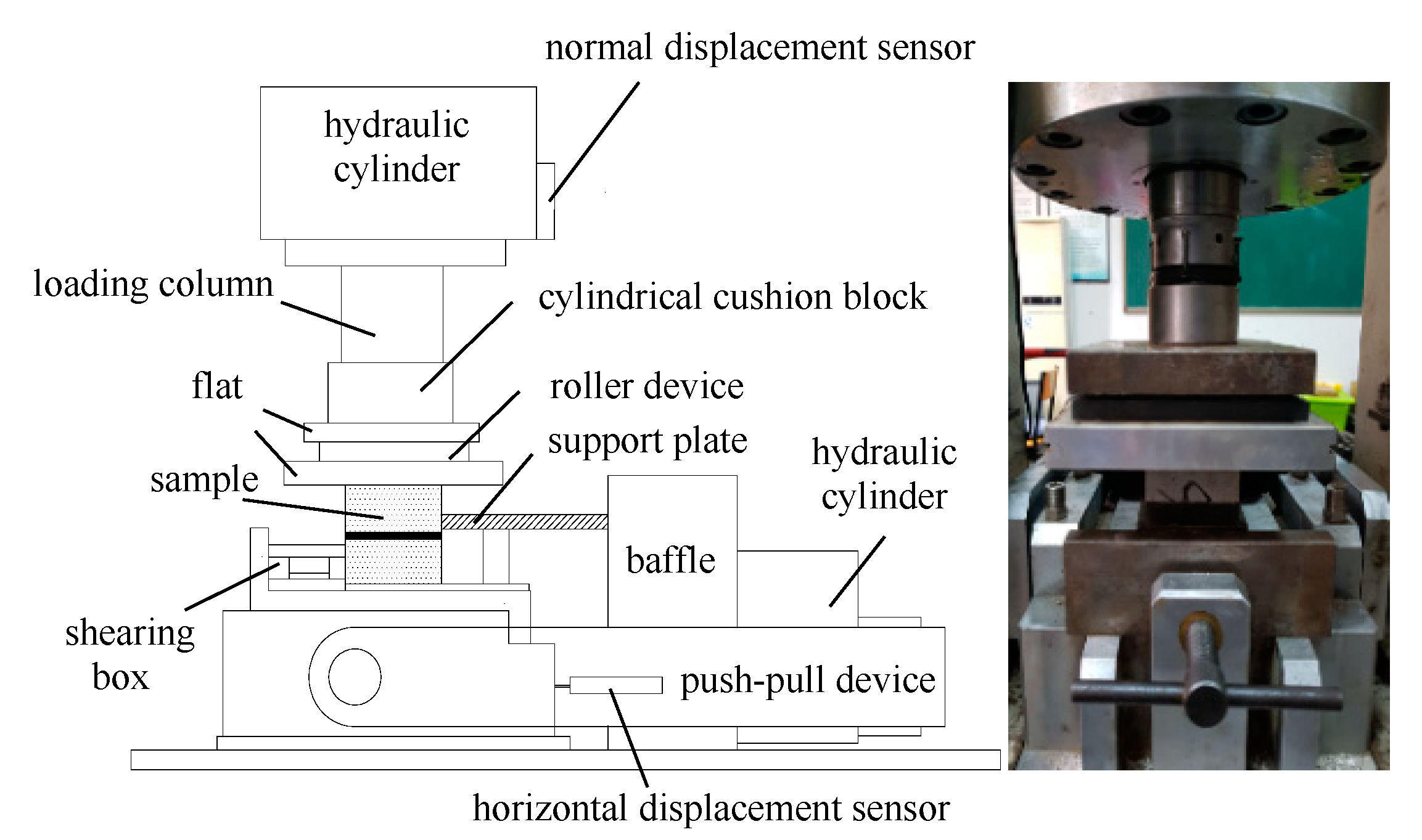
2.3. ExperimentalGrouting System
2.4. Shearing Experimental System and Scheme
3. Results of the Shearing Experiment
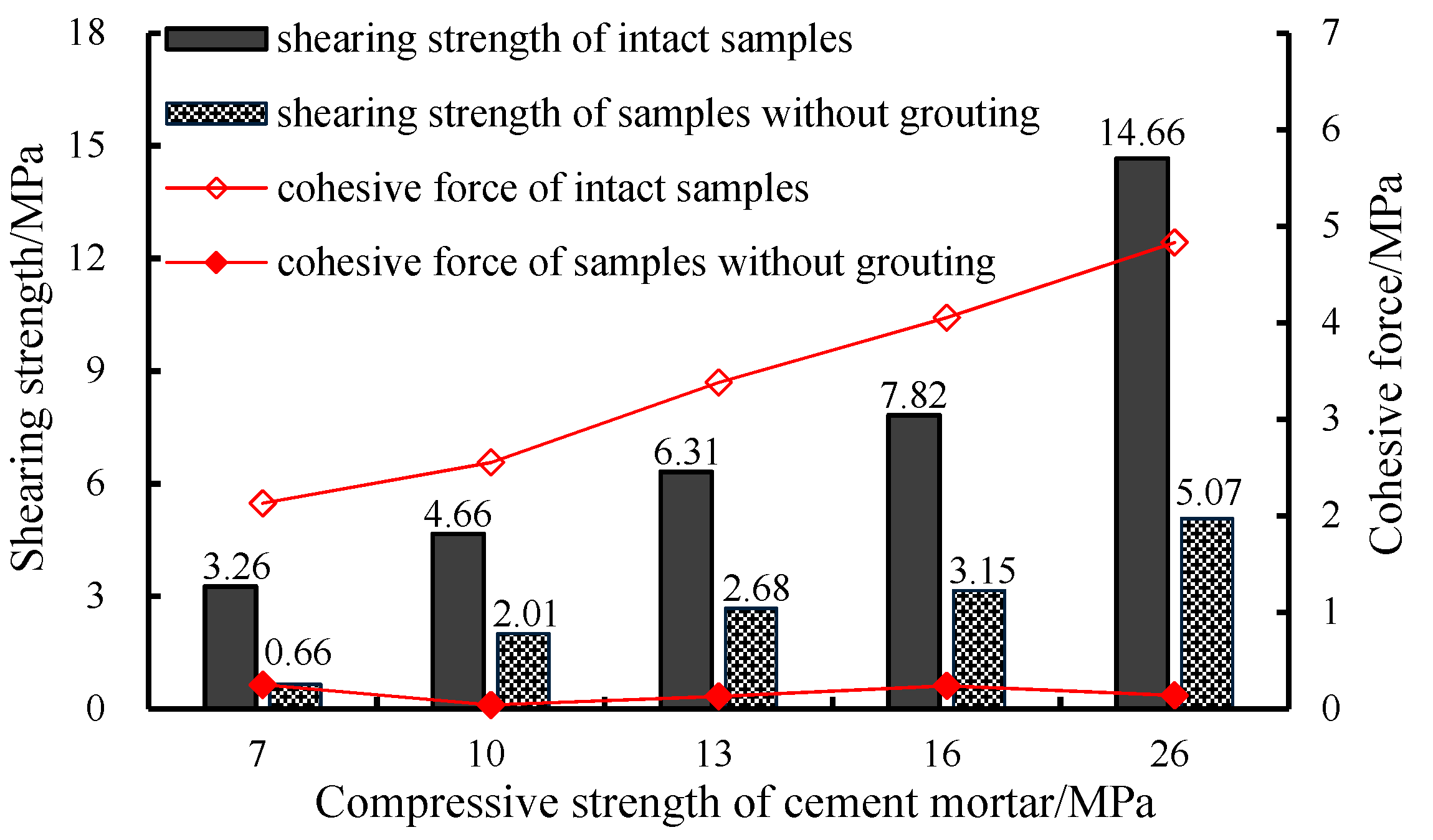
3.1. Controlled Experimental Results
- (1)
- With the increase of N, cohesion, and internal friction angle of the intact samples increase. Because samples without grouting are mainly affected by the normal stress, though the strength of samples increased, the internal friction angle and cohesion are only slightly increased
- (2)
- Under the same condition of normal stress, the shearing strength of the sample only accounts for 18.33% to 34.58% of the strength of intact samples, and the cohesion only accounts for 1.6% to 2.9% of cohesion of the intact samples.
3.2. Results of the Shearing Experiment of Grouting Samples on the Structural Plane
- (1)
- Under the same normal stress, with the decrease of W/C (the strength of grouting material increases), the τ(the shearing strength of the samples) increases.
- (2)
- The larger the N is, the greater the influence of the increasing W/C is on the sampleswith the grouted structural plane.
- (3)
- By fitting the data of the samples in the same W/C, the curves are all following the characteristics of an exponential function. That means with the increase of N, the τincreases continuously, and the reduction rate is close tozero gradually.
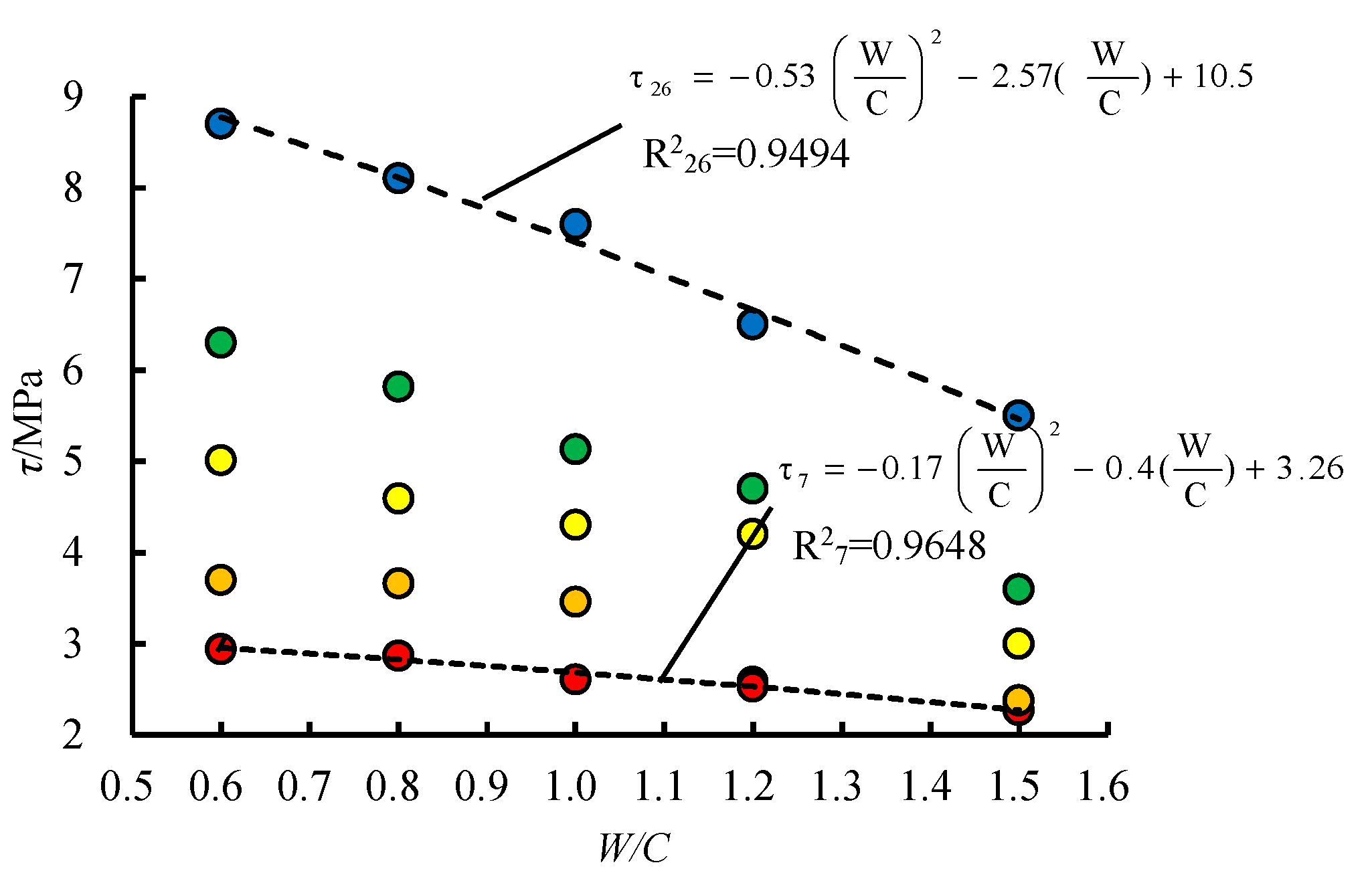
- (1)
- For the samples in the same N, with the increase of W/C, the τ decreases continuously. The reduction rate of τ increases, which is more significant for the samples with larger N.
- (2)
- The smaller the W/C is, the greater the difference of τ is in different N.
- (3)
- The fitting degree of the quadratic function is high when N and τ are fitted. With the decrease of W/C (the strength of grouting material increases), τ increases slowly and finally tends to be steady.
4. Analysis of Grouting Reinforcement Effect and Failure Characteristics of Samples
4.1. Grouting Effect of the Samples with the Prefabricated Structural Plane
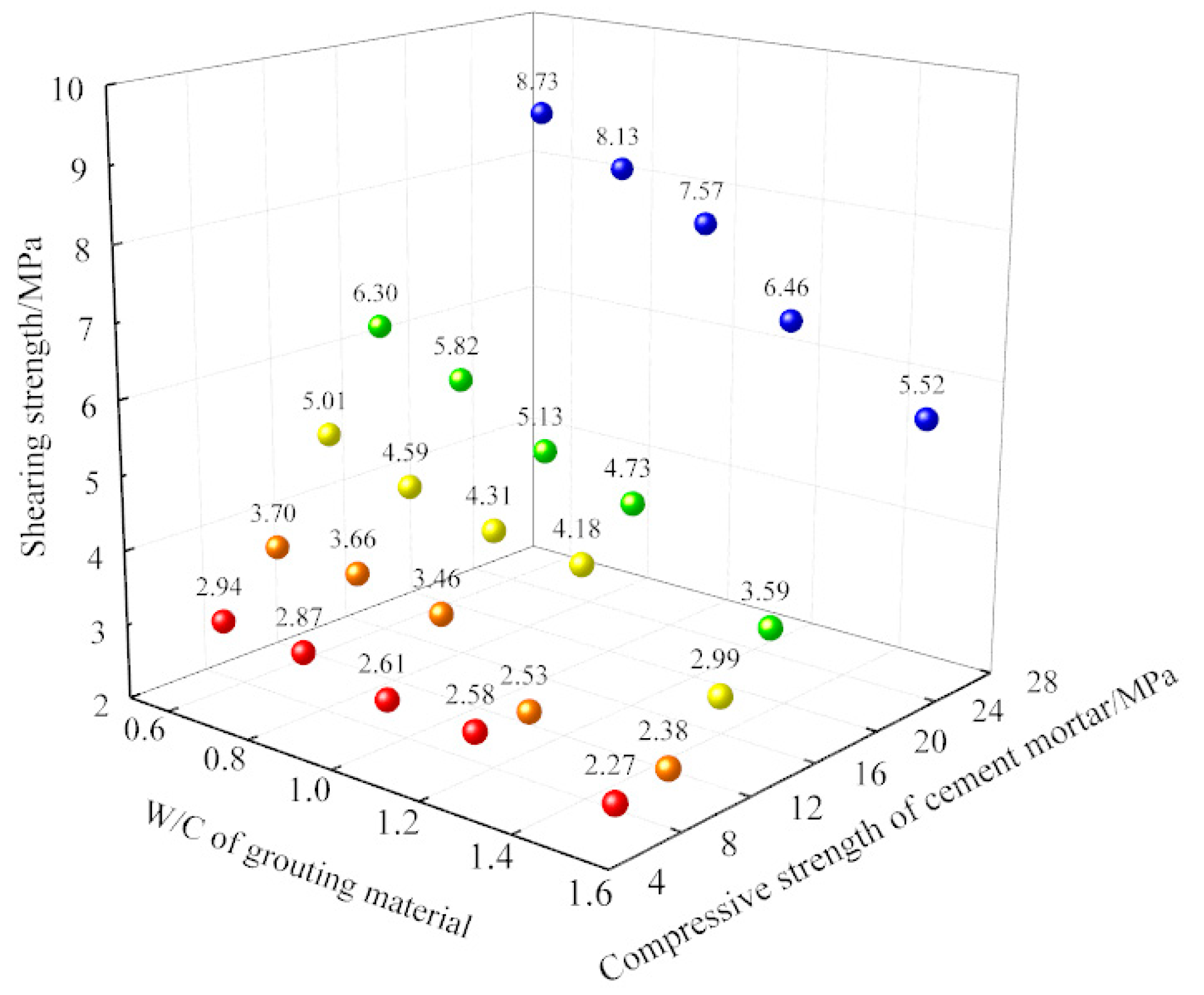
4.2. Characteristics of Shearing Strength of Grouted Sample on Prefabricated Structural Planes
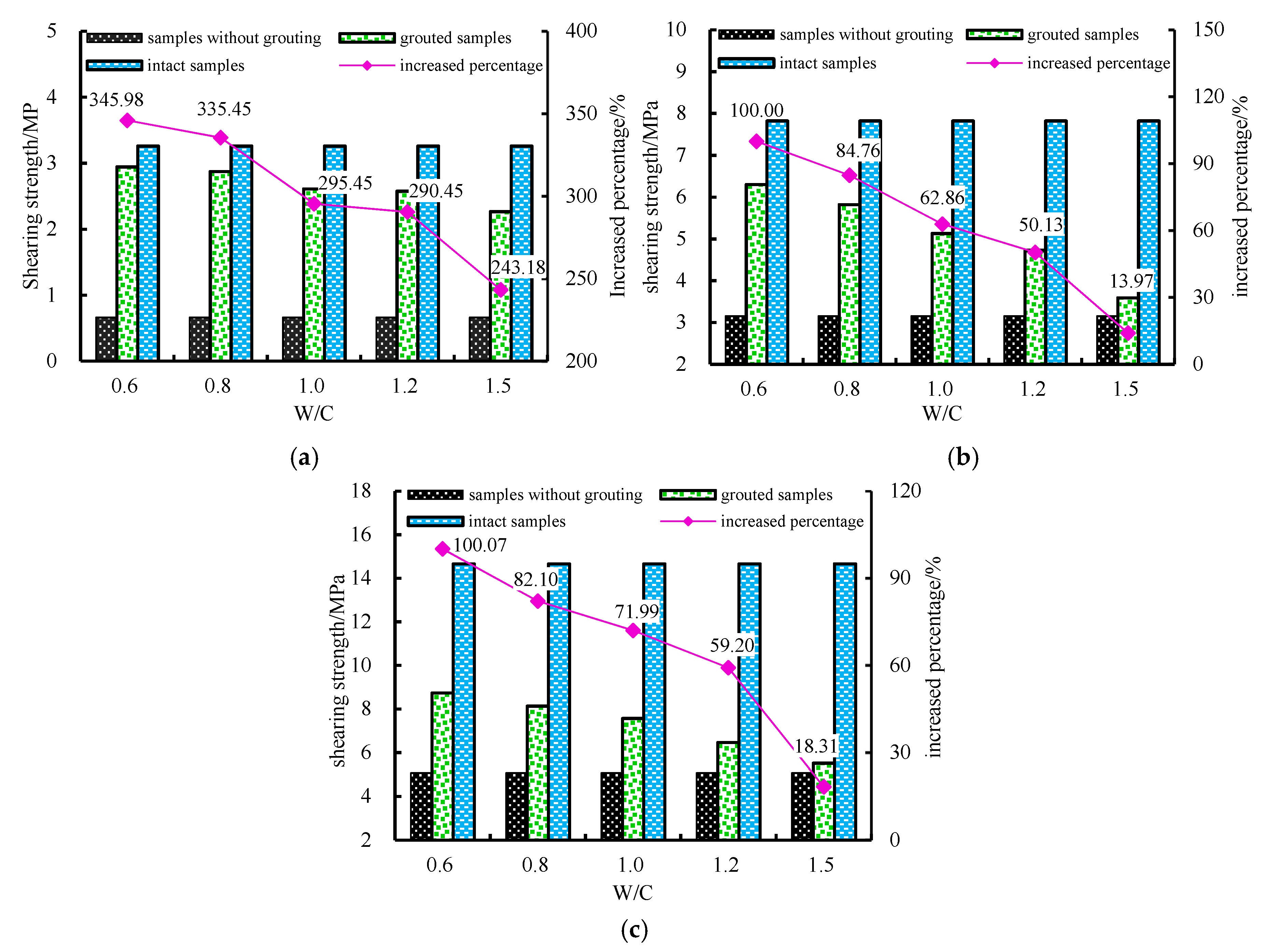
- (1)
- Grouting can effectively improve the shearing strength of samples with the structural plane, but no matter how big the M is, it cannot reach the strength value of the complete sample.
- (2)
- The relationship between τ and M is quadratic. With the increase of M, the growth rate of τ decreases gradually.
- (3)
- With the increase of N, the upside of the effect of grouting reinforcement is becoming limited. The U decreases from 0.9 to 0.6.
4.3. Shearing Failure Process and Morphology Characteristics of Grouted Samples
5. Discussion on the Reasonable Grouting Strength of Fractured Rock Mass
6. Conclusions
- (1)
- N is in the range from 7 MPa to 26 MPa, and M is in the range from 9.3 MPa to 23.2 MPa. No matter which combination of M and N, the shearing strength of samples cannot reach the shearing strength of the intact samples.
- (2)
- The increase of M can enhance the effect of grouting reinforcement. The lower N is, the more obvious the reinforcement effect is. With the increase of N, the influence of the increase of M on the strength of samples decreases. With the increase of N, the growth rate of τ decreases.
- (3)
- When M increases, the failure morphology of the grouted samples is consistent with the plastic failure of the sample without grouting at the initial stage, and it gradually changes to the brittle shearing slip failure which is like that of intact samples.
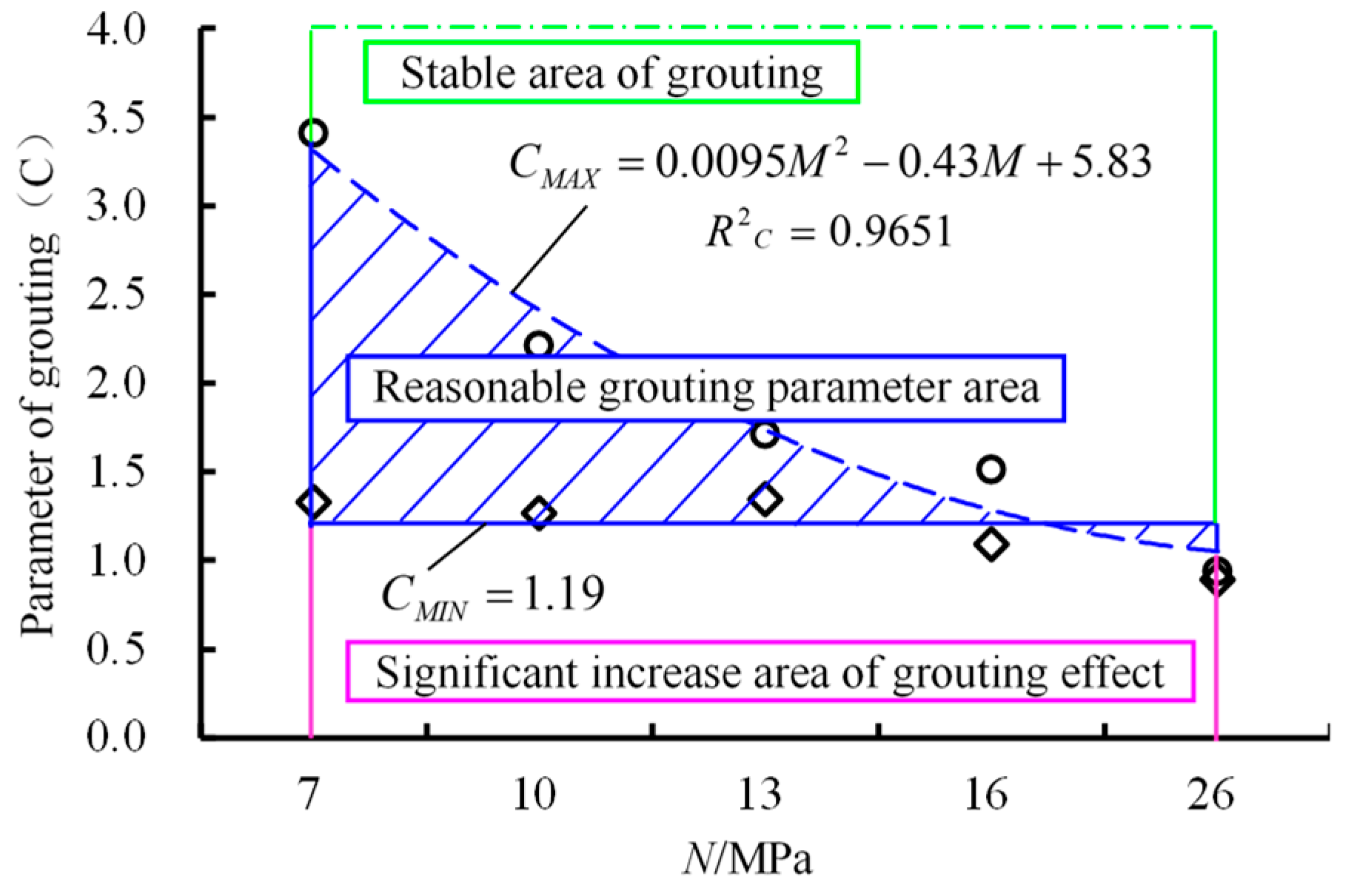
- (4)
- The C is reasonable in the range (1.19 ≤ C ≤ Cmax). When C is less than 1.19, τincreases obviously with M increasing. When C is larger than CMAX, the grouting reinforcement effect will not be improved, and if M increases continuously, the cost of engineering will increase. Thus, C can provide a reference for grouting reinforcement in engineering.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, S.R.; Sun, H.Y.; Wang, Y.J.; Wei, J.H.; Liu, J.; Kanungo, D.P. Effect of the combination characteristics of rock structural plane on the stability of a rock-mass slope. Bull. Eng. Geol. Environ. 2014, 73, 987–995. [Google Scholar] [CrossRef]
- Fraternali, F.; Farina, I.; Carpentieri, G. A discrete-to-continuum approach to the curvatures of membrane networks and parametric surfaces. Mech. Res. Commun. 2014, 56, 18–25. [Google Scholar] [CrossRef]
- Fraternali, F.; Farina, I.; Modano, M. Loading noise effects on the system identification of composite structures by dynamic tests with vibrodyne. Compos. Part. B Eng. 2016, 115, 376–383. [Google Scholar]
- Wang, Z.; Ii, L. Experimental study on bending fatigue behavior of grouting reinforced rock with a fracture. Chin. J. Rock Mech. Eng. 2018, 37, 1823–1832. [Google Scholar]
- Meng, B.; Jing, H.; Chen, K.; Su, H. Failure mechanism and stability control of a large section of very soft roadway surrounding rock shear slip. Int J. Min. Sci. Technol. 2013, 23, 127–134. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Zhu, X.X.; Xu, S.X.; Wang, Z.Y.; Li, W. Experimental study on properties of a new type of grouting material for the reinforcement of fractured seam floor. J. Mater. Res. Technol. 2019, 8, 5271–5282. [Google Scholar] [CrossRef]
- Liu, R.; Zheng, Z.; Shucai, L.; Zhang, Q. Study on grouting penetration in soil rock mixture and the mechanical behavior after grouting reinforcement. J. Test. Eval. 2019, 47, 2240–2254. [Google Scholar] [CrossRef]
- Sha, F.; Lin, C.; Li, Z.; Liu, R. Reinforcement simulation of water-rich and broken rock with Portland cement-based grout. Constr. Build. Mater. 2019, 221, 292–300. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, Q.; Jiang, B.; Yu, H.C.; Pan, R.; Li, S.C. Study and engineering application on the bolt-grouting reinforcement effect in underground engineering with the fractured surrounding rock. Tunn. Undergr. Space Technol. 2019, 84, 237–247. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.F.; Xiong, Z.Q.; Wang, C.; Su, C.D.; Zhang, Y.H. Experimental study on the effect of grouting reinforcement on the shear strength of a fractured rock mass. PLoS ONE 2019, 14, e0220643. [Google Scholar] [CrossRef] [Green Version]
- He, Z.L.; Zhu, Z.D.; Ni, X.H.; Li, Z.J. Shear creep tests and creep constitutive model of marble with the structural plane. Eur. J. Environ. Civ. Eng. 2019, 23, 1275–1293. [Google Scholar] [CrossRef]
- He, Z.M.; Xiong, Z.Y.; Hu, Q.G.; Yang, M. Analytical and numerical solutions for shear mechanical behaviors of a structural plane. J. Cent. South. Univ. 2014, 21, 2944–2949. [Google Scholar] [CrossRef]
- Ji, F.; Liu, C.J.; Zhang, Y.; Zheng, L.B.; Pan, K.; Tan, X. High-strength model material production for structural plane replica and its shear testing. Eur. J. Environ. Civ. Eng. 2018, 22, 174–184. [Google Scholar] [CrossRef]
- Lu, Z.D.; Chen, C.X. A study of shear strength property and deformability of hard structural planes under hydro-mechanical coupling. Disaster Adv. 2012, 5, 158–163. [Google Scholar]
- Liu, Q.S.; Zhou, Y.S.; Lu, C.B.; Zhang, J.M. Experimental study on mechanical properties of mudstone fracture before and after grouting. Chin. J. Min. Saf. Eng. 2016, 33, 509–514, 520. [Google Scholar]
- Zhang, J.L.; Shen, M.R.; Liang, Z.R. Experimental study on shearing strength characteristics of irregular rock mass discontinuities. Chin. J. Southwest JiaoTong Univ. 2015, 50, 993–1000. [Google Scholar]
- Shen, M.R.; Zhang, Q.Z. Model test study on shearing characteristics of regular toothed structure surface. Chin. J. Rock Mech. Eng. 2010, 29, 713–719. [Google Scholar]
- Shi, L.; Cai, M.F.; Zhao, J. Fracture mechanism and experiment of infilled rock joints. Chin. J. Univ. Sci. Technol. Beijing 2012, 34, 253–259. [Google Scholar]
- Liu, R.T.; Zheng, Z.; Li, S.C.; Yang, H.L. Mechanical properties of fractured rock mass with consideration of grouting reinforcement. ChinaJ Highw. Transp. 2018, 10, 284–291. [Google Scholar]
- Zhang, Q.Z.; Shen, M.R.; Zhi, W. Investigation of mechanical behavior of a rock plane using rheological tests. J. Mater. Civ. Eng. 2011, 23, 1220–1226. [Google Scholar] [CrossRef]
- Wang, D.-J.; Tang, H.M.; Elsworth, D.; Wang, C.Y. Fracture evolution in artificial bedded rocks containing a structural flaw under uniaxial compression. Eng. Geol. 2019, 250, 130–140. [Google Scholar] [CrossRef]
- Gratchev, I.B.; Sassa, K. Shear Strength of Clay at Different Shear Rates. J. Geotech. Geoenviron. Eng. 2015, 141, 06015002. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.H.; Song, L.B.; Jiang, Q.; Yang, C.X.; Liu, C.; Yang, B. Shearing performance of naturally matched joints with different wall strength under direct shearing tests. Geotech. Test. J. 2018, 41, 371–389. [Google Scholar] [CrossRef]
- Li, Z.P.; Zhang, L.Z.; Chu, Y.T.; Zhang, Q.S. Research on the influence of water-cement ratio on reinforcement effect for permeation grouting in the sand layer. Adv. Mater. Sci. Eng. 2020, 2020, 5329627. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.S.; Lei, G.F.; Peng, X.X.; Lu, C.B.; Lai, W. Rheological characteristics of cement grout and its effect on mechanical properties of a rock fracture. Rock Mech. Rock Eng. 2018, 51, 613–625. [Google Scholar] [CrossRef]
- Liu, Q.S.; Lei, G.F.; Lu, C.B.; Peng, X.X.; Zhang, J.; Wang, J.T. Experimental study of grouting reinforcement influence on mechanical properties of rock fracture. Chin. J. Rock Mech. Eng. 2017, 36, 3140–3147. [Google Scholar]
- Zheng, C.F.; Chen, C.J.; Zhao, D.J.; Song, Z.F.; Zheng, S. Test technology study on mesoscopic shear strength of mineral aggregate contact surface. J. Mater. Civ. Eng. 2014, 26, 90–98. [Google Scholar]
- Kim, C.G.; Park, H.G.; Hong, G.H.; Kang, S.M.; Lee, H. Shear strength of concrete composite beams with shear reinforcements. ACI Struct. J. 2017, 114, 827–838. [Google Scholar] [CrossRef]
- Lee, J.Y.; Choi, I.J.; Kim, S.W. Shear behavior of reinforced concrete beams with high-strength stirrups. ACI Struct. J. 2011, 108, 620–629. [Google Scholar]
- Tian, J.; Wu, X.; Zheng, Y.; Hu, S.; Du, Y.; Wang, W.; Sun, C.; Zhang, L. Investigation of interface shear properties and mechanical model between ECC and concrete. Constr. Build. Mater. 2019, 223, 12–27. [Google Scholar] [CrossRef]







| Number | Proportion of Sand | Proportion of Cement | Proportion of Water | Uniaxial Compressive Strength/MPa |
|---|---|---|---|---|
| A | 4.5 | 1 | 1 | 7 |
| B | 4 | 1 | 0.9 | 10 |
| C | 3.5 | 1 | 0.8 | 13 |
| D | 3 | 1 | 0.7 | 16 |
| E | 2 | 1 | 0.6 | 26 |
| Group | Number | Strength of Samples/MPa | Normal Load/MPa | Strength of Grouting Material/MPa |
|---|---|---|---|---|
| Intact samples | A1 | 7 | 1.75 | / |
| B1 | 10 | 2.5 | / | |
| C1 | 13 | 3.25 | / | |
| D1 | 16 | 4 | / | |
| E1 | 26 | 6.5 | / | |
| Samples without grouting | A2 | 7 | 1.75 | / |
| B2 | 10 | 2.5 | / | |
| C2 | 13 | 3.25 | / | |
| D2 | 16 | 4 | / | |
| E2 | 26 | 6.5 | / | |
| Grouted samples | Aa | 7 | 1.75 | 9.3 |
| Ab | 12.7 | |||
| Ac | 14.7 | |||
| Ad | 17.5 | |||
| Ae | 23.2 | |||
| Ba | 10 | 2.5 | 9.3 | |
| Bb | 12.7 | |||
| Bc | 14.7 | |||
| Bd | 17.5 | |||
| Be | 23.2 | |||
| Ca | 13 | 3.25 | 9.3 | |
| Cb | 12.7 | |||
| Cc | 14.7 | |||
| Cd | 17.5 | |||
| Ce | 23.2 | |||
| Da | 16 | 4 | 9.3 | |
| Db | 12.7 | |||
| Dc | 14.7 | |||
| Dd | 17.5 | |||
| De | 23.2 | |||
| Ea | 26 | 6.5 | 9.3 | |
| Eb | 12.7 | |||
| Ec | 14.7 | |||
| Ed | 17.5 | |||
| Ee | 23.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xiong, Z.-q.; Wang, C.; Su, C.-d.; Li, X.-f. Research on the Reasonable Grouting Strength of Rock-Like Samples in Different Strengths. Materials 2020, 13, 3161. https://doi.org/10.3390/ma13143161
Wang Y, Xiong Z-q, Wang C, Su C-d, Li X-f. Research on the Reasonable Grouting Strength of Rock-Like Samples in Different Strengths. Materials. 2020; 13(14):3161. https://doi.org/10.3390/ma13143161
Chicago/Turabian StyleWang, Yan, Zu-qiang Xiong, Chun Wang, Cheng-dong Su, and Xue-feng Li. 2020. "Research on the Reasonable Grouting Strength of Rock-Like Samples in Different Strengths" Materials 13, no. 14: 3161. https://doi.org/10.3390/ma13143161
APA StyleWang, Y., Xiong, Z.-q., Wang, C., Su, C.-d., & Li, X.-f. (2020). Research on the Reasonable Grouting Strength of Rock-Like Samples in Different Strengths. Materials, 13(14), 3161. https://doi.org/10.3390/ma13143161






