Weak Antilocalization Tailor-Made by System Topography in Large Scale Bismuth Antidot Arrays
Abstract
:1. Introduction
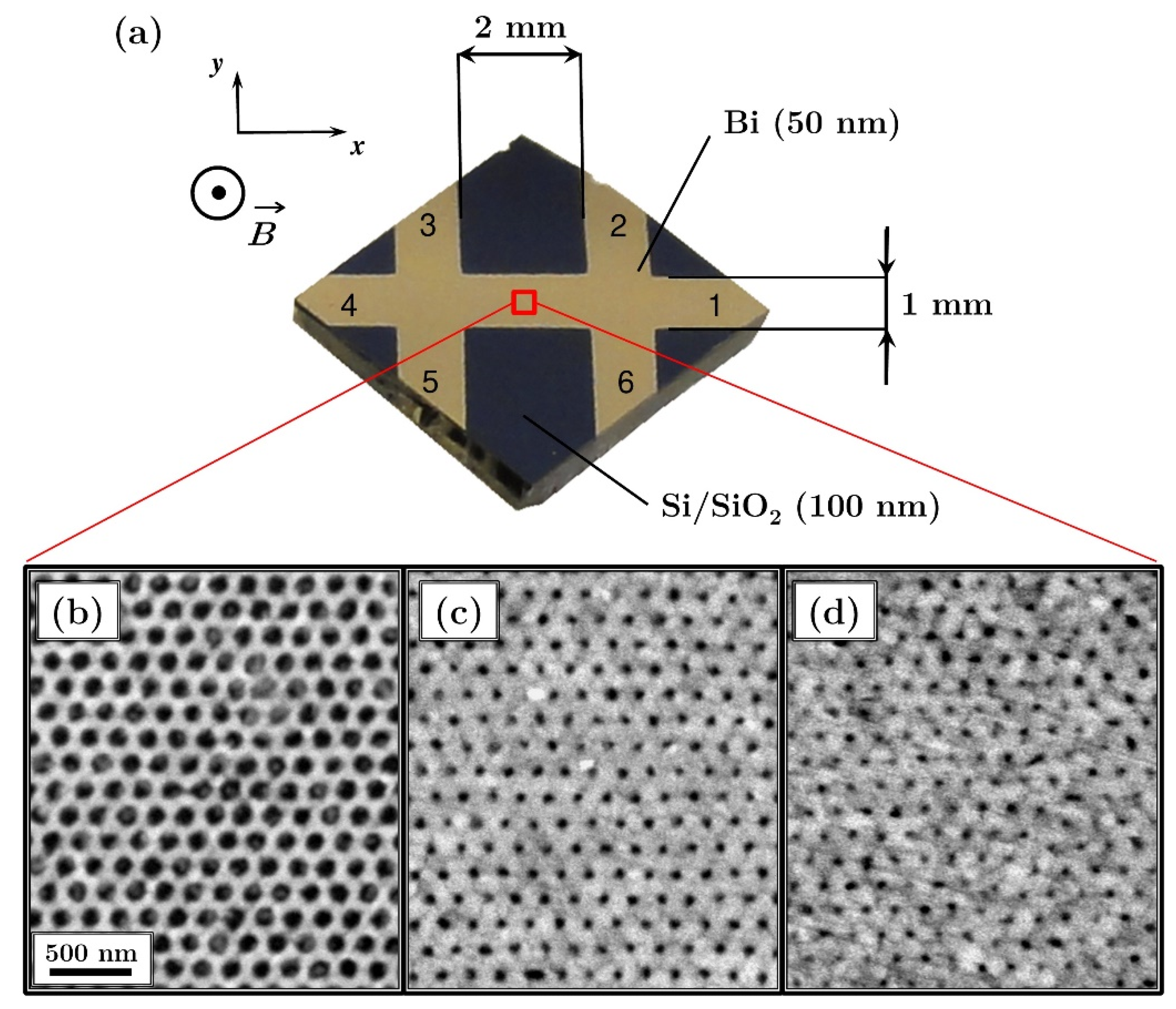
2. Materials and Methods
3. Results and Discussion
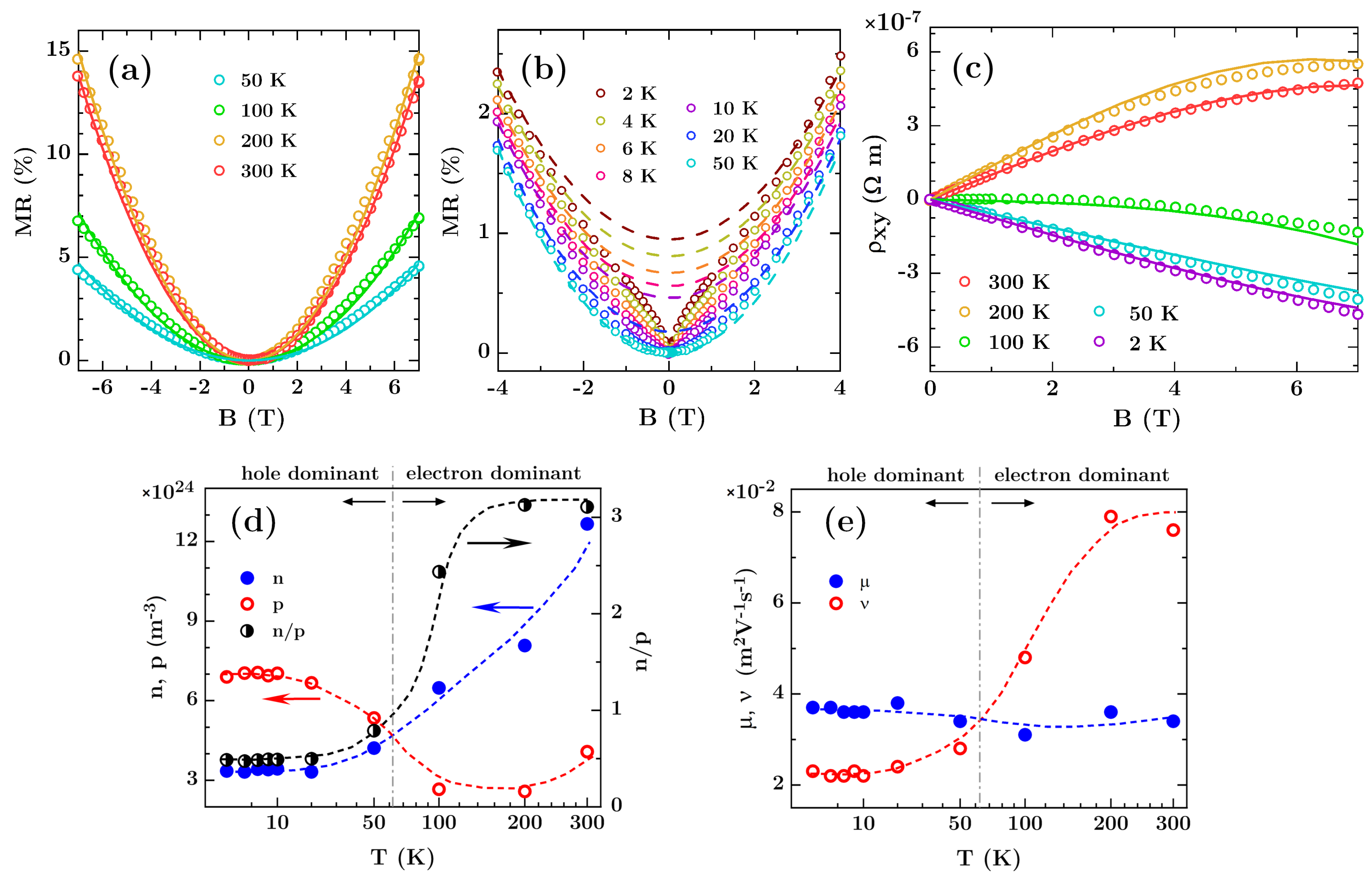
3.1. Non-Patterned Film
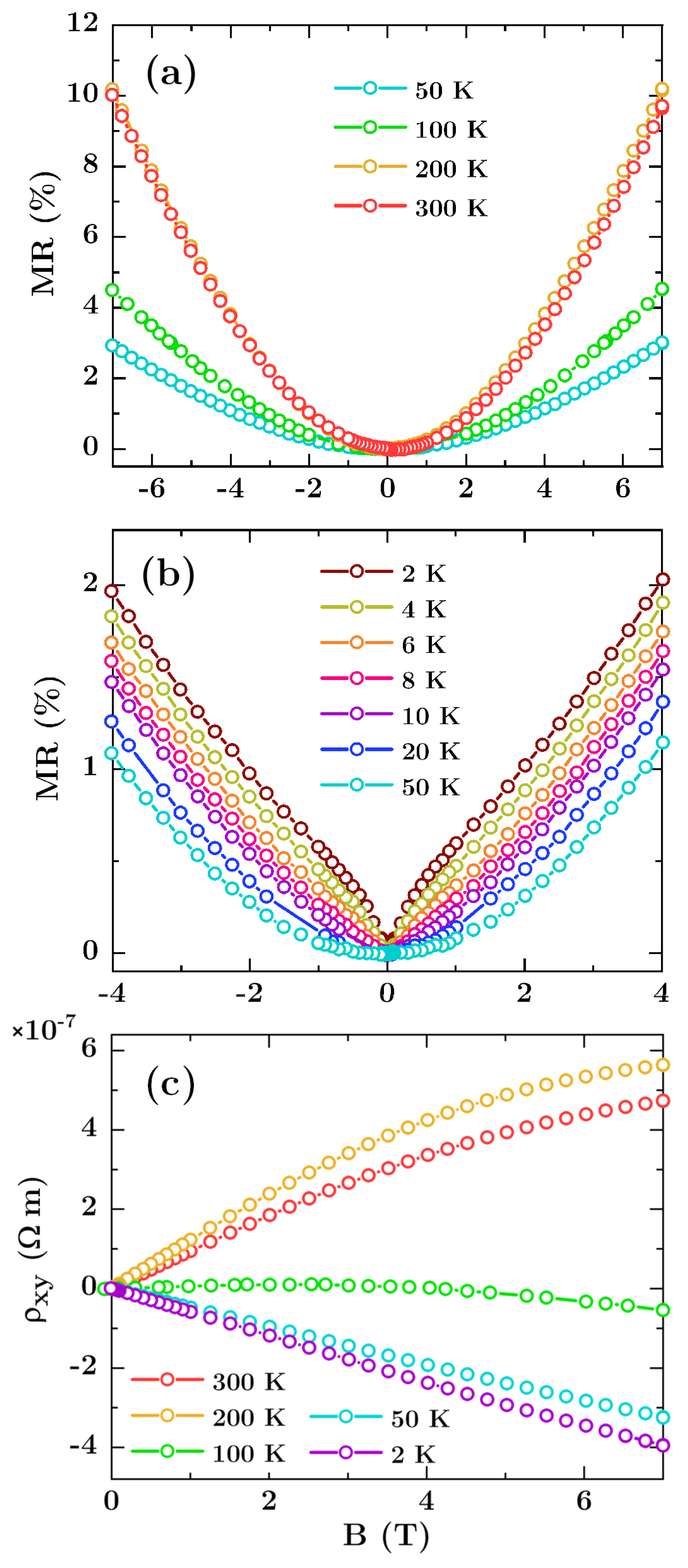
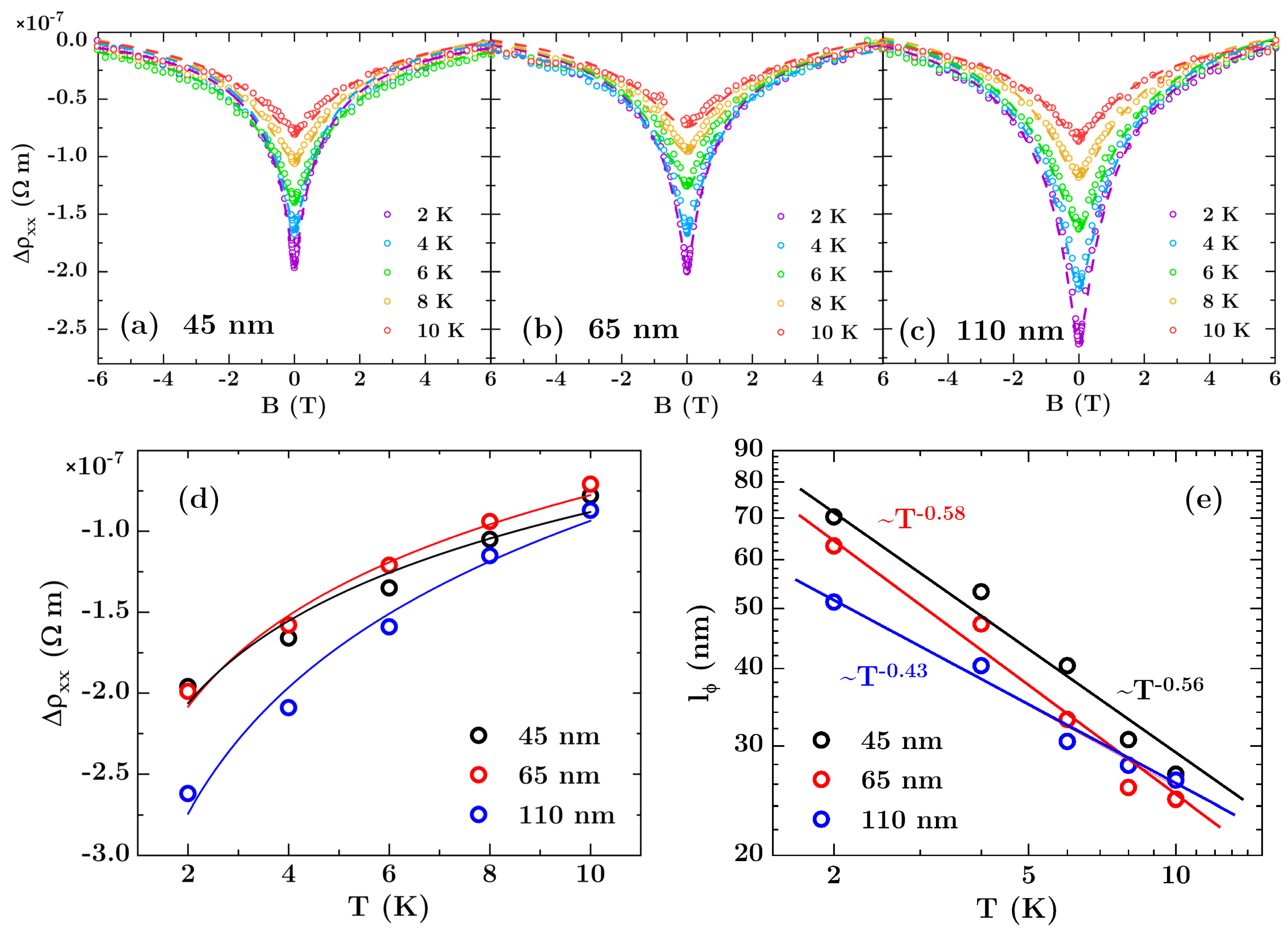
3.2. Antidot Arrays
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kim, G.-S.; Lee, M.-R.; Lee, S.-Y.; Hyung, J.-H.; Park, N.-W.; Lee, E.S.; Lee, S.-K. Reduction in thermal conductivity of Bi thin films with high-density ordered nanoscopic pores. Nanoscale Res. Lett. 2013, 8, 371. [Google Scholar] [CrossRef] [Green Version]
- Heremans, J.; Thrush, C.M.; Lin, Y.-M.; Cronin, S.; Zhang, Z.; Dresselhaus, M.S.; Mansfield, J.F. Bismuth nanowire arrays: Synthesis and galvanomagnetic properties. Phys. Rev. B 2000, 61, 2921. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Hirose, Y.; Nakao, S.; Fukumura, T.; Xu, J.; Hasegawa, T. Quantum confinement effect in Bi anti-dot thin films with tailored pore wall widths and thicknesses. Appl. Phys. Lett. 2014, 104, 023106. [Google Scholar] [CrossRef]
- Shim, W.; Ham, J.; Kim, J.; Lee, W. Shubnikov–de Haas oscillations in an individual single-crystalline bismuth nanowire grown by on-film formation of nanowires. Appl. Phys. Lett. 2009, 95, 232107. [Google Scholar] [CrossRef] [Green Version]
- Zhu, K.; Wu, L.; Gong, X.; Xiao, S.; Jin, X. Quantum transport in the surface states of epitaxial Bi(111) thin films. Phys. Rev. B 2016, 94, 121401. [Google Scholar] [CrossRef]
- De Haas, W.J.; van Alphen, P.M. The dependence of the susceptibility of diamagnetic metals upon the field. Proc. Neth. R. Acad. Sci. 1930, 33, 1106. [Google Scholar]
- Abrikosov, A.A. Quantum linear magnetoresistance. Europhys. Lett. 2000, 49, 789. [Google Scholar] [CrossRef]
- Zhu, K.; Tian, D.; Wu, L.; Xu, J.; Jin, X. Impurity effect on surface states of Bi (111) ultrathin films. Chin. Phys. B 2016, 25, 087303. [Google Scholar] [CrossRef]
- White, H.; McLachlan, D.S. Morphology dependence of weak-anti-localisation parameters in bismuth films. J. Phys. Condens. Matter 1989, 1, 6665. [Google Scholar] [CrossRef]
- Sangiao, S.; Marcano, N.; Fan, J.; Morellon, L.; Ibarra, M.R.; De Teresa, J.M. Quantitative analysis of the weak anti-localization effect in ultrathin bismuth films. Europhys. Lett. 2011, 95, 37002. [Google Scholar] [CrossRef]
- Rudolph, M.; Heremans, J.J. Electronic and quantum phase coherence properties of bismuth thin films. Appl. Phys. Lett. 2012, 100, 241601. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.Y.; Liu, K.; Hong, K.; Reich, D.H.; Searson, P.C.; Chien, C.L. Large magnetoresistance of electrodeposited single-crystal bismuth thin films. Science 1999, 284, 1335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hackens, B.; Minet, J.P.; Faniel, S.; Farhi, G.; Gustin, C.; Issi, J.P.; Heremans, J.P.; Bayot, V. Quantum transport, anomalous dephasing, and spin-orbit coupling in an open ballistic bismuth nanocavity. Phys. Rev B 2003, 67, 121403(R). [Google Scholar] [CrossRef]
- Heremans, J.; Thrush, C.M.; Zhang, Z.; Sun, X.; Dresselhaus, M.S.; Ying, J.Y.; Morelli, D.T. Magnetoresistance of bismuth nanowire arrays: A possible transition from one-dimensional to three-dimensional localization. Phys. Rev. B 1998, 58, R10091. [Google Scholar] [CrossRef]
- Lin, Y.-M.; Cronin, S.B.; Ying, J.Y.; Dresselhaus, M.S.; Heremans, J.P. Transport properties of Bi nanowire arrays. Appl. Phys. Lett. 2000, 76, 3944. [Google Scholar] [CrossRef] [Green Version]
- Rudolph, M.; Heremans, J.J. Spin-orbit interaction and phase coherence in lithographically defined bismuth wires. Phys. Rev. B 2011, 83, 205410. [Google Scholar] [CrossRef] [Green Version]
- Marcano, N.; Sangiao, S.; Plaza, M.; Perez, L.; Fernandez Pacheco, A.; Cordoba, R.; Sanchez, M.C.; Morellon, L.; Ibarra, M.R.; De Teresa, J.M. Weak-antilocalization signatures in the magnetotransport properties of individual electrodeposited Bi nanowires. Appl. Phys. Lett. 2010, 96, 082110. [Google Scholar] [CrossRef] [Green Version]
- Murata, M.; Hasegawa, Y.; Komine, T.; Kobayashi, T. Preparation of bismuth nanowire encased in quartz template for Hall measurements using focused ion beam processing. Nanoscale Res. Lett. 2012, 7, 505. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z.A. Topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970. [Google Scholar] [CrossRef] [Green Version]
- Tian, M.; Wang, J.; Zhang, Q.; Kumar, N.; Mallouk, T.E.; Chan, M.H.W. Superconductivity and quantum oscillations in crystalline Bi nanowire. Nano Lett. 2009, 9, 3196–3202. [Google Scholar] [CrossRef] [Green Version]
- Rabin, O.; Dresselhaus, M.S. Anomalous magnetoresistance behavior of bismuth antidot arrays. MRS Online Proc. Libr. Arch. 2004, 788, L12.1. [Google Scholar] [CrossRef]
- Rabin, O.; Nielsch, K.; Dresselhaus, M.S. Enhancement of weak anti-localization signatures in the magneto-resistance of bismuth anti-dot thin films. Appl. Phys. A 2006, 82, 471–474. [Google Scholar] [CrossRef]
- Strijkers, G.J.; Yang, F.Y.; Reich, D.H.; Chien, C.L.; Searson, P.C.; Strelniker, Y.M.; Bergman, D.J. Magnetoresistance anisotropy of a Bi antidot array. IEEE Trans. Magn. 2001, 37, 2067–2069. [Google Scholar] [CrossRef]
- Gao, J.; Kempa, K.; Giersig, M.; Akinoglu, E.M.; Han, B.; Li, R. Physics of transparent conductors. Adv. Phys. 2016, 65, 553–617. [Google Scholar] [CrossRef]
- Kobayashi, N.; Masumoto, H.; Takahashi, S.; Maekawa, S. Optically transparent ferromagnetic nanogranular films with tunable transmittance. Sci. Rep. 2016, 6, 34227. [Google Scholar] [CrossRef] [PubMed]
- Krupinski, M.; Mitin, D.; Zarzycki, A.; Szkudlarek, A.; Giersig, M.; Albrecht, M.; Marszałek, M. Magnetic transition from dot to antidot regime in large area Co/Pd nanopatterned arrays with perpendicular magnetization. Nanotechnology 2017, 28, 085302. [Google Scholar] [CrossRef]
- Krupinski, M.; Bali, R.; Mitin, D.; Sobieszczyk, P.; Gregor-Pawlowski, J.; Zarzycki, A.; Böttger, R.; Albrecht, M.; Potzger, K.; Marszałek, M. Ion induced ferromagnetism combined with self-assembly for large area magnetic modulation of thin films. Nanoscale 2019, 11, 8930–8939. [Google Scholar] [CrossRef]
- White, G.K.; Woods, S.B. The Thermal and electrical resistivity of bismuth and antimony at low temperatures. Philos. Mag. 1958, 3, 342–359. [Google Scholar] [CrossRef]
- Gallo, C.F.; Chandrasekhar, B.S.; Sutter, P.H. Transport properties of bismuth single crystals. J. Appl. Phys. 1963, 34, 144. [Google Scholar] [CrossRef]
- Cornelius, T.W.; Toimil-Molares, M.E.; Neumann, R.; Karim, S. Finite-size effects in the electrical transport properties of single bismuth nanowires. J. Appl. Phys. 2006, 100, 114307. [Google Scholar] [CrossRef]
- Marcano, N.; Sangiao, S.; De Teresa, J.M.; Morellon, L.; Ibarra, M.R.; Plaza, M.; Perez, L. Structural and magnetotransport properties of Bi thin films grown by thermal evaporation. J. Magn. Magn. Mater. 2010, 322, 1460–1463. [Google Scholar] [CrossRef]
- Lukermann, D.; Sologub, S.; Pfnur, H.; Tegenkamp, C. Sensing surface states of Bi films by magnetotransport. Phys. Rev. B 2011, 83, 245425. [Google Scholar] [CrossRef]
- Li, C.-Z.; Li, J.-G.; Wang, L.-X.; Zhang, L.; Zhang, J.-M.; Yu, D.; Liao, Z.-M. Two-carrier transport induced Hall anomaly and large tunable magnetoresistance in Dirac semimetal Cd3As2 nanoplates. ACS Nano 2016, 10, 6020–6028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emoto, H.; Ando, Y.; Eguchi, G.; Ohshima, R.; Shikoh, E.; Fuseya, Y.; Shinjo, T.; Shiraishi, M. Transport and spin conversion of multicarriers in semimetal bismuth. Phys. Rev. B 2016, 93, 174428. [Google Scholar] [CrossRef] [Green Version]
- Dillner, U.; Schnelle, W. Electrical and galvanomagnetic properties of undoped and doped polycrystalline bismuth films III. Analysis in an anisotropic two-carrier model. Phys. Status Solidi 1989, 116, 715–723. [Google Scholar] [CrossRef]
- Vu, D.M.; Shon, W.; Rhyee, J.-S.; Sasaki, M.; Ohnishi, A.; Kim, K.-S.; Kim, H.-J. Weak antilocalization and two-carrier electrical transport in Bi1−xSbx single crystals (0% < x < 17.0%). Phys. Rev. B 2019, 100, 125162. [Google Scholar]
- Marcano, N.; Sangiao, S.; Magén, C.; Morellón, L.; Ibarra, M.R.; Plaza, M.; Pérez, L.; De Teresa, J.M. Role of the surface states in the magnetotransport properties of ultrathin bismuth films. Phys. Rev. B 2010, 82, 125326. [Google Scholar] [CrossRef] [Green Version]
- Rosenbaum, R.; Galibert, J. Unusual electronic transport properties of a thin polycrystalline bismuth film. J. Phys. Condens. Matter 2004, 16, 5849. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.; Nagaoka, Y. Spin-orbit interaction and magnetoresistance in the two dimensional random system. Prog. Theor. Phys. 1980, 63, 707–710. [Google Scholar] [CrossRef]
- Chiu, S.-P.; Lin, J.-J. Weak antilocalization in topological insulator Bi2Te3 microflakes. Phys. Rev. B 2013, 87, 035122. [Google Scholar] [CrossRef] [Green Version]
- Beutler, D.E.; Giordano, N. Localization and electron-electron interaction effects in thin Bi wires and films. Phys. Rev. B 1988, 38, 8. [Google Scholar] [CrossRef] [PubMed]
- Takagaki, Y.; Giussani, A.; Perumal, K.; Calarco, R.; Friedland, K.-J. Robust topological surface states in Sb2Te3 layers as seen from the weak antilocalization effect. Phys. Rev. B 2012, 86, 125137. [Google Scholar] [CrossRef] [Green Version]
- Hamdou, B.; Gooth, J.; Dorn, A.; Pippel, E.; Nielsch, K. Aharonov-Bohm oscillations and weak antilocalization in topological insulator Sb2Te3 nanowires. Appl. Phys. Lett. 2013, 102, 223110. [Google Scholar] [CrossRef] [Green Version]
- Dorn, A.; Sigrist, M.; Fuhrer, A.; Ihn, T.; Heinzel, T.; Ensslin, K.; Wegscheider, W.; Bichler, M. Electronic properties of antidot lattices fabricated by atomic force lithography. Appl. Phys. Lett. 2002, 80, 252. [Google Scholar] [CrossRef] [Green Version]
- Castano, F.J.; Nielsch, K.; Ross, C.A.; Robinson, J.W.A.; Krishnan, R. Anisotropy and magnetotransport in ordered magnetic antidot arrays. Appl. Phys. Lett. 2004, 85, 2872. [Google Scholar] [CrossRef]
- Park, N.-W.; Lee, W.-Y.; Park, T.-H.; Kim, D.-J.; Cho, S.-H.; Lee, S.-Y.; Lee, S.-K. Temperature-dependent thermal conductivity of nanoporous Bi thin films by controlling pore size and porosity. J. Alloys Compd. 2015, 639, 289–295. [Google Scholar] [CrossRef]
- Krupinski, M.; Sobieszczyk, P.; Zieliński, P.; Marszałek, M. Magnetic reversal in perpendicularly magnetized antidot arrays with intrinsic and extrinsic defects. Sci. Rep. 2019, 9, 13276. [Google Scholar] [CrossRef] [Green Version]
- Perzanowski, M.; Krupinski, M.; Zarzycki, A.; Dziedzic, A.; Zabila, Y.; Marszalek, M. Exchange bias in the [CoO/Co/Pd]10 antidot large area arrays. ACS Appl. Mater. Interfaces 2017, 9, 33250–33256. [Google Scholar] [CrossRef] [Green Version]
- Tornow, M.; Weiss, D.; Klitzing, K.V.; Eberl, K.; Bergman, D.J.; Strelniker, Y.M. Anisotropic magnetoresistance of a classical antidot array. Phys. Rev. Lett. 1996, 77, 147–150. [Google Scholar] [CrossRef] [Green Version]
- Bergman, D.J.; Strelniker, Y.M. Calculation of strong-field magnetoresistance in some periodic composites. Phys. Rev. B 1994, 49, 16256. [Google Scholar] [CrossRef]
- Meckler, S.; Heinzel, T.; Cavanna, A.; Faini, G.; Gennser, U.; Mailly, D. Commensurability effects in hexagonal antidot lattices with large antidot diameters. Phys. Rev. B 2005, 72, 035319. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.Q.; Yang, C.L.; Du, R.R.; Pfeiffer, L.N.; West, K.W. Microwave photoresistance of a high-mobility two-dimensional electron gas in a triangular antidot lattice. Phys. Rev. B 2006, 74, 075313. [Google Scholar] [CrossRef] [Green Version]


| Flat Film | Antidot Arrays | |||
|---|---|---|---|---|
| 45 nm | 65 nm | 110 nm | ||
| ρxx (T = 300 K, B = 0) (10−6 Ωm) | 8.4 | 9.6 | 10.7 | 17 |
| Δρxx (T = 2 K, B = 0) (10−7 Ωm) | −1.63 | −1.96 | −1.99 | −2.62 |
| l0 (nm) | 60–90 | 50–70 | 50–70 | 50–70 |
| lso (nm) | 25–40 | 20–30 | 25–30 | 25–30 |
| lϕ (T = 2 K) (nm) | 86 | 71 | 64 | 51 |
| 1.05 ± 0.07 | 1.12 ± 0.14 | 1.16 ± 0.14 | 0.86 ± 0.08 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krupinski, M.; Zarzycki, A.; Zabila, Y.; Marszałek, M. Weak Antilocalization Tailor-Made by System Topography in Large Scale Bismuth Antidot Arrays. Materials 2020, 13, 3246. https://doi.org/10.3390/ma13153246
Krupinski M, Zarzycki A, Zabila Y, Marszałek M. Weak Antilocalization Tailor-Made by System Topography in Large Scale Bismuth Antidot Arrays. Materials. 2020; 13(15):3246. https://doi.org/10.3390/ma13153246
Chicago/Turabian StyleKrupinski, Michal, Arkadiusz Zarzycki, Yevhen Zabila, and Marta Marszałek. 2020. "Weak Antilocalization Tailor-Made by System Topography in Large Scale Bismuth Antidot Arrays" Materials 13, no. 15: 3246. https://doi.org/10.3390/ma13153246
APA StyleKrupinski, M., Zarzycki, A., Zabila, Y., & Marszałek, M. (2020). Weak Antilocalization Tailor-Made by System Topography in Large Scale Bismuth Antidot Arrays. Materials, 13(15), 3246. https://doi.org/10.3390/ma13153246





