A Micromechanical Fatigue Limit Stress Model of Fiber-Reinforced Ceramic-Matrix Composites under Stochastic Overloading Stress
Abstract
:1. Introduction
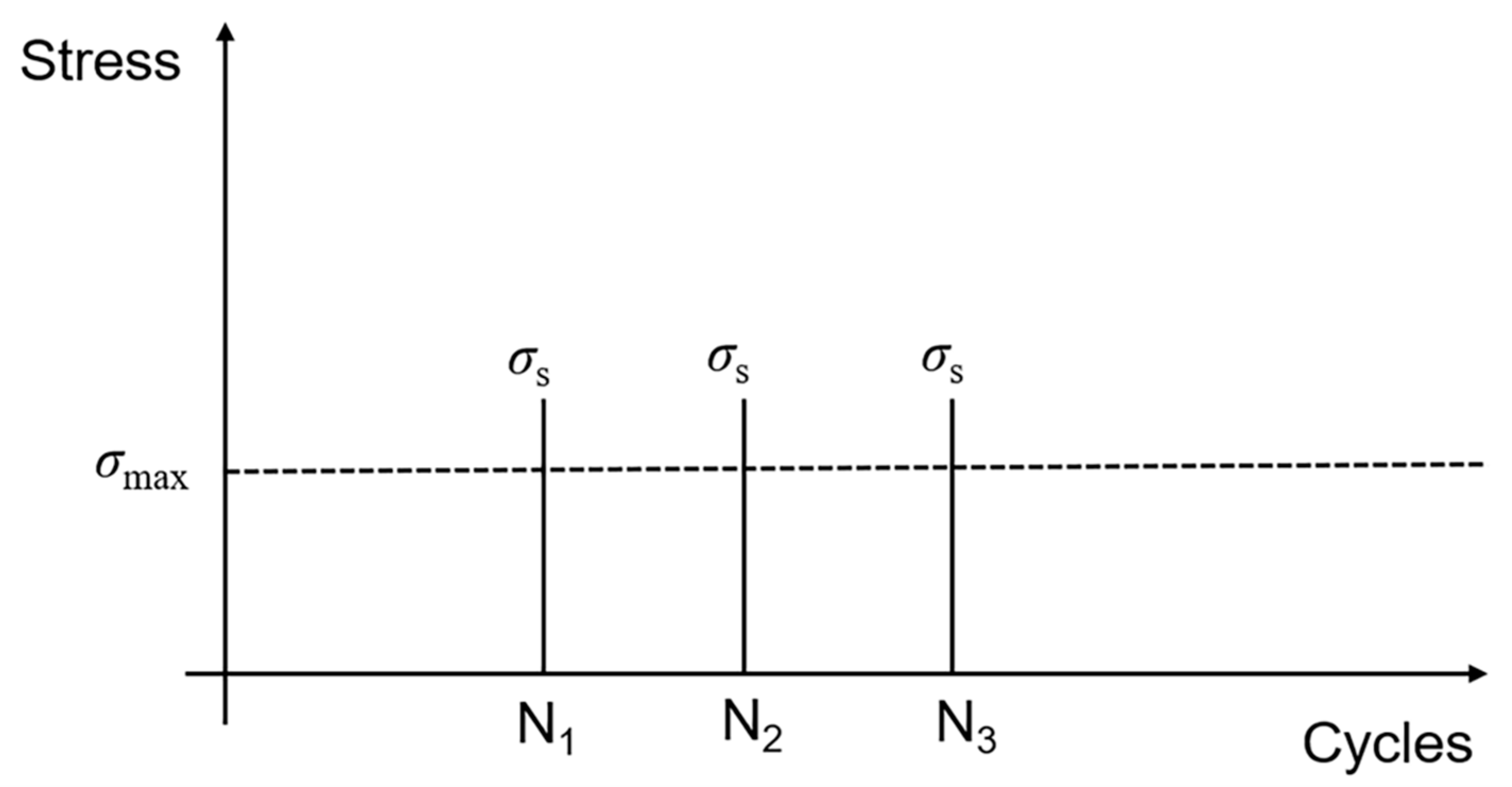
2. Theoretical Model
3. Experimental Comparisons
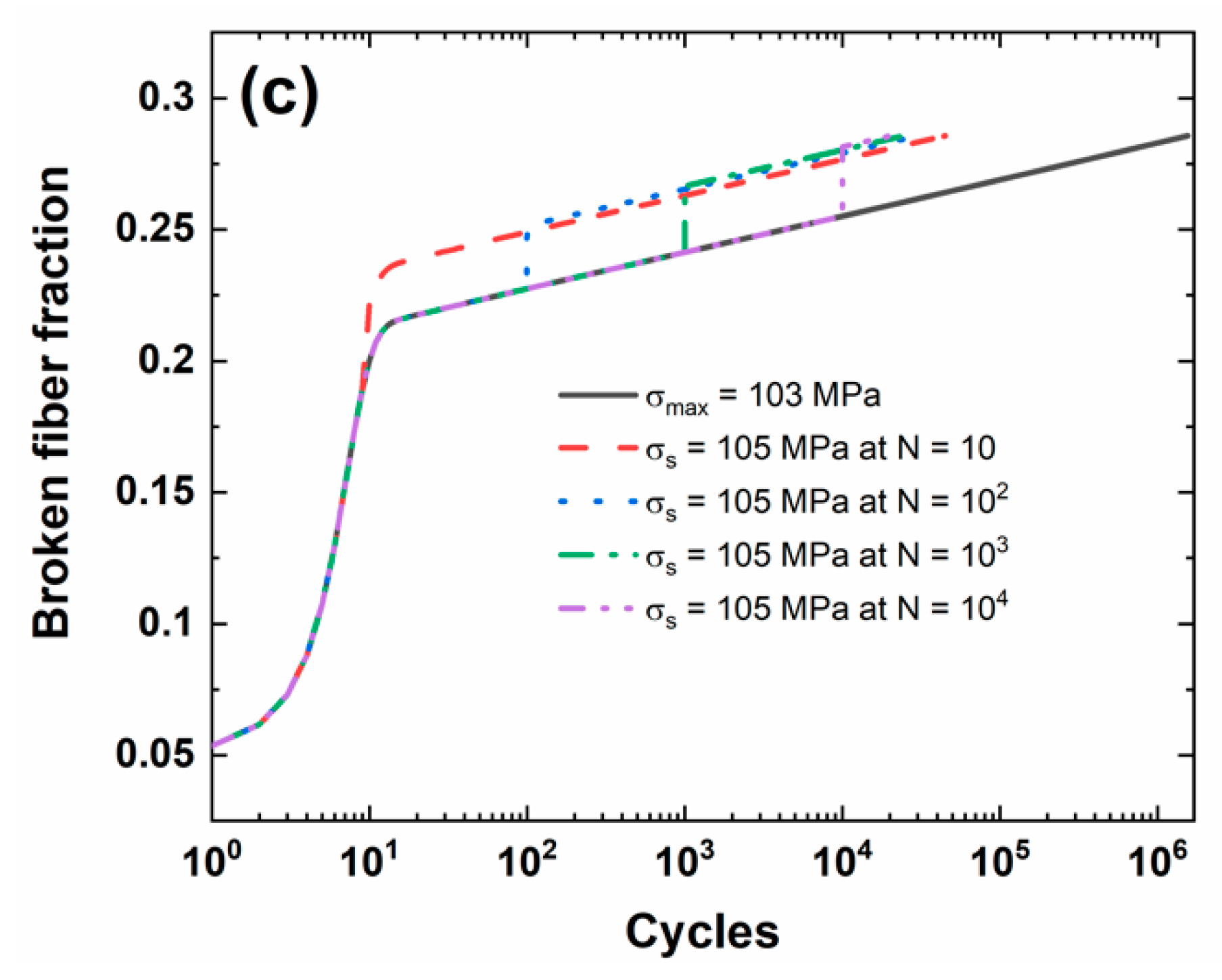
3.1. Unidirectional C/SiC Composite
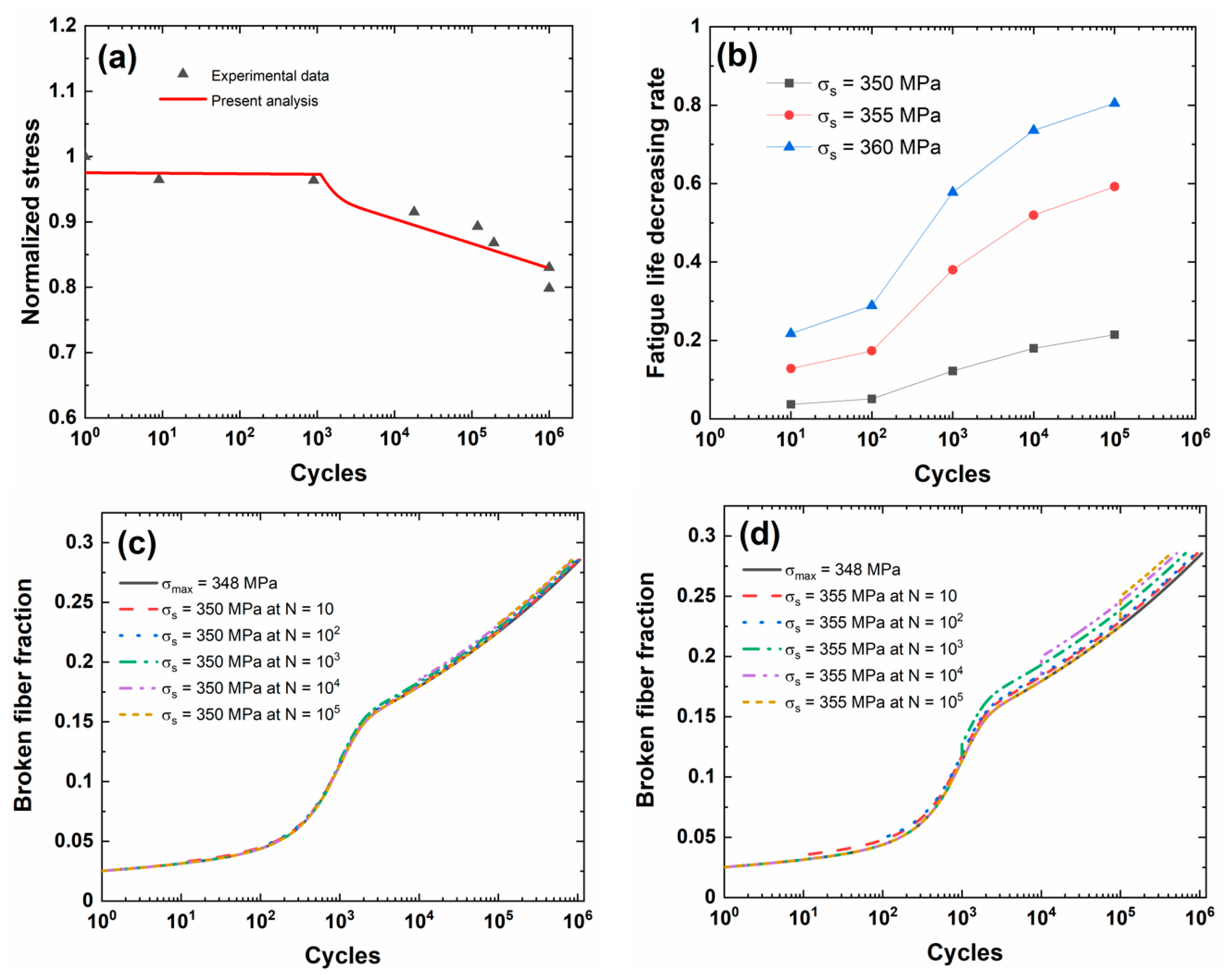
3.2. Cross-Ply C/SiC Composite
3.3. The 2D C/SiC Composite
3.4. The 2.5D C/SiC Composite
3.5. The 3D C/SiC Composite
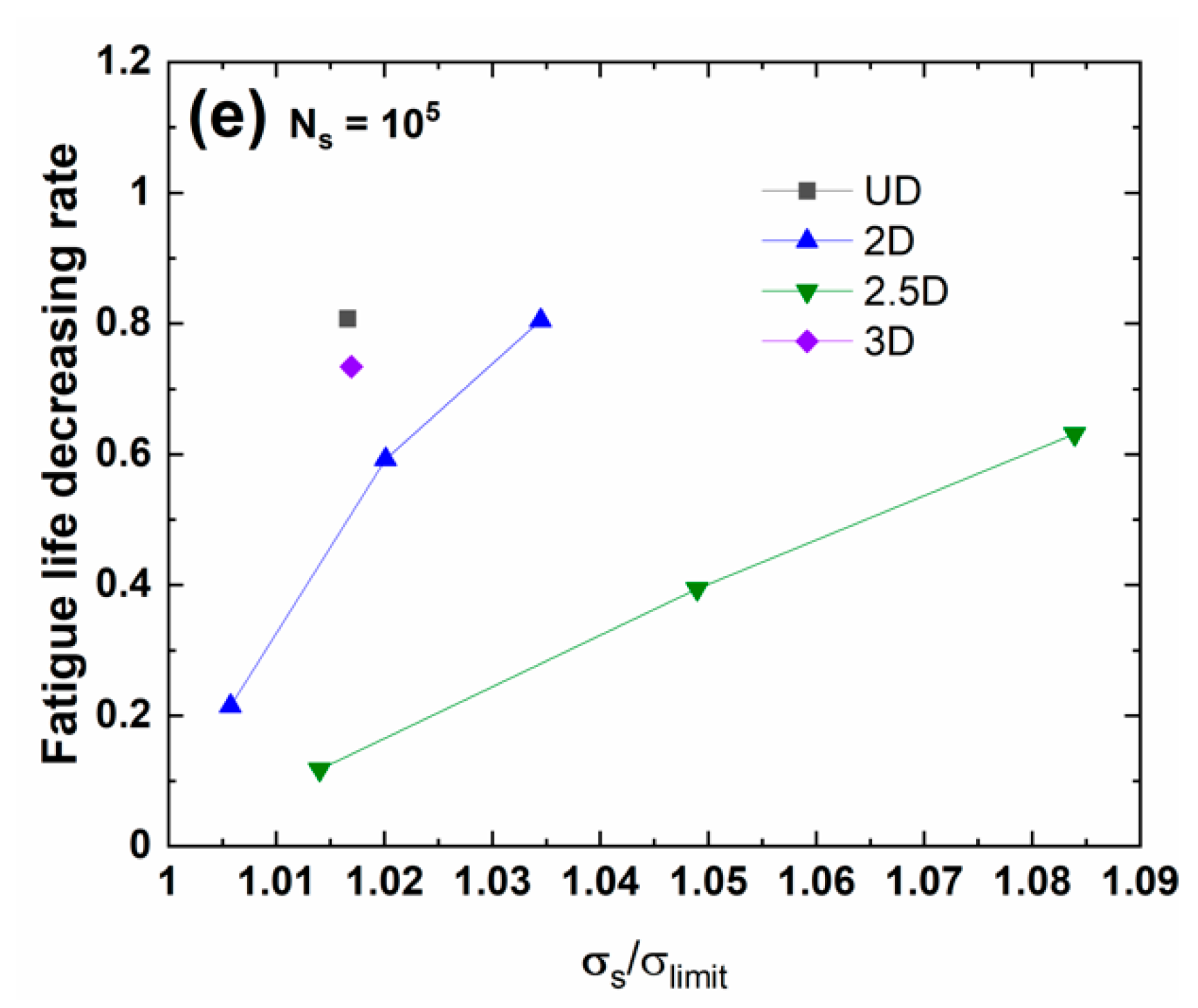
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Naslain, R. Design, Preparation and properties of non-oxide CMCs for application in engines and nuclear reactors: An overview. Compos. Sci. Technol. 2004, 64, 155–170. [Google Scholar] [CrossRef]
- Wing, B.L.; Halloran, J.W. Subsurface oxidation of boron nitride coatings on silicon carbide fibers in SiC/SiC ceramic matrix composites. Ceram. Int. 2018, 44, 17491–17505. [Google Scholar] [CrossRef]
- Li, L.B. Time-Dependent Mechanical Behavior of Ceramic-Matrix Composites at Elevated Temperatures; Springer Nature Singapore Pte Ltd.: Singapore, 2020. [Google Scholar]
- Li, L.B. Thermomechanical Fatigue of Ceramic-Matrix Composites; Wiley-VCH: Weinheim, Germany, 2019. [Google Scholar]
- Reynaud, P. Cyclic fatigue of ceramic-matrix composites at ambient and elevated temperatures. Compos. Sci. Technol. 1996, 56, 809–814. [Google Scholar] [CrossRef]
- Zhu, S.; Mizuno, M.; Kagawa, Y.; Mutoh, Y. Monotonic tension, fatigue and creep behavior of SiC-fiber-reinforced SiC-matrix composites: A review. Compos. Sci. Technol. 1999, 59, 833–851. [Google Scholar] [CrossRef]
- Li, L.B. Tension-tension fatigue behavior of unidirectional C/SiC ceramic-matrix composite at room and elevated temperature and 800 °C in air atmosphere. Materials 2015, 8, 3316–3333. [Google Scholar] [CrossRef] [Green Version]
- Yang, F. Research on Fatigue Behavior of 2.5d Woven Ceramic Matrix Composites. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, December 2011. [Google Scholar]
- Du, S.M.; Qiao, S.R.; Ji, G.C.; Han, D. Tension-tension fatigue behavior of 3D-C/SiC composite at room temperature and 1300 °C. Mater. Eng. 2002, 9, 22–25. [Google Scholar]
- Shuler, S.F.; Holmes, J.W.; Wu, X.; Roach, D. Influence of loading frequency on the room-temperature fatigue of a carbon-fiber/SiC-matrix composite. J. Am. Ceram. Soc. 1993, 76, 2327–2336. [Google Scholar] [CrossRef] [Green Version]
- Ruggles-Wrenn, M.B.; Christensen, D.T.; Chamberlain, A.L.; Lane, J.E.; Cook, T.S. Effect of frequency and environment on fatigue behavior of a CVI SiC/SiC ceramic matrix composite at 1200 °C. Compos. Sci. Technol. 2011, 71, 190–196. [Google Scholar] [CrossRef]
- Li, L.B.; Reynaud, P.; Fantozzi, G. Cyclic-dependent damage evolution in self-healing woven SiC/[Si-B-C] ceramic-matrix composites at elevated temperatures. Materials 2020, 13, 1478. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.B. Damage evolution and life prediction of cross-ply C/SiC ceramic-matrix composite under cyclic fatigue loading at room temperature and 800 °C in air. Materials 2015, 8, 8539–8560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruggles-Wrenn, M.B.; Sharma, V. Effects of steam environment on fatigue behavior of two SiC/[SiC+Si3N4] ceramic composites at 1300 °C. Appl. Compos. Mater. 2011, 18, 385–396. [Google Scholar] [CrossRef]
- Ruggles-Wrenn, M.B.; Lee, M.D. Fatigue behavior of an advanced SiC/SiC ceramic composite with a self-healing matrix at 1300 °C in air and in steam. Mater. Sci. Eng. A 2016, 677, 438–445. [Google Scholar] [CrossRef]
- Ruggles-Wrenn, M.B.; Boucher, N.; Przybyla, C. Fatigue of three advanced SiC/SiC ceramic matrix composites at 1200 °C in air and in steam. Int. J. Appl. Ceram. Technol. 2018, 15, 3–15. [Google Scholar] [CrossRef]
- Suzuki, T.; Mahfuz, H.; Takanashi, M. A new stiffness degradation model for fatigue life prediction of GFRPs under random loading. Int. J. Fatigue 2019, 119, 220–228. [Google Scholar] [CrossRef]
- Li, L.B. Stress-rupture of fiber-reinforced ceramic-matrix composites with stochastic loading at intermediate temperatures. Part I: Theoretical analysis. Materials 2019, 12, 3123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evans, A.G. Design and life prediction issues for high-temperature engineering ceramics and their composites. Acta Mater. 1997, 45, 23–40. [Google Scholar] [CrossRef]
- Li, L.B. Fatigue life prediction of carbon fiber-reinforced ceramic-matrix composites at room and elevated temperatures. Part I: Experimental analysis. Appl. Compos. Mater. 2016, 23, 101–117. [Google Scholar] [CrossRef]
- Li, L.B. Fatigue life prediction of carbon fiber-reinforced ceramic-matrix composites at room and elevated temperatures. Part II: Experimental comparisons. Appl. Compos. Mater. 2015, 22, 961–972. [Google Scholar]
- Li, L.B. Fatigue life prediction of fiber-reinforced ceramic-matrix composites with different fiber preforms at room and elevated temperatures. Materials 2016, 9, 207. [Google Scholar] [CrossRef] [Green Version]
- Curtin, W.A. Theory of mechanical properties of ceramic-matrix composites. J. Am. Ceram. Soc. 1991, 74, 2837–2845. [Google Scholar] [CrossRef]








| Items | Unidirectional [7] | Cross-Ply [13] | 2D [10] | 2.5D [8] | 3D [9] |
|---|---|---|---|---|---|
| Manufacturing Process | Hot Pressing | Hot Pressing | Chemical Vapor Infiltration (CVI) | CVI | CVI |
| Stress Ratio | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Frequency/(Hz) | 10 | 10 | 10 | 10 | 60 |
| Fiber Type | T−700TM | T−700TM | T−300TM | T−300TM | T−300TM |
| Vf | 0.4 | 0.4 | 0.45 | 0.4 | 0.4 |
| σuts1/(MPa) | 270 | 124 | 420 | 225 | 276 |
| rf2/(μm) | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 |
| τio 3/(MPa) | 8 | 6.2 | 25 | 20 | 20 |
| τimin 4/(MPa) | 0.3 | 1.5 | 8 | 8 | 5 |
| ω5 | 0.04 | 0.06 | 0.002 | 0.001 | 0.02 |
| Λ 5 | 1.5 | 1.8 | 1.0 | 1.0 | 1.0 |
| p16 | 0.01 | 0.01 | 0.018 | 0.02 | 0.012 |
| p26 | 1.0 | 0.8 | 1.0 | 1.2 | 1.0 |
| m7 | 5 | 5 | 5 | 5 | 5 |
| σmax = 241 MPa | Nf2 | N3 = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,431,993 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.20077 | 0.22431 | 0.25085 | |
| σs1 = 245 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,225,895 | Pf | 0.00609 | 0.02329 | 0.18207 | 0.20294 | 0.22648 | 0.25302 | |
| σs = 245 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 418,087 | Pf | 0.00609 | 0.02113 | 0.19662 | 0.21749 | 0.24103 | 0.26757 | |
| σs = 245 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 368,186 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.21915 | 0.24269 | 0.26923 | |
| σs = 245 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 320,486 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.20077 | 0.2445 | 0.27104 | |
| σs = 245 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 275,798 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.20077 | 0.22431 | 0.27298 | |
| σs = 250 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 989,365 | Pf | 0.00609 | 0.02626 | 0.18504 | 0.2059 | 0.22944 | 0.25598 | |
| σs = 250 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 70,700 | Pf | 0.00609 | 0.02113 | 0.21897 | 0.23983 | 0.26338 | 0.28571 | |
| σs = 250 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 51,311 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.24365 | 0.26719 | 0.28571 | |
| σs = 250 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 36,095 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.20077 | 0.27131 | 0.28571 | |
| σs = 255 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 779,144 | Pf | 0.00609 | 0.02952 | 0.1883 | 0.20917 | 0.23271 | 0.25925 | |
| σs = 255 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 8593 | ||
| 8593 | Pf | 0.00609 | 0.02113 | 0.24295 | 0.26381 | 0.28571 | ||
| σs = 255 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 4870 | ||
| 4870 | Pf | 0.00609 | 0.02113 | 0.17991 | 0.26984 | 0.28571 |
| σmax = 103 MPa | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
|---|---|---|---|---|---|---|---|---|
| 1,568,296 | Pf | 0.05349 | 0.20047 | 0.22748 | 0.24133 | 0.25508 | 0.26892 | |
| σs = 105 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 45,256 | |
| 45,256 | Pf | 0.05349 | 0.22205 | 0.24906 | 0.26291 | 0.27666 | 0.28571 | |
| σs = 105 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 30,243 | |
| 30,243 | Pf | 0.05349 | 0.20047 | 0.25148 | 0.26533 | 0.27908 | 0.28571 | |
| σs = 105 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 24,787 | |
| 24,787 | Pf | 0.05349 | 0.20047 | 0.22748 | 0.26653 | 0.28028 | 0.28571 | |
| σs = 105 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 20,455 | |
| 20,455 | Pf | 0.05349 | 0.20047 | 0.22748 | 0.24133 | 0.28143 | 0.28571 |
| σmax = 348 MPa | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
|---|---|---|---|---|---|---|---|---|
| 1,067,612 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.1795 | 0.22527 | |
| σs = 350 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,028,121 | Pf | 0.02529 | 0.03261 | 0.04505 | 0.11466 | 0.18059 | 0.22635 | |
| σs = 350 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,013,262 | Pf | 0.02529 | 0.03153 | 0.04547 | 0.11508 | 0.18101 | 0.22677 | |
| σs = 350 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 937,226 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11731 | 0.18323 | 0.229 | |
| σs = 350 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 875,603 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.18516 | 0.23093 | |
| σs = 350 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 838,274 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.1795 | 0.23215 | |
| σs = 355 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 930,683 | Pf | 0.02529 | 0.03546 | 0.0479 | 0.11751 | 0.18342 | 0.2292 | |
| σs = 355 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 882,390 | Pf | 0.02529 | 0.03153 | 0.04941 | 0.11902 | 0.18493 | 0.23071 | |
| σs = 355 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 661,586 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.12704 | 0.19295 | 0.23873 | |
| σs = 355 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 513,025 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.19983 | 0.24561 | |
| σs = 355 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 435,308 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.17949 | 0.24996 | |
| σs = 360 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 835,692 | Pf | 0.02529 | 0.0385 | 0.05094 | 0.12055 | 0.18646 | 0.23224 | |
| σs = 360 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 759,497 | Pf | 0.02529 | 0.03153 | 0.05361 | 0.12323 | 0.18914 | 0.23491 | |
| σs = 360 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 450,695 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.13736 | 0.20327 | 0.24905 | |
| σs = 360 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 282,293 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.2153 | 0.26108 | |
| σs = 360 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 208,007 | Pf | 0.02529 | 0.03153 | 0.04397 | 0.11358 | 0.17949 | 0.26861 |
| σmax = 143 MPa | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
|---|---|---|---|---|---|---|---|---|
| 1,012,346 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.07519 | 0.14038 | |
| σs = 145 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,005,026 | Pf | 0.00574 | 0.00834 | 0.01317 | 0.03724 | 0.07585 | 0.14105 | |
| σs = 145 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,000,463 | Pf | 0.00574 | 0.00767 | 0.01359 | 0.03766 | 0.07627 | 0.14146 | |
| σs = 145 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 978,311 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03969 | 0.0783 | 0.1435 | |
| σs = 145 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 944,705 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.08145 | 0.14664 | |
| σs = 145 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 893,212 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.07519 | 0.15161 | |
| σs = 150 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 984,589 | Pf | 0.00574 | 0.01021 | 0.01504 | 0.03911 | 0.07772 | 0.14292 | |
| σs = 150 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 967,500 | Pf | 0.00574 | 0.00767 | 0.01663 | 0.0407 | 0.07931 | 0.1445 | |
| σs = 150 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 886,901 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.04842 | 0.08703 | 0.15223 | |
| σs = 150 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 772,084 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.09888 | 0.16408 | |
| σs = 150 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 613,579 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.07519 | 0.1825 | |
| σs = 155 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 960,848 | Pf | 0.00574 | 0.01241 | 0.01725 | 0.04132 | 0.07993 | 0.14512 | |
| σs = 155 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 929,613 | Pf | 0.00574 | 0.00767 | 0.02021 | 0.04427 | 0.08288 | 0.14808 | |
| σs = 155 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 787,301 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.05864 | 0.09725 | 0.16245 | |
| σs = 155 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 599,723 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.11905 | 0.18425 | |
| σs = 155 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 373,608 | Pf | 0.00574 | 0.00767 | 0.01251 | 0.03658 | 0.07519 | 0.21754 |
| σmax = 236 MPa | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
|---|---|---|---|---|---|---|---|---|
| 1,383,192 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.18509 | 0.2122 | 0.24367 | |
| σs = 240 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 1,066,666 | Pf | 0.03314 | 0.04771 | 0.12242 | 0.18957 | 0.21668 | 0.24815 | |
| σs = 240 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 696,321 | Pf | 0.03314 | 0.04324 | 0.12961 | 0.19676 | 0.22387 | 0.25534 | |
| σs = 240 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 488,262 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.2026 | 0.22971 | 0.26118 | |
| σs = 240 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 426,789 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.18509 | 0.23189 | 0.26336 | |
| σs = 240 MPa N = 105 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 367,609 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.18509 | 0.2122 | 0.26575 | |
| σs = 245 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 742,891 | Pf | 0.03314 | 0.05383 | 0.12853 | 0.19568 | 0.22279 | 0.25426 | |
| σs = 245 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 262,035 | Pf | 0.03314 | 0.04324 | 0.14538 | 0.21253 | 0.23963 | 0.2711 | |
| σs = 245 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 107,854 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.22602 | 0.25313 | 0.2846 | |
| σs = 245 MPa N = 104 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 76,689 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.18509 | 0.25812 | 0.28571 | |
| σs = 250 MPa N = 10 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 494,186 | Pf | 0.03314 | 0.06055 | 0.13525 | 0.2024 | 0.22951 | 0.26098 | |
| σs = 250 MPa N = 102 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 84,191 | Pf | 0.03314 | 0.04324 | 0.1625 | 0.22966 | 0.25676 | 0.28571 | |
| σs = 250 MPa N = 103 | Nf | N = 1 | N = 10 | N = 102 | N = 103 | N = 104 | N = 105 | |
| 17,798 | Pf | 0.03314 | 0.04324 | 0.11794 | 0.25116 | 0.27827 | 0.28571 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L. A Micromechanical Fatigue Limit Stress Model of Fiber-Reinforced Ceramic-Matrix Composites under Stochastic Overloading Stress. Materials 2020, 13, 3304. https://doi.org/10.3390/ma13153304
Li L. A Micromechanical Fatigue Limit Stress Model of Fiber-Reinforced Ceramic-Matrix Composites under Stochastic Overloading Stress. Materials. 2020; 13(15):3304. https://doi.org/10.3390/ma13153304
Chicago/Turabian StyleLi, Longbiao. 2020. "A Micromechanical Fatigue Limit Stress Model of Fiber-Reinforced Ceramic-Matrix Composites under Stochastic Overloading Stress" Materials 13, no. 15: 3304. https://doi.org/10.3390/ma13153304
APA StyleLi, L. (2020). A Micromechanical Fatigue Limit Stress Model of Fiber-Reinforced Ceramic-Matrix Composites under Stochastic Overloading Stress. Materials, 13(15), 3304. https://doi.org/10.3390/ma13153304





