Active IR Thermography Evaluation of Coating Thickness by Determining Apparent Thermal Effusivity
Abstract
:1. Introduction
2. Apparent Thermal Effusivity Implementation
3. Analytical Model
4. Experimental Setup
5. Results and Discussion
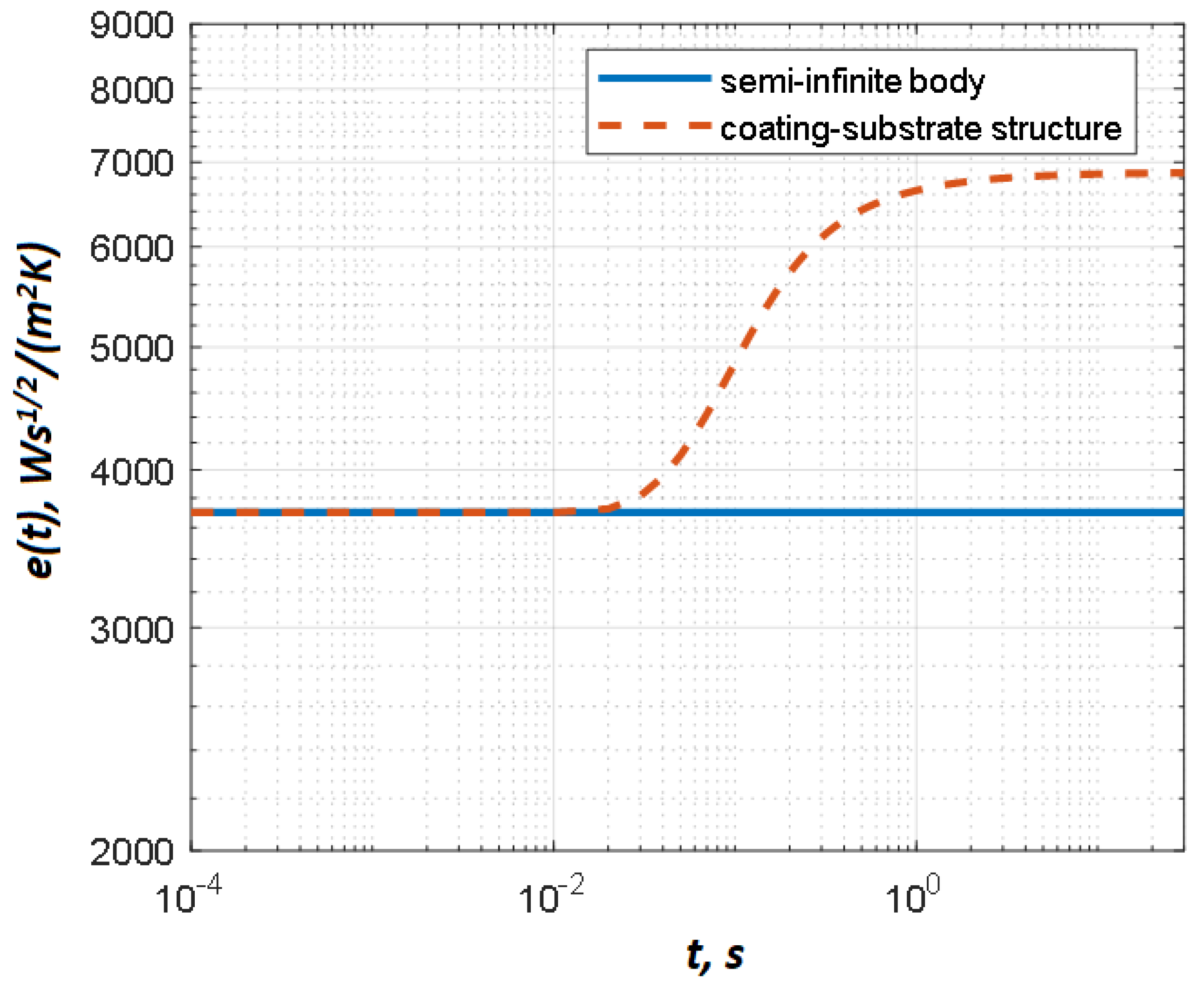
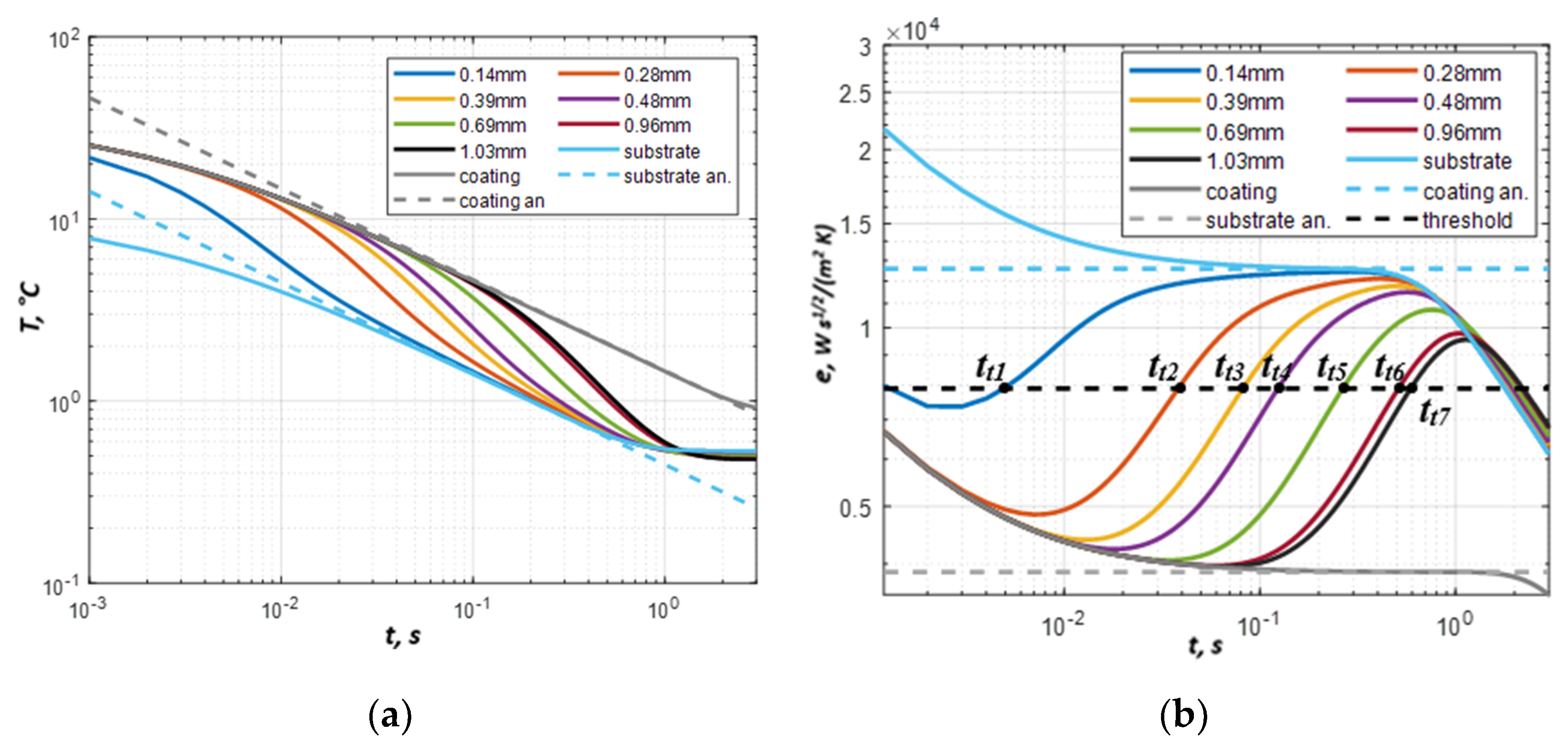
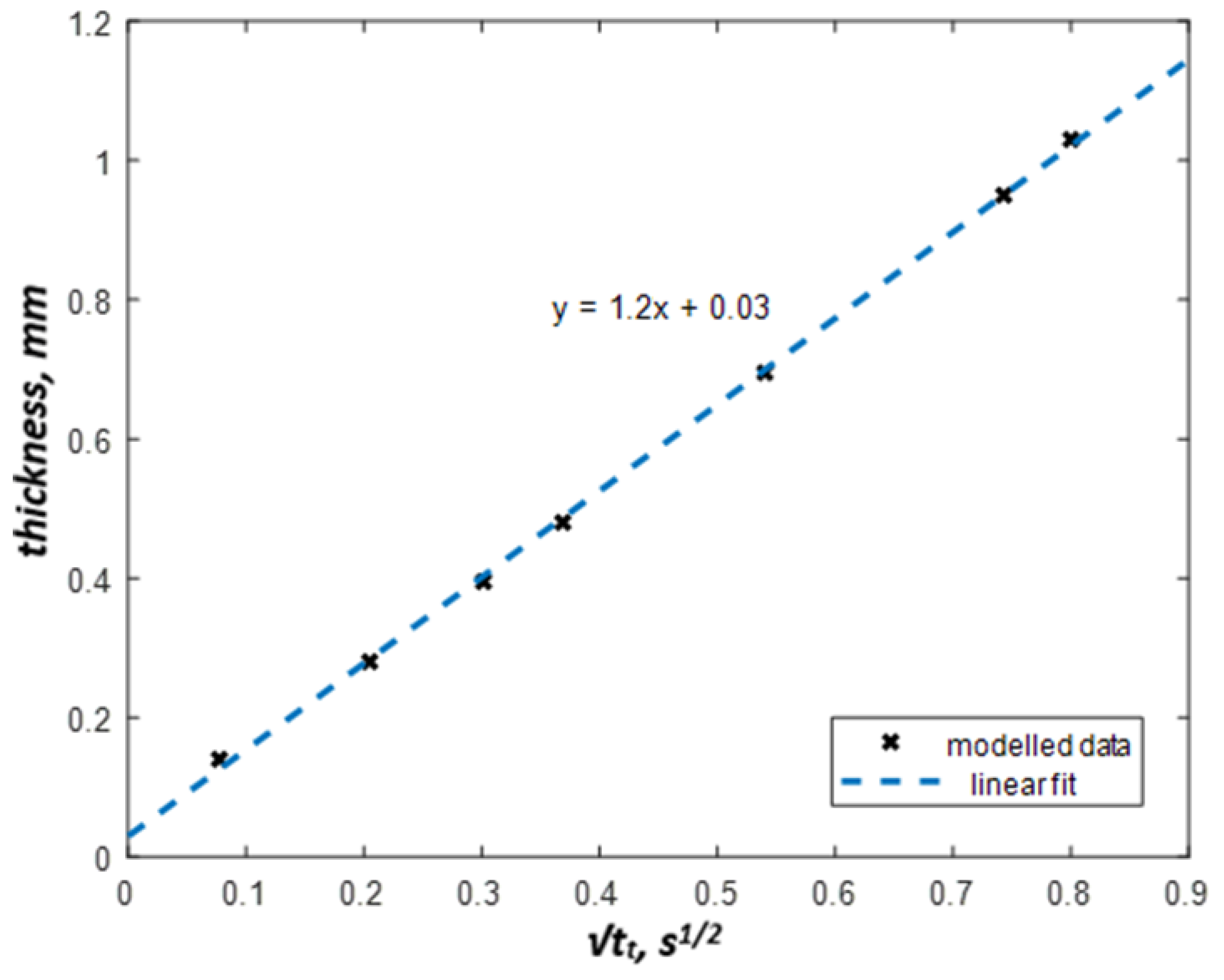
5.1. Modeling Results
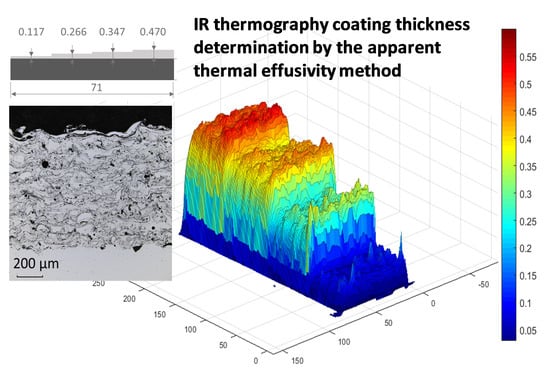
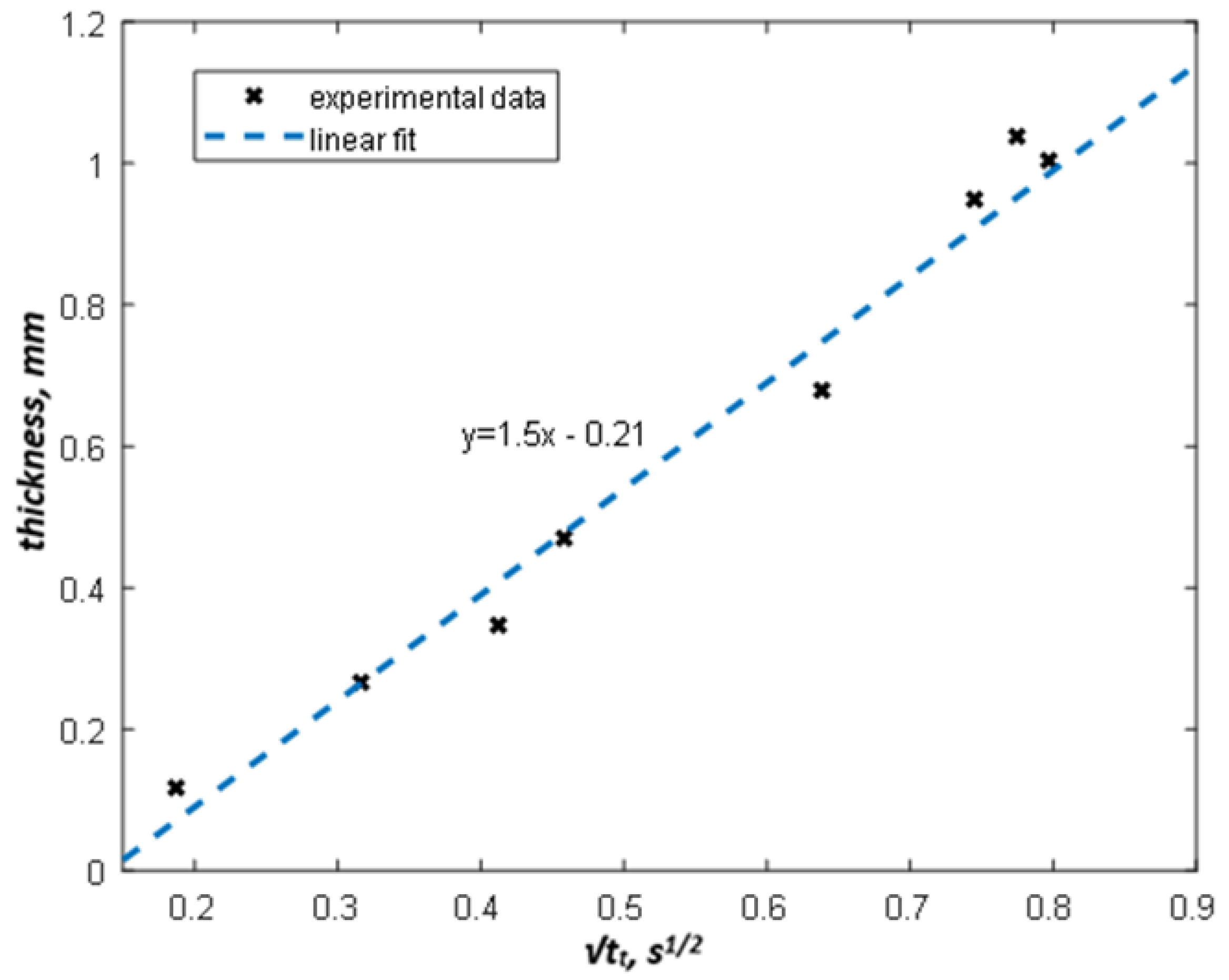
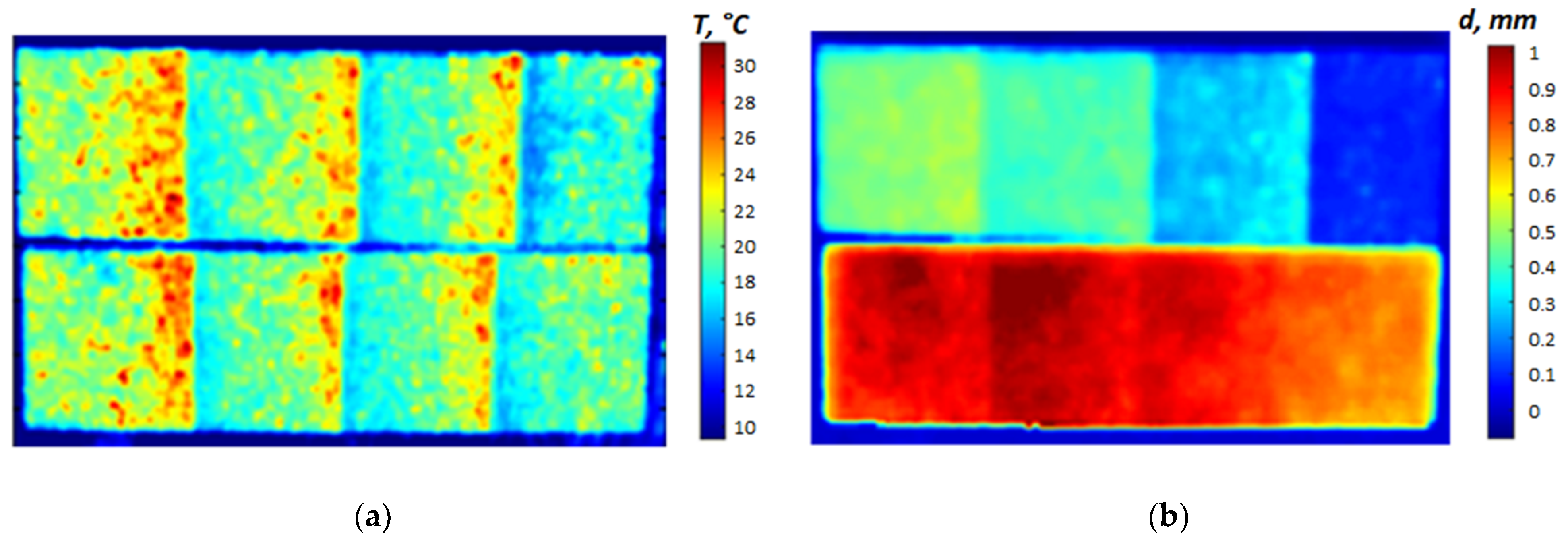
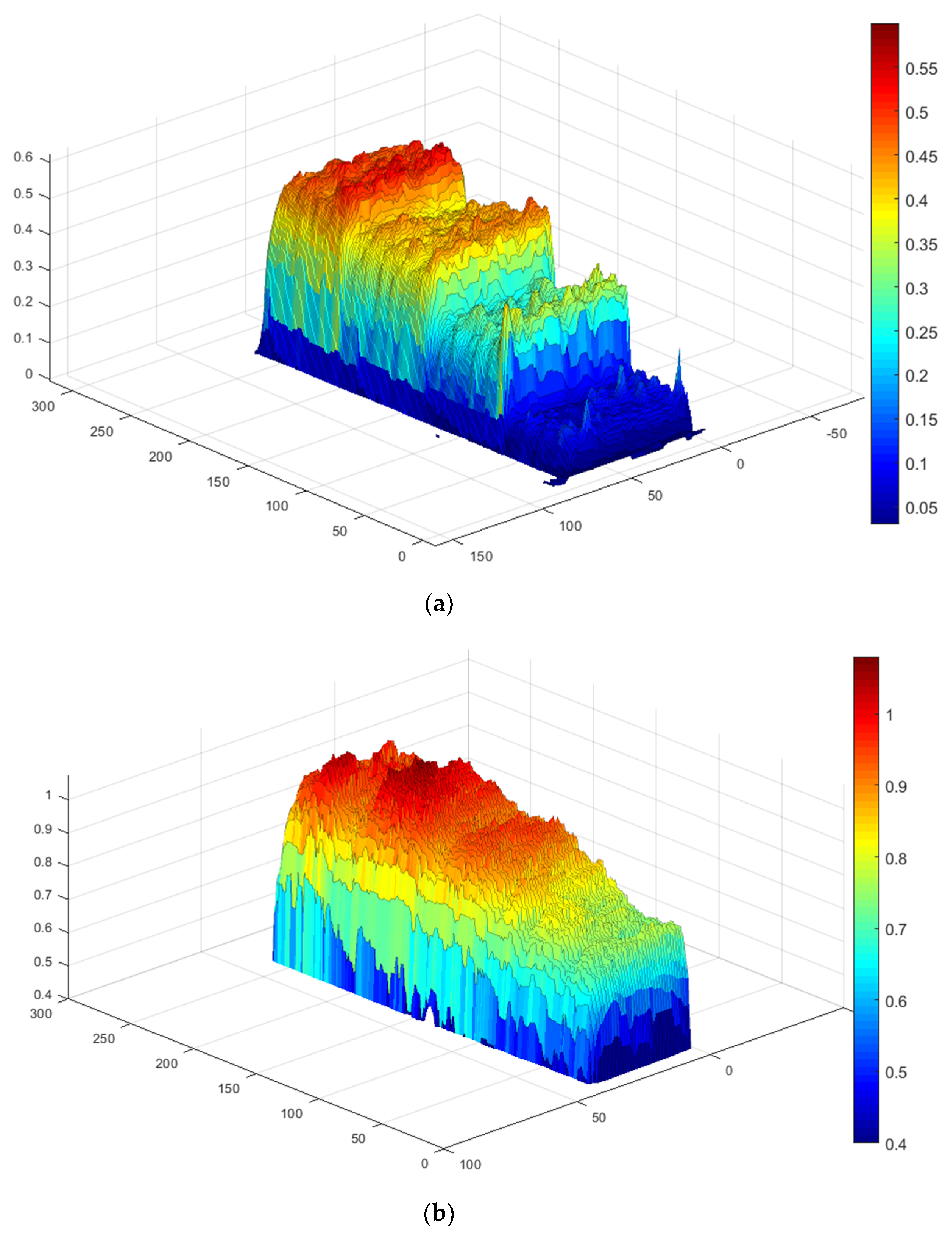
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parker, G. Encyclopedia of materials: Science and technology. In Guide-Wave Optical Communications: Materials; Elsevier: Amsterdam, The Netherlands, 2001; pp. 3703–3707. [Google Scholar]
- Kutz, M. Handbook of Environmental Degradation of Materials; William Andrew: Amsterdam, The Netherlands, 2018. [Google Scholar]
- García-Martín, J.; Gomez-Gil, J.; Vazquez-Sanchez, E. Non-destructive techniques based on eddy current testing. Sensors 2011, 11, 2525–2565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russe, I.-S.; Brock, D.; Knop, K.; Kleinebudde, P.; Zeitler, J.A. Validation of terahertz coating thickness measurements using X-ray microtomography. Mol. Pharm. 2012, 9, 3551–3559. [Google Scholar] [CrossRef] [PubMed]
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; Wiley-Interscience: New York, NY, USA, 2001. [Google Scholar]
- Vavilov, V.P.; Burleigh, D.D. Review of pulsed thermal NDT: Physical principles, theory and data processing. NDT E Int. 2015, 73, 28–52. [Google Scholar] [CrossRef]
- Shrestha, R.; Kim, W. Evaluation of coating thickness by thermal wave imaging: A comparative study of pulsed and lock-in infrared thermography—Part I: Simulation. Infrared Phys. Technol. 2017, 83, 124–131. [Google Scholar] [CrossRef]
- Tang, Q.; Liu, J.; Dai, J.; Yu, Z. Theoretical and experimental study on thermal barrier coating (TBC) uneven thickness detection using pulsed infrared thermography technology. Appl. Therm. Eng. 2017, 114, 770–775. [Google Scholar] [CrossRef]
- Ranjit, S.; Chung, Y.; Kim, W. Thermal behavior variations in coating thickness using pulse phase thermography. J. Korean Soc. Nondestruct. Test. 2016, 36, 259–265. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.-B.; Zhang, C.-L.; Wu, N.-M.; Wang, H.-M. Quality evaluation for air plasma spray thermal barrier coatings with pulsed thermography. Prog. Nat. Sci. 2011, 21, 301–306. [Google Scholar] [CrossRef] [Green Version]
- Svantner, M.; Muzika, L.; Houdková, Š. Quantitative inspection of coatings thickness by time-power transformation flash pulse thermographic method. Proc. 2019, 27, 32. [Google Scholar] [CrossRef] [Green Version]
- Bison, P.G.; Marinetti, S.; Grinzato, E.G.; Vavilov, V.P.; Cernuschi, F.; Robba, D. Inspecting thermal barrier coatings by IR thermography. In Thermosense XXV; International Society for Optics and Photonics: Bellingham, WA, USA, 2003. [Google Scholar] [CrossRef]
- Winfree, W.P.; Cramer, K.E.; Howell, P.A.; Burke, E.R. Principal component analysis of thermographic data. In Thermosense: Thermal Infrared Applications XXXVII; International Society for Optics and Photonics: Bellingham, WA, USA, 2015. [Google Scholar]
- Balageas, D.L.; Krapez, J.-C.; Cielo, P. Pulsed photothermal modeling of layered materials. J. Appl. Phys. 1986, 59, 348–357. [Google Scholar] [CrossRef]
- Cernuschi, F.; Marinetti, S. Discrimination between over-thickness and delamination of thermal barrier coatings by apparent thermal effusivity thermographic technique. J. Therm. Spray Technol. 2010, 19, 958–963. [Google Scholar] [CrossRef]
- Marinetti, S.; Robba, D.; Cernuschi, F.; Bison, P.G.; Grinzato, E. Thermographic inspection of TBC coated gas turbine blades: Discrimination between coating over-thicknesses and adhesion defects. Infrared Phys. Technol. 2007, 49, 281–285. [Google Scholar] [CrossRef]
- Boué, C.; Fournier, D. Infrared thermography measurement of the thermal parameters (effusivity, diffusivity and conductivity) of materials. Quant. Infrared Thermogr. J. 2009, 6, 175–188. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Almond, D.P.; Patel, P.; Patel, P.M. Photothermal Science and Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Sun, J. Method for Thermal Tomography of Thermal Effusivity from Pulsed Thermal Imaging. U.S. Patent 7,365,330, 29 April 2008. [Google Scholar]
- Maillet, D. Thermal Quadrupoles: Solving the Heat Equation through Integral Transforms; John Wiley & Sons Inc: Hoboken, NJ, USA, 2000. [Google Scholar]
- OVAKO. Material Data Sheet Steel Grade S235JR. 2017. Available online: https://steelnavigator.ovako.com/steel-grades/s235/ (accessed on 1 June 2020).
- Arizmendi-Morquecho, A.; Campa-Castilla, A.; Leyva-Porras, C.; Aguilar-Martínez, J.; Gutiérrez, G.V.; Moreno, K.; López, L.L. Microstructural characterization and wear properties of fe-based amorphous-crystalline coating deposited by twin wire arc spraying. Adv. Mater. Sci. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.H.; Zhou, Z.; Wang, G.H.; He, D.Y.; Bobzin, K.; Zhao, L.; Öte, M.; Königstein, T. Influence of feedstock materials and spray parameters on thermal conductivity of wire-arc-sprayed coatings. J. Mater. Eng. Perform. 2017, 26, 1108–1113. [Google Scholar] [CrossRef]
- Svantner, M.; Muzika, L.; Houdková, Š. Quantitative inspection of coating thickness by flash-pulse thermography and time-power transformation evaluation. Appl. Opt. 2020, 59, E29–E35. [Google Scholar] [CrossRef]

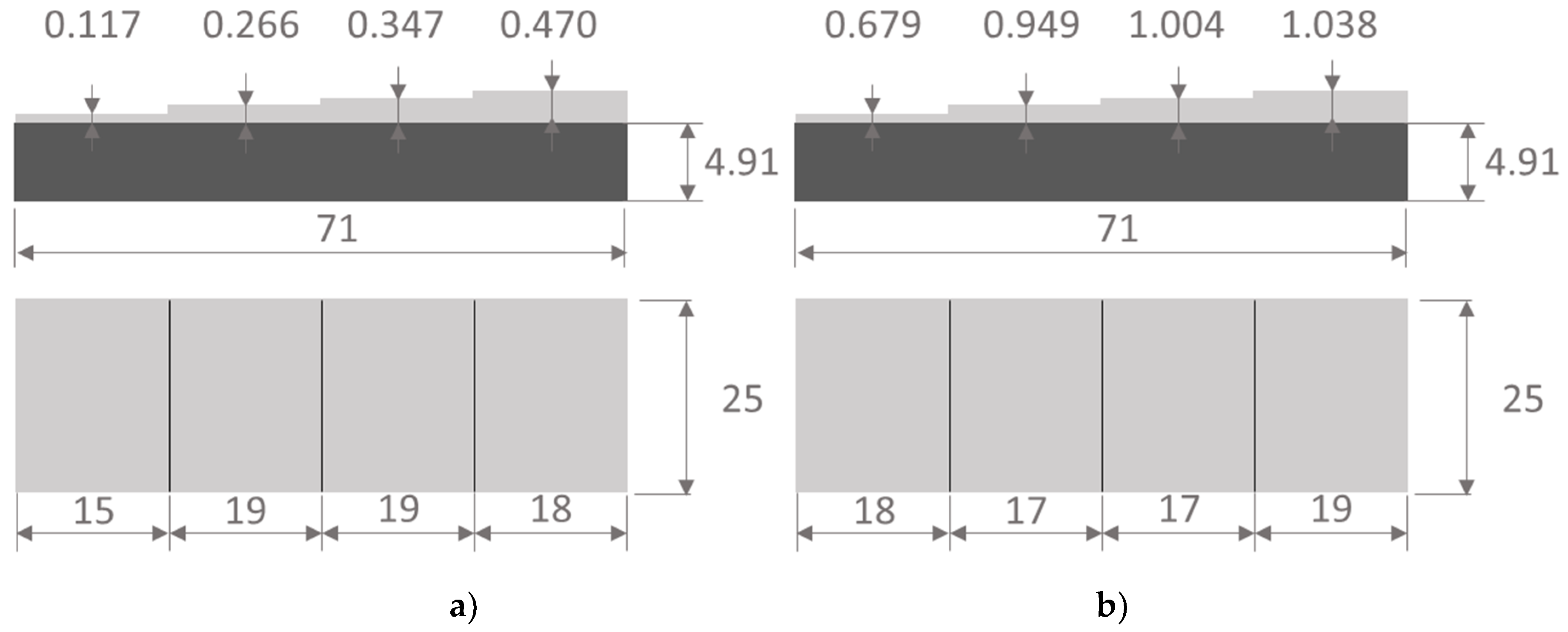


| Parameter | Coating | Substrate * |
|---|---|---|
| Thickness d, mm | 0.117, 0.266, 0.347, 0.470, 0.679, 0.949, 1.038 | 4.91 |
| Conductivity, W∙m∙K−1 | 6.12 | 40 |
| Diffusivity, m2 s−1 | 2.74 × 10−6 | 1.11 × 10−5 |
| Effusivity, W∙s1/2 m−2 K−1 | 0.37 × 104 | 1.21 × 104 |
| Area | Micrometry Thickness Measurement, µm | Thermography Thickness Measurement, µm | Difference, µm/% | ||||
|---|---|---|---|---|---|---|---|
| Min/Max Value | Mean | Standard Deviation | Min/Max Value | Mean | Standard Deviation | ||
| d1 | 77/176 | 117 | 37.7 | 71/179 | 93 | 12.5 | −24/−20.5 |
| d2 | 222/334 | 266 | 40.6 | 227/371 | 283 | 24.9 | 17/6.4 |
| d3 | 281/408 | 347 | 37.5 | 361/486 | 414 | 19.2 | 67/19.3 |
| d4 | 422/507 | 470 | 24.9 | 409/551 | 483 | 19.6 | 13/2.8 |
| d5 | 617/735 | 679 | 39.1 | 661/818 | 747 | 26.3 | 68/10 |
| d6 | 914/972 | 949 | 17.6 | 751/969 | 876 | 45.6 | −73/−7.7 |
| d7 | 948/1058 | 1004 | 39.4 | 818/1076 | 954 | 44.5 | −50/−5 |
| d8 | 987/1065 | 1038 | 24.6 | 799/1050 | 919 | 42.1 | −0.119/−11.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moskovchenko, A.; Vavilov, V.; Švantner, M.; Muzika, L.; Houdková, Š. Active IR Thermography Evaluation of Coating Thickness by Determining Apparent Thermal Effusivity. Materials 2020, 13, 4057. https://doi.org/10.3390/ma13184057
Moskovchenko A, Vavilov V, Švantner M, Muzika L, Houdková Š. Active IR Thermography Evaluation of Coating Thickness by Determining Apparent Thermal Effusivity. Materials. 2020; 13(18):4057. https://doi.org/10.3390/ma13184057
Chicago/Turabian StyleMoskovchenko, Alexey, Vladimir Vavilov, Michal Švantner, Lukáš Muzika, and Šárka Houdková. 2020. "Active IR Thermography Evaluation of Coating Thickness by Determining Apparent Thermal Effusivity" Materials 13, no. 18: 4057. https://doi.org/10.3390/ma13184057
APA StyleMoskovchenko, A., Vavilov, V., Švantner, M., Muzika, L., & Houdková, Š. (2020). Active IR Thermography Evaluation of Coating Thickness by Determining Apparent Thermal Effusivity. Materials, 13(18), 4057. https://doi.org/10.3390/ma13184057