Configuration of Novel Experimental Fractographic Reverse Engineering Approach Based on Relationship between Spectroscopy of Ruptured Surface and Fracture Behaviour of Rubber Sample
Abstract
:1. Introduction
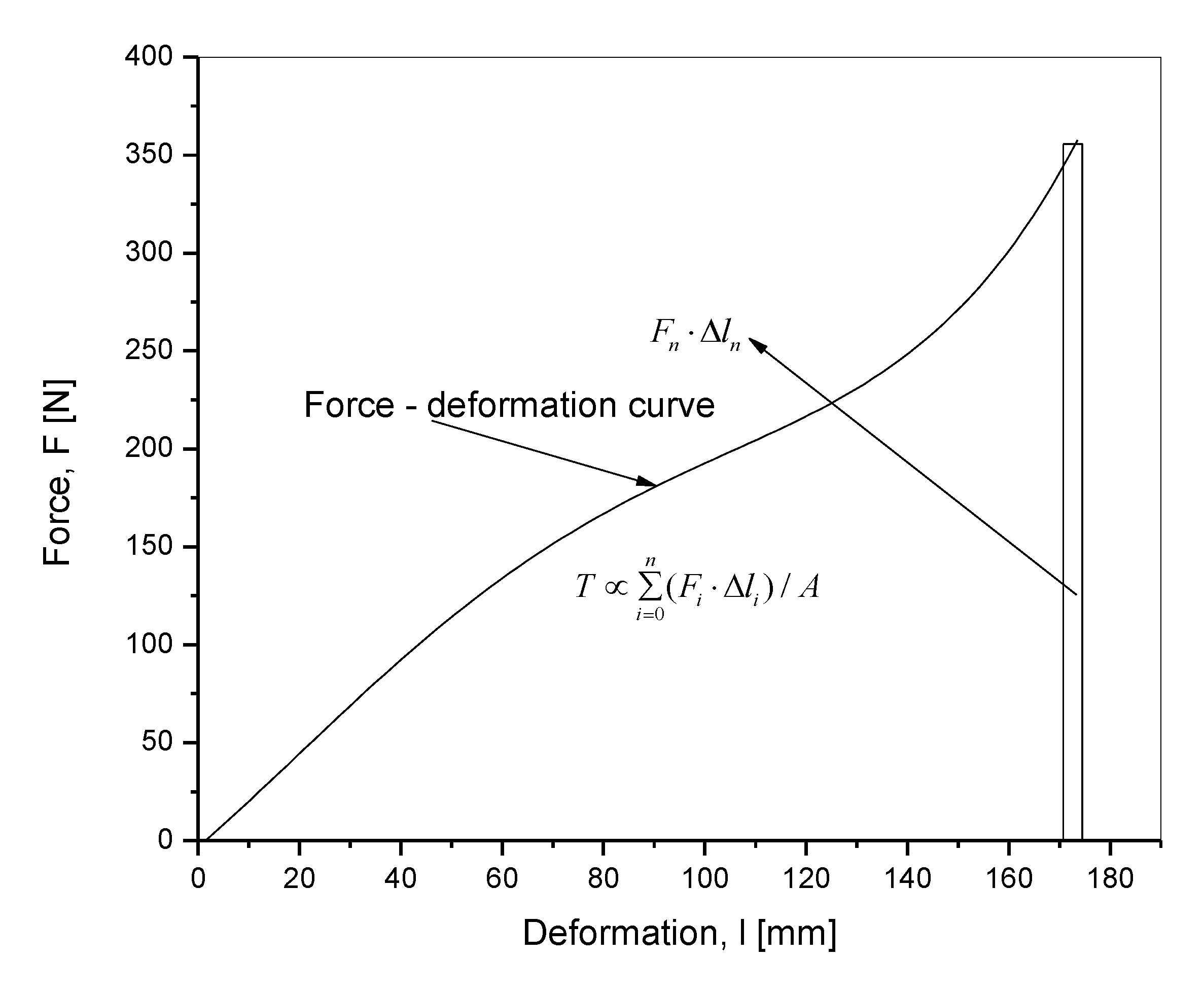
2. Materials and Methods
3. Results
4. Discussion
- (a)
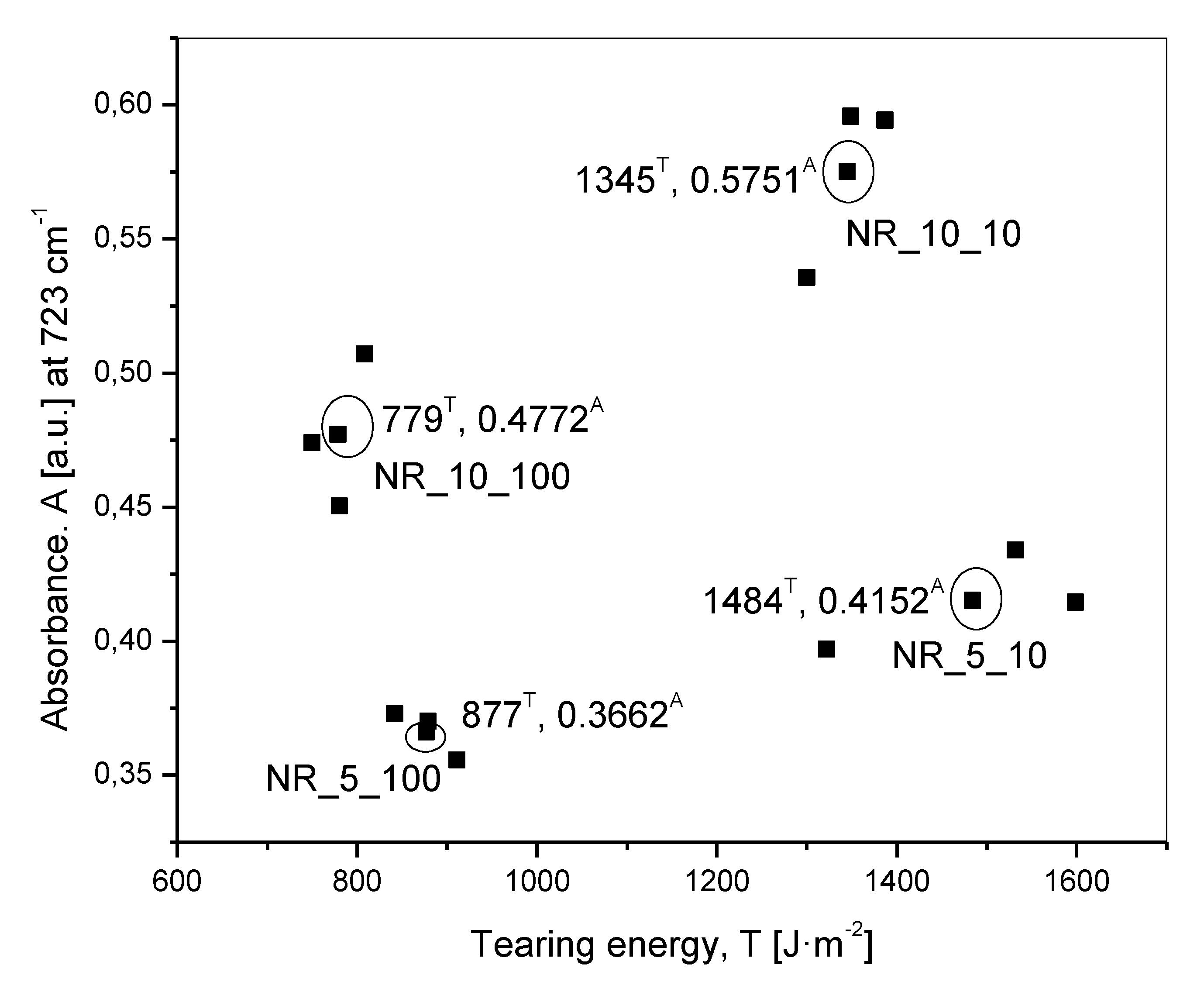
- At a fixed initial oil concentration, the deformation speed determined the tearing energy. The tearing energy was found to be higher at a slower deformation speed of 10 mm·min−1 compared to that at a faster deformation speed of 100 mm·min−1.
- (b)
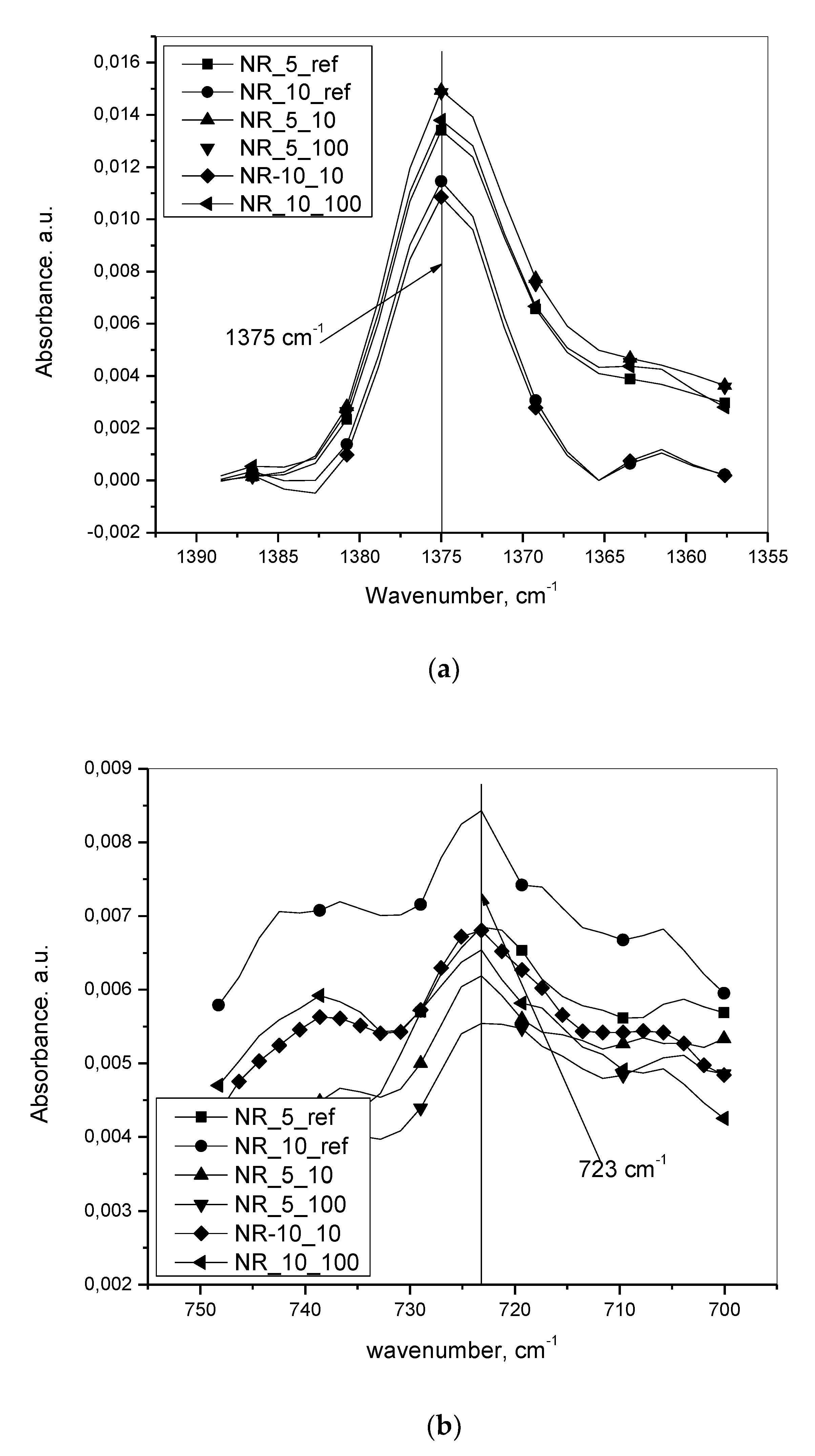
- The IR absorbance peak height at 723 cm−1 at a given initial oil concentration was more at slower deformation speed. This was the most important observation pertaining to the title of the present work
- (c)
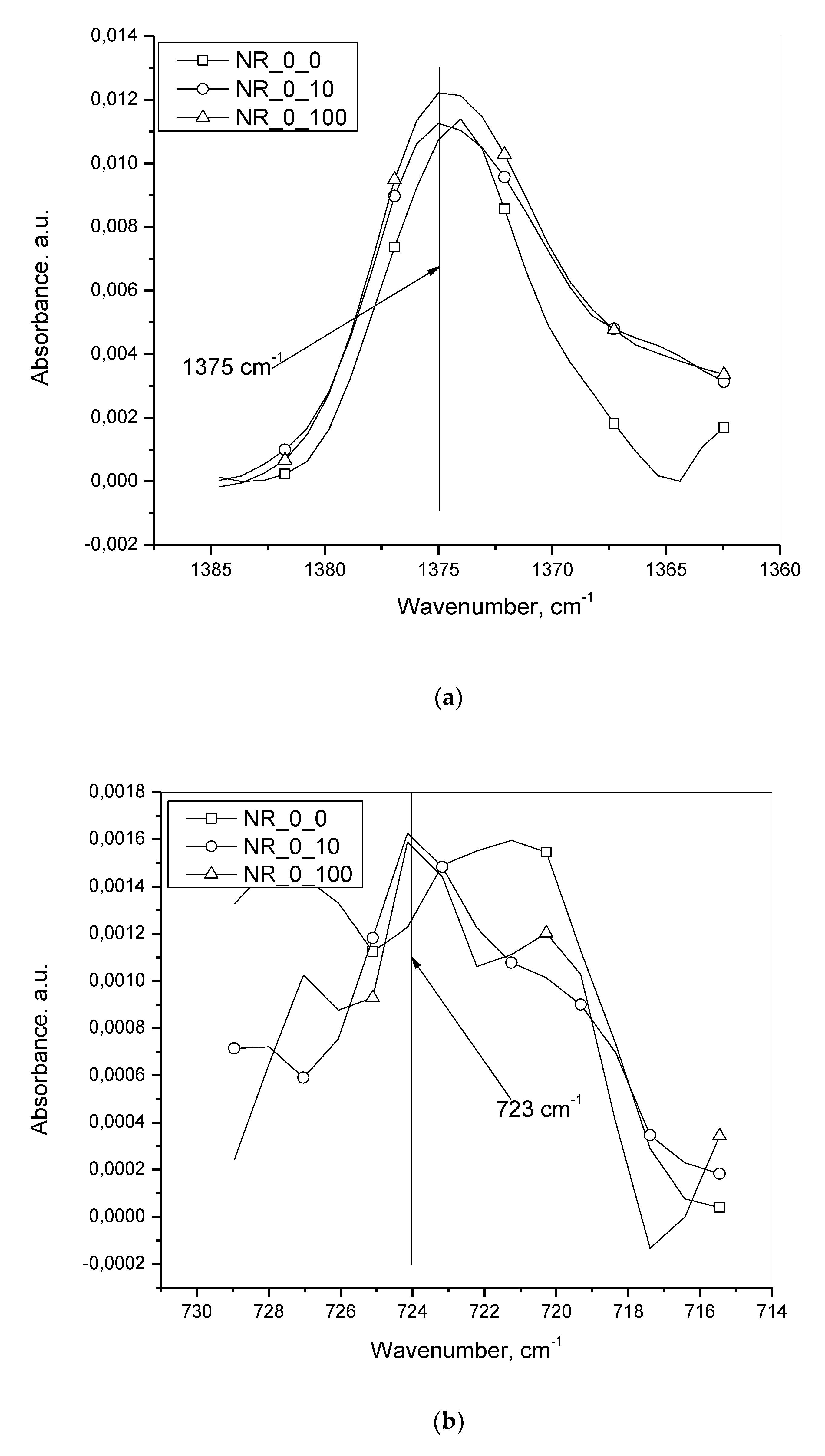
- With an increase in initial oil concentration at any of the two defined deformation speeds, the absorbance peak height for oil at 723 cm−1 increased. However, as reflected in Table 3, the ratio of this peak height for 5 and 10 phr of oil did not show up as 5/10, simplified to 1/2 (0.5). This was probably due to the presence of a compound in the rubber compounding which had a peak at the same wavenumber of 723 cm−1. In effect, 1/2 (0.5) worked out to (1+p)/(2+p) = 0.7, which is greater than 0.5, where p was the additional peak height from the compound. To prove that another compound was adding to this absorbance peak height, a set of experiments with no oil at three defined deformation speeds of 0, 10 and 100 mm·min−1 were done, the result of which is shown in Table 4. It shows that this additional peak height was almost a constant, in effect proving that even in the presence of another compound having a peak at the same wavenumber as that of the oil, the scientific approach of the work was not affected, meaning that even without the subtraction of this peak height from the peak height of oil, the conclusions of the present work remained unaffected.
- (d)
- At a given deformation speed, the tearing energy was higher for the lower initial concentration of the oil at 5 phr. This was attributed to the elongation at break, which was a little higher and at comparable elastic modulus (comparable slopes of all the force—displacement curves) an important parameter to determine the tearing energy.
- (e)
- The percent changes in tearing energy and IR absorbance peak height between 10 and 100 mm·min−1 deformation speeds as calculated in Equations (5) and (6), respectively, at any defined initial oil concentration after the incidence of rupture revealed an interesting trend. Calculations show that for 5 and 10 phr of oil, the percent changes in tearing energy were 69.21 and 72.66 respectively and the percent changes in IR peak height were 13.37 and 20.54, respectively. The results revealed that the percent changes in all the cases were positive, proving that after redistribution, more of a redistributed concentration of oil was observed at higher tearing energy or at lower deformation speed.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghosh, P.; Stoček, R.; Gehde, M.; Mukhopadhyay, R.; Krishnakumar, R. Investigation of fatigue crack growth characteristics of NR/BR blend based tyre tread compounds. Int. J. Fract. 2014, 188, 9–21. [Google Scholar] [CrossRef]
- Ghosh, P.; Mukhopadhyay, R.; Stocek, R. Durability prediction of NR/BR and NR/SBR blend tread compounds using tear fatigue analyser. Kgk-Kautschuk Gummi Kunststoffe 2016, 69, 53–55. [Google Scholar]
- Andreini, G.; Straffi, P.; Cotugno, S.; Gallone, G.; Polacco, G. Crack growth behavior of styrene-butadiene rubber, natural rubber, and polybutadiene rubber compounds: Comparison of pure-shear versus strip tensile test. Rubber Chem. Technol. 2013, 86, 132–145. [Google Scholar] [CrossRef]
- Hamed, G.R. Materials and Compounds. In Engineering with Rubber: How to Design Rubber Components; Gent, A.N., Ed.; Hanser Publishers: Munich, Germany, 2012; p. 29. [Google Scholar]
- Kaliske, M.; Dal, H.; Fleischhauer, R.; Jenkel, C.; Netzker, C. Characterization of fracture processes by continuum and discrete modelling. Comput. Mech. 2011, 50, 303–320. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Thomas, A.G. Rupture of rubber. I. Characteristic energy for tearing. J. Polym. Sci. 2003, 10, 291–318. [Google Scholar] [CrossRef]
- Griffith, A.A. VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character (1896–1934) 1921, 221, 163–198. [Google Scholar] [CrossRef] [Green Version]
- Stoček, R.; Horst, T.; Reincke, K. Tearing energy as fracture mechanical quantity for elastomers. In Designing of Elastomer Nanocomposites: From Theory to Applications; Stöckelhuber, K.W., Das, A., Klüppel, M., Eds.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Reincke, K.; Grellmann, W.; Lach, R.; Heinrich, G. Toughness optimization of SBR elastomers—Use of fracture mechanics methods for characterization. Macromol. Mater. Eng. 2003, 288, 181–189. [Google Scholar] [CrossRef]
- Torabizadeh, M.; Putnam, Z.A.; Sankarasubramanian, M.; Moosbrugger, J.C.; Krishnan, S. The effects of initial crack length on fracture characterization of rubbers using the J-Integral approach. Polym. Test. 2019, 73, 327–337. [Google Scholar] [CrossRef]
- Agnelli, S.; Balasooriya, W.; Bignotti, F.; Schrittesser, B. On the experimental measurement of fracture toughness in SENT rubber specimens. Polym. Test. 2020, 87, 106508. [Google Scholar] [CrossRef]
- Stoček, R.; Heinrich, G.; Gehde, M.; Kipscholl, R. A new testing concept for determination of dynamic crack propagation in rubber material. KGK-Kautschuk Gummi Kunststoffe 2012, 65, 49–53. [Google Scholar]
- Stoček, R.; Heinrich, G.; Gehde, M.; Kipscholl, R. Analysis of Dynamic Crack Propagation in Elastomers by Simultaneous Tensile- and Pure-Shear-Mode Testing. In Fracture Mechanics; Springer Science and Business Media LLC: Berlin, Germany, 2013; Volume 70, pp. 269–301. [Google Scholar]
- Chow, C.L.; Wang, J.; Tse, P.N. Rubber Fracture Characterization UsingJ-Integral. Tire Sci. Technol. 1988, 16, 44–60. [Google Scholar] [CrossRef]
- Caimmi, F.; Calabro, R.; Vangosa, F.B.; Marano, C.; Rink, M. J-Integral from Full Field Kinematic Data for Natural Rubber Compounds. Strain 2015, 51, 343–356. [Google Scholar] [CrossRef] [Green Version]
- Shahani, A.R.; Shooshtar, H.; Baghaee, M. On the determination of the critical J-integral in rubber-like materials by the single specimen test method. Eng. Fract. Mech. 2017, 184, 101–120. [Google Scholar] [CrossRef]
- Rice, J.R.; Paris, P.C.; Merkle, J.G.; Kaufman, J.G.; Swedlow, J.L.; Corten, H.T.; Srawley, J.E.; Heyer, R.H.; Wessel, E.T.; Irwin, G.R. Some Further Results of J-Integral Analysis and Estimates. Prog. Flaw Growth Fract. Toughness Test. 1973, 536, 231–245. [Google Scholar] [CrossRef]
- Reincke, K.; Grellmann, W.; Heinrich, G. Investigation of Mechanical and Fracture Mechanical Properties of Elastomers Filled with Precipitated Silica and Nanofillers Based upon Layered Silicates. Rubber Chem. Technol. 2004, 77, 662–677. [Google Scholar] [CrossRef]
- Bhowmick Anil, K.; De, S.K. (Eds.) Fractography of Rubbery Materials; Elsevier Applied Science: London, UK, 1991. [Google Scholar]
- Ganesan, L.; Bhattacharyya, P.; Bhowmick, A.K. Quantitative Fractography of Rubber by Image Processing Technique. Rubber Chem. Technol. 1995, 68, 132–145. [Google Scholar] [CrossRef]
- Ducrot, E.; Chen, Y.; Bülters, M.; Sijbesma, R.P.; Creton, C. Toughening Elastomers with Sacrificial Bonds and Watching Them Break. Science 2014, 344, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, S.; Mukhopadhyay, R.; Baranwal, K.C.; Bhowmick, A.K. Tools and Techniques—Chapter 5. Reverse Engineering of Rubber Products: Concepts; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Datta, S.; Antoš, J.; Stoček, R. Smart numerical method for calculation of simple general infrared parameter identifying binary rubber blends. Polym. Test. 2017, 57, 192–202. [Google Scholar] [CrossRef]
- Datta, S.; Antoš, J.; Stoček, R. Characterisation of ground tyre rubbery using combination of FT-IR numerical parameter and DTG analysis to determine the composition of ternary rubber blend. Polym. Test. 2017, 59, 308–315. [Google Scholar] [CrossRef]
- Datta, S.; Harea, D.; Harea, E.; Stoček, R. An advanced method for calculation of infrared parameter to quantitatively identify rubber grade in a multi-component rubber blend. Polym. Test. 2019, 73, 308–315. [Google Scholar] [CrossRef]




| Compounding Ingredients | phr * |
|---|---|
| NR (SVR CV-60) | 100.00 |
| Zinc oxide (ZnO) | 3.00 |
| Stearic acid | 1.00 |
| Carbon black, N-330 | 50.00 |
| Paraffin Oil, Tudalen 3912B | 5.00 (Batch-1) 10.00 (Batch-2). 0.00 (Batch-3) |
| Rubber Accelerator, CBS ** | 2.50 |
| Sulphur | 1.70 |
| Sample Designation | Initial Oil Concentration, phr | Deformation Speed, mm·min−1 |
|---|---|---|
| NR_5_ref * | 5.00 | 0 |
| NR_10_ref | 10.00 | 0 |
| NR_5_10 | 5.00 | 10 |
| NR_5_100 | 5.00 | 100 |
| NR_10_10 | 10.00 | 10 |
| NR_10_100 | 10.00 | 100 |
| NR_0_0 | 0.00 | 0 |
| NR_0_10 | 0.00 | 10 |
| NR_0_100 | 0.00 | 100 |
| Sample Designation | Tearing Energy. J·m−2 | IR Absorbance at 1375 cm−1(NR). as Obtained after Baseline Subtraction | IR Absorbance at 723 cm−1 (oil). as Obtained after Baseline Subtraction | IR Absorbance at 723 cm−1 (oil) Calculated against Normalized Peak at 1375 cm−1 ** |
|---|---|---|---|---|
| NR_5_0 | not applicable | 0.0136 | 0.0074 | 0.5456 |
| 0.0132 | 0.0068 | 0.5168 | ||
| 0.0134 | 0.0068 | 0.5109 | ||
| 0.0134 (±0.0001) * | 0.0070 (±0.0003) | 0.5244 (±0.0151) | ||
| NR_10_0 | not applicable | 0.0115 | 0.0084 | 0.7363 |
| 0.0109 | 0.0086 | 0.7967 | ||
| 0.0115 | 0.0079 | 0.6902 | ||
| 0.0113 (±0.0003) | 0.0083 (±0.0003) | 0.7411 (±0.0436) | ||
| NR_5_10 | 1322 | 0.0146 | 0.0058 | 0.3970 |
| 1599 | 0.0149 | 0.0062 | 0.4145 | |
| 1532 | 0.0150 | 0.0065 | 0.4340 | |
| 1484 (±118) | 0.0148 (±0.0001) | 0.0062 (±0.0003) | 0.4152 (±0.0151) | |
| NR_5_100 | 842 | 0.0149 | 0.0055 | 0.3729 |
| 911 | 0.0151 | 0.0054 | 0.3556 | |
| 879 | 0.0150 | 0.0056 | 0.3701 | |
| 877 (±28) | 0.0150 (±0.0001) | 0.0055 (±0.0001) | 0.3662 (±0.0076) | |
| NR_10_10 | 1387 | 0.0115 | 0.0068 | 0.5943 |
| 1349 | 0.0109 | 0.0065 | 0.5958 | |
| 1300 | 0.0115 | 0.0061 | 0.5356 | |
| 1345 (±35) | 0.0113 (±0.0003) | 0.0065 (±0.0003) | 0.5751 (±0.0093) | |
| NR_10_100 | 780 | 0.0135 | 0.0061 | 0.4504 |
| 808 | 0.0134 | 0.0068 | 0.5072 | |
| 750 | 0.0138 | 0.0065 | 0.4740 | |
| 779 (±23) | 0.0136 (±0.0002) | 0.0065 (±0.0003) | 0.4772 (±0.0233) |
| Sample Designation | IR Absorbance at 1375cm−1 (NR). as Obtained after Baseline Subtraction | IR Absorbance at 723 cm−1 (without oil). as Obtained after Baseline Subtraction | IR Absorbance at 723 cm−1 (without oil) Calculated against Normalized Peak at 1375 cm−1 ** |
|---|---|---|---|
| NR_0_0 | 0.0101 | 0.0020 | 0.1972 |
| 0.0114 | 0.0016 | 0.1400 | |
| 0.0128 | 0.0016 | 0.1211 | |
| 0.0115 (±0.0011) * | 0.0017 (±0.0002) | 0.1528 (±0.0323) | |
| NR_0_10 | 0.0113 | 0.0016 | 0.1445 |
| 0.0113 | 0.0021 | 0.1662 | |
| 0.0132 | 0.0017 | 0.1313 | |
| 0.0119 (±0.0009) | 0.0018 (±0.0002) | 0.1473 (±0.01439) | |
| NR_0_100 | 0.0122 | 0.0016 | 0.1302 |
| 0.0127 | 0.0014 | 0.1121 | |
| 0.0124 | 0.0019 | 0.1542 | |
| 0.0124 (±0.0002) | 0.0016 (±0.0002) | 0.1322 (±0.0172) |
| % Change in Tearing Energy | % Change in IR Absorbance Peak Height | ||
|---|---|---|---|
| defined for 5 phr of oil | defined for 10 phr of oil | defined for 5 phr of oil | defined for 10 phr of oil |
| 69.21 | 72.66 | 13.37 | 20.54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datta, S.; Stoček, R.; Harea, E.; Kratina, O.; Stěnička, M. Configuration of Novel Experimental Fractographic Reverse Engineering Approach Based on Relationship between Spectroscopy of Ruptured Surface and Fracture Behaviour of Rubber Sample. Materials 2020, 13, 4445. https://doi.org/10.3390/ma13194445
Datta S, Stoček R, Harea E, Kratina O, Stěnička M. Configuration of Novel Experimental Fractographic Reverse Engineering Approach Based on Relationship between Spectroscopy of Ruptured Surface and Fracture Behaviour of Rubber Sample. Materials. 2020; 13(19):4445. https://doi.org/10.3390/ma13194445
Chicago/Turabian StyleDatta, Sanjoy, Radek Stoček, Evghenii Harea, Ondřej Kratina, and Martin Stěnička. 2020. "Configuration of Novel Experimental Fractographic Reverse Engineering Approach Based on Relationship between Spectroscopy of Ruptured Surface and Fracture Behaviour of Rubber Sample" Materials 13, no. 19: 4445. https://doi.org/10.3390/ma13194445
APA StyleDatta, S., Stoček, R., Harea, E., Kratina, O., & Stěnička, M. (2020). Configuration of Novel Experimental Fractographic Reverse Engineering Approach Based on Relationship between Spectroscopy of Ruptured Surface and Fracture Behaviour of Rubber Sample. Materials, 13(19), 4445. https://doi.org/10.3390/ma13194445





