Effects of Applied Voltages on the Charge Transport Properties in a ZnO Nanowire Field Effect Transistor
Abstract
:1. Introduction
2. Materials and Methods
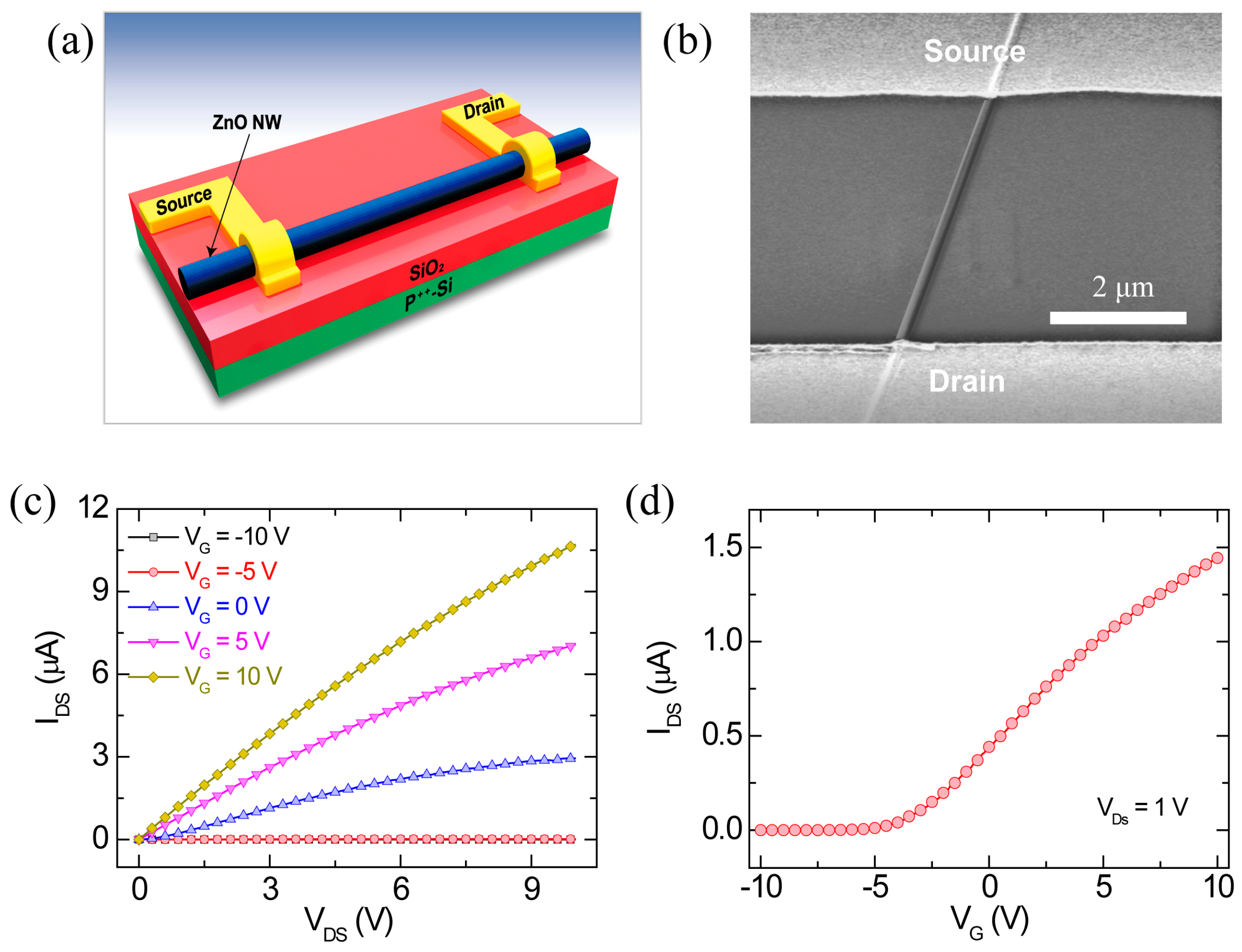
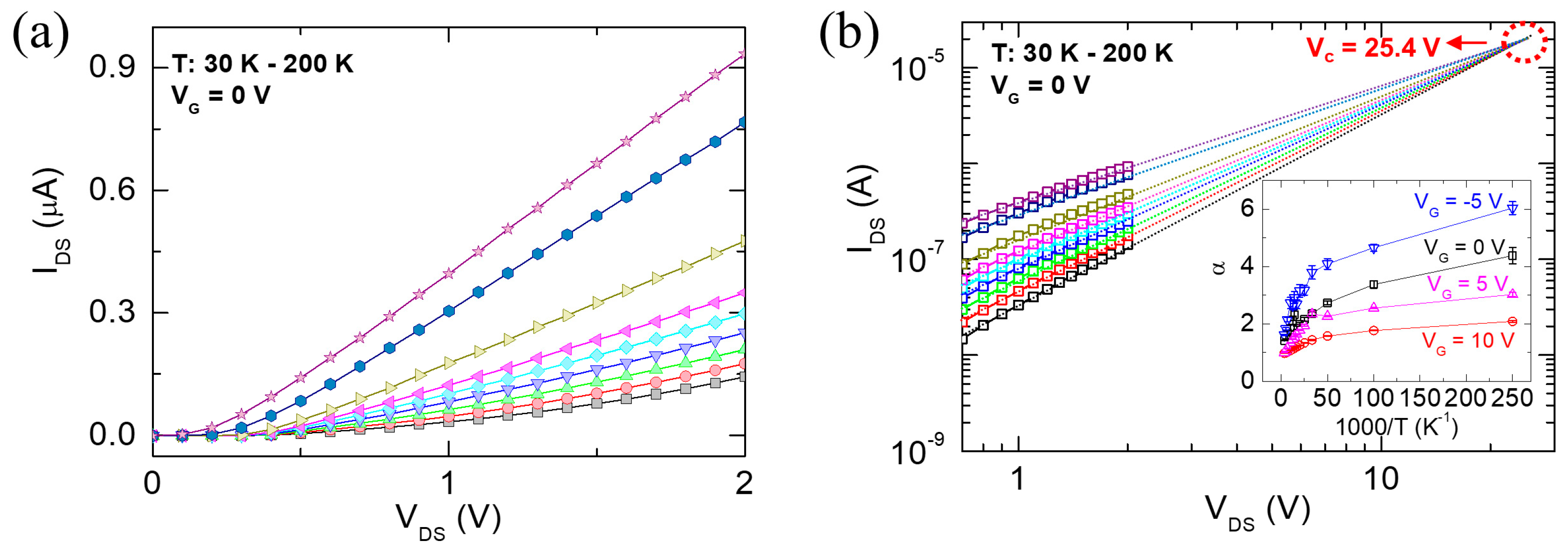
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Z.L. Zinc oxide nanostructures: Growth, properties and applications. J. Phys. Condens. Matter 2004, 16, R829–R858. [Google Scholar] [CrossRef]
- Yang, P.; Yan, H.; Mao, S.; Russo, R.; Johnson, J.; Saykally, R.; Morris, N.; Pham, J.; He, R.; Choi, H.-J. Controlled growth of ZnO nanowires and their optical properties. Adv. Funct. Mater. 2002, 12, 323–331. [Google Scholar] [CrossRef]
- Rackauskas, S.; Barbero, N.; Barolo, C.; Viscardi, G. ZnO nanowire application in chemoresistive sensing: A review. Nanomaterials 2017, 7, 381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Consonni, V.; Briscoe, J.; Kärber, E.; Li, X.; Cossuet, T. ZnO nanowires for solar cells: A comprehensive review. Nanotechnology 2019, 30, 362001. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Çelik-Buter, Z.; Butler, D.P. An integrated piezoelectric zinc oxide nanowire micro-energy harvester. Nano Energy 2016, 26, 456–465. [Google Scholar] [CrossRef]
- Bao, J.; Zimmler, M.A.; Capasso, F.; Wang, X.; Ren, Z.F. Broadband ZnO single-nanowire light-emitting diode. Nano Lett. 2006, 6, 1719–1722. [Google Scholar] [CrossRef] [Green Version]
- Hong, W.-K.; Sohn, J.I.; Hwang, D.-K.; Kwon, S.-S.; Jo, G.; Song, S.; Kim, S.-M.; Ko, H.-J.; Park, S.-J.; Welland, M.E.; et al. Tunable electronic Transport Characteristics of Surface-Architecture-Controlled ZnO Nanowire Field Effect Transistors. Nano Lett. 2008, 8, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Lieber, C.M. One- dimensional nanostructures: Chemistry, physics & applications. Solid State Commun. 1998, 107, 607–616. [Google Scholar]
- Schmidt-Mende, L.; MacManus-Driscoll, J.L. ZnO—Nanostructures, defects, and devices. Mater. Today 2007, 10, 40–48. [Google Scholar] [CrossRef]
- Lord, A.M.; Maffeis, T.G.; Kryvchenkova, O.; Cobley, R.J.; Kalna, K.; Kepaptsoglou, D.M.; Ramasse, Q.M.; Walton, A.S.; Ward, M.B.; Köble, J.; et al. Controlling the electrical transport properties of nanocontacts to nanowire. Nano Lett. 2015, 15, 4248–4254. [Google Scholar] [CrossRef]
- Jo, G.; Maeng, J.; Kim, T.-W.; Hong, W.-K.; Choi, B.-S.; Lee, T. Channel-length and gate-bias dependence of contact resistance and mobility for In2O3 nanowire field effect transistors. J. Appl. Phys. 2007, 102, 084508. [Google Scholar] [CrossRef]
- He, J.-H.; Ke, J.-J.; Chang, P.-H.; Tsai, K.-T.; Yang, P.C.; Chan, I.-M. Development of Ohmic nanocontacts via surface modification for nanowire-based electronic and optoelectronic devices: ZnO nanowires as an example. Nanoscale 2012, 4, 3399–3404. [Google Scholar] [CrossRef] [PubMed]
- Ju, S.; Janes, D.B.; Lu, G.; Facchetti, A.; Marks, T.J. Effects of bias stress on ZnO nanowire field-effect transistors fabricated with organic gate nanodielectrics. Appl. Phys. Lett. 2006, 89, 193506. [Google Scholar] [CrossRef]
- Choe, M.; Park, W.; Kang, J.W.; Jeong, S.; Hong, W.-K.; Lee, B.H.; Park, S.-J.; Lee, T. Investigation of threshold voltage instability induced by gate bias stress in ZnO nanowire field effect transistors. Nanotechnology 2012, 23, 485201. [Google Scholar] [CrossRef]
- Hong, W.-K.; Hwang, D.-K.; Park, I.-K.; Jo, G.; Song, S.; Park, S.-J.; Lee, T.; Kim, B.-J.; Stach, E.A. Realization of highly reproducible ZnO nanowire field effect transistors with n-channel depletion and enhancement modes. Appl. Phys. Lett. 2007, 90, 243103. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.-Y.; Amani, M.; Ahn, G.H.; Song, Y.; Javey, A.; Chung, S.; Lee, T. Electrical properties of synthesized large-area MoS2 field-effect transistors fabricated with inkjet-printed contacts. ACS Nano 2016, 10, 2819–2826. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, X.; Huo, Y.; Wang, Y.; Zhang, T.; Jiang, K.; Wang, J.; Fan, S.; Li, Q. Influence of asymmetric contact form on contact resistance and Schottky barrier, and corresponding applications of diode. ACS Appl. Mater. Interfaces 2017, 9, 18945–18955. [Google Scholar] [CrossRef]
- Jo, G.; Maeng, J.; Kim, T.-W.; Hong, W.-K.; Jo, M.; Hwang, H.; Lee, T. Effects of channel-length scaling on In2O3 nanowire field effect transistors studied by conducting atomic force microscopy. Appl. Phys. Lett. 2007, 90, 173106. [Google Scholar] [CrossRef]
- Liao, Z.-M.; Lv, Z.-K.; Zhou, Y.-B.; Xu, J.; Zhang, J.-M.; Yu, D.-P. The effect of adsorbates on the space–charge-limited current in single ZnO nanowires. Nanotechnology 2008, 19, 335204. [Google Scholar] [CrossRef]
- Xu, W.; Chin, A.; Ye, L.; Ning, C.Z.; Yu, H. Charge transport and trap characterization in individual GaSb nanowires. J. Appl. Phys. 2012, 111, 104515. [Google Scholar] [CrossRef] [Green Version]
- Fang, D.Q.; Zhang, R.Q. Size effects on formation energies and electronic structures of oxygen and zinc vacancies in ZnO nanowires: A first-principle study. J. Appl. Phys. 2011, 109, 044306. [Google Scholar] [CrossRef]
- Shao, Y.; Yoon, J.; Kim, H.; Lee, T.; Lu, W. Analysis of surface states in ZnO nanowire field effect transistors. Appl. Surf. Sci. 2014, 301, 2–8. [Google Scholar] [CrossRef]
- Chang, P.-C.; Lu, J.G. Temperature dependent conduction and UV induced metal-to-insulator transition in ZnO nanowires. Appl. Phys. Lett. 2008, 92, 212113. [Google Scholar] [CrossRef]
- Lin, Y.-F.; Jian, W.-B.; Wang, C.P.; Suen, Y.-W.; Wu, Z.-Y.; Chen, F.-R.; Kai, J.-J.; Lin, J.-J. Contact to ZnO and intrinsic resistances of individual ZnO nanowires with a circular cross section. Appl. Phys. Lett. 2007, 90, 223117. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-F.; Chen, T.-H.; Chang, C.-H.; Chang, Y.-W.; Chiu, Y.-C.; Hung, H.-C.; Kai, J.-J.; Liu, Z.; Fang, J.; Jian, W.-B. Electron transport in high-resistance semiconductor nanowires through two-probe measurements. Phys. Chem. Chem. Phys. 2010, 12, 10928–10932. [Google Scholar] [CrossRef] [PubMed]
- Ko, D. Charge Transport Properties in Semiconductor Nanowires. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2011. [Google Scholar]
- Liu, X.; Liu, J.; Antipina, L.Y.; Hu, J.; Yue, C.; Sanchez, A.M.; Sorokin, P.B.; Mao, Z.; Wei, J. Direct fabrication of functional ultrathin single-crystal nanowires from quasi-one-dimensional van der Waals crystals. Nano Lett. 2016, 16, 6188–6195. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, A.B.; Gómez-Navarro, C.; Sundaram, R.S.; Burghard, M.; Kern, K. Electrical conduction mechanism in chemically derived graphene monolayers. Nano Lett. 2009, 9, 1787–1792. [Google Scholar] [CrossRef]
- Varade, V.; Anjaneyulu, P.; Sangeeth, C.S.S.; Ramesh, K.P.; Menon, R. Electric field activated nonlinear anisotropic charge transport in doped polypyrrole. Appl. Phys. Lett. 2013, 103, 233305. [Google Scholar] [CrossRef]
- Radisavljevic, B.; Kis, A. Mobility engineering and a metal-insulator transition in monolayer MoS2. Nat. Mater. 2013, 12, 815–820. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Cai, J.; Hui, C.; Zhang, C.; Bao, L.; Gao, M.; Shen, C.; Gao, H. Boron nanowires for flexible electronics. Appl. Phys. Lett. 2008, 93, 122105. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.-J.; Zhang, Z.; Zhou, F.; Lu, L.; Jin, A.; Gu, C. Hopping conduction in single ZnO nanowires. Nanotechnology 2005, 16, 746–749. [Google Scholar] [CrossRef]
- Ayari, A.; Cobas, E.; Ogundadegbe, O.; Fuhrer, M.S. Realization and electrical characterization of ultrathin crystals of layered transition-metal dichalcogenides. J. Appl. Phys. 2007, 101, 014507. [Google Scholar] [CrossRef] [Green Version]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.; Huang, F.; Shin, K.H.; Sohn, J.I.; Hong, W.-K. Effects of Applied Voltages on the Charge Transport Properties in a ZnO Nanowire Field Effect Transistor. Materials 2020, 13, 268. https://doi.org/10.3390/ma13020268
Yoon J, Huang F, Shin KH, Sohn JI, Hong W-K. Effects of Applied Voltages on the Charge Transport Properties in a ZnO Nanowire Field Effect Transistor. Materials. 2020; 13(2):268. https://doi.org/10.3390/ma13020268
Chicago/Turabian StyleYoon, Jongwon, Fu Huang, Ki Hoon Shin, Jung Inn Sohn, and Woong-Ki Hong. 2020. "Effects of Applied Voltages on the Charge Transport Properties in a ZnO Nanowire Field Effect Transistor" Materials 13, no. 2: 268. https://doi.org/10.3390/ma13020268
APA StyleYoon, J., Huang, F., Shin, K. H., Sohn, J. I., & Hong, W. -K. (2020). Effects of Applied Voltages on the Charge Transport Properties in a ZnO Nanowire Field Effect Transistor. Materials, 13(2), 268. https://doi.org/10.3390/ma13020268




