Multi-Terminal Transistor-Like Devices Based on Strongly Correlated Metallic Oxides for Neuromorphic Applications
Abstract
:1. Introduction
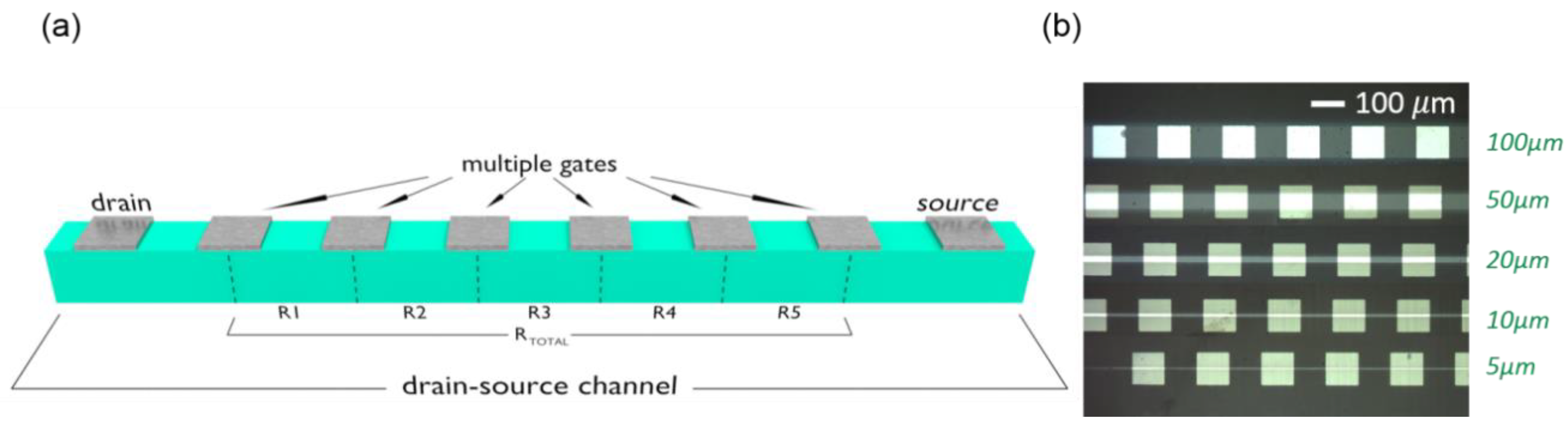
2. Materials and Methods
3. Results and Discussion
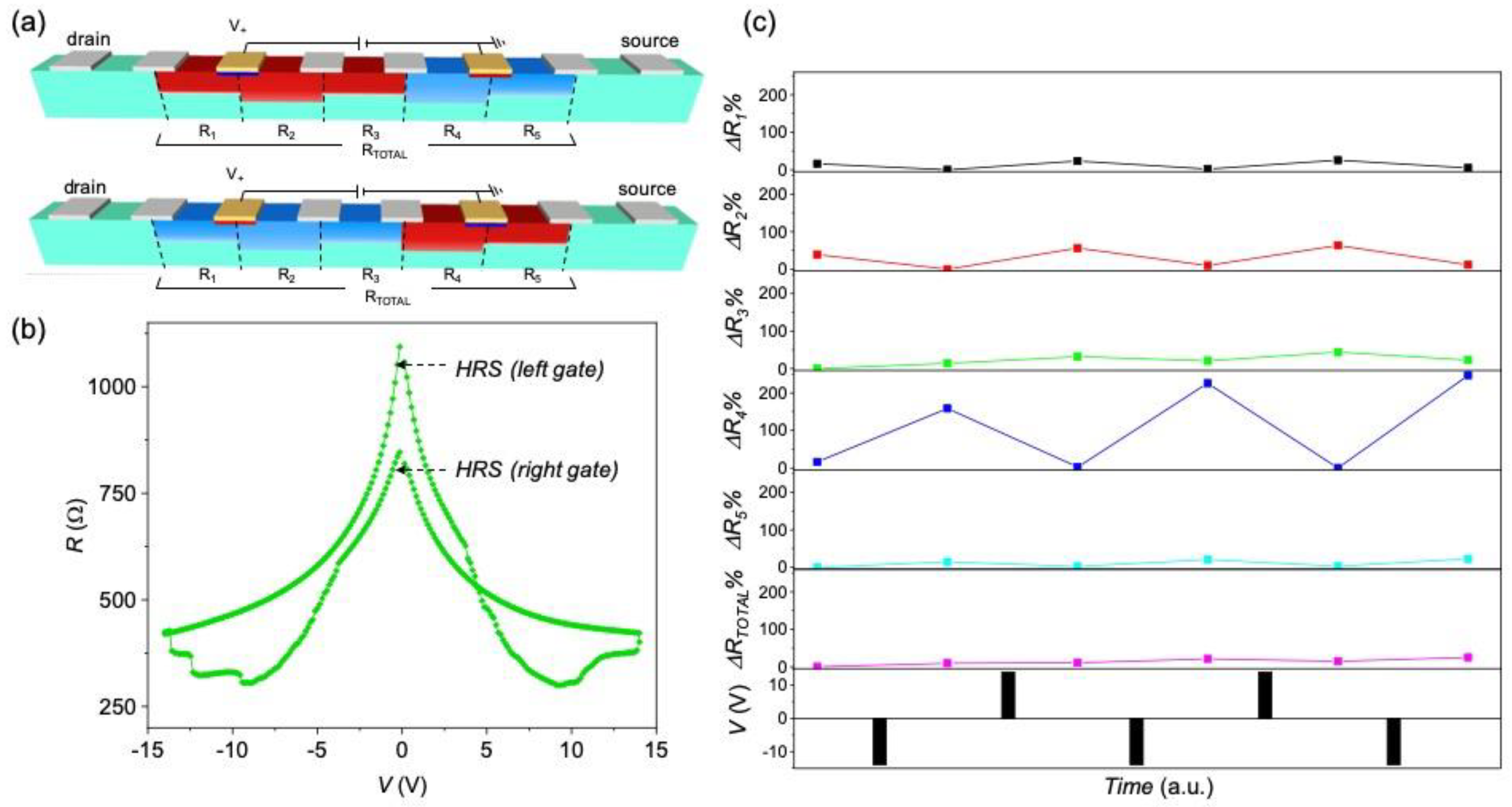
3.1. Switching Characteristics between Two Gates
3.2. Conductance Modulation in a Drain-Source Channel
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Solomon, P.M. Analog neuromorphic computing using programmable resistor arrays. Solid-State Electron. 2019, 155, 82–92. [Google Scholar] [CrossRef]
- Gokmen, T.; Vlasov, Y. Acceleration of deep neural network training with resistive cross-point devices: Design considerations. Front. Neurosci. 2016, 10, 333. [Google Scholar] [CrossRef] [Green Version]
- Burr, G.W.; Shelby, R.M.; Sebastian, A.; Kim, S.; Sidler, S.; Virwani, K.; Ishii, M.; Narayanan, P.; Fumarola, A.; Sanches, L.L.; et al. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2017, 2, 89–124. [Google Scholar] [CrossRef]
- Suri, M.; Querlioz, D.; Bichler, O.; Palma, G.; Vianello, E.; Vuillaume, D.; Gamrat, C.; De Salvo, B.; Suri, M.; Querlioz, D.; et al. Bio-inspired stochastic computing using binary CBRAM synapses. IEEE Trans. Electron Devices 2013, 60, 2402–2409. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Gao, B.; Fang, Z.; Yu, H.; Kang, J.; Wong, H.-S.P. Stochastic learning in oxide binary synaptic device for neuromorphic computing. Front. Neurosci. 2013, 7, 186. [Google Scholar] [CrossRef] [Green Version]
- Zidan, M.A.; Strachan, J.P.; Lu, W.D. The future of electronics based on memristive systems. Nat. Electron. 2018, 1, 22–29. [Google Scholar] [CrossRef]
- Sawa, A. Resistive switching in transition metal oxides. Mater. Today 2008, 11, 28–36. [Google Scholar] [CrossRef]
- Janod, E.; Tranchant, J.; Corraze, B.; Querré, M.; Stoliar, P.; Rozenberg, M.; Cren, T.; Roditchev, D.; Phuoc, V.T.; Besland, M.P.; et al. Resistive switching in Mott insulators and correlated systems. Adv. Funct. Mater. 2015, 25, 6287–6305. [Google Scholar] [CrossRef]
- Bagdzevicius, S.; Maas, K.; Boudard, M.; Burriel, M. Interface-type resistive switching in perovskite materials. J. Electroceramics 2017, 39, 157–184. [Google Scholar] [CrossRef]
- Bi, C.; Meng, X.; Almasi, H.; Rosales, M.; Wang, W. Metal based nonovolatile field-effect transistors. Adv. Funct. Mater. 2016, 26, 3490–3495. [Google Scholar] [CrossRef]
- Zhou, B.Y.; Ramanathan, S. Mott memory and neuromorphic devices. Proc. IEEE 2015, 103, 1289–1310. [Google Scholar] [CrossRef] [Green Version]
- Stoliar, P.; Tranchant, J.; Corraze, B.; Janod, E.; Besland, M.P.; Tesler, F.; Rozenberg, M.; Cario, L. A leaky-integrate-and-fire neuron analog realized with a Mott insulator. Adv. Funct. Mater. 2017, 27, 1604740. [Google Scholar] [CrossRef]
- Kuzum, D.; Yu, S.; Wong, H.S. Synaptic electronics: Materials, devices and applications. Nanotechnology 2013, 24, 382001. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef]
- Han, H.; Yu, H.; Wei, H.; Gong, J.; Xu, W. Recent progress in three-terminal artificial synapses: From device to system. Small 2019, 15, 1900695. [Google Scholar] [CrossRef]
- Yang, C.S.; Shang, D.S.; Liu, N.; Fuller, E.J.; Agrawal, S.; Talin, A.A.; Li, Y.Q.; Shen, B.G.; Sun, Y. All-solid-state synaptic transistor with ultralow conductance for neuromorphic computing. Adv. Funct. Mater. 2018, 28, 1804170. [Google Scholar] [CrossRef]
- Gkoupidenis, P.; Koutsouras, D.A.; Lonjaret, T.; Fairfield, J.A.; Malliaras, G.G. Orientation selectivity in a multi-gated organic electrochemical transistor. Sci. Rep. 2016, 6, 27007. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Dodda, A.; Das, S. A biomimetic 2D transistor for audiomorphic computing. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Sangwan, V.K.; Lee, H.-S.; Bergeron, H.; Balla, I.; Beck, M.E.; Chen, K.-S.; Hersam, M.C. Multi-terminal memtransistors from polycrystalline monolayer molybdenum disulfide. Nature 2018, 554, 500–504. [Google Scholar] [CrossRef]
- Stoddart, A. Electronic devices: Making multi-terminal memtransistors. Nat. Rev. Mater. 2018, 3, 18014. [Google Scholar] [CrossRef]
- Gou, G.; Sun, J.; Qian, C.; He, Y.; Kong, L.A.; Fu, Y.; Dai, G.; Yang, J.; Gao, Y. Artificial synapses based on biopolymer electrolyte-coupled SnO2 nanowire transistors. J. Mater. Chem. C 2016, 4, 11110–11117. [Google Scholar] [CrossRef]
- Zhu, L.Q.; Wan, C.J.; Guo, L.Q.; Shi, Y.; Wan, Q. Artificial synapse network on inorganic proton conductor for neuromorphic systems. Nat. Commun. 2014, 5, 3158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palau, A.; Fernandez-rodriguez, A.; Gonzalez-rosillo, J.C.; Granados, X.; Coll, M.; Bozzo, B.; Ortega-hernandez, R.; Sun, J.; Obradors, X.; Puig, T. Electrochemical tuning of metal insulator transition and nonvolatile resistive switching in superconducting films. ACS Appl. Mater. Interfaces 2018, 10, 30522–30531. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Rosillo, J.C.; Ortega-Hernandez, R.; Arndt, B.; Coll, M.; Dittmann, R.; Obradors, X.; Palau, A.; Suñe, J.; Puig, T. Engineering oxygen migration for homogeneous volume resistive switching in 3-terminal devices. Adv. Electron. Mater. 2019, 5, 1800629. [Google Scholar] [CrossRef]
- Wuyts, B.; Moshchalkov, V.V.; Bruynseraede, Y. Resistivity and Hall effect of metallic oxygen-deficient YBa2Cu3Ox films in the normal state. Phys. Rev. B 1996, 53, 9418. [Google Scholar] [CrossRef]
- Sakai, J.; Ito, N.; Imai, S. Oxygen content of La1−xSrxMnO3−y thin films and its relation to electric-magnetic properties. J. Appl. Phys. 2006, 99, 08Q318. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, C.; Szot, K. Redox-based resistive switching memories nanoionic mechanisms, prospects, and challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Linn, E.; Rosezin, R.; Kügeler, C.; Waser, R. Complementary resistive switches for passive nanocrossbar memories. Nat. Mater. 2010, 9, 403–406. [Google Scholar] [CrossRef]
- Nardi, F.; Balatti, S.; Larentis, S.; Gilmer, D.C.; Ielmini, D. Complementary switching in oxide-based bipolar resistive-switching random memory. IEEE Trans. Electron Devices 2012, 60, 70–77. [Google Scholar] [CrossRef]
- Lee, Y.S.; Segawa, K.; Li, Z.Q.; Padilla, W.J.; Dumm, M.; Dordevic, S.V.; Homes, C.C.; Ando, Y.; Basov, D.N. Electrodynamics of the nodal metal state in weakly doped high-Tc cuprates. Phys. Rev. B-Condens. Matter Mater. Phys. 2005, 72, 054529. [Google Scholar] [CrossRef] [Green Version]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Rodríguez, A.; Alcalà, J.; Suñe, J.; Mestres, N.; Palau, A. Multi-Terminal Transistor-Like Devices Based on Strongly Correlated Metallic Oxides for Neuromorphic Applications. Materials 2020, 13, 281. https://doi.org/10.3390/ma13020281
Fernández-Rodríguez A, Alcalà J, Suñe J, Mestres N, Palau A. Multi-Terminal Transistor-Like Devices Based on Strongly Correlated Metallic Oxides for Neuromorphic Applications. Materials. 2020; 13(2):281. https://doi.org/10.3390/ma13020281
Chicago/Turabian StyleFernández-Rodríguez, Alejandro, Jordi Alcalà, Jordi Suñe, Narcis Mestres, and Anna Palau. 2020. "Multi-Terminal Transistor-Like Devices Based on Strongly Correlated Metallic Oxides for Neuromorphic Applications" Materials 13, no. 2: 281. https://doi.org/10.3390/ma13020281
APA StyleFernández-Rodríguez, A., Alcalà, J., Suñe, J., Mestres, N., & Palau, A. (2020). Multi-Terminal Transistor-Like Devices Based on Strongly Correlated Metallic Oxides for Neuromorphic Applications. Materials, 13(2), 281. https://doi.org/10.3390/ma13020281







