Numerical Studies on Damage Behavior of Recycled Aggregate Concrete Based on a 3D Model
Abstract
1. Introduction
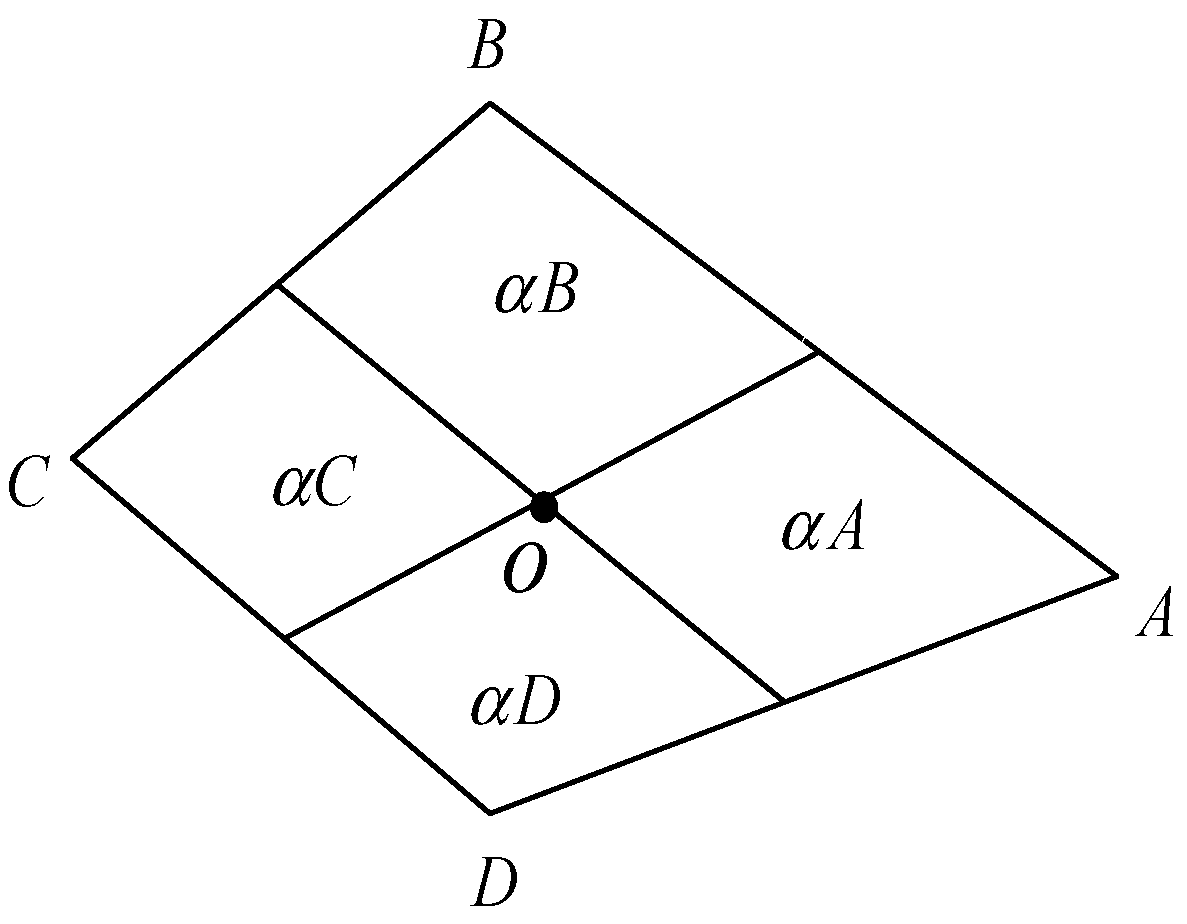
2. Basic Formula of 3D Base Force Theory
3. BFEM Model of Hexahedron Element
3.1. Strain Tensor
3.2. Stiffness Matrix
4. Random Model of RAC
4.1. Aggregate Number
4.2. Placing Algorithm
- (1)
- The aggregate particles must be completely located in the specimen.
- (2)
- The aggregate particles must not overlap with each other.
- (3)
- The distance between centers of any two adjacent aggregate particles must be larger than that of 1.20 (), where and are the radii of the two adjacent aggregates.
4.3. Numerical Model of RAC
4.4. Mechanical Parameters
5. Simulation of Uniaxial Compressive Test
5.1. Effect of Aggregate Substitution
5.2. Effect of Adhered Mortar Percentage
5.3. Failure Mechanism
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paul, S.C.; van Zijl, G.P.A.G. Mechanical and durability properties of recycled concrete aggregate for normal strength structural concrete. Int. J. Sustain. Constr. Eng. Technol. 2013, 4, 89–103. [Google Scholar]
- Mardani-Aghabaglou, A.; Yüksel, C.; Beglarigale, A.; Ramyar, K. Improving the mechanical and durability performance of recycled concrete aggregate-bearing mortar mixtures by using binary and ternary cementitious systems. Constr. Build. Mater. 2019, 196, 295–306. [Google Scholar] [CrossRef]
- Meesala, C.R. Influence of different types of fiber on the properties of recycled aggregate concrete. Struct. Concr. 2019, 20, 1656–1669. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, B. Discrete Element Mesoscale Modeling of Recycled Lump Concrete under Axial Compression. Materials 2019, 12, 3140. [Google Scholar] [CrossRef]
- Xie, J.; Zhao, J.; Wang, J.; Wang, C.; Huang, P.; Fang, C. Sulfate Resistance of Recycled Aggregate Concrete with GGBS and Fly Ash-Based Geopolymer. Materials 2019, 12, 1247. [Google Scholar] [CrossRef]
- Paul, S.C.; Panda, B.; Garg, A. A novel approach in modelling of concrete made with recycled aggregates. Measurement 2018, 115, 64–72. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.; Kamel, M.M.; Ying, L. 2D numerical investigation on damage mechanism of recycled aggregate concrete prism. Constr. Build. Mater. 2019, 213, 91–99. [Google Scholar] [CrossRef]
- Clough, R. The finite element method in plane stress analysis. In Proceedings of the 2nd ASCE Conference on Electronic Computation, Pittsburgh, PA, USA, 8–9 September 1960. [Google Scholar]
- Wang, Y.; Peng, Y.; Kamel, M.M.A.; Ying, L. Mesomechanical properties of concrete with different shapes and replacement ratios of recycled aggregate based on base force element method. Struct. Concr. 2019, 20, 1425–1437. [Google Scholar] [CrossRef]
- Jin, L.; Yu, W.; Du, X.; Zhang, S.; Li, N.; Xiuli, D. Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates. Int. J. Impact Eng. 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Xiao, J.; Li, W.; Corr, D.J.; Shah, S.P. Effects of interfacial transition zones on the stress–strain behavior of modeled recycled aggregate concrete. Cem. Concr. Res. 2013, 52, 82–99. [Google Scholar] [CrossRef]
- Li, W.; Luo, Z.; Sun, Z.; Hu, Y.; Duan, W.H. Numerical modelling of plastic–damage response and crack propagation in RAC under uniaxial loading. Mag. Concr. Res. 2018, 70, 459–472. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, Q.; Ying, L.; Kamel, M.M.A.; Peng, H. Numerical Simulation of Dynamic Mechanical Properties of Concrete under Uniaxial Compression. Materials 2019, 12, 643. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, F.; Roelfstra, P.; Sadouki, H. Simulation and analysis of composite structures. Mater. Sci. Eng. 1985, 68, 239–248. [Google Scholar] [CrossRef]
- Zaitsev, Y.B.; Wittmann, F.H. Simulation of crack propagation and failure of concrete. Mater. Struct. 1981, 14, 357–365. [Google Scholar]
- Peng, Y.; Wang, Y.; Guo, Q.; Ni, J. Application of Base Force Element Method to Mesomechanics Analysis for Concrete. Math. Probl. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Walraven, J.; Reinhardt, H. Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to shear loading. Heron 1981, 26, 1–68. [Google Scholar]
- Bazant, Z.P.; Tabbara, M.R.; Kazemi, M.T.; Pijaudier-Cabot, G. Random Particle Model for Fracture of Aggregate or Fiber Composites. J. Eng. Mech. 1990, 116, 1686–1705. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elements Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Chen, H.; Ma, H.; Tu, J.; Cheng, G.; Tang, J. Parallel computation of seismic analysis of high arch dam. Earthq. Eng. Eng. Vib. 2008, 7, 1–11. [Google Scholar] [CrossRef]
- Sun, C.; Xiao, J.; Lange, D.A. Simulation study on the shear transfer behavior of recycled aggregate concrete. Struct. Concr. 2018, 19, 255–268. [Google Scholar] [CrossRef]
- Chen, A.; Xia, X.; Zhang, Q.; Wu, M. The Meso-level Numerical Experiment Research of the Mechanics Properties of Recycled Concrete. J. Softw. 2012, 7, 1932–1940. [Google Scholar] [CrossRef]
- Jayasuriya, A.; Adams, M.P.; Bandelt, M.J. Understanding variability in recycled aggregate concrete mechanical properties through numerical simulation and statistical evaluation. Constr. Build. Mater. 2018, 178, 301–312. [Google Scholar] [CrossRef]
- Gao, Y.C. A new description of the stress state at a point with applications. Arch. Appl. Mech. 2003, 73, 171–183. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, Y. Base force element method of complementary energy principle for large rotation problems. Acta Mech. Sin. 2009, 25, 507–515. [Google Scholar] [CrossRef]
- Ottosen, N.S. Constitutive model for short-time loading of concrete. J. Eng. Mech. Div. 1979, 105, 127–141. [Google Scholar]
- Zhang, Z.; Chen, C.; Zhang, J. Yield Criterion in Plastic-Damage Models for Concrete. Acta Mech. Solida Sin. 2010, 23, 220–230. [Google Scholar] [CrossRef]
- Darwin, D.; Pecknold, D.A. Nonlinear biaxial stress-strain law for concrete. J. Eng. Mech. Div. 1977, 103, 229–241. [Google Scholar]
- Lutz, M.P.; Monteiro, P.J.; Zimmerman, R.W. Inhomogeneous Interfacial Transition Zone Model for the Bulk Modulus of Mortar. Cem. Concr. Res. 1997, 27, 1113–1122. [Google Scholar] [CrossRef]
- Li, W.; Xiao, J.; Sun, Z.; Kawashima, S.; Shah, S.P. Interfacial transition zones in recycled aggregate concrete with different mixing approaches. Constr. Build. Mater. 2012, 35, 1045–1055. [Google Scholar] [CrossRef]
- Bittnar, Z.; Bartos, P.J.; Nemecek, J.; Smilauer, V.; Zeman, J. (Eds.) Nanotechnology in Construction 3: Proceedings of the NICOM3; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mondal, P.; Shah, S.P.; Marks, L.D. Nanomechanical Properties of Interfacial Transition Zone in Concrete. In Nanotechnology in Construction 3; Springer: Berlin/Heidelberg, Germany, 2009; pp. 315–320. [Google Scholar]
- Xiao, J.; Li, W.; Sun, Z.; Lange, D.A.; Shah, S.P. Properties of interfacial transition zones in recycled aggregate concrete tested by nanoindentation. Cem. Concr. Compos. 2013, 37, 276–292. [Google Scholar] [CrossRef]
- Xiao, J.; Li, J.; Zhang, C. Mechanical properties of recycled aggregate concrete under uniaxial loading. Cem. Concr. Res. 2005, 35, 1187–1194. [Google Scholar] [CrossRef]
- Abid, S.R.; Nahhab, A.H.; Al-Aayedi, H.K.; Nuhair, A.M. Expansion and strength properties of concrete containing contaminated recycled concrete aggregate. Case Stud. Constr. Mater. 2018, 9, e00201. [Google Scholar] [CrossRef]
- Verian, K.P.; Ashraf, W.; Cao, Y. Properties of recycled concrete aggregate and their influence in new concrete production. Resour. Conserv. Recycl. 2018, 133, 30–49. [Google Scholar] [CrossRef]
- Folino, P.; Xargay, H. Recycled aggregate concrete—Mechanical behavior under uniaxial and triaxial compression. Constr. Build. Mater. 2014, 56, 21–31. [Google Scholar] [CrossRef]
- de Sánchez, J.M.; Gutiérrez, P.A. Study on the influence of attached mortar content on the properties of recycled concrete aggregate. Constr. Build. Mater. 2009, 23, 872–877. [Google Scholar]
- Etxeberria, M.; Vázquez, E.; Mari, A.; Barra, M. Influence of amount of recycled coarse aggregates and production process on properties of recycled aggregate concrete. Cem. Concr. Res. 2007, 37, 735–742. [Google Scholar] [CrossRef]
- Li, W.; Xiao, J.; Sun, Z.; Shah, S.P. Failure processes of modeled recycled aggregate concrete under uniaxial compression. Cem. Concr. Compos. 2012, 34, 1149–1158. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, Q.; Wu, Y.C. Numerical and experimental studies on fracture process of recycled concrete. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 801–808. [Google Scholar] [CrossRef]
- Akçaoğlu, T.; Tokyay, M.; Celik, T. Assessing the ITZ microcracking via scanning electron microscope and its effect on the failure behavior of concrete. Cem. Concr. Res. 2005, 35, 358–363. [Google Scholar] [CrossRef]
- Huang, Y.; He, X.; Sun, H.; Sun, Y.; Wang, Q. Effects of coral, recycled and natural coarse aggregates on the mechanical properties of concrete. Constr. Build. Mater. 2018, 192, 330–347. [Google Scholar] [CrossRef]







| Replacement Ratio | Aggregate Radius (mm) | |||||
|---|---|---|---|---|---|---|
| 7.5 | 12.5 | 17.5 | ||||
| RA | NA | RA | NA | RA | NA | |
| 0% | 0 | 468 | 0 | 77 | 0 | 23 |
| 15% | 70 | 398 | 12 | 65 | 3 | 20 |
| 30% | 140 | 328 | 23 | 54 | 7 | 16 |
| 50% | 234 | 234 | 38 | 39 | 11 | 12 |
| 100% | 468 | 0 | 77 | 0 | 23 | 0 |
| Mechanical Properties | Five Phases | ||||
|---|---|---|---|---|---|
| Natural Aggregate | Old ITZ | Adhered Mortar | New ITZ | New Cement Mortar | |
| Elastic modulus/GPa | 75 | 13.75 | 25 | 16.50 | 30 |
| Poisson’s ratio | 0.16 | 0.20 | 0.22 | 0.20 | 0.22 |
| Tensile strength/MPa | 10.0 | 2.0 | 2.5 | 2.0 | 3.0 |
| Mechanical Properties | Replacement Ratio | ||||
|---|---|---|---|---|---|
| 0% | 15% | 30% | 50% | 100% | |
| Elastic modulus/GPa | 25.56 | 24.29 | 22.36 | 22.06 | 21.34 |
| Compressive stress/MPa | 28.09 | 26.08 | 25.23 | 25.19 | 25.06 |
| Mechanical Properties | Percentage of Adhered Mortar | |||||
|---|---|---|---|---|---|---|
| 0% | 5% | 10% | 30% | 40% | 50% | |
| Elastic modulus/GPa | 1 | 0.96 | 0.93 | 0.86 | 0.84 | 0.82 |
| Compressive stress/MPa | 1 | 0.97 | 0.95 | 0.92 | 0.91 | 0.88 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, H.; Xu, M.; Wu, C.; Fu, J.; Gao, L.; Kamel, M.M.A. Numerical Studies on Damage Behavior of Recycled Aggregate Concrete Based on a 3D Model. Materials 2020, 13, 355. https://doi.org/10.3390/ma13020355
Wang Y, Zhao H, Xu M, Wu C, Fu J, Gao L, Kamel MMA. Numerical Studies on Damage Behavior of Recycled Aggregate Concrete Based on a 3D Model. Materials. 2020; 13(2):355. https://doi.org/10.3390/ma13020355
Chicago/Turabian StyleWang, Yao, Huawei Zhao, Minyao Xu, Chunyang Wu, Jiajia Fu, Lili Gao, and Mahmoud M. A. Kamel. 2020. "Numerical Studies on Damage Behavior of Recycled Aggregate Concrete Based on a 3D Model" Materials 13, no. 2: 355. https://doi.org/10.3390/ma13020355
APA StyleWang, Y., Zhao, H., Xu, M., Wu, C., Fu, J., Gao, L., & Kamel, M. M. A. (2020). Numerical Studies on Damage Behavior of Recycled Aggregate Concrete Based on a 3D Model. Materials, 13(2), 355. https://doi.org/10.3390/ma13020355





