Spark Plasma Sintering Apparatus Used for High-temperature Compressive Creep Tests
Abstract
:1. Introduction
2. Test Setup and Procedure
2.1. SPS Apparatus Technical Details
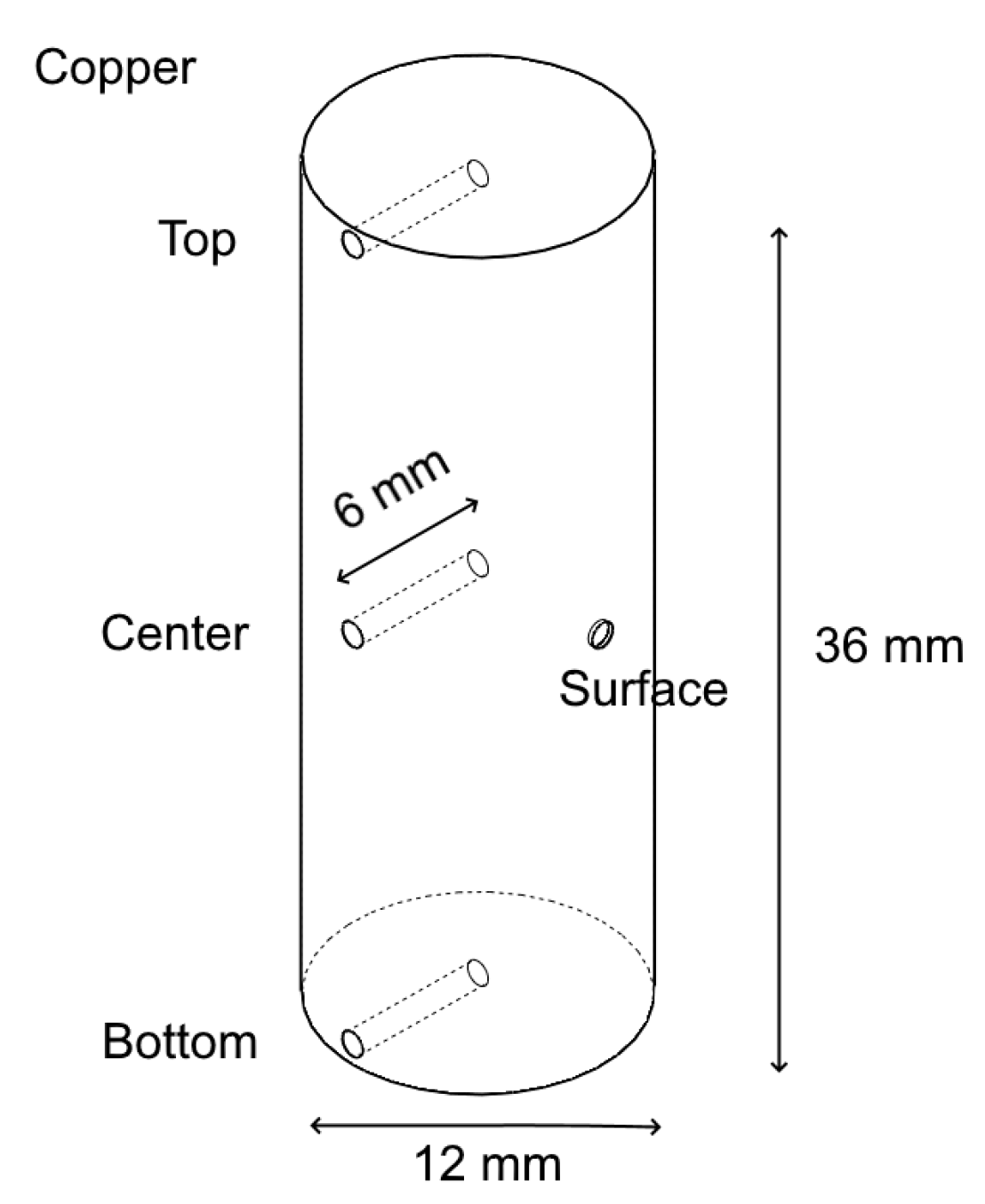
2.2. Test Configurations and Temperature Considerations
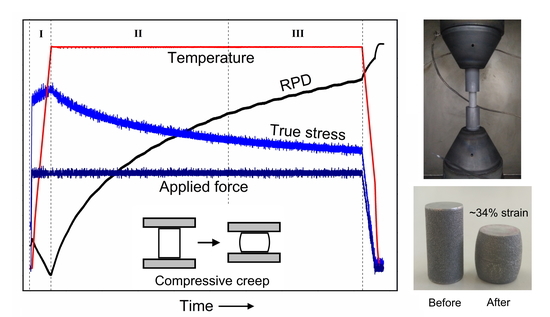
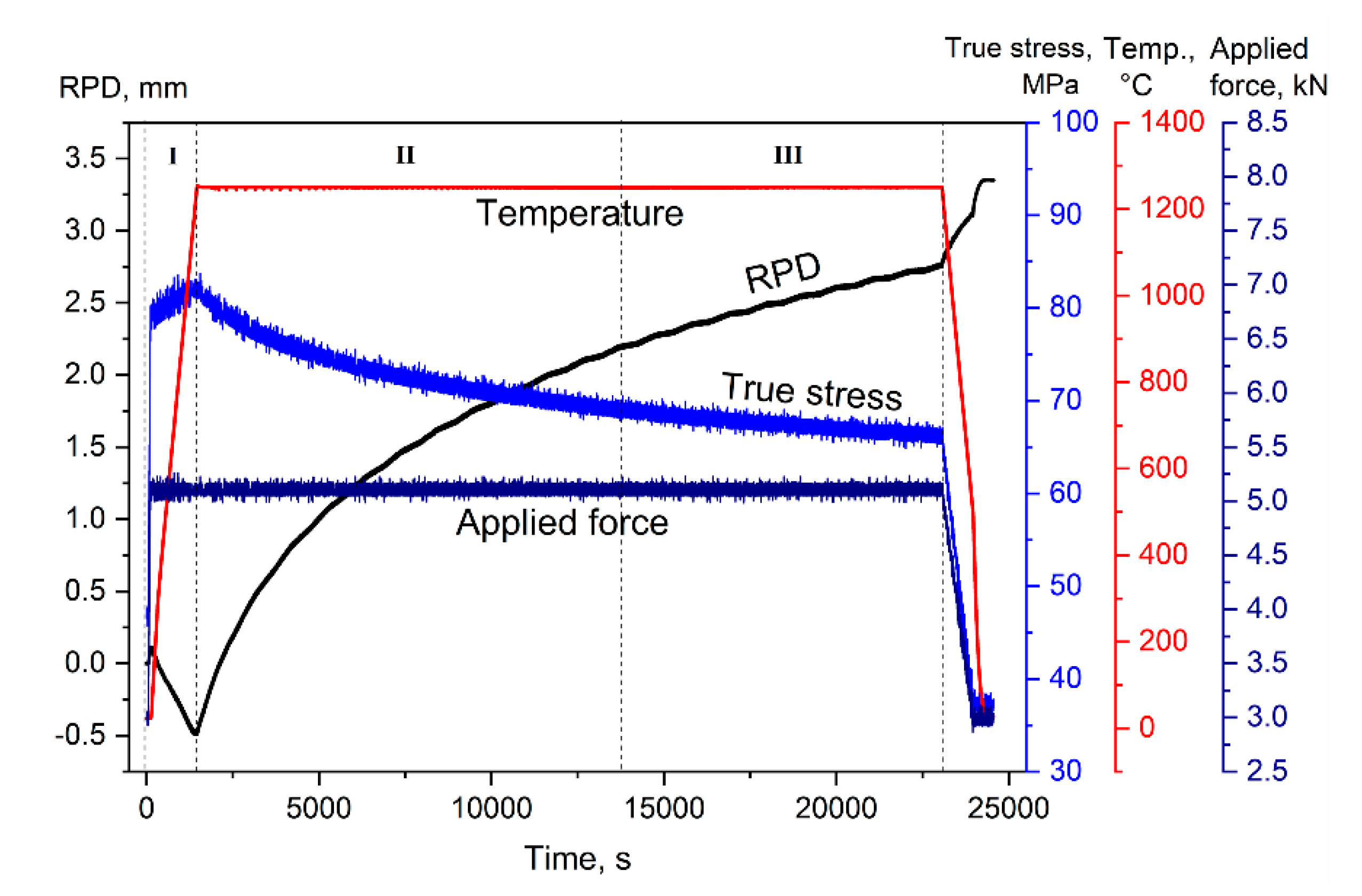
2.3. Creep Testing Procedure
3. Results and Discussion
3.1. Creep Testing of Metals
3.2. Creep Testing of Ceramics
3.3. High-Pressure Creep Tests
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kassner, M.E. Fundamentals of Creep in Metals and Alloys, 3rd ed.; Butterworth Heinemann imprint of Elsevier: Waltham, MA, USA, 2015. [Google Scholar]
- Carroll, D.F.; Wiederhorn, S.M. High temperature creep testing of ceramics. Int. J. High Technol. Ceram. 1988, 4, 227–241. [Google Scholar] [CrossRef]
- Yoon, K.J.; Wiederhorn, S.M.; Luecke, W.E. Comparison of tensile and compressive creep behavior in silicon nitride. J. Am. Ceram. Soc. 2004, 83, 2017–2022. [Google Scholar] [CrossRef]
- Longhin, M.E.; Shelleman, D.L.; Hellmann, J.R. A methodology for the accurate measurement of uniaxial compressive creep of refractory ceramics. meas. J. Int. Meas. Confed. 2017, 111, 69–83. [Google Scholar] [CrossRef]
- Cannon, W.R.; Langdon, T.G. Review creep of ceramics-Part 1 mechanical characteristics. J. Mater. Sci. 1983, 18, 1–50. [Google Scholar]
- Langdon, T.G. Identifying creep mechanisms in plastic flow. Z. Für Met. 2005, 96, 522–531. [Google Scholar] [CrossRef]
- Raj, R.; Ashby, M.F. On grain boundary sliding and diffusional creep. Metall. Trans. 1971, 2, 1113–1127. [Google Scholar] [CrossRef]
- Gibeling, J.C. ASM Handbook Volume 8: Mechanical Testing and Evaluation; ASM International: Novelty, OH, USA, 2000. [Google Scholar]
- Guillon, O.; Gonzalez-Julian, J.; Dargatz, B.; Kessel, T.; Schierning, G.; Räthel, J.; Herrmann, M. Field-assisted sintering technology/spark plasma sintering: mechanisms, materials, and technology developments. Adv. Eng. Mater. 2014, 16, 830–849. [Google Scholar] [CrossRef]
- Cavaliere, P. Spark Plasma Sintering of Materials; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Orru, R.; Licheri, R.; Locci, A.M.; Cincotti, A.; Cao, G. Consolidation/Synthesis of materials by electric current activated/assisted sintering. Mater. Sci. Eng. R Rep. 2009, 63, 127–287. [Google Scholar] [CrossRef]
- Ratzker, B.; Sokol, M.; Kalabukhov, S.; Frage, N. Using a spark plasma sintering apparatus as a tool in a compressive creep study of fine-grained alumina. Ceram. Int. 2017, 43, 9369–9376. [Google Scholar] [CrossRef]
- Ratzker, B.; Sokol, M.; Kalabukhov, S.; Frage, N. Creep of polycrystalline magnesium aluminate spinel studied by an SPS apparatus. Materials 2016, 9, 493. [Google Scholar] [CrossRef] [Green Version]
- Ratzker, B.; Sokol, M.; Kalabukhov, S.; Frage, N. compression creep of copper under electric current studied by a spark plasma sintering (SPS) apparatus. Mater. Sci. Eng. A 2018, 712, 424–429. [Google Scholar] [CrossRef]
- Uzan, N.E.; Ratzker, B.; Landau, P.; Kalabukhov, S.; Frage, N. Compressive creep of AlSi10Mg parts produced by selective laser melting additive manufacturing technology. Addit. Manuf. 2019, 29, 100788. [Google Scholar] [CrossRef]
- Li, W.; Olevsky, E.A.; McKittrick, J.; Maximenko, A.L.; German, R.M. Densification mechanisms of spark plasma sintering: Multi-step pressure dilatometry. J. Mater. Sci. 2012, 47, 7036–7046. [Google Scholar] [CrossRef]
- Lee, G.; Olevsky, E.A.; Manière, C.; Maximenko, A.; Izhvanov, O.; Back, C.; McKittrick, J. Effect of electric current on densification behavior of conductive ceramic powders consolidated by spark plasma sintering. Acta Mater. 2018, 144, 524–533. [Google Scholar] [CrossRef]
- E209-18 Standard Practice for Compression Tests of Metallic Materials at Elevated Temperatures with Conventional or Rapid Heating Rates and Strain Rates; ASTM E209-18; ASTM International: West Conshohocken, PA, USA, 2018.
- Achenani, Y.; Saâdaoui, M.; Cheddadi, A.; Fantozzi, G. Finite element analysis of the temperature uncertainty during spark plasma sintering: Influence of the experimental procedure. Ceram. Int. 2017, 43, 15281–15287. [Google Scholar] [CrossRef]
- Manière, C.; Durand, L.; Brisson, E.; Desplats, H.; Carré, P.; Rogeon, P.; Estournès, C. Contact resistances in spark plasma sintering: From in-situ and ex-situ determinations to an extended model for the scale up of the process. J. Eur. Ceram. Soc. 2017, 37, 1593–1605. [Google Scholar] [CrossRef] [Green Version]
- Sweidan, F.B.; Kim, D.H.; Ryu, H.J. Minimization of the sample temperature deviation and the effect of current during high-temperature compressive creep testing by the spark plasma sintering apparatus. Materialia 2020, 9, 100550. [Google Scholar] [CrossRef]
- Conrad, H. Thermally activated plastic flow of metals and ceramics with an electric field or current. Mater. Sci. Eng. A. 2002, 322, 100–107. [Google Scholar] [CrossRef]
- Chokshi, A.H.; Porter, J.R. Analysis of concurrent grain growth during creep of polycrystalline alumina. J. Am. Ceram. Soc. 1986, 37, 36–37. [Google Scholar] [CrossRef]
- Xue, L.A.; Chen, I. Deformation and grain growth of low-temperature-sintered high-purity alumina. J. Am. Ceram. Soc. 1990, 73, 3518–3521. [Google Scholar] [CrossRef]
- Venkatachari, K.R.; Raj, R. Superplastic flow in fine-grained alumina. J. Am. Ceram. Soc. 1986, 38, 135–138. [Google Scholar] [CrossRef]
- Feltham, P.; Meakin, J.D. Creep in face-centred cubic metals with special reference to copper. Acta Metall. 1959, 7, 614–627. [Google Scholar] [CrossRef]
- Raj, S.V.; Langdon, T.G. Creep behavior of copper at intermediate temperatures-I. Mechanical characteristics. Acta Metall. 1989, 37, 843–852. [Google Scholar] [CrossRef]
- Klypin, A.A. Plastic deformation of metals in the presence of electric influences. Strength Mater. 1975, 7, 810–815. [Google Scholar] [CrossRef]
- Cao, W.D.; Conrad, H. Effect of Stacking Fault Energy and Temperature on the Electroplastic Effect in FCC Metals. In Micromechanics of Advanced Materials: A Symposium in Honor of Professor James C.M. Li’s 70th Birthday; Minerals, Metals & Materials Society: Warrendale, PA, USA, 1995. [Google Scholar]
- Giuntini, D.; Olevsky, E.A.; Garcia-cardona, C.; Maximenko, A.L.; Yurlova, M.S.; Haines, C.D.; Martin, D.G.; Kapoor, D. Localized overheating phenomena and optimization of spark-plasma sintering tooling design. Materials 2013, 6, 2612–2632. [Google Scholar] [CrossRef] [Green Version]
- Bernard-Granger, G.; Guizard, C.; Duclos, R. Compressive creep behavior in air of a slightly porous as-sintered polycrystalline α-alumina material. J. Mater. Sci. 2007, 42, 2807–2819. [Google Scholar] [CrossRef]
- Ruano, O.A.; Wadsworth, J.; Sherby, O.D. Deformation of fine-grained alumina by grain boundary sliding accommodated by slip. Acta Mater. 2003, 51, 3617–3634. [Google Scholar] [CrossRef]
- Xu, Q.; Hayhurst, D.R. The evaluation of high-stress creep ductility for 316 stainless steel at 550 °C by extrapolation of constitutive equations derived for lower stress levels. Int. J. Press. Vessel. Pip. 2003, 80, 689–694. [Google Scholar] [CrossRef]
- Izuno, H.; Yokokawa, T.; Harada, H. An applicability of a creep constitutive equation for Ni-base superalloys on low temperature high stress condition. J. Jpn. Inst. Met. 2006, 70, 674–677. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Dlouhy, A.; Eggeler, Y.M.; Spiecker, E.; Kostka, A.; Somsen, C.; Eggeler, G. On the nucleation of planar faults during low temperature and high stress creep of single crystal Ni-base superalloys. Acta Mater. 2018, 144, 642–655. [Google Scholar] [CrossRef]
- Munro, R.G. Material properties of a sinterd α-SiC. J. Phys. Chem. Ref. Data. 1997, 26, 1195–1203. [Google Scholar] [CrossRef]






| Temperature Range, °C | Pressing Force, kN | Displacement Resolution, mm | Programmable Test Segments | Electric Current Applied to Sample | Chamber Atmosphere |
|---|---|---|---|---|---|
| Up to 2400 | 3–100 (stress depends on sample cross-section) | 0.001 | Yes | Possible for conductive samples | Vacuum (10−2 mbar) with argon flow |
| Test Configuration | Temperature at the Surface, °C | Temperature at the Center, °C | Temperature at the Top, °C | Temperature at the Bottom, °C |
|---|---|---|---|---|
| With electric current | 450 | 473 * | ||
| 500 | 524 * | 515 * | 501 * | |
| 550 | 579 * | |||
| Insulated from the electric current | 450 | 438 | ||
| 500 | 486 | |||
| 550 | 536 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratzker, B.; Kalabukhov, S.; Frage, N. Spark Plasma Sintering Apparatus Used for High-temperature Compressive Creep Tests. Materials 2020, 13, 396. https://doi.org/10.3390/ma13020396
Ratzker B, Kalabukhov S, Frage N. Spark Plasma Sintering Apparatus Used for High-temperature Compressive Creep Tests. Materials. 2020; 13(2):396. https://doi.org/10.3390/ma13020396
Chicago/Turabian StyleRatzker, Barak, Sergey Kalabukhov, and Nachum Frage. 2020. "Spark Plasma Sintering Apparatus Used for High-temperature Compressive Creep Tests" Materials 13, no. 2: 396. https://doi.org/10.3390/ma13020396
APA StyleRatzker, B., Kalabukhov, S., & Frage, N. (2020). Spark Plasma Sintering Apparatus Used for High-temperature Compressive Creep Tests. Materials, 13(2), 396. https://doi.org/10.3390/ma13020396