Magnetocaloric Effect in Cu5-NIPA Molecular Magnet: A Theoretical Study
Abstract
1. Introduction
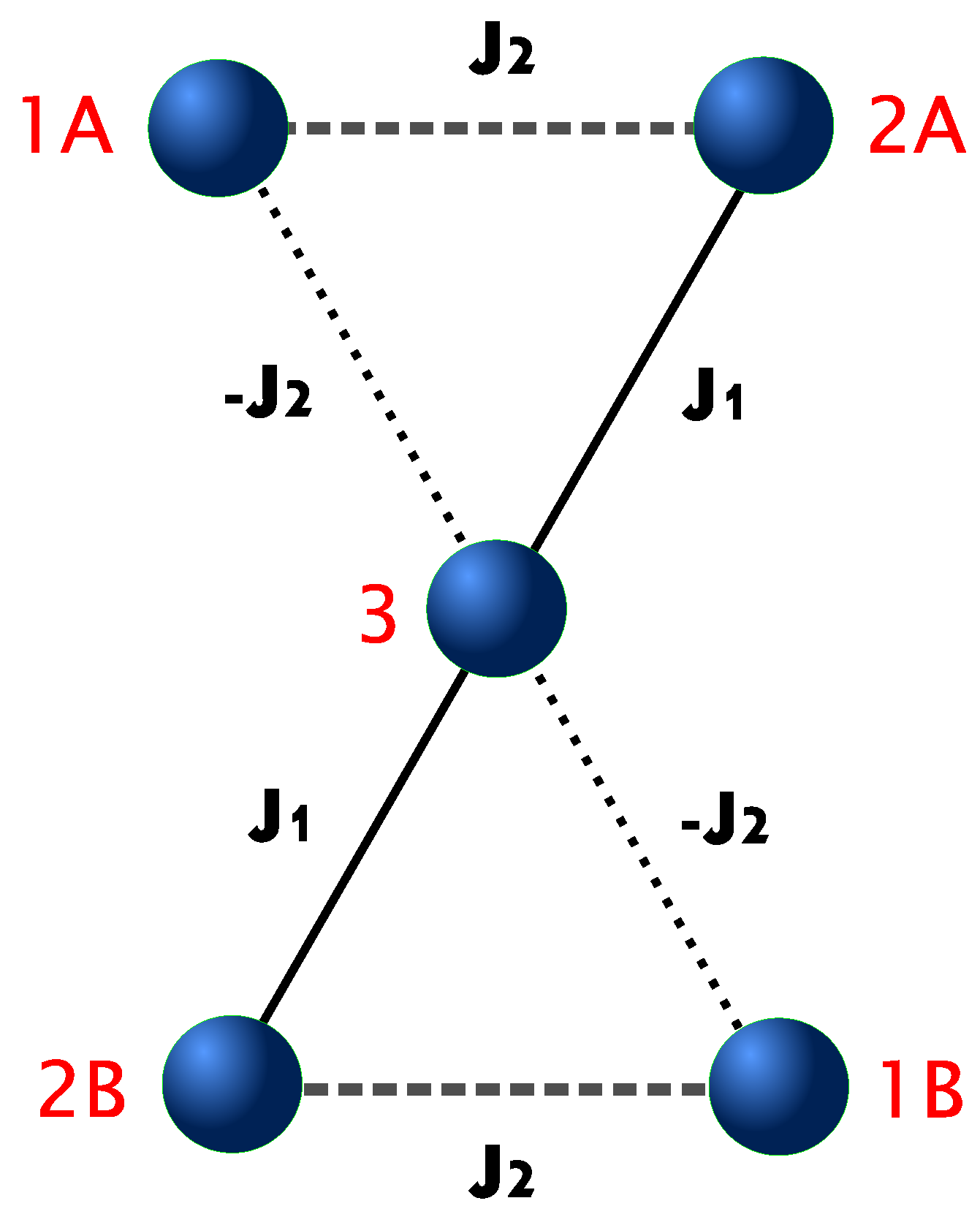
2. Theoretical Model and Computational Methods
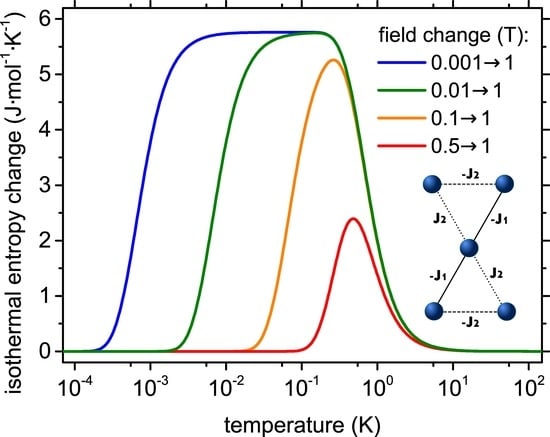
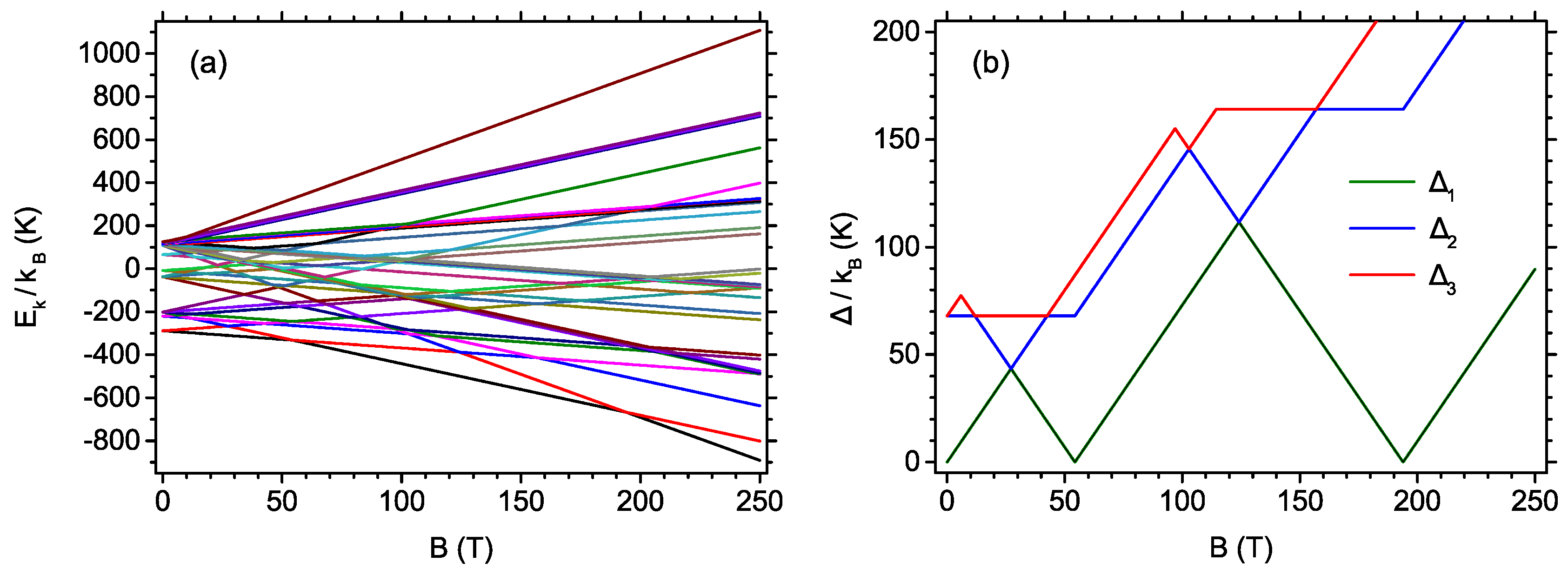
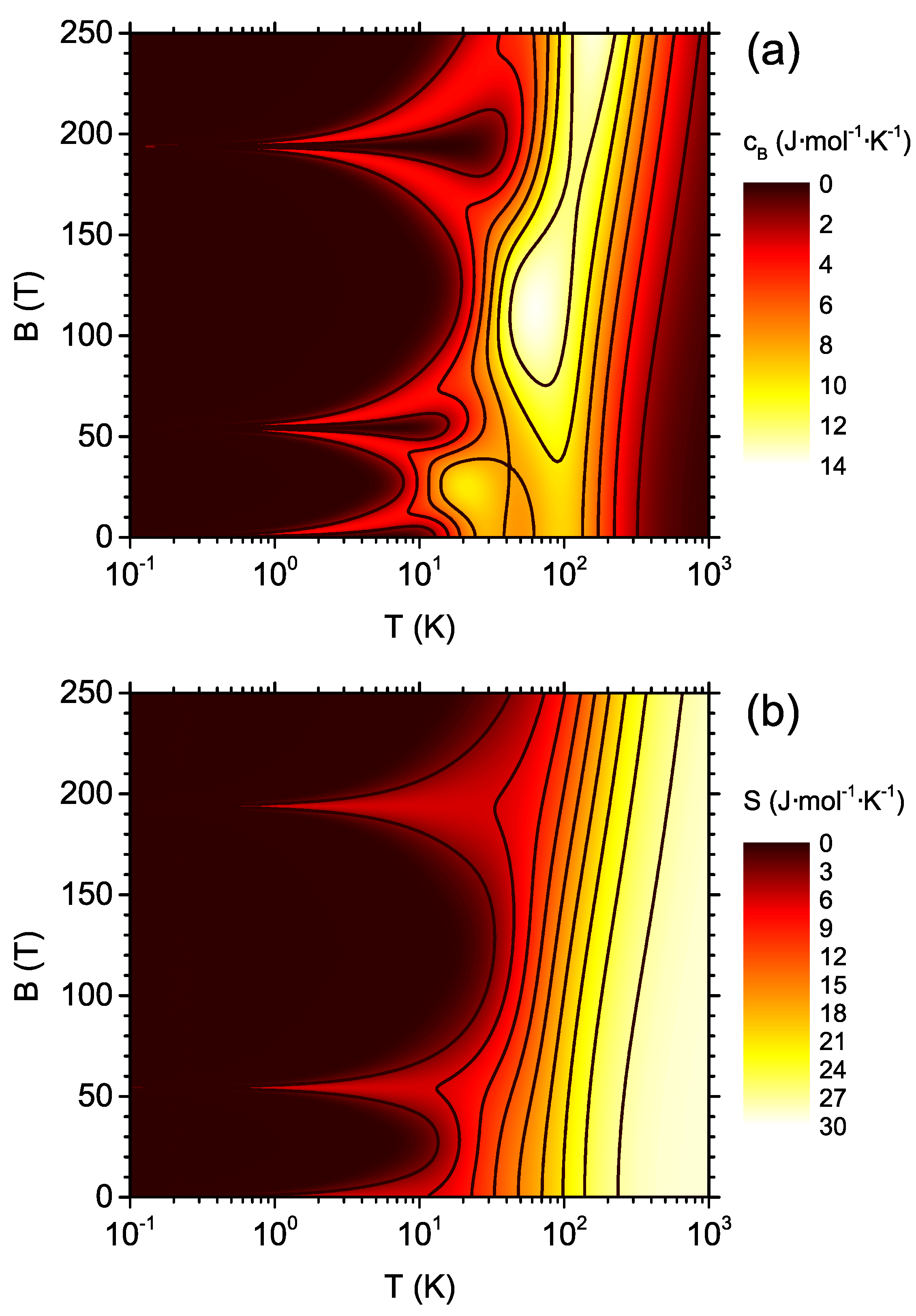
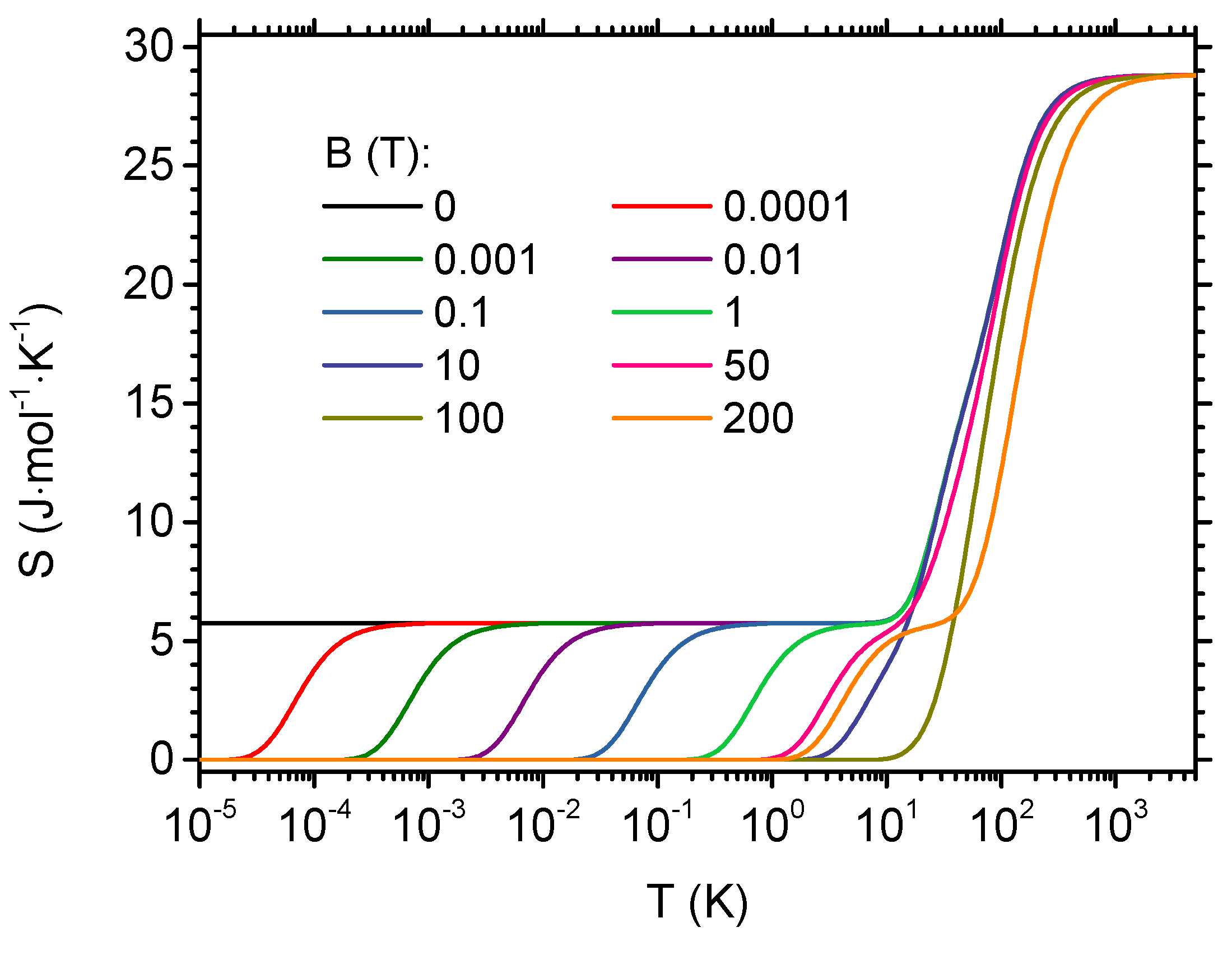
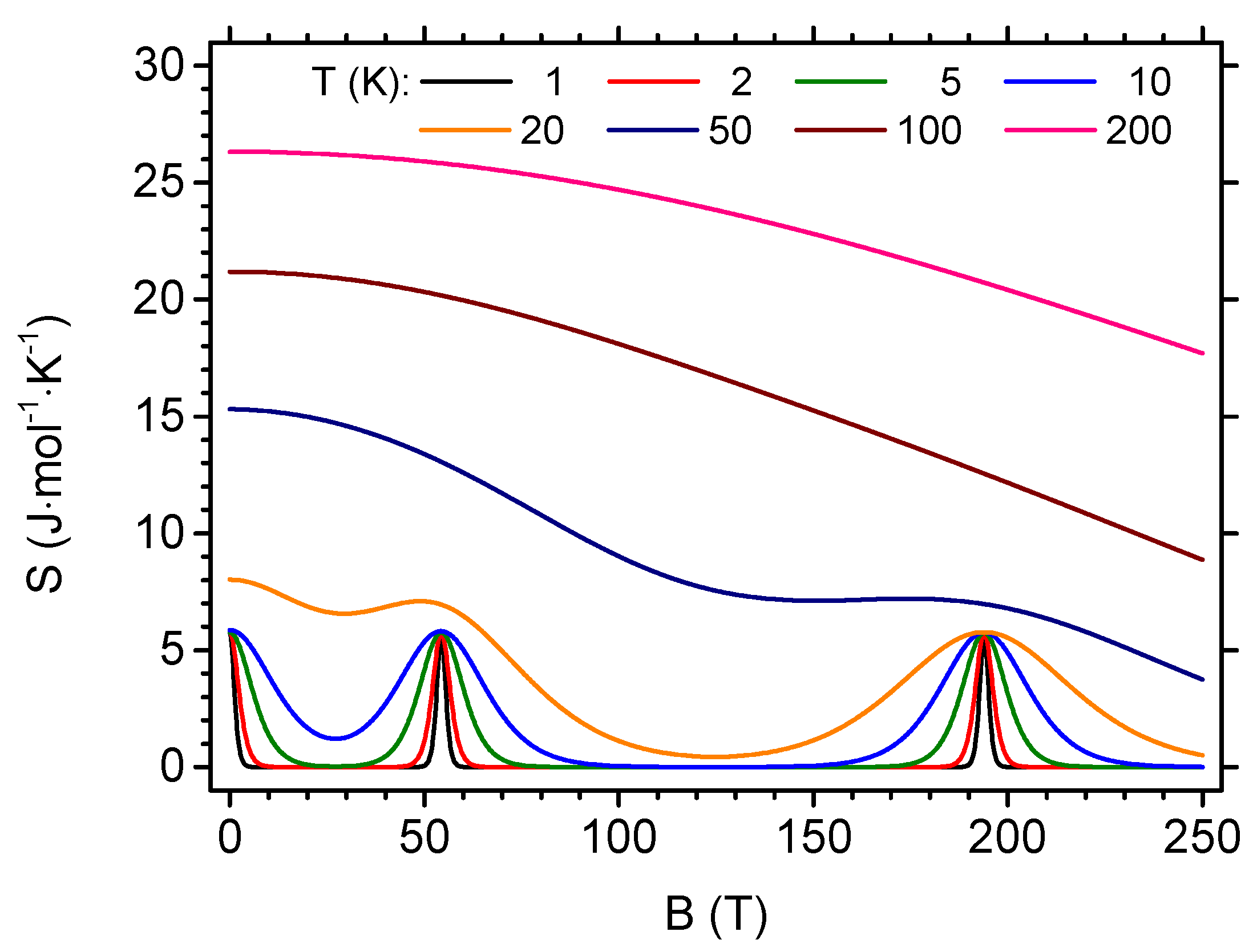
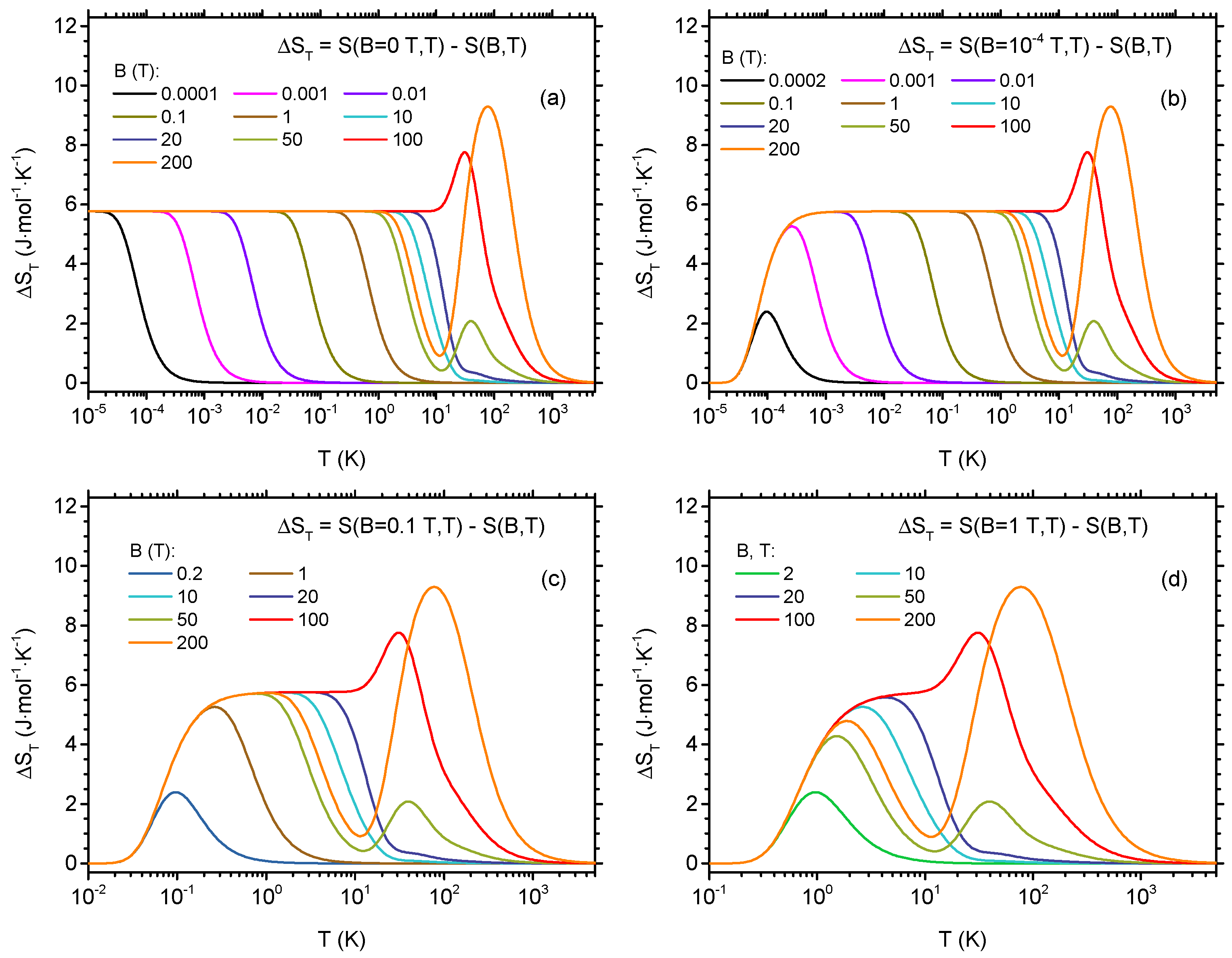
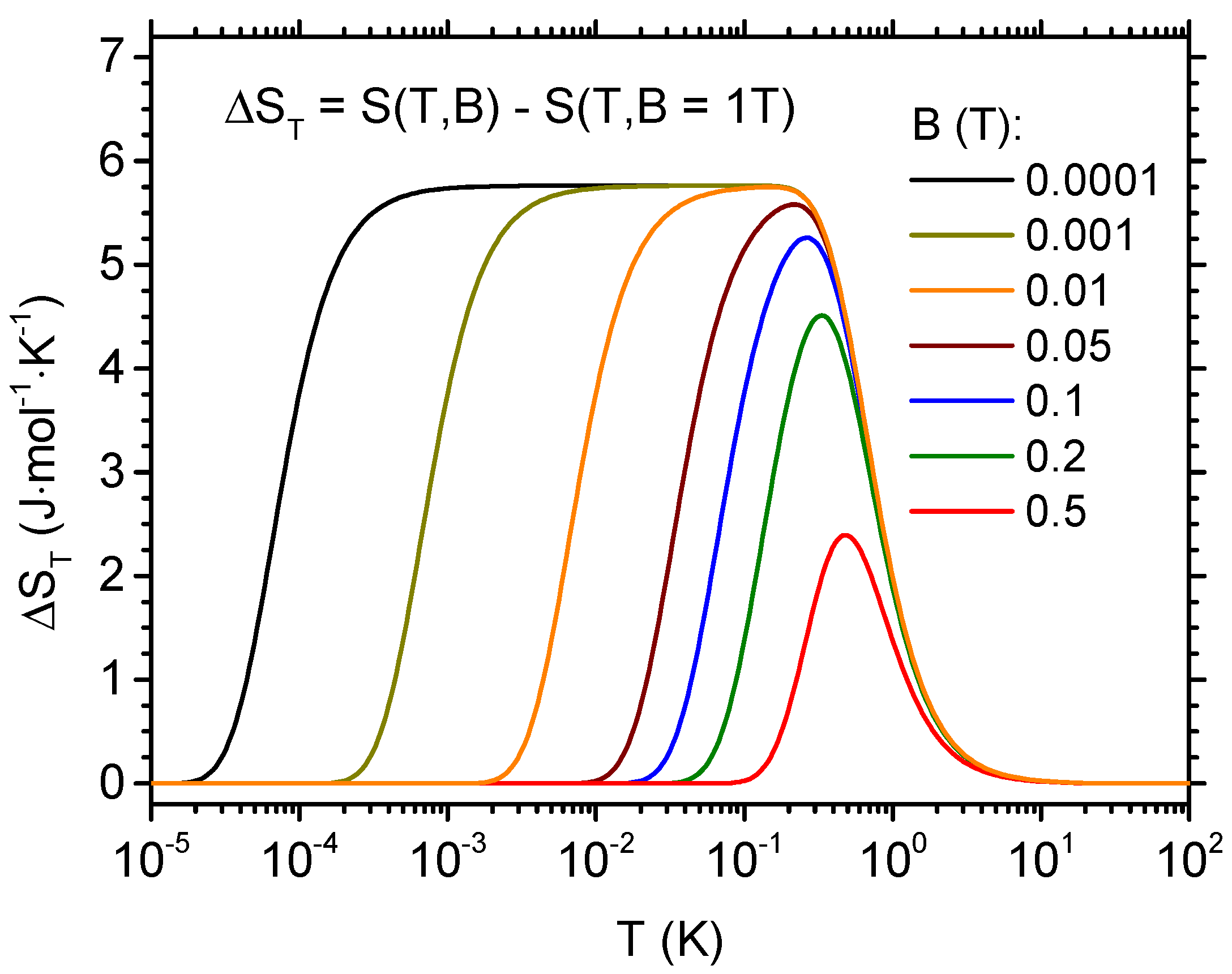
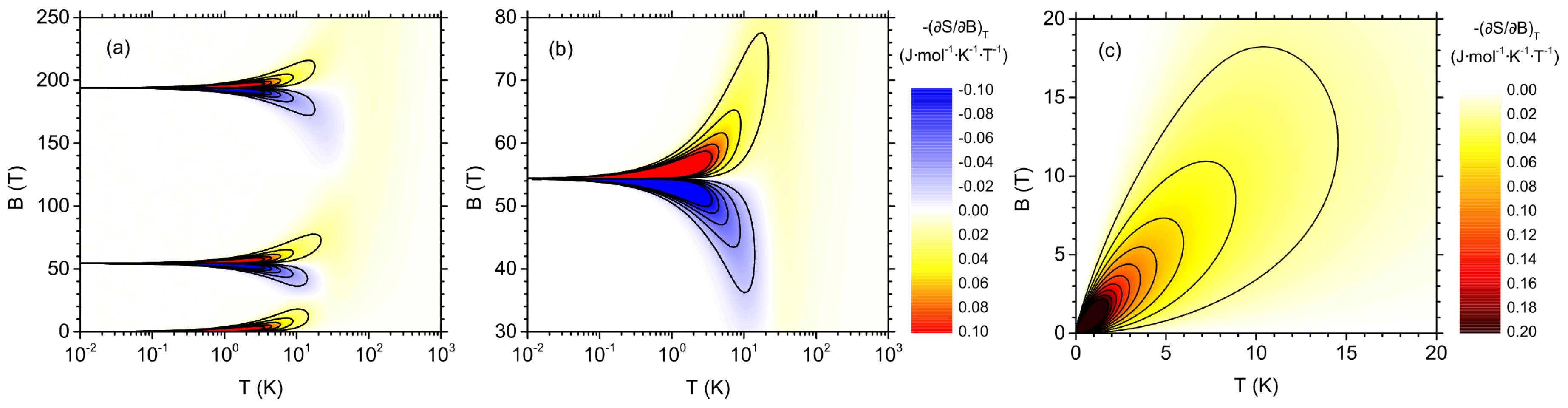
3. Results and Discussion
4. Final Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MCE | Magnetocaloric effect |
| NIPA | 5-nitro-isophthalic acid ligand |
| Cu5-NIPA | Cu5(OH)2(NIPA)4·10H2O |
Appendix A. The Ground States and Critical Magnetic Fields
References
- Pinkowicz, D.; Chorąży, S.; Stefańczyk, O. An Invitation to Molecular Magnetism. Sci. Prog. 2011, 94, 139–183. [Google Scholar] [CrossRef]
- Sieklucka, B.; Pinkowicz, D. (Eds.) Molecular Magnetic Materials: Concepts and Applications; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
- Blundell, S.J.; Pratt, F.L. Organic and Molecular Magnets. J. Phys. Condens. Matter 2004, 16, R771–R828. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Molecular Nanomagnets: The First 10 Years. J. Magn. Magn. Mater. 2004, 272–276, 1030–1036. [Google Scholar] [CrossRef]
- Blundell, S.J. Molecular Magnets. Contemp. Phys. 2007, 48, 275–290. [Google Scholar] [CrossRef]
- Schnack, J. Large Magnetic Molecules and What We Learn from Them. Contemp. Phys. 2019, 60, 127–144. [Google Scholar] [CrossRef]
- Coronado, E. Molecular Magnetism: From Chemical Design to Spin Control in Molecules, Materials and Devices. Nat. Rev. Mater. 2019, 1–18. [Google Scholar] [CrossRef]
- Friedman, J.R.; Sarachik, M.P. Single-Molecule Nanomagnets. Ann. Rev. Condens. Matter Phys. 2010, 1, 109–128. [Google Scholar] [CrossRef]
- Hołyńska, M. Introduction to Single-Molecule Magnets. In Single-Molecule Magnets; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2018; pp. 1–39. [Google Scholar]
- Bertaina, S.; Gambarelli, S.; Mitra, T.; Tsukerblat, B.; Müller, A.; Barbara, B. Quantum Oscillations in a Molecular Magnet. Nature 2008, 453, 203–206. [Google Scholar] [CrossRef]
- Fitta, M.; Pełka, R.; Konieczny, P.; Bałanda, M. Multifunctional Molecular Magnets: Magnetocaloric Effect in Octacyanometallates. Crystals 2019, 9, 9. [Google Scholar] [CrossRef]
- Evangelisti, M.; Luis, F.; de Jongh, L.J.; Affronte, M. Magnetothermal Properties of Molecule-Based Materials. J. Mater. Chem. 2006, 16, 2534–2549. [Google Scholar] [CrossRef]
- Sessoli, R. Chilling with Magnetic Molecules. Angew. Chem. Int. Ed. 2012, 51, 43–45. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.Z.; Zhou, G.J.; Zheng, Z.; Winpenny, R.E.P. Molecule-Based Magnetic Coolers. Chem. Soc. Rev. 2014, 43, 1462–1475. [Google Scholar] [CrossRef] [PubMed]
- Evangelisti, M. Molecule-Based Magnetic Coolers: Measurement, Design and Application. In Molecular Magnets: Physics and Applications; Bartolomé, J., Luis, F., Fernández, J.F., Eds.; NanoScience and Technology, Springer: Berlin/Heidelberg, Germany, 2014; pp. 365–387. [Google Scholar]
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and its Applications; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Romero Gómez, J.; Ferreiro Garcia, R.; De Miguel Catoira, A.; Romero Gómez, M. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renew. Sustain. Energy Rev. 2013, 17, 74–82. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Sharples, J.W.; Collison, D.; McInnes, E.J.L.; Schnack, J.; Palacios, E.; Evangelisti, M. Quantum Signatures of a Molecular Nanomagnet in Direct Magnetocaloric Measurements. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef]
- Ciccarelli, C.; Campion, R.P.; Gallagher, B.L.; Ferguson, A.J. Intrinsic Magnetic Refrigeration of a Single Electron Transistor. Appl. Phys. Lett. 2016, 108, 053103. [Google Scholar] [CrossRef]
- Bradley, D.I.; Guénault, A.M.; Gunnarsson, D.; Haley, R.P.; Holt, S.; Jones, A.T.; Pashkin, Y.A.; Penttilä, J.; Prance, J.R.; Prunnila, M.; et al. On-Chip Magnetic Cooling of a Nanoelectronic Device. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Affronte, M.; Ghirri, A.; Carretta, S.; Amoretti, G.; Piligkos, S.; Timco, G.A.; Winpenny, R.E.P. Engineering Molecular Rings for Magnetocaloric Effect. Appl. Phys. Lett. 2004, 84, 3468–3470. [Google Scholar] [CrossRef]
- Evangelisti, M.; Brechin, E.K. Recipes for Enhanced Molecular Cooling. Dalton Trans. 2010, 39, 4672–4676. [Google Scholar] [CrossRef]
- Garlatti, E.; Carretta, S.; Schnack, J.; Amoretti, G.; Santini, P. Theoretical Design of Molecular Nanomagnets for Magnetic Refrigeration. Appl. Phys. Lett. 2013, 103, 202410. [Google Scholar] [CrossRef]
- Liu, J.L.; Chen, Y.C.; Guo, F.S.; Tong, M.L. Recent Advances in the Design of Magnetic Molecules for Use as Cryogenic Magnetic Coolants. Coord. Chem. Rev. 2014, 281, 26–49. [Google Scholar] [CrossRef]
- Holleis, L.; Shivaram, B.S.; Balachandran, P.V. Machine Learning Guided Design of Single-Molecule Magnets for Magnetocaloric Applications. Appl. Phys. Lett. 2019, 114, 222404. [Google Scholar] [CrossRef]
- Torres, F.; Hernández, J.M.; Bohigas, X.; Tejada, J. Giant and Time-Dependent Magnetocaloric Effect in High-Spin Molecular Magnets. Appl. Phys. Lett. 2000, 77, 3248–3250. [Google Scholar] [CrossRef]
- Gajewski, M.; Pełka, R.; Fitta, M.; Miyazaki, Y.; Nakazawa, Y.; Bałanda, M.; Reczyński, M.; Nowicka, B.; Sieklucka, B. Magnetocaloric Effect of High-Spin Cluster with Ni9W6 Core. J. Magn. Magn. Mater. 2016, 414, 25–31. [Google Scholar] [CrossRef]
- Chen, W.-P.; Qin, L.; Camón, A.; Engelhardt, L.; Luis, F.; Winpenny, R.E.P.; Zheng, Y.-Z. Quantum Monte Carlo simulations of a giant {Ni21Gd20} cage with a S=91 spin ground state. Nat. Commun. 2018, 9, 2107. [Google Scholar] [CrossRef]
- Schnack, J. Frustration Effects in Magnetic Molecules. J. Low Temp. Phys. 2006, 142, 279–284. [Google Scholar] [CrossRef][Green Version]
- Schnack, J.; Schmidt, R.; Richter, J. Enhanced Magnetocaloric Effect in Frustrated Magnetic Molecules with Icosahedral Symmetry. Phys. Rev. B 2007, 76, 054413. [Google Scholar] [CrossRef]
- Pakhira, S.; Mazumdar, C.; Ranganathan, R.; Avdeev, M. Magnetic Frustration Induced Large Magnetocaloric Effect in the Absence of Long Range Magnetic Order. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- Chakraborty, T.; Mitra, C. Magnetocaloric Effect as a Signature of Quantum Level-Crossing for a Spin-Gapped System. J. Phys. Condens. Matter 2019, 31, 475802. [Google Scholar] [CrossRef]
- Lorusso, G.; Roubeau, O.; Evangelisti, M. Rotating Magnetocaloric Effect in an Anisotropic Molecular Dimer. Angew. Chem. Int. Ed. 2016, 55, 3360–3363. [Google Scholar] [CrossRef]
- Beckmann, C.; Ehrens, J.; Schnack, J. Rotational Magnetocaloric Effect of Anisotropic Giant-Spin Molecular Magnets. J. Magn. Magn. Mater. 2019, 482, 113–119. [Google Scholar] [CrossRef]
- Engelhardt, L.; Luban, M. Simple Models and Powerful Tools for Seeking a Comprehensive Understanding of the Magnetic Properties of Molecular Magnets. Dalton Trans. 2010, 39, 4687–4692. [Google Scholar] [CrossRef] [PubMed]
- Strečka, J.; Karľová, K.; Madaras, T. Giant Magnetocaloric Effect, Magnetization Plateaux and Jumps of the Regular Ising Polyhedra. Phys. B Condens. Matter 2015, 466–467, 76–85. [Google Scholar] [CrossRef]
- Karľová, K.; Strečka, J.; Madaras, T. The Schottky-Type Specific Heat as an Indicator of Relative Degeneracy between Ground and First-Excited States: The Case Study of Regular Ising Polyhedra. Phys. B Condens. Matter 2016, 488, 49–56. [Google Scholar] [CrossRef]
- Karľová, K.; Strečka, J.; Richter, J. Enhanced Magnetocaloric Effect in the Proximity of Magnetization Steps and Jumps of Spin-1/2 XXZ Heisenberg Regular Polyhedra. J. Phys. Condens. Matter 2017, 29, 125802. [Google Scholar] [CrossRef]
- Karľová, K.; Strečka, J.; Madaras, T. Isothermal Entropy Change and Adiabatic Change of Temperature of the Antiferromagnetic Spin-1/2 Ising Octahedron and Dodecahedron. Acta Phys. Pol. A 2017, 131, 630–632. [Google Scholar] [CrossRef]
- Žukovič, M.; Bobák, A. Entropy of Spin Clusters with Frustrated Geometry. Phys. Lett. A 2014, 378, 1773–1779. [Google Scholar] [CrossRef][Green Version]
- Žukovič, M. Thermodynamic and Magnetocaloric Properties of Geometrically Frustrated Ising Nanoclusters. J. Magn. Magn. Mater. 2015, 374, 22–35. [Google Scholar] [CrossRef]
- Žukovič, M.; Semjan, M. Magnetization Process and Magnetocaloric Effect in Geometrically Frustrated Ising Antiferromagnet and Spin Ice Models on a ‘Star of David’ Nanocluster. J. Magn. Magn. Mater. 2018, 451, 311–318. [Google Scholar] [CrossRef]
- Mohylna, M.; Žukovič, M. Magnetocaloric Properties of Frustrated Tetrahedra-Based Spin Nanoclusters. Phys. Lett. A 2019, 383, 2525–2534. [Google Scholar] [CrossRef]
- Strečka, J.; Čisárová, J. Magnetization Process and Adiabatic Demagnetization of the Antiferromagnetic Spin-1/2 Heisenberg Cubic Cluster. Acta Phys. Pol. A 2014, 126, 26–27. [Google Scholar] [CrossRef]
- Karľová, K.; Strečka, J. Magnetization process and magnetocaloric effect of the spin-1/2 XXZ Heisenberg cuboctahedron. J. Low. Temp. Phys. 2017, 187, 727–733. [Google Scholar] [CrossRef]
- Strečka, J.; Karľová, K. Magnetization Curves and Low-Temperature Thermodynamics of Two Spin-1/2 Heisenberg Edge-Shared Tetrahedra. AIP Adv. 2018, 8, 101403. [Google Scholar] [CrossRef]
- Deb, M.; Ghosh, A.K. Studies of Magnetocaloric Effect on Spin-1/2 J1-J2 Heisenberg Hexagons. AIP Conf. Proc. 2016, 1728, 020058. [Google Scholar]
- Haldar, S.; Ramasesha, S. Magnetocaloric effect in molecular spin clusters and their assemblies: Exact and Monte Carlo studies using exact cluster eigenstates. J. Magn. Magn. Mater. 2020, 500, 166424. [Google Scholar] [CrossRef]
- Arian Zad, H.; Kenna, R.; Ananikian, N. Magnetic and Thermodynamic Properties of the Octanuclear Nickel Phosphonate-Based Cage. Phys. A Stat. Mech. Appl. 2020, 538, 122841. [Google Scholar] [CrossRef]
- Kowalewska, P.; Szałowski, K. Magnetocaloric Properties of V6 Molecular Magnet. J. Magn. Magn. Mater. 2020, 496, 165933. [Google Scholar] [CrossRef]
- Schnack, J.; Hage, P.; Schmidt, H.J. Efficient Implementation of the Lanczos Method for Magnetic Systems. J. Comput. Phys. 2008, 227, 4512–4517. [Google Scholar] [CrossRef]
- Schnack, J.; Ummethum, J. Advanced Quantum Methods for the Largest Magnetic Molecules. Polyhedron 2013, 66, 28–33. [Google Scholar] [CrossRef]
- Ummethum, J.; Schnack, J.; Läuchli, A.M. Large-Scale Numerical Investigations of the Antiferromagnetic Heisenberg Icosidodecahedron. J. Magn. Magn. Mater. 2013, 327, 103–109. [Google Scholar] [CrossRef]
- Hanebaum, O.; Schnack, J. Thermodynamic Observables of Mn12-Acetate Calculated for the Full Spin Hamiltonian. Phys. Rev. B 2015, 92, 064424. [Google Scholar] [CrossRef]
- Mentrup, D.; Schmidt, H.J.; Schnack, J.; Luban, M. Transition from Quantum to Classical Heisenberg Trimers: Thermodynamics and Time Correlation Functions. Phys. A Stat. Mech. Appl. 2000, 278, 214–221. [Google Scholar] [CrossRef]
- Luban, M.; Borsa, F.; Bud’ko, S.; Canfield, P.; Jun, S.; Jung, J.K.; Kögerler, P.; Mentrup, D.; Müller, A.; Modler, R.; et al. Heisenberg Spin Triangles in {V6}-Type Magnetic Molecules: Experiment and Theory. Phys. Rev. B 2002, 66, 054407. [Google Scholar] [CrossRef]
- Haraldsen, J.T.; Barnes, T.; Musfeldt, J.L. Neutron Scattering and Magnetic Observables for S=1/2 Spin Clusters and Molecular Magnets. Phys. Rev. B 2005, 71, 064403. [Google Scholar] [CrossRef]
- Schmidt, H.J. The General Spin Triangle. Int. J. Modern Phys. B 2013, 27, 1350064. [Google Scholar] [CrossRef]
- Brumfield, A.; Haraldsen, J.T. Thermodynamics and Magnetic Excitations in Quantum Spin Trimers: Applications for the Understanding of Molecular Magnets. Crystals 2019, 9, 93. [Google Scholar] [CrossRef]
- Angaridis, P.A.; Baran, P.; Boča, R.; Cervantes-Lee, F.; Haase, W.; Mezei, G.; Raptis, R.G.; Werner, R. Synthesis and Structural Characterization of Trinuclear CuII-Pyrazolato Complexes Containing μ3-OH, μ3-O, and μ3-Cl Ligands. Magnetic Susceptibility Study of [PPN]2[(μ3-O)Cu3(μ-pz)3Cl3]. Inorg. Chem. 2002, 41, 2219–2228. [Google Scholar] [CrossRef]
- Iida, K.; Qiu, Y.; Sato, T.J. Dzyaloshinsky-Moriya Interaction and Long Lifetime of the Spin State in the Cu3 Triangular Spin Cluster by Inelastic Neutron Scattering Measurements. Phys. Rev. B 2011, 84, 094449. [Google Scholar] [CrossRef]
- Ponomaryov, A.N.; Kim, N.; Jang, Z.H.; van Tol, J.; Koo, H.J.; Law, J.M.; Suh, B.J.; Yoon, S.; Choi, K.Y. Spin Decoherence Processes in the S = 1/2 Scalene Triangular Cluster (Cu3(OH)). New J. Phys. 2015, 17, 033042. [Google Scholar] [CrossRef]
- Spielberg, E.T.; Gilb, A.; Plaul, D.; Geibig, D.; Hornig, D.; Schuch, D.; Buchholz, A.; Ardavan, A.; Plass, W. A Spin-Frustrated Trinuclear Copper Complex Based on Triaminoguanidine with an Energetically Well-Separated Degenerate Ground State. Inorg. Chem. 2015, 54, 3432–3438. [Google Scholar] [CrossRef]
- Kintzel, B.; Böhme, M.; Liu, J.; Burkhardt, A.; Mrozek, J.; Buchholz, A.; Ardavan, A.; Plass, W. Molecular Electronic Spin Qubits from a Spin-Frustrated Trinuclear Copper Complex. Chem. Commun. 2018, 54, 12934–12937. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Mrozek, J.; Myers, W.K.; Timco, G.A.; Winpenny, R.E.P.; Kintzel, B.; Plass, W.; Ardavan, A. Electric Field Control of Spins in Molecular Magnets. Phys. Rev. Lett. 2019, 122, 037202. [Google Scholar] [CrossRef] [PubMed]
- Alécio, R.C.; Lyra, M.L.; Strečka, J. Ground States, Magnetization Plateaus and Bipartite Entanglement of Frustrated Spin-1/2 Ising-Heisenberg and Heisenberg Triangular Tubes. J. Magn. Magn. Mater. 2016, 417, 294–301. [Google Scholar] [CrossRef]
- Zad, H.A.; Ananikian, N.; Kenna, R. The Specific Heat and Magnetic Properties of Two Species of Spin-1/2 Ladders with Butterfly-Shaped Unit Blocks. J. Phys. Condens. Matter 2019, 31, 445802. [Google Scholar] [CrossRef] [PubMed]
- Schnack, J.; Nojiri, H.; Kögerler, P.; Cooper, G.J.T.; Cronin, L. Magnetic Characterization of the Frustrated Three-Leg Ladder Compound [(CuCl2 tach H)3Cl]Cl2. Phys. Rev. B 2004, 70, 174420. [Google Scholar] [CrossRef]
- Ivanov, N.B.; Schnack, J.; Schnalle, R.; Richter, J.; Kögerler, P.; Newton, G.N.; Cronin, L.; Oshima, Y.; Nojiri, H. Heat Capacity Reveals the Physics of a Frustrated Spin Tube. Phys. Rev. Lett. 2010, 105, 037206. [Google Scholar] [CrossRef]
- Nath, R.; Tsirlin, A.A.; Khuntia, P.; Janson, O.; Förster, T.; Padmanabhan, M.; Li, J.; Skourski, Y.; Baenitz, M.; Rosner, H.; et al. Magnetization and Spin Dynamics of the Spin S=1/2 Hourglass Nanomagnet Cu5(OH)2(NIPA)4·10H2O. Phys. Rev. B 2013, 87, 214417. [Google Scholar] [CrossRef]
- Bi, L.-H.; Kortz, U. Synthesis and Structure of the Pentacopper(II) Substituted Tungstosilicate [Cu5(OH)4(H2O)2(A-α-SiW9O33)2]10−. Inorg. Chem. 2004, 43, 7961–7962. [Google Scholar] [CrossRef]
- Nellutla, S.; van Tol, J.; Dalal, N.S.; Bi, L.H.; Kortz, U.; Keita, B.; Nadjo, L.; Khitrov, G.A.; Marshall, A.G. Magnetism, Electron Paramagnetic Resonance, Electrochemistry, and Mass Spectrometry of the Pentacopper(II)- Substituted Tungstosilicate [Cu5(OH)4(H2O)2(A-α-SiW9O33)2]10−, A Model Five-Spin Frustrated Cluster. Inorg. Chem. 2005, 44, 9795–9806. [Google Scholar] [CrossRef]
- Ishikawa, R.; Nakano, M.; Fuyuhiro, A.; Takeuchi, T.; Kimura, S.; Kashiwagi, T.; Hagiwara, M.; Kindo, K.; Kaizaki, S.; Kawata, S. Construction of a Novel Topological Frustrated System: A Frustrated Metal Cluster in a Helical Space. Chem. Eur. J. 2010, 16, 11139–11144. [Google Scholar] [CrossRef]
- Liu, Z.-Y.; Chu, J.; Ding, B.; Zhao, X.-J.; Yang, E.-C. A novel cluster-based 3D magnetic framework with an overall S=1/2 spin ground state. Inorg. Chem. Commun. 2011, 14, 925–928. [Google Scholar] [CrossRef]
- Mathematica, Version 8.0.4; Wolfram Research, Inc.: Champaign, IL, USA, 2010.
- Plascak, J.A. Ensemble Thermodynamic Potentials of Magnetic Systems. J. Magn. Magn. Mater. 2018, 468, 224–229. [Google Scholar] [CrossRef]
- Fu, Z.; Xiao, Y.; Su, Y.; Zheng, Y.; Kögerler, P.; Brückel, T. Low-lying magnetic excitations and magnetocaloric effect of molecular magnet K6[V15As6O42(H2O)]·8H2O. EPL 2015, 112, 27003. [Google Scholar] [CrossRef]
- Waldmann, O. Field-induced level crossings in spin clusters: Thermodynamics and magnetoelastic instability. Phys. Rev. B 2007, 75, 174440. [Google Scholar] [CrossRef]
- Chakraborty, T.; Singh, H.; Mitra, C. Experimental evidences of singlet to triplet transition in a spin cluster compound. J. Magn. Magn. Mater. 2015, 396, 247–253. [Google Scholar] [CrossRef]
- Julien, M.-H.; Jang, Z.H.; Lascialfari, A.; Borsa, F.; Horvatič, M.; Caneschi, A.; Gatteschi, D. Proton NMR for Measuring Quantum Level Crossing in the Magnetic Molecular Ring Fe10. Phys. Rev. Lett. 1999, 83, 227–230. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Magnetocaloric Materials. Ann. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szałowski, K.; Kowalewska, P. Magnetocaloric Effect in Cu5-NIPA Molecular Magnet: A Theoretical Study. Materials 2020, 13, 485. https://doi.org/10.3390/ma13020485
Szałowski K, Kowalewska P. Magnetocaloric Effect in Cu5-NIPA Molecular Magnet: A Theoretical Study. Materials. 2020; 13(2):485. https://doi.org/10.3390/ma13020485
Chicago/Turabian StyleSzałowski, Karol, and Pamela Kowalewska. 2020. "Magnetocaloric Effect in Cu5-NIPA Molecular Magnet: A Theoretical Study" Materials 13, no. 2: 485. https://doi.org/10.3390/ma13020485
APA StyleSzałowski, K., & Kowalewska, P. (2020). Magnetocaloric Effect in Cu5-NIPA Molecular Magnet: A Theoretical Study. Materials, 13(2), 485. https://doi.org/10.3390/ma13020485