Giant Vertical Magnetization Shift Caused by Field-Induced Ferromagnetic Spin Reconfiguration in Ni50Mn36Ga14 Alloy
Abstract
1. Introduction
2. Material and Methods
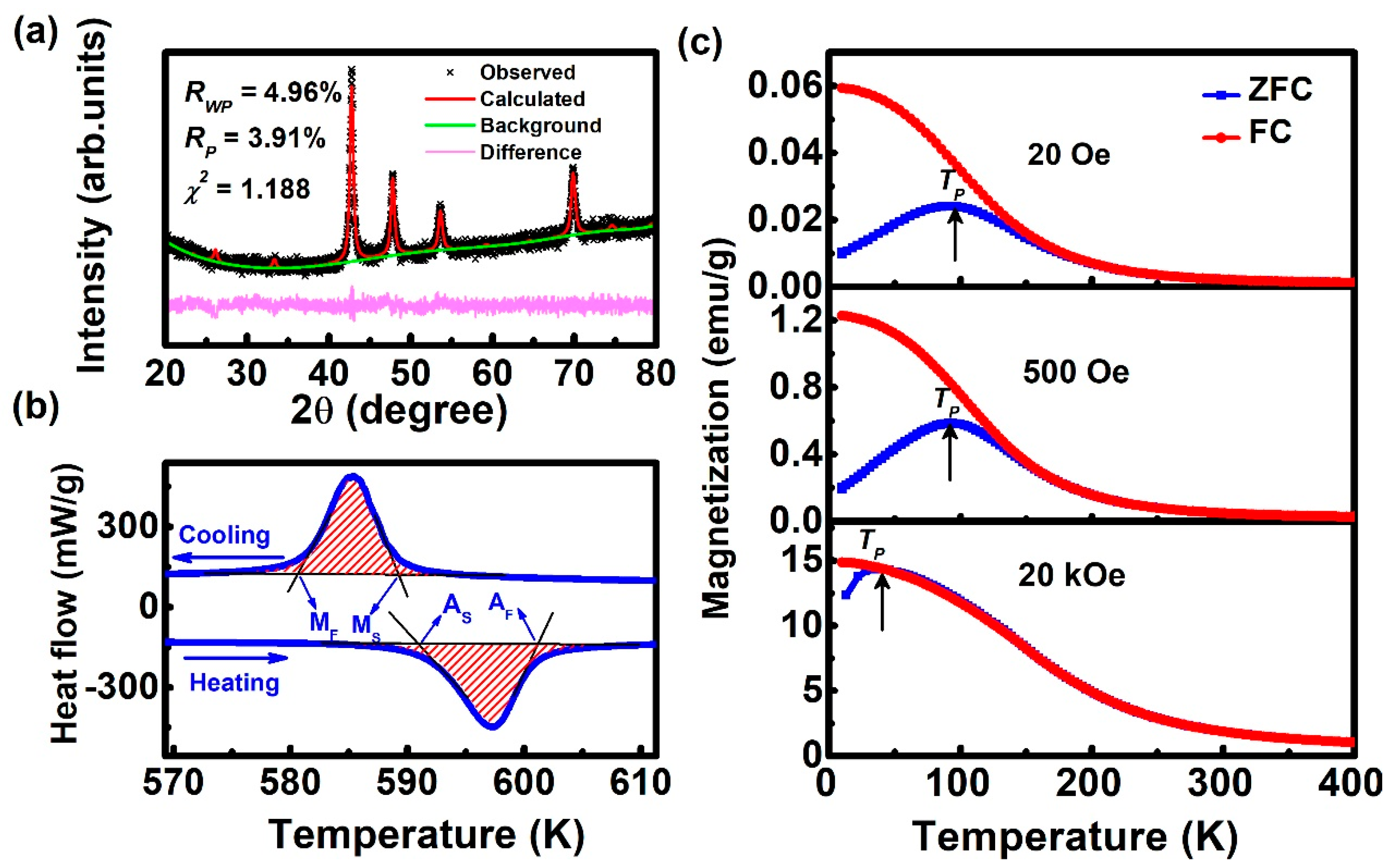
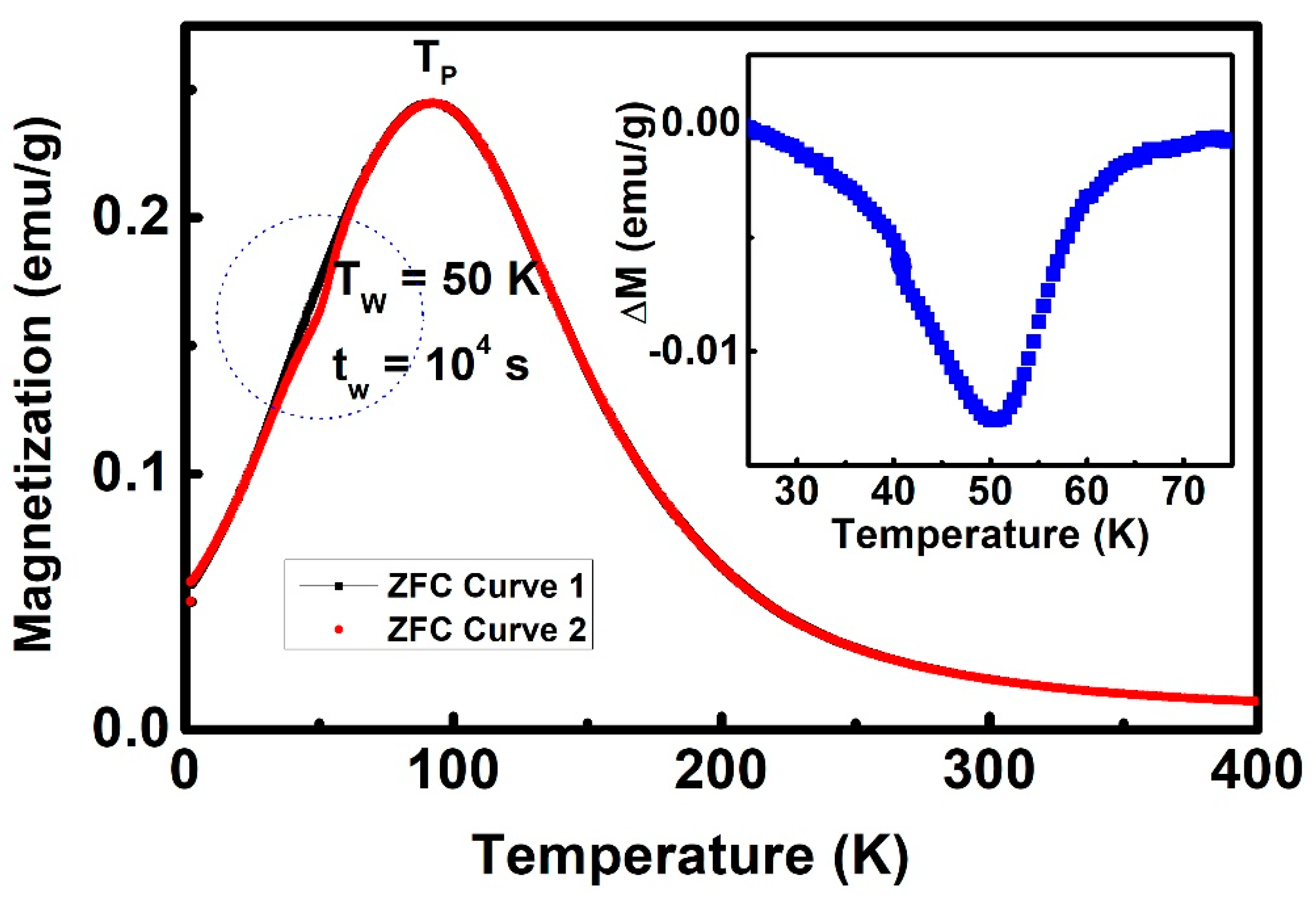
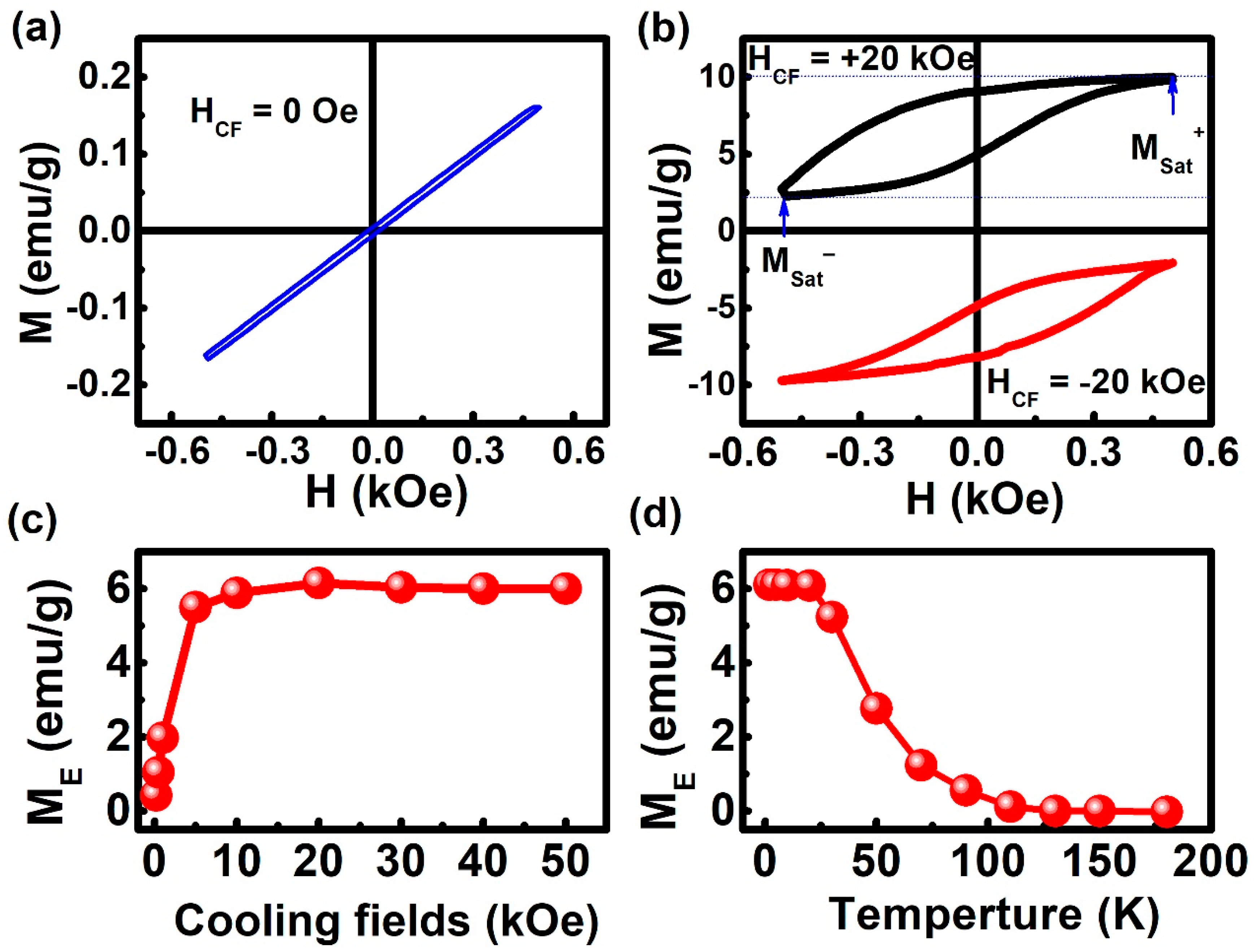
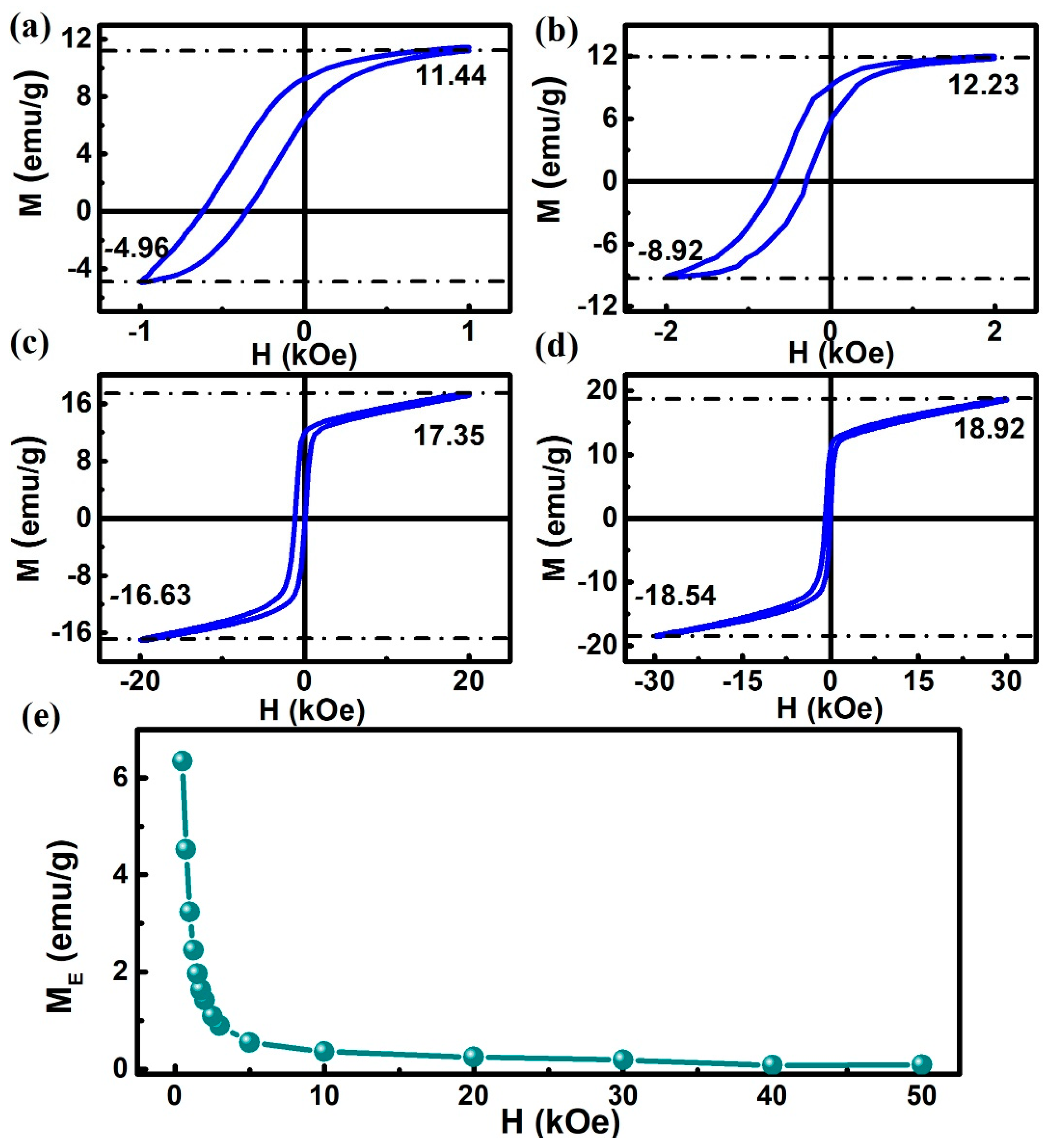
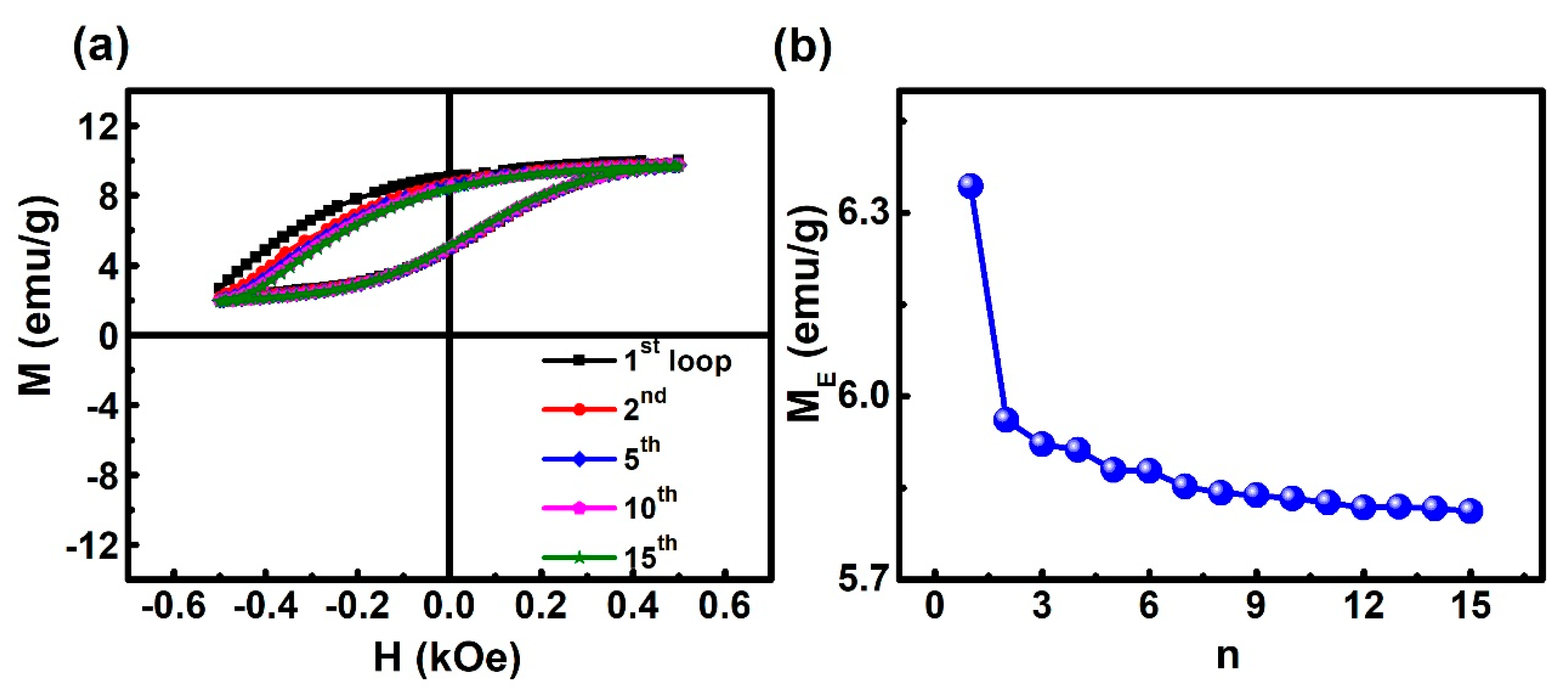
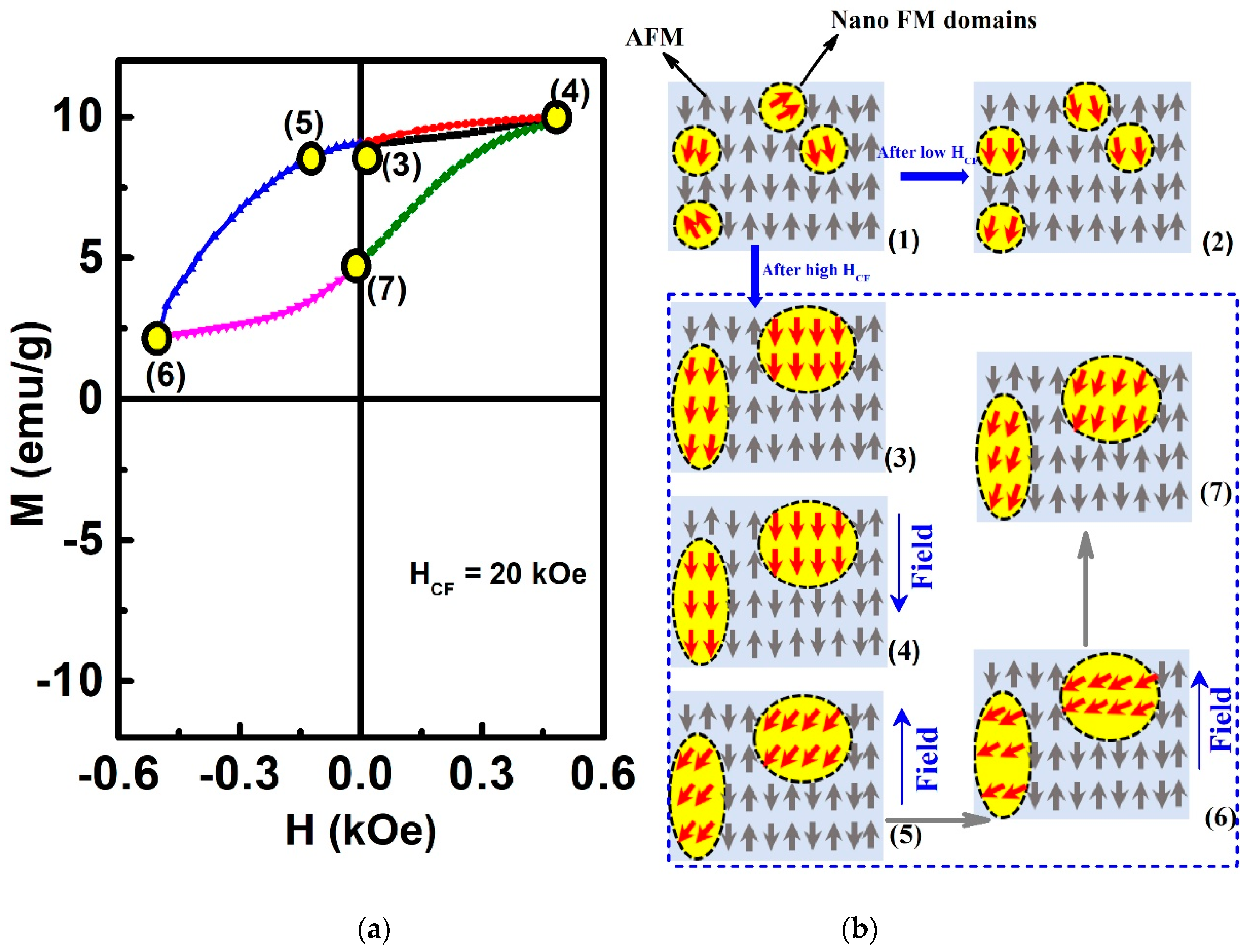
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Meiklejohn, W.H.; Bean, C.P. New Magnetic Anisotropy. Phys. Rev. 1956, 102, 3866–3876. [Google Scholar] [CrossRef]
- Elphck, K.; Vallejo-Fernandez, G.; Klemmer, T.J.; Thiele, J.U.; O’Grady, K. HAMR media based on exchange bias. Appl. Phys. Lett. 2016, 109, 052402. [Google Scholar] [CrossRef]
- Albisetti, E.; Scaramuzzi, G.; Rinaldi, C.; Cantoni, M.; Bertacco, R.; Petti, D. Temperature Dependence of the Magnetic Properties of IrMn/CoFeB/Ru/CoFeB Exchange Biased Synthetic Antiferromagnets. Materials 2020, 13, 387. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.J.; Song, C.; Cui, B.; Wang, G.Y.; Xiao, L.R.; Pan, F. Room temperature spontaneous exchange bias in (La,Sr)MnO3/PbZr0.8Ti0.2O3/(La,Sr)MnO3 sandwich structure. J. Appl. Phys. 2013, 114, 167. [Google Scholar] [CrossRef]
- Çakır, A.C.; Acet, M.; Farle, M. Exchange bias caused by field-induced spin reconfiguration in Ni-Mn-Sn. Phys. Rev. B 2016, 93, 094411. [Google Scholar] [CrossRef]
- Kim, G.; Khaydukov, Y.; Bluschke, M.; Suyolcu, Y.E.; Christiani, G.; Son, K.; Dietl, C.; Keller, T.; Weschke, E.; Van Aken, P.A.; et al. Tunable perpendicular exchange bias in oxide heterostructures. Phys. Rev. Mater. 2019, 3, 084420. [Google Scholar] [CrossRef]
- Ding, S.; Xue, M.; Liang, Z.; Liu, Z.; Li, R.; Cao, S.; Sun, Y.; Zhao, J.; Yang, W.; Yang, J. Spin switching temperature modulated by the magnetic field and spontaneous exchange bias effect in single crystal SmFeO3. J. Phys. Condens. Matter 2019, 31, 435801. [Google Scholar] [CrossRef] [PubMed]
- Coutrim, L.T.; Rigitano, D.; Macchiutti, C.; Mori, T.J.A.; Lora-Serrano, R.; Granado, E.; Sadrollahi, E.; Litterst, F.J.; Fontes, M.B.; Baggio-Saitovitch, E.; et al. Zero-field-cooled exchange bias effect in phase-segregated La2-xAxCoMnO6-δ (A = Ba,Ca,Sr; x = 0, 0.5). Phys. Rev. B 2019, 100, 054428. [Google Scholar] [CrossRef]
- Liu, J.; Singh, A.; Liu, Y.Y.F.; Ionescu, A.; Kuerbanjiang, B.; Barnes, C.H.W.; Hesjedal, T. Exchange Bias in Magnetic Topological Insulator Superlattices. Nano Lett. 2020, 20, 5315–5322. [Google Scholar] [CrossRef]
- Wang, X.X.; Gao, S.; Yan, X.; Li, Q.; Zhang, J.C.; Long, Y.Z.; Ruan, K.Q.; Li, X.G. Giant spontaneous exchange bias obtained by tuning magnetic compensation in samarium ferrite single crystal. Phys. Chem. Chem. Phys. 2018, 20, 3687–3693. [Google Scholar] [CrossRef]
- Gumieniczek-Chłopek, E.; Odrobińska, J.; Strączek, T.; Radziszewska, A.; Zapotoczny, S.; Kapusta, C. Hydrophobically Coated Superparamagnetic Iron Oxides Nanoparticles Incorporated into Polymer-Based Nanocapsules Dispersed in Water. Materials 2020, 13, 1219. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Cao, K.; Zhang, Y.; Zeng, Y.; Zhang, R.; Chang, T.; Zhou, C.; Xu, M.; Song, X.; Yang, S. Giant spontaneous exchange bias triggered by crossover of superspin glass in Sb-doped Ni50Mn38Ga12 Heusler alloys. Sci. Rep. 2016, 6, 30801. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.M.; Yuan, S.L.; Yin, S.Y.; Liu, L.; He, J.H.; Duan, H.N.; Li, P.; Wang, C.H. Exchange bias effect in a granular system of NiFe2O4 nanoparticles embedded in an antiferromagnetic NiO matrix. Appl. Phys. Lett. 2008, 93, 222505. [Google Scholar] [CrossRef]
- Singamaneni, S.R.; Fan, W.; Prater, J.T. Complete vertical MH loop shift in La0. 7Sr0. 3MnO3/SrRuO3 thin film heterostructures. J. Appl. Phys. 2015, 117, 17B711. [Google Scholar] [CrossRef]
- Zheng, M.; Li, X.; Xiao, W.; Wang, W.; Ni, H. Oxygen deficiency and cooling field driven vertical hysteretic shift in epitaxial SrRuO3/SrTiO3 heterostructures. Appl. Phys. Lett. 2017, 111, 152405. [Google Scholar] [CrossRef]
- Zhou, G.; Ji, H.; Lin, W.; Zhang, J.; Bai, Y.; Chen, J.; Wu, M.; Xu, X. Orbital reconstruction mediated giant vertical magnetization shift and insulator-to-metal transition in superlattices based on antiferromagnetic manganites. Phys. Rev. B. 2020, 101, 024422. [Google Scholar] [CrossRef]
- Tho, P.T.; Kim, D.H.; Phan, T.L.; Dang, N.V.; Lee, B.W. Intrinsic exchange bias and vertical hysteresis shift in Bi0.84La0.16Fe0.96Ti0.04O3. J. Magn. Magn. Mater. 2018, 462, 172–177. [Google Scholar] [CrossRef]
- Zheng, M.; Wang, W. Tunable Ferromagnetic Transition Temperature and Vertical Hysteretic Shift in SrRuO3 Films Integrated on Si(001). ACS Appl. Mater. Interfaces 2016, 8, 14012–14018. [Google Scholar] [CrossRef]
- Krenke, T.; Duman, E.; Acet, M.; Wassermann, E.F.; Moya, X.; Manosa, L.; Planes, A. Inverse magnetocaloric effect in ferromagnetic Ni–Mn–Sn alloys. Nat. Mater. 2005, 4, 450–454. [Google Scholar] [CrossRef]
- Sutou, Y.; Imano, Y.; Koeda, N.; Omori, T.; Kainuma, R.; Ishida, K.; Oikawa, K. Magnetic and martensitic transformations of NiMnX (X = In, Sn, Sb) ferromagnetic shape memory alloys. Appl. Phys. Lett. 2004, 85, 4358. [Google Scholar] [CrossRef]
- Lünser, K.; Diestel, A.; Nielsch, K.; Fähler, S. Influencing Martensitic Transition in Epitaxial Ni-Mn-Ga-Co Films with Large Angle Grain Boundaries. Materials 2020, 13, 3674. [Google Scholar] [CrossRef] [PubMed]
- Krenke, T.; Acet, M.; Wassermann, E.F.; Moya, X.; Mañosa, L.; Planes, A. Martensitic transitions and the nature of ferromagnetism in the austenitic and martensitic states of Ni-Mn-Sn alloys. Phys. Rev. B 2005, 72, 014412. [Google Scholar] [CrossRef]
- Tian, F.; Zeng, Y.; Xu, M.; Yang, S.; Lu, T.; Wang, J.; Chang, T.; Adil, M.; Zhang, Y.; Zhou, C.; et al. A magnetocaloric effect arising from a ferromagnetic transition in the martensitic state in Heusler alloy of Ni50Mn36Sb8Ga6. Appl. Phys. Lett. 2015, 107, 012406. [Google Scholar] [CrossRef]
- Raji, G.R.; Uthaman, B.; Rajan, R.K.; Sharannia, M.P.; Thomas, S.; Suresh, K.G.; Varma, M.R. Martensitic transition, spin glass behavior and enhanced exchange bias in Si substituted Ni50Mn36Sn14 Heusler alloys. RSC Adv. 2016, 6, 32037–32045. [Google Scholar] [CrossRef]
- Barandiarán, J.M.; Chernenko, V.A.; Gutiérrez, J.; Orúe, I.; Lázpita, P. Magnetostriction in the vicinity of structural transitions in Ni2MnGa. Appl. Phys. Lett. 2012, 100, 262410. [Google Scholar] [CrossRef]
- Hinterleitner, B.; Knapp, I.; Poneder, M.; Shi, Y.; Müller, H.; Eguchi, G.; Eisenmenger-Sittner, C.; Stöger-Pollach, M.; Kakefuda, Y.; Kawamoto, N.; et al. Thermoelectric performance of a metastable thin-film Heusler alloy. Nature 2019, 576, 85–90. [Google Scholar] [CrossRef]
- Ye, M.; Kimura, A.; Miura, Y.; Shirai, M.; Cui, Y.T.; Shimada, K.; Namatame, H.; Taniguchi, M.; Ueda, S.; Kobayashi, K.; et al. Role of Electronic Structure in the Martensitic Phase Transition of Ni2Mn1+xSn1-x Studied by Hard-X-Ray Photoelectron Spectroscopy and Ab Initio Calculation. Phys. Rev. Lett. 2010, 104, 176401. [Google Scholar] [CrossRef]
- Xu, X.; Nagasako, M.; Ito, W.; Umetsu, R.Y.; Kanomata, T.; Kainuma, R. Magnetic properties and phase diagram of Ni50Mn50-xGax ferromagnetic shape memory alloys. Acta Mater. 2013, 61, 6712–6723. [Google Scholar] [CrossRef]
- Han, Z.D.; Qian, B.; Wang, D.H.; Zhang, P.; Jiang, X.F.; Zhang, C.L.; Du, Y.W. Magnetic phase separation and exchange bias in off-stoichiometric Ni-Mn-Ga alloys. Appl. Phys. Lett. 2013, 103, 172403. [Google Scholar] [CrossRef]
- Vasil’ev, A.N.; Buchel’nikov, V.D.; Takagi, T.; Khovaĭlo, V.V.; Éstrin, É.I. Shape memory ferromagnets. Phys.-Usp. 2003, 46, 559. [Google Scholar] [CrossRef]
- Nayak, A.K.; Shekhar, C.; Winterlik, J.; Gupta, A.; Felser, C. Mn2PtIn: A tetragonal Heusler compound with exchange bias behavior. Appl. Phys. Lett. 2012, 100, 152404. [Google Scholar] [CrossRef]
- Winkelmann, A.; Przybylski, M.; Luo, F.; Shi, Y.; Barthel, J. Perpendicular magnetic anisotropy induced by tetragonal distortion of FeCo alloy films grown on Pd (001). Phys. Rev. Lett. 2006, 96, 257205. [Google Scholar] [CrossRef] [PubMed]
- Machavarapu, R.; Jakob, G. Exchange bias effect in the martensitic state of Ni-Co-Mn-Sn film. Appl. Phys. Lett. 2013, 102, 232406. [Google Scholar] [CrossRef]
- Sharma, J.; Suresh, K.G. Observation of giant exchange bias in bulk Mn50Ni42Sn8 Heusler alloy. Appl. Phys. Lett. 2015, 106, 072405. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, J.; Iyer, K.K.; Sampathkumaran, E.V. Reentrant spin-glass and transport behavior of Gd4PtAl, a compound with three sites for Gd. J. Magn. Magn. Mater. 2019, 490, 165515. [Google Scholar] [CrossRef]
- Zheng, R.K.; Wen, G.H.; Fung, K.K.; Zhang, X.X. Giant exchange bias and the vertical shifts of hysteresis loops in γ- Fe2O3 -coated Fe nanoparticles. J. Appl. Phys. 2004, 95, 5244. [Google Scholar] [CrossRef]
- Polisetty, S.; Sahoo, S.; Binek, C. Scaling behavior of the exchange-bias training effect. Phys. Rev. B. 2007, 76, 184423. [Google Scholar] [CrossRef]
- Proenca, M.P.; Ventura, J.; Sousa, C.T.; Vazquez, M.; Araujo, J.P. Exchange bias, training effect, and bimodal distribution of blocking temperatures in electrodeposited core-shell nanotubes. Phys. Rev. B. 2013, 87, 134404. [Google Scholar] [CrossRef]
- Bitla, Y.; Kaul, S.N.; Barquín, L.F. Nonlinear susceptibilities as a probe to unambiguously distinguish between canonical and cluster spin glasses. Phys. Rev. B. 2012, 86, 094405. [Google Scholar] [CrossRef]
- Bedanta, S.; Kleemann, W. Topical review superparamagnetism. J. Phys. D-Appl. Phys. 2009, 42, 013001. [Google Scholar] [CrossRef]
- Liao, P.; Jing, C.; Wang, X.L.; Yang, Y.J.; Zheng, D.; Li, Z.; Kang, B.J.; Deng, D.M.; Cao, S.X.; Zhang, J.C.; et al. Strongly enhanced antiferromagnetism and giant spontaneous exchange bias in Ni50Mn36Co4Sn10 Heusler alloy. Appl. Phys. Lett. 2014, 104, 092410. [Google Scholar] [CrossRef]
- Windsor, Y.W.; Gerber, A.; Karpovski, M. Dynamics of successive minor hysteresis loops. Phys. Rev. B 2012, 85, 064409. [Google Scholar] [CrossRef]

| Cooling Field (kOe) | T0 (K) | τ0 (s) | Ea/KB (K) |
|---|---|---|---|
| 0 | 87.1 | 5.1 × 10−9 | 621.5 |
| 10 | 89.3 | 9.7 × 10−7 | 648.2 |
| 20 | 90.1 | 8.4 × 10−6 | 669.1 |
| 30 | 91.7 | 3.5 × 10−5 | 752.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, F.; Zhang, Y.; Zhou, C.; Zhao, Q.; Yu, Z.; Murtaza, A.; Zuo, W.; Yang, S.; Song, X. Giant Vertical Magnetization Shift Caused by Field-Induced Ferromagnetic Spin Reconfiguration in Ni50Mn36Ga14 Alloy. Materials 2020, 13, 4701. https://doi.org/10.3390/ma13214701
Tian F, Zhang Y, Zhou C, Zhao Q, Yu Z, Murtaza A, Zuo W, Yang S, Song X. Giant Vertical Magnetization Shift Caused by Field-Induced Ferromagnetic Spin Reconfiguration in Ni50Mn36Ga14 Alloy. Materials. 2020; 13(21):4701. https://doi.org/10.3390/ma13214701
Chicago/Turabian StyleTian, Fanghua, Yin Zhang, Chao Zhou, Qizhong Zhao, Zhonghai Yu, Adil Murtaza, Wenliang Zuo, Sen Yang, and Xiaoping Song. 2020. "Giant Vertical Magnetization Shift Caused by Field-Induced Ferromagnetic Spin Reconfiguration in Ni50Mn36Ga14 Alloy" Materials 13, no. 21: 4701. https://doi.org/10.3390/ma13214701
APA StyleTian, F., Zhang, Y., Zhou, C., Zhao, Q., Yu, Z., Murtaza, A., Zuo, W., Yang, S., & Song, X. (2020). Giant Vertical Magnetization Shift Caused by Field-Induced Ferromagnetic Spin Reconfiguration in Ni50Mn36Ga14 Alloy. Materials, 13(21), 4701. https://doi.org/10.3390/ma13214701





