Tool Path Design of the Counter Single Point Incremental Forming Process to Decrease Shape Error
Abstract
1. Introduction
2. Experimental Set-Up
2.1. Equipment for the Experiments
2.2. Experimental Conditions
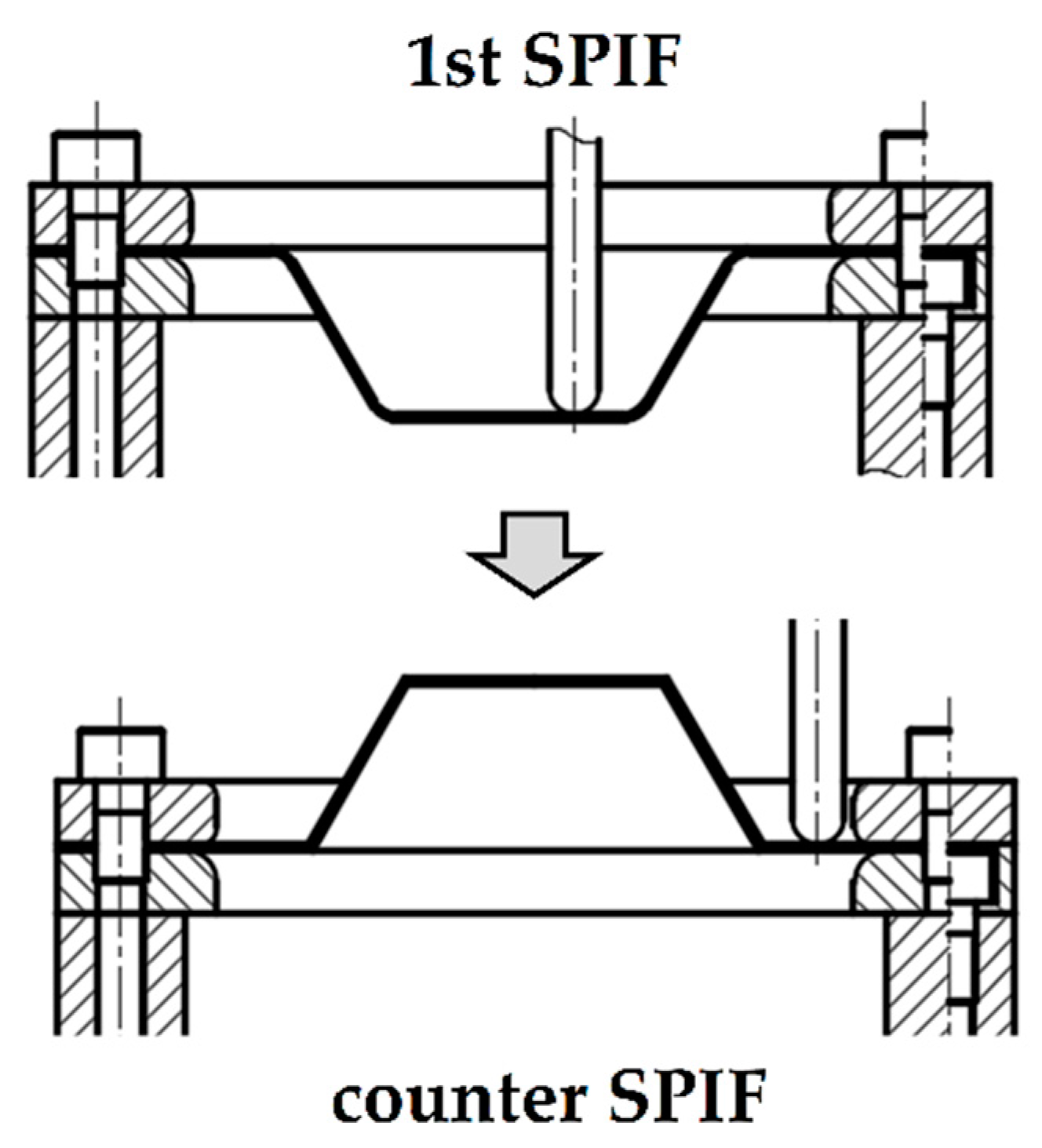
3. Tool Path Design for the Counter SPIF
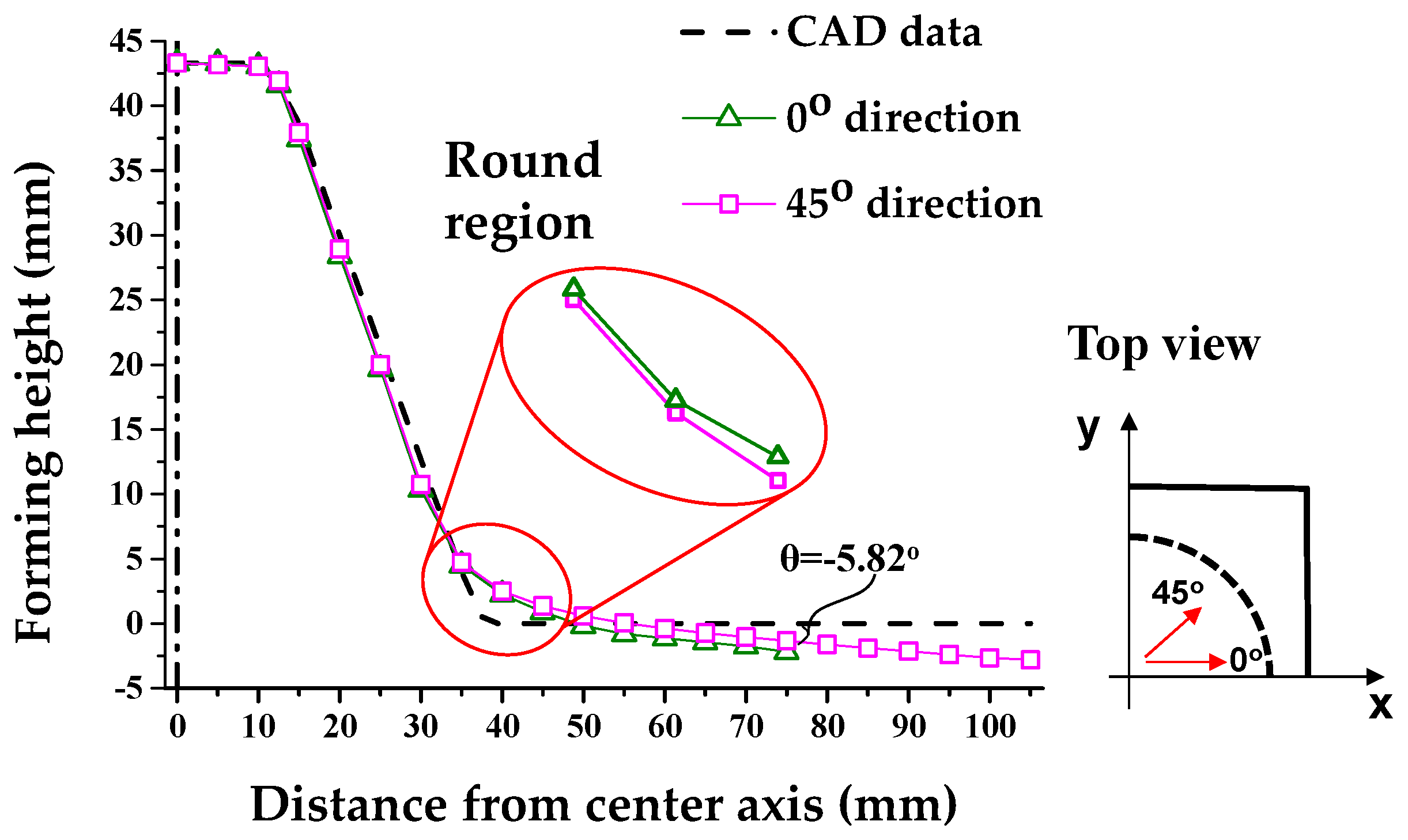
3.1. Definition of the Shape Error
3.2. Tool Path Modification to Increase the Geometric Accuracy
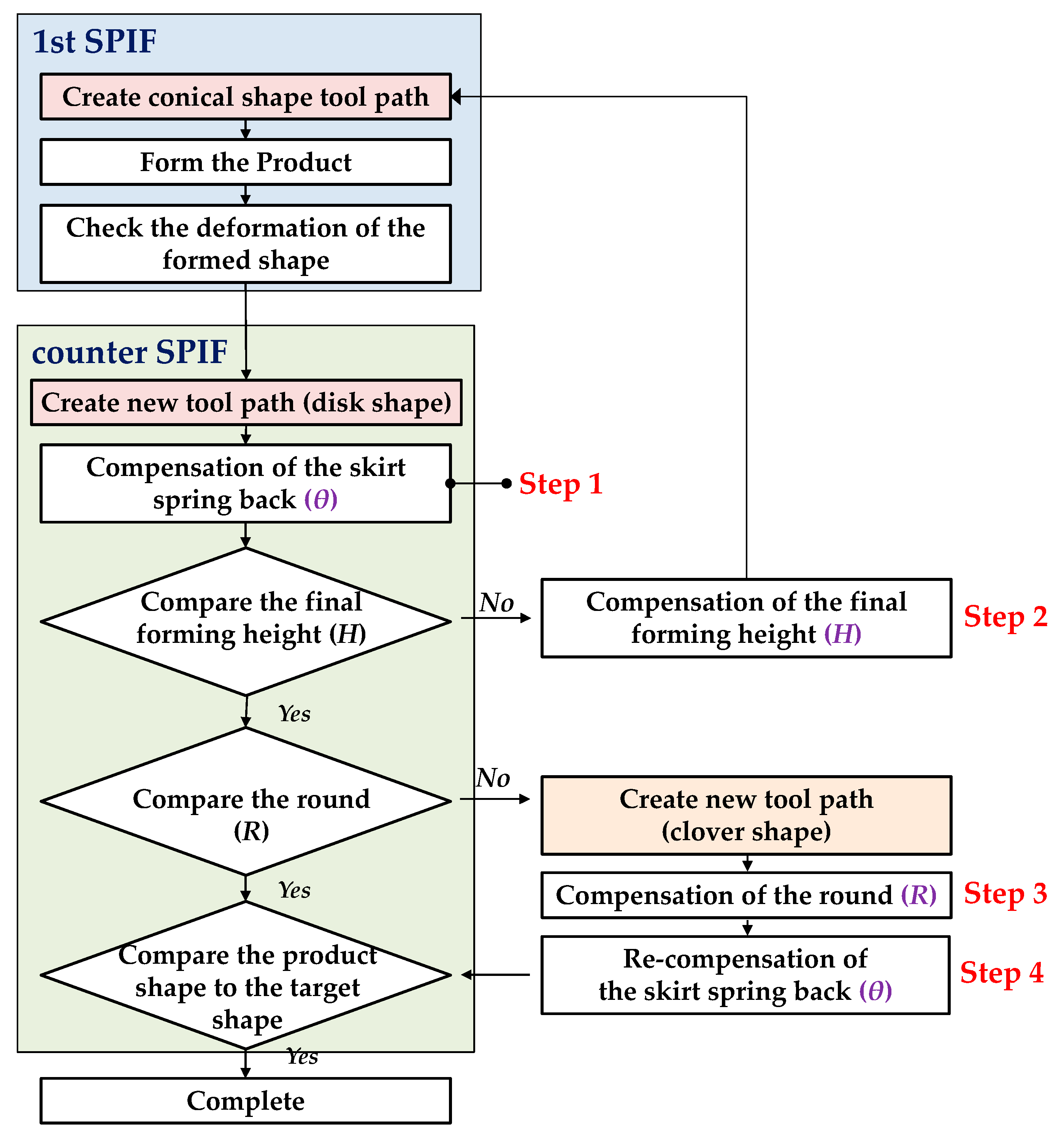
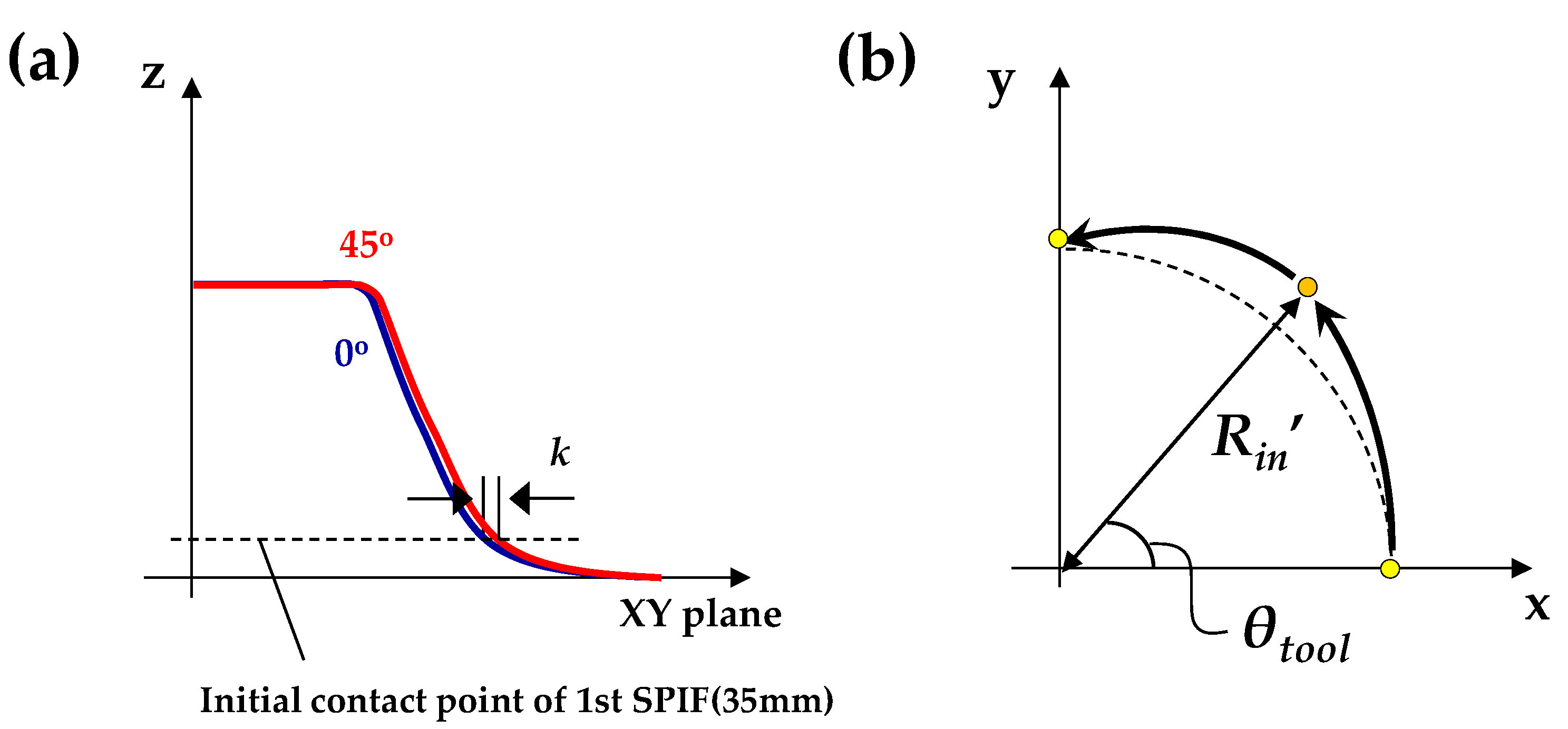
3.3. Compensation Process of the Tool Path for the Counter SPIF
3.4. Experimental Conditions and Measurement Method
4. Experiments of Incremental Forming to Reduce Shape Error
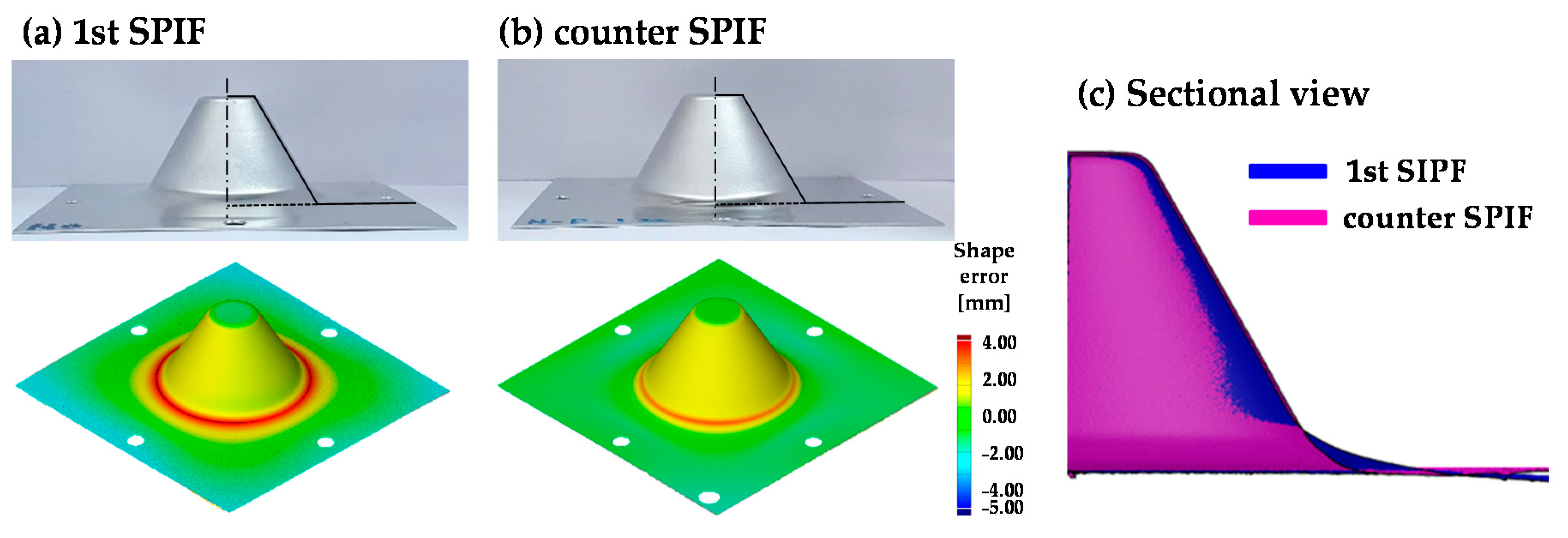
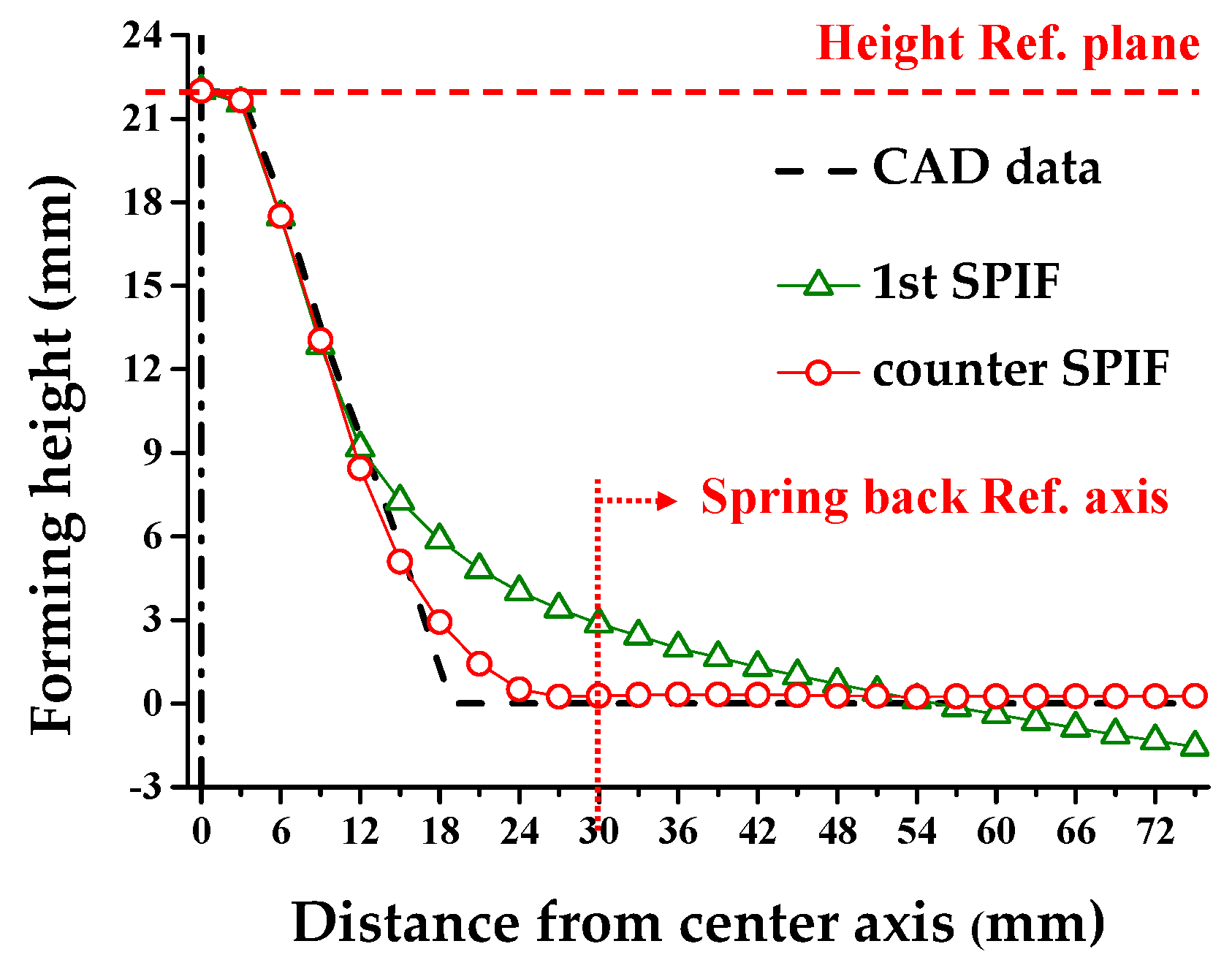
4.1. Experimental Results of the 1st SPIF
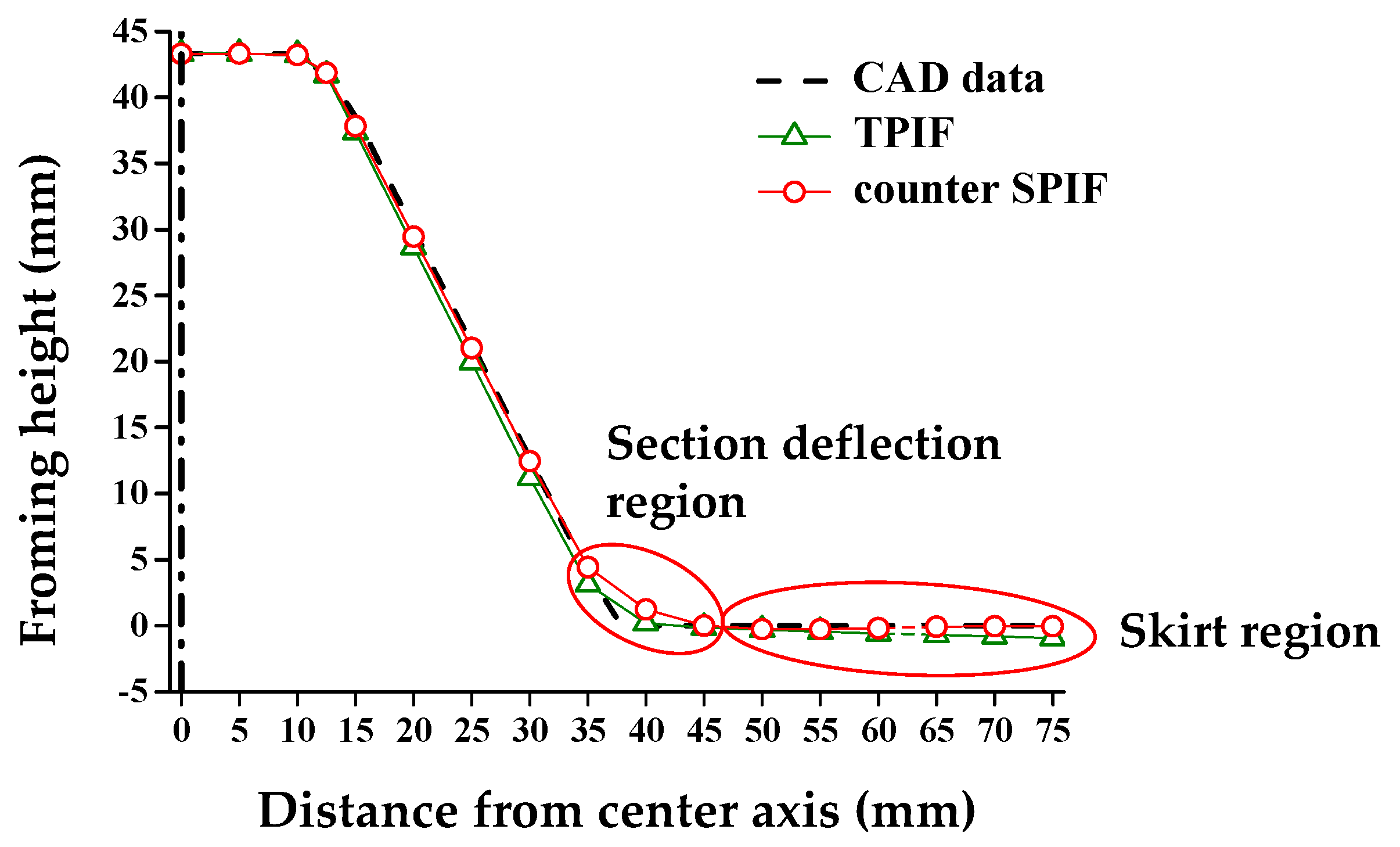
4.2. Compensation Results in the Counter SPIF
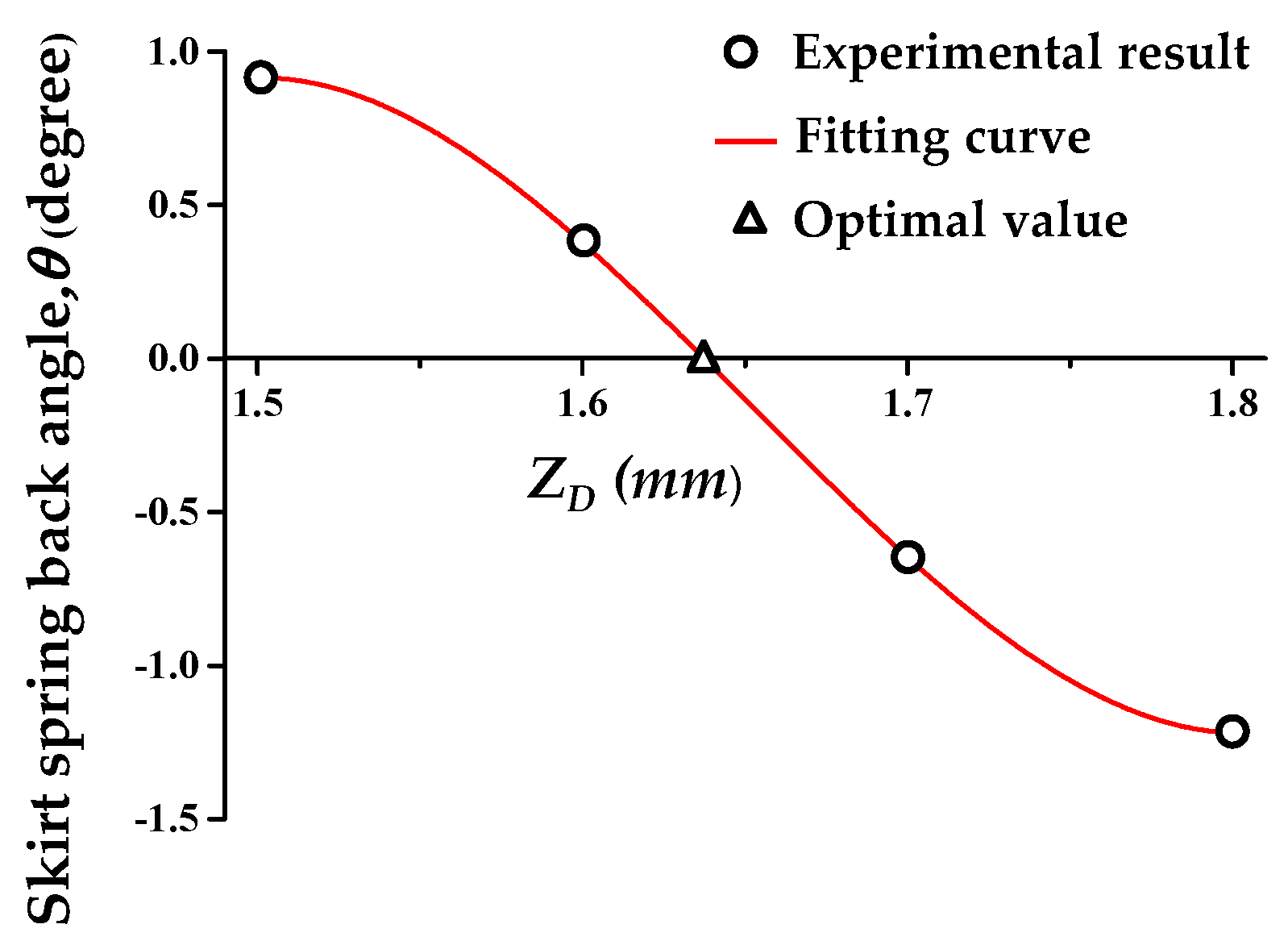
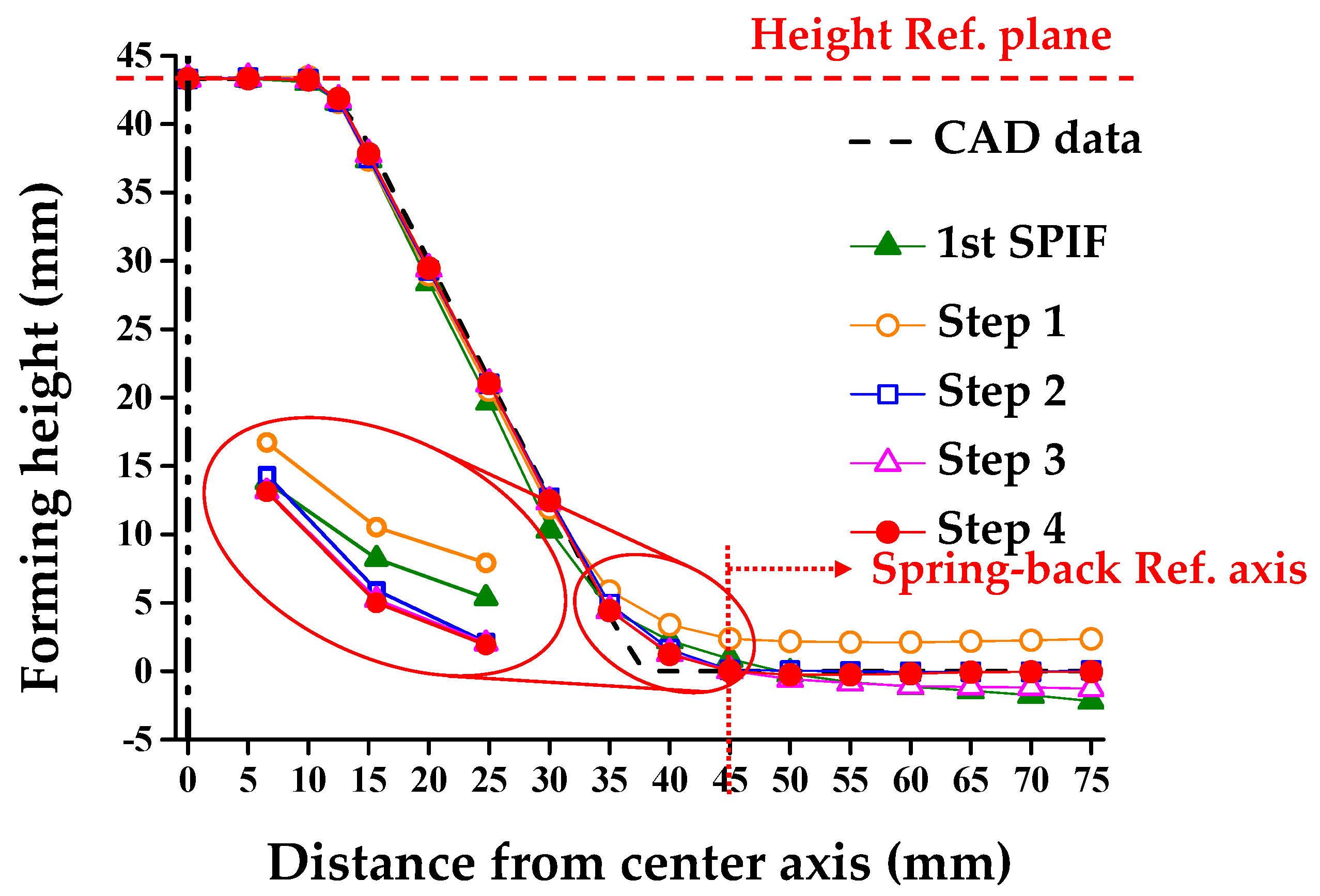
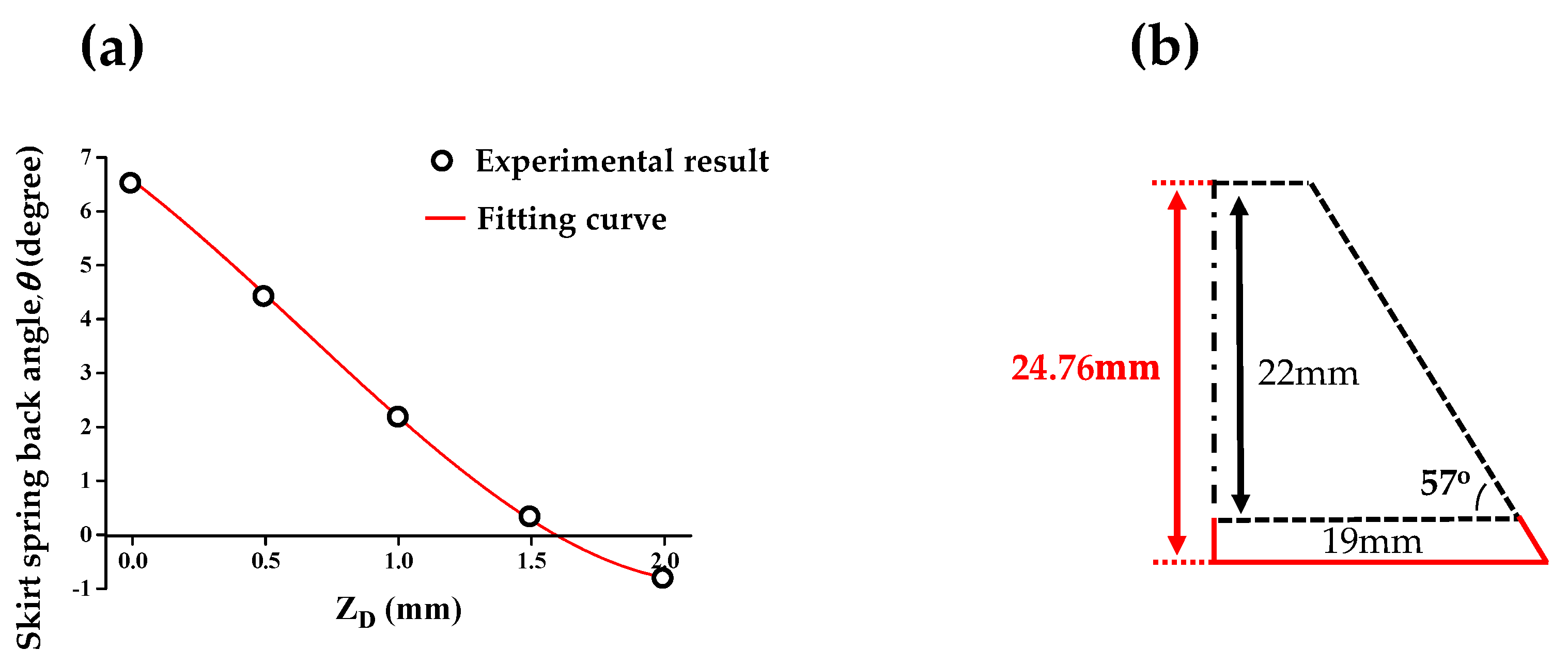
4.2.1. Step 1—Compensation of the Skirt Spring-Back (θ)
4.2.2. Step 2—Compensation of the Final Forming Height (H)
4.2.3. Step 3—Compensation of the Round (R)
4.2.4. Step 4—Recompensation of the Skirt Spring-Back (θ)
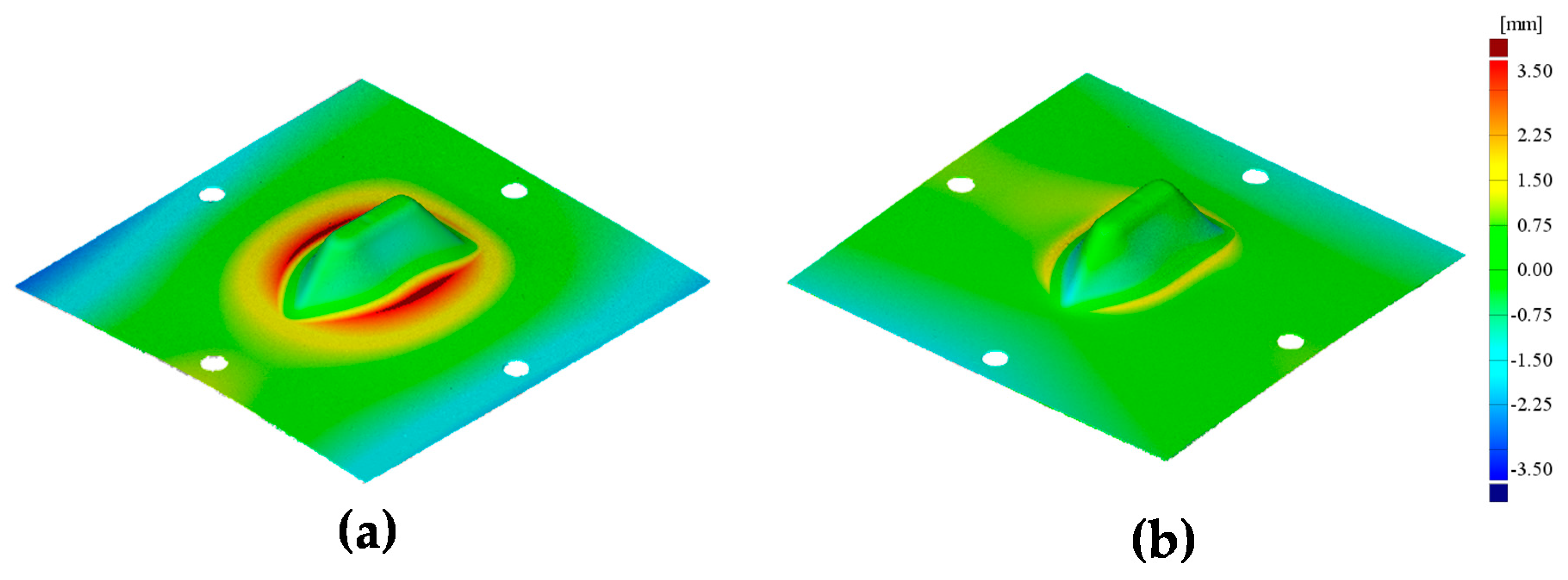
4.3. Experimental Results of the Proposed Method
4.4. Experimental Results of the Conventional and Proposed Methods
4.5. Discussion: Cross-Sectional Shape According to the Compensation Steps
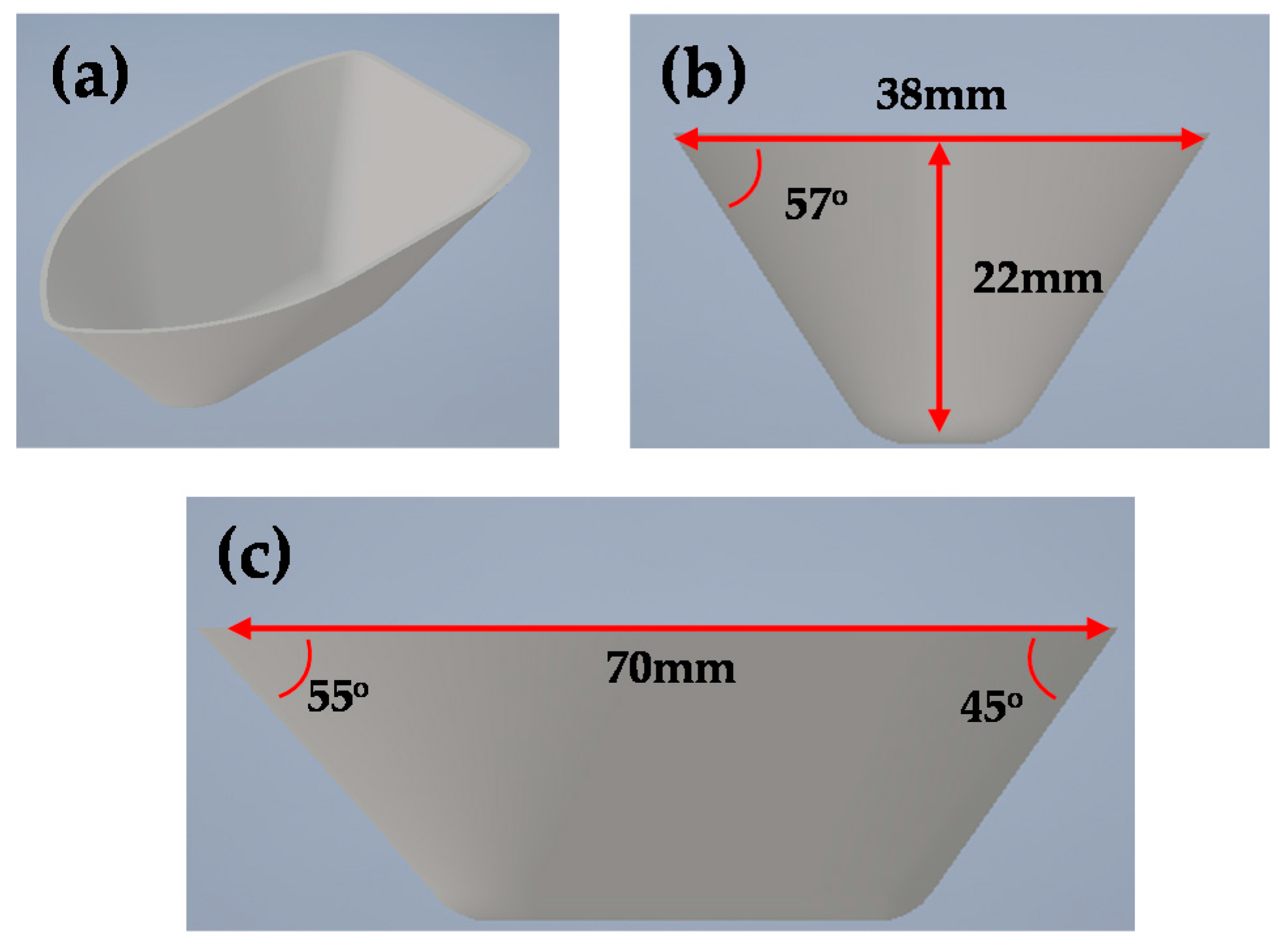
5. Application
5.1. Target Geometry
5.2. Experimental Results
6. Conclusions
- (1)
- The tool path of the proposed counter SPIF was disk-shaped. The main process variable in the counter SPIF was the entry depth of the tool (ZD). From experiments and the simple optimization methods, optimal ZD was obtained. It was found that the counter SPIF decreases the skirt spring-back angle effectively. However, the height of the product decreased.
- (2)
- To increase the geometric accuracy, the tool path in the 1st and the counter SPIF was compensated with the 4-step compensation process. The skirt spring-back, section deflection, final forming height, and round were compensated. Through the developed tool paths, the skirt spring-back angle was decreased to 0.05° in the cup shape manufacturing process. At the same time, the section deflection (δ) decreased by 67.30%, and the mean value of shape error (δm) decreased by 37.57%.
- (3)
- For another example, the ship-hull shape was adopted. The section deflection (δ) decreased by 78.14%, and the mean value of shape error (δm) decreased by 40.28% in the counter incremental forming process compared to the first incremental forming process.
- (4)
- It was found that the proposed two-stage SPIF was very effective at increasing the geometric accuracy. The two-stage SPIF does not require additional experimental devices such as a die-set or robot arm. The two-stage SPIF is expected to be helpful in the sheet metal forming industry, because it improves geometric accuracy and reduces manufacturing equipment cost.
Author Contributions
Funding
Conflicts of Interest
References
- Yang, D.; Bambach, M.; Cao, J.; Duflou, J.; Groche, P.; Kuboki, T.; Sterzing, A.; Tekkaya, A.; Lee, C. Flexibility in metal forming. CIRP Ann. 2018, 67, 743–765. [Google Scholar] [CrossRef]
- Duflou, J.; Habraken, A.-M.; Cao, J.; Malhotra, R.; Bambach, M.; Adams, D.; Vanhove, H.; Mohammadi, A.; Jeswiet, J. Single point incremental forming: State-of-the-art and prospects. Int. J. Mater. Form. 2017, 11, 743–773. [Google Scholar] [CrossRef]
- Iseki, H.; Kato, K.; Sakamoto, S. Flexible and incremental sheet metal forming using a spherical roller. Proc. 40th JJCTP 1989, 41, 44. [Google Scholar]
- Jeswiet, J.; Micari, F.; Hirt, G.; Bramley, A.; Duflou, J.; Allwood, J. Asymmetric single point incremental forming of sheet metal. CIRP Ann. 2005, 54, 88–114. [Google Scholar] [CrossRef]
- Bambach, M.; Araghi, B.T.; Hirt, G. Strategies to improve the geometric accuracy in asymmetric single point incremental forming. Prod. Eng. 2009, 3, 145–156. [Google Scholar] [CrossRef]
- Kopač, J.; Kampus, Z. Incremental sheet metal forming on CNC milling machine-tool. J. Mater. Process. Technol. 2005, 162, 622–628. [Google Scholar] [CrossRef]
- Duflou, J.; Callebaut, B.; Verbert, J.; De Baerdemaeker, H. Laser assisted incremental forming: Formability and accuracy improvement. CIRP Ann. 2007, 56, 273–276. [Google Scholar] [CrossRef]
- Allwood, J.M.; Music, O.; Raithathna, A.; Duncan, S.R. Closed-loop feedback control of product properties in flexible metal forming processes with mobile tools. CIRP Ann. 2009, 58, 287–290. [Google Scholar] [CrossRef]
- Malhotra, R.; Reddy, N.V.; Cao, J. Automatic 3D spiral toolpath generation for single point incremental forming. J. Manuf. Sci. Eng. 2010, 132, 061003. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, H.; Liu, Y. Tool path generation for the point-pressing-based 5-axis CNC incremental forming. Int. J. Adv. Manuf. Technol. 2019, 103, 3459–3477. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, F. Mechanism of twist in incremental sheet forming of thermoplastic polymer. Mater. Des. 2020, 195, 108997. [Google Scholar] [CrossRef]
- Matsubara, S. Incremental backward bulge forming of a sheet metal with a hemispherical head tool-a study of a numerical control forming system II. J. Jpn. Soc. Technol. Plast. 1994, 35, 1311–1316. [Google Scholar]
- Duc-Toan, N.; Seung-Han, Y.; Dong-Won, J.; Tae-Hoon, C.; Young-Suk, K. Incremental sheet metal forming: Numerical simulation and rapid prototyping process to make an automobile white-body. Steel Res. Int. 2011, 82, 795–805. [Google Scholar] [CrossRef]
- Silva, M.B.; Martins, P.A. Two-point incremental forming with partial die: Theory and experimentation. J. Mater. Eng. Perform. 2012, 22, 1018–1027. [Google Scholar] [CrossRef]
- Panjwani, D.; Priyadarshi, S.; Jain, P.K.; Samal, M.K.; Roy, J.J.; Roy, D.; Tandon, P. A novel approach based on flexible supports for forming non-axisymmetric parts in SPISF. Int. J. Adv. Manuf. Technol. 2017, 92, 2463–2477. [Google Scholar] [CrossRef]
- Ou, L.; An, Z.; Gao, Z.; Zhou, S.; Men, Z. Effects of process parameters on the thickness uniformity in Two-Point Incremental Forming (TPIF) with a positive die for an irregular stepped part. Materials 2020, 13, 2634. [Google Scholar] [CrossRef]
- Meier, H.; Smukala, V.; Dewald, O.; Zhang, J. Two point incremental forming with two moving forming tools. Key Eng. Mater. 2007, 344, 599–605. [Google Scholar] [CrossRef]
- Maidagan, E.; Zettler, J.; Bambach, M.; Rodríguez, P.; Hirt, G. A new incremental sheet forming process based on a flexible supporting die system. Key Eng. Mater. 2007, 344, 607–614. [Google Scholar] [CrossRef]
- Malhotra, R.; Cao, J.; Beltran, M.; Xu, D.; Magargee, J.; Kiridena, V.; Xia, Z.C. Accumulative-DSIF strategy for enhancing process capabilities in incremental forming. CIRP Ann. 2012, 61, 251–254. [Google Scholar] [CrossRef]
- Moser, N.; Zhang, Z.; Ren, H.; Zhang, H.; Shi, Y.; Ndip-Agbor, E.E.; Lu, B.; Chen, J.; Ehmann, K.F.; Cao, J. Effective forming strategy for double-sided incremental forming considering in-plane curvature and tool direction. CIRP Ann. 2016, 65, 265–268. [Google Scholar] [CrossRef]
- Praveen, K.; Lingam, R.; Reddy, N.V. Tool path design system to enhance accuracy during double sided incremental forming: An analytical model to predict compensations for small/large components. J. Manuf. Process. 2020, 58, 510–523. [Google Scholar] [CrossRef]
- Jung, K.-S.; Yu, J.-H.; Chung, W.-J.; Lee, C.-W. Incremental Forming Method and Incremental Forming Apparatus. Korean Patent 10-2018-0172398, 28 December 2018. [Google Scholar]
- Jung, K.-S.; Yu, J.-H.; Chung, W.-J.; Lee, C.-W. Analysis of the section deflection in the incremental sheet metal forming process of the circular cup shape according to the cup geometry. J. Korean Soc. Precis. Eng. 2020, 37, 675–683. [Google Scholar] [CrossRef]
- Ben Said, L.; Mars, J.; Wali, M.; Dammak, F. Numerical prediction of the ductile damage in single point incremental forming process. Int. J. Mech. Sci. 2017, 131, 546–558. [Google Scholar] [CrossRef]
- Kim, H.; Park, T.; Esmaeilpour, R.; Pourboghrat, F. Numerical study of incremental sheet forming processes. J. Physics: Conf. Ser. 2018, 1063, 012017. [Google Scholar] [CrossRef]
- Guzmán, C.; Yuan, S.; Duchêne, L.; Flores, E.I.S.; Habraken, A.-M. Damage prediction in single point incremental forming using an extended Gurson model. Int. J. Solids Struct. 2018, 151, 45–56. [Google Scholar] [CrossRef]
- Bouhamed, A.; Jrad, H.; Ben Said, L.; Wali, M.; Dammak, F. A non-associated anisotropic plasticity model with mixed isotropic–kinematic hardening for finite element simulation of incremental sheet metal forming process. Int. J. Adv. Manuf. Technol. 2018, 100, 929–940. [Google Scholar] [CrossRef]
- Elford, M.; Saha, P.; Seong, D.; Haque, Z.; Yoon, J.W. Benchmark 3 - Incremental sheet forming. In Proceedings of the NUMISHEET 2014: The 9th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes: Part A Benchmark Problems and Results and Part B General Papers, Melbourne, Australia, 6 January 2014; pp. 227–261. [Google Scholar]
- Hamilton, K.; Jeswiet, J. Single point incremental forming at high feed rates and rotational speeds: Surface and structural consequences. CIRP Ann. 2010, 59, 311–314. [Google Scholar] [CrossRef]



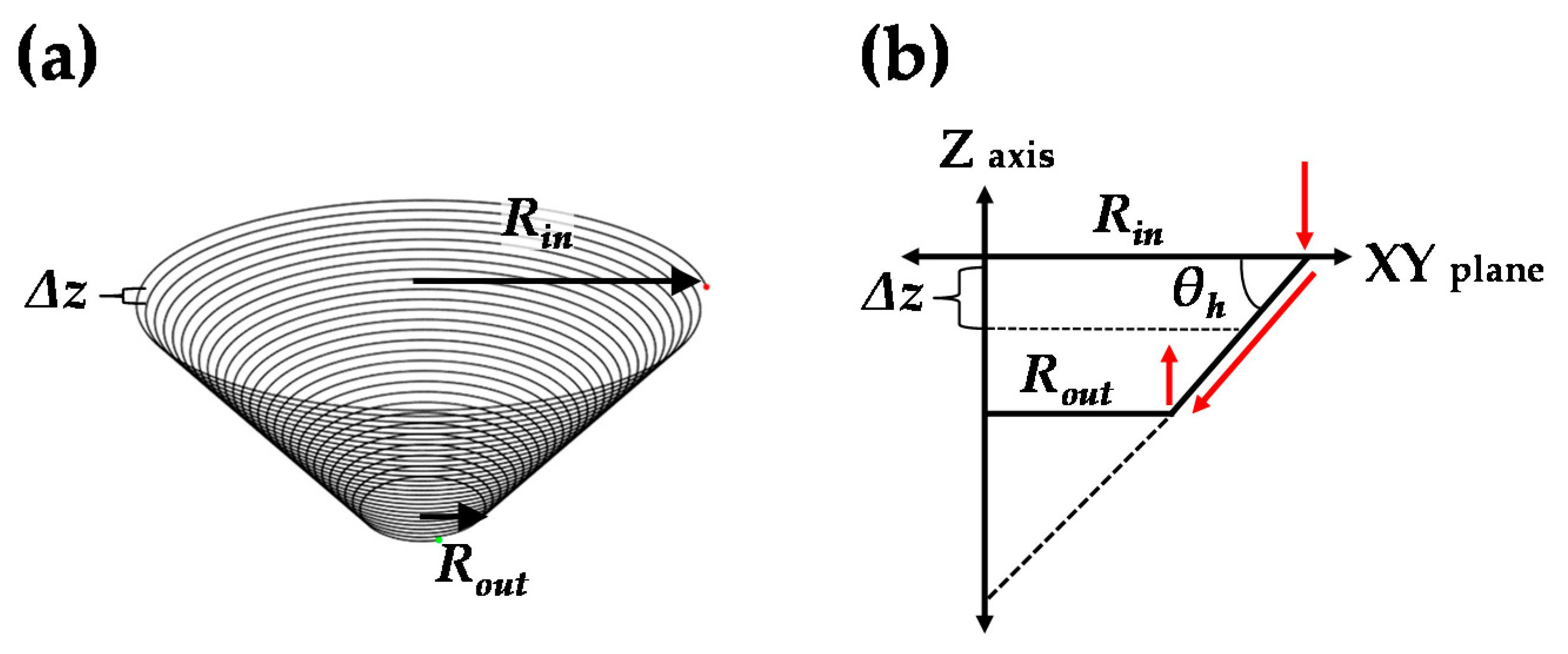
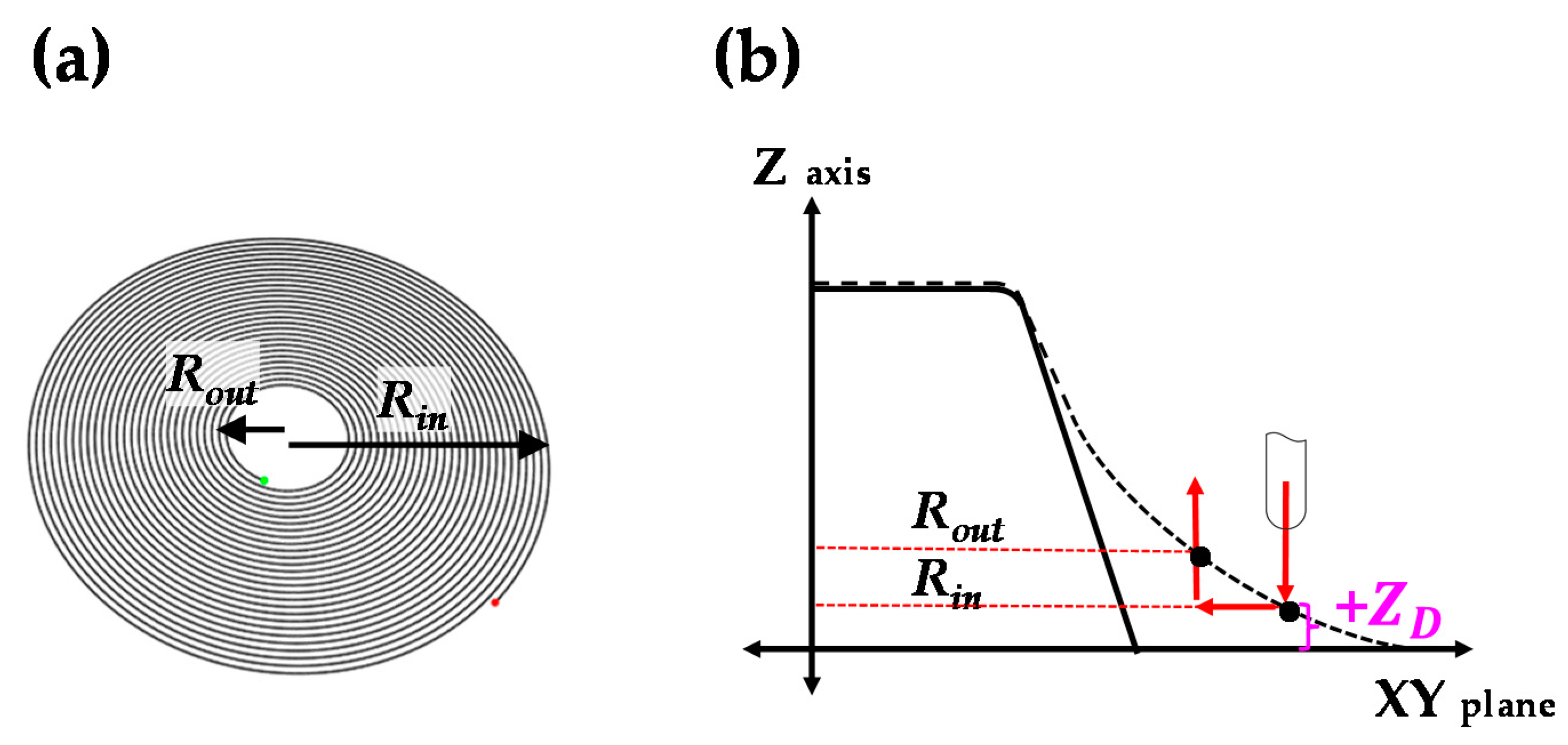
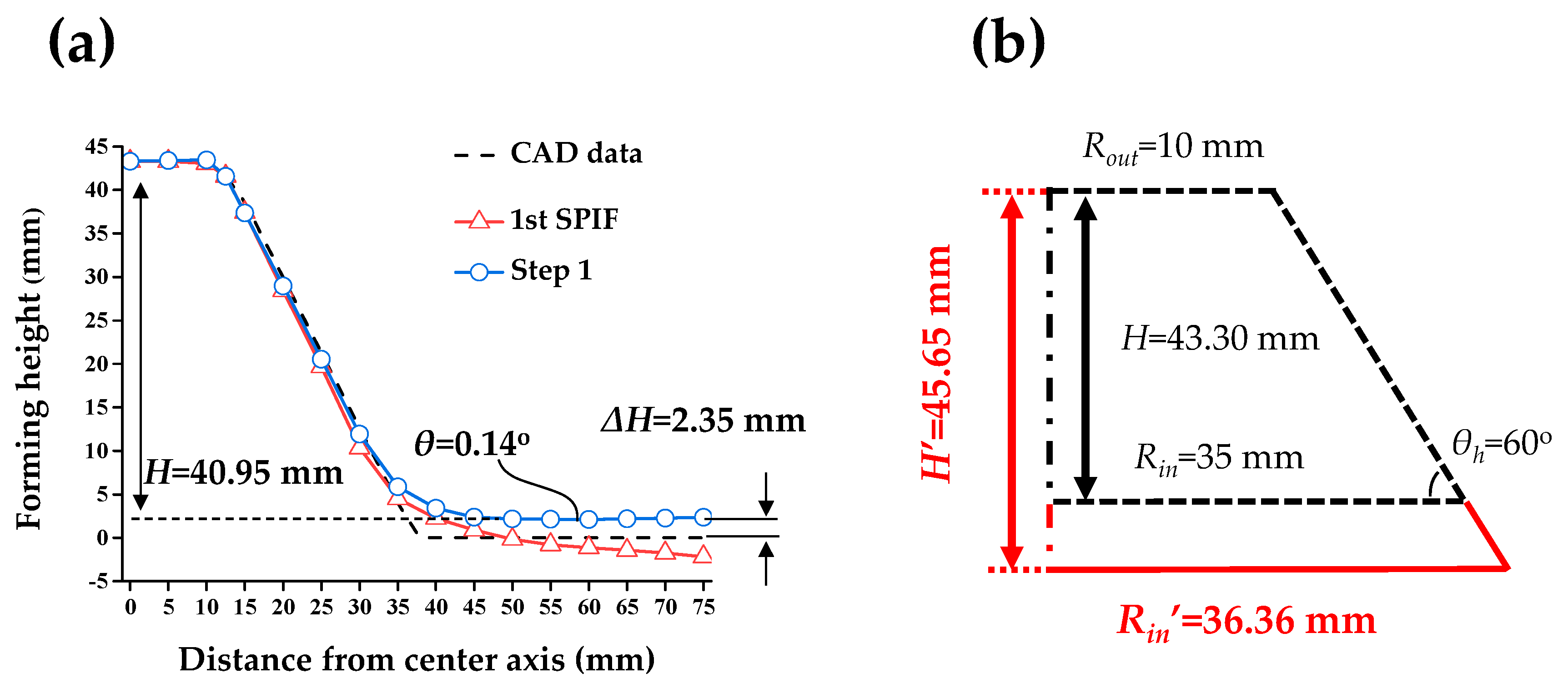


| Stage | Tool Path Shape | Rin (mm) | Rout (mm) | θh (degree) | ∆z (mm) |
|---|---|---|---|---|---|
| 1st SPIF | circular cup | 35 | 10 | 60 | 0.3 |
| counter SPIF | disk | 45 | 39 | - | 0 |
| ZD (mm) | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
| θ (degree) | 0.72 | 0.28 | −0.33 | −0.95 | −1.71 |
| SPIF | Tool Path Shape | Rin (mm) | Rout (mm) | θh (°) | ∆z (mm) | ZD (mm) |
|---|---|---|---|---|---|---|
| (a) 1st SPIF | circular cup | 36.36 | 10 | 60 | 0.3 | - |
| (b) counter SPIF | clover (according to step 3) | 46.36 | 40.36 | - | 0.3 | 1.25 |
| Shape Error | CAD Data | 1st SPIF | Counter SPIF |
|---|---|---|---|
| δ (mm) | 0 | 3.15 | 1.03 |
| δm(mm) | 0 | 1.73 | 1.08 |
| Parameter | CAD Data | 1st SPIF | Counter SPIF | |||
|---|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 4 | |||
| θ (degree) | 0 | −5.82 | 0.14 | 0.11 | −2.57 | 0.05 |
| H (mm) | −43.30 | −45.49 | −40.95 | −43.25 | −44.58 | −43.35 |
| R0/R45 (mm) | - | 33.18/27.19 | 21.18/15.68 | 19.08/13.65 | 17.81/17.79 | 12.49/12.12 |
| Parameter | CAD Data | 1st SPIF | Counter SPIF | |
|---|---|---|---|---|
| Step 1 | Step 2 | |||
| θ (degree) | 0 | −5.61 | 0.08 | 0.03 |
| H (mm) | −22 | −23.56 | −19.24 | 21.73 |
| δ (mm) | 0 | 3.75 | 3.75 | 0.82 |
| δm(mm) | 0 | 1.44 | 1.44 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, K.-S.; Yu, J.-H.; Chung, W.-J.; Lee, C.-W. Tool Path Design of the Counter Single Point Incremental Forming Process to Decrease Shape Error. Materials 2020, 13, 4719. https://doi.org/10.3390/ma13214719
Jung K-S, Yu J-H, Chung W-J, Lee C-W. Tool Path Design of the Counter Single Point Incremental Forming Process to Decrease Shape Error. Materials. 2020; 13(21):4719. https://doi.org/10.3390/ma13214719
Chicago/Turabian StyleJung, Kyu-Seok, Jae-Hyeong Yu, Wan-Jin Chung, and Chang-Whan Lee. 2020. "Tool Path Design of the Counter Single Point Incremental Forming Process to Decrease Shape Error" Materials 13, no. 21: 4719. https://doi.org/10.3390/ma13214719
APA StyleJung, K.-S., Yu, J.-H., Chung, W.-J., & Lee, C.-W. (2020). Tool Path Design of the Counter Single Point Incremental Forming Process to Decrease Shape Error. Materials, 13(21), 4719. https://doi.org/10.3390/ma13214719





