A Review of Permeability and Flow Simulation for Liquid Composite Moulding of Plant Fibre Composites
Abstract
:1. Introduction
1.1. Liquid Composite Moulding (LCM)
1.2. Plant Fibre Composites in LCM Processes
- Low processing temperatures (often ambient, if not <150 °C), thereby avoiding thermal degradation of plant fibres (which decompose above ca 200 °C, although both temperature and time of exposure are pertinent parameters [15]);
- Minimal fibre damage during composite processing due to low shear rate range (as opposed to injection–extrusion moulding), thereby allowing retention of high reinforcement length, alignment, and mechanical properties;
- Use of liquid resins with low viscosities (0.1–1 Pa·s), thereby allowing good preform impregnation with low porosity, even at low compaction or injection pressures;
- Relatively low-cost tooling, making the process compatible with low-cost plant fibres, particularly when manufacturing in low- and middle-income countries with an abundance of indigenous plant fibres;
- Closed-mould LCM processes reduce exposure to harmful emissions, therefore offering worker-friendly conditions, much like non-hazardous plant fibres.
2. Plant Fibre Reinforcements in LCM Processes
2.1. Specificities of Plant Fibre Reinforcements
2.1.1. Plant Fibre Morphology
2.1.2. Fibre Surface Properties
2.2. Compaction and Packing of Plant Fibre Reinforcements
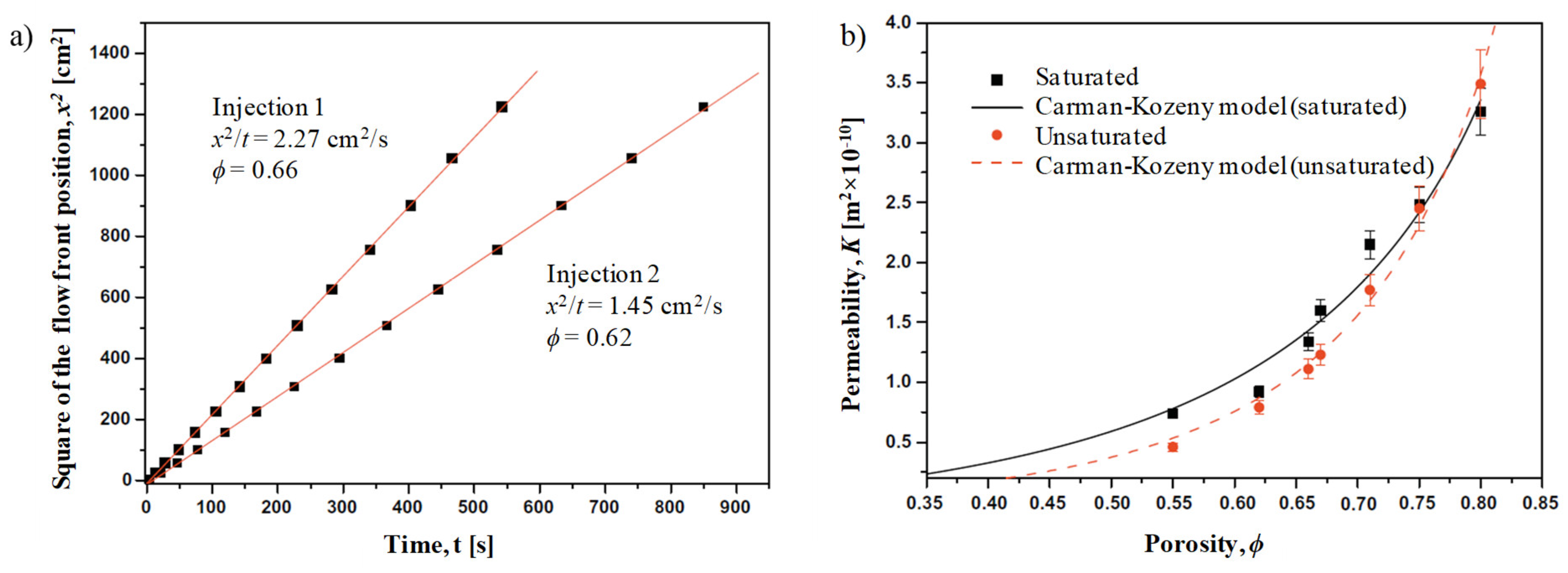
2.3. In-Plane Permeability of Plant Fibre Reinforcements
2.3.1. Permeability Anisotropy: Direction Matters
2.4. Summary
3. Flow Modelling and Simulation of Natural Fibre Composites
3.1. Classical Flow Models
3.1.1. Dual-Scale Flow and Capillarity
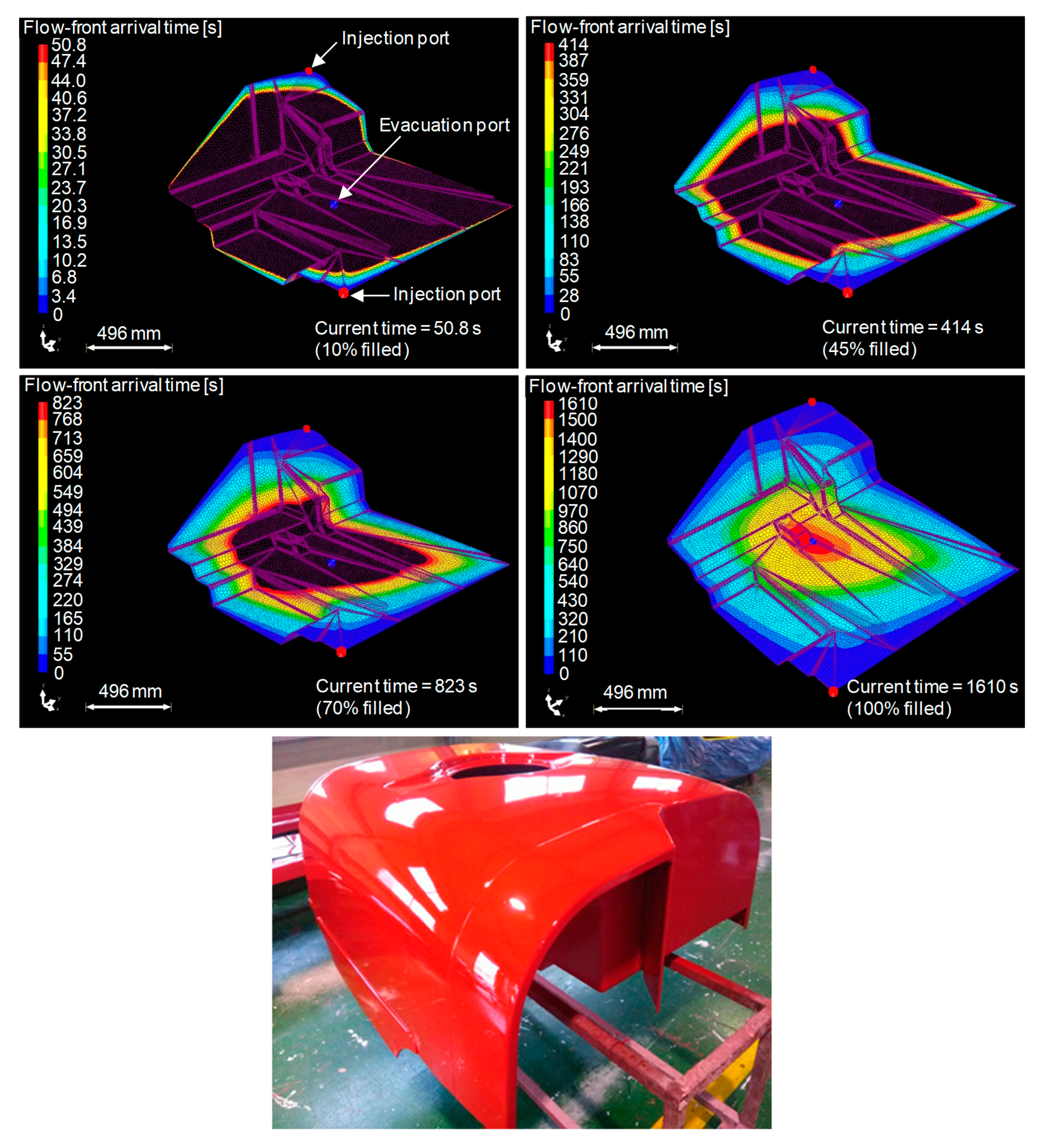
3.1.2. Simulating Impregnation in Plant Fibre Preforms by Classical Approaches
3.2. Modifying Flow Models to Accommodate Plant Fibre Specificities
3.2.1. Sink Effects
3.2.2. Capillarity and Swelling Effects
3.2.3. Models Suitable for Natural Fibre Reinforcements
3.3. Summary
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- JEC Observer. Overview of the Global Composites Market, 2019–2024; JEC Group: Paris, France, 2020. [Google Scholar]
- Khan, L.A.; Mehmood, A.H. Cost-effective composites manufacturing processes for automotive applications. In Lightweight Composite Structures in Transport: Design, Manufacturing, Analysis and Performance; Njuguna, J., Ed.; Woodhead Publishing Limited: Cambridge, UK, 2016; pp. 93–120. [Google Scholar]
- Long, A.C. Design and Manufacture of Textile Composites; Woodhead Publishing Limited: Cambridge, UK; CRC Press LLC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Delgado, J.M.P.Q.; de Lima, A.G.B.; Santos, M.J.N. Transport Phenomena in Liquid Composite Molding Processes; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Faruk, O.; Bledzki, A.K.; Fink, H.-P.; Sain, M. Biocomposites reinforced with natural fibers: 2000–2010. Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Ho, M. Critical factors on manufacturing processes of natural fibre composites. Compos. Part B Eng. 2012, 43, 3549–3562. [Google Scholar] [CrossRef]
- Shah, D.U. Developing plant fibre composites for structural applications by optimising composite parameters: A critical review. J. Mater. Sci. 2013, 48, 6083–6107. [Google Scholar] [CrossRef]
- Summerscales, J. A review of bast fibres and their composites. Part 2—Composites. Compos. Part Appl. Sci. Manuf. 2010, 41, 1336–1344. [Google Scholar] [CrossRef] [Green Version]
- Pickering, K.L. Properties and Performance of Natural-Fibre Composites; CRC Press LLC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Chaudhary, V.; Ahmad, F. A review on plant fiber reinforced thermoset polymers for structural and frictional composites. Polym. Test. 2020, 91, 106792. [Google Scholar] [CrossRef]
- Carus, M. Wood-Plastic Composites (WPC) and Natural Fibre Composites (NFC): European and Global Markets 2012 and Future Trends; WPC/NFC Market Study 2014-03; nova-Institut GmbH: Hürth, Germany, 2014. [Google Scholar]
- Carus, M. Natural Fibre Reinforced Plastics—Material with Future; nova-Institut GmbH: Hürth, Germany, 2008. [Google Scholar]
- Francucci, G. Experimental study of the compaction response of jute fabrics in liquid composite molding processes. J. Compos. Mater. 2012, 46, 155–167. [Google Scholar] [CrossRef]
- Shah, D.U. Mechanical property characterization of aligned plant yarn reinforced thermoset matrix composites manufactured via vacuum infusion. Polym. Plast. Technol. Eng. 2014, 53, 239–253. [Google Scholar] [CrossRef]
- Baley, C.; Gomina, M.; Breard, J.; Bourmaud, A.; Drapier, S.; Ferreira, M.; Le Duigou, A.; Liotier, P.J.; Ouagne, P.; Soulat, D.; et al. Specific features of flax fibres used to manufacture composite materials. Int. J. Mater. Form. 2019, 12, 1023–1052. [Google Scholar] [CrossRef] [Green Version]
- Madsen, B. Properties of plant fibre yarn polymer composites—An experimental study. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2004. [Google Scholar]
- Francucci, G.; Vázquez, A.; Rodríguez, E.S. Key differences on the compaction response of natural and glass fiber preforms in liquid composite molding. Text. Res. J. 2012, 82, 1774–1785. [Google Scholar] [CrossRef]
- van Wyk, C.M. 20—Note on the compressibility of wool. J. Text. Inst. Trans. 1946, 37, T285–T292. [Google Scholar] [CrossRef]
- Xue, D.; Miao, M.; Hu, H. Permeability anisotropy of flax nonwoven mats in vacuum-assisted resin transfer molding. J. Text. Inst. 2011, 102, 612–620. [Google Scholar] [CrossRef]
- Umer, R.; Bickerton, S.; Fernyhough, A. The effect of yarn length and diameter on permeability and compaction response of flax fibre mats. Compos. Part A Appl. Sci. Manuf. 2011, 42, 723–732. [Google Scholar] [CrossRef]
- Shah, D.U. Opportunities for silk textiles in reinforced biocomposites: Studying through-thickness compaction behaviour. Compos. Part A Appl. Sci. Manuf. 2014, 62, 1–10. [Google Scholar] [CrossRef]
- Masoodi, R.; Pillai, K.M. Modeling the Processing of Natural Fiber Composites Made Using Liquid Composite Molding. In Handbook of Bioplastics and Biocomposites Engineering Applications; Pilla, S., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 43–73. ISBN 978-1-118-20369-9. [Google Scholar]
- Rodriguez, E. Permeability-porosity relationship in RTM for different fiberglass and natural reinforcements. J. Compos. Mater. 2004, 38, 259–268. [Google Scholar] [CrossRef]
- Francucci, G.; Rodríguez, E.S.; Vázquez, A. Study of saturated and unsaturated permeability in natural fiber fabrics. Compos. Part A Appl. Sci. Manuf. 2010, 41, 16–21. [Google Scholar] [CrossRef]
- Richardson, M.O.W. Experimental investigation and flow visualisation of the resin transfer mould filling process for non-woven hemp reinforced phenolic composites. Compos. Part A Appl. Sci. Manuf. 2000, 31, 1303–1310. [Google Scholar] [CrossRef]
- Rodriguez, E.S.; Stefani, P.M.; Vazquez, A. Effects of Fibers’ Alkali Treatment on the Resin Transfer Molding Processing and Mechanical Properties of Jute—Vinylester Composites. J. Compos. Mater. 2007, 41, 1729–1741. [Google Scholar] [CrossRef]
- Bourmaud, A.; Beaugrand, J.; Shah, D.U.; Placet, V.; Baley, C. Towards the design of high-performance plant fibre composites. Prog. Mater. Sci. 2018, 97, 347–408. [Google Scholar] [CrossRef]
- Wu, G.; Shah, D.U.; Janeček, E.-R.; Burridge, H.C.; Reynolds, T.P.S.; Fleming, P.H.; Linden, P.F.; Ramage, M.H.; Scherman, O.A. Predicting the pore-filling ratio in lumen-impregnated wood. Wood Sci. Technol. 2017, 51, 1277–1290. [Google Scholar] [CrossRef] [Green Version]
- Mikshina, P. Cellulosic Fibers: Role of Matrix Polysaccharides in Structure and Function. In Cellulose—Fundamental Aspects; van de Ven, T., Ed.; IntechOpen: London, UK, 2013; pp. 91–112. [Google Scholar]
- Baley, C.; Goudenhooft, C.; Gibaud, M.; Bourmaud, A. Flax stems: From a specific architecture to an instructive model for bioinspired composite structures. Bioinspir. Biomim. 2018, 13, 026007. [Google Scholar] [CrossRef]
- le Duigou, A.; Bourmaud, A.; Balnois, E.; Davies, P.; Baley, C. Improving the interfacial properties between flax fibres and PLLA by a water fibre treatment and drying cycle. Ind. Crops Prod. 2012, 39, 31–39. [Google Scholar] [CrossRef]
- Mbakop, R.S.; Lebrun, G.; Brouillette, F. Effect of compaction parameters on preform permeability and mechanical properties of unidirectional flax fiber composites. Compos. Part B Eng. 2019, 176, 107083. [Google Scholar] [CrossRef]
- Melelli, A.; Arnould, O.; Beaugrand, J.; Bourmaud, A. The Middle Lamella of Plant Fibers Used as Composite Reinforcement: Investigation by Atomic Force Microscopy. Molecules 2020, 25, 632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merotte, J.; Le Duigou, A.; Kervoelen, A.; Bourmaud, A.; Behlouli, K.; Sire, O.; Baley, C. Flax and hemp nonwoven composites: The contribution of interfacial bonding to improving tensile properties. Polym. Test. 2018, 66, 303–311. [Google Scholar] [CrossRef]
- Long, A.C. Mechanical analysis of textiles. In Design and Manufacture of Textile Composites; Long, A.C., Ed.; Woodhead Publishing Limited: Cambridge, UK; CRC Press LLC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Chen, B. Experimental and theoretical studies of fabric compaction behavior in resin transfer molding. Mater. Sci. Eng. A 2001, 317, 188–196. [Google Scholar] [CrossRef]
- Chen, B. Compaction of woven-fabric preforms in liquid composite molding processes: Single-layer deformation. Compos. Sci. Technol. 1999, 59, 1519–1526. [Google Scholar] [CrossRef]
- Chen, B. Compaction of woven-fabric preforms: Nesting and multi-layer deformation. Compos. Sci. Technol. 2000, 60, 2223–2231. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J.; Clifford, M.J.; Licence, P. The tensile behavior of off-axis loaded plant fiber composites: An insight on the nonlinear stress-strain response. Polym. Compos. 2012, 33, 1494–1504. [Google Scholar] [CrossRef]
- Lundquist, L.; Willi, F.; Leterrier, Y.; Månson, J.-A.E. Compression behavior of pulp fiber networks. Polym. Eng. Sci. 2004, 44, 45–55. [Google Scholar] [CrossRef]
- Shah, D.U. Characterisation and Optimisation of the Mechanical Performance of Plant Fibre Composites for Structural Applications. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2013. [Google Scholar]
- Shah, D.U. Mechanical characterization of vacuum infused thermoset matrix composites reinforced with aligned hydroxyethylcellulose sized plant bast fibre yarns. In Proceedings of the 4th International Conference on Sustainable Materials, Polymers and Composites (EcoComp), Birmingham, UK, 6–7 July 2011. [Google Scholar]
- Goutianos, S. Textile reinforcements based on aligned flax fibres for structural composites. In Proceedings of the Composites Innovation 2007—Improved Sustainability and Environmental Performance, Barcelona, Spain, 4–5 October 2007. [Google Scholar]
- Gassan, J. Calculation of elastic properties of natural fibers. J. Mater. Sci. 2001, 36, 3715–3720. [Google Scholar] [CrossRef]
- Placet, V. Diameter dependence of the apparent tensile modulus of hemp fibres: A morphological, structural or ultrastructural effect? Compos. Part A Appl. Sci. Manuf. 2012, 43, 275–287. [Google Scholar] [CrossRef]
- Umer, R.; Bickerton, S.; Fernyhough, A. Modelling the application of wood fibre reinforcements within liquid composite moulding processes. Compos. Part A Appl. Sci. Manuf. 2008, 39, 624–639. [Google Scholar] [CrossRef]
- Li, Y. Processing of sisal fiber reinforced composites by resin transfer molding. Mater. Manuf. Process. 2006, 21, 181–190. [Google Scholar] [CrossRef]
- de Oliveira, D.M.; de Carvalho Benini, K.C.C.; Monticeli, F.M.; Schukraft, J.P.; de Bomfim, A.S.C.; Cioffi, M.O.H.; Voorwald, H.J.C. Permeability of untreated and atmospheric plasma treated coconut fiber mats. Mater. Res. Express 2019, 6, 095323. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, J.; Qin, Y.; Liu, D.; Yan, C.; Zhang, H. Effects of liquid absorption and swelling on the permeability of natural fiber fabrics in liquid composite moulding. Polym. Compos. 2017, 38, 996–1004. [Google Scholar] [CrossRef]
- Ouagne, P.; Ouahbi, T.; Park, C.H.; Bréard, J.; Saouab, A. Continuous measurement of fiber reinforcement permeability in the thickness direction: Experimental technique and validation. Compos. Part B Eng. 2013, 45, 609–618. [Google Scholar] [CrossRef] [Green Version]
- Liotier, P.-J.; Govignon, Q.; Swery, E.; Drapier, S.; Bickerton, S. Characterisation of woven flax fibres reinforcements: Effect of the shear on the in-plane permeability. J. Compos. Mater. 2015, 49, 3415–3430. [Google Scholar] [CrossRef] [Green Version]
- Ehresmann, M.; Amiri, A.; Ulven, C. The effect of different variables on in-plane radial permeability of natural fiber mats. J. Reinf. Plast. Compos. 2018, 37, 1191–1201. [Google Scholar] [CrossRef]
- Goutianos, S. The optimisation of flax fibre yarns for the development of high-performance natural fibre composites. Adv. Compos. Lett. 2003, 12, 237–241. [Google Scholar] [CrossRef] [Green Version]
- Umer, R. Characterising wood fibre mats as reinforcements for liquid composite moulding processes. Compos. Part A Appl. Sci. Manuf. 2007, 38, 43–448. [Google Scholar] [CrossRef]
- Mekic, S. Radial infusion models for permeability measurements of compressed fibrous beds. Int. J. Multiph. Flow 2013, 48, 1–10. [Google Scholar] [CrossRef]
- Neuman, S.P. Theoretical derivation of Darcy’s law. Acta Mech. 1977, 25, 153–170. [Google Scholar] [CrossRef]
- Parnas, R.S. Permeability characterization. Part 1: A proposed standard reference fabric for permeability. Polym. Compos. 1995, 16, 429–445. [Google Scholar] [CrossRef]
- Cai, Z. Analysis of mold filling in RTM process. J. Compos. Mater. 1992, 26, 1310–1338. [Google Scholar]
- Gauvin, R. Variation of mat surface density and its effect on permeability evaluation for RTM modelling. J. Reinf. Plast. Compos. 1994, 13, 371–383. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid Flow through Granular Beds; Transactions; Institution of Chemical Engineers: London, UK, 1937; pp. 150–166. [Google Scholar]
- Caglar, B.; Tekin, C.; Karasu, F.; Michaud, V. Assessment of capillary phenomena in liquid composite molding. Compos. Part A Appl. Sci. Manuf. 2019, 120, 73–83. [Google Scholar] [CrossRef]
- Michaud, V. A Review of Non-saturated Resin Flow in Liquid Composite Moulding processes. Transp. Porous Media 2016, 115, 581–601. [Google Scholar] [CrossRef]
- Shah, D.U. Determining the minimum, critical and maximum fibre content for twisted yarn reinforced plant fibre composites. Compos. Sci. Technol. 2012, 72, 1909–1917. [Google Scholar] [CrossRef] [Green Version]
- Kong, C. Design of natural fiber composites chemical container using resin flow simulation of VARTML process. Int. J. Mater. Mech. Manuf. 2014, 2, 256–260. [Google Scholar] [CrossRef] [Green Version]
- Pillai, K.M. A model for unsaturated flow in woven fiber preforms during mold filling in resin transfer molding. J. Compos. Mater. 1998, 32, 1753–1783. [Google Scholar] [CrossRef]
- Francucci, G.; Vázquez, A.; Ruiz, E.; Rodríguez, E.S. Capillary effects in vacuum-assisted resin transfer molding with natural fibers. Polym. Compos. 2012, 33, 1593–1602. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, X.; Ma, J. Capillary effect in the impregnation of jute fiber mat reinforced polypropylene composites. J. Compos. Mater. 2014, 48, 447–453. [Google Scholar] [CrossRef]
- Yin, T.; Li, Y.; Yuan, B. The multi-scale flow behaviors of sisal fiber reinforced composites during resin transfer molding process. Sci. China Technol. Sci. 2018, 61, 1925–1934. [Google Scholar] [CrossRef]
- Moudood, A.; Rahman, A.; Öchsner, A.; Islam, M.; Francucci, G. Flax fiber and its composites: An overview of water and moisture absorption impact on their performance. J. Reinf. Plast. Compos. 2018, 38. [Google Scholar] [CrossRef] [Green Version]
- Testoni, G.A.; Kim, S.; Pisupati, A.; Park, C.H. Modeling of the capillary wicking of flax fibers by considering the effects of fiber swelling and liquid absorption. J. Colloid Interface Sci. 2018, 525, 166–176. [Google Scholar] [CrossRef]
- Vo, H.N.; Pucci, M.F.; Corn, S.; Le Moigne, N.; Garat, W.; Drapier, S.; Liotier, P.J. Capillary wicking in bio-based reinforcements undergoing swelling—Dual scale consideration of porous medium. Compos. Part A Appl. Sci. Manuf. 2020, 134, 105893. [Google Scholar] [CrossRef]
- Masoodi, R. Darcy’s law-based model for wicking in paper-like swelling porous media. Am. Inst. Chem. Eng. J. 2010, 56, 2257–2267. [Google Scholar] [CrossRef]
- Francucci, G.; Rodríguez, E.S.; Morán, J. Novel approach for mold filling simulation of the processing of natural fiber reinforced composites by resin transfer molding. J. Compos. Mater. 2014, 48, 191–200. [Google Scholar] [CrossRef]
- Nguyen, V.H. Experimental analysis of flow behavior in the flax fiber reinforcement with double scale porosity. In Proceedings of the 12th International Conference on Flow Processes in Composite Materials (FPCM-12), Enschede, The Netherlands, 14–16 July 2014. [Google Scholar]
- Masoodi, R. Flow modeling in natural-fiber preforms used in liquid composite molding. In Proceedings of the 1st Joint American-Canadian International Conference on Composites, Newark, DE, USA, 15–17 September 2009. [Google Scholar]
- Languri, E.M. An approach to model resin flow through swelling porous media made of natural fibers. In Proceedings of the 10th International Conference on Flow Processes in Composite Materials (FPCM10), Ascona, Switzerland, 11–15 July 2010. [Google Scholar]
- Nguyen, V.H.; Lagardère, M.; Park, C.H.; Panier, S. Permeability of natural fiber reinforcement for liquid composite molding processes. J. Mater. Sci. 2014, 49, 6449–6458. [Google Scholar] [CrossRef]







| Scale | Mechanism | Dominant in | Secondary in | |
|---|---|---|---|---|
Fibre/filament | cell wall/lumen collapse (fibre cross-section deformation) | 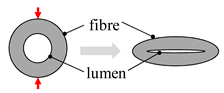 | all plant fibre preforms | - |
| Yarn/tow, Unidirectional tape  | yarn cross-section deformation | 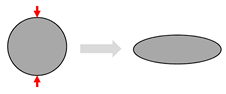 | all | - |
| void condensation (i.e., closing gaps between fibres) | 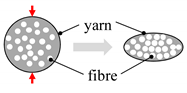 | random mat, unidirectional tape | woven and non-woven | |
| yarn flattening | 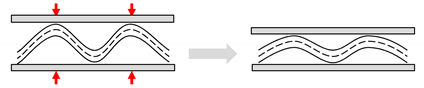 | woven | random mat | |
| fibre/yarn bending deformation |  | - | all | |
Fabric/preform | nesting and packing | 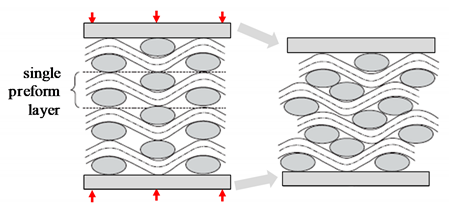 | woven | non-woven |
| Reinforcement | C [×108 m−2] | n | K at vf = 0.2 (or ϕ = 0.8) [×10−8 m−2] | K at vf = 0.5 (or ϕ = 0.5) [×10−8 m−2] | Unsaturated or Saturated, Test fluid, Viscosity and Temperature | Source |
|---|---|---|---|---|---|---|
| Wood fibre—random mat | 2460 | 1.80 | 0.00394 | 0.000203 | Saturated Mineral oil, 0.066–0.095 Pa·s, 14–23 °C | [46] |
| Wood fibre—random mat | 4000 | 1.76 | 0.00229 | 0.000125 | Saturated Mineral oil, 0.066–0.095 Pa·s, 14–23 °C | [46] |
| Sisal— random mat | 4.8 | 1.48 | 1.30 | 0.104 | Unsaturated, Glycerin solution, 1.2 Pa·s, ambient | [23] |
| Jute— plain-woven | 5.3 | 1.48 | 1.17 | 0.0943 | Unsaturated, Glycerin solution, 1.2 Pa·s, ambient | [23] |
| Sisal— plain-woven | 22.5 | 2.00 | 0.569 | 0.0222 | Unsaturated, Vinylester resin, 0.5–0.9 Pa·s | [47] |
| Jute— plain-woven | 81.0 | 0.88 | 0.0335 | 0.00617 | Saturated, Glycerin solution, 0.13 Pa·s, ambient | [17] |
| Jute— plain woven | 133.8 | 1.29 | 0.0357 | 0.00373 | Unsaturated, Glycerin solution, 0.15 Pa·s, ambient | [24] |
| Jute— plain woven | 84.6 | 0.91 | 0.0334 | 0.00591 | Saturated, Glycerin solution, 0.15 Pa·s, ambient | [24] |
| Coconut— random mat | 0.21 | 1.45 | 0.0160 | - | Unsaturated, Glycerin solution, 0.085 Pa.s, ambient | [48] |
| Jute— plain-woven | - | - | 0.00351 | 0.00197 | Saturated Mineral oil, 0.180 Pa.s, ambient | [49] |
| Jute— plain-woven | - | - | 0.00270 | 0.00060 | Saturated, corn syrup solution, 0.180 Pa.s, ambient | [49] |
| Flax– random mat | - | - | 0.00028 | 0.00005 | Transverse saturated, Silicon oil, 0.1 Pa.s, ambient | [50] |
| Flax– plain-woven | - | - | 0.00090 (at vf = 0.3) | 0.00006 | Transverse saturated, mineral oil, 0.14 Pa.s, 20 °C | [51] |
| Flax– plain-woven | - | - | 0.080 (at vf = 0.3) | 0.00030 | K1 In-plane saturated, mineral oil, 0.14 Pa.s, 20 °C | [51] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantaloni, D.; Bourmaud, A.; Baley, C.; Clifford, M.J.; Ramage, M.H.; Shah, D.U. A Review of Permeability and Flow Simulation for Liquid Composite Moulding of Plant Fibre Composites. Materials 2020, 13, 4811. https://doi.org/10.3390/ma13214811
Pantaloni D, Bourmaud A, Baley C, Clifford MJ, Ramage MH, Shah DU. A Review of Permeability and Flow Simulation for Liquid Composite Moulding of Plant Fibre Composites. Materials. 2020; 13(21):4811. https://doi.org/10.3390/ma13214811
Chicago/Turabian StylePantaloni, Delphin, Alain Bourmaud, Christophe Baley, Mike J. Clifford, Michael H. Ramage, and Darshil U. Shah. 2020. "A Review of Permeability and Flow Simulation for Liquid Composite Moulding of Plant Fibre Composites" Materials 13, no. 21: 4811. https://doi.org/10.3390/ma13214811
APA StylePantaloni, D., Bourmaud, A., Baley, C., Clifford, M. J., Ramage, M. H., & Shah, D. U. (2020). A Review of Permeability and Flow Simulation for Liquid Composite Moulding of Plant Fibre Composites. Materials, 13(21), 4811. https://doi.org/10.3390/ma13214811








