On the Evolution of Temperature and Combined Stress in a Work Roll under Cyclic Thermo-Mechanical Loadings during Hot Strip Rolling and Idling
Abstract
:1. Introduction
2. FEM Simulations
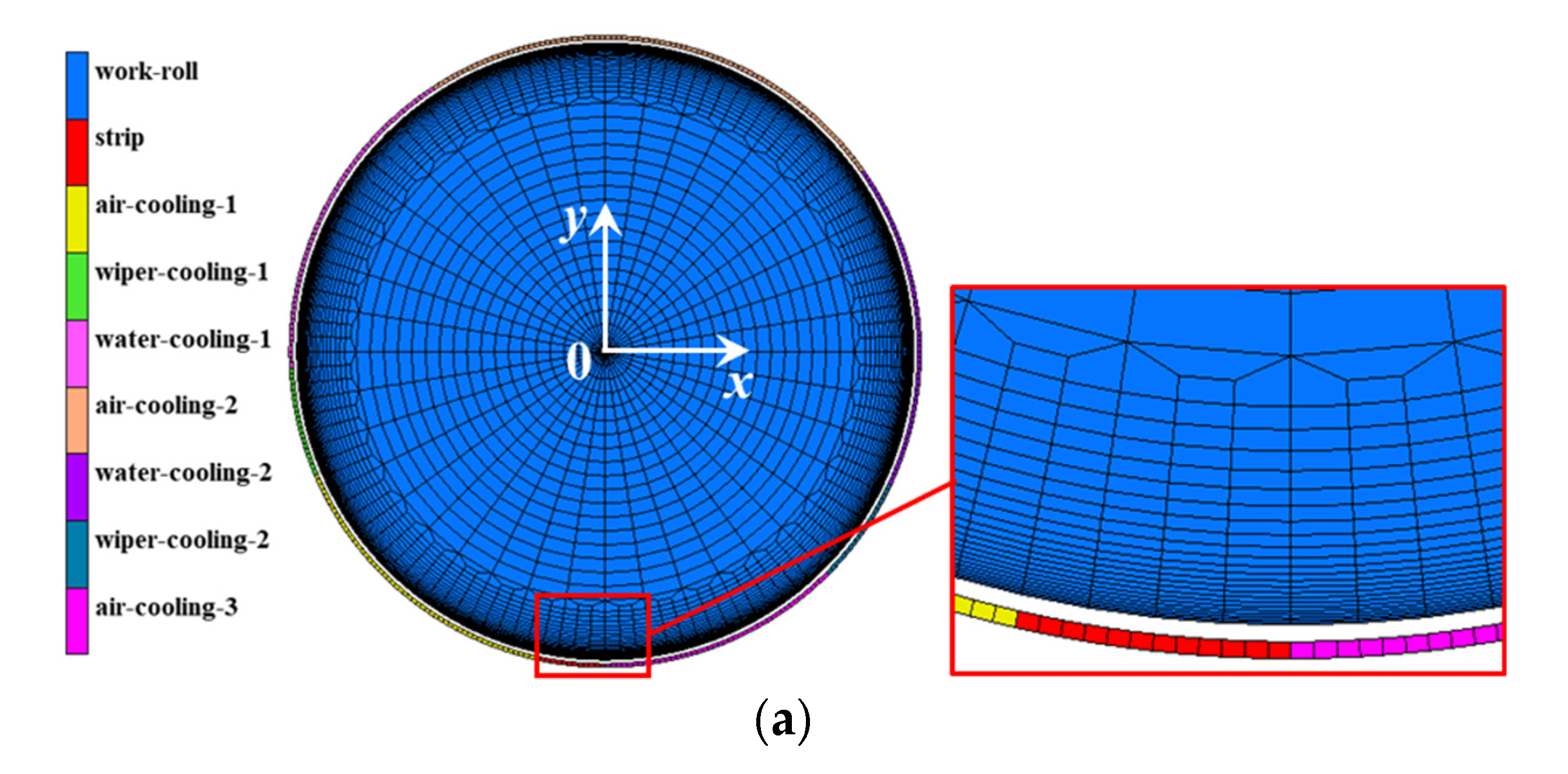
2.1. FEM Model Description
2.2. Heat Transfer Description
2.3. Material Properties Description
3. Results and Discussion
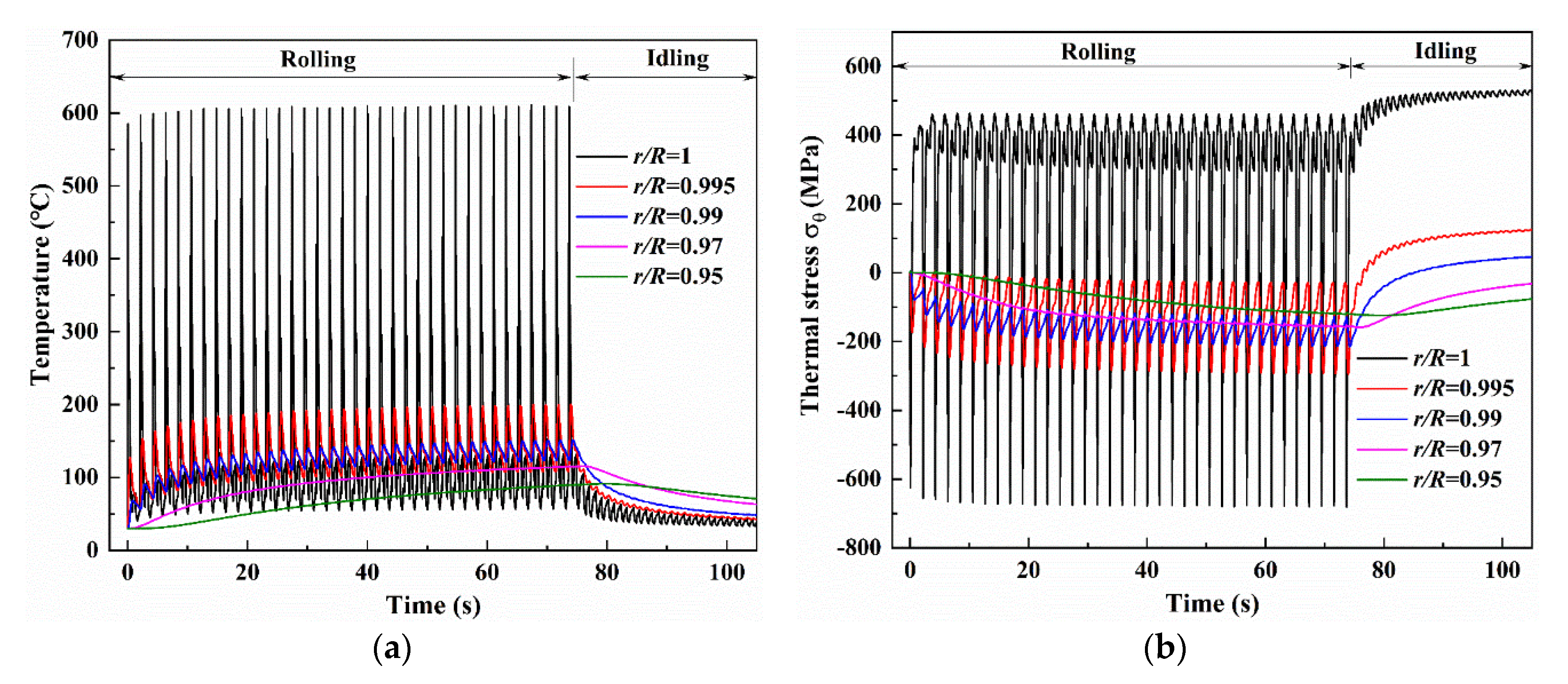
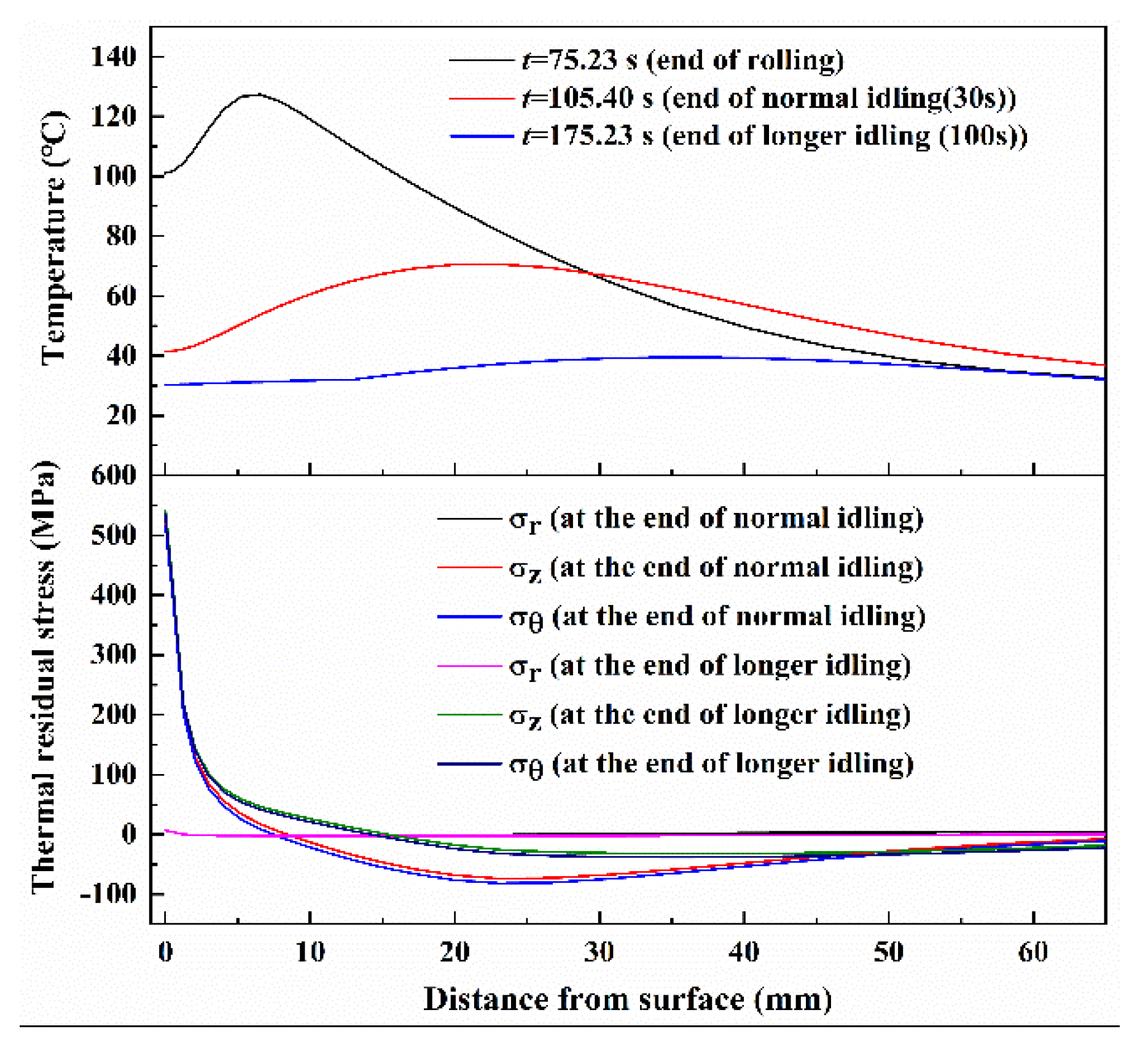
3.1. Temperature and Thermal Stress of Work Rolls during Rolling and Idling
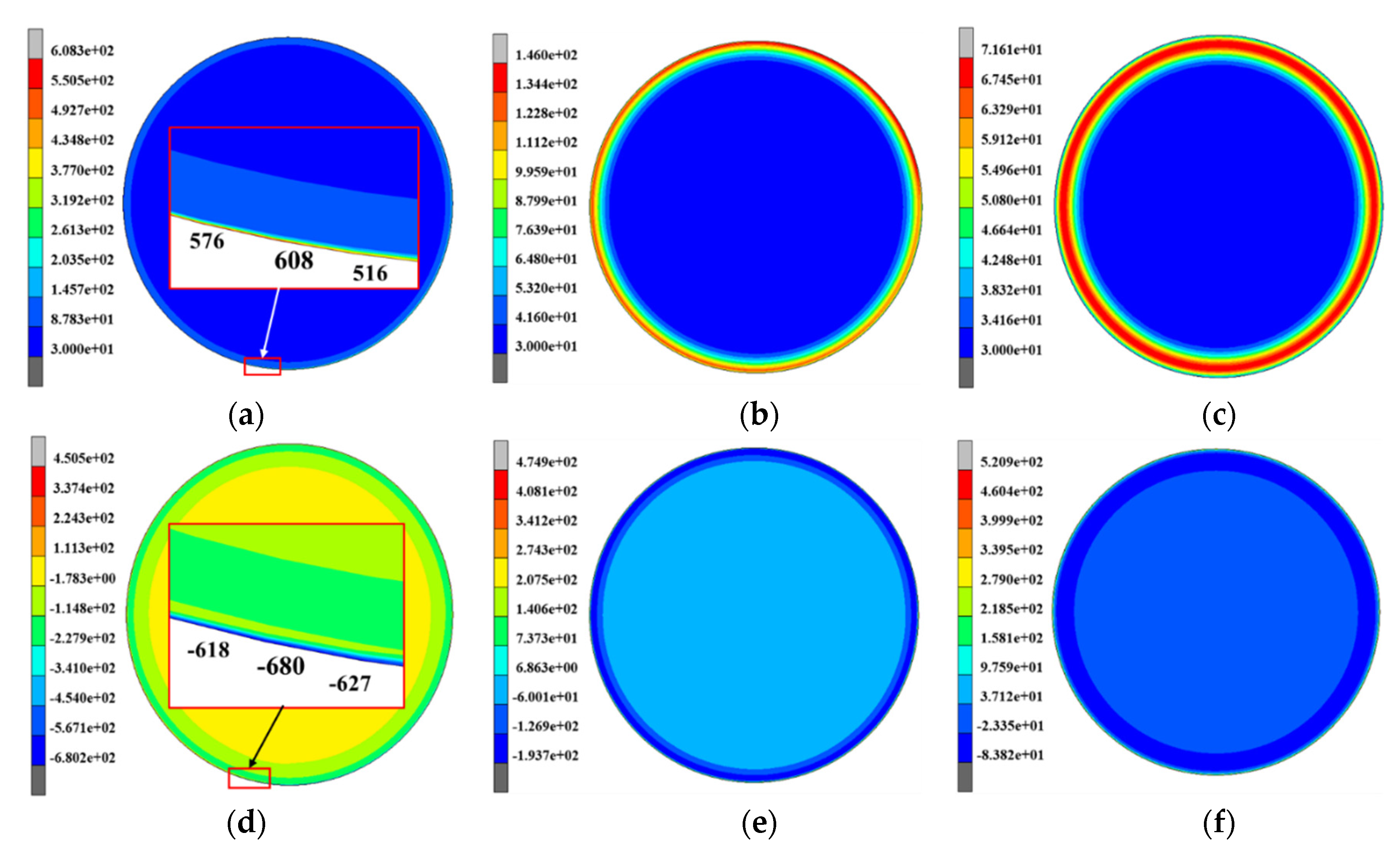
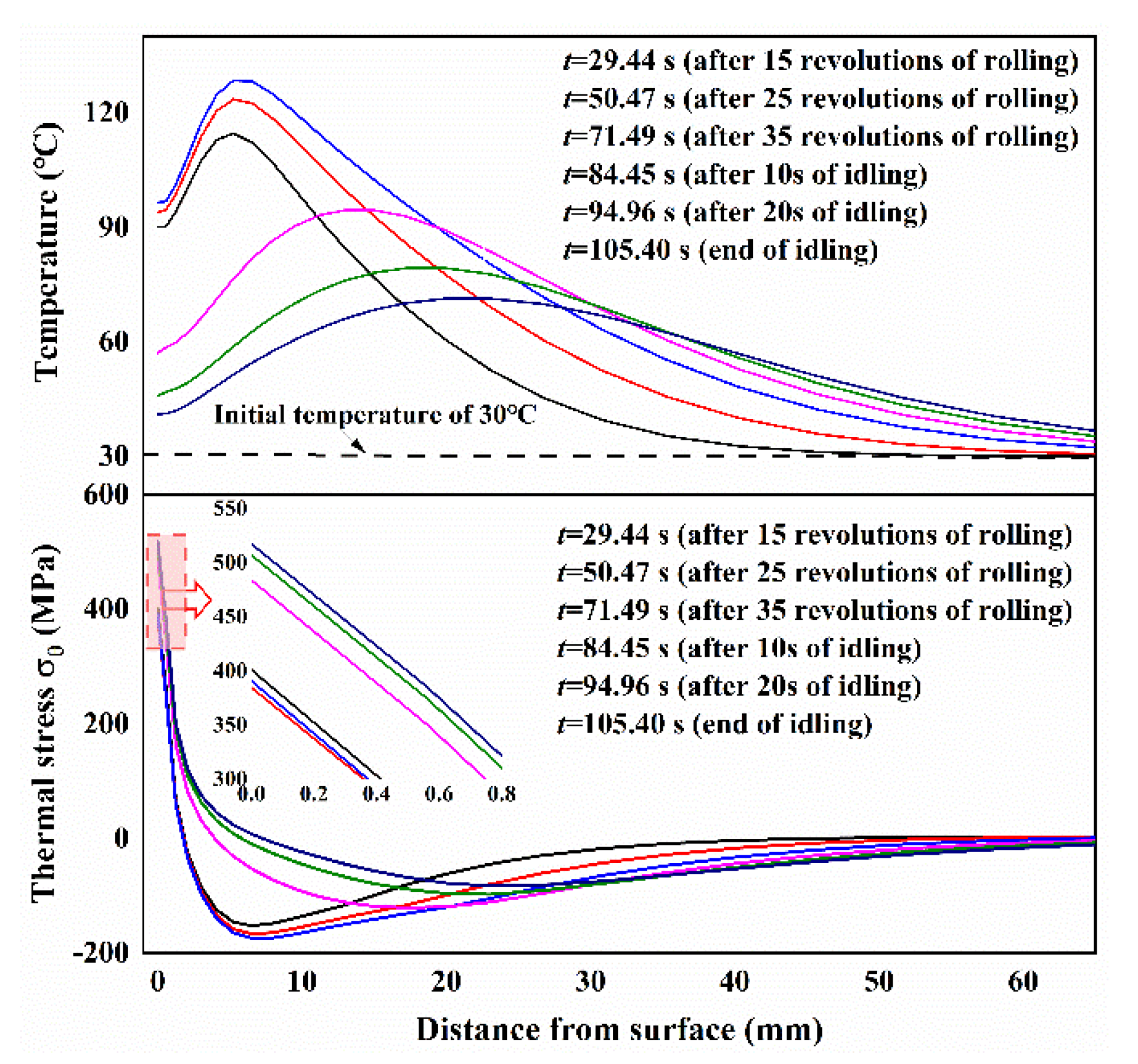
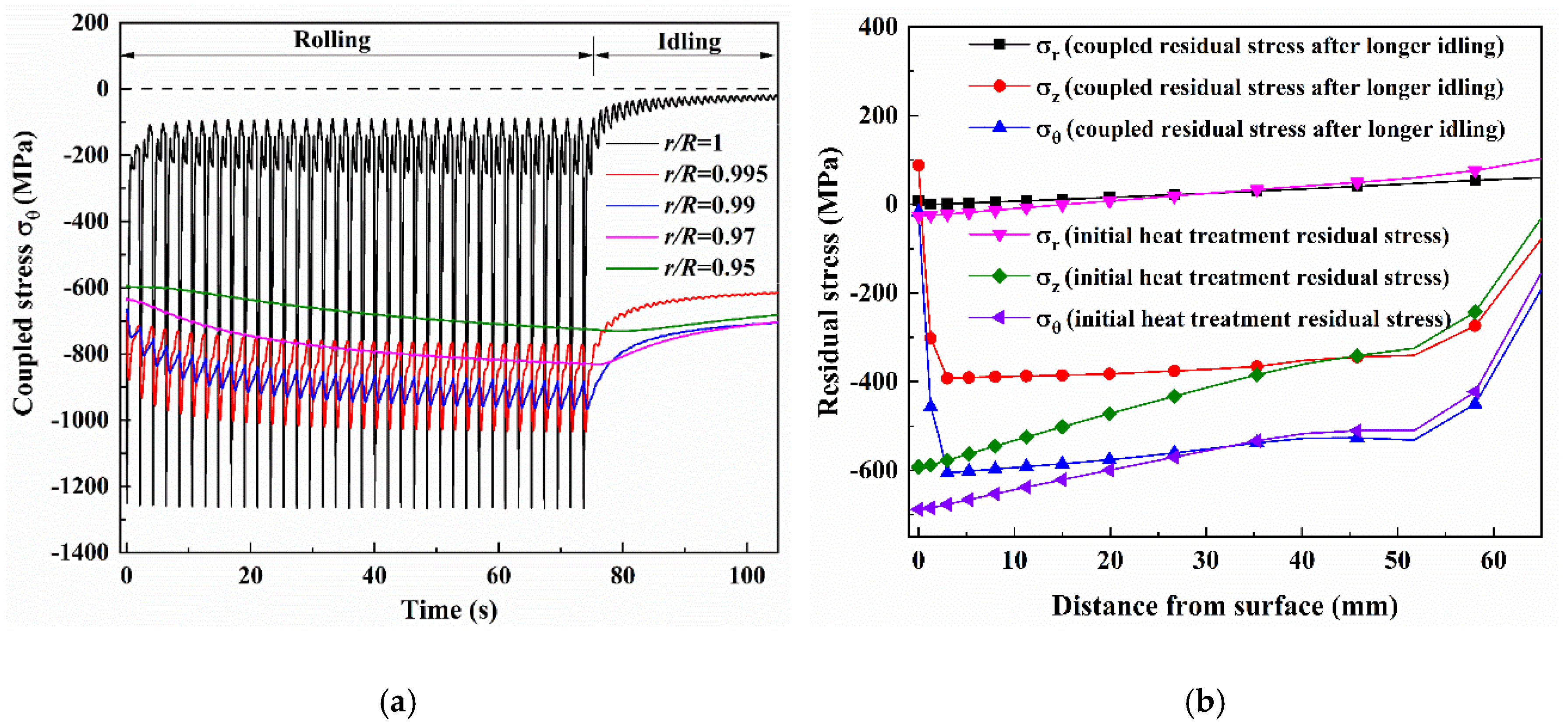
3.2. Thermo-Mechanical Stress in Work Rolls during Rolling
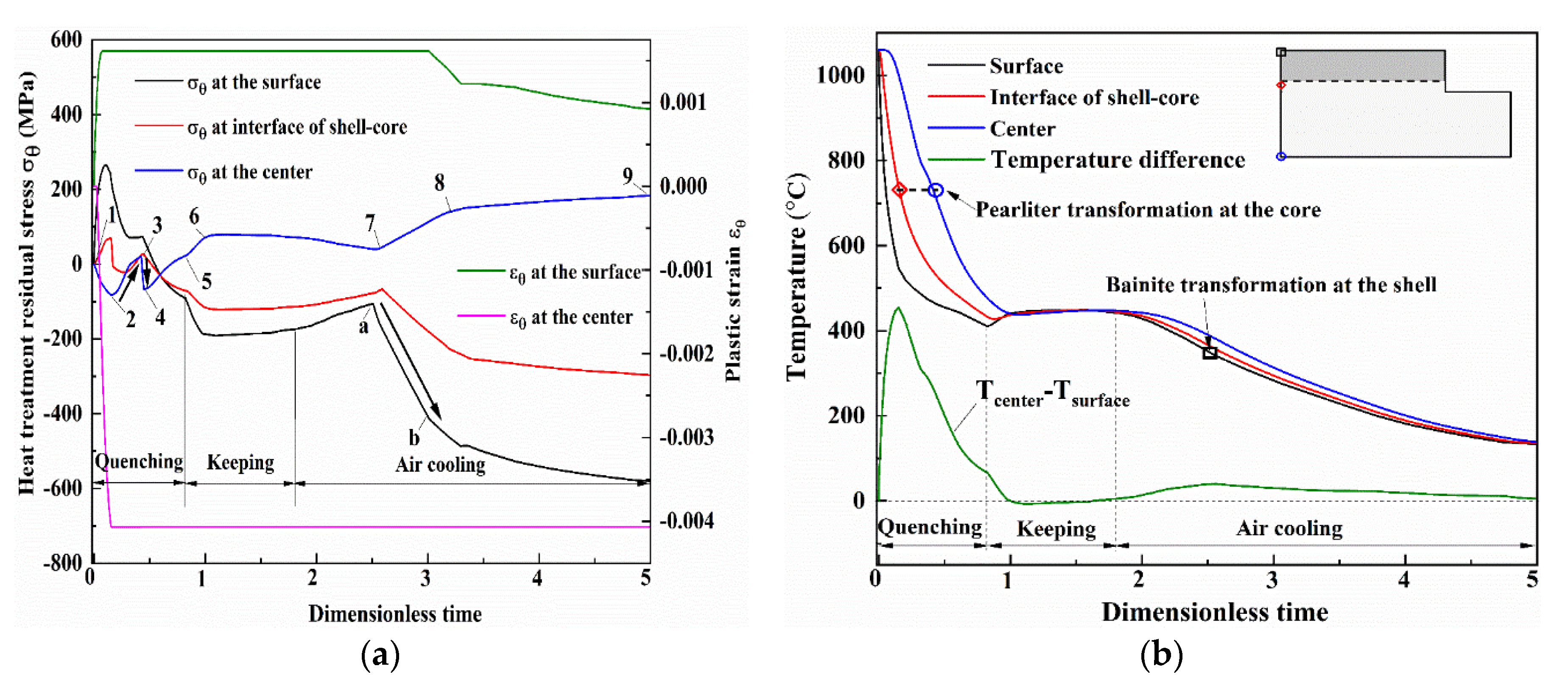
3.3. Redistribution of Heat Treatment Residual Stress in Work Rolls during Hot Rolling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sano, Y.; Hattori, T.; Haga, M. Characteristics of high-carbon high speed steel rolls for hot strip mill. ISIJ Int. 1992, 32, 1194–1201. [Google Scholar] [CrossRef]
- Shimizu, M.; Shitamura, O.; Matsuo, S.; Kamata, T.; Kondo, Y. Development of high performance new composite roll. ISIJ Int. 1992, 32, 1244–1249. [Google Scholar] [CrossRef]
- Mercado-Solis, R.D.; Talamantes-Silva, J.; Beynon, J.H.; Hernandez-Rodriguez, M.A.L. Modelling surface thermal damage to hot mill rolls. Wear 2007, 263, 1560–1567. [Google Scholar] [CrossRef]
- Beynon, J.H. Tribology of hot metal forming. Tribol. Int. 1998, 31, 73–77. [Google Scholar] [CrossRef]
- Montmitonnet, P.; Bucssla, P. A review on theoretical analyses of rolling in Europe. ISIJ Int. 1991, 31, 525–538. [Google Scholar] [CrossRef] [Green Version]
- Stevens, P.G.; Ivens, K.P.; Harper, P. Increasing work roll life by improved roll cooling practice. J. Iron Steel Inst. 1971, 209, 1–11. [Google Scholar]
- Patula, E. Steady-state temperature distribution in a rotating roll subject to surface heat fluxes and convective cooling. ASME J. Heat Transf. 1981, 103, 36–41. [Google Scholar] [CrossRef]
- Tseng, A.A. A numerical heat transfer analysis of strip rolling. J. Heat Transf. 1984, 106, 512–517. [Google Scholar] [CrossRef]
- Tseng, A.A.; Tong, S.; Lin, F.H. Thermal stresses of rotating rolls in rolling processing. J. Therm. Stresses 1989, 12, 427–450. [Google Scholar] [CrossRef]
- Lai, W.; Chen, T.C.; Weng, C. Transient thermal stresses of work roll by coupled thermoelasticity. Comput. Mech. 1991, 9, 55–71. [Google Scholar] [CrossRef]
- Yiannopoulos, A.C.; Anifantis, N.; Dimarogonas, A. Thermal stress optimization in metal rolling. J. Therm. Stresses 1997, 20, 569–590. [Google Scholar] [CrossRef]
- Lin, Z.C.; Chen, C.C. Three-dimensional heat-transfer and thermal-expansion analysis of the work roll during rolling. J. Mater. Process. Technol. 1995, 49, 125–147. [Google Scholar] [CrossRef]
- Shang, W.X.; Rodrigues, J.M.C.; Martins, P.A.F. Simulation of plane strain rolling through a combined finite element–boundary element approach. J. Mater. Process. Technol. 1999, 96, 173–181. [Google Scholar] [CrossRef]
- Chang, D.F. Thermal stresses in work rolls during the rolling of metal strip. J. Mater. Process. Technol. 1999, 94, 45–51. [Google Scholar] [CrossRef]
- Guo, R.M. Two-dimensional transient thermal behaviour of work rolls in rolling process. J. Manuf. Sci. Eng. 1998, 120, 28–33. [Google Scholar] [CrossRef]
- Hwang, S.M.; Sun, C.G.; Ryoo, S.R.; Kwak, W.J. An integrated FE process model for precision analysis of thermo-mechanical behaviors of rolls and strip in hot strip rolling. Comput. Methods Appl. Mech. Eng. 2002, 191, 4015–4033. [Google Scholar] [CrossRef]
- Lee, J.D.; Manzari, M.T.; Shen, Y.; Zeng, W. A finite element approach to transient thermal analysis of work rolls in rolling process. Trans. ASME J. Manuf. Sci. Eng. 2000, 122, 706–716. [Google Scholar] [CrossRef]
- Hsu, P.T.; Yang, Y.T.; Chen, C.O.K. A three-dimensional inverse problem of estimating the surface thermal behavior of the working roll in rolling process. J. Manuf. Sci. Eng. 2000, 122, 76–82. [Google Scholar] [CrossRef]
- Sun, C.G.; Hwang, S.M.; Yun, C.S.; Chung, J.S. Investigation of thermomechanical behavior of a work roll and of roll life in hot strip rolling. Metall. Mater. Trans. A 1998, 29, 2407–2424. [Google Scholar] [CrossRef] [Green Version]
- Li, C.S.; Liu, X.H.; Wang, G.D.; He, X.M. Three-dimensional FEM analysis of work roll temperature field in hot strip rolling. Mater. Sci. Technol. 2002, 18, 1147–1150. [Google Scholar] [CrossRef]
- Li, C.S.; Yu, H.L.; Deng, G.Y.; Liu, X.H.; Wang, G.D. Numerical simulation of temperature field and thermal stress field of work roll during hot strip rolling. J. Iron Steel Res. Int. 2007, 14, 18–21. [Google Scholar] [CrossRef]
- Serajzadeh, S.; Taheri, A.K.; Mucciardi, F. Unsteady state work-roll temperature distribution during continuous hot slab rolling. Int. J. Mech. Sci. 2002, 44, 2447–2462. [Google Scholar] [CrossRef]
- Serajzadeh, S.; Mucciardi, F. Modelling of work-roll temperature variation at unsteady state condition. Model Simul. Mater. Sci. Eng. 2003, 11, 179–194. [Google Scholar] [CrossRef]
- Sonboli, A.; Serajzadeh, S. A model for evaluating thermo-mechanical stresses within work-rolls in hot-strip rolling. J. Eng. Math. 2012, 72, 73–85. [Google Scholar] [CrossRef]
- Fischer, F.D.; Schreiner, W.E.; Werner, E.A.; Sun, C.G. The temperature and stress fields developing in rolls during hot rolling. J. Mater. Process. Technol. 2004, 150, 263–269. [Google Scholar] [CrossRef]
- Benasciutti, D.; Brusa, E.; Bazzaro, G. Finite elements prediction of thermal stresses in work roll of hot rolling mills. Procedia Eng. 2010, 2, 707–716. [Google Scholar] [CrossRef] [Green Version]
- Benasciutti, D. On thermal stress and fatigue life evaluation in work rolls of hot rolling mill. J. Strain Anal. Eng. Des. 2012, 47, 297–312. [Google Scholar] [CrossRef]
- Benasciutti, D.; Bona, F.D.; Munteanu, M.G. A harmonic one-dimensional element for non-linear thermo-mechanical analysis of axisymmetric structures under asymmetric loads: The case of hot strip rolling. J. Strain Anal. Eng. 2016, 51, 518–531. [Google Scholar] [CrossRef]
- Qayyum, F.; Shah, M.; Manzoor, S.; Abbas, M. Comparison of thermomechanical stresses produced in work rolls during hot and cold rolling of Cartridge Brass 1101. Mater. Sci. Technol. 2015, 31, 317–324. [Google Scholar] [CrossRef]
- Koohbor, B. Finite element modeling of thermal and mechanical stresses in work-rolls of warm strip rolling process. Proc. Inst. Mech. Eng. Part B 2016, 230, 1076–1086. [Google Scholar] [CrossRef]
- Gao, J.H.; Huang, C.Q.; Wang, M.; Huang, J.P. Determination and application of surface temperature field on hss hot work roll. Mater. Mech. Eng. 2009, 33, 46–49. [Google Scholar]
- Dünckelmeyer, M.; Krempaszky, C.; Werner, E.; Hein, G.; Schörkhuber, K. Analytical modeling of thermo-mechanically induced residual stresses of work rolls during hot rolling. Steel Res. Int. 2010, 81, 86–89. [Google Scholar]
- Na, D.H.; Moon, C.H.; Lee, Y. Thermal stress evolution of the roll during rolling and idling in hot strip rolling process. J. Therm. Stresses 2014, 37, 981–1001. [Google Scholar] [CrossRef]
- Deng, G.Y.; Zhu, H.T.; Tieu, A.K.; Su, L.H.; Reid, M.; Zhang, L.; Wei, P.T.; Zhao, X.; Wang, H.; Zhang, J.; et al. Theoretical and experimental investigation of thermal and oxidation behaviours of a high speed steel work roll during hot rolling. Int. J. Mech. Sci. 2017, 131, 811–826. [Google Scholar] [CrossRef] [Green Version]
- Deng, G.Y.; Zhu, Q.; Tieu, A.K.; Zhu, H.T.; Reid, M.; Saleh, A.A.; Su, L.H.; Ta, T.D.; Zhang, J.; Lu, C.; et al. Evolution of microstructure, temperature and stress in a high speed steel work roll during hot rolling: Experiment and modelling. J. Mater. Process. Technol. 2017, 240, 200–208. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Q. A Calculation of thermal stress affecting strip flatness change during run-out table cooling in hot steel strip rolling. J. Mater. Process Technol. 2008, 207, 130–146. [Google Scholar] [CrossRef]
- Hlady, C.; Brimacombe, J.; Samarasekera, I.; Hawbolt, E. Heat transfer in the hot rolling of metals. Metall. Mater. Trans. B 1995, 26, 1019–1027. [Google Scholar] [CrossRef]
- Zhou, J.H.; Guan, K.Z. Plastic Deformation Resistance of Metal; Mechanic Industry Publishing Company: Beijing, China, 1989. [Google Scholar]
- Wang, X.H.; Liu, C.Y.; Deng, Y.C.; Nie, Y.Z.; Han, Y.G. Model of deformation resistance of Q235 steel. Metal World 2011, 40–43. [Google Scholar]
- Mohanty, A.K.; Tawfek, A.A.; Prasad, B. Heat transfer from a rotating cylinder in cross flow. Exp. Therm. Fluid Sci. 1995, 10, 54–61. [Google Scholar] [CrossRef]
- Li, W.G.; Liu, X.H.; Guo, Z.H. Numerical simulation of temperature field and thermal crown of work roll during hot strip rolling. Chin. J. Nonferr. Met. 2012, 22, 3176–3184. [Google Scholar]
- Sims, R.B. The calculation of roll force and torque in hot rolling mills. Proc. Inst. Mech. Eng. 1954, 168, 191–201. [Google Scholar] [CrossRef]






| Parameters | Value | |
|---|---|---|
| Velocity of the work roll (m/s) | 1.24 | |
| Roll diameter (mm) | 830 | |
| Initial work roll temperature (°C) | 30 | |
| Entry strip temperature (°C) | 1030 | |
| Air/water temperature (°C) | 30 | |
| Entry strip temperature (°C) | 1030 | |
| Entry strip width (mm) | 964 | |
| Initial strip thickness (mm) | 44 | |
| Rolling reduction (%) | 43.6 | |
| Rolling force (kN) | 19,350 | |
| Water pressure (MPa) | 1.47 | |
| Water flow (L/min) | 2500 | |
| Heat transfer coefficient (W/(m2 K)) | Bite region | 45,000 |
| Wiper cooling | 14,600 | |
| Water cooling | 32,600 | |
| Air cooling | 5 |
| Property | HSS | DCI | Q235 |
|---|---|---|---|
| Young’s modulus (GPa) | 233 | 173 | 210 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| Density (kg/m3) | 7600 | 7300 | 7850 |
| Thermal expansion coefficient (/K) | 12.6 × 10−6 | 13.0 × 10−6 | 11.9 × 10−6 |
| Thermal conductivity (W/(m K)) | 20.2 | 23.4 | 56.9 |
| Specific heat (J/(kg K)) | 461 | 460 | 461 |
| Tensile strength (MPa) | 1280 | 415 | 235 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Shi, Q.; Han, W.; Zhu, F.; Chen, J. On the Evolution of Temperature and Combined Stress in a Work Roll under Cyclic Thermo-Mechanical Loadings during Hot Strip Rolling and Idling. Materials 2020, 13, 5054. https://doi.org/10.3390/ma13215054
Hu K, Shi Q, Han W, Zhu F, Chen J. On the Evolution of Temperature and Combined Stress in a Work Roll under Cyclic Thermo-Mechanical Loadings during Hot Strip Rolling and Idling. Materials. 2020; 13(21):5054. https://doi.org/10.3390/ma13215054
Chicago/Turabian StyleHu, Kejun, Qinghe Shi, Wenqin Han, Fuxian Zhu, and Jufang Chen. 2020. "On the Evolution of Temperature and Combined Stress in a Work Roll under Cyclic Thermo-Mechanical Loadings during Hot Strip Rolling and Idling" Materials 13, no. 21: 5054. https://doi.org/10.3390/ma13215054
APA StyleHu, K., Shi, Q., Han, W., Zhu, F., & Chen, J. (2020). On the Evolution of Temperature and Combined Stress in a Work Roll under Cyclic Thermo-Mechanical Loadings during Hot Strip Rolling and Idling. Materials, 13(21), 5054. https://doi.org/10.3390/ma13215054




