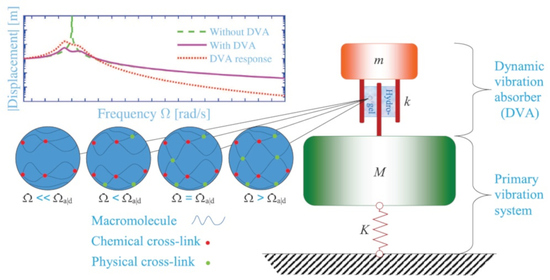
Are Single Polymer Network Hydrogels with Chemical and Physical Cross-Links a Promising Dynamic Vibration Absorber Material? A Simulation Model Inquiry †
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
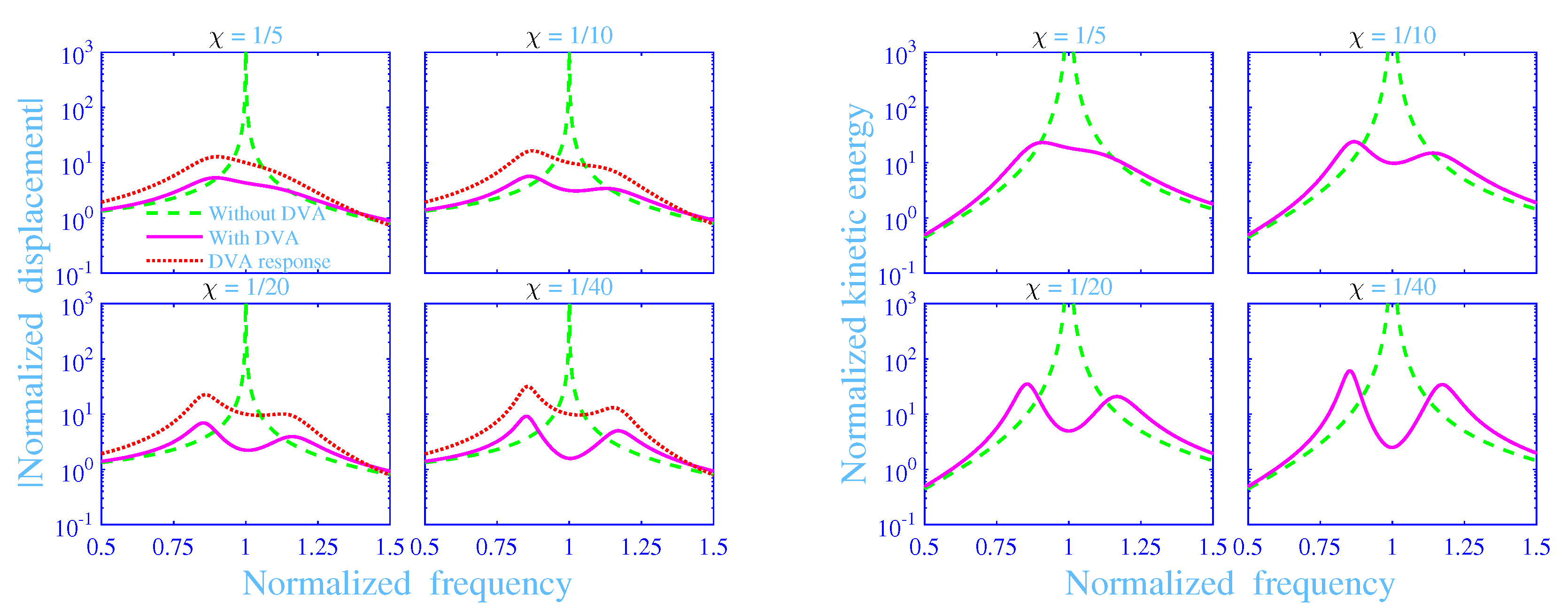
3.1. Material and Dynamic Vibration Absorber Parameters
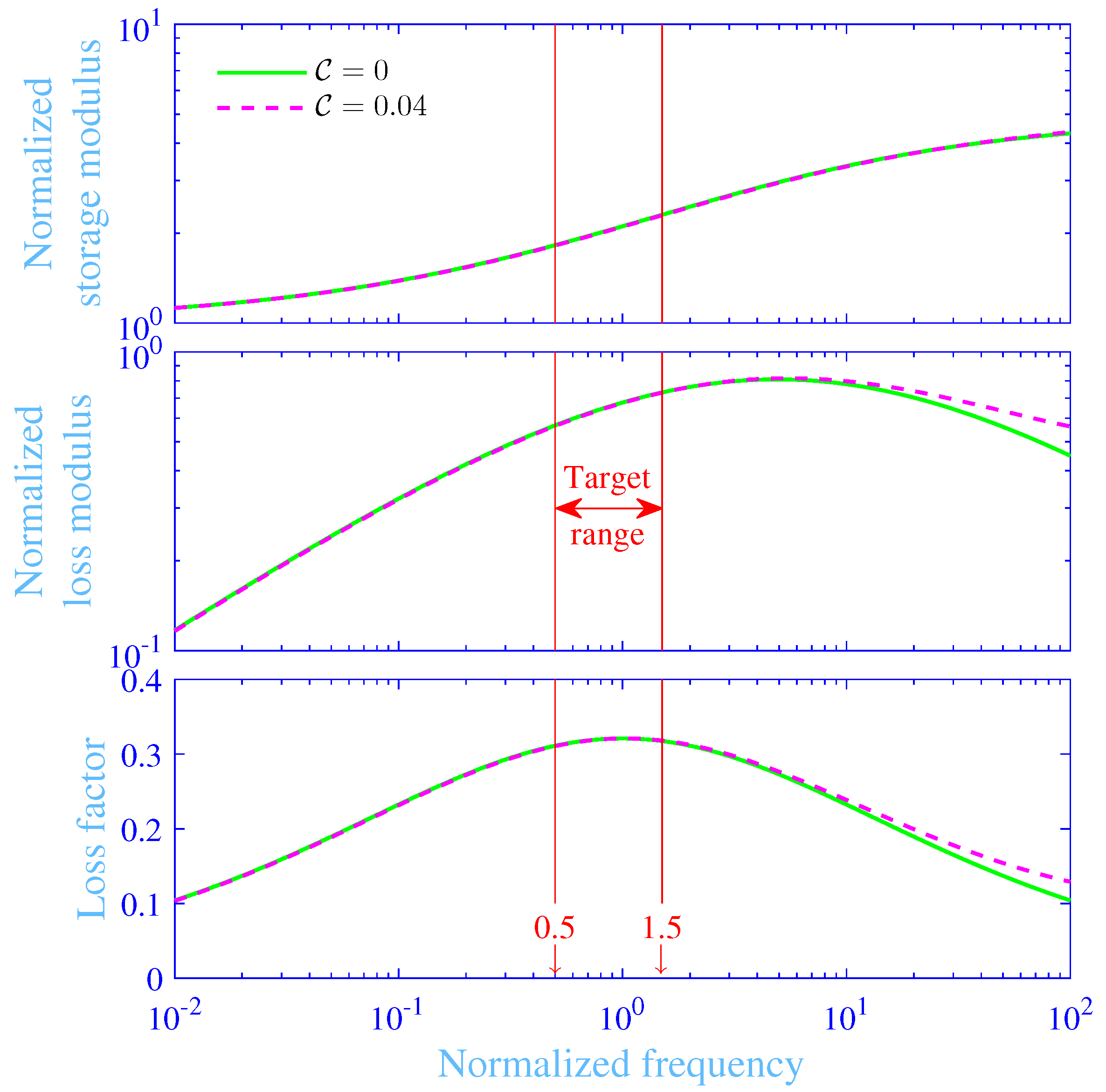
3.2. Shear Modulus
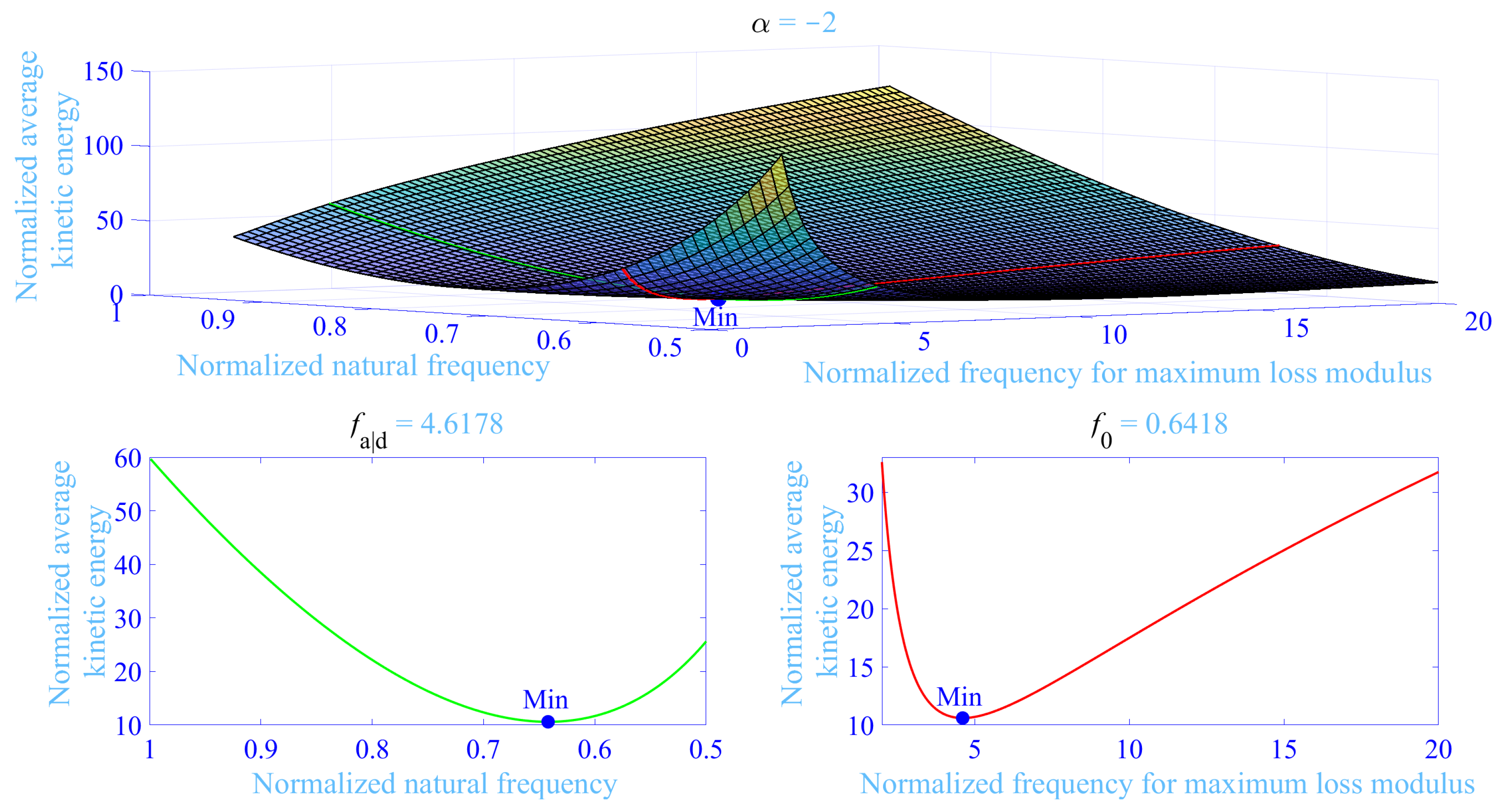
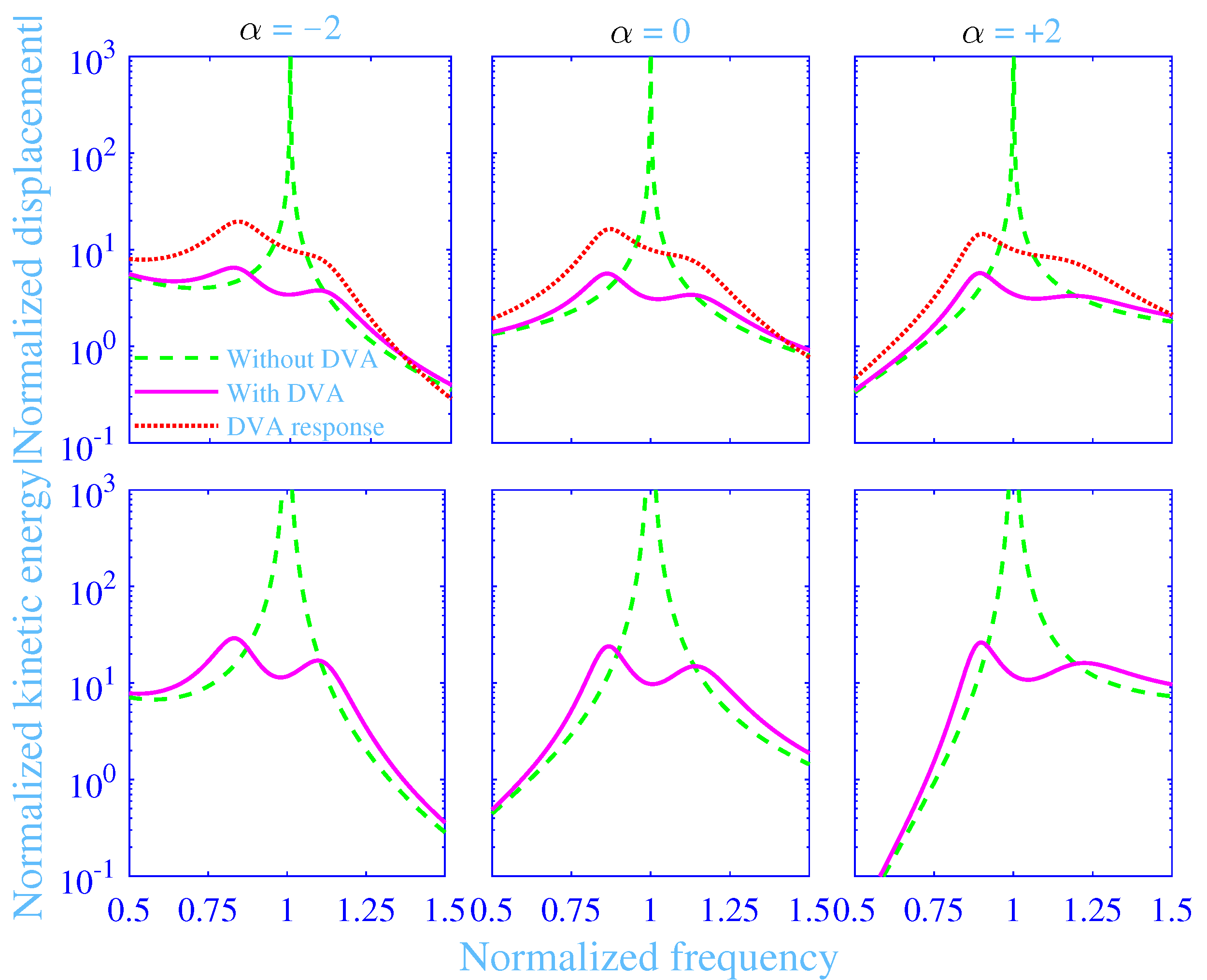
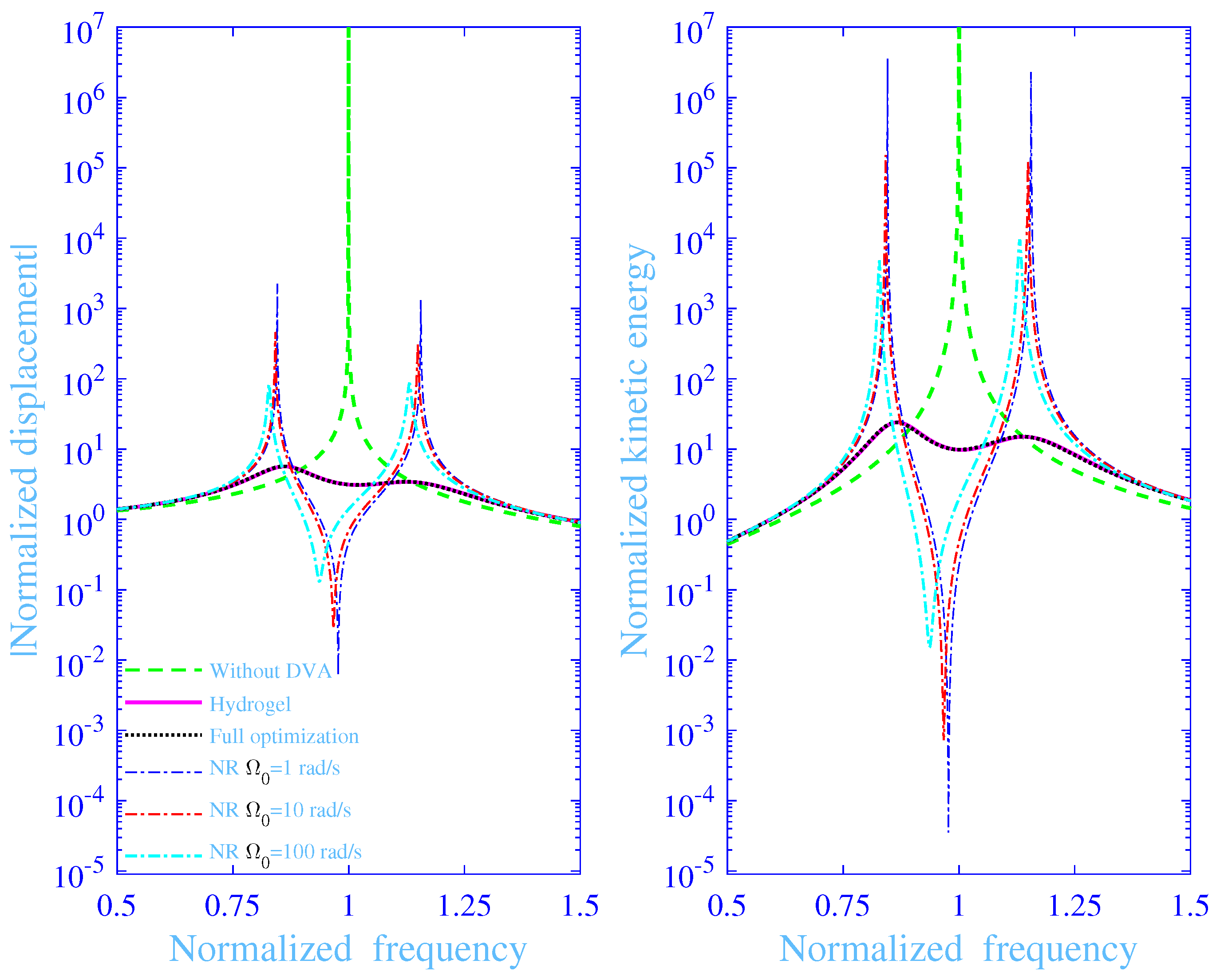
3.3. Optimization
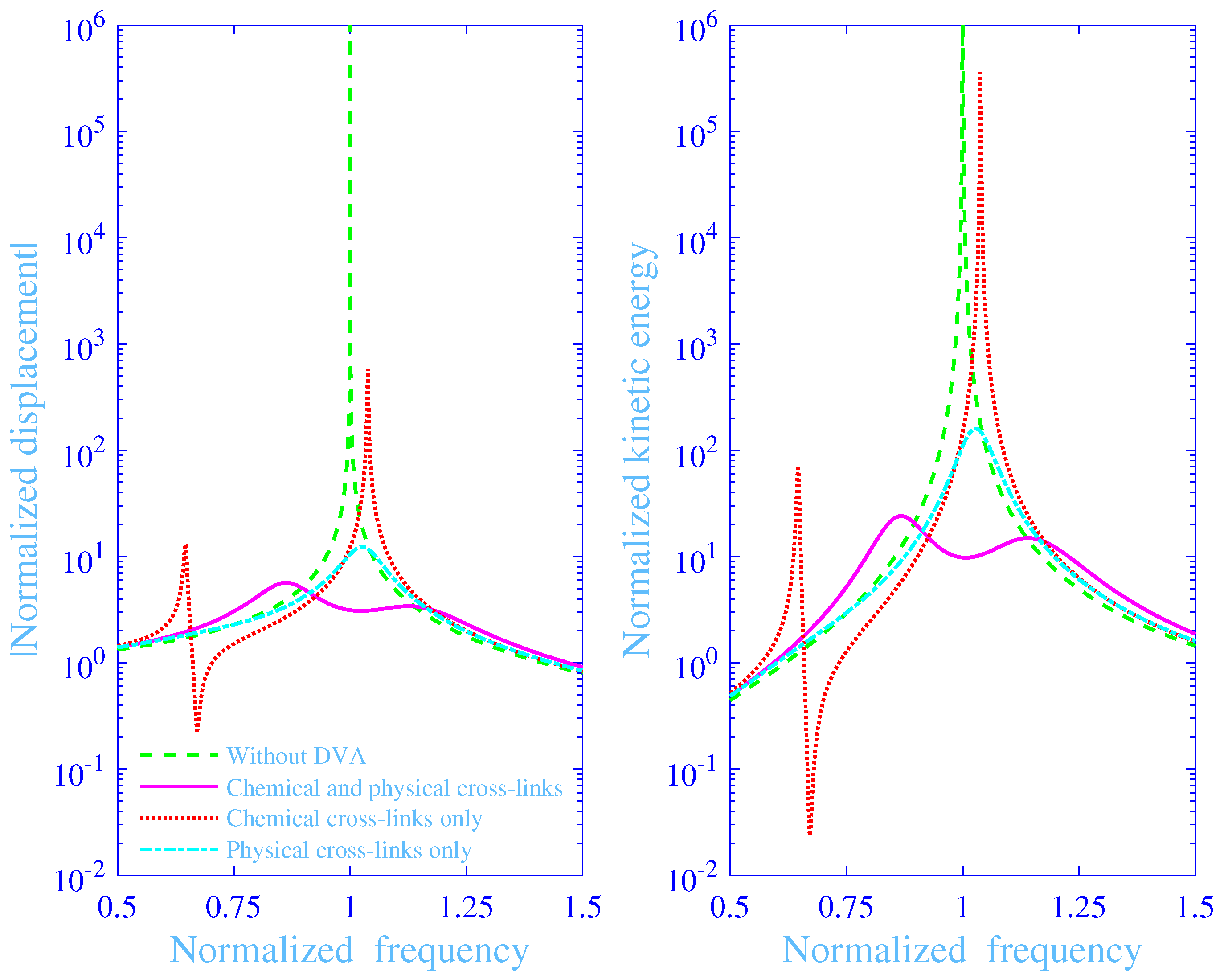
3.4. Chemical and Physical Cross-Links
4. Conclusions
Funding
Conflicts of Interest
References
- Frahm, H. Device for Damping Vibrations of Bodies. U.S. Patent 989,958, 18 April 1911. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; Civil, Mechanical and Other Engineering Series; Dover Publications: New York, NY, USA, 1985. [Google Scholar]
- Korenev, B.G.; Reznikov, L.M. Dynamic Vibration Absorbers: Theory and Technical Applications; John Wiley and Sons Ltd.: Chichester, UK, 1993. [Google Scholar]
- Sun, J.Q.; Jolly, M.R.; Norris, M.A. Passive, adaptive and active tuned vibration absorbers—A survey. J. Mech. Des. 1995, 117, 234–242. [Google Scholar] [CrossRef]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Mead, D.J. Passive Vibration Control; John Wiley and Sons Ltd.: Chichester, UK, 1998. [Google Scholar]
- Kari, L. Dynamic Vibration Absorbers. In Handbook of Noise and Vibration Control; Crocker, M.J., Ed.; Wiley InterScience, John Wiley and Sons Ltd.: Hooboken, NJ, USA, 2007; Chapter 61; pp. 745–752. [Google Scholar] [CrossRef]
- Gutierrez Soto, M.; Adeli, H. Tuned mass dampers. Arch. Comput. Methods Eng. 2013, 20, 419–431. [Google Scholar] [CrossRef]
- Berbyuk, V. Design optimization of torsional vibration absorbers for heavy-duty truck drivetrain systems. Vibration 2019, 2, 240–264. [Google Scholar] [CrossRef] [Green Version]
- Wramner, L. Dual mass flywheels with tuned vibration absorbers for application in heavy-duty truck powertrains. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2020, 234, 2500–2508. [Google Scholar] [CrossRef]
- Arfiadi, Y. Nonlinear controllers for active composite tuned mass dampers. Procedia Eng. 2017, 171, 1178–1185. [Google Scholar] [CrossRef]
- Lavazec, D.; Cumunel, G.; Duhamel, D.; Soize, C. Experimental evaluation and model of a nonlinear absorber for vibration attenuation. Commun. Nonlinear Sci. Numer. Simulat. 2019, 69, 386–397. [Google Scholar] [CrossRef] [Green Version]
- Nishihara, O.; Asami, T. Closed-form solutions to the exact optimizations of dynamic vibration absorbers (Minimizations of the maximum amplitude magnification factors). J. Vib. Acoust. 2002, 124, 576–582. [Google Scholar] [CrossRef]
- Asami, T.; Nishihara, O. H2 Optimization of the three-element type dynamic vibration absorbers. J. Vib. Acoust. 2002, 124, 583–592. [Google Scholar] [CrossRef]
- Yang, C.H.; Wang, M.X.; Haider, H.; Yang, J.H.; Sun, J.Y.; Chen, Y.M.; Zhou, J.; Suo, Z. Strengthening alginate/polyacrylamide hydrogels using various multivalent cations. ACS Appl. Mater. Interfaces 2013, 5, 10418–10422. [Google Scholar] [CrossRef]
- Lin, W.C.; Fan, W.; Marcellan, A.; Hourdet, D.; Creton, C. Large strain and fracture properties of poly(dimethylacrylamide)/silica hybrid hydrogels. Macromolecules 2010, 43, 2554–2563. [Google Scholar] [CrossRef]
- Carlsson, L.; Rose, S.; Hourdet, D.; Marcellan, A. Nano-hybrid self-crosslinked PDMA/silica hydrogels. Soft Matter 2010, 6, 3619–3631. [Google Scholar] [CrossRef]
- Peak, C.W.; Wilker, J.J.; Schmidt, G. A review on tough and sticky hydrogels. Colloid Polym. Sci. 2013, 291, 2031–2047. [Google Scholar] [CrossRef]
- Mayumi, K.; Marcellan, A.; Ducouret, G.; Creton, C.; Narita, T. Stress–strain relationship of highly stretchable dual cross-link gels: Separability of strain and time effect. ACS Macro Lett. 2013, 2, 1065–1068. [Google Scholar] [CrossRef]
- Hao, J.; Weiss, R.A. Mechanical behavior of hybrid hydrogels composed of a physical and a chemical network. Polymer 2013, 54, 2174–2182. [Google Scholar] [CrossRef]
- Rose, S.; Dizeux, A.; Narita, T.; Hourdet, D.; Marcellan, A. Time dependence of dissipative and recovery processes in nanohybrid hydrogels. Macromolecules 2013, 46, 4095–4104. [Google Scholar] [CrossRef]
- Narita, T.; Mayumi, K.; Ducouret, G.; Hébraud, P. Viscoelastic properties of poly(vinyl alcohol) hydrogels having permanent and transient cross-links studied by microrheology, classical rheometry, and dynamic light scattering. Macromolecules 2013, 46, 4174–4183. [Google Scholar] [CrossRef]
- Long, R.; Mayumi, K.; Creton, C.; Narita, T.; Hui, C.Y. Time dependent behavior of a dual cross-link self-healing gel: Theory and experiments. Macromolecules 2014, 47, 7243–7250. [Google Scholar] [CrossRef]
- Zhao, X. Multi-scale multi-mechanism design of tough hydrogels: Building dissipation into stretchy networks. Soft Matter 2014, 10, 672–687. [Google Scholar] [CrossRef] [Green Version]
- Long, R.; Mayumi, K.; Creton, C.; Narita, T.; Hui, C.Y. Rheology of a dual crosslink self-healing gel: Theory and measurement using parallel-plate torsional rheometry. J. Rheol. 2015, 59, 643–665. [Google Scholar] [CrossRef]
- Branca, C.; Crupi, C.; D’Angelo, G.; Khouzami, K.; Rifici, S.; Visco, A.; Wanderlingh, U. Effect of montmorillonite on the rheological properties of dually crosslinked guar gum-based hydrogels. J. Appl. Polym. Sci. 2015, 132, 41373. [Google Scholar] [CrossRef]
- Lin, P.; Ma, S.; Wang, X.; Zhou, F. Molecularly engineered dual-crosslinked hydrogel with ultrahigh mechanical strength, toughness, and good self-recovery. Adv. Mater. 2015, 27, 2054–2059. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Peng, H.; Li, Y.; Xu, Y.; Weng, W. Compositional- and time-dependent dissipation, recovery and fracture toughness in hydrophobically reinforced hybrid hydrogels. Polymer 2015, 80, 130–137. [Google Scholar] [CrossRef]
- Haraguchi, K.; Li, H.J.; Xu, Y.; Li, G. Copolymer nanocomposite hydrogels: Unique tensile mechanical properties and network structures. Polymer 2016, 96, 94–103. [Google Scholar] [CrossRef]
- Karobi, S.N.; Sun, T.L.; Kurokawa, T.; Luo, F.; Nakajima, T.; Nonoyama, T.; Gong, J.P. Creep behavior and delayed fracture of tough polyampholyte hydrogels by tensile test. Macromolecules 2016, 49, 5630–5636. [Google Scholar] [CrossRef] [Green Version]
- Czarnecki, S.; Rossow, T.; Seiffert, S. Hybrid polymer-network hydrogels with tunable mechanical response. Polymers 2016, 8, 82. [Google Scholar] [CrossRef] [Green Version]
- Mayumi, K.; Guo, J.; Narita, T.; Hui, C.Y.; Creton, C. Fracture of dual crosslink gels with permanent and transient crosslinks. Extreme Mech. Lett. 2016, 6, 52–59. [Google Scholar] [CrossRef] [Green Version]
- Zhong, M.; Liu, Y.T.; Liu, X.Y.; Shi, F.K.; Zhang, L.Q.; Zhu, M.F.; Xie, X.M. Dually cross-linked single network poly(acrylic acid) hydrogels with superior mechanical properties and water absorbency. Soft Matter 2016, 12, 5420–5428. [Google Scholar] [CrossRef]
- Creton, C. 50th Anniversary perspective: Networks and gels: Soft but dynamic and tough. Macromolecules 2017, 50, 8297–8316. [Google Scholar] [CrossRef]
- Zhao, J.; Mayumi, K.; Creton, C.; Narita, T. Rheological properties of tough hydrogels based on an associating polymer with permanent and transient crosslinks: Effects of crosslinking density. J. Rheol. 2017, 61, 1371–1383. [Google Scholar] [CrossRef]
- Zou, X.; Kui, X.; Zhang, R.; Zhang, Y.; Wang, X.; Wu, Q.; Chen, T.; Sun, P. Viscoelasticity and structures in chemically and physically dual-cross-linked hydrogels: Insights from rheology and proton multiple-quantum NMR spectroscopy. Macromolecules 2017, 50, 9340–9352. [Google Scholar] [CrossRef]
- Liu, M.; Guo, J.; Hui, C.Y.; Creton, C.; Narita, T.; Zehnder, A. Time–temperature equivalence in a PVA dual cross-link self-healing hydrogel. J. Rheol. 2018, 62, 991–1000. [Google Scholar] [CrossRef]
- Nicol, E.; Nicolai, T.; Zhao, J.; Narita, T. Photo-cross-linked self-assembled poly(ethylene oxide)-based hydrogels containing hybrid junctions with dynamic and permanent cross-links. ACS Macro Lett. 2018, 7, 683–687. [Google Scholar] [CrossRef] [Green Version]
- Kari, L. Effective visco-elastic models of tough, doubly cross-linked, single-network polyvinyl alcohol (PVA) hydrogels. Additively separable fractional-derivative based models for chemical and physical cross-links. Contin. Mech. Thermodyn. 2020, in press. [Google Scholar] [CrossRef] [Green Version]
- Kari, L. Torsional energy flow trough a tough hydrogel vibration isolator. In Proceedings of the MEDYNA2020, 3rd Euro-Mediterranean Conference on Structural Dynamics and Vibroacoustics, Napoli, Italy, 17–19 February 2020; pp. 237–240. [Google Scholar]
- Guo, J.; Long, R.; Mayumi, K.; Hui, C.Y. Mechanics of a dual cross-link gel with dynamic bonds: Steady state kinetics and large deformation effects. Macromolecules 2016, 49, 3497–3507. [Google Scholar] [CrossRef]
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 2, 1272–1280. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Pritz, T. Analysis of four-parameter fractional derivative model of real solid materials. J. Sound Vib. 1996, 195, 103–115. [Google Scholar] [CrossRef]
- Enelund, M.; Olssson, P. Damping described by fading memory—Analysis andapplication to fractional derivative models. Int. J. Solids Struct. 1999, 36, 939–970. [Google Scholar] [CrossRef]
- Pritz, T. Verification of local Kramers–Kronig relations for complex modulus by means of fractional derivative model. J. Sound Vib. 1999, 228, 1145–1165. [Google Scholar] [CrossRef]
- Kari, L. On the waveguide modelling of dynamic stiffness of cylindrical vibration isolators. Part I: The model, solution and experimental comparison. J. Sound Vib. 2001, 244, 211–233. [Google Scholar] [CrossRef]
- Kari, L.; Eriksson, P.; Stenberg, B. Dynamic stiffness of natural rubber cylinders in the audible frequency range using wave guides. Kaut. Gummi Kunstst. 2001, 54, 106–111. [Google Scholar]
- Surguladze, T.A. On certain applications of fractional calculus to viscoelasticity. J. Math. Sci. 2002, 112, 4517–4557. [Google Scholar] [CrossRef]
- Sjöberg, M.; Kari, L. Non-linear behavior of a rubber isolator system using fractional derivatives. Vehicle Syst. Dyn. 2002, 37, 217–236. [Google Scholar] [CrossRef]
- Kari, L. Dynamic stiffness matrix of a long rubber bush mounting. Rubber Chem. Technol. 2002, 75, 747–770. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M. Fractional derivative viscoelasticity at large deformations. Nonlinear Dyn. 2003, 33, 301–321. [Google Scholar] [CrossRef]
- Sjöberg, M.; Kari, L. Nonlinear isolator dynamics at finite deformations: An effective hyperelastic, fractional derivative, generalized friction model. Nonlinear Dyn. 2003, 33, 323–336. [Google Scholar] [CrossRef]
- Kari, L. Audible-frequency stiffness of a primary suspension isolator on a high speed tilting bogie. Proc. Inst. Mech. Eng. F-J. Rail Rapid Transit 2003, 217, 47–62. [Google Scholar] [CrossRef]
- Kari, L. On the dynamic stiffness of preloaded vibration isolators in the audible frequency range: Modeling and experiments. J. Acoust. Soc. Am. 2003, 113, 1909–1921. [Google Scholar] [CrossRef] [PubMed]
- Pritz, T. Five-parameter fractional derivative model for polymeric damping materials. J. Sound Vib. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Coja, M.; Kari, L. Axial audio-frequency stiffness of a bush mounting—The waveguide solution. Appl. Math. Modell. 2007, 31, 38–53. [Google Scholar] [CrossRef]
- García Tárrago, M.J.; Kari, L.; Vinolas, J.; Gil-Negrete, N. Frequency and amplitude dependence of the axial and radial stiffness of carbon-black filled rubber bushings. Polym. Test. 2007, 26, 629–638. [Google Scholar] [CrossRef]
- Hanyga, A. Fractional-order relaxation laws in non-linear viscoelasticity. Contin. Mech. Thermodyn. 2007, 19, 25–36. [Google Scholar] [CrossRef]
- García Tárrago, M.J.; Vinolas, J.; Kari, L. Axial stiffness of carbon black filled rubber bushings. Kaut. Gummi Kunsts. 2007, 60, 43–48. [Google Scholar]
- García Tárrago, M.J.; Kari, L.; Viñolas, J.; Gil-Negrete, N. Torsion stiffness of a rubber bushing: A simple engineering design formula including the amplitude dependence. J. Strain Anal. Eng. 2007, 42, 13–21. [Google Scholar] [CrossRef]
- Gil-Negrete, N.; Vinolas, J.; Kari, L. A nonlinear rubber material model combining fractional order viscoelasticity and amplitude dependent effects. J. Appl. Mech. 2009, 76, 011009. [Google Scholar] [CrossRef]
- Lewandowski, R.; Pawlak, Z. Dynamic analysis of frames with viscoelastic dampers modelled by rheological models with fractional derivatives. J. Sound Vib. 2011, 330, 923–936. [Google Scholar] [CrossRef]
- Blom, P.; Kari, L. A nonlinear constitutive audio frequency magneto-sensitive rubber model including amplitude, frequency and magnetic field dependence. J. Sound Vib. 2011, 330, 947–954. [Google Scholar] [CrossRef]
- Östberg, M.; Kari, L. Transverse, tilting and cross-coupling stiffness of cylindrical rubber isolators in the audible frequency range—The wave-guide solution. J. Sound Vib. 2011, 330, 3222–3244. [Google Scholar] [CrossRef]
- Müller, S.; Kästner, M.; Brummund, J.; Ulbricht, V. A nonlinear fractional viscoelastic material model for polymers. Comput. Mater. Sci. 2011, 50, 2938–2949. [Google Scholar] [CrossRef]
- Blom, P.; Kari, L. The frequency, amplitude and magnetic field dependent torsional stiffness of a magneto-sensitive rubber bushing. Int. J. Mech. Sci. 2012, 60, 54–58. [Google Scholar] [CrossRef]
- Wharmby, A.W.; Bagley, R.L. Generalization of a theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 2013, 57, 1429–1440. [Google Scholar] [CrossRef]
- Alberdi-Muniain, A.; Gil-Negrete, N.; Kari, L. Modelling energy flow through magneto-sensitive vibration isolators. Int. J. Eng. Sci. 2013, 65, 22–39. [Google Scholar] [CrossRef]
- Müller, S.; Kästner, M.; Brummund, J.; Ulbricht, V. On the numerical handling of fractional viscoelastic material models in a FE analysis. Comput. Mech. 2013, 51, 999–1012. [Google Scholar] [CrossRef]
- Östberg, M.; Coja, M.; Kari, L. Dynamic stiffness of hollowed cylindrical rubber vibration isolators—The wave-guide solution. Int. J. Solids Struct. 2013, 50, 1791–1811. [Google Scholar] [CrossRef]
- Wollscheid, D.; Lion, A. The benefit of fractional derivatives in modelling the dynamics of filler-reinforced rubber under large strains: A comparison with the Maxwell-element approach. Comput. Mech. 2014, 53, 1015–1031. [Google Scholar] [CrossRef]
- Rouleau, L.; Pirk, R.; Pluymers, B.; Desmet, W. Characterization and modeling of the viscoelastic behavior of a self-adhesive rubber using dynamic mechanical analysis tests. J. Aerosp. Technol. Manag. 2015, 7, 200–208. [Google Scholar] [CrossRef] [Green Version]
- Pirk, R.; Rouleau, L.; Desmet, W.; Pluymers, B. Validating the modeling of sandwich structures with constrained layer damping using fractional derivative models. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1959–1972. [Google Scholar] [CrossRef]
- Fredette, L.; Singh, R. Estimation of the transient response of a tuned, fractionally damped elastomeric isolator. J. Sound Vib. 2016, 382, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Yan, G.; Benyahia, L.; Sahraoui, S. Fitting stress relaxation experiments with fractional Zener model to predict high frequency moduli of polymeric acoustic foams. Mech. Time-Depend. Mater. 2016, 20, 523–533. [Google Scholar] [CrossRef]
- Rouleau, L.; Deü, J.F.; Legay, A. A comparison of model reduction techniques based on modal projection for structures with frequency-dependent damping. Mech. Syst. Sig. Process. 2017, 90, 110–125. [Google Scholar] [CrossRef]
- Fredette, L.; Singh, R. High frequency, multi-axis dynamic stiffness analysis of a fractionally damped elastomeric isolator using continuous system theory. J. Sound Vib. 2017, 389, 468–483. [Google Scholar] [CrossRef]
- Kim, S.; Singh, R. A comparison between fractional-order and integer-order differential finite deformation viscoelastic models: Effects of filler content and loading rate on material parameters. Int. J. Appl. Mech. 2018, 10, 1850099. [Google Scholar] [CrossRef]
- Rouleau, L.; Legay, A.; Deü, J.F. Interface finite elements for the modelling of constrained viscoelastic layers. Compos. Struct. 2018, 204, 847–854. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L. A nonlinear constitutive model by spring, fractional derivative and modified bounding surface model to represent the amplitude, frequency and the magnetic dependency for magneto-sensitive rubber. J. Sound Vib. 2019, 438, 344–352. [Google Scholar] [CrossRef]
- Sahraoui, S.; Zekri, N. On fractional modeling of viscoelastic foams. Mech. Res. Commun. 2019, 96, 62–66. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L. Modeling and vibration control of a smart vibration isolation system based on magneto-sensitive rubber. Smart Mater. Struct. 2019, 28, 065026. [Google Scholar] [CrossRef]
- Freundlich, J. Transient vibrations of a fractional Kelvin–Voigt viscoelastic cantilever beam with a tip mass and subjected to a base excitation. J. Sound Vib. 2019, 438, 99–115. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L. A visco-elastic-plastic constitutive model of isotropic magneto-sensitive rubber with amplitude, frequency and magnetic dependency. Int. J. Plast. 2020, 132, 102756. [Google Scholar] [CrossRef]
- Henriques, I.R.; Rouleau, L.; Castello, D.A.; Borges, L.A.; Deü, J.F. Viscoelastic behavior of polymeric foams: Experiments and modeling. Mech. Mater. 2020, 148, 103506. [Google Scholar] [CrossRef]
- Kari, L. Dynamic stiffness of chemically and physically ageing rubber vibration isolators in the audible frequency range. Part 1: Constitutive equations. Contin. Mech. Thermodyn. 2017, 29, 1027–1046. [Google Scholar] [CrossRef] [Green Version]
- Kari, L. Dynamic stiffness of chemically and physically ageing rubber vibration isolators in the audible frequency range. Part 2: Waveguide solution. Contin. Mech. Thermodyn. 2017, 29, 1047–1059. [Google Scholar] [CrossRef] [Green Version]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef] [Green Version]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
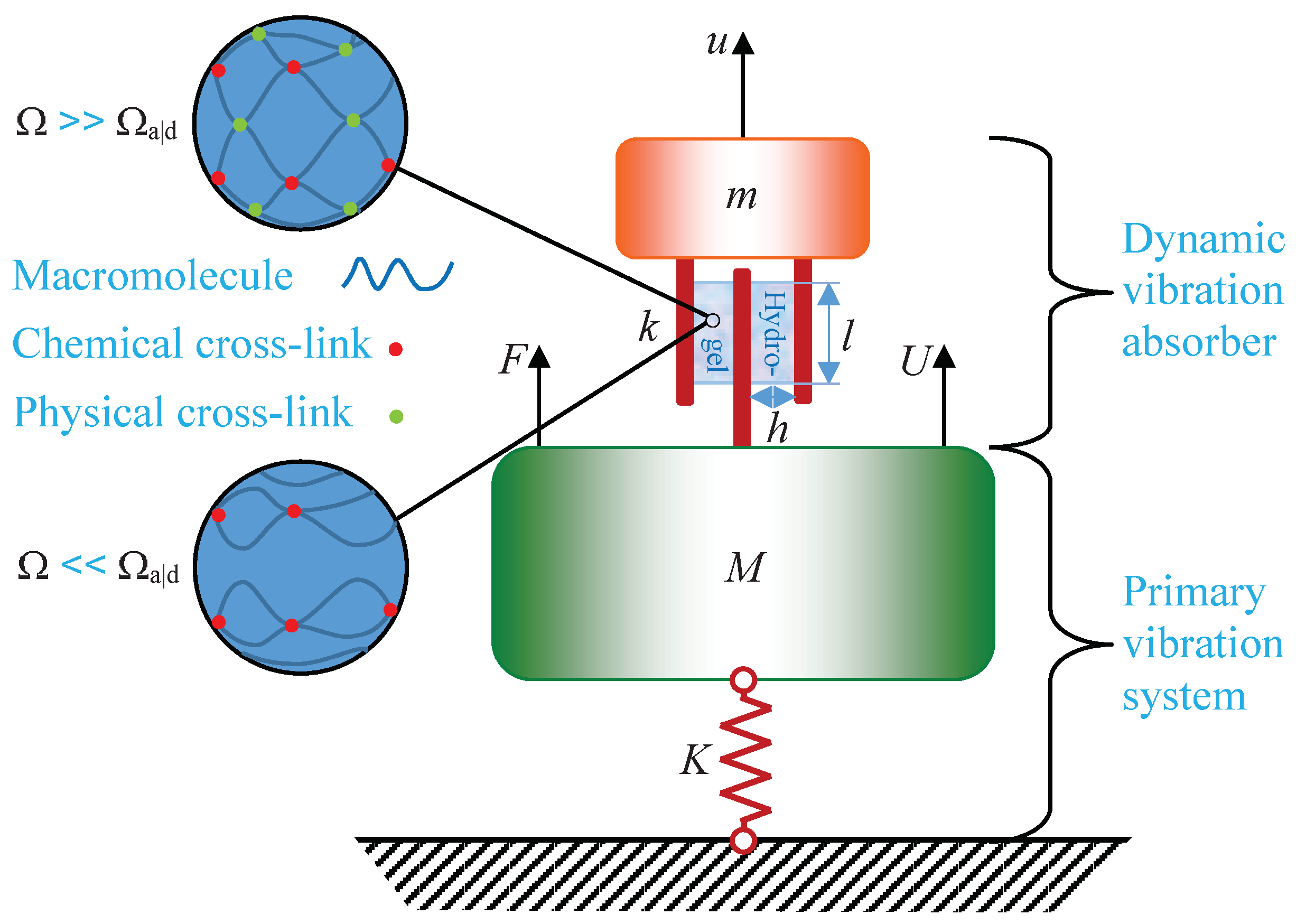
| 0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| △ | △ | △ | |||||||
| 0.5139 | 8.3062 | 9.3062 | 0.5527 | 9.1548 | 10.1548 | 0.5760 | 13.1228 | 14.1228 | |
| 0.6408 | 3.7198 | 4.7198 | 0.6661 | 3.9055 | 4.9055 | 0.6630 | 5.2817 | 6.2817 | |
| 0.7396 | 1.9690 | 2.9690 | 0.7554 | 2.0106 | 3.0106 | 0.7594 | 2.2679 | 3.2679 | |
| 0.8133 | 1.1520 | 2.1520 | 0.8224 | 1.1625 | 2.1625 | 0.8273 | 1.2207 | 2.2207 | |
| 0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| △ | △ | △ | |||||||
| 0.5141 | 8.2145 | 9.2145 | 0.5529 | 9.0587 | 10.0587 | 0.5762 | 13.0316 | 14.0316 | |
| 0.6418 | 3.6178 | 4.6178 | 0.6672 | 3.8005 | 4.8005 | 0.6639 | 5.1755 | 6.1755 | |
| 0.7423 | 1.8576 | 2.8576 | 0.7582 | 1.8975 | 2.8975 | 0.7620 | 2.1538 | 3.1538 | |
| 0.8184 | 1.0325 | 2.0325 | 0.8277 | 1.0422 | 2.0422 | 0.8325 | 1.0998 | 2.0998 | |
| Material | △ | Exponent Equation (9) | Equation (20) | |||
|---|---|---|---|---|---|---|
| Hydrogel from Table 2 | 0.6672 | 3.8005 | 4.8005 | 0.04 | 8.1488 | |
| Hydrogel full optimization | 0.7336 | 4.7051 | 0.04 | 8.1372 | ||
| NR rad/s | 0.9773 | 276 | 0 | |||
| NR rad/s | 0.9665 | 276 | 0 | |||
| NR rad/s | 0.9333 | 276 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kari, L. Are Single Polymer Network Hydrogels with Chemical and Physical Cross-Links a Promising Dynamic Vibration Absorber Material? A Simulation Model Inquiry. Materials 2020, 13, 5127. https://doi.org/10.3390/ma13225127
Kari L. Are Single Polymer Network Hydrogels with Chemical and Physical Cross-Links a Promising Dynamic Vibration Absorber Material? A Simulation Model Inquiry. Materials. 2020; 13(22):5127. https://doi.org/10.3390/ma13225127
Chicago/Turabian StyleKari, Leif. 2020. "Are Single Polymer Network Hydrogels with Chemical and Physical Cross-Links a Promising Dynamic Vibration Absorber Material? A Simulation Model Inquiry" Materials 13, no. 22: 5127. https://doi.org/10.3390/ma13225127