Effects of Multiple-Hole Baffle Arrangements on Flow Fields in a Five-Strand Asymmetric Tundish
Abstract
1. Introduction
2. Water Model Experiment
2.1. Experimental Principle
2.2. Experiment Instruments
3. Numerical Simulation
3.1. Governing Equations
3.2. Simulation Details
3.3. Validation of the Simulation Model
4. Results and Discussions
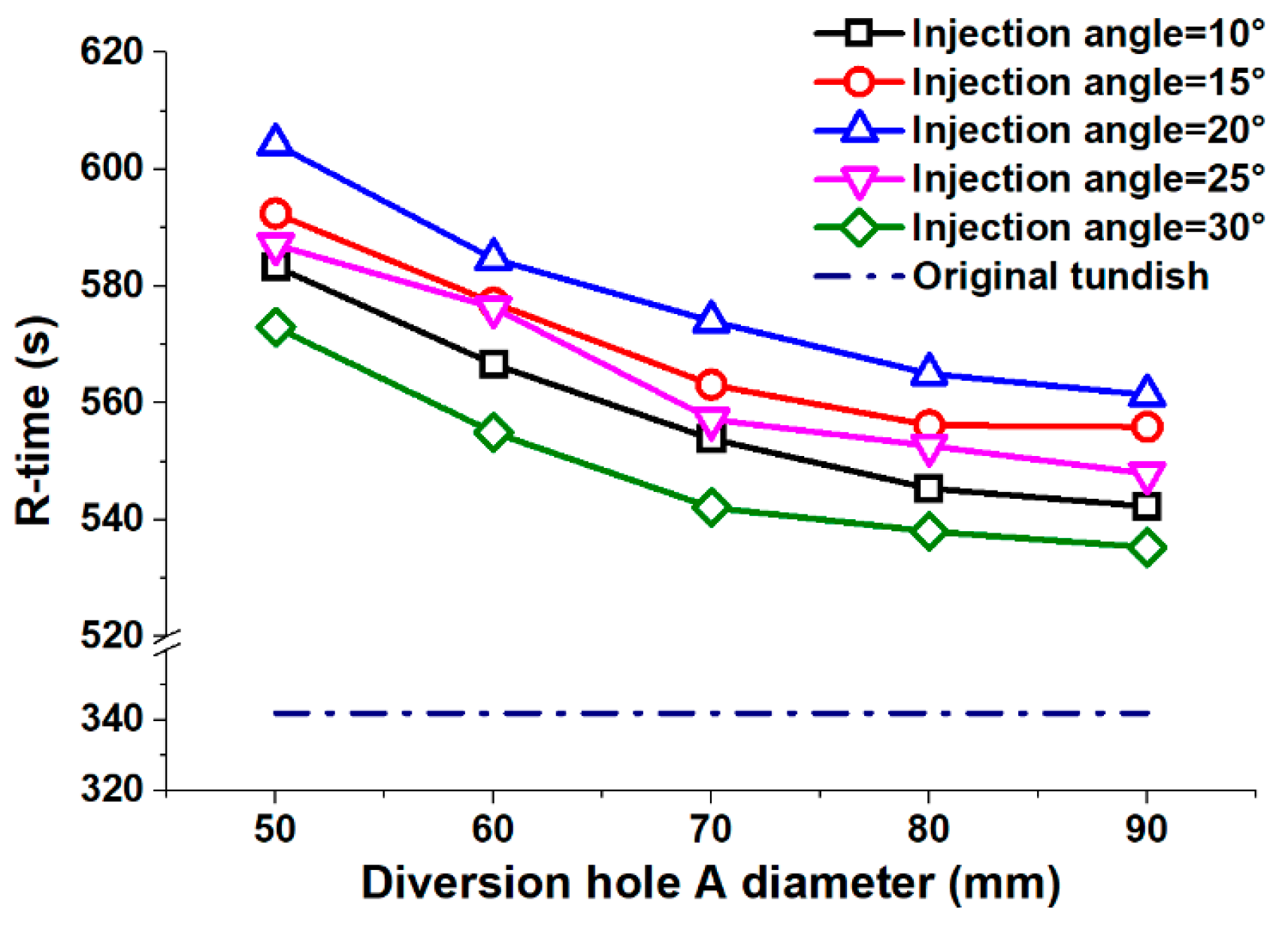
4.1. Average Residence Time Distributions
4.2. Residence Time Standard Deviation Distributions
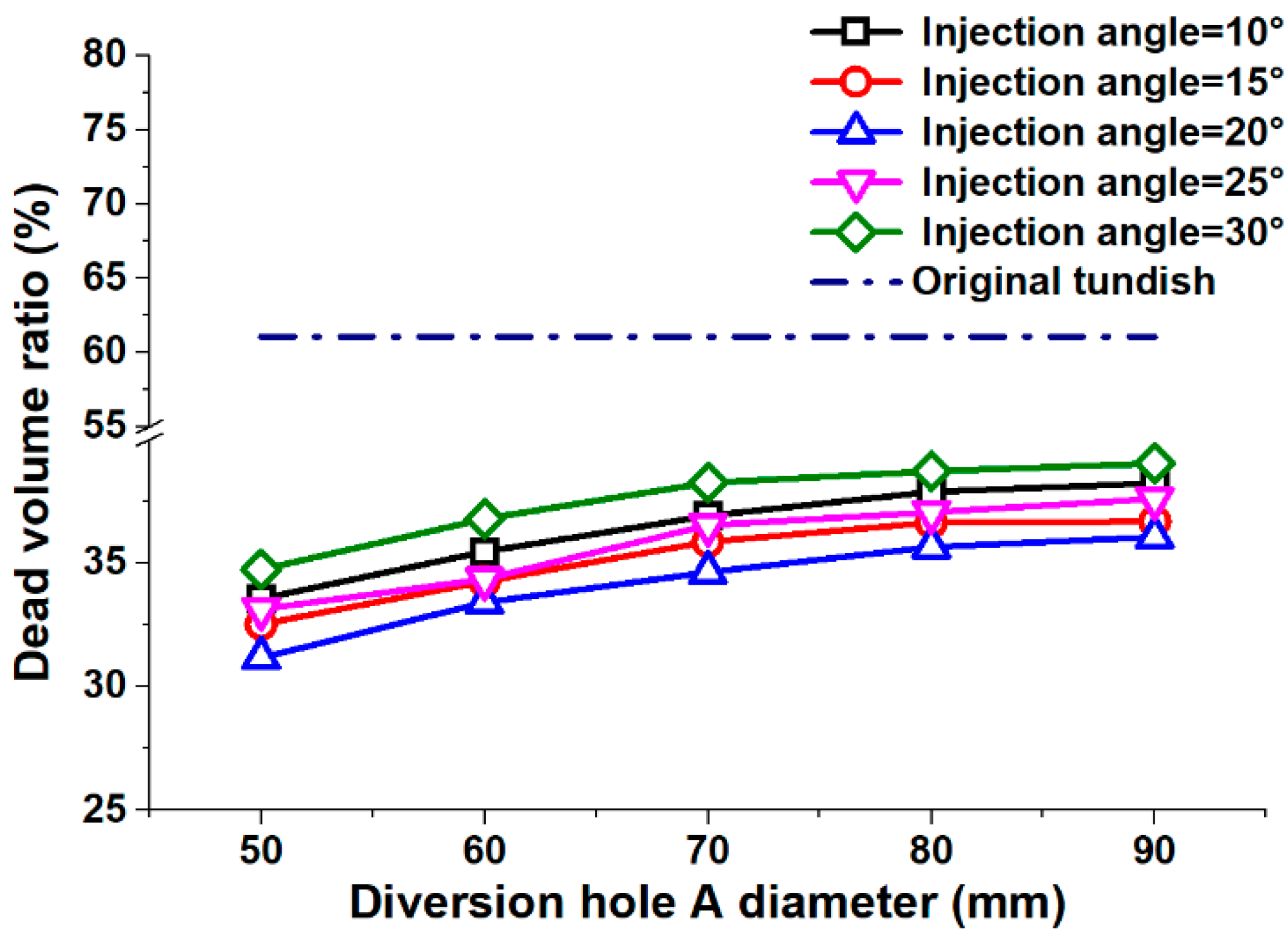
4.3. Dead Volume Distributions
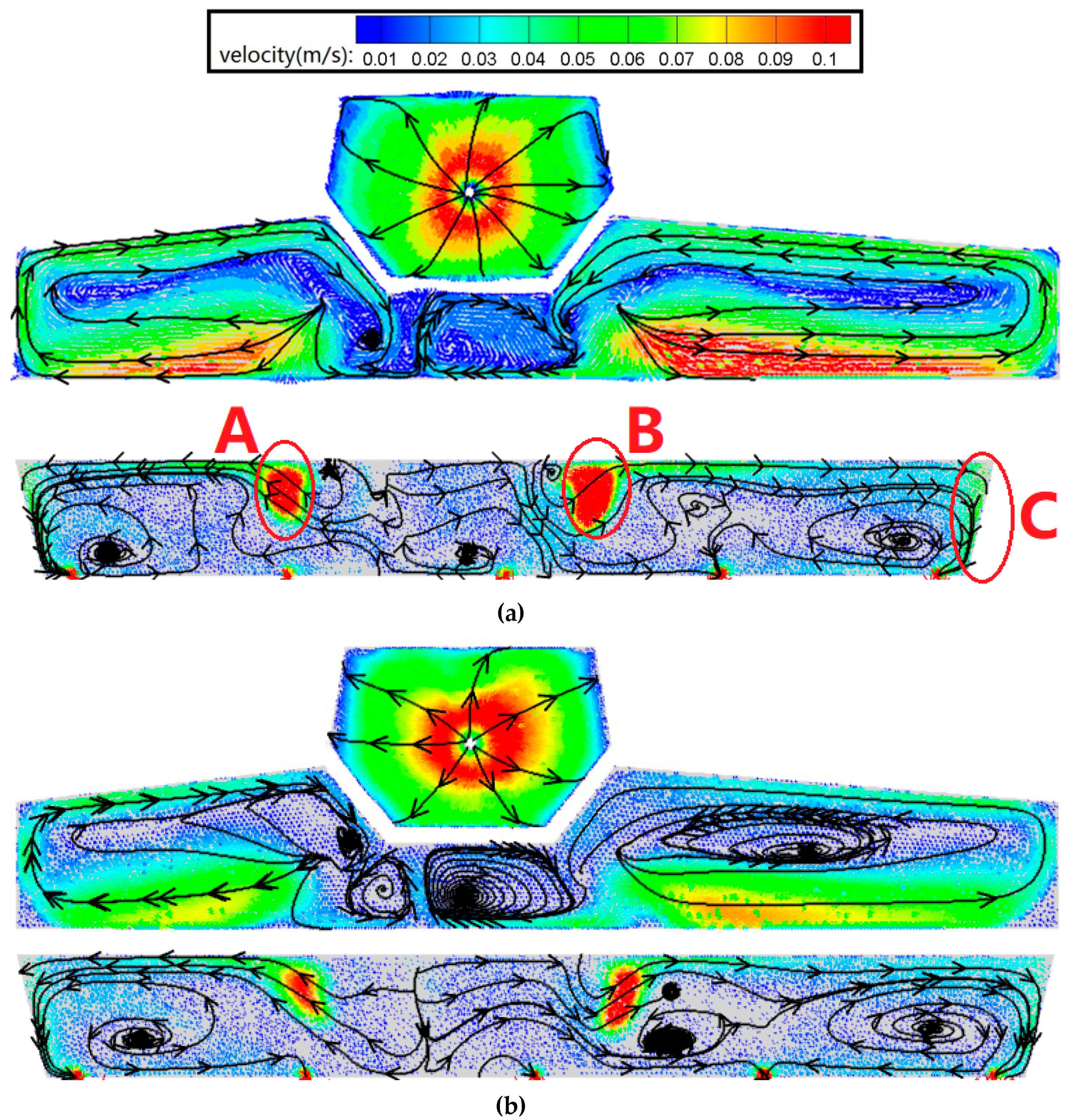
4.4. Velocity and Vector Distributions
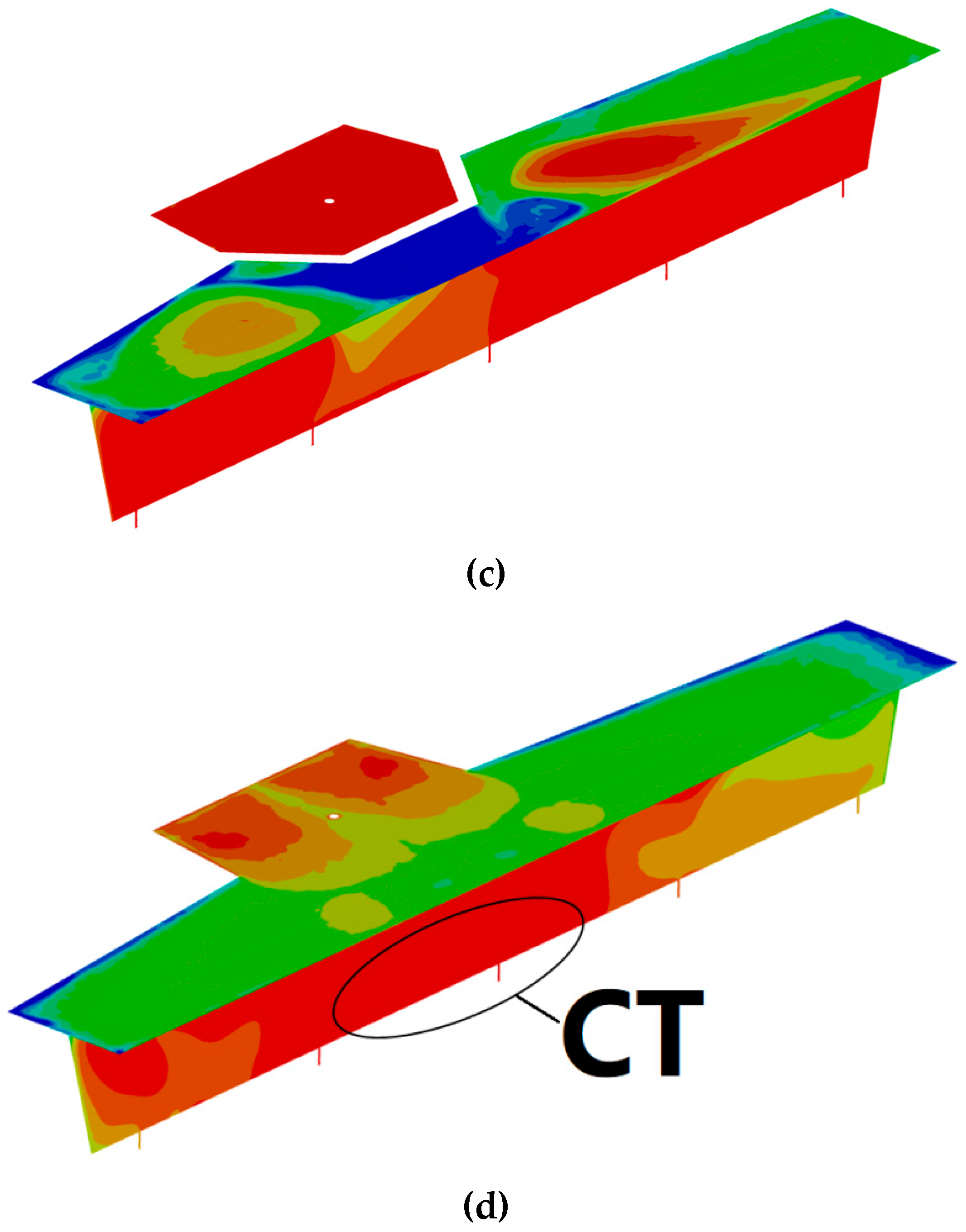
4.5. Static Temperature Distributions
4.6. Inclusion Removel Rate Distributions
5. Conclusions
- The average residence time reduced as the diameter of the diversion hole increased. However, the average standard deviation for each strand first increased and then decreased with an increase in the diversion hole diameter. With regard to the injection angle, both the average residence time and standard deviation first decreased and then increased as the injection angle increased.
- For the original tundish, the speed of the liquid steel at the bottom of the wall below the ladle shroud (region D) was much higher than it was in a tundish with a diversion hole arrangement. As a result, the liquid steel traversed two of the strands (#2 and #3), creating a bias phenomenon and leading to a lower residence time.
- The average temperature of the molten bath increased as the diameter of the diversion hole reduced. The average temperature in the original tundish was 1833.6 K, which was 1.8 K lower than the tundish using a diversion hole arrangement.
- The different-sized inclusion will be directed to the slag layer by the diversion wall and turbulence suppressor, resulting in a larger average IRR when using a diversion hole arrangement. As a result, the original tundish achieved the smallest average IRR of 46.8%, which was 10.7% lower than the overall IRR average for a tundish using a diversion hole arrangement.
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, J.; Xie, J.; Wang, B.; Lei, H.; Zhang, H.; Ni, H. Heat Transfer of Steel in a Slab Tundish with Vacuum Chambe. ISIJ Int. 2017, 57, 1037–1044. [Google Scholar] [CrossRef]
- Lopez-Ramirez, S.; Barreto, J.d.; Palafox-Ramos, J.; Morales, R.D.; Zacharias, D. Optimization of a Six-Strand Continuous Casting Tundish: Industrial Measurements and Numerical Investigation of the Tundish Modifications. Metall. Trans. B 2001, 32, 615–627. [Google Scholar]
- Cwudzinski, A. Investigation of Eccentric Open Eye Formation in a Slab Caster Tundish. Steel Res. Int. 2013, 85, 902–917. [Google Scholar]
- Ni, P.; Ersson, M.; Jonsson, L.T.I.; Jonsson, P.G. A Study on the Nonmetallic Inclusion Motions in a Swirling Flow Submerged Entry Nozzle in a New Cylindrical Tundish Design. Metall. Trans. B 2018, 49, 723–736. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D.; Qiu, S.; Zou, Z. Effect of Tunnel Filters on Flow Characteristics in an Eight-strand Tundish. ISIJ Int. 2017, 57, 1990–1999. [Google Scholar] [CrossRef]
- Chen, C.; Jonsson, L.T.I.; Tilliander, A.; Cheng, G.G.; Jonsson, P.G. A Mathematical Modeling Study of Tracer Mixing in a Continuous Casting Tundish. Metall. Trans. B 2015, 46, 169–190. [Google Scholar] [CrossRef]
- Chen, D.; Xie, X.; Long, M.; Zhang, M.; Zhang, L.; Liao, Q. Hydraulics and mathematics simulation on the weir and gas curtain in tundish of ultrathick slab continuous casting. Metall. Trans. B 2014, 45, 392–398. [Google Scholar] [CrossRef]
- Vargas-Zamora, A.; Morales, R.D.; Diaz-Cruz, M.; Palafox-Ramos, J.; Barreto-Sandoval, J.D. Inertial and buoyancy driven water flows under gas bubbling and thermal stratification conditions in a tundish model. Metall. Trans. B 2004, 35, 247–257. [Google Scholar] [CrossRef]
- Merder, T.; Warzecha, M. Optimization of a Six-Strand Continuous Casting Tundish:Industrial Measurements and Numerical Investigationof the Tundish Modifications. Metall. Trans. B 2012, 43, 856–868. [Google Scholar] [CrossRef]
- Chen, C.; Cheng, G.; Sun, H.; Hou, Z.; Wang, X.; Zhang, J. Effects of salt tracer amount, concentration and kind on the fluid flow behavior in a hydrodynamic model of continuous casting tundish. Steel Res. Int. 2012, 83, 1141–1151. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chattopadhyay, K. Transient steel quality under non-isothermal conditions in a multi-strand billet caster tundish: Part I. Analysis of fluid flow, thermal behaviour and inclusion behaviour. Ironmak. Steelmak. 2017, 44, 403–412. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Isac, M.; Guthrie, R.I.L. Effect of flow modifiers on liquid metal cleanliness in four-strand delta shaped billet caster tundish. Ironmak. Steelmak. 2012, 39, 454–462. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Zhang, Y.; Zhang, Y.; Ye, X.; Wang, B. Study of flow characteristics of tundish based on digital image velocimetry technique. Metall. Trans. B 2016, 47, 3144–3157. [Google Scholar] [CrossRef]
- He, F.; Wang, H.; Zhu, Z. Numerical Investigation of Effect of Casting Speed on Flow Characteristics of Molten Steel in Multistrand Tundish. ISIJ Int. 2019, 59, 1250–1258. [Google Scholar] [CrossRef]
- Sarkar, S.; Sambasivam, R.; Ajmani, S.K.; Denys, M.B. Numerical analysis of unsteady hydrodynamics and thermal transport in five-strand asymmetric tundish. Ironmak. Steelmak. 2012, 39, 540–549. [Google Scholar] [CrossRef]
- Ramirez, O.S.D.; Torres, E.A.; Banderas, J.A.R. Thermal and Fluid-Dynamic Optimization of a Five Strand Asymmetric Delta Shaped Billet Caster Tundish. Steel Res. Int. 2018, 89, 1–10. [Google Scholar]
- Koria, C.; Singh, S. Physical modeling of the effects of the flow modifier on the dynamics of molten steel flowing in a tundish satish. ISIJ Int. 1994, 34, 784–793. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Isac, M.; Ian, R.; Guthrie, L. Modelling of non-isothermal melt flows in a four strand delta shaped billet caster tundish validated by water model experiments. ISIJ Int. 2012, 52, 2026–2035. [Google Scholar] [CrossRef]
- Jones, W.; Launder, B. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transfer. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Yakhot, V.; Spalding, D.B. Lectures in Mathematical Model of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Henkes, R.A.W.M.; van der Flugt, F.F.; Hoogendoorn, C.J. A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure. Int. J. Heat Mass Transfer. 1991, 34, 1543–1557. [Google Scholar]
- Rogler, J.; Heaslip, L.; Mehrvar, M. Physical modelling of inclusion removal in a tundish by gas bubbling. Can. Metall. Q. 2005, 44, 357–368. [Google Scholar] [CrossRef]
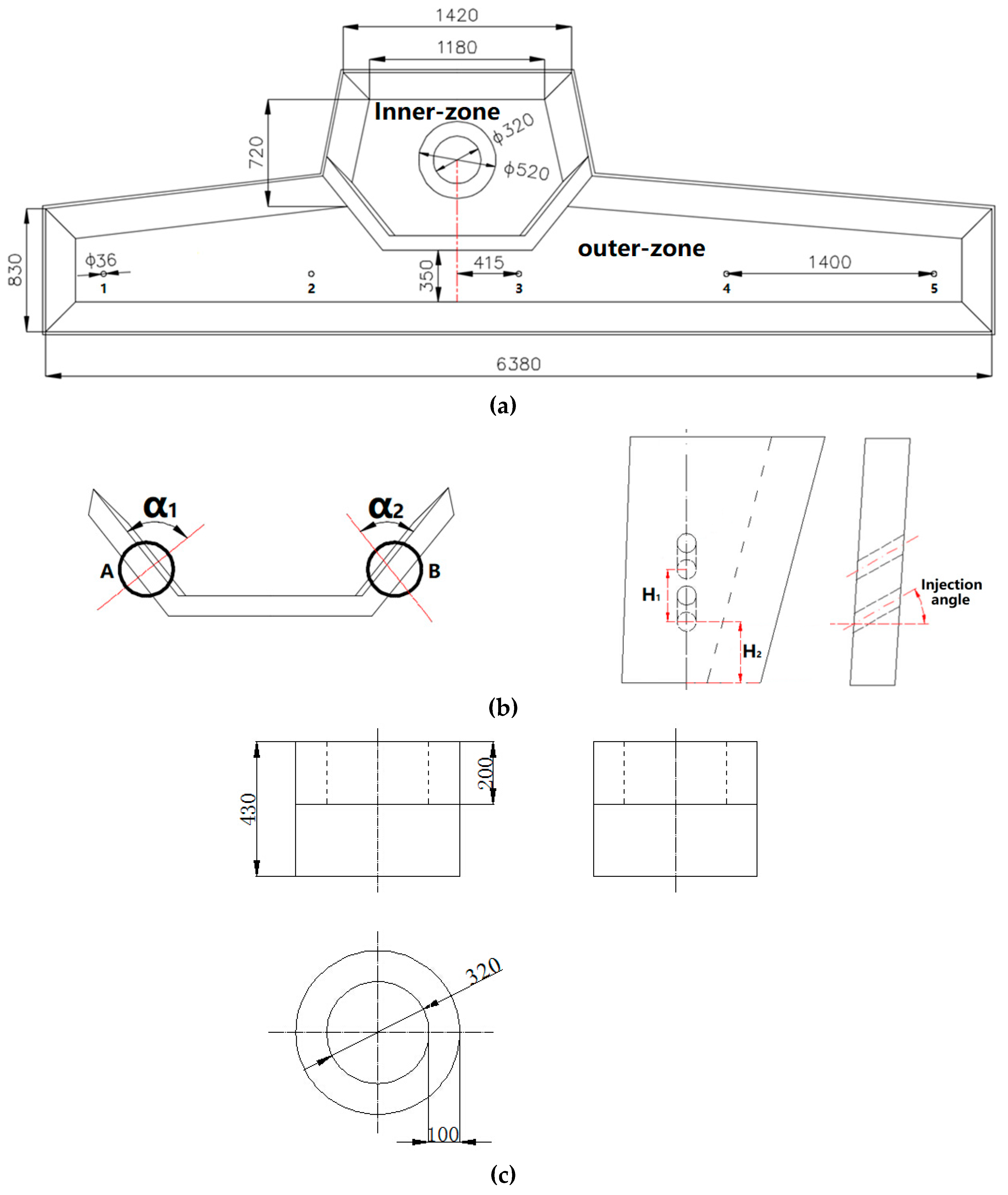
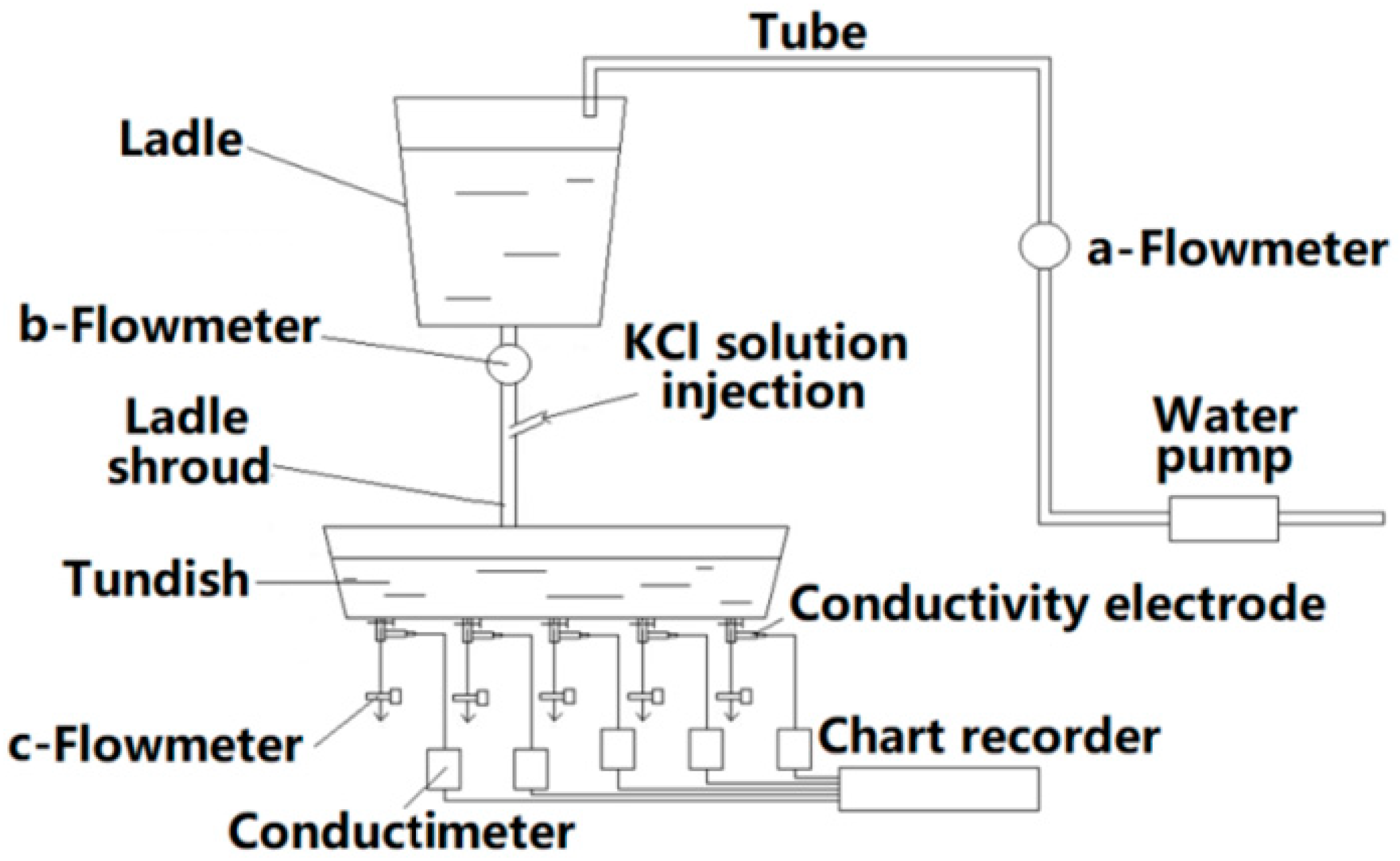

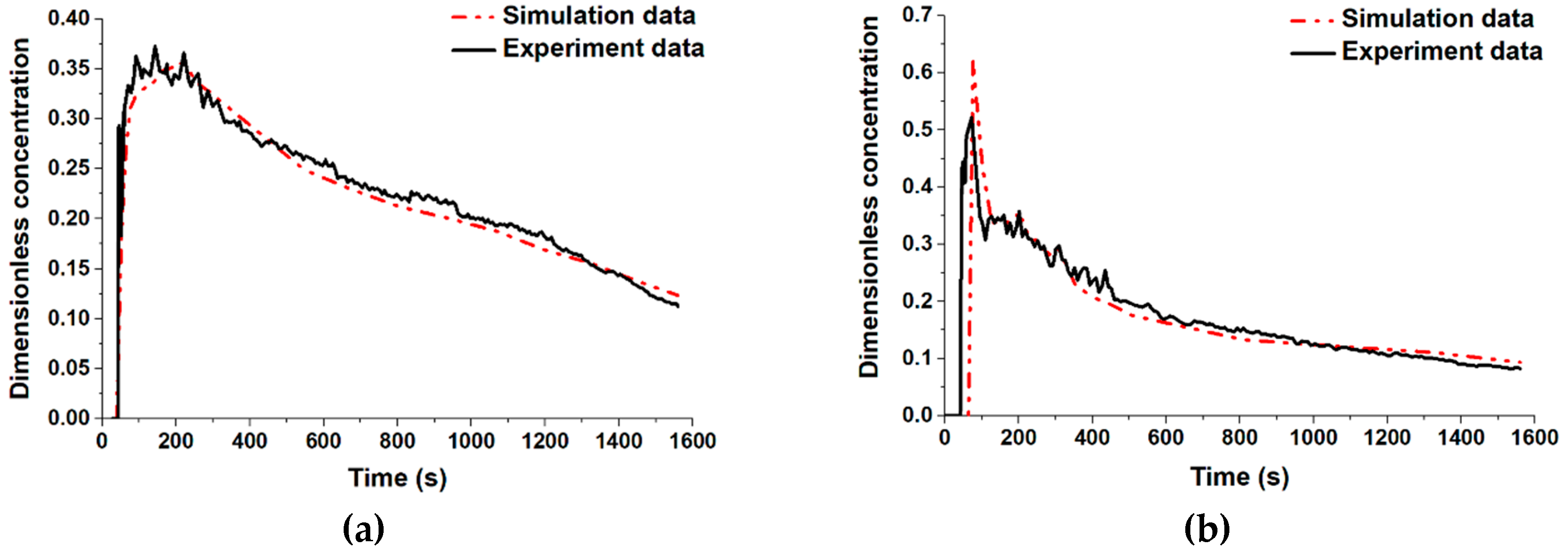




| Parameter | Prototype | Model |
|---|---|---|
| Flow rate (m3/h) | 16.5 | 1.058 |
| Depth of the liquid steel (mm) | 750 | 250 |
| Ladle shroud diameter (mm) | 55 | 18.3 |
| Immersion depth of Ladle Shroud diameter (mm) | 180 | 60 |
| α1 and α2 (°) | 15 | 15 |
| Injection angle (°) | 10, 15, 20, 25 and 30 | 10, 15, 20, 25 and 30 |
| A diversion hole diameter (mm) | 50, 60, 70, 80 and 90 | 16.7, 20.0, 23.3, 26.7 and 30.0 |
| B diversion hole diameter (mm) | 65, 75, 85, 95 and 105 | 21.7, 25.0, 28.3, 31.7 and 35.0 |
| H1/H2 (mm) | 150/200 | 50.0/66.7 |
| Material/Interphase | Density (kg/m3) | Viscosity (kg/m·s) | Cp (J/kg·K) | Thermal Conductivity (W/m·K) | Surface Tension (N/m) |
|---|---|---|---|---|---|
| Steel | 7010 | 0.0061 | 755 | 41 | — |
| Slag | 2650 | 0.34 | 875 | 8.1 | — |
| Air | 1.225 | 1.789·10−5 | 1006 | 0.0242 | — |
| Steel-slag | — | — | — | — | 0.12 |
| Air-steel | — | — | — | — | 1.60 |
| Air-slag | — | — | — | — | 1.40 |
| Label | 50 mm−20° | 60 mm−20° | 70 mm−20° | 80 mm−20° | 90 mm−20° | Original Tundish | |
|---|---|---|---|---|---|---|---|
| Average Temperature (K) | Molten bath | 1835.8 | 1835.7 | 1835.5 | 1835.2 | 1835.0 | 1833.6 |
| Surface of the molten steel | 1833.1 | 1832.8 | 1832.5 | 1831.8 | 1831.5 | 1830.2 | |
| Bottom of the molten steel | 1836.4 | 1836.3 | 1836.1 | 1836.0 | 1835.8 | 1834.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Liu, F.; Zhu, R.; Zhu, J. Effects of Multiple-Hole Baffle Arrangements on Flow Fields in a Five-Strand Asymmetric Tundish. Materials 2020, 13, 5129. https://doi.org/10.3390/ma13225129
Zhang B, Liu F, Zhu R, Zhu J. Effects of Multiple-Hole Baffle Arrangements on Flow Fields in a Five-Strand Asymmetric Tundish. Materials. 2020; 13(22):5129. https://doi.org/10.3390/ma13225129
Chicago/Turabian StyleZhang, Binglong, Fuhai Liu, Rong Zhu, and Jinfeng Zhu. 2020. "Effects of Multiple-Hole Baffle Arrangements on Flow Fields in a Five-Strand Asymmetric Tundish" Materials 13, no. 22: 5129. https://doi.org/10.3390/ma13225129
APA StyleZhang, B., Liu, F., Zhu, R., & Zhu, J. (2020). Effects of Multiple-Hole Baffle Arrangements on Flow Fields in a Five-Strand Asymmetric Tundish. Materials, 13(22), 5129. https://doi.org/10.3390/ma13225129




