Dynamic Mechanical Analysis Investigations of PLA-Based Renewable Materials: How Are They Useful?
Abstract
:1. Introduction
2. Poly(Lactic Acid) (PLA)—General Outlook
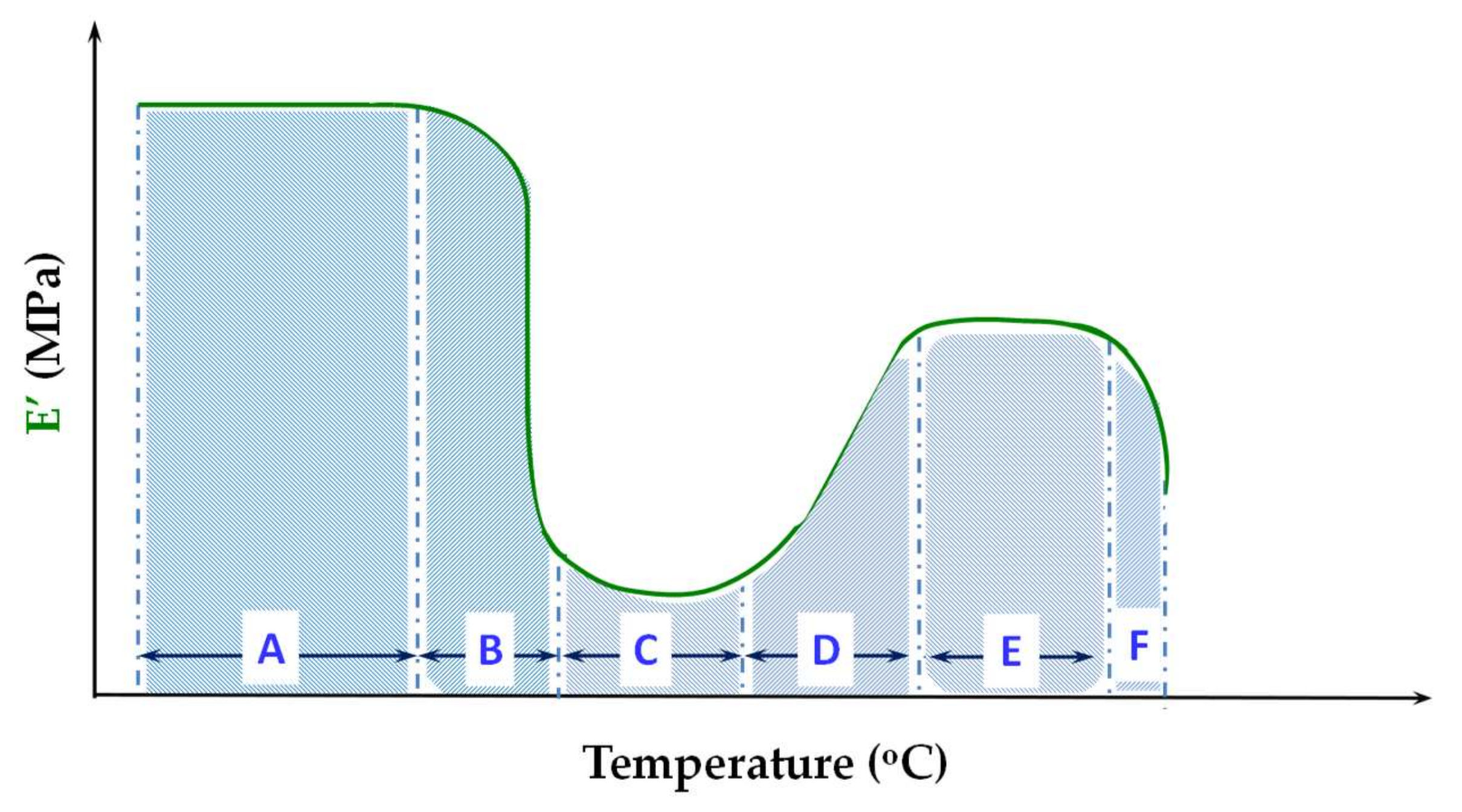
3. Dynamic Mechanical Analysis—Basics and Rationale of Its Usefulness for PLA
4. Dynamic Mechanical Analysis—The Unique Viscoelastic Behavior of PLA
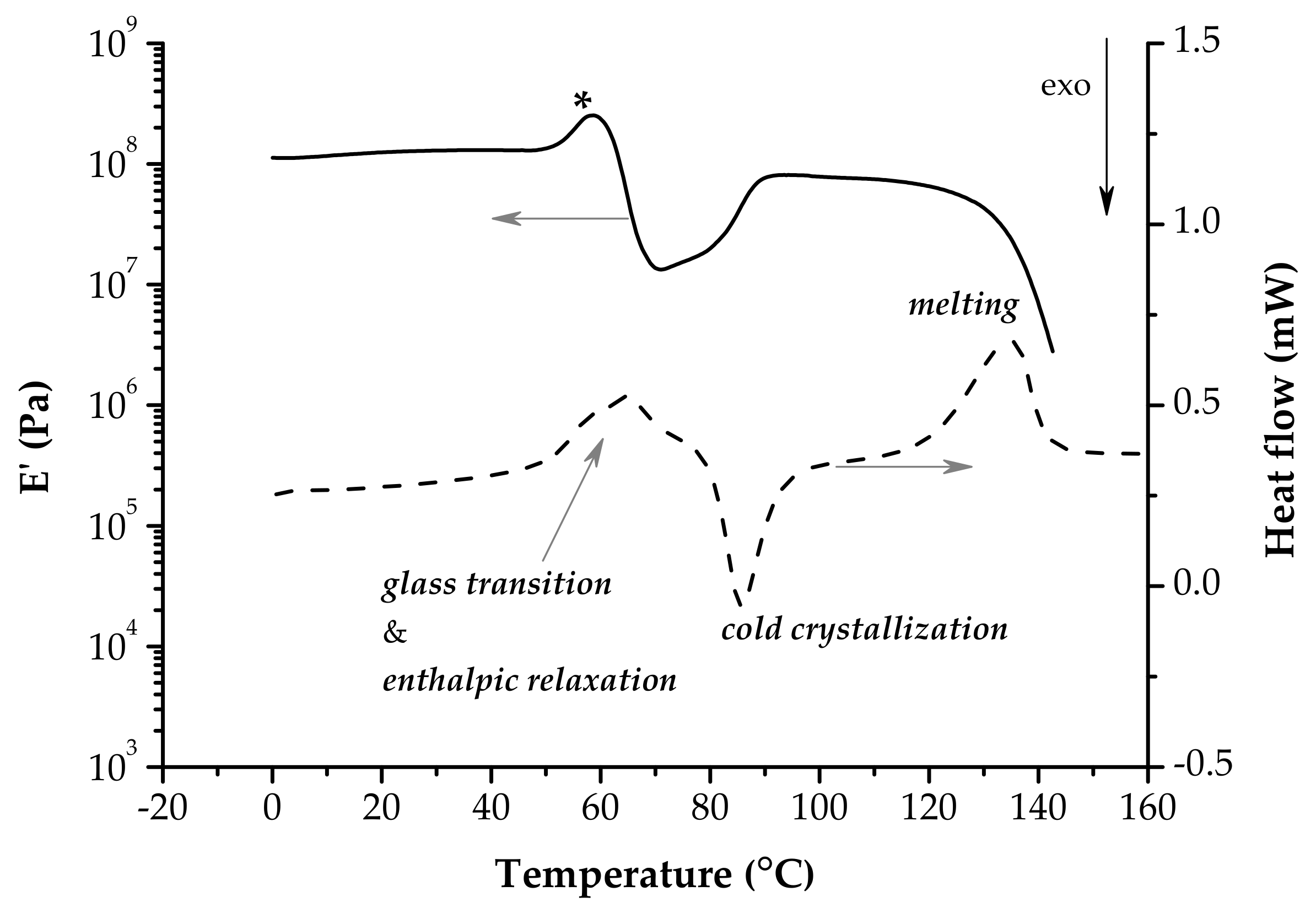
4.1. The Glassy Region
4.2. The Glass Transition Region
4.3. The Cold-Crystallization Region
4.4. The Melting Region
5. Conclusions
- In the glassy region (T < Tg) the secondary relaxations are incidentally mentioned at −50 °C or lower. The β-relaxation was evidenced as a faint drop of E’ modulus or a shallow tan δ peak. Because of the brittleness of PLA, the DMA device is not able to perform reliable experiments at negative temperatures on samples that have a propensity toward cracking.
- When dealing with PLA, the glassy region means also room temperature condition. Therefore, the DMA investigations allow the determination of the elastic modulus E’ under usual working conditions.
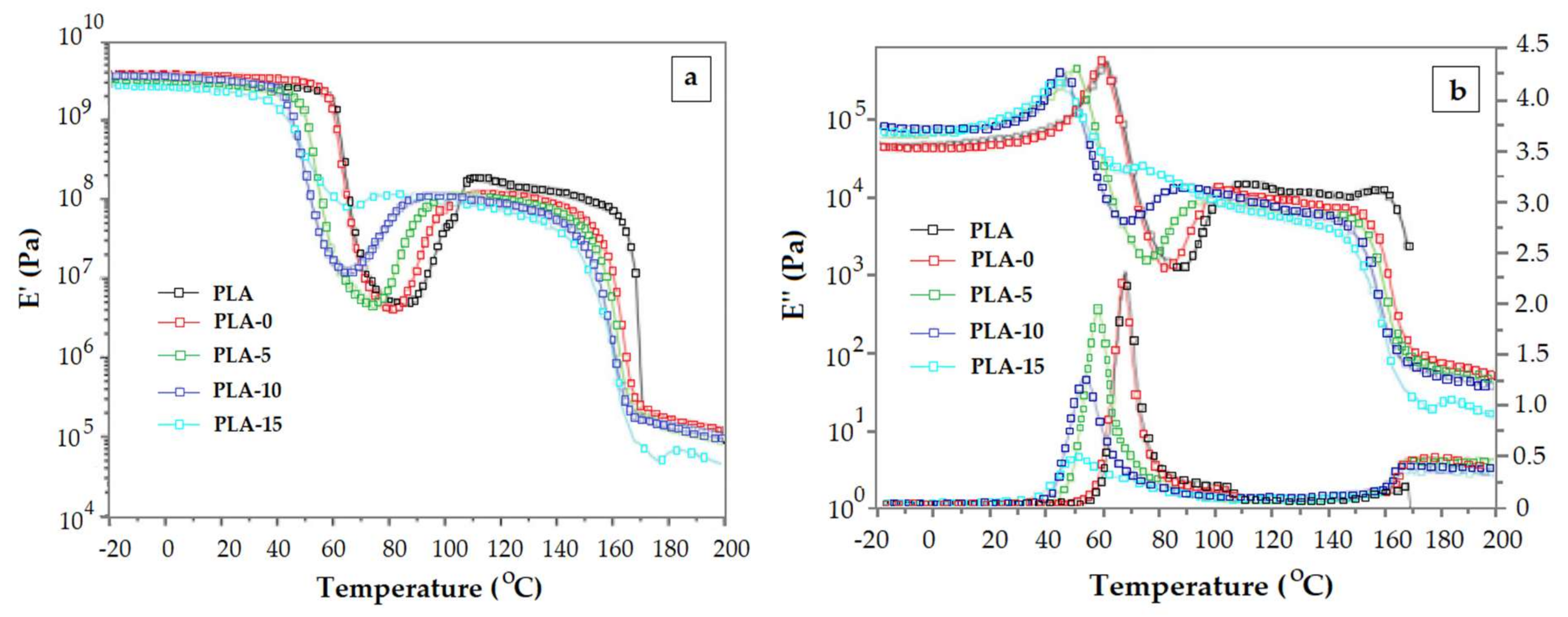
- The effects that are noticed in the glassy region during composition-dependent studies are reported also for other classes of polymer. The particularity comes from the semicrystalline character of PLA. The processing conditions, the nature and the content of stereoisomers determine decisively the morphology of PLA in terms of crystallinity. Crystalline content can be tuned during the processing stage, inducing an envisaged change of the E’ modulus.
- By far the most challenging zone is the glass transition region. The chain mobility may be influenced, besides the temperature, by the history of the polymer (aging phenomena) and the applied stress/strain that can induce orientation effects.
- Typically, the glass transition temperature is considered to be the onset of E’ drop or the peaks of E’’ or tan δ. These indicators are often ambiguous in the situation of PLA because of overlapping phenomena that happen during the glass transition. The synergism of enthalpic relaxation, coordinated molecular movements and orientation/crystallization phenomena makes the determination of Tg by DMA fraught with difficulties.
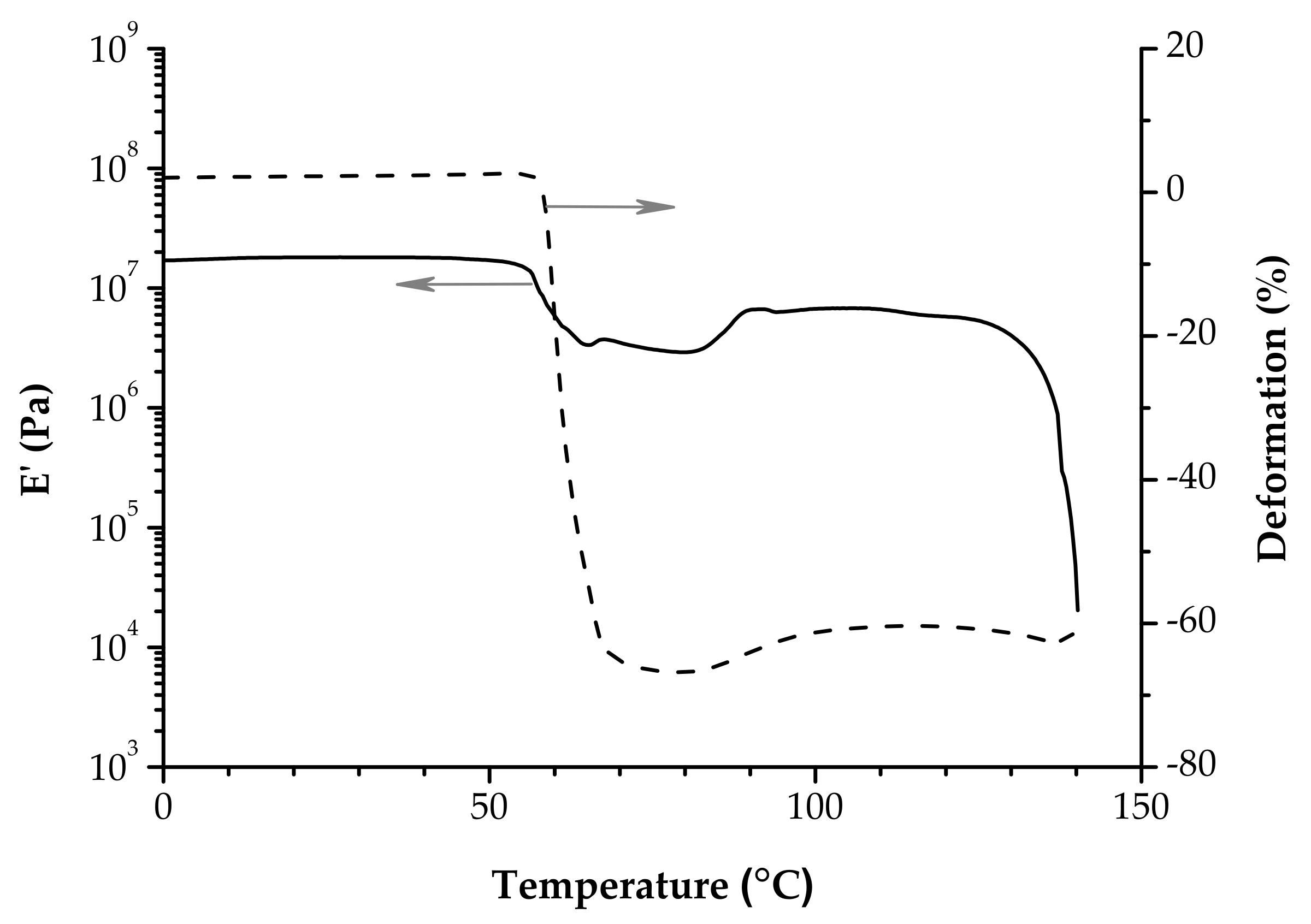
- The E’ onset is often hidden by a hump that could appear just at the beginning of the glass transition on the E’ vs. T plot, because of enthalpic relaxation. As a result, contraction of the samples is obvious when the DMA experiment is performed under tension loading.
- The peaks of E’’ and tan δ for PLA are also deformed as compared to those of a well-behaved polymer that records during the glass transition only the coordinated movements of chain segments.
- The E’’ peak appears very sharp. This E’’ shape accounts for an instantaneous break of mobility growth due to refolding of polymer chains (shrinking).
- The tan δ peak is at least bimodal, its descending side is less abrupt, larger than the ascending side, and it may span partially the first rubbery plateau and the cold crystallization region. This is consistent with few underlying processes. Therefore, under the simultaneous action of temperature and force, orientation/crystallization phenomena are triggered even during the glass transition.
- The increase of crystalline content does not entail necessarily the increase of the glass transition temperature. From a certain level of the crystalline content upward, the values of the glass transition temperature decrease with the crystalline content. These results should be discussed in terms of cooperatively rearranging regions (rigid amorphous phase and mobile amorphous phase).
- The increased toughness that is obtained by adding a plasticizer is reflected in a lower Tg, but very often the height of tan δ peak monitored during the glass transition region decreases with the toughener quantity. Similarly, a reinforcement agent augments the E’ modulus. However, an opposite effect is reflected in the height of tan δ, i.e., it may increase as more reinforcement is included in the DMA. These patterns are consistent with the effects of already mentioned overlapping phenomena happening during the glass transition (enthalpic relaxation, shrinking, orientation/crystallization).
- The length of the first rubbery plateau depends on the PLA molecular weight. It can be considered as a gauge for the PLA level degradation in decomposition studies.
- In the presence of efficient plasticizers the first rubbery plateau is absent because the cold crystallization begins during or immediately the glass transition region.
- The cold crystallization is evidenced by a sudden increase of E’ modulus. When it follows the glass transition region (the first rubbery plateau is absent), the E’ vs. T plot has a V-shape.
- There are instances where the cold-crystallization is not encompassed by the extended tan δ descending side. It can appear as a separate, smaller, frequency-independent peak.
- The E’ value of the second rubbery plateau is lower than that of the glassy region; however it is stable until the abrupt decrease at melting.
- With regard to the heating rate, it is evident that its value is meaningful firstly for the point of view of DMA investigation accuracy. Then, the kinetic events that might take place as the temperature is raised require time for completion. Heating rates higher than 2–3 °C/min are not adequate for fulfillment of both conditions.
Author Contributions
Funding
Conflicts of Interest
References
- Tolinski, M. Plastics and Sustainability: Towards a Peaceful Coexistence between Bio-based and Fossil Fuel-Based Plastics; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 1–30. [Google Scholar]
- Haider, T.P.; Völker, C.; Kramm, J.; Landfester, K.; Wurm, F. Plastics of the future? The impact of biodegradable polymers on the environment and on society. Angew. Chem. Int. Ed. 2019, 58, 50–62. [Google Scholar] [CrossRef] [Green Version]
- Lamontagne, N.D. Putting the bio in bio-based plastics: The latest in sustainable materials. Plast. Eng. 2018, 74, 26–29. [Google Scholar] [CrossRef]
- Nampoothiri, K.M.; Nair, N.R.; John, R.P. An overview of the recent developments in polylactide (PLA) research. Bioresour. Technol. 2010, 101, 8493–8501. [Google Scholar] [CrossRef]
- Basu, A.; Langer, R.; Domb, A.J. Special issue: Polylactide (PLA) based polymers. Adv. Drug Deliv. Rev. 2016, 107, 1–2. [Google Scholar]
- Hamad, K.; Kaseem, M.; Ayyoob, M.; Joo, J.; Deri, F. Polylactic acid blends: The future of green, light and tough. Prog. Polym. Sci. 2018, 85, 83–127. [Google Scholar] [CrossRef]
- Kaseem, M. Poly(Lactic Acid) composites. Materials 2019, 12, 3586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bogaert, J.-C.; Coszach, P. Poly(lactic acids): A potential solution to plastic waste dilemma. Macromol. Symp. 2000, 153, 287–303. [Google Scholar] [CrossRef]
- Tyler, B.; Gullotti, D.; Mangraviti, A.; Utsuki, T.; Brem, H. Polylactic acid (PLA) controlled delivery carriers for biomedical applications. Adv. Drug Deliv. Rev. 2016, 107, 163–175. [Google Scholar] [CrossRef]
- Musiol, M.; Sikorska, W.; Adamus, G.; Janeczek, H.; Richert, J.; Malinowski, R.; Jiang, G.Z.; Kowalczuk, M. Forensic engineering of advanced polymeric materials. Part III—Biodegradation of thermoformed rigid PLA packaging under industrial composting conditions. Waste Manag. 2016, 52, 69–76. [Google Scholar] [CrossRef] [Green Version]
- Vasile, C.; Pamfil, D.; Rapa, M.; Darie-Nita, R.N.; Mitelut, A.C.; Popa, E.E.; Popescu, P.A.; Draghici, M.C.; Popa, M.E. Study of soil burial degradation of some PLA/CS biocomposites. Compos. Part B Eng. 2018, 142, 251–262. [Google Scholar] [CrossRef]
- Spiridon, I.; Darie Nita, R.N.; Kozlowski, M.; Nechita, A.; Ursu, R.G. Influence of accelerated weathering on the performance of polylactic acid based materials. Cell. Chem. Technol. 2016, 50, 629–635. [Google Scholar]
- Anderson, K.S.; Schreck, K.M.; Hillmyer, M.A. Toughening polylactide. Polym. Rev. 2008, 48, 85–108. [Google Scholar] [CrossRef]
- Sperling, L.H. Introduction to Physical Polymer Science, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 349–375. [Google Scholar]
- Garlotta, D. A literature review of poly(lactic acid). J. Polym Environ. 2001, 9, 63–84. [Google Scholar] [CrossRef]
- Södergård, A.; Stolt, M. Properties of lactic acid based polymers and their correlation with composition. Prog. Polym. Sci. 2002, 27, 1123–1163. [Google Scholar] [CrossRef]
- Petrula, J.; Slomkowski, S.; Penczek, S. Polylactides—Methods of synthesis and characterization. Adv. Drug Deliv. Rev. 2016, 107, 3–16. [Google Scholar]
- Jin, F.-L.; Hu, R.-R.; Park, S.-J. Improvement of thermal behaviors of biodegradable poly(lactic acid) polymer: A review. Compos. B Eng. 2019, 164, 287–296. [Google Scholar] [CrossRef]
- Sin, L.T.; Tueen, B.S. Polylactic Acid. A Practical Guide for the Processing, Manufacturing and Applications of PLA, 2nd ed.; Plastics Design Library, William Andrew Publishing: Chadds Ford, PA, USA, 2019; pp. 53–95. [Google Scholar]
- Saeidlou, S.; Huneault, M.A.; Hongbo, L.; Chul, B.P. Poly(lactic acid) crystallization. Prog. Polym. Sci. 2012, 37, 1657–1677. [Google Scholar] [CrossRef]
- Jiang, L.; Shen, T.; Xu, P.; Zhao, X.; LI, X.; Dong, W.; Ma, P.; Chen, M. Crystallization modification of poly(lactide) by using nucleating agents and stereocomplexation. e-Polymers 2016, 16, 1–13. [Google Scholar] [CrossRef]
- Gonzáles-López, M.E.; Del Campo, A.S.M.; Robledo-Ortíz, J.R.; Arellano, M.; Pérez-Fonseca, A.A. Accelerated weathering of poly(lactic acid) and its biocomposites: A review. Polym. Degrad. Stab. 2020, 179, 109290. [Google Scholar] [CrossRef]
- Murariu, M.; Dubois, P. PLA composites: From production to properties. Adv. Drug Deliv. Rev. 2016, 107, 17–46. [Google Scholar] [CrossRef]
- Kaseem, M.; Hamad, K.; Rehman, Z.U. Review of recent advances in polylactic acid/TiO2 composites. Materials 2019, 12, 3659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, S.; Kopitzky, R.; Tolga, S.; Kabasci, S. Polylactide (PLA) and its blends with poly(butylene succinate) (PBS): A brief review. Polymers 2019, 11, 1193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Auras, R.; Harte, B.; Selke, S. An overview of polylactides as packaging materials. Macromol. Biosci. 2004, 4, 835–864. [Google Scholar] [CrossRef]
- Hamad, K.; Kaseem, M.; Yang, H.W.; Deri, F.; Ko, Y.G. Properties and medical applications of polylactic acid: A review. EXPRESS Polym. Let. 2015, 9, 435–455. [Google Scholar] [CrossRef]
- Saini, P.; Arora, M.; Ravi Kumar, M.N.V. Poly(lactic acid) blends in biomedical applications. Adv. Drug Deliv. Rev. 2016, 107, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Auras, R. Poly(lactic acid). In Encyclopedia of Polymer Science and Technology, 4th ed.; Mark, H.F., Ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 1–10. [Google Scholar]
- Bigg, D.M. Polylactide copolymers: Effect of copolymer ratio and end capping on their properties. Adv. Polym. Tech. 2005, 24, 69–82. [Google Scholar] [CrossRef]
- Tabi, T. The application of the synergistic effect between the crystal structure of poly(lactic acid) (PLA) and the presence of ethylene vinyl acetate copolymer (EVA) to produce highly ductile PLA/EVA blends. J. Therm. Anal. Calorim. 2019, 138, 1287–1297. [Google Scholar] [CrossRef] [Green Version]
- Picciochi, R.; Wang, Y.; Alves, N.A.; Mano, J.F. Glass transition of semi-crystalline PLLA with different morphologies as studied by dynamic mechanical analysis. Colloid Polym. Sci. 2007, 285, 575–580. [Google Scholar] [CrossRef] [Green Version]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications – A comprehensive review. Adv. Drug Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Deng, C.; Hong, R.; Fu, Q.; Zhang, J. Effect of thermal annealing on crystal and properties of PLLA/PCL blend. J. Polym. Res. 2020, 27, 221. [Google Scholar] [CrossRef]
- Tabi, T.; Sajo, I.E.; Szabo, F.; Luyt, A.S.; Kovacs, J.G. Crystalline structure of annealed polylactic acid and its relation to processing. Express Polym. Lett. 2010, 4, 659–668. [Google Scholar] [CrossRef]
- Bubeck, R.A.; Merrington, A.; Dumitrascu, A.; Smith, P.B. Thermal analyses of poly(lactic acid) PLA and micro-ground paper blends. J. Therm. Anal. Calorim. 2018, 131, 309–316. [Google Scholar] [CrossRef]
- Kong, W.; Tong, B.; Ye, A.; Ma, R.; Gou, J.; Wang, Y.; Liu, C.; Shen, C. Crystallization behavior and mechanical properties of poly(lactic acid)/polyethylene oxide) blends nucleated by a self-assembly nucleator. J. Therm. Anal. Calorim. 2019, 135, 3107–3114. [Google Scholar] [CrossRef]
- Petchwattana, N.; Sanetuntikul, J.; Narupai, B. Plasticization of biodegradable poly(lactic acid) by different triglyceride molecular sizes: A comparative study with glycerol. J. Polym. Environ. 2018, 26, 1160–1168. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, J.; Wolcott, M.P. Comparison of polylactide/nano-sized calcium carbonate and polylactide/montmorillonite composites: Reinforcing effects and toughening mechanisms. Polymer 2007, 48, 7632–7644. [Google Scholar] [CrossRef]
- Li, H.; Huneault, M.A. Effect of nucleation and plasticization on the crystallization of poly(lactic acid). Polymer 2007, 48, 6855–6866. [Google Scholar] [CrossRef] [Green Version]
- Rapa, M.; Darie-Nita, R.N.; Vasile, C. Influence of plasticizers over some physic-chemical properties of PLA. Mater. Plast. 2017, 54, 73–78. [Google Scholar] [CrossRef]
- Piorkowska, E.; Kulinski, Z.; Galeski, A.; Masirek, R. Plasticization of semicrystalline poly(l-lactide) with poly(propylene glycol). Polymer 2006, 47, 7178–7188. [Google Scholar] [CrossRef]
- Chartoff, P.R.; Menczel, J.D.; Dillman, S.H. Dynamic mechanical analysis. In Thermal Analysis of Polymers. Fundamentals and Applications; Menczel, J.D., Prime, R.B., Eds.; Jonn Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 387–495. [Google Scholar]
- Menard, K.P.; Menard, N.R. Dynamic mechanical analysis in the analysis of polymers and rubbers. In Encyclopedia of Polymer Science and Technology, 4th ed.; Mark, H.F., Ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–33. [Google Scholar]
- Wunderlich, B. Thermal Analysis of Polymeric Materials; Springer: Berlin/Heidelberg, Germany, 2005; pp. 412–424. [Google Scholar]
- Mano, J.F.; Reis, R.L.; Cunha, A.M. Dynamic mechanical analysis in polymers for medical applications. In Polymer Based Systems on Tissue Engineering, Replacement and Regeneration; NATO Science Series (Series II: Mathematics, Physics and Chemistry); Reis, R.L., Cohn, D., Eds.; Springer: Dordrecht, Germany, 2002; Volume 86, pp. 139–164. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1980. [Google Scholar]
- Menczel, J.D. Dynamic mechanical analysis (DMA) in fiber research. In Thermal Analysis of Textiles and Fibers; Jaffe, M., Menczel, J.D., Eds.; Elsevier Ltd.: Cambridge, MA, USA, 2020; pp. 95–104. [Google Scholar]
- Sepe, P.M. Dynamic Mechanical Analysis for Plastics Engineering; Plastics Design Library: Norwich, NY, USA, 1998. [Google Scholar]
- Mezger, T.G. The Rheology Handbook, 2nd ed.; Vincentz Network: Hannover, Germany, 2006; pp. 114–118. [Google Scholar]
- Cristea, M. Dynamic mechanical analysis in polymeric multiphase systems. In Multiphase Polymer Systems. Micro- to Nanostructural Evolution in Advanced Technologies; Barzic, A.I., Ioan, S., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 173–191. [Google Scholar]
- Cristea, M.; Ionita, D.; Simionescu, B.C. A new insight in the dynamo-mechanical behavior of poly(ethylene tereftalate). Eur. Polym. J. 2010, 10, 2005–2012. [Google Scholar] [CrossRef]
- Sepe, M. Heat Deflection Temperature vs. Dynamic Mechanical Analysis. Part 1–4. Plastics Technologies. 2019. Available online: www.ptonline.com (accessed on 25 September 2020).
- Migliaresi, C.; Cohn, D.; De Lollis, A.; Fambri, L. Dynamic mechanical and calorimetric analysis of compression-molded PLLA of different molecular weights: Effect of thermal treatments. Polymer 1991, 43, 83–95. [Google Scholar] [CrossRef]
- Celli, A.; Scandola, M. Thermal properties and physical ageing of poly(L-lactic acid). Polymer 1992, 33, 2699–2703. [Google Scholar] [CrossRef]
- Starkweather, H.W., Jr.; Avakian, P.; Fontanella, J.J.; Wintersgill, M.G. Internal motions in polylactide and related polymers. Macromolecules 1993, 26, 5084–5087. [Google Scholar] [CrossRef]
- Badia, J.D.; Stromberg, E.; Karlsson, S.; Ribes-Greus, A. Material valorization of amorphous polylactide. Influence of thermo-mechanical degradation on the morphology, segmental dynamics, thermal and mechanical performance. Polym. Degrad. Stab. 2012, 97, 670–678. [Google Scholar] [CrossRef]
- Courgneau, C.; Domenek, S.; Guinault, A.; Averous, L.; Ducruet, V. Analysis of the structure-properties relationships of different multiphase systems based on plasticized poly(lactic acid). J. Polym. Environ. 2011, 19, 362–371. [Google Scholar] [CrossRef]
- Akindoyo, J.O.; Beg, M.D.H.; Ghazali, S.; Heim, H.P.; Feldmann, M.; Mariatti, M. Simultaneous impact modified and chain extended glass fiber reinforced poly(lactic) composites: Mechanical, thermal, crystallization and dynamic mechanical performance. J. Appl. Polym. Sci. 2020, 138, 49752. [Google Scholar] [CrossRef]
- Qin, S.; Hu, Y.; Tian, X.; Tian, Y.; Liu, W.; Zhao, L. Modification of cellulose nanocrystals by self-assembly nucleation agents to improve poly(L-lactide) nanocomposite properties. Cellulose 2020, 27, 4337–4353. [Google Scholar] [CrossRef]
- Lee, J.-S.; Hwang, G.H.; Kwon, Y.S.; Jeong, Y.G. Impacts of cellulose nanofobril and physical aging on the enthalpy relaxation behavior and dynamic mechanical thermal properties of poly(lactic acid) composite films. Polymer 2020, 202, 122677. [Google Scholar] [CrossRef]
- Shojaeiarani, J.; Bajwa, D.S.; Hartman, K. Esterified cellulose nanocrystals as reinforcement in poly(lactic acid) nanocomposites. Cellulose 2019, 26, 2349–2362. [Google Scholar] [CrossRef]
- Espinach, F.X.; Boufi, S.; Delgado-Aguilar, M.; Julian, F.; Mutje, P.; Mendez, J.A. Composites from poly(lactic acid) and bleached chemical fibres: Thermal properties. Compos. Part B 2018, 134, 169–176. [Google Scholar] [CrossRef]
- Yazdaninia, A.; Khonakdar, H.A.; Jafari, S.H.; Asadi, V. Influence of trifluoropropyl-POSS nanoparticles on microstructure, rheological, thermal and thermomechanical properties of PLA. RSC Adv. 2016, 6, 37149–37159. [Google Scholar] [CrossRef]
- Ferreira, W.H.; Andrade, C.T. The role of graphene on thermally induced shape memory properties of poly(lactic acid) extruded composites. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Cao, Y.; Ju, Y.; Liao, F.; Jin, X.; Dai, X.; Li, J.; Wang, X. Improving the flame retardancy and mechanical properties of poly(lactic acid) with a novel nanorod-shaped hybrid flame retardant. RSC Adv. 2016, 6, 14852–14858. [Google Scholar] [CrossRef]
- Yu, F.; Liu, T.; Zhao, X.; Yu, X.; Lu, A.; Wang, J. Effects of talc on the mechanical and thermal properties of polylactide. J. Appl. Polym. Sci. 2012, 125, E99–E109. [Google Scholar] [CrossRef]
- Santonja-Blasco, L.; Moriana, R.; Badia, J.D.; Ribes-Greus, A. Thermal analysis applied to the characterization of degradation in soil of polylactide: I. Calorimetric and viscoelastic analyses. Polym. Degrad. Stab. 2010, 95, 2185–2191. [Google Scholar] [CrossRef] [Green Version]
- Sikorska, W.; Adamus, G.; Dobrzynski, P.; Libera, M.; Rychter, P.; Krucinska, I.; Komisarczyk, A.; Cristea, M.; Kowalczuk, M. Forensic engineering of advanced polymeric materials—Part II: The effect of the solvent-free non-woven fabrics formation method on the release rate of lactic acid and glycolic acids from the tin-free poly(lactide-co-glycolide) nonwovens. Polym. Degrad. Stab. 2014, 110, 518–528. [Google Scholar] [CrossRef]
- Suksut, B.; Deeprasertkul, C. Effect of nucleating agents on physical properties of poly(lactic acid) and its blends with natural rubber. J. Polym. Environ. 2011, 19, 288–296. [Google Scholar] [CrossRef]
- Pluta, M.; Galeski, A. Plastic deformation of amorphous poly(L/D,L-lactide): Structure evolution and physical properties. Biomacromolecules 2007, 8, 1836–1843. [Google Scholar] [CrossRef]
- Ali, F.; Chang, Y.-W.; Kang, S.C.; Yoon, J.Y. Thermal, mechanical and rheological properties of poly(lactic acid)/epoxidized soybean oil blends. Polym. Bull. 2009, 62, 91–98. [Google Scholar] [CrossRef]
- Martino, V.P.; Jimenez, A.; Ruseckaite, R.A. Processing and characterization of poly(lactic acid) films plasticized with commercial adipates. J. Appl. Polym. Sci. 2009, 112, 2010–2018. [Google Scholar] [CrossRef]
- Yang, S.-L.; Wu, Z.-H.; Meng, B.; Yang, W. The effects of dioctyl phthalate plasticization on the morphology and thermal, mechanical and rheological properties of chemical crosslinked polylactide. J. Polym. Sci. Polym. Phys. 2009, 47, 1136–1145. [Google Scholar] [CrossRef]
- Martin, O.; Averous, L. Poly(lactic acid): Plasticization and properties of biodegradable multiphase systems. Polymer 2001, 42, 6209–6219. [Google Scholar] [CrossRef]
- Ljungberg, N.; Colombini, D.; Wesslen, B. Plasticization of poly(lactic acid) with oligomeric malonate esteramides: Dynamic mechanical and thermal film properties. J. Appl. Polym. Sci. 2005, 96, 992–1002. [Google Scholar] [CrossRef]
- Hu, Y.; Rogunova, M.; Topolkaraev, V.; Hiltner, A.; Baer, E. Aging of poly(lactide)/poly(ethylene glycol) blends. Part 1. Poly(lactide) with low stereoregularity. Polymer 2003, 44, 5701–5710. [Google Scholar] [CrossRef]
- Hu, Y.; Hu, Y.S.; Topolkaraev, V.; Hiltner, A.; Baer, E. Aging of poly(lactide)/poly(ethylene glycol) blends. Part 2. Poly(lactide) with high stereoregularity. Polymer 2003, 44, 5711–5720. [Google Scholar] [CrossRef]
- Yang, S.L.; Wu, Z.H.; Yang, W.; Yang, M.B. Thermal and mechanical properties of chemical crosslinked polylactide (PLA). Polym. Test. 2008, 27, 957–963. [Google Scholar] [CrossRef]
- Hao, Y.; Li, Y.; Liu, Z.; Yan, X.; Tong, Y.; Zhang, H. Thermal, mechanical and rheological properties of poly(lactic acid) chain extended with polyaryl polymethylene isocyanate. Fiber Polym. 2019, 20, 1766–1773. [Google Scholar] [CrossRef]
- Wunderlich, B. Reversible crystallization and the rigid-amorphous phase in semicrystalline macromolecules. Prog. Polym. Sci. 2003, 28, 383–450. [Google Scholar] [CrossRef]
- Varol, N.; Delpouve, N.; Araujo, S.; Domenek, S.; Guinault, A.; Golovchak, R.; Ingram, A.; Delbreilh, L.; Dargent, E. Amorphous rigidification and cooperativity drop in semi-crystalline plasticized polylactide. Polymer 2020, 194, 122373. [Google Scholar] [CrossRef]
- Radjabian, M.; Kish, M.H.; Mohammadi, N. Structure-property relationship for poly(lactic acid) (PLA) filaments: Physical, thermomechanical and shape memory characterization. J. Polym. Res. 2012, 19, 9870. [Google Scholar] [CrossRef]
- White, J.R. Polymer ageing: Physics, chemistry or engineering. Time to reflect. C.R. Chim. 2006, 9, 1396–1408. [Google Scholar] [CrossRef]
- Aou, K.; Kang, S.; Hsu, S.L. Morphological study on thermal shrinkage and dimensional stability associated with oriented poly(lactic acid). Macromolecules 2005, 38, 7730–7735. [Google Scholar] [CrossRef]
- Trznadel, M.; Kryszewski, M. Thermal shrinkage of oriented polymers. J.M.S. Rev. Macromol. Chem. Phys. C 1992, 32, 259–300. [Google Scholar] [CrossRef]
- Manich, A.M.; Carilla, J.; Miguel, R.A.L.; Lucas, J.M.; Franco, F.G.F.; Montero, L.A.; Cayuela, D. Thermal transitions of polylactide false-twist textured multifilaments determined by DSC and TMA. J. Therm. Anal. Calorim. 2010, 99, 723–731. [Google Scholar] [CrossRef]
- Okuzaki, H.; Kubota, I.; Kunugi, T. Mechanical properties and structure of the zone-drawn poly(L-lactic acid) fibers. J. Polym. Sci. Polym. Phys. 1999, 37, 991–996. [Google Scholar] [CrossRef]
- Smola, A.; Dobrzynski, P.; Cristea, M.; Kasperczyk, J.; Sobota, M.; Gebarowska, K.; Janeczek, H. Bioresorbable terpolymers based on L-lactide, glycolide and trimethylene carbonate with shape memory behaviour. Polym. Chem. 2014, 5, 2442–2452. [Google Scholar] [CrossRef]
- Mulligan, J.; Cakmak, M. Nonlinear mechanooptical behavior of uniaxially stretched poly(lactic acid): Dynamic phase behavior. Macromolecules 2005, 38, 2333–2344. [Google Scholar] [CrossRef]
- Stoclet, G.; Seguela, R.; Lefebvre, J.M.; Elkoun, S.; Vanmansart, C. Strain-induced molecular ordering in polylactide upon uniaxial stretching. Macromolecules 2020, 43, 1488–1498. [Google Scholar] [CrossRef]
- Stoclet, G.; Seguela, R.; Lefebvre, J.M.; Rochas, C. New insights on the strain-induces mesophase of poly(D,L-lactide): In situ WAXS and DSC study of the thermo-mechanical stability. Macromolecules 2010, 43, 7228–7237. [Google Scholar] [CrossRef]
- Ljungberg, N.; Wesslen, B. Tributyl citrate oligomers as plasticizers for poly(lactic acid): Thermo-mechanical film properties and aging. Polymer 2003, 44, 7679–7688. [Google Scholar] [CrossRef]
- Ljungberg, N.; Andersson, T.; Wesslen, B. Film extrusion and film weldability of poly(lactic acid) plasticized with triacetine and tributyl citrate. J. Appl. Polym. Sci. 2003, 88, 3239–3247. [Google Scholar] [CrossRef]
- Pluta, M.; Paul, M.-A.; Alexandre, M.; Dubois, P. Plasticized polylactide/clay nanocomposites. I. The role of filler content and its surface organo-modification on the physic-chemical properties. J. Polym. Sci. B Polym. Phys. 2005, 44, 299–311. [Google Scholar] [CrossRef]



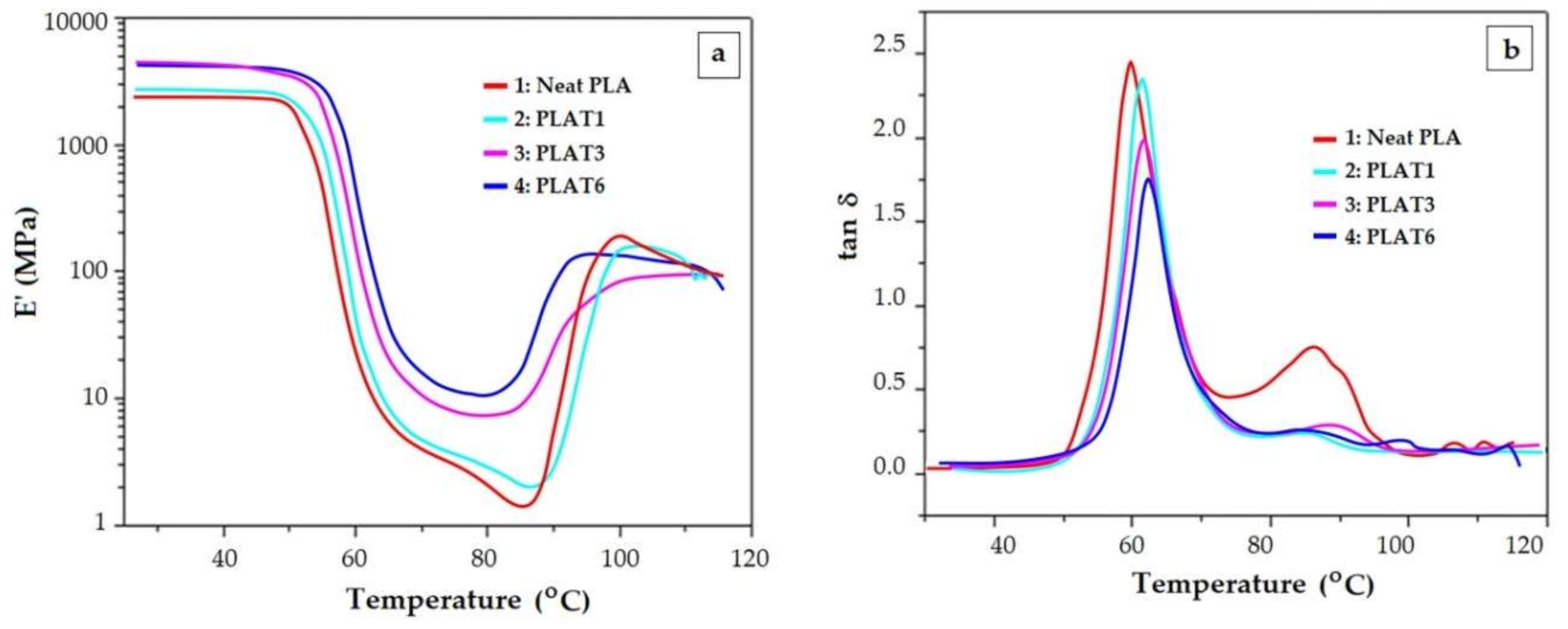
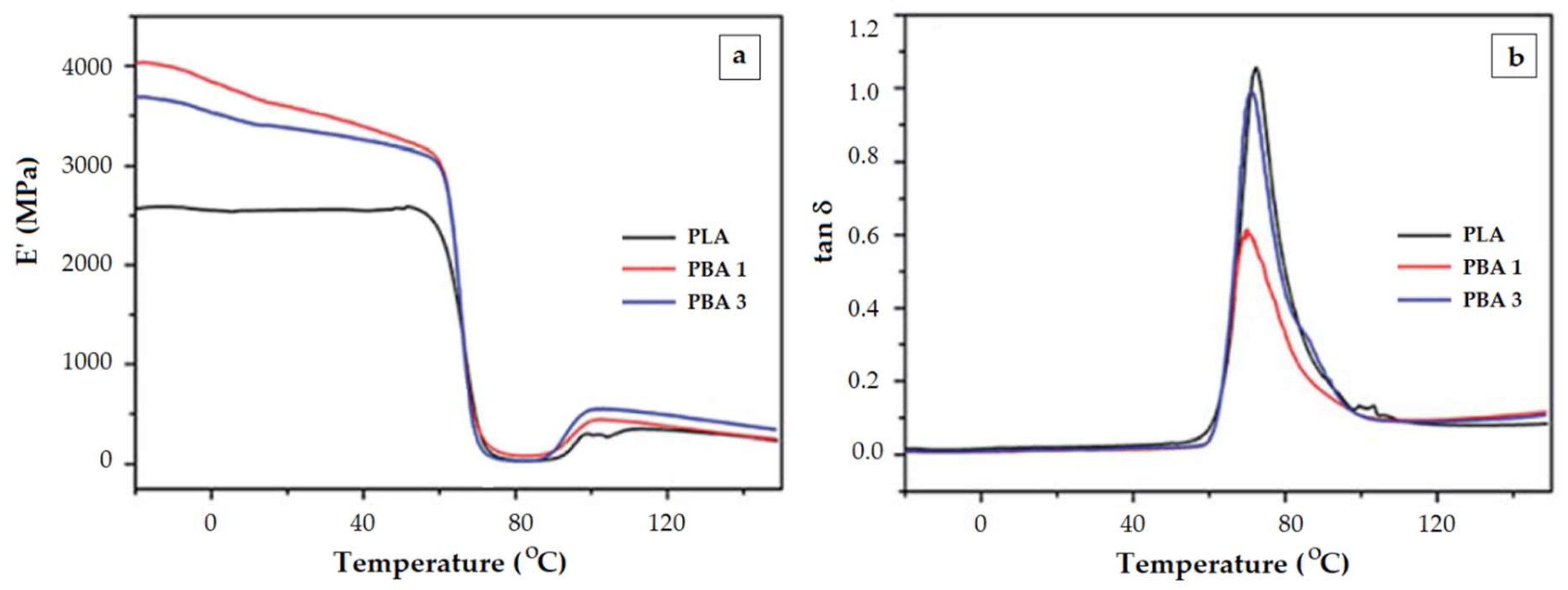
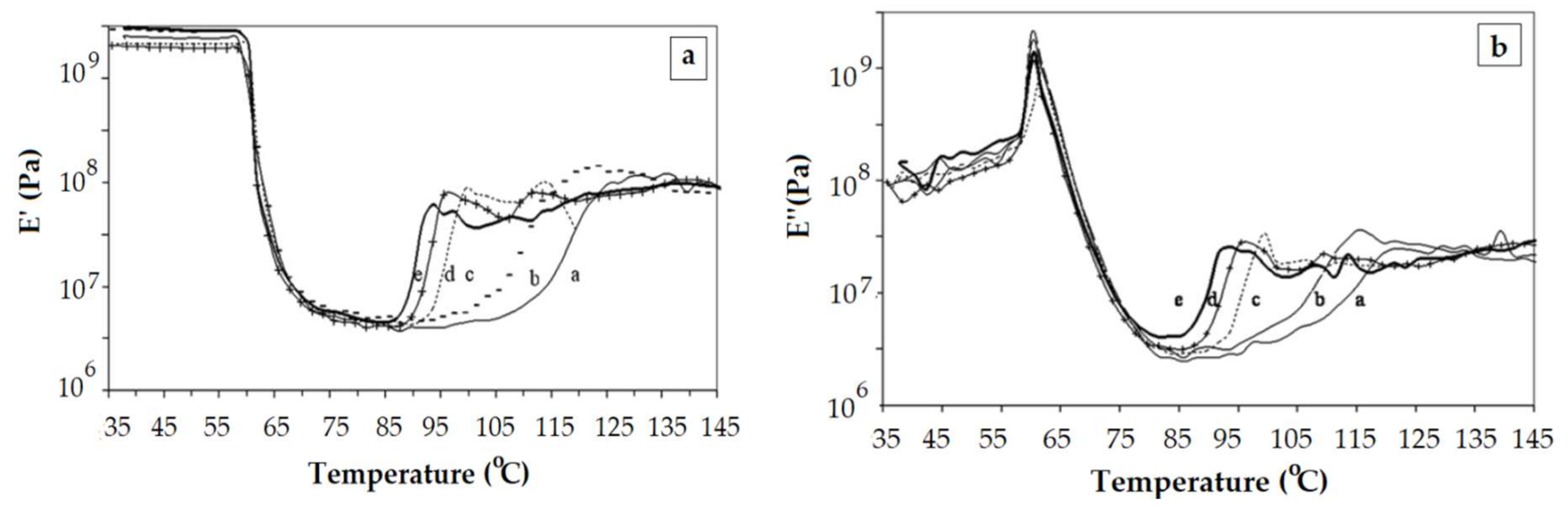



| PLA Samples | DMA Experimental Conditions | Glass Transition Temperature (Tg, °C) 1 | Observations | Ref. |
|---|---|---|---|---|
| ▪ semi-crystalline PLLA from Boehringer Ingelheim (Resomer® (Mn 180,000, Mw 22 × 104 g mol−1) | Perkin Elmer DMA 7e: 3 °C/min; 1 Hz; 20–110 °C; loading mode: tension | 60 (tan δ peak) | Investigation of the glass transition region The apparent unusual decrease of Tg with increasing crystallinity is associated with the changes in the thickness of the rigid amorphous phase. | [32] |
| ▪ PLA 3051D type from Nature Works (4% D-lactide) | Perkin Elmer Diamond DMA: 2, 5, 10, 15, 20 °C/min; 1 Hz; 0–150 °C; loading mode: ns | 60–70 (onset of E’ drop) | The whole behavior (also Tg) depends on the heating rate | [35] |
| ▪ PLLA from Boehringer, Ingelheim or synthesized in the laboratory | Polymer Laboratories DMTA 2: 2 °C/min; 1 Hz; 30–150 °C; loading mode: bending | 65 (tan δ peak) | The effect of thermal treatment, processing conditions and molecular weight on crystallization phenomena occurring in the PLLA | [54] |
| ▪ PLLA from Boehringer (Resomer L206: Mv 20,000 and L214: Mv 691,000) or synthesized in the laboratory (Mv 5,300) | Polymer Laboratories DMTA: 3 °C/min; 3 Hz; −150–160 °C; loading mode: dual cantilever bending | 70 (tan δ peak) | Dynamic mechanical characterization of optically active PLA depending on effect of physical ageing | [55] |
| ▪ PLA synthesized in the laboratory (~95% L-isomer) | Polymer Laboratories DMTA: 1 Hz; −150–150 °C; loading mode: ns | 50 (tan δ peak) | Study of internal motions; Broad secondary relaxations mentioned near −50 °C | [56] |
| ▪ PLA, 2002D type from Nature Works (4.25% D-lactic enantiomer) | Mettler Toledo DMA: Isothermal steps at 2°; 1 Hz; 20–140 °C; loading mode: three point bending | 58 (onset of E’ drop) | PLA mechanically reprocessed up to 5 cycles The shortening of the first rubbery plateau denotes the chain cleavage | [57] |
| ▪ PLA from Nature Works (92% L-lactide, Mw 9 × 104 g mol−1, PI 2.75) | TA Instruments DMTA V: 2 °C/min; 1 Hz; −140–130 °C; loading mode: tension | 67 (tan δ peak) | Study of the effect of plasticizers like ATBC 3 and PEG 4; Broad β-relaxation centered at −80 °C. V-shape E’ vs. T plot. | [58] |
| ▪ PLA 3052D type from Nature Works IngeoTM (Mw 13.9 × 104 g mol−1) | TA Instruments Q800 DMA: 3 °C/min; 1 Hz; −60–130 °C; loading mode: single cantilever bending | 65.6 (tan δ peak) | Glass fiber-reinforced PLA composites | [59] |
| ▪ PLLA 4032D type from Nature Works (1.2–1.6% D-lactide, Mw 20.7 × 104 g mol−1, PI 1.74) | Mettler Toledo DMA 1: 2 °C/min; 1 Hz; 30–100 °C; loading mode: tension | 60 (onset of E’ drop) | Nanocomposites of PLLA with CNC 5 and modified CNC (with TMC 6 300); Improved HDT at T < Tm 7 | [60] |
| ▪ PLA 2002D type from Nature Works (4.2% D-lactide, Mw 4 × 104 g mol−1) | Perkin Elmer Inc. DMA 8000 3 °C/min; −500–150 °C; loading mode: tension | 60 (onset of E’ drop) | PLA composite films with 0.5–7.0 wt% CNF 8; Cold crystallization starts at the end of the glass transition: A slope change is noticed on E’vs. T during the glass transition. | [61] |
| ▪ PLA 2003D type from Nature Works LLC (Mw 9.8 × 104 and 20 × 104 g mol−1) | TA Instruments Q800 DMA: 1 °C/min; 1 Hz; 25–120 °C; loading mode: bending | 66 (tan δ peak) | PLA nanocomposites with esterified cellulose nanocrystals | [62] |
| ▪ PLA 3251D type from Nature Works (Naarden, The Netherlands) | Mettler Toledo DMA: 3 °C/min; 1 Hz; 0–160 °C; loading mode: dual cantilever bending | 60 (onset of E’ drop) | PLA composites with BKSW 9 (15–35%) | [63] |
| ▪ PLA 4043D type from Nature Works (2% D-lactide, Mw 10 × 104 g mol−1) | TA Instruments Q800 DMA: 3 °C/min; 1 Hz; 20–140 °C; loading mode: bending | 70 (tan δ peak) | PLA-trifluoropropyl-POSS 10 composites | [64] |
| ▪ PLA 3251D type from Nature Works (Mn 11.6 × 104 g mol−1) | TA Instruments Q800 DMA: 3 °C/min; 1 Hz; 0–100 °C; loading mode: single cantilever bending | 55 (onset of E’ drop) | Graphene-PLA composites | [65] |
| ▪ PLA 290, Zhejiang, Haizheng Biological Materials Co. Ltd. (Dhejiang, China) | TA Instruments Q800 DMA: 3 °C/min; 1 Hz; −20–150 °C; loading mode: dual cantilever bending | 60 (tan δ peak) | Nanocomposites of PLA with nanorod-shaped hybrid flame retardant based on ATH and BPA 11 | [66] |
| ▪ PLA REvode 201, Zhejiang Hisaiv Biomaterials | TA Instruments Q800 DMA: 3 °C/min; 1 Hz; 25–120 °C; loading mode: single cantilever bending | 50 (onset of E’ drop) | PLA-talc composites; Cold crystallization is marked as a small peak the tan δ curve | [67] |
| ▪ PLLA from Nature Works (3.8% meso-lactide, Mw 10.2 × 104 g mol−1) | Rheometric Scientific DMTA Mark IV: Isostep mode; step 2 °C; 35–150 °C; loading mode: dual cantilever bending | 60 | PLA plates that were subjected to controlled degradation in soil test under controlled conditions (T, water, pH) Decrease of E’ in the glassy region as a result of formation of shorter chain Unusual sharp E’’ peak | [68] |
| ▪ PLGA poly(lactide-co-glycolide) in the form of non-woven fabrics | Perkin Elmer Diamond DMA: 2 °C/min; 1 Hz; 0–150 °C; loading mode: tension | 55.5 (onset of E’ drop) 63 (tan δ peak) | Degradation investigations of non-woven fabrics made from PLGA Emphasizing of shrinking during the glass transition | [69] |
| ▪ PLA 4042D type from Nature works | Perkin Elmer DMA 7e: 5 °C/min; 1 Hz; 20–90 °C; loading mode: three-point bending | 59 (tan δ peak) | Effect of nucleating agents (α-cyclodextrin, CaCO3, talc) on PLA/natural rubber mixtures A hump is noticed on the E’ vs. T curve, before Tg (enthalpic relaxation). | [70] |
| ▪ PDLLA (L/DL 70/30), LR 708, CCA Purac Biochem, Gorinchem, Holland (Mw 22.6 × 104 g mol−1, PI 1.36) | Rheometric Scientific, Inc. MkIII DMTA: 3 °C/min; 1 Hz; −100–145 °C; loading mode: dual cantilever bending | 57.2 (E’’ peak) | Investigations on amorphous PDLLA samples, deformed above Tg, at different compression ratios | [71] |
| ▪ PLA, Cargill-Dow (Mw 14.8 × 104 g mol−1, PI 1.9) | TA Instruments DMA 2980: 2 °C/min; 1 Hz; 0–140 °C; loading mode: dual cantilever bending | 65 (onset of E’ drop) | The plasticization effects exerted by ESO 12. ESO increases the ability of PLA to cold crystallization which starts right after the glass transition; the first rubbery plateau is absent. Unusual: tan δ peak height decreases with ESO content | [72] |
| ▪ PLA, CML type, Hycail Finland Oy (Turku, Finland) | TA Instruments DMA Q800: 3 °C/min; 1 Hz; −90–140 °C; loading mode: tension | 60 (onset of E’ drop) | PLA films plasticized with adipates (monomeric and polymeric structures) The plasticizers decrease the cold crystallization temperature. | [73] |
| ▪ PLA (90% L-lactide, 8% mesolactide), 3001D type from NatureWorks (Mw 10.7 × 104 g mol−1, Mn 15.2 × 104) | TA Instruments DMA Q800: 3 °C/min; 1 Hz; −20–200 °C; loading mode: tension | 61.9 (E’’ peak) 68.1 (tan δ peak) (linear PLA) | Crosslinked PLA plasticized with DOP 13 | [74] |
| ▪ PLA (90% L-lactide, 8% mesolactide), from Cargill-Dow (Mw 4.9 × 104 g mol−1) | TA Instruments DMA 2980: 1.5 °C/min; 1 Hz; −100–160 °C; loading mode: dual-cantilever bending | 67 (tan δ) | Plasticization of PLA with thermoplastic starch | [75] |
| ▪ PLA, Fortum Corp. (Keilaniemi, Finland) Mw 10 × 104 g mol−1, PI 2.4 | TA Instruments DMA 2980 3 °C/min; 1 Hz; −60–150 °C; loading mode: tension | 60 (onset of E’ drop) | PLA films plasticized with oligomeric malonate esteramides | [76] |
| ▪ PLA with low and high stereogularity (13% D-lactide and 5% D-lactide) | Polymer laboratories DMTA Mk II: 3 °C/min; 1 Hz; −60–80 °C; loading mode: tension | 60 (onset of E’ drop) | Aging phenomena in PLA/PEG4 No cold crystallization for PLA with low stereogularity | [77,78] |
| ▪ PLA 3001D type, Nature Works | TA Instruments DMA Q800: 3 °C/min; 1 Hz; −20–200 °C; loading mode: tension | 60 (onset of E’ drop) | Crosslinked PLA, crosslinking agent: TAIC and DCP 14 Higher crosslinking degree means larger rubbery plateau | [79] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cristea, M.; Ionita, D.; Iftime, M.M. Dynamic Mechanical Analysis Investigations of PLA-Based Renewable Materials: How Are They Useful? Materials 2020, 13, 5302. https://doi.org/10.3390/ma13225302
Cristea M, Ionita D, Iftime MM. Dynamic Mechanical Analysis Investigations of PLA-Based Renewable Materials: How Are They Useful? Materials. 2020; 13(22):5302. https://doi.org/10.3390/ma13225302
Chicago/Turabian StyleCristea, Mariana, Daniela Ionita, and Manuela Maria Iftime. 2020. "Dynamic Mechanical Analysis Investigations of PLA-Based Renewable Materials: How Are They Useful?" Materials 13, no. 22: 5302. https://doi.org/10.3390/ma13225302
APA StyleCristea, M., Ionita, D., & Iftime, M. M. (2020). Dynamic Mechanical Analysis Investigations of PLA-Based Renewable Materials: How Are They Useful? Materials, 13(22), 5302. https://doi.org/10.3390/ma13225302






