Effect of Asymmetric Accumulative Roll-Bonding process on the Microstructure and Strength Evolution of the AA1050/AZ31/AA1050 Multilayered Composite Materials
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Analysis of the Numerical Modeling Results
3.2. Analysis of the Experimental Results
4. Conclusions
- (1)
- favourable impact of the introduction of the ARB into the roll rotational speed asymmetry increases tangential stresses τyz, which was proved in experimental tests;
- (2)
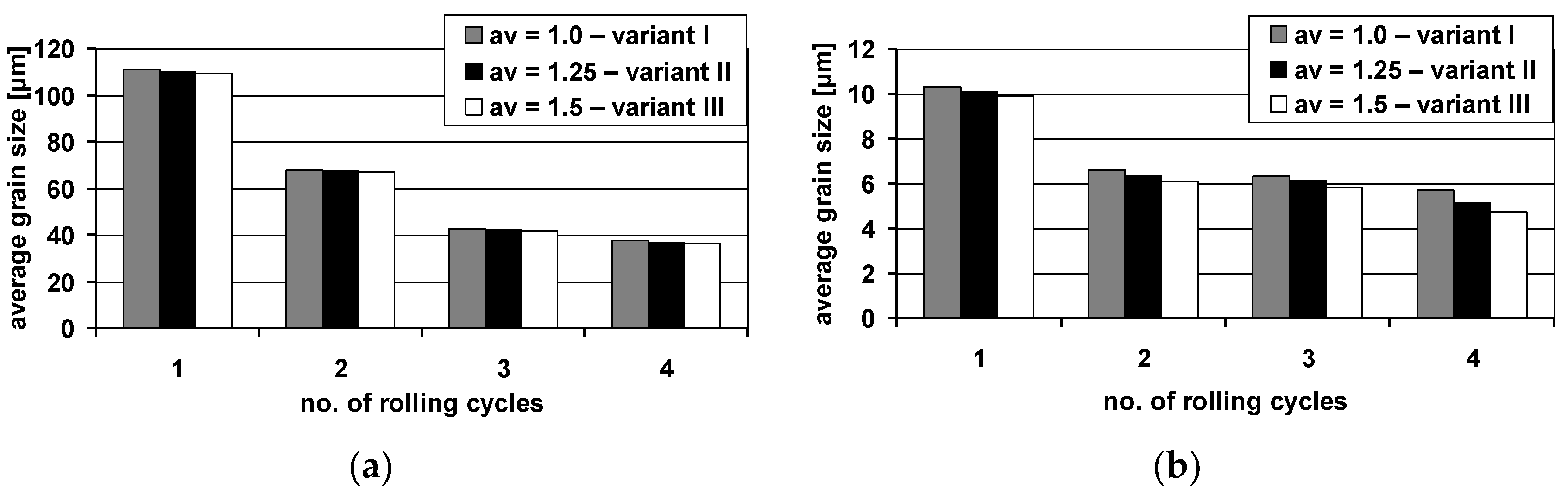
- the application of roll rotational speed asymmetry in the first rolling cycle has a beneficial effect on the activation of additional shear bands, especially in magnesium alloy, which was demonstrated in numerical calculations and microstructural examinations. It results in increased grain refinement as compared to the ARB process. The values of the asymmetry introduced into the ARB contributed to the decrease by 17% of grain dimension in the last rolling cycle of the AZ31 alloy relative to the ARB;
- (3)
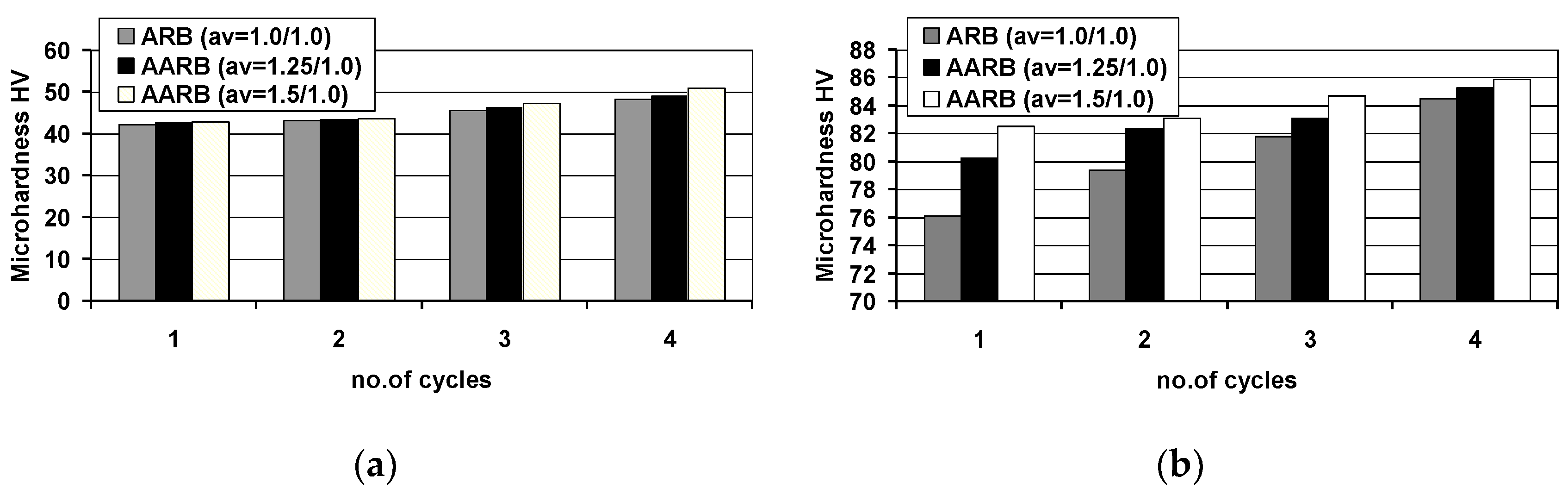
- the suggested modification of the ARB caused an increase in microhardness of each layer and an improvement of strength properties of the Al/Mg/Al multilayered composite subjected to rolling;
- (4)
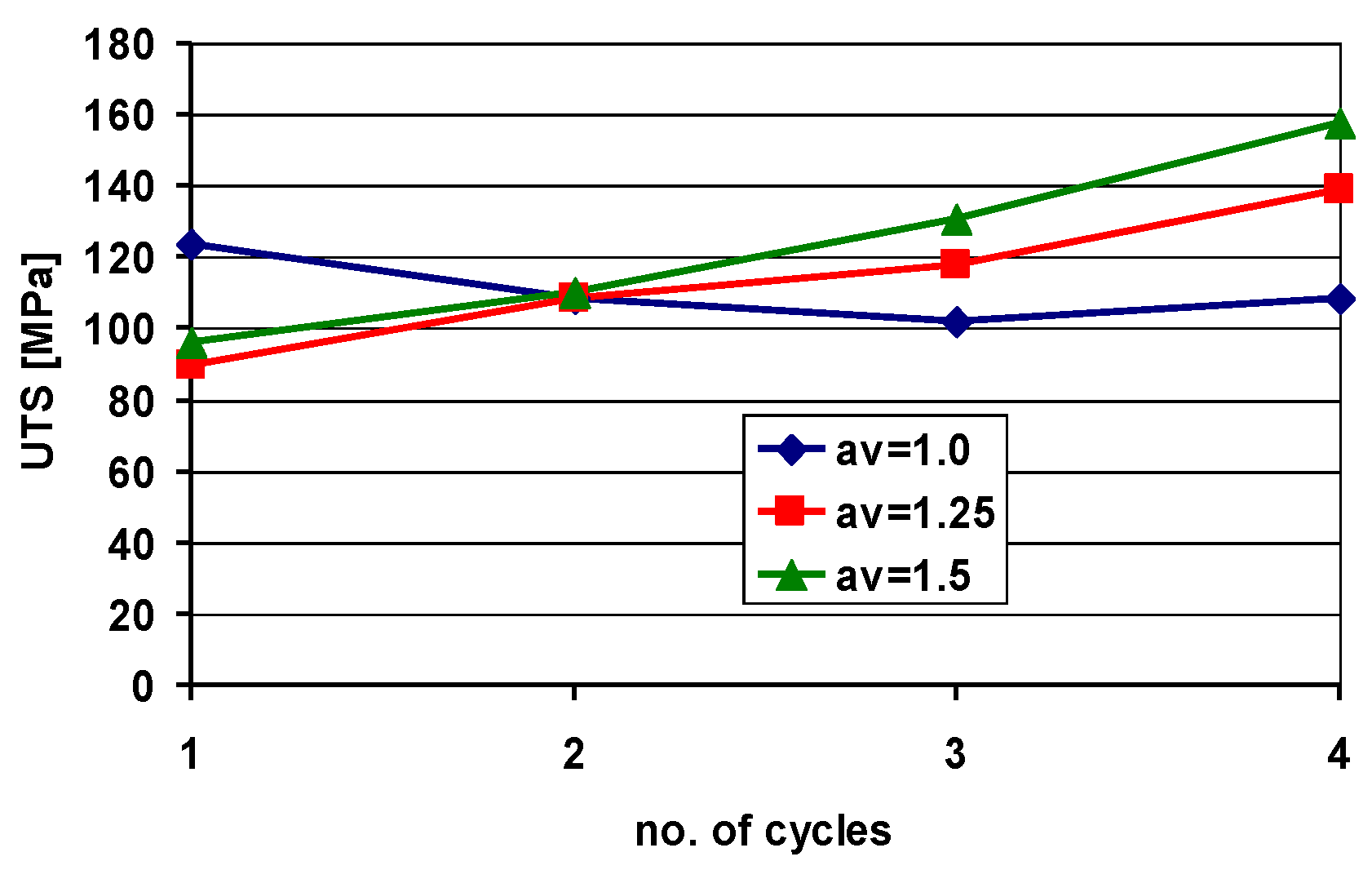
- the results of strength tests obtained revealed that the introduction of rolling speed asymmetry increases the tensile strength of the fabricated Al/Mg/Al composite, as compared to the composite obtained via the classic ARB process;
- (5)
- after the last rolling cycle, high fragmentation of the magnesium alloy layer is observed in the finished Al/Mg/Al composite. This increases along with the growth of the asymmetry coefficient in the first rolling cycle. The introduction of too high a roll circumferential speed asymmetry has an impact on the formation of a higher number of cracks.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A1, m1÷m9 | coefficient of function (2) |
| AARB | asymmetric accumulative roll bonding |
| ACR | accumulative clad rolling |
| AR | asymmetric rolling |
| ARB | accumulative roll bonding |
| ECAP | equal-channel angular pressing |
| HPT | high-pressure torsion |
| K | consistence being dependent on the flow stress σf |
| Sij | deviatoric stress tensor |
| SPD | severe plastic deformation |
| T | temperature, °C |
| Ttool | tool temperature, °C |
| Tair | ambient temperature, °C |
| UFG | ultrafine-grained |
| UTS | ultimate tensile strength, MPa |
| YS | yield strength, MPa |
| av | coefficient of asymmetry |
| m | factor characterizing hot metal deformation (0 < m < 1) |
| vz | longitudinal component of the plastic flow rate, mm/s |
| α | heat exchange coefficient between the band and the rolls, W/(m2K) |
| αb | heat exchange coefficient between aluminium and magnesium layers, W/(m2K) |
| αair | heat exchange coefficient between the band and the environment, W/(m2K) |
| ε | true strain |
| εij | the equivalent strain rate tensor |
| equivalent plastic strain | |
| strain rate, s–1 | |
| equivalent strain rate | |
| σf | flow stress, MPa |
| τyz | tangential stress component, MPa |
References
- Kainer, K.U. Magnesium—Alloys and Technology; Wiley-VCH Verlag GmbH & Co. KGaA.: Weinheim, Germany, 2004. [Google Scholar]
- Wang, J.L.; Shi, Q.N. Orientation evolution and nucleation mechanism of UFG copper prepared by SD-AARB with heat treatment. Appl. Mech. Mater. 2010, 33, 63–167. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Korznikov, A.V.; Mulyukov, R.R. Structure and Properties of Ultrafine-grained Materials Produced by Severe Plastic Deformation. Mat. Sci. Eng. A 1993, 168, 141–148. [Google Scholar] [CrossRef]
- Azushima, A.; Kopp, R.; Korhonen, A.; Yang, D.Y.; Micari, F.; Lahoti, G.D.; Groche, P.; Yanagimoto, J.; Tsuji, N.; Rosochowski, A.; et al. Severe plastic deformation (SPD) processes for metals. CIRP Ann. Man. Technol. 2008, 57, 716–735. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, N.; Starink, M.J. Al-Mg-Cu based alloys and pure Al processed by high pressure torsion, The influence of alloying additions on strengthening. Mater. Sci. Eng. A 2010, 527, 3472–3479. [Google Scholar] [CrossRef][Green Version]
- Loucif, A.; Figueiredo, R.B.; Baudin, T.; Brisset, F.; Langdon, T.G. Microstructural evolution in an Al-6061 alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2010, 527, 4864–4869. [Google Scholar] [CrossRef]
- Jin, Y.G.; Baek, H.M.; Hwang, S.K.; Im, Y.T.; Jeon, B.C. Continuous high strength aluminum bolt manufacturing by the spring-loaded ECAP system. J. Mater. Process. Technol. 2012, 212, 848–855. [Google Scholar] [CrossRef]
- Soliman, M.S.; El-Danaf, E.A.; Almajid, A.A. Effect of equal-channel angular pressing process on properties of 1050 Al alloy. Mater. Manuf. Process. 2012, 27, 746–750. [Google Scholar] [CrossRef]
- Yu, H.L.; Lu, C.; Tieu, K.; Liu, X.H.; Sun, Y.; Yu, Q.; Kong, C. Asymmetric cryorolling for fabrication of nanostructural aluminum sheets. Sci. Rep. 2012, 2, 772. [Google Scholar] [CrossRef]
- Yu, H.L.; Tieu, K.; Lu, C.; Liu, X.H.; Godbole, A.; Kong, C. Mechanical properties of Al-Mg-Si alloy sheets produced using asymmetric cryorolling and ageing treatment. Mater. Sci. Eng. A 2013, 568, 212–218. [Google Scholar] [CrossRef]
- Pirgazi, H.; Akbarzadeh, A.; Petrov, R.; Kestens, L. Microstructure evolution and mechanical properties of AA1100 aluminum sheet processed by accumulative roll bonding. Mater. Sci. Eng. A 2008, 497, 132–138. [Google Scholar] [CrossRef]
- Rezaei, M.R.; Toroghinejad, M.R.; Ashrafizadeh, F. Effects of ARB and ageing processes on mechanical properties and microstructure of 6061 aluminum alloy. J. Mater. Process. Technol. 2011, 211, 1184–1190. [Google Scholar] [CrossRef]
- Wierzba, A.; Mroz, S.; Szota, P.; Stefanik, A.; Mola, R. The influence of the asymmetric ARB process on the properties of Al-Mg-Al multi-layer. Arch. Metal. Mater. 2015, 60, 2821–2825. [Google Scholar] [CrossRef]
- Cui, Q.; Ohori, K. Grain refinement of a 6061 aluminum alloy by asymmetric warm-rolling. J. Jpn. Inst. Light Met. 2002, 52, 185–189. [Google Scholar] [CrossRef][Green Version]
- Eizadjou, M.; Kazemi Talachi, A.; Danesh Manesh, H.; Shakur Shahabi, H.; Janghorban, K. Investigation of structure and mechanical properties of multi-layered Al/Cu composite produced by accumulative roll bonding (ARB) process. Compos. Sci. Technol. 2008, 68, 2003–2009. [Google Scholar] [CrossRef]
- Min, G.H.; Lee, J.M.; Kang, S.B.; Kim, H.W. Evolution of microstructure for multilayered Al/Ni composites by accumulative roll bonding process. Mater. Lett. 2006, 60, 3255–3259. [Google Scholar] [CrossRef]
- Ruppert, M.; Böhm, W.; Nguyen, H.; Höppel, H.W.; Merklein, M.; Göken, M. Influence of upscaling accumulative roll bonding on the homogeneity and mechanical properties of AA1050A. J. Mater. Sci. 2013, 48, 8377–8385. [Google Scholar] [CrossRef]
- Li, L.; Nagai, K.; Yin, F. Progress in cold roll bonding of metals. Sci. Technol. Adv. Mater. 2008, 9, 023001. [Google Scholar] [CrossRef]
- Bay, N. Cold welding. Part 1: Characteristics, bonding mechanisms, bond strength. Met. Constr. 1986, 18, 369–372. [Google Scholar]
- Bay, N.; Clemensen, C.; Juelstorp, O.; Wanheim, T. Bond Strength in Cold Roll Bonding. CIRP Ann. 1985, 34, 221–224. [Google Scholar] [CrossRef]
- Luo, J.G.; Aco, V.L. Using cold roll bonding and annealing to process Ti/Al multi-Layered composites from elemental foils. Mater. Sci. Eng. A. 2004, 379, 164–172. [Google Scholar] [CrossRef]
- Mozaari, A.; Hosseini, M.; Manesh, H.D. Al/Ni metal intermetallic composite produced by accumulative roll bonding and reaction annealing. J. Alloys Compd. 2011, 509, 9938–9945. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Zarei-Hanzaki, A.; Abedi, H.; Rokni, M. An investigation into the mechanical behavior and microstructural evolution of the accumulative roll bonded AZ31 Mg alloy upon annealing. Mater. Des. 2011, 32, 2963–2968. [Google Scholar] [CrossRef]
- Kamikawa, N.; Tsuji, N. Microstructure and Mechanical Properties of ARB Processed Aluminium with Different Purities. Mat. Trans. 2016, 57, 1720–1728. [Google Scholar] [CrossRef]
- Cheng, L.S.; Li, L.H.; Deng, G.; Tieu, K. Investigation of ultrafine grained AA1050 fabricated by accumulative roll bonding. Mat. Sc. Eng. A. 2014, 614, 148–155. [Google Scholar]
- Trojanová, Z.; Džugan, J.; Halmešová, J.; Németh, G.; Minárik, P.; Lukác, P.; Bohlen, J. Influence of Accumulative Roll Bonding on the Texture and Tensile Properties of an AZ31 Magnesium Alloy Sheets. Materials 2018, 11, 73. [Google Scholar] [CrossRef] [PubMed]
- Trojanová, Z.; Džugan, J.; Halmešová, K.; Németh, G.; Minárik, P.; Lukác, P. Effect of Accumulative Roll Bonding of an AZ31 Alloy on the Microstructure and Tensile Stress. Act. Phys. Pol. A 2017, 134, 863–866. [Google Scholar] [CrossRef]
- Zhan, M.; Li, C.; Zhang, W.; Zhang, D. Processing of AZ31 magnesium alloy by accumulative roll-bonding at gradient temperature. Acta Metall. Sin. Engl. Lett. 2012, 25, 65–75. [Google Scholar]
- Ghalehbandi, S.M.; Malaki, M.; Gupta, M. Accumulative roll bonding—A review. Appl. Sci. 2019, 9, 3627. [Google Scholar] [CrossRef]
- Su, L.; Lu, C.; Tieu, A.K.; Deng, G.; Sun, X. Ultrafine grained AA1050/AA6061 composite produced by accumulative roll bonding. Mater. Sci. Eng. A 2013, 559, 345–351. [Google Scholar] [CrossRef]
- Roy, S.; Nataraj, B.R.; Suwas, S.; Kumar, S.; Chattopadhyay, K. Microstructure and texture evolution during accumulative roll bonding of aluminum alloys AA2219/ AA5086 composite laminates. J. Mater. Sci. 2012, 47, 6402–6419. [Google Scholar] [CrossRef]
- Mozaffari, A.; Manesh, H.D.; Janghorban, K. Evaluation of mechanical properties and structure of multilayered Al/Ni composites produced by accumulative roll bonding (ARB) process. J. Alloys Compd. 2010, 489, 103–109. [Google Scholar] [CrossRef]
- Dehsorkhi, R.N.; Qods, F.; Tajally, M. Investigation on microstructure and mechanical properties of Al–Zn composite during accumulative roll bonding (ARB) process. Mater. Sci. Eng. A 2011, 530, 63–72. [Google Scholar] [CrossRef]
- Yang, D.; Cizek, P.; Hodgson, P.; Wen, C. Ultrafine equiaxed-grain Ti/Al composite produced by accumulative roll bonding. Scr. Mater. 2010, 62, 321–324. [Google Scholar] [CrossRef]
- Ohsaki, S.; Kato, S.; Tsuji, N.; Ohkubo, T.; Hono, K. Bulk mechanical alloying of Cu–Ag and Cu/Zr two-phase microstructures by accumulative roll-bonding process. Acta Mater. 2007, 55, 2885–2895. [Google Scholar] [CrossRef]
- Tayyebi, M.; Eghbali, B. Study on the microstructure and mechanical properties of multilayer Cu/Ni composite processed by accumulative roll bonding. Mater. Sci. Eng. A 2013, 559, 759–764. [Google Scholar] [CrossRef]
- Chen, M.C.; Hsieh, H.C.; Wu, W. The evolution of microstructures and mechanical properties during accumulative roll bonding of Al/Mg composite. J. Alloys Compd. 2006, 416, 169–172. [Google Scholar] [CrossRef]
- Wu, K.; Chang, H.; Maawad, E.; Gan, W.M.; Brokmeier, H.G.; Zheng, M.Y. Microstructure and mechanical properties of the Mg/Al laminated composite fabricated by accumulative roll bonding (ARB). Mat. Sc. Eng. A 2010, 527, 3073–3078. [Google Scholar] [CrossRef]
- Bahmani, A.; Kim, W.J. Effect of Grain Refinement and Dispersion of Particles and Reinforcements on Mechanical Properties of Metals and Metal Matrix Composites through High-Ratio Differential Speed Rolling. Materials 2020, 13, 4159. [Google Scholar] [CrossRef]
- Wang, J.L.; Shi, Q.N.; Qian, T.C.; Wang, S.H.; Yang, X.K. Recrystallized microstructural evolution of UFG copper prepared by asymmetrical accumulative roll bonding process. Trans. Nonferrous Met. Soc. China 2010, 20, 559–563. [Google Scholar] [CrossRef]
- Chen, L.; Shi, Q.; Chen, D.; Zhou, S.; Wang, J.; Luo, X. Research of textures of ultrafine grains pure copper produced by accumulative-roll bonding. Mater. Sci. Eng. A 2009, 508, 37–42. [Google Scholar] [CrossRef]
- Lee, S.H.; Sakai, T.; Shin, D.H. Fabrication of ultrafine grained aluminum by differential speed accumulative roll-bonding (ARB) process. Mater. Trans. 2003, 44, 1382–1385. [Google Scholar] [CrossRef]
- Kim, W.J.; Park, J.D.; Kim, W.Y. Effect of differential speed rolling on microstructure and mechanical properties of an AZ91 magnesium alloy. J. Alloys Compd. 2008, 1–2, 289–293. [Google Scholar] [CrossRef]
- Romberg, J.; Freudenberger, J.; Watanabe, H.; Scharnweber, J.; Eschke, A.; Kühn, U.; Klauß, H.; Oertel, K.G.; Skrotzki, W.; Eckert, J.; et al. Ti/Al Multi-Layered Sheets: Differential Speed Rolling (Part B). Metals 2016, 6, 31. [Google Scholar] [CrossRef]
- Magalhães, D.C.; Sordi, V.L.; Kliauga, A.M. Microstructure evolution of multilayered composite sheets of AA1050/AA7050 Al alloys produced by Asymmetric Accumulative Roll-Bonding. Mat. Char. 2020, 162, 110226. [Google Scholar] [CrossRef]
- Wierzba, A. Obtaining of a Fine-Grained Multilayered Al-Mg-Al Materials with Use of ARB Modified Method. Ph.D. Thesis, Czestochowa University of Technology, Czestochowa, Poland, 2016. (In Polish). [Google Scholar]
- Mróz, S.; Szota, P.; Stefanik, A. FE and physical modelling of plastic flow the two-layer Mg/Al materials. Comp. Meth. Mat. Sci. 2017, 17, 148–155. [Google Scholar]
- Hensel, A.; Spittel, T. Kraft und Arbeitsbedarf Bildsomer Formgeburgs; VEB Deutscher Verlang für Grundstoffindustrie: Lipsk, Germany, 1979. (In German) [Google Scholar]
- Norton, F.H. Creep of Steel at High Temperature; McGraw Hill: New York, NY, USA, 1929. [Google Scholar]
- Hoff, N.J. Approximate Analysis of Structures in the Presence of Moderately Large Steps Deformation. Quart. Appl. Mech. 1954, 2, 49. [Google Scholar]
- Anibal, M.; Timokhina, I.; Molotnikov, A.; Hodgson, P.D.; Lapovok, R. Role of shear in interface formation of aluminium-steel multilayered composite sheets. Mat. Sci. Eng. A 2017, 705, 142–152. [Google Scholar]
- Gontarz, A.; Dziubińska, A.; Okoń, Ł. Determination of friction coefficients at elevated temperatures for some Al, Mg and Ti alloys. Arch. Metall. Mater. 2011, 56, 379–384. [Google Scholar] [CrossRef]
- Pesin, A.; Pustovoytov, D. Novel technique for physical simulation of asymmetric rolling. Proc. Manuf. 2018, 15, 137–143. [Google Scholar] [CrossRef]
- Ji, Y.H.; Park, J.J. Development of severe plastic deformation by various asymmetric rolling processes. Mat. Sci. Eng. A 2009, 499, 14–17. [Google Scholar] [CrossRef]

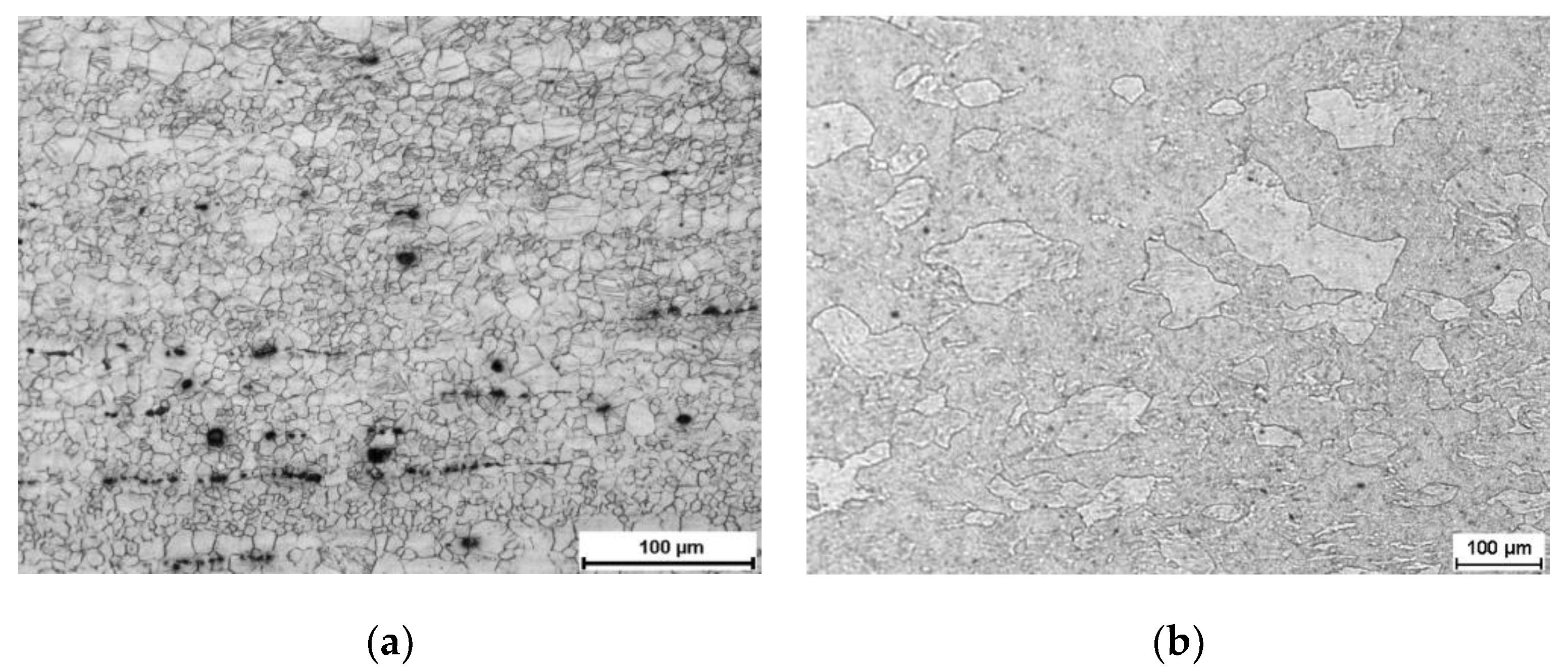


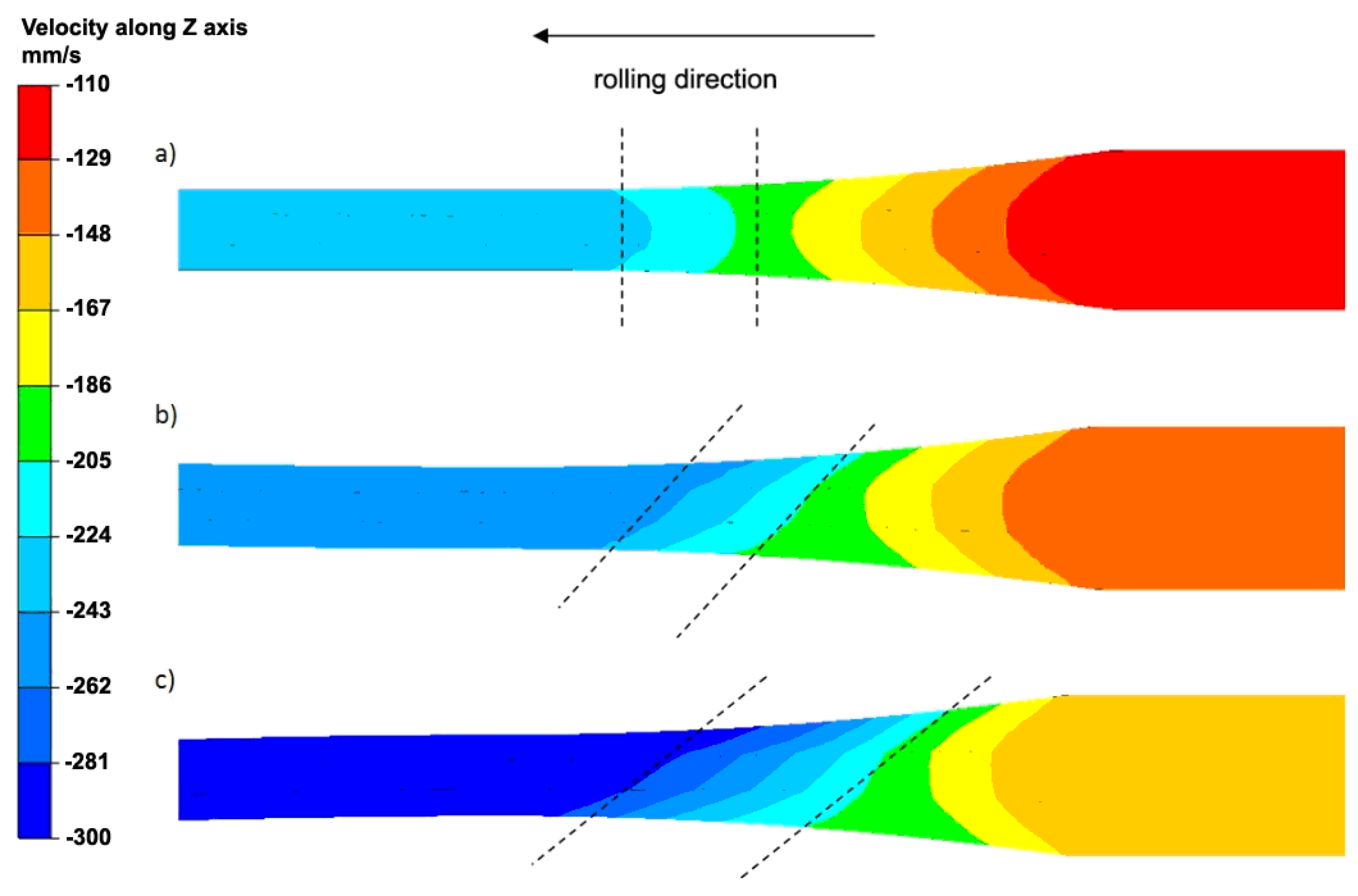
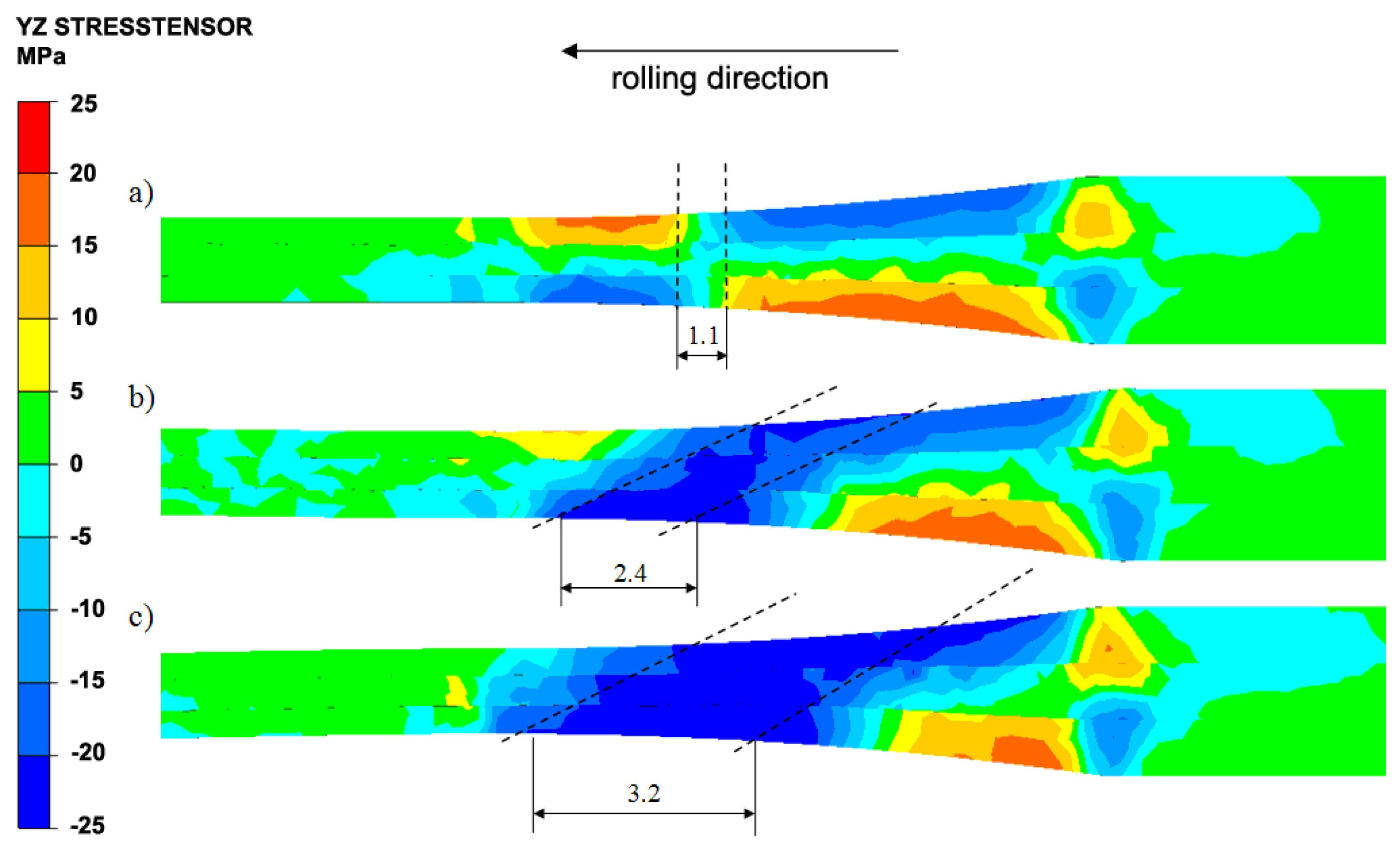



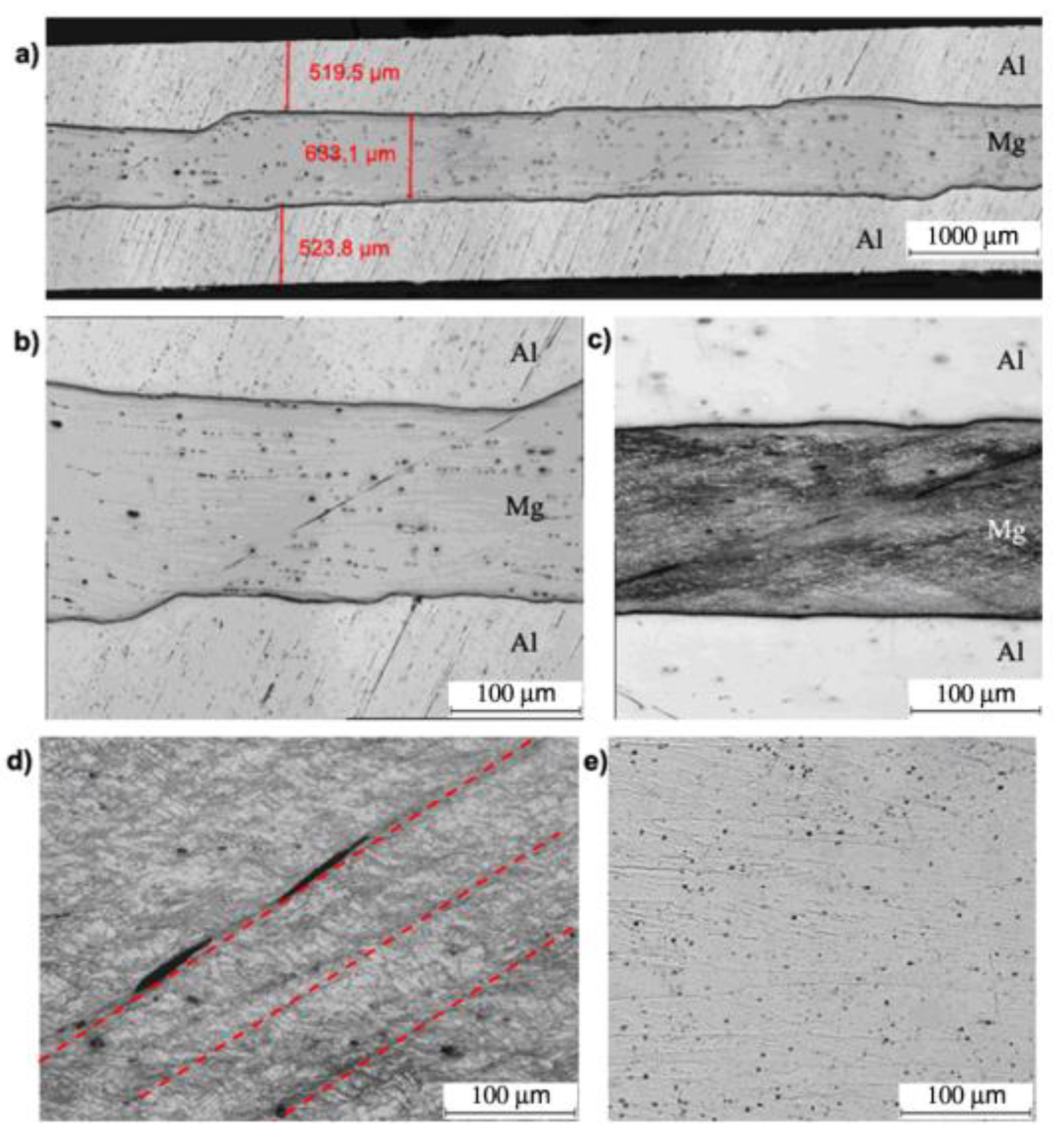
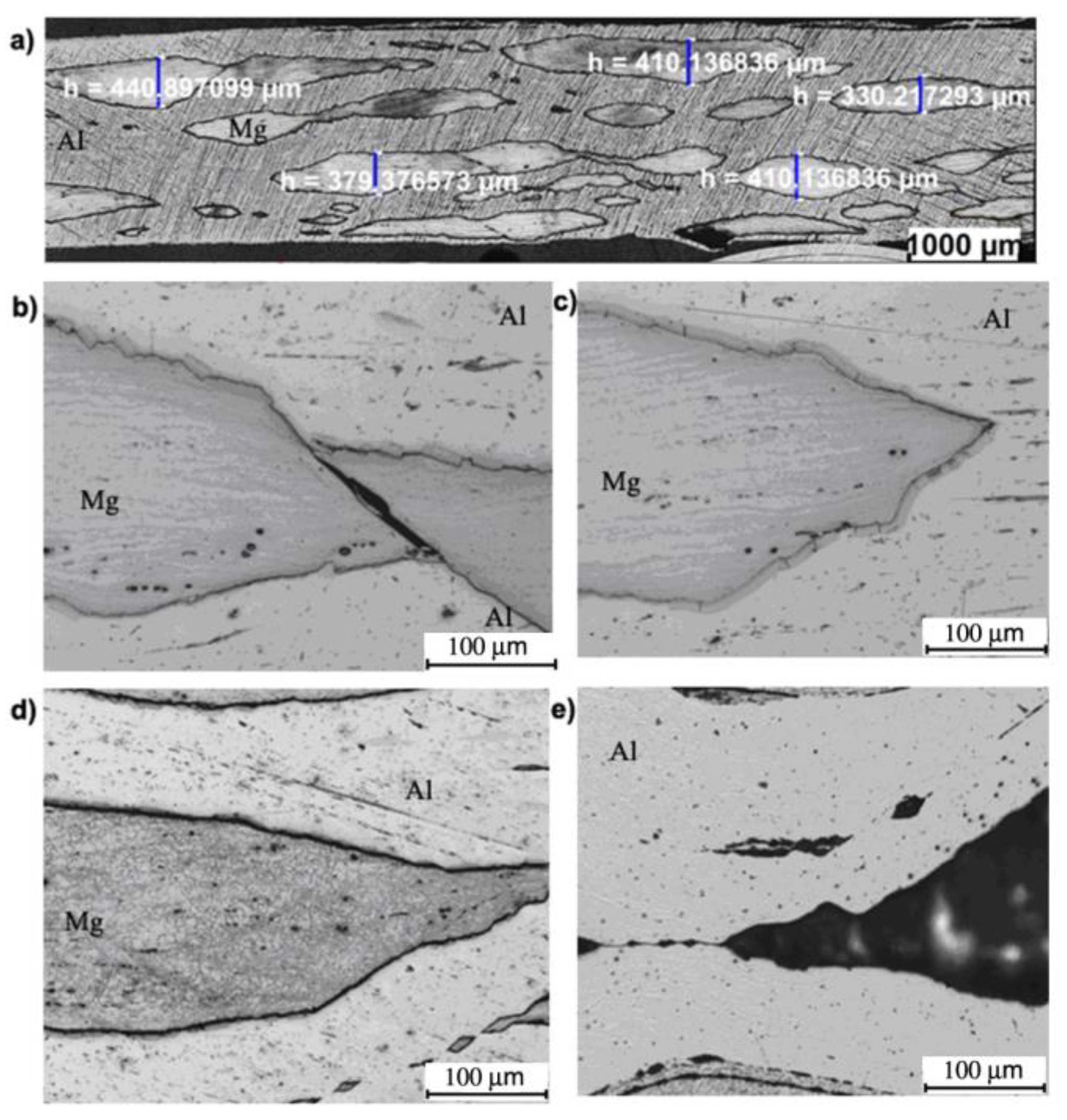


| Material | Al | Mg | Fe | Mn | Ni | Si | Zn | Cu |
|---|---|---|---|---|---|---|---|---|
| 1050A | 99.50 | 0.047 | 0.32 | 0.005 | 0.01 | 0.06 | 0.008 | 0.05 |
| AZ31 | 3.5 | 95.0 | 0.01 | 0.4 | 0.01 | 0.1 | 0.8 | 0.05 |
| Method | Asymmetry Coefficient, av | Cycle no. | Initial Thickness [mm] | Final Thickness [mm] | Reduction [%] | True Strain | |
|---|---|---|---|---|---|---|---|
| ARB | 1.0 | 1 | 3.00 | 1.57 | 47 | 0.64 | 2.75 |
| 2 | 3.14 | 1.49 | 52 | 0.74 | |||
| 3 | 2.98 | 1.52 | 48 | 0.67 | |||
| 4 | 3.04 | 1.51 | 50 | 0.70 | |||
| AARB | 1.25 | 1 | 3.00 | 1.56 | 48 | 0.65 | 2.76 |
| 1.0 | 2 | 3.12 | 1.47 | 53 | 0.75 | ||
| 3 | 2.94 | 1.50 | 49 | 0.67 | |||
| 4 | 3.00 | 1.50 | 50 | 0.69 | |||
| 1.5 | 1 | 3.00 | 1.56 | 48 | 0.65 | 2.77 | |
| 1.0 | 2 | 3.12 | 1.47 | 53 | 0.75 | ||
| 3 | 2.95 | 1.50 | 49 | 0.68 | |||
| 4 | 3.00 | 1.50 | 50 | 0.69 | |||
| Material | Yield Strength, YS, [MPa] | Ultimate Tensile Strength, UTS [MPa] | Elongation A10 [%] |
|---|---|---|---|
| AZ31 | 130 | 240 | 10 |
| 1050A | 30 | 80 | 40 |
| Material | Temperature [°C] | Strain Rate [s−1] | True Strain [–] |
|---|---|---|---|
| 1050A | 350, 400, 450 | 0.1; 1.0; 10 | up to 1.2 |
| AZ31 | 350, 400, 450 | 0.1; 1.0; 10 | up to 1.0 |
| Material | A1 | m1 | m2 | m3 | m4 | m5 | m7 | m8 | m9 |
|---|---|---|---|---|---|---|---|---|---|
| 1050A | 0.08743 | −0.0099 | 0.11325 | −0.08845 | −0.00058 | −0.00153 | 0.196267 | 0.00048 | 1.71527 |
| AZ31 | 0.68478 | −0.0072 | 0.34242 | 0.02864 | −0.08199 | −0.00023 | −0.00439 | 0.00022 | 1.41094 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mroz, S.; Wierzba, A.; Stefanik, A.; Szota, P. Effect of Asymmetric Accumulative Roll-Bonding process on the Microstructure and Strength Evolution of the AA1050/AZ31/AA1050 Multilayered Composite Materials. Materials 2020, 13, 5401. https://doi.org/10.3390/ma13235401
Mroz S, Wierzba A, Stefanik A, Szota P. Effect of Asymmetric Accumulative Roll-Bonding process on the Microstructure and Strength Evolution of the AA1050/AZ31/AA1050 Multilayered Composite Materials. Materials. 2020; 13(23):5401. https://doi.org/10.3390/ma13235401
Chicago/Turabian StyleMroz, Sebastian, Arkadiusz Wierzba, Andrzej Stefanik, and Piotr Szota. 2020. "Effect of Asymmetric Accumulative Roll-Bonding process on the Microstructure and Strength Evolution of the AA1050/AZ31/AA1050 Multilayered Composite Materials" Materials 13, no. 23: 5401. https://doi.org/10.3390/ma13235401
APA StyleMroz, S., Wierzba, A., Stefanik, A., & Szota, P. (2020). Effect of Asymmetric Accumulative Roll-Bonding process on the Microstructure and Strength Evolution of the AA1050/AZ31/AA1050 Multilayered Composite Materials. Materials, 13(23), 5401. https://doi.org/10.3390/ma13235401







