Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Glued Laminated Timber
2.1.2. Solid Wood
2.1.3. CFRP
2.1.4. Epoxy Resin
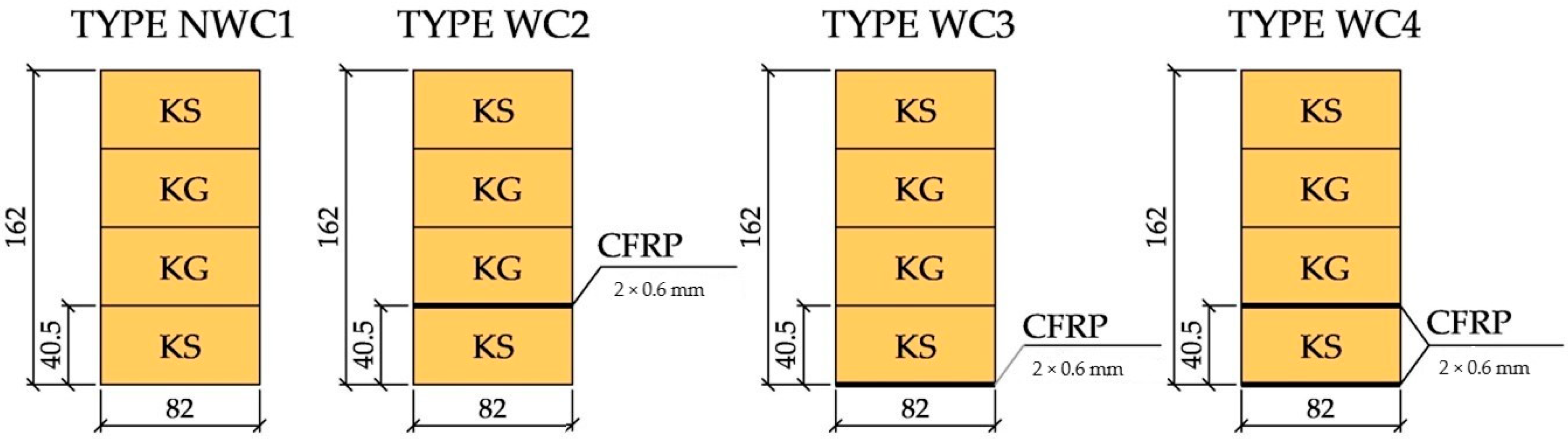
2.1.5. CFRP Reinforcement Preparations
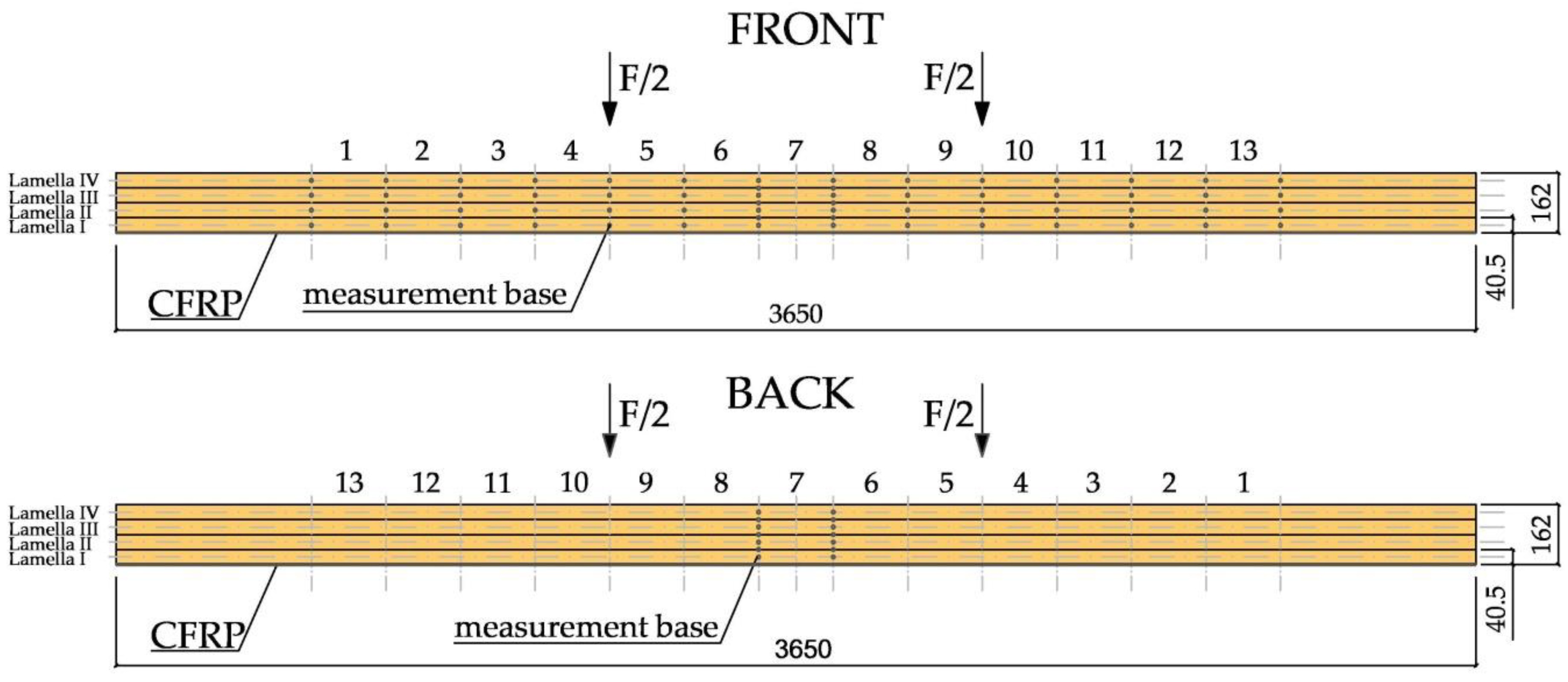
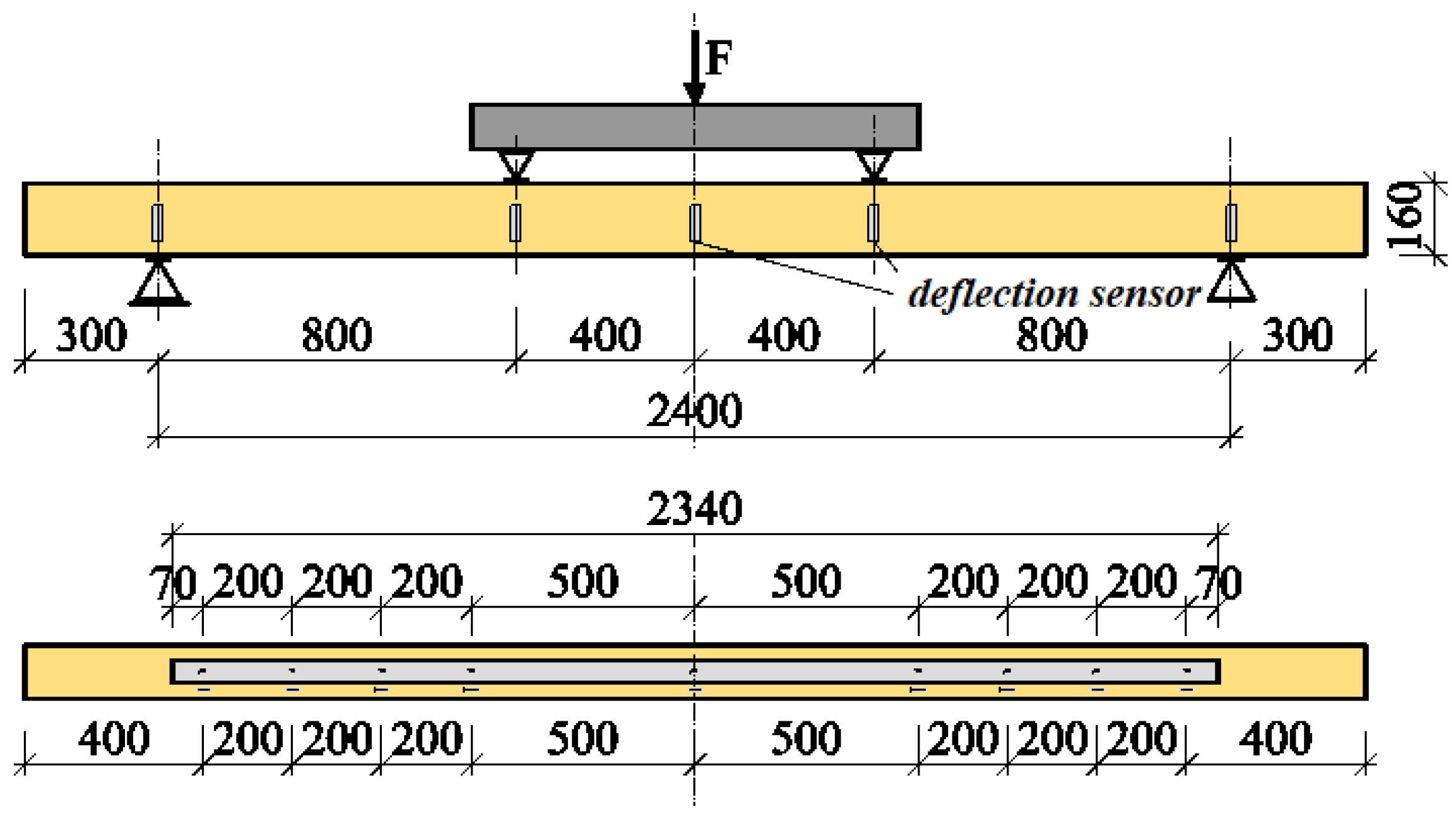
2.2. Method
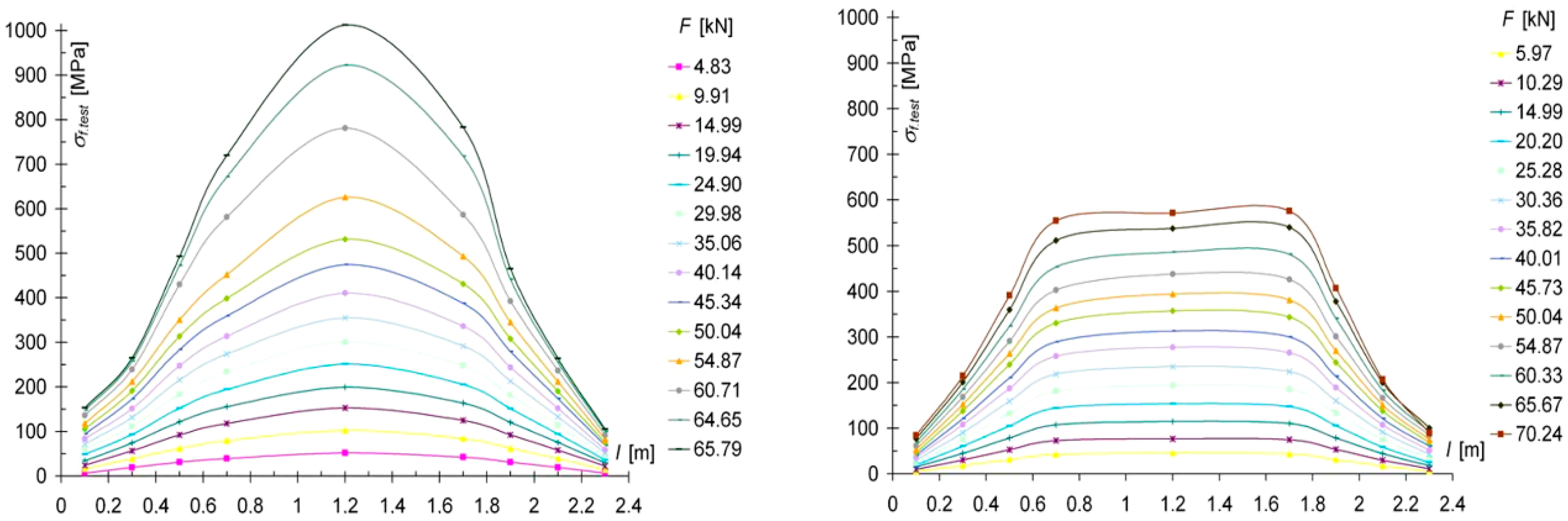
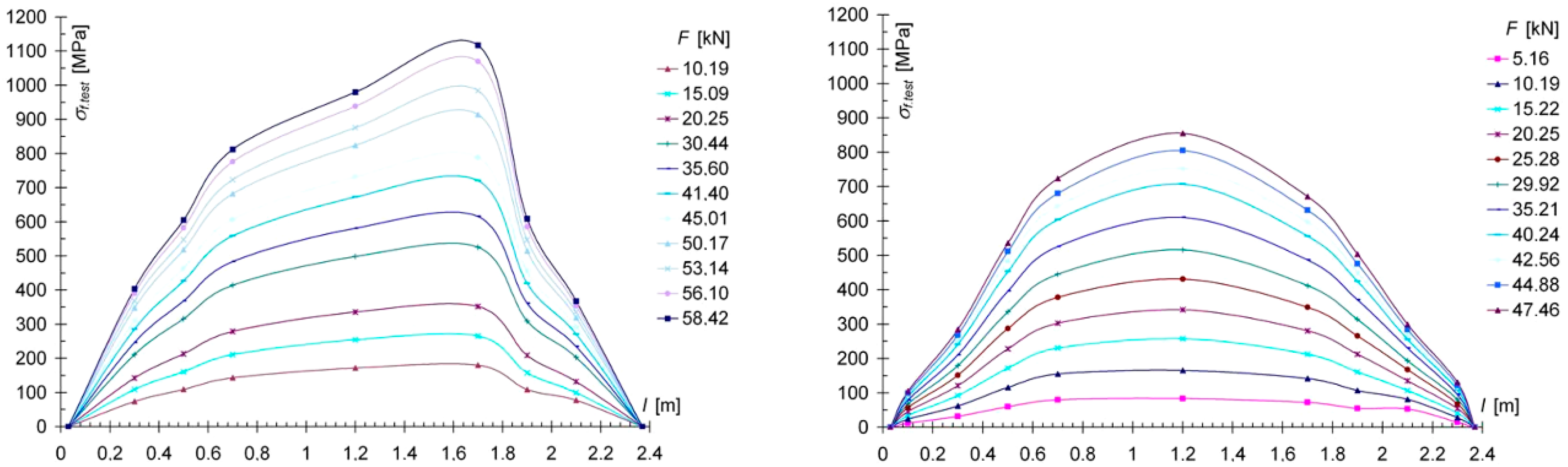
3. Results
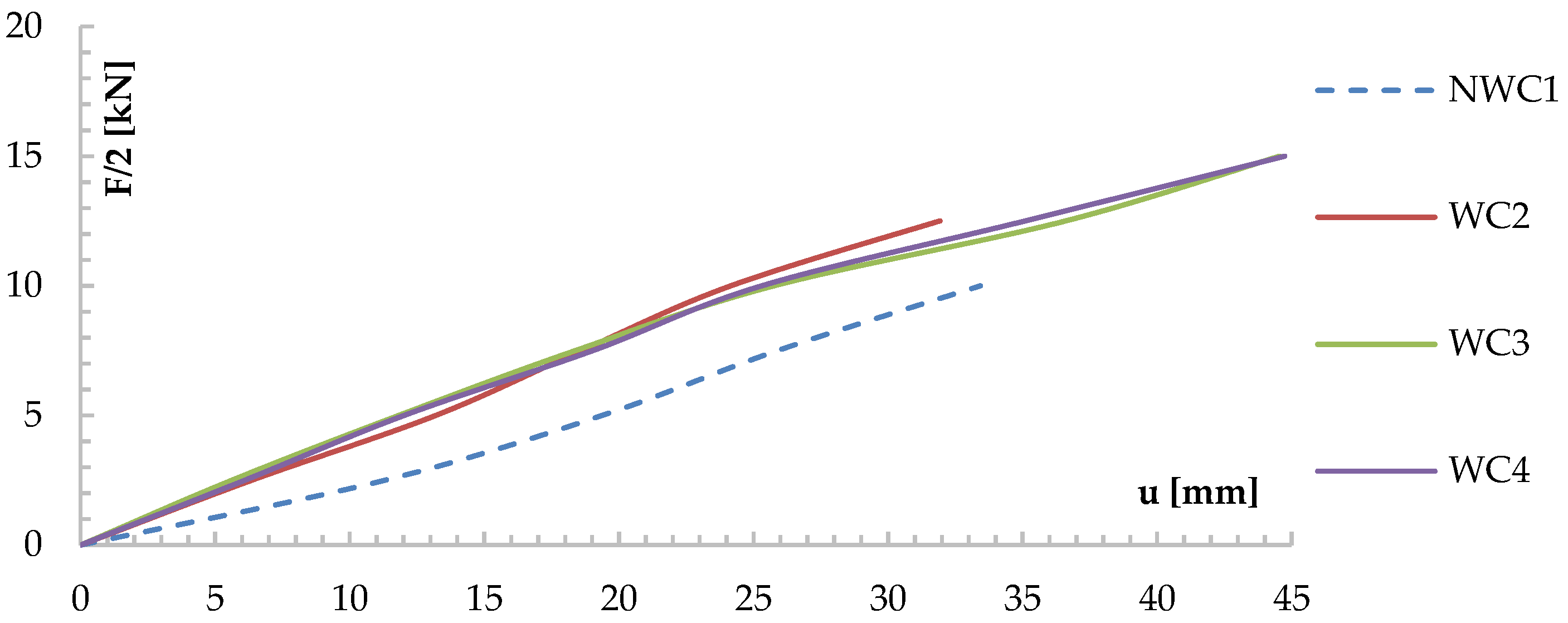
3.1. Results for Reinforced Glued Laminated Beams
3.2. Results for Reinforced Solid Wood Beams
4. Analytical Validation
5. Conclusions
- For the models tested here, an increase in the bending strength of the reinforced beams was observed. The increase in the load capacity of beams with natural wood defects was due to the use of CFRP materials in the tension zone, which increased the ductility of the wood. The load-bearing capacity of the reinforced and glued beams increased by about 23% compared to the control beams, and about 28% for the solid timber beams. Due to the continuity of the tension zone in beams containing defects and reinforced with CFRP materials, an increase in bending stiffness of 36.29% was observed for the glued beams, and about 20% for the solid wood beams. It should be emphasized that the quantitative increases in stiffness and load capacity depend directly on the cross-sectional dimensions and the percentage of reinforcement.
- The applied reinforcement method has a favorable effect on structural elements with reduced mechanical properties in the tension zones. In the case of solid timber and glued timber, there are natural defects in the structure, such as knots, twisted fibers, or others, which have a negative impact, especially in the tension zones, causing discontinuity in this zone, both in bent and tension elements. Due to their high tensile stiffness, CFRP materials effectively reduce the impact of wood weakening caused by e.g., knots, which has a direct impact on the safety of the structure.
- In the course of the above-mentioned research, it was observed that in reinforced beams, in the case of a wood defect in the lower part of the bending beams, these defects did not significantly affect the stiffness of the beams, and the reserve capacity of the tapes allowed them to absorb and safely transfer additional stresses, which effectively improved the safety of the beams.
- The proposed analytical approach seems to show a satisfactory convergence with the results obtained from laboratory tests, but nevertheless it still requires further comparison analyses with the other tests.
- Due to the limited number of studies described in the literature, further research should be continued on the reinforcement of non-homogeneous glued and solid beams with FRP materials, and the impact of structural and geometric characteristics of wood (including wood defects) on the effect of strengthening these beams or checking the behavior of reinforced beams composite materials at the time of their destruction.
Author Contributions
Funding
Conflicts of Interest
References
- Glišović, I.; Stevanović, B.; Petrović, M. Bending behaviour of glulam beams reinforced with carbon FRP plates. J. Civ. Eng. Manag. 2015, 21, 923–932. [Google Scholar] [CrossRef]
- Jacob, J.; Barragan, O.L.G. Flexural Strengthening of Glued Laminated Timber Beams with Steel and Carbon Fiber Reinforced Polymers. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2010. [Google Scholar]
- Juvandes, L.F.P.; Barbosa, R.M.T. Bond analysis of timber structures strengthened with FRP systems. Strain 2012, 48, 124–135. [Google Scholar] [CrossRef]
- Wdowiak, A.; Brol, J. Effectiveness of Reinforcing Bent Non-Uniform Pre-Stressed Glulam Beams with Basalt Fibre Reinforced Polymers Rods. Materials 2019, 12, 3141. [Google Scholar] [CrossRef] [Green Version]
- Brol, J.; Wdowiak-Postulak, A. Old Timber Reinforcement with FRP. Materials 2019, 12, 4197. [Google Scholar] [CrossRef] [Green Version]
- Borri, A.; Corradi, M.; Speranzini, E. Bending Tests on Natural Fiber Reinforced Fir Wooden Elements. Adv. Mat. Res. 2013, 778, 537–544. [Google Scholar] [CrossRef]
- Nadir, Y.; Nagarajan, P.; Ameen, M.; Muhammed, A.M. Flexural stiffness and strength enhancement of horizontally glued laminated wood beams with GFRP and CFRP composite sheets. Constr. Build. Mater. 2016, 112, 547–555. [Google Scholar] [CrossRef]
- Li, Y.F.; Xie, Y.M.; Tsai, M.J. Enhancement of the flexural performance of retrofitted wood beams using CFRP composite sheets. Constr. Build. Mater. 2009, 23, 411–422. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Grazini, A. A method for flexural reinforcement of old wood beams with CFRP materials. Compos. Part B Eng. 2005, 36, 143–153. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A. Fir and chestnut timber beams reinforced with GFRP pultruded elements. Compos. Part B Eng. 2007, 38, 172–181. [Google Scholar] [CrossRef]
- Johnsson, H.; Blanksvärd, T.; Carolin, A. Glulam members strengthened by carbon fibre reinforcement. Mater. Struct. 2006, 40, 47–56. [Google Scholar] [CrossRef]
- Plevris, N.; Triantafillou, T.C. FRP Reinforced Wood as Structural Material. J. Mater. Civ. Eng. ASCE 1992, 4, 300–315. [Google Scholar] [CrossRef]
- Schober, K.U.; Rautenstrauch, K. Experimental investigations on flexural strengthening of timber structures with CFRP. In International Symposium on Bond Behaviour of FRP in Structures (BBFS 2005); International Institute for FRP in Construction: Hong Kong, China, 2005. [Google Scholar]
- Schober, K.U.; Rautenstrauch, K. Post-strengthening of timber structures with CFRP’s. Mater. Struct. 2007, 40, 27–35. [Google Scholar] [CrossRef]
- Jankowski, L.J.; Jasieńko, J.; Nowak, T.P. Experimental assessment of CFRP reinforced wooden beams by 4-point bending tests and photoelastic coating technique. Mater. Struct. 2010, 43, 141. [Google Scholar] [CrossRef]
- Meier, U. Strengthening of structures using carbon fibre/epoxy composites. Constr. Build. Mater. 1995, 9, 341–351. [Google Scholar] [CrossRef]
- Parisi, M.A.; Piazza, M. Rehabilitation of timber structures by new materials and connectors. In Proceedings of the 10th International Conference Structural Faults & Repair 2003—Extending the Life of Bridges, Concrete & Composites, Buildings, Masonry & Civil Structures’, London, UK, 1–3 July 2003. [Google Scholar]
- Johns, K.C.; Lacroix, S. Composite reinforcement of timber in bending. Can. J. Civ. Eng. 2000, 27, 899–906. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Shear reinforcement of wood using FRP materials. J. Mater. Civ. Eng. ASCE 1997, 9, 65–69. [Google Scholar] [CrossRef]
- Gentile, C.; Svecova, D.; Saltzberg, W.; Rizkalla, S.H. Strengthening for Timber Bridges. In Proceedings of the World Wise’99, Winnipeg, MB, Canada, 6–8 December 1999. [Google Scholar]
- Brol, J.; Wdowiak, A. The Use of Glass and Aramid Fibres for the Strengthening of Timber Structures; Annals of Warsaw University of Life Sciences, Forestry and Wood Technology: Warsaw, Poland, 2017; pp. 128–138. [Google Scholar]
- Brol, J.; Nowak, T.; Wdowiak, A. Numerical Analysis and Modelling of Timber Elements Strengthened with FRP Materials; Annals of Warsaw University of Life Sciences, Forestry and Wood Technology: Warsaw, Poland, 2018; pp. 274–282. [Google Scholar]
- Wdowiak, A. Analysis of bent timber beam reinforcement with the application of composite materials. Struct. Environ. 2016, 8, 10–16. [Google Scholar]
- Wdowiak, A. Właściwości Strukturalno—Wytrzymałościowe Zginanych Belek Drewnianych Wzmocnionych Kompozytami Włóknistymi [Structural and Strength Properties of Bent Wooden Beams Reinforced with Fibre Composites]. Ph.D. Thesis, Kielce University of Technology, Kielce, Poland, 12 April 2019. [Google Scholar]
- Wdowiak, A.; Kroner, A. Wpływ niejednorodności struktury zginanych belek z drewna klejonego na efekt ich wzmocnienia. Mater. Bud. 2017, 1, 87–89. [Google Scholar] [CrossRef]
- Wdowiak, A.; Brol, J. Methods of strength grading of structural timber—Comparative analysis of visual and machine grading on the example of Scots pine timber from four natural forest regions of Poland. Struct. Environ. 2019, 11, 210–224. [Google Scholar] [CrossRef]
- Fiorelli, J.; Dias, A.A. Evaluation of the Structural Behavior of Wood Beams Reinforced with FRP″. In Proceedings of the 7th World Conference on Timber Engineering, WCTE 2002, Perpustakaan Negara Malaysia, Kuala Lumpur, Malaysia, 12–15 August 2002; pp. 225–262. [Google Scholar]
- Buell, T.W.; Saadatmanesh, H. Strengthening Timber Bridge Beams Using Carbon Fibre. J. Struct. Eng. 2005, 131, 173–187. [Google Scholar] [CrossRef]
- Alam, P.; Ansell, M.P.; Smedley, D. Mechanical Repair of Timber Beams Fractured in Flexure Using Bonded-in Reinforcements. Compos. B Eng. 2009, 40, 95–106. [Google Scholar] [CrossRef]
- Brol, J. Analiza Doświadczalno-Teoretyczna Wzmacniania Konstrukcji Drewnianych Kompozytami Polimerowo-Węglowymi [Experimental and Theoretical Analysis of Wooden Structures Strengthening with Polymer-Carbon Composites]. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2005. [Google Scholar]
- Nowak, T. Analiza Pracy Statycznej Zginanych Belek Drewnianych Wzmacnianych Przy Użyciu CFRP [Analysis of the Static Work of Bent Wooden Beams Reinforced with CFRP]. Ph.D. Thesis, Wrocław University of Science and Technology, Wroclaw, Poland, 2005. [Google Scholar]
- Mukhopadhyaya, T.; Naskarb, S.; Deyc, S.; Chakrabartid, A. Condition assessment and strengthening of aged structures: Perspectives based on a critical case study. Pract. Period. Struct. Des. Constr. 2019, 24, 05019003. [Google Scholar] [CrossRef]
- Moisture Content of a Piece of Sawn Timber—Part 2: Estimation by Electrical Resistance Method; PN-EN 13183-2:2004; Polish Committee for Standardization: Warsaw, Poland, 2004.
- Moisture Content of a Piece of Sawn Timber—Part 3: Estimation by Capacitance Method; PN-EN 13183-3:2007; Polish Committee for Standardization: Warsaw, Poland, 2007.
- Coniferous Construction Timber Sorted by Strength Methods; PN-D-94021:2013-10; Polish Committee for Standardization: Warsaw, Poland, 2013.
- Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties; PN-EN 408+A1:2012; Polish Committee for Standardization: Warsaw, Poland, 2012.
- Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings; PN-EN 1995-1-1: 2010, Eurocode 5; Polish Committee for Standardization: Warsaw, Poland, 2010.



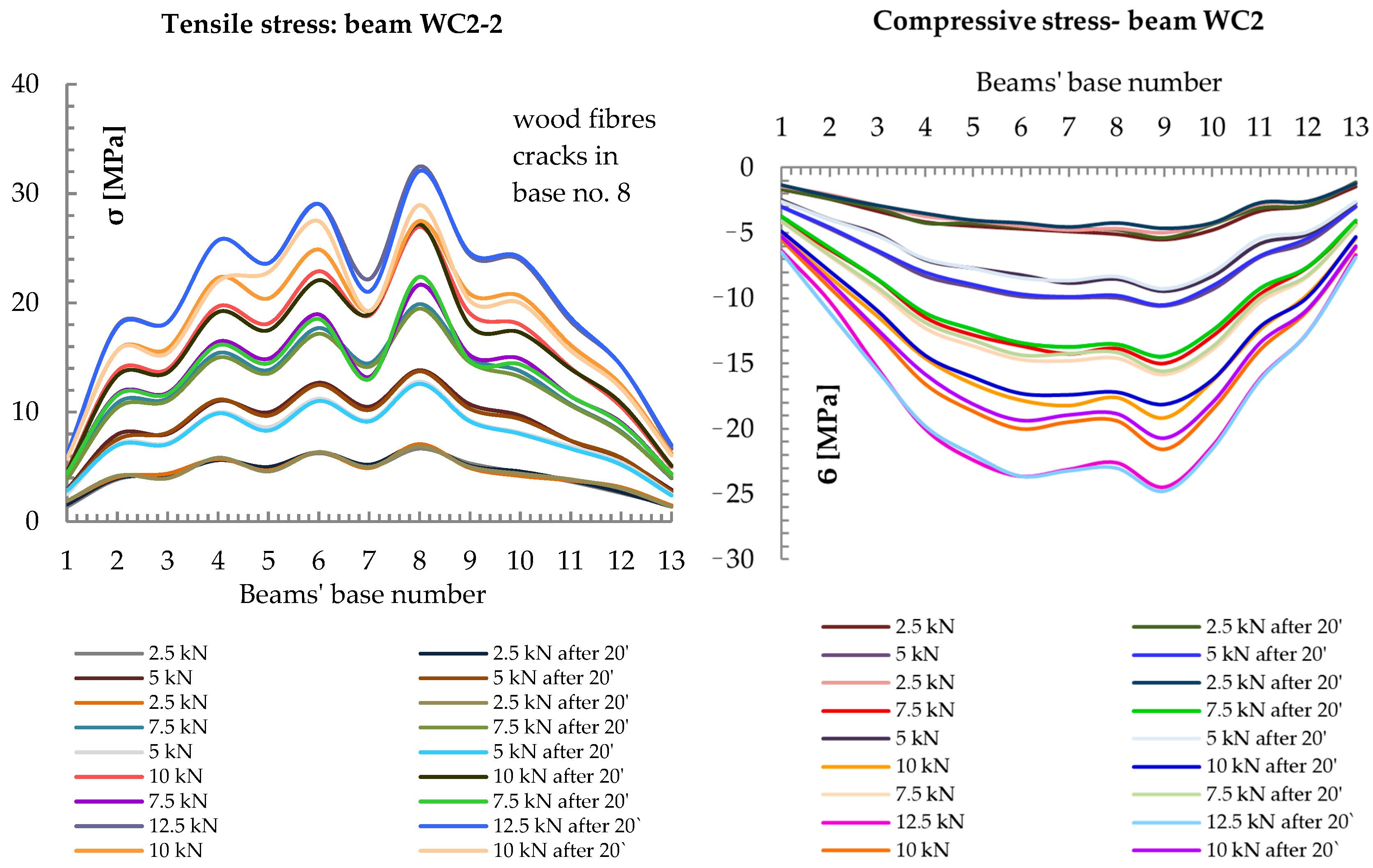
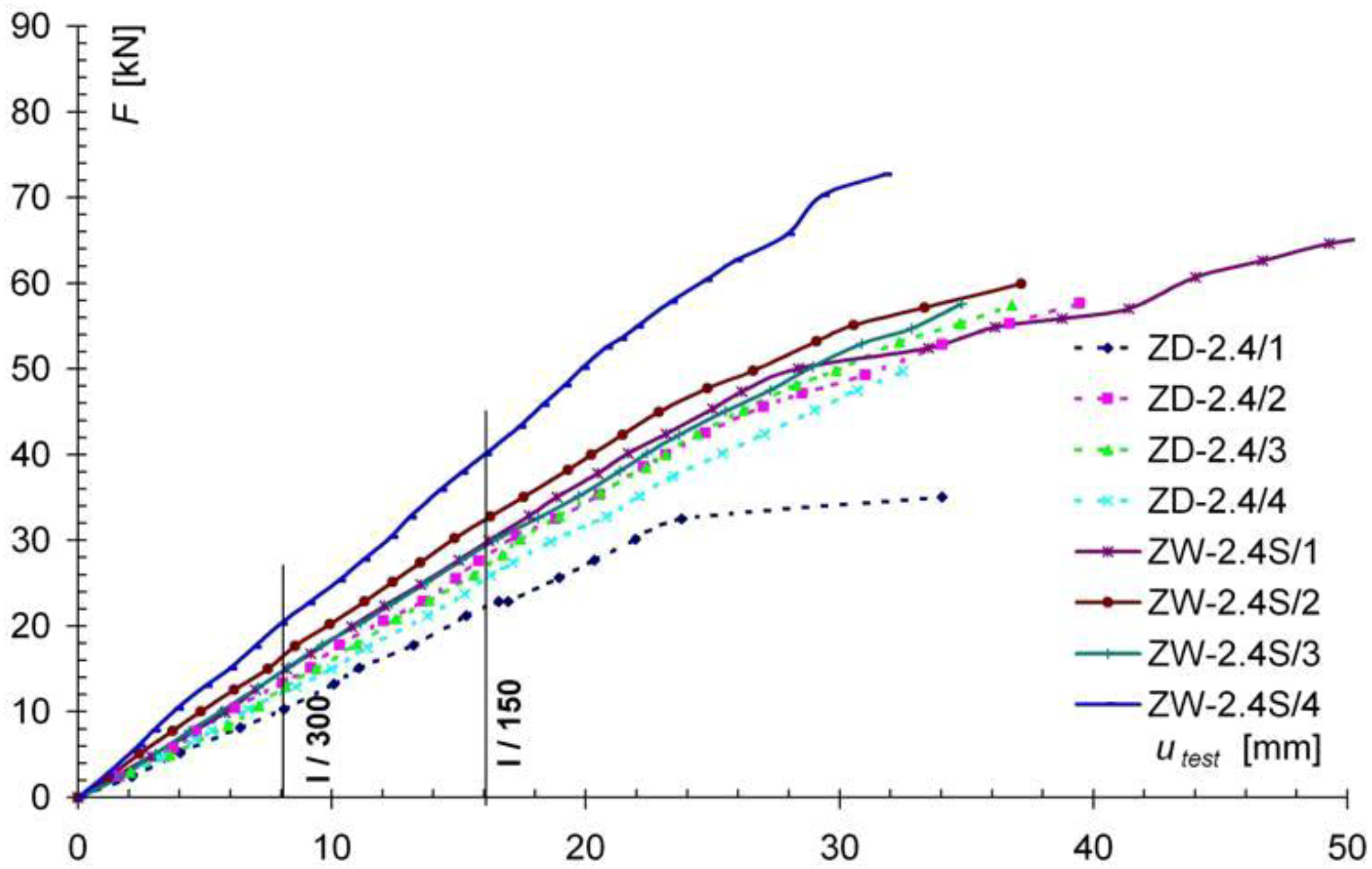
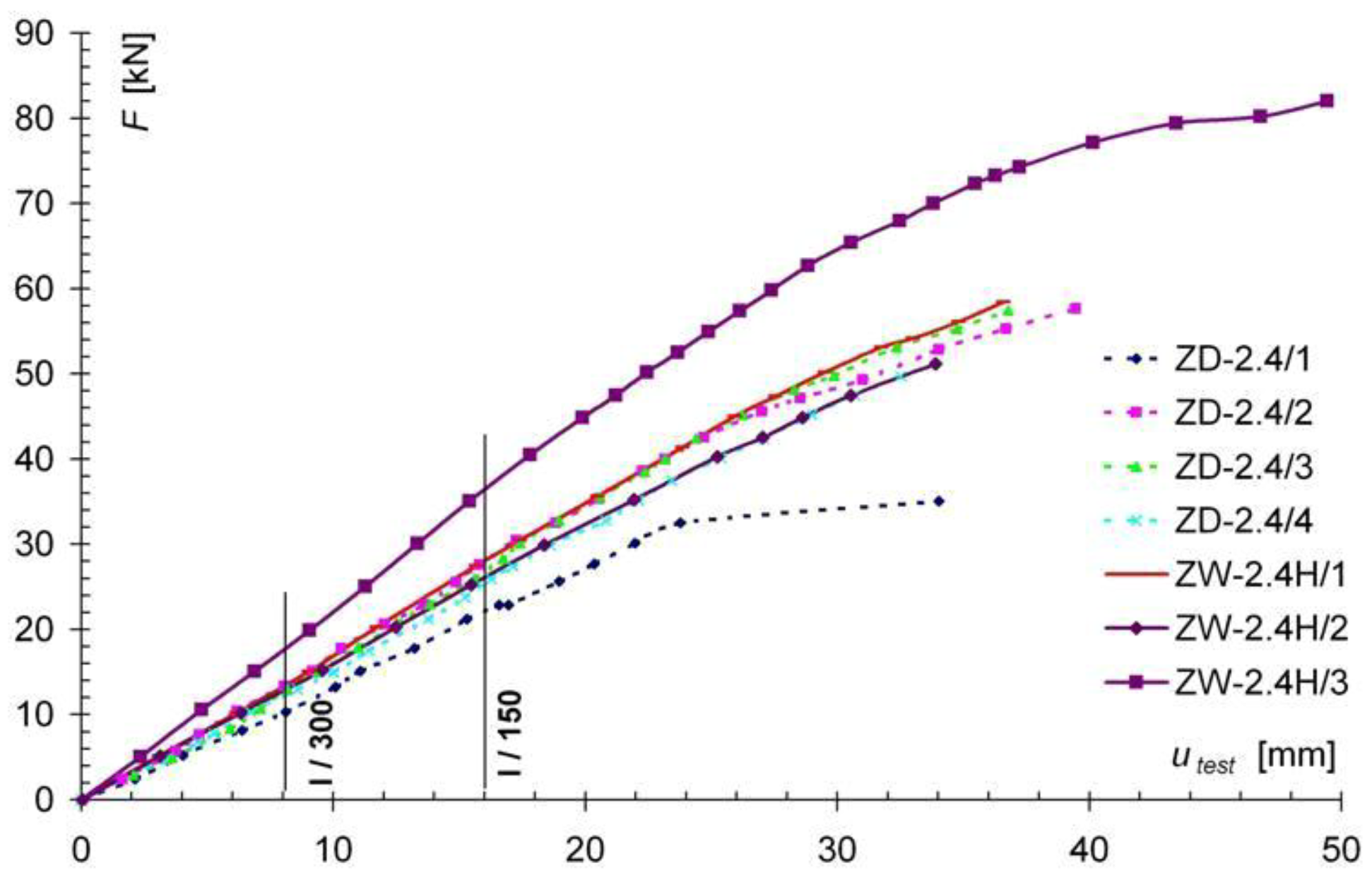

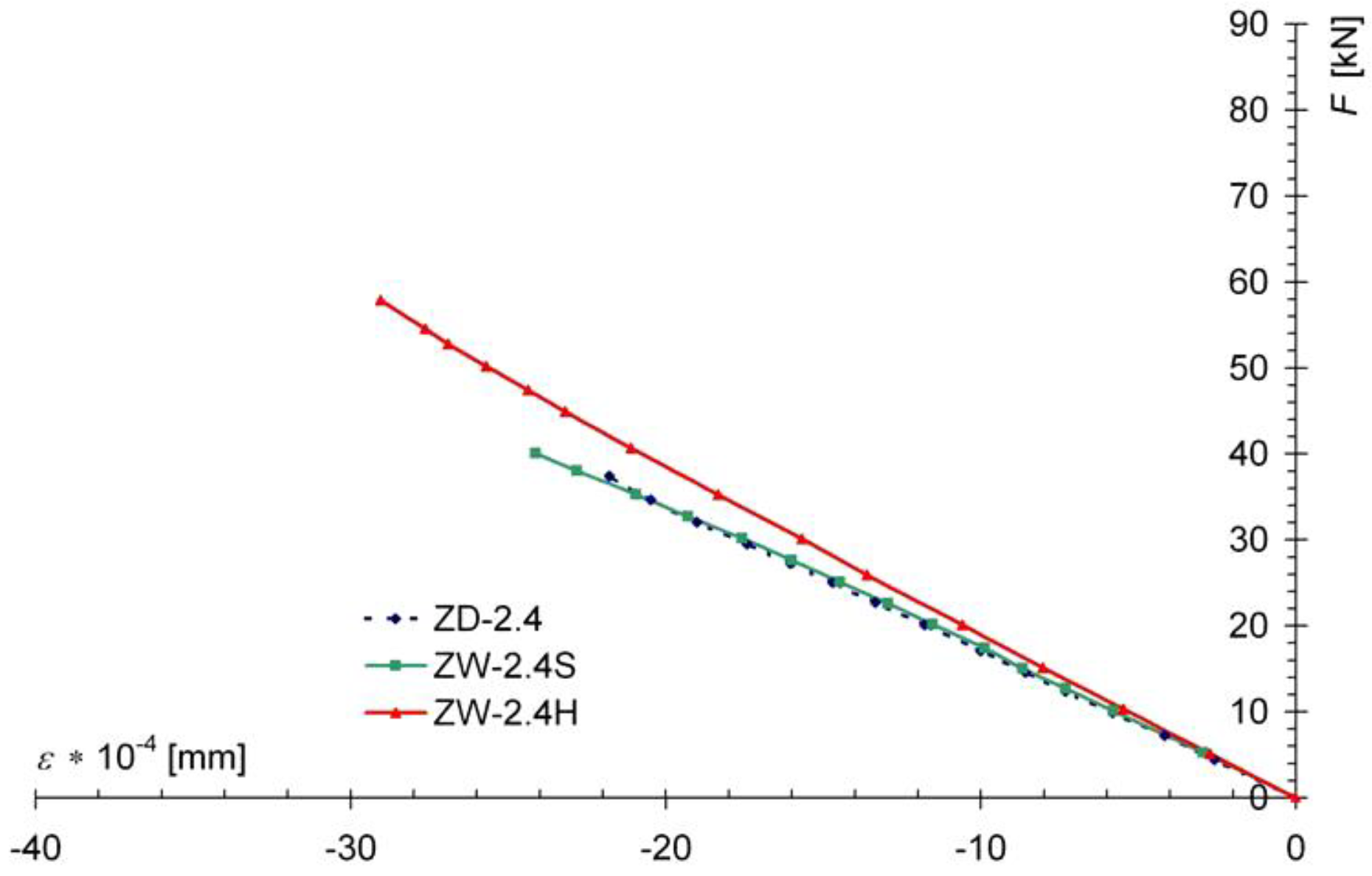


| Model | Fmax,(mean) [kN] | Mmax [kNm] |
|---|---|---|
| NWC1-1 | 30.40 | 15.20 |
| NWC1-2 | 32.82 | 16.41 |
| NWC1-3 | 27.48 | 13.74 |
| Mean | 30.23 | 15.12 |
| Standard deviation | 2.67 | 1.34 |
| WC2-1 | 37.96 | 18.98 |
| WC2-2 | 38.30 | 19.15 |
| WC2-3 | 33.44 | 16.72 |
| Mean | 36.57 | 18.28 |
| Standard deviation | 2.71 | 1.36 |
| WC3-1 | 38.04 | 19.02 |
| WC3-2 | 37.70 | 18.85 |
| WC3-3 | 34.24 | 17.12 |
| Mean | 36.66 | 18.33 |
| Standard deviation | 2.10 | 1.05 |
| WC4-1 | 40.04 | 20.02 |
| WC4-2 | 38.12 | 19.06 |
| WC4-3 | 37.98 | 18.99 |
| Mean | 38.71 | 19.36 |
| Standard deviation | 1.15 | 0.58 |
| Model | Fmax,(mean) [kN] | Mmax [kNm] |
|---|---|---|
| ZD-2.4/1 | 35.03 | 14.01 |
| ZD-2.4/2 | 57.66 | 23.06 |
| ZD-2.4/3 | 57.41 | 22.96 |
| ZD-2.4/4 | 49.73 | 16.89 |
| Mean | 49.96 | 19.98 |
| Standard deviation | 10.61 | 4.24 |
| ZW-2.4S/1 | 65.79 | 26.32 |
| ZW-2.4S/2 | 59.95 | 23.98 |
| ZW-2.4S/3 | 57.60 | 23.04 |
| ZW-2.4S/4 | 72.65 | 29.06 |
| Mean | 64.00 | 25.60 |
| Standard deviation | 6.72 | 2.69 |
| ZW-2.4H/1 | 60.32 | 24.13 |
| ZW-2.4H/2 | 51.20 | 20.48 |
| ZW-2.4H/3 | 82.02 | 32.81 |
| Mean | 64.51 | 25.81 |
| Standard deviation | 15.83 | 6.33 |
| Model | Mmax [kNm] | Mr [kNm] |
|---|---|---|
| WC2 (Mean) | 18.28 | 18.51 |
| WC3 (Mean) | 18.33 | 19.40 |
| WC4(Mean) | 19.36 | 20.03 |
| ZW-2.4S (Mean) | 25.60 | 25.23 |
| ZW-2.4H (Mean) | 25.81 | 25.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wdowiak-Postulak, A.; Brol, J. Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials. Materials 2020, 13, 5451. https://doi.org/10.3390/ma13235451
Wdowiak-Postulak A, Brol J. Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials. Materials. 2020; 13(23):5451. https://doi.org/10.3390/ma13235451
Chicago/Turabian StyleWdowiak-Postulak, Agnieszka, and Janusz Brol. 2020. "Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials" Materials 13, no. 23: 5451. https://doi.org/10.3390/ma13235451
APA StyleWdowiak-Postulak, A., & Brol, J. (2020). Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials. Materials, 13(23), 5451. https://doi.org/10.3390/ma13235451






