Numerical Simulation and Experimental Investigation of the Preparation of Aluminium Alloy 2A50 Semi-Solid Billet by Electromagnetic Stirring
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methodology
2.1.1. Simulation Method
2.1.2. Model Assumptions
- (a)
- The influence of displacement current and metal paste movement on the electromagnetic field is not considered.
- (b)
- The influence of the cooling water pipe, the insulation layer, and the corundum pipe on the magnetic field is negligible.
- (c)
- The Joule heat generated by the electromagnetic field in the slurry is ignored due to the low stirring frequency and short stirring time.
- (d)
- The metal slurry is regarded as an incompressible single-phase non-Newtonian fluid.
- (e)
- The average EMS force during one cycle is used to couple with other field variables instead of the instantaneous EMS force.
2.1.3. Simulation Model
2.1.4. Governing Equations
2.2. Experimental Design
2.2.1. Experimental Setup and Materials
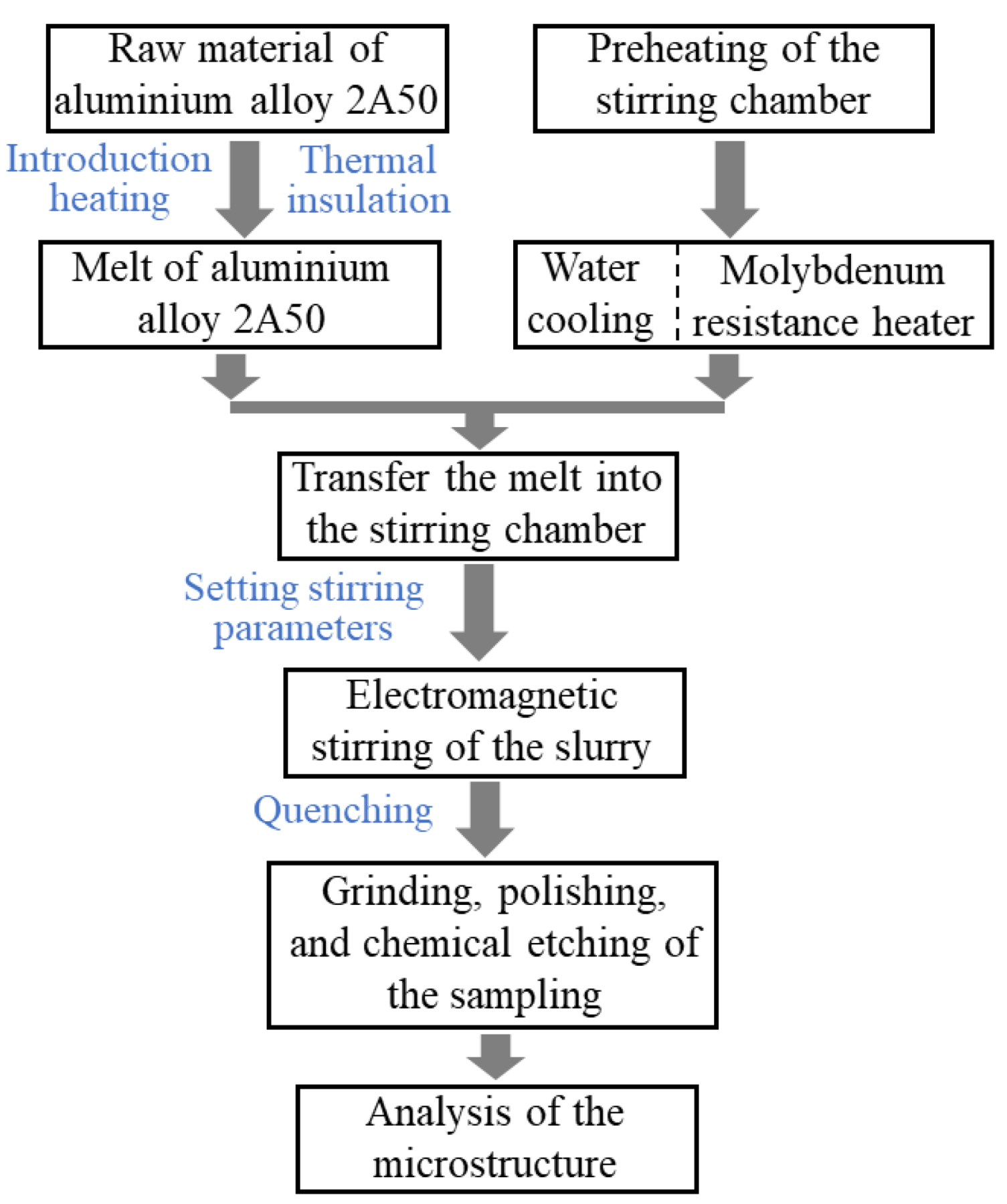
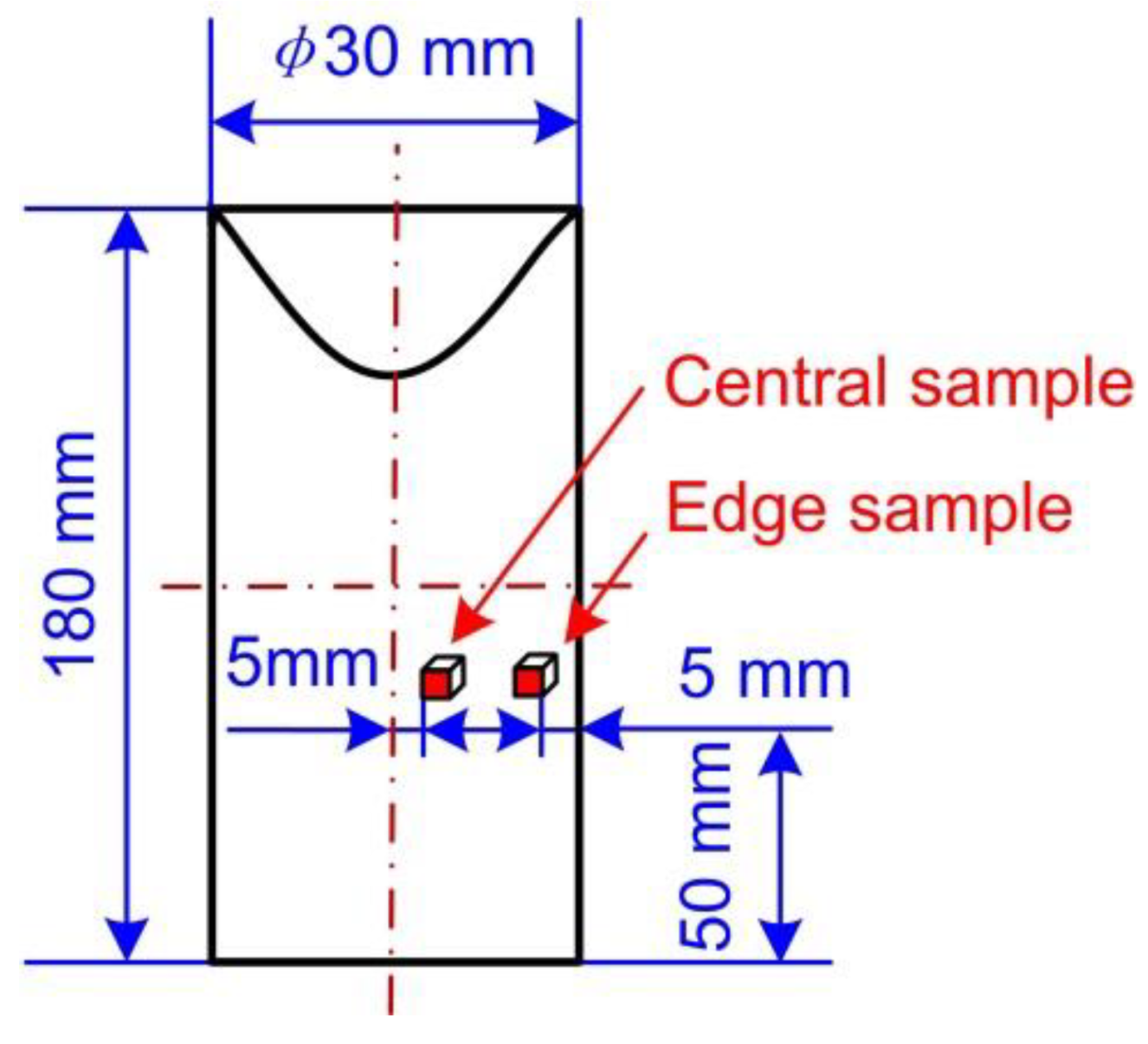
2.2.2. Experimental Procedure
3. Results and Discussion
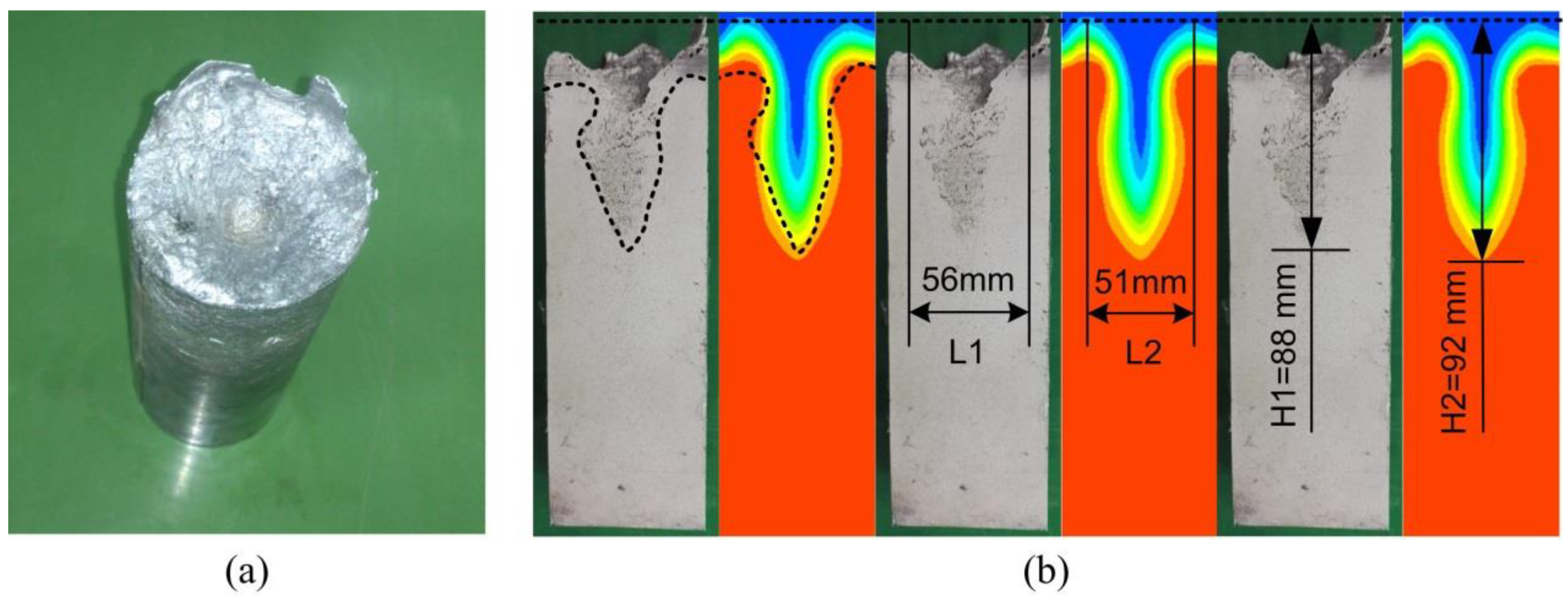
3.1. Verification of the Numerical Model
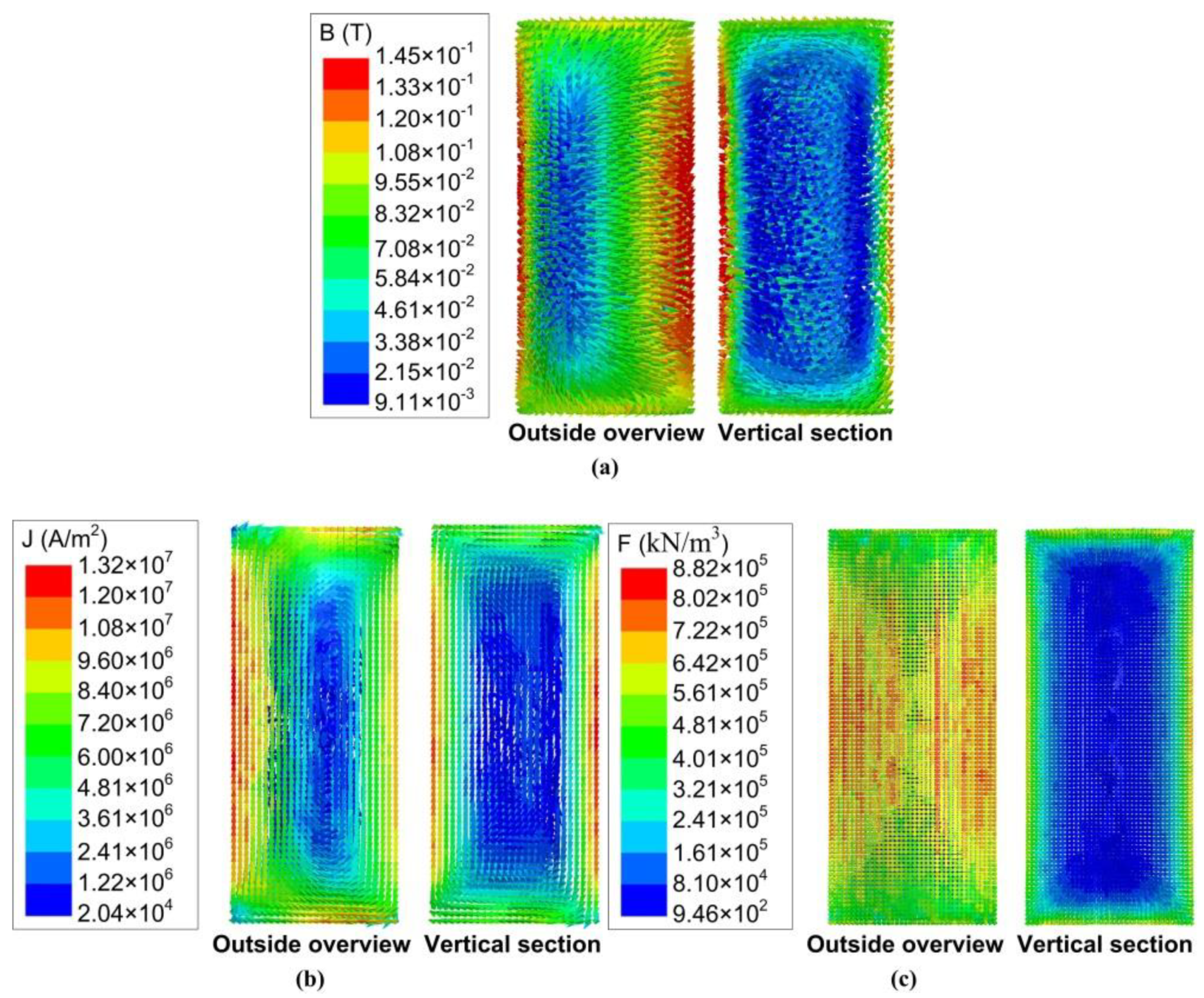
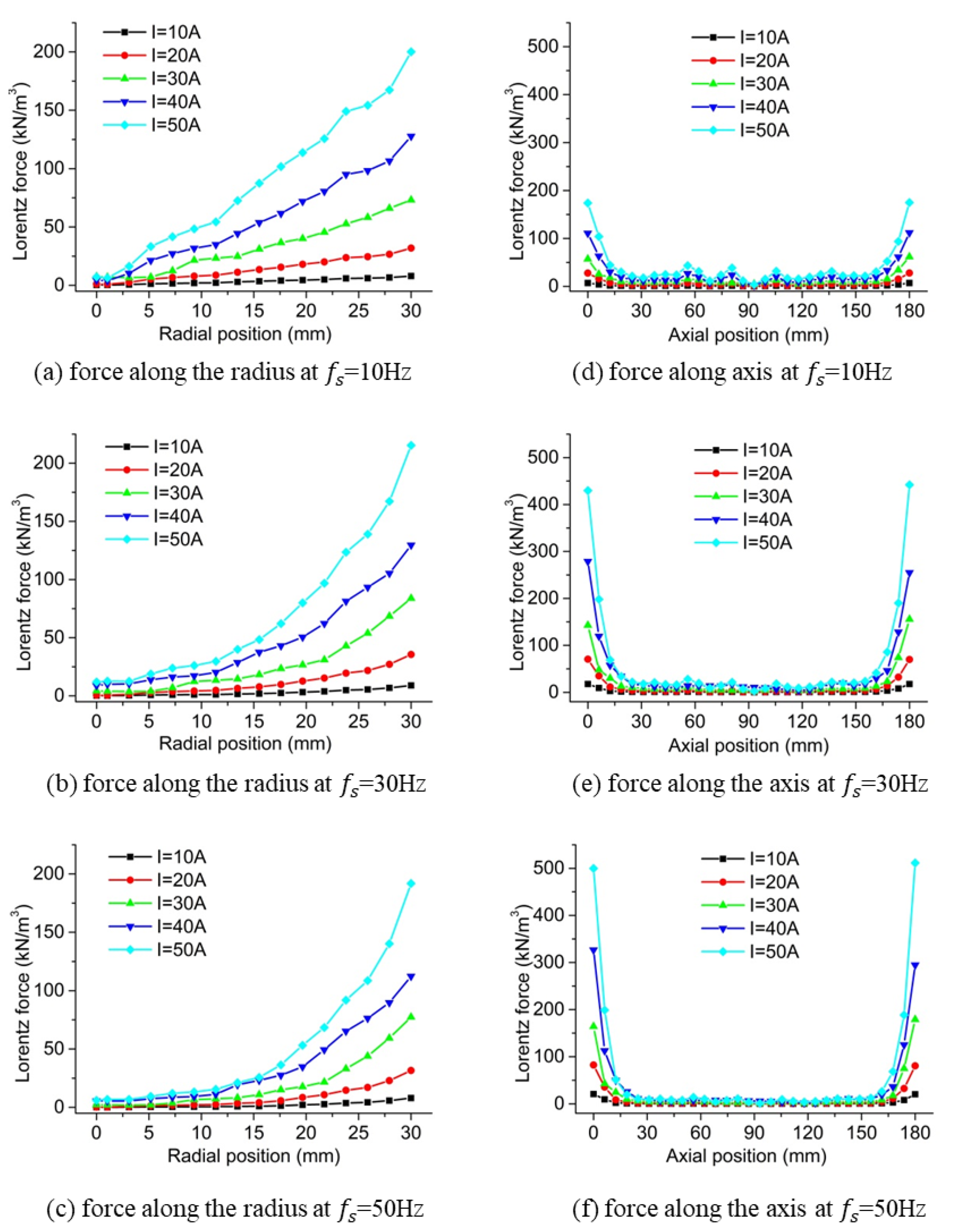
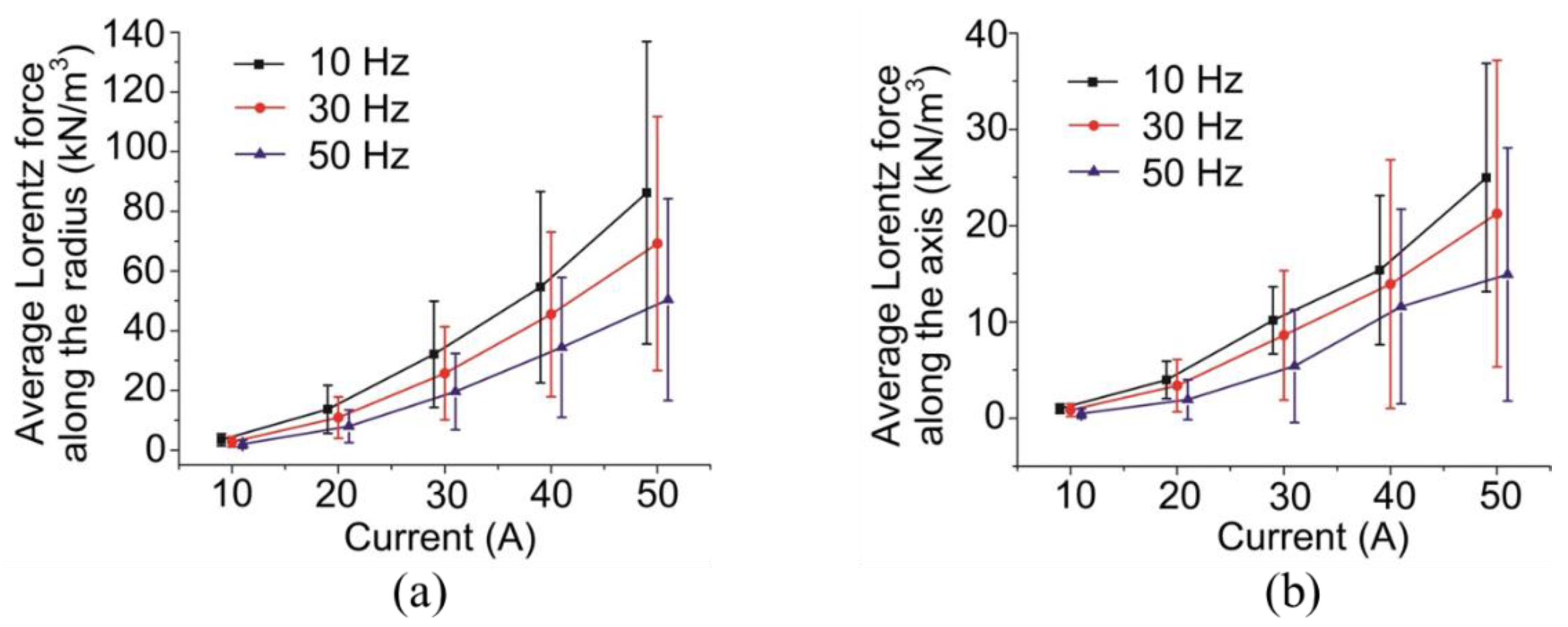
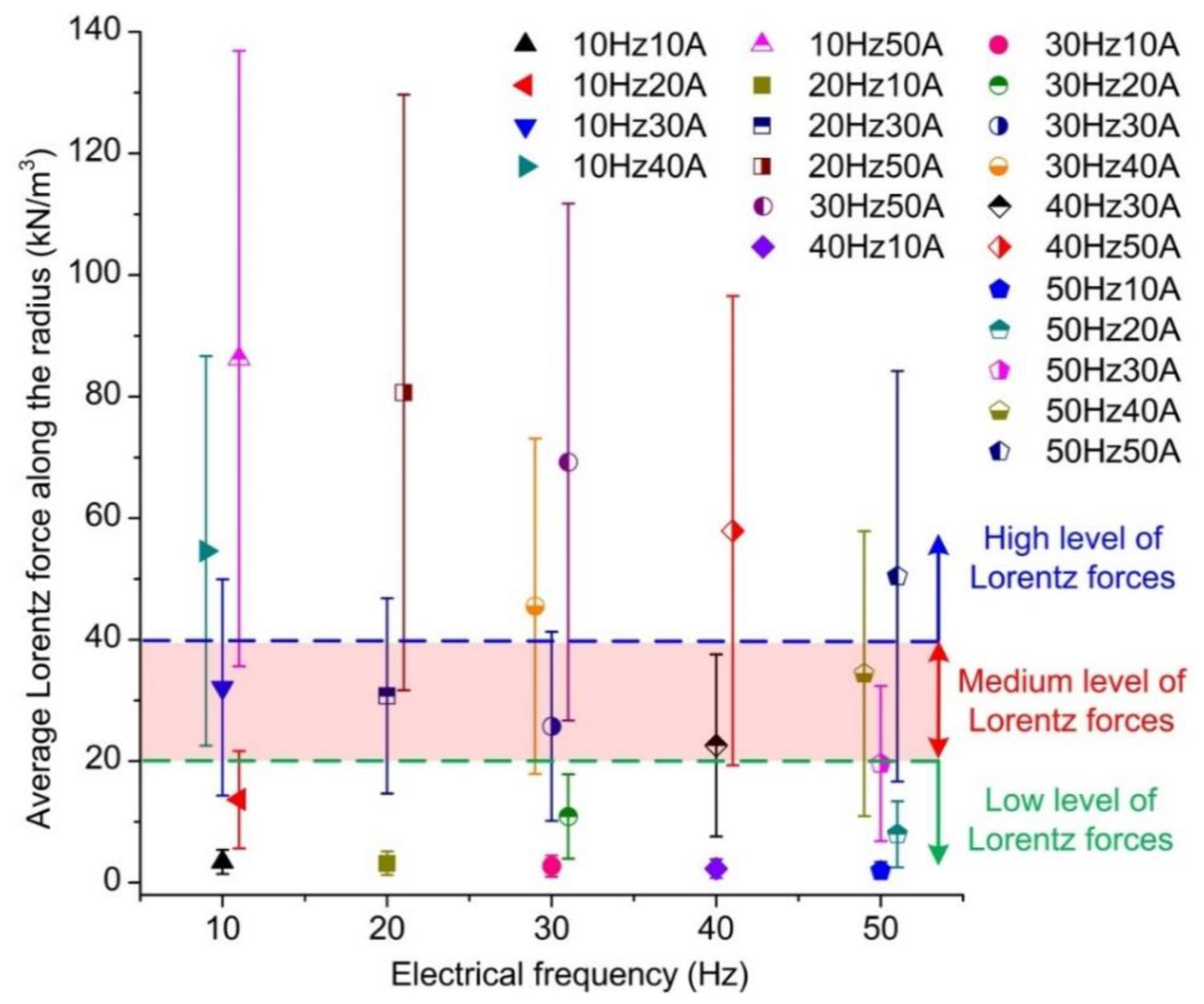
3.2. Results of the Magnetohydrodynamics Analysis
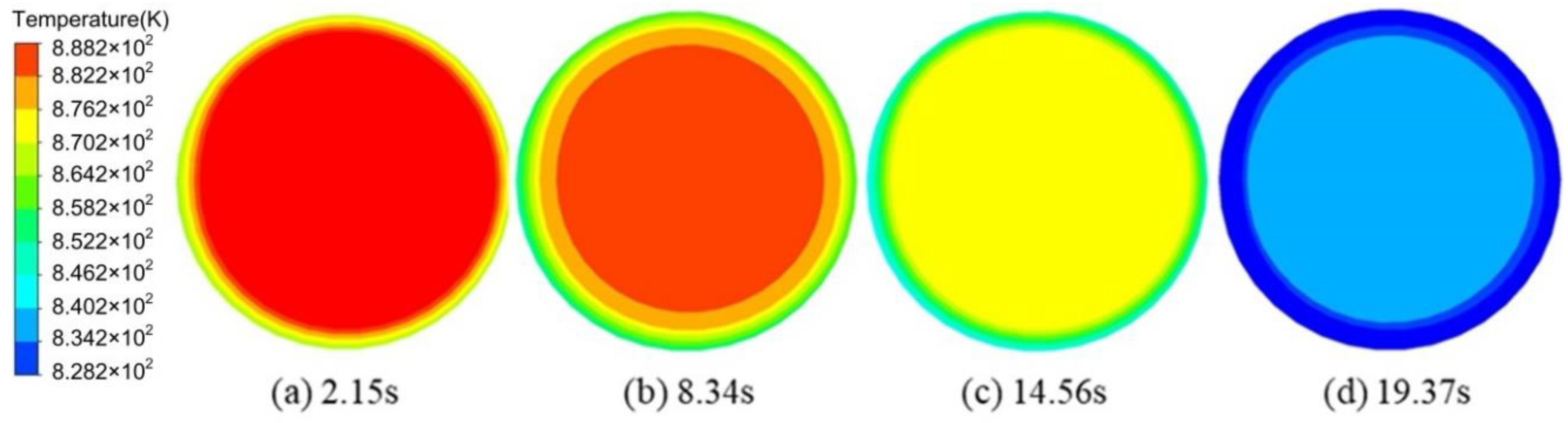
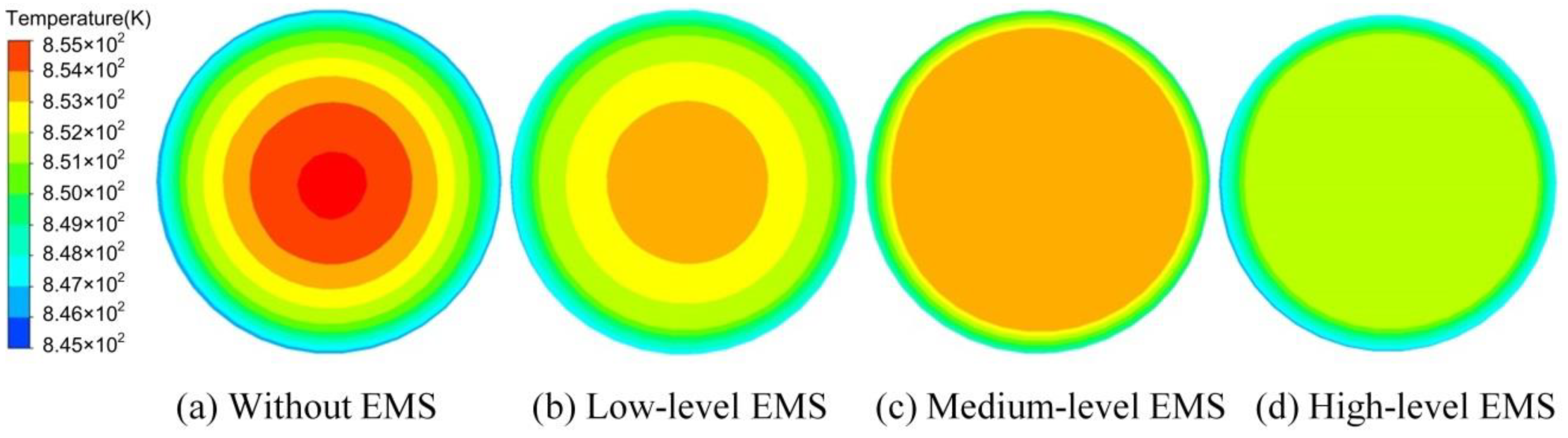
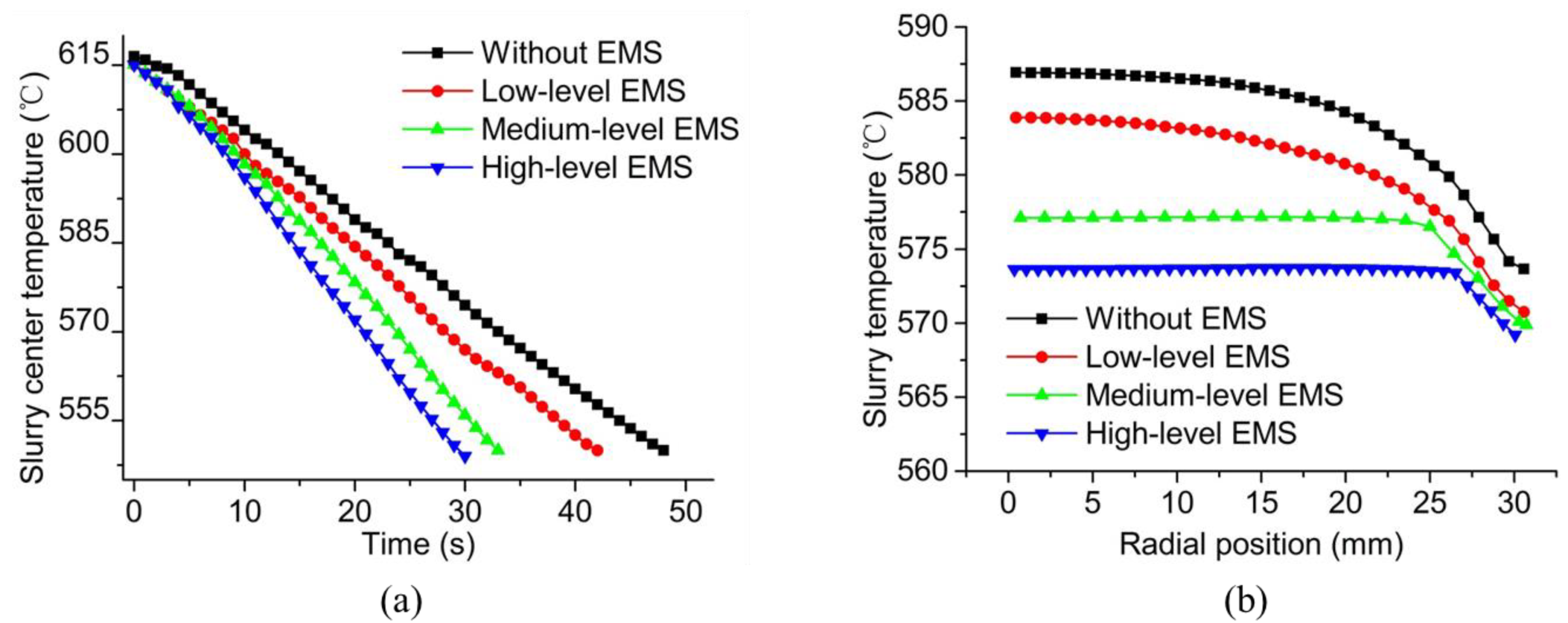
3.3. Effects of the Operating Conditions on the Temperature Field
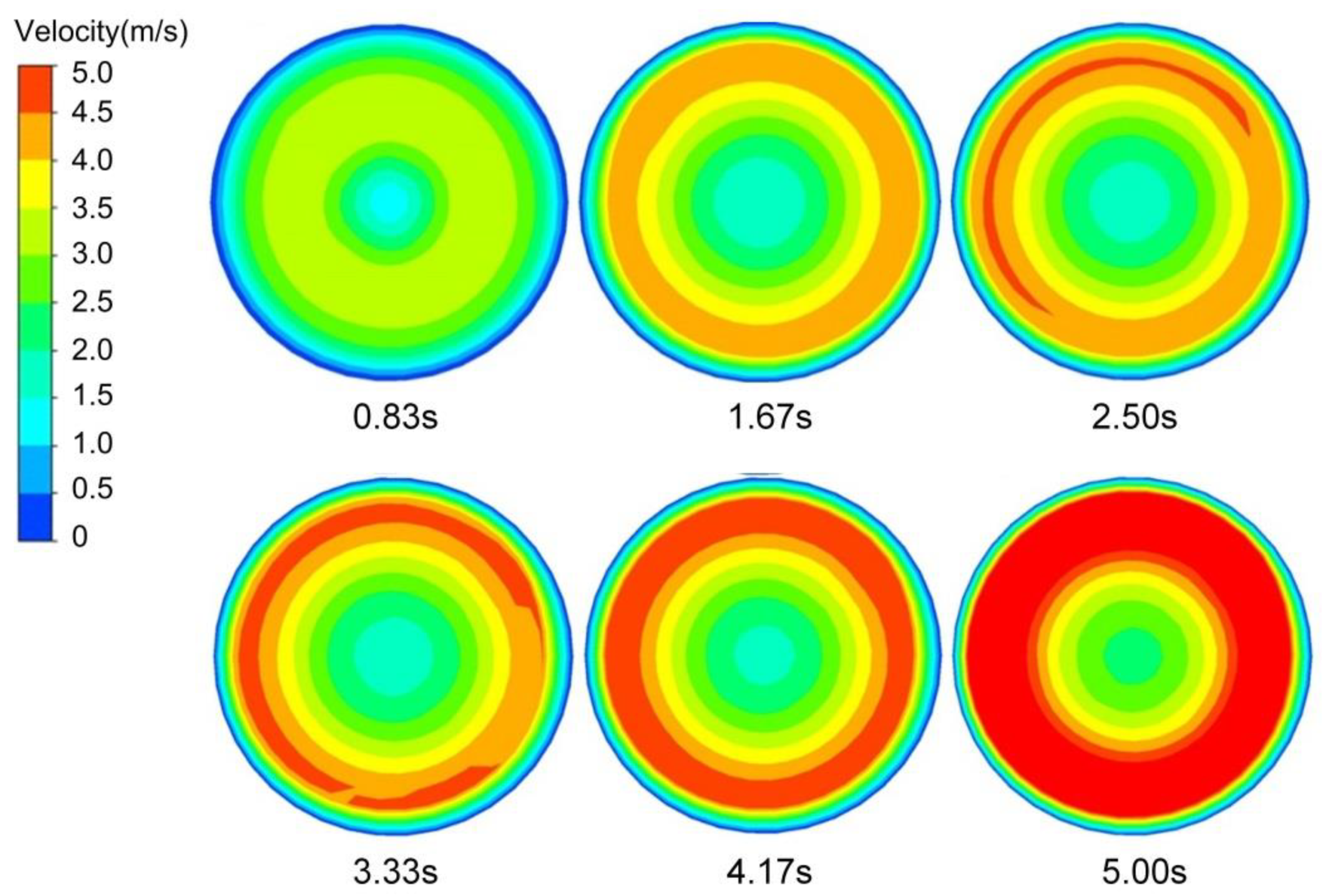
3.4. Effects of the Operating Conditions on the Flow Field
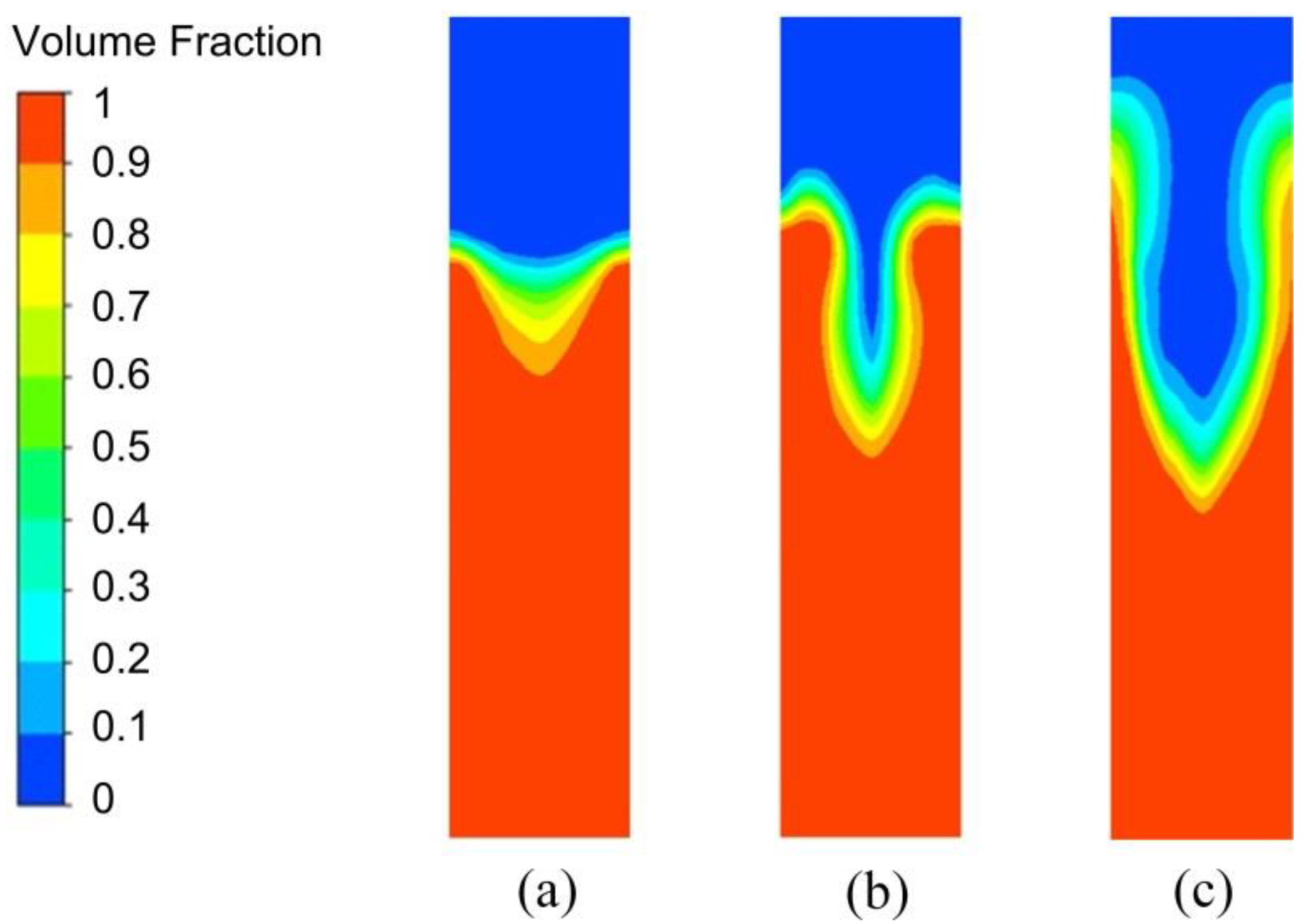
3.5. Effects of the Operating Conditions on the Vortex-Shaped Structure
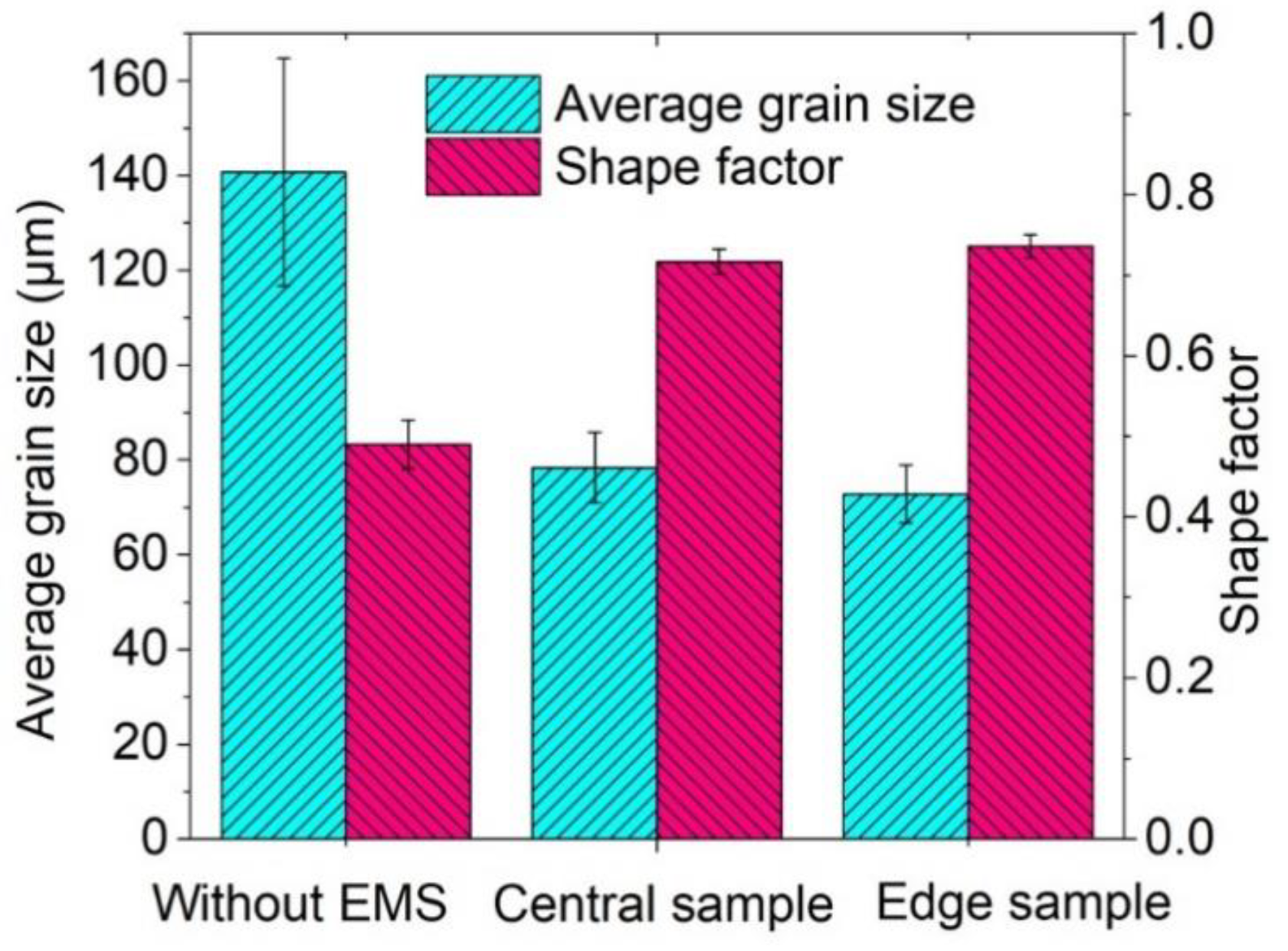
3.6. Effects of the Operating Conditions on the Microstructure
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Horikiri, G.; Kitazumi, T.; Natori, K.; Tanaka, T. Improvement in mechanical properties of semi-solid AA7075 aluminum alloys by Equal-Channel Angular Pressing. Procedia Eng. 2017, 207, 1451–1456. [Google Scholar] [CrossRef]
- Kim, Y.-M.; Choi, S.-W.; Hong, S.-K. Influence of Si content on thermal expansion characteristic of Al–Si alloys. Mater. Sci. Technol. 2020, 36, 709–716. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Liu, Y.; Shi, Y.; Ren, J.; Wang, C. Mechanical property and corrosion behavior of SiCp/2A50 composites prepared by liquid forging. Xiyou Jinshu Cailiao Yu Gongcheng/Rare Met. Mater. Eng. 2015, 44, 1307–1313. [Google Scholar]
- Xu, H.; Zhang, X.; Li, H.; Li, S.; Wang, C.; Wang, Y.; Zhang, B. Hot deformation behavior of squeeze casting SiCp/2A50 matrix composites. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2012, 27, 443–449. [Google Scholar] [CrossRef]
- Du, Z.-M.; Chen, G.; Han, F.; Cao, G.-X.; Liu, J.; Li, H.-W.; Zhang, X.; Xie, S.-S. Homogenization on microstructure and mechanical properties of 2A50 aluminum alloy prepared by liquid forging. Trans. Nonferrous Met. Soc. 2011, 21, 2384–2390. [Google Scholar] [CrossRef]
- Jiang, W.-J.; Zhang, W.-X.; Li, J.; Liu, X.-Q.; Xia, J.-K.; LV, D. Effect of die-forging process on properties of 2A50 aluminium alloy propeller blades. Light Alloy Fabr. Technol. 2006, 35, eht329. [Google Scholar]
- Fridlyander, I.N.; Sister, V.G.; Grushko, O.E.; Berstenev, V.V.; Sheveleva, L.M.; Ivanova, L.A. Aluminum alloys: Promising materials in the automotive industry. Metal Sci. Heat Treat. 2002, 44, 365–370. [Google Scholar] [CrossRef]
- Li, X.-J.; Zhang, M.; Wen, S.; Mao, X.; Huo, W.-G.; Guo, Y.-Y.; Wang, Y.-X. Microstructure and wear resistance of micro-arc oxidation ceramic coatings prepared on 2A50 aluminum alloys. Surf. Coat. Technol. 2020, 394, 125853. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Y.; Zhou, D.; Sun, L.; Li, R.; Xu, W. Influence of Homogenization on Microstructural Response and Mechanical Property of Al-Cu-Mn Alloy. Materials 2018, 11, 914. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Lu, Y.; Wang, T.; Li, T.; Zhang, G. Effect of electromagnetic stirring on microstructure and properties of Al0.5CoCrCuFeNi alloy. Procedia Eng. 2012, 27, 1129–1134. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, S.; Ghose, A.K.; Chakrabarty, I. Effect of rotary electromagnetic stirring during solidification of In-situ Al-TiB2 composites. Mater. Des. 2017, 113, 195–206. [Google Scholar] [CrossRef]
- Li, M.; Tamura, T.; Omura, N.; Murakami, Y.; Tada, S. Grain refinement of AZCa912 alloys solidified by an optimized electromagnetic stirring technique. J. Mater. Process. Technol. 2016, 235, 114–120. [Google Scholar] [CrossRef]
- Wang, B.; Wang, X.-D.; Kolesnikov, Y.; Zhang, S.; Tan, Y.-Q.; NA, X.-Z. An Experimental Prototype of an Innovative Fluid-driven Electromagnetic Stirring Technique. J. Iron Steel Res. Int. 2016, 23, 422–427. [Google Scholar] [CrossRef]
- Yu, H.Q.; Zhu, M.Y. Influence of electromagnetic stirring on transport phenomena in round billet continuous casting mould and macrostructure of high carbon steel billet. Ironmak. Steelmak. 2012, 39, 574–584. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Mi, G.; Zhong, Y. Microstructural evolution caused by electromagnetic stirring in superheated AlSi7Mg alloys. J. Mater. Process. Technol. 2010, 210, 1652–1659. [Google Scholar] [CrossRef]
- Ning, L.; Hong, Y.; Zhi-Wei, W. Effects of Heat Treatment on the Tribological Properties of Sicp/Al-5Si-1Cu-0.5Mg Composite Processed by Electromagnetic Stirring Method. Appliedences 2018, 8, 372. [Google Scholar]
- Chen, Y.; Zhang, L.; Liu, W.; Wu, G.; Ding, W. Preparation of Mg–Nd–Zn–(Zr) alloys semisolid slurry by electromagnetic stirring. Mater. Des. 2016, 95, 398–409. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, E.-G.; Li, Z.; Deng, A.-Y. Effects of vertical electromagnetic stirring on grain refinement and macrosegregation control of bearing steel billet in continuous casting. J. Iron Steel Res. Int. 2017, 24, 483–489. [Google Scholar] [CrossRef]
- Zhang, W.; Luo, S.; Chen, Y.; Wang, W.; ZHu, M. Numerical Simulation of Fluid Flow, Heat Transfer, Species Transfer, and Solidification in Billet Continuous Casting Mold with M-EMS. Metals 2019, 9, 66. [Google Scholar] [CrossRef] [Green Version]
- Çadırlı, E.; Kaya, H.; Räbiger, D.; Eckert, S.; Gündüz, M. Effect of rotating magnetic field on the microstructures and physical properties of Al–Cu–Co ternary eutectic alloy. J. Alloys Compd. 2015, 647, 471–480. [Google Scholar] [CrossRef]
- Zuo, Y.; Cui, J.; Zhao, Z.; Zhang, H.; Li, L.; Zhu, Q. Mechanism of grain refinement of an Al–Zn–Mg–Cu alloy prepared by low-frequency electromagnetic casting. J. Mater. Sci. 2012, 47, 5501–5508. [Google Scholar] [CrossRef]
- Mapelli, C.; Gruttadauria, A.; Peroni, M. Application of electromagnetic stirring for the homogenization of aluminium billet cast in a semi-continuous machine. J. Mater. Process. Technol. 2010, 210, 306–314. [Google Scholar] [CrossRef]
- Meng, X.; Bachmann, M.; Artinov, A.; Rethmeier, M. Experimental and numerical assessment of weld pool behavior and final microstructure in wire feed laser beam welding with electromagnetic stirring. J. Manuf. Process. 2019, 45, 408–418. [Google Scholar] [CrossRef]
- Wang, T.; Hachani, L.; Fautrelle, Y.; Delannoy, Y.; Wang, E.; Wang, X.; Budenkova, O. Numerical modeling of a benchmark experiment on equiaxed solidification of a Sn–Pb alloy with electromagnetic stirring and natural convection. Int. J. Heat Mass Transf. 2020, 151, 119414. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, S.; Zhang, C. Grain Refinement of Aluminum Alloy Bar by a Modified RAP Process for Semi-Solid Forming. Mater. Trans. 2017, 58, 176–181. [Google Scholar] [CrossRef] [Green Version]
- Binesh, B.; Aghaie-Khafri, M. Phase Evolution and Mechanical Behavior of the Semi-Solid SIMA Processed 7075 Aluminum Alloy. Metals 2016, 6, 42. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, H.V.; Liu, D. Microstructural coarsening of semi-solid aluminium alloys. Mater. Sci. Eng. A 2008, 496, 439–446. [Google Scholar] [CrossRef] [Green Version]

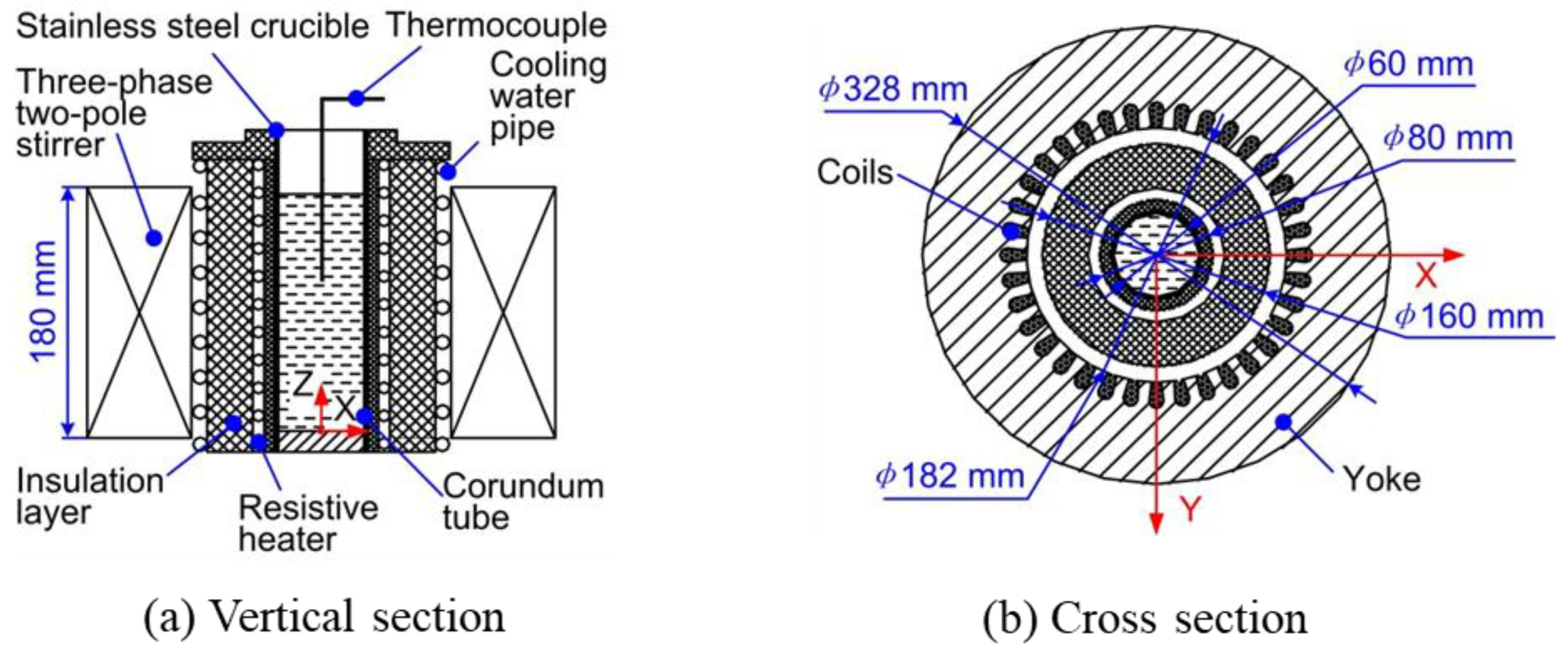







| Item | External Diameter (mm) | Inner Diameter (mm) | Height (mm) |
|---|---|---|---|
| Yoke | 328 | 182 | 180 |
| Corundum tube | 80 | 62 | 200 |
| Stainless steel crucible | 62 | 60 | 220 |
| Aluminium alloy blank | 60 | - | 180 |
| Simulation Category | Parameter | Value |
|---|---|---|
| Electromagnetic field | Relative permeability of three-phase two-pole electromagnetic stirrer coil, | 0.999991 |
| Resistivity of three-phase two-pole electromagnetic stirrer coil, (Ω·m) | 1.5 × 10−7 | |
| Relative permeability of silicon steel yoke of three-phase two-pole electromagnetic stirrer, | 2000 | |
| Resistivity of silicon steel yoke of three-phase two-pole electromagnetic stirrer, (Ω·m) | 8.0 × 10−6 | |
| Relative permeability of aluminium alloy paste, | 1 | |
| Resistivity of aluminium alloy paste, (Ω·m) | 2.1 × 10−7 | |
| Relative permeability of stainless steel mixing drum and other parts, | 1 | |
| Resistivity of other parts such as stainless steel mixing drum, (Ω·m) | 9.1 × 10−7 | |
| Flow and temperature fields | Density of aluminium alloy paste, (kg/m3) | 2405 |
| Thermal conductivity of aluminium alloy paste, (W/m·K) | 204 | |
| Specific heat capacity of aluminium alloy paste, (J/kg·K) | 900 | |
| Thermal conductivity of stainless steel mixing drum, (W/m·K) | 26 | |
| Specific heat capacity of stainless steel mixing drum, (J/kg·K) | 500 | |
| Aluminium alloy slurry-stainless steel mixing drum interface heat transfer coefficient, (W/m2·K) | 1000 | |
| Stainless steel mixing drum-air interface heat transfer coefficient, (W/m2·K) | 10 |
| Item | Specifications |
|---|---|
| Intermediate frequency electricity input | Three-phase, 380 V, 50 Hz |
| Intermediate frequency electricity output | Three-phase, 2000–3000 Hz, 0–380 V, 0–60 A |
| Rated power | 25 kW (adjustable) |
| Control mode | PID closed-loop control |
| Maximum temperature difference | ±5 °C |
| Rated power of the cooling water pump | 1.5 kW |
| Flow rate of the cooling water | 12.5 m3/h |
| Water pump head | 20 m |
| Heating time | ≤300 s |
| Ingredient | Element | Cu | Si | Mg | Mn | Zn | Ti | Ni | Fe | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| Proportion (wt.%) | 2.43 | 0.82 | 0.68 | 0.53 | 0.12 | 0.06 | 0.05 | 0.01 | Bal. | |
| Temperature | Liquidus (°C) | 615 | ||||||||
| Solidus (°C) | 521 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, S.; Guo, Y. Numerical Simulation and Experimental Investigation of the Preparation of Aluminium Alloy 2A50 Semi-Solid Billet by Electromagnetic Stirring. Materials 2020, 13, 5470. https://doi.org/10.3390/ma13235470
Wang Y, Zhao S, Guo Y. Numerical Simulation and Experimental Investigation of the Preparation of Aluminium Alloy 2A50 Semi-Solid Billet by Electromagnetic Stirring. Materials. 2020; 13(23):5470. https://doi.org/10.3390/ma13235470
Chicago/Turabian StyleWang, Yongfei, Shengdun Zhao, and Yi Guo. 2020. "Numerical Simulation and Experimental Investigation of the Preparation of Aluminium Alloy 2A50 Semi-Solid Billet by Electromagnetic Stirring" Materials 13, no. 23: 5470. https://doi.org/10.3390/ma13235470
APA StyleWang, Y., Zhao, S., & Guo, Y. (2020). Numerical Simulation and Experimental Investigation of the Preparation of Aluminium Alloy 2A50 Semi-Solid Billet by Electromagnetic Stirring. Materials, 13(23), 5470. https://doi.org/10.3390/ma13235470







