Heat Losses Caused by the Temporary Influence of Wind in Timber Frame Walls Insulated with Fibrous Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of Materials
2.2. Simulation
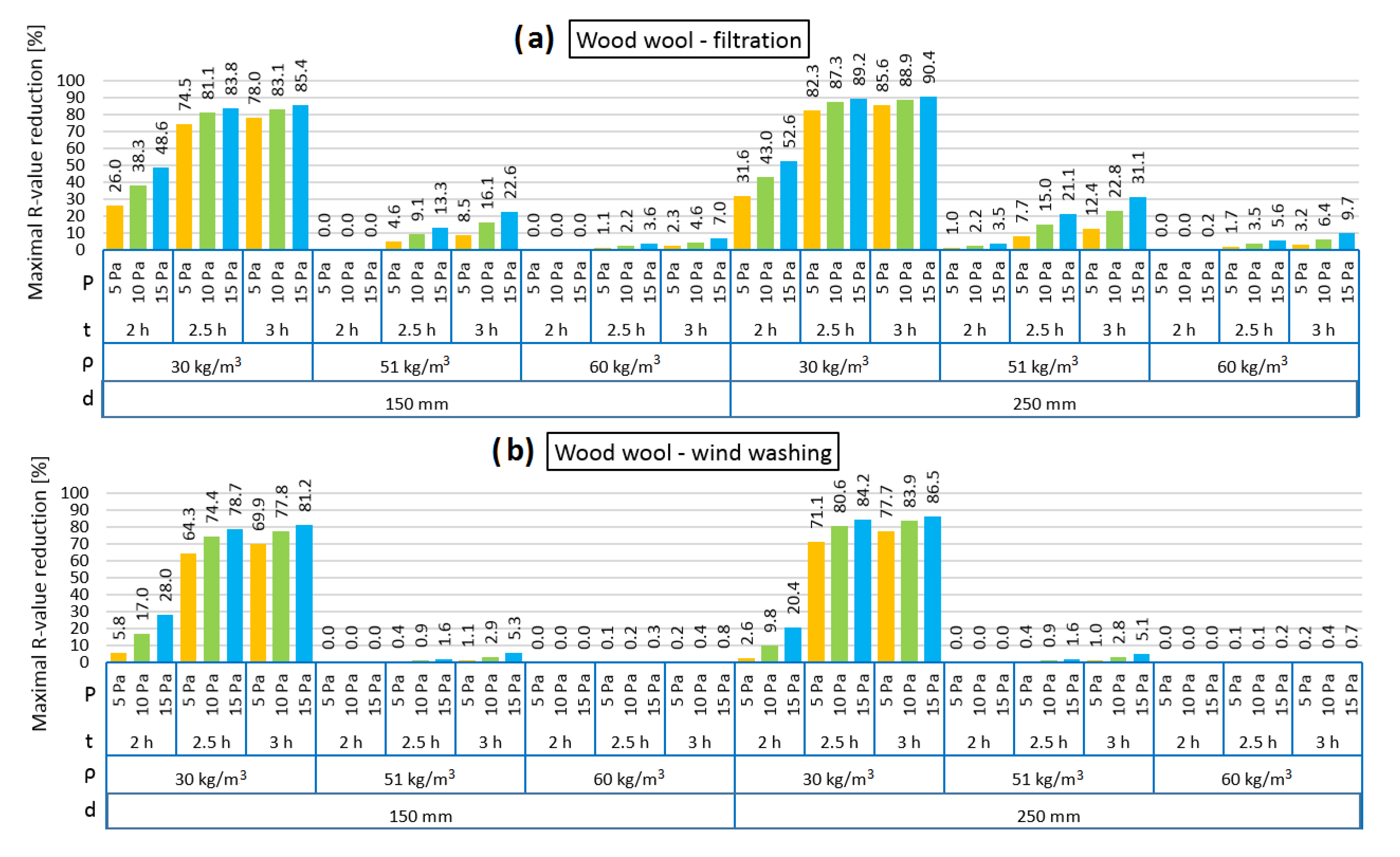
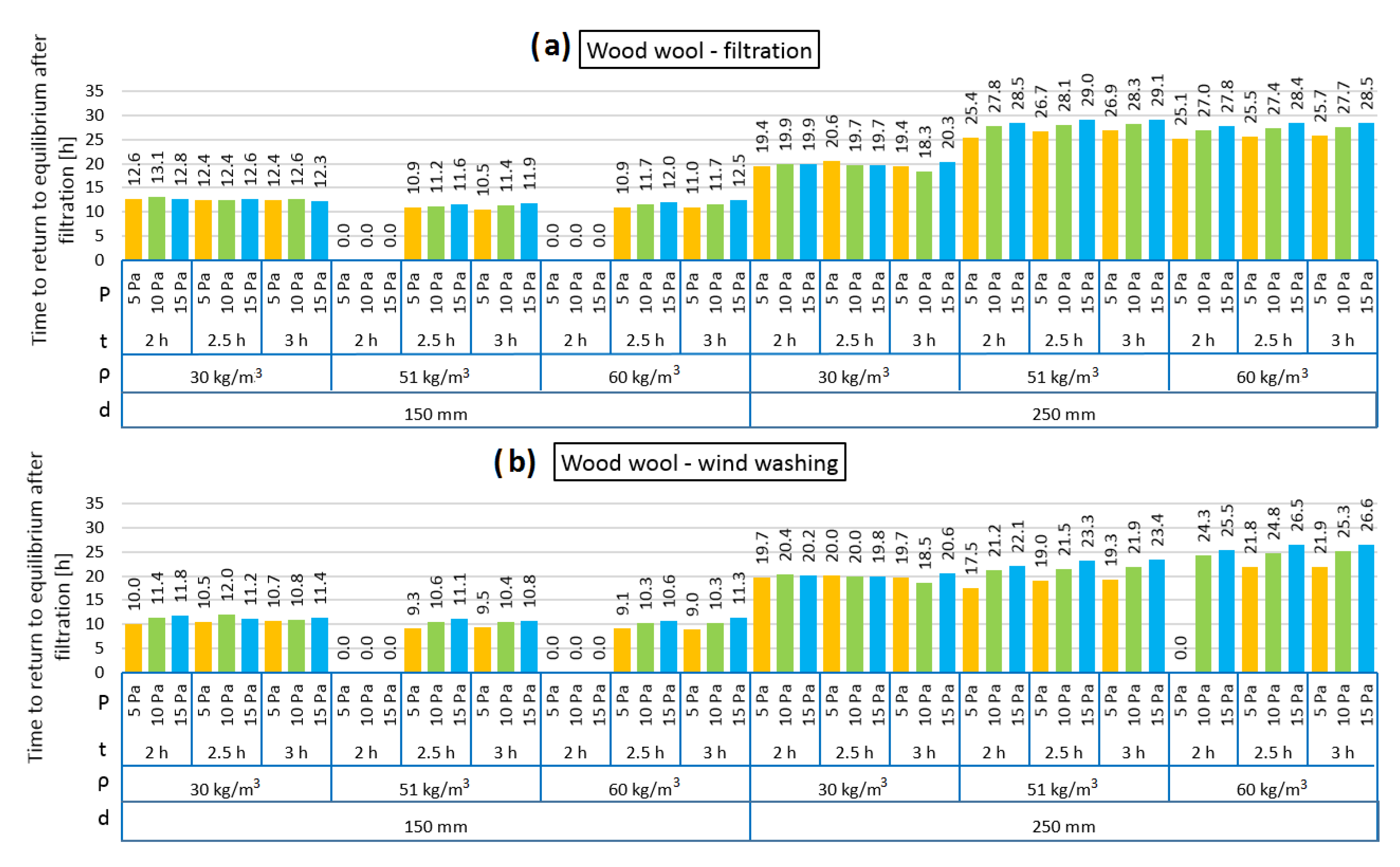
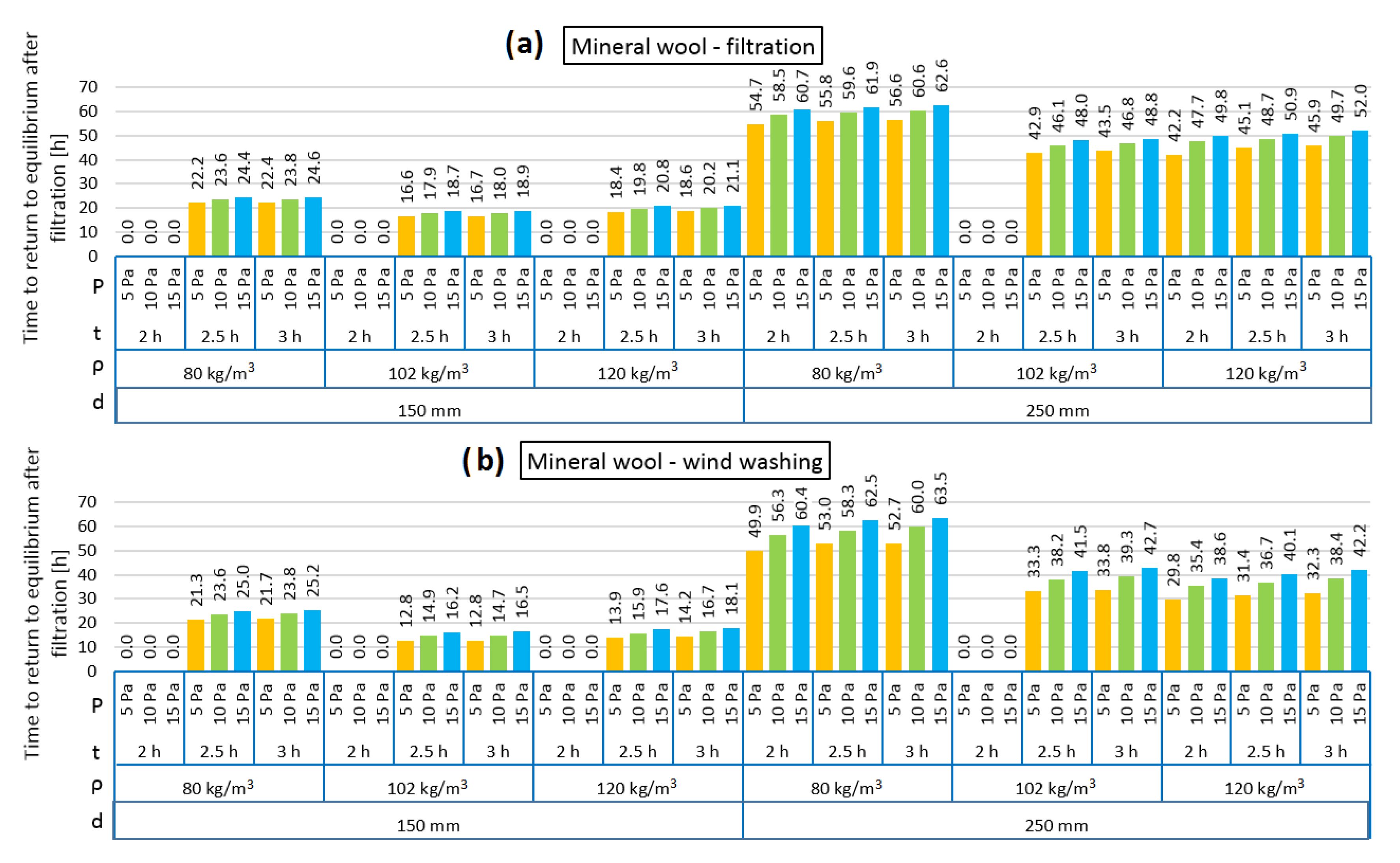
3. Results and Discussion
4. Conclusions
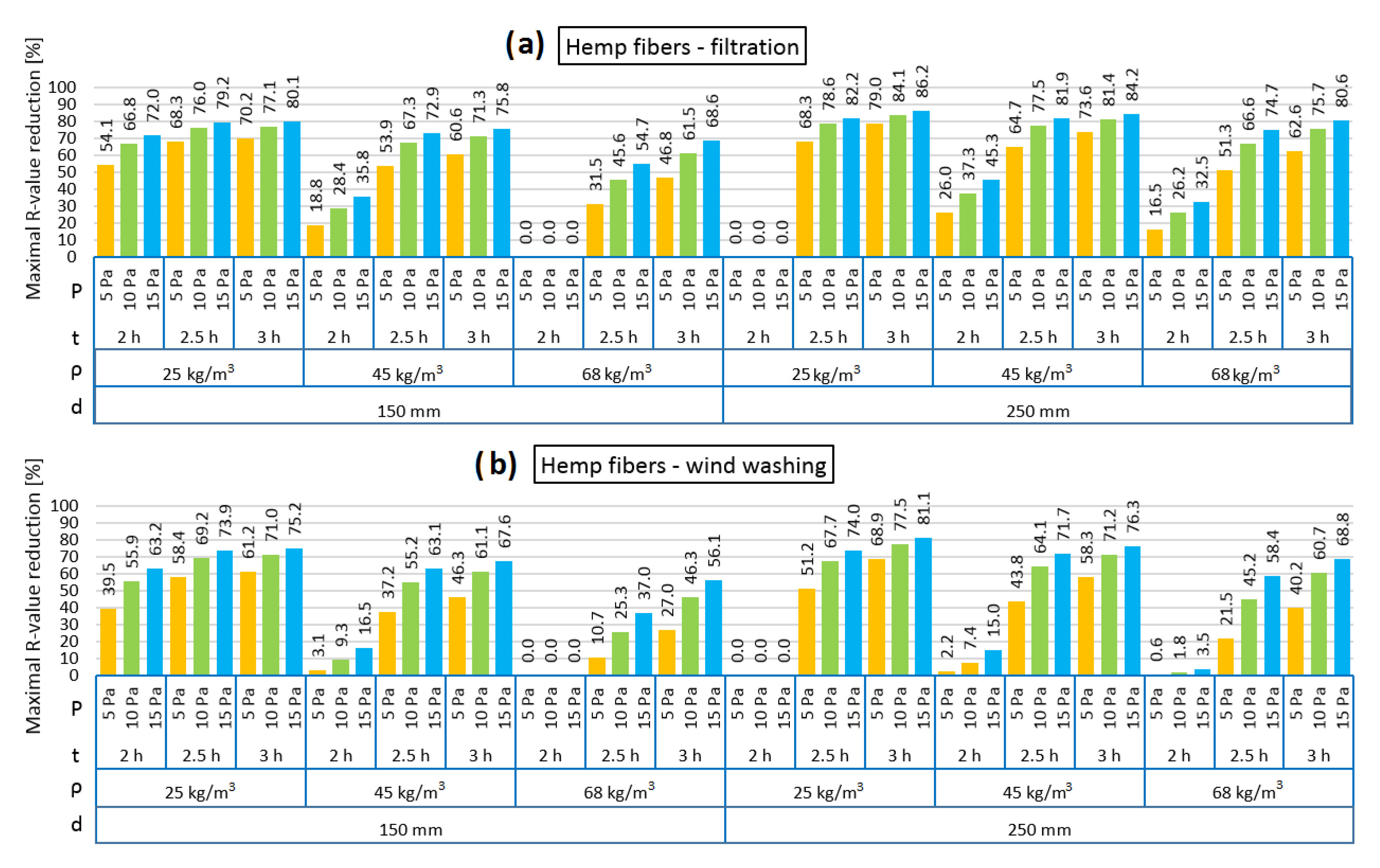
- The reduction in thermal resistance (R) in the analyzed cases depends on the density of thermal insulation, its thickness, but also time and pressure load. With increasing density, the R reduction is lower due to the lower air permeability of the material (both air filtration and wind washing cases). The most remarkable influence of insulation material density on the R value reduction can be observed in the case of wood wool. Wind washing causes lower R reduction than air filtration in all models.
- The longer the time and the higher the pressure load, the higher the R reduction. Higher R reduction was observed in the thicker models. After 2 h of exposure of the mineral wool model to air pressure, the reduction in the R value is clearly smaller (equal to zero in almost all cases) in comparison to 2.5 and 3 h of exposure. In the walls insulated with natural fibers, these differences are less visible (air filtration case), especially in the case of hemp fibers (thickness 150 mm, density 25 kg/m3).
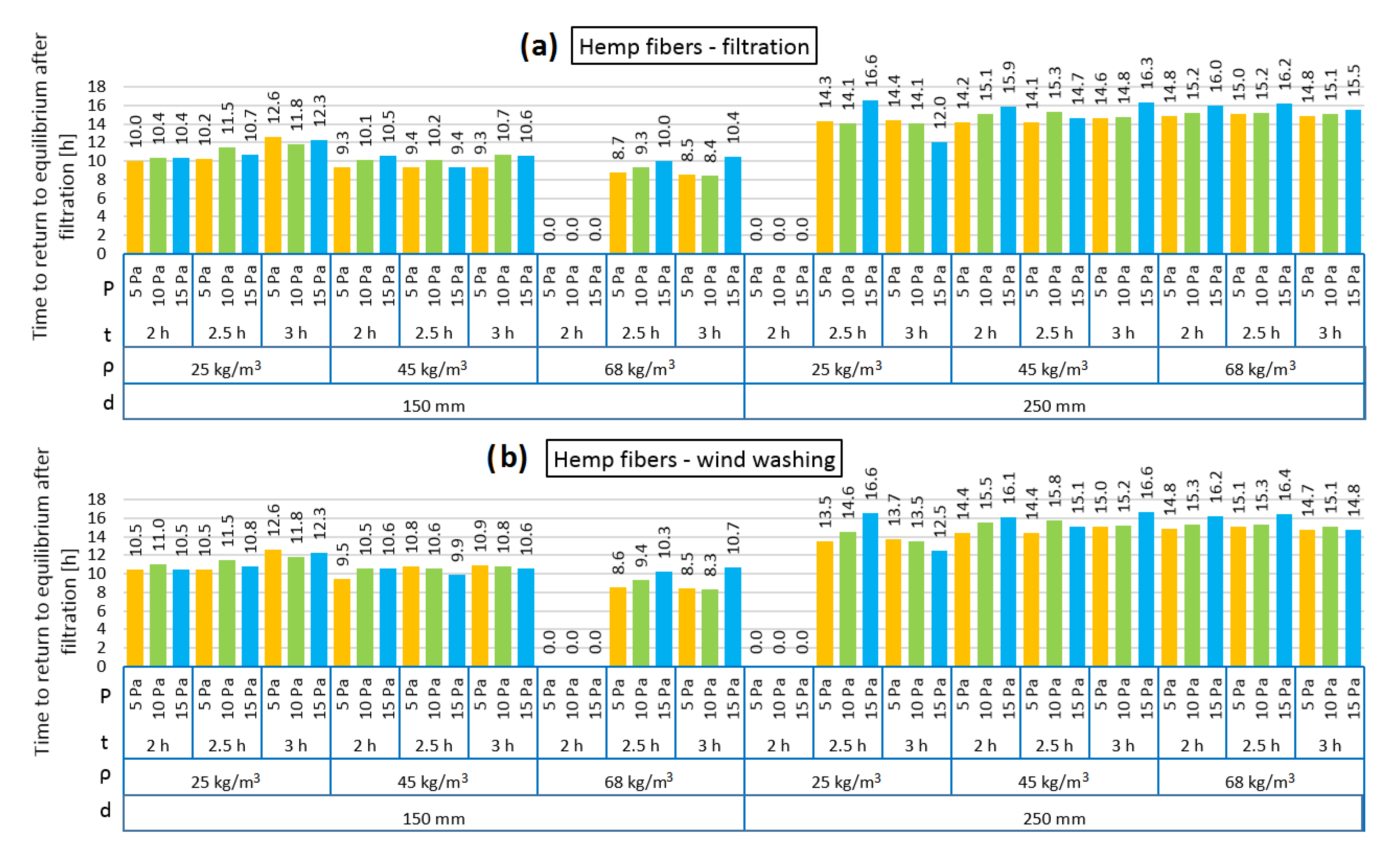
- The period needed for the models after air filtration (wind washing as well) to return to the equilibrium state depends strongly on the thermal insulation thickness. The higher the thickness, the longer the time. The period is comparable for both air filtration and wind washing. In the case of mineral wool, the time to return to equilibrium after filtration increases along with wind pressure and the time period of its exposure. There are no such clear relationships in the case of the walls insulated with natural fibers.
- It can be clearly seen that the R reduction depends on the time of the pressure load and that a 3 h period does not enable the maximum change. The intention was to identify the results of short periods, which occur quite often in the Polish climate due to wind operation. It should be also mentioned that the authors did not analyze thermal buoyancy, which will increase the convection in the thermal insulation layer. The time period of returning to the equilibrium state is three or four times longer than the time period of pressure load in the case of the 150 mm model but up to ten times longer in the 250 mm model (wood wool and hemp fibers) or twenty times longer (mineral wool).
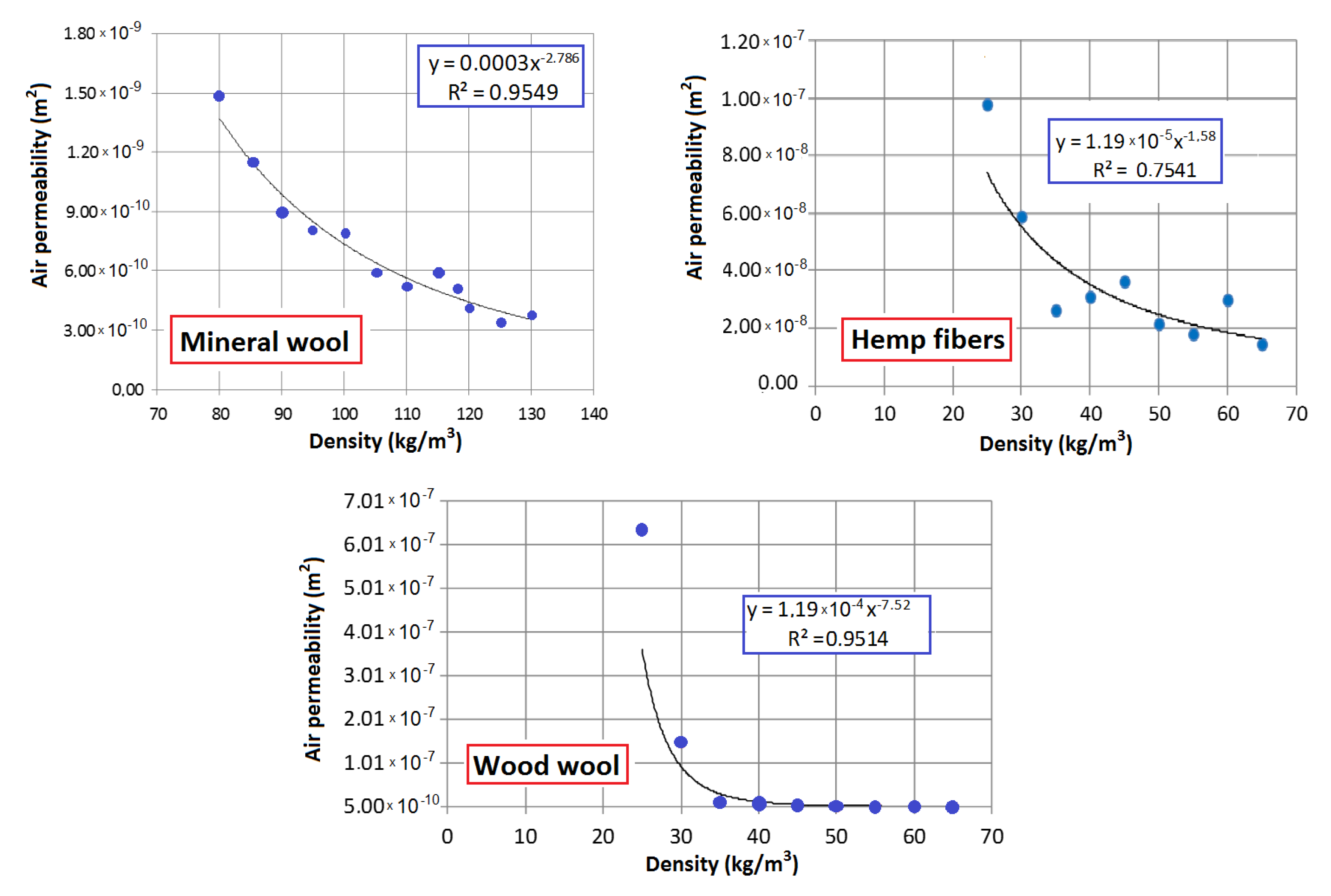
- The difference between the natural and the synthetic fiber materials can be identified mostly in the air transport properties. Mineral wool is characterized by low air permeability even for the lower analyzed densities, in contract to natural materials. Air permeability as a function of wood wool density, due to the dusty fraction content, is characterized by a rapidly decreasing shape. Hemp fibers, because of the preparation process, are devoid of the dusty fraction and this is why this material is the most porous amongst those analyzed. These properties were presented in the results of the simulation; hemp fibers were characterized by the strongest susceptibility to air filtration, and wood wool was also high, but lower than hemp fibers, while mineral wool displayed the lowest values.
- It should be noted that the numerical software calculations are based on the simplification of the material properties. Unlike in reality, the air permeability and thermal conductivity of fiber materials were the same in every area of the model. Almost always, there are gaps between the fibers and the filled frame; thus, the risk of air filtration in the insulation material is higher. As a result, the heat loses in such elements are higher than in the simulations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grudzińska, M.; Brzyski, P. The occurrence of thermal bridges in hemp-lime construction junctions. Period. Polytech. Civil Eng. 2019, 63, 377–387. [Google Scholar] [CrossRef]
- Brzyski, P.; Grudzińska, M.; Majerek, D. Analysis of the occurrence of thermal bridges in several variants of connections of the wall and the ground floor in construction technology with the use of a hemp–lime composite. Materials 2019, 12, 2392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kosiński, P.; Wójcik, R. An impact of air permeability on heat transfer through partitions insulated with loose fiber materials. Appl. Mech. Mater. 2017, 861, 190–197. [Google Scholar] [CrossRef]
- Younes, C.; Abi Shdid, C.; Bitsuamlak, G. Air infiltration through building envelopes: A review. J. Build. Physics 2012, 35, 267–302. [Google Scholar] [CrossRef]
- Raczkowski, A.; Suchorab, Z.; Połednik, B.; Zarzeka-Raczkowska, E.; Życzyńska, A. Computational fluid dynamics simulation of thermal comfort in naturally ventilated room by the fresh air valve installed in an external wall. AIP Conf. Proc. 2018, 1988, 020041. [Google Scholar] [CrossRef]
- Powell, F.; Moncef, K.; Tuluca, A. Air movement influence on the effective thermalresistance of porous insulation: A literature survey. J. Build. Phys. 1989, 12, 239–251. [Google Scholar] [CrossRef]
- Claesson, J.; Hellstrom, G. Forced convective-diffusive heat flow in insulations: Anew analytical technique applied to air leakage through a slit. J. Build. Phys. 1995, 18, 216–228. [Google Scholar] [CrossRef]
- Arens, E.A.; Williams, P.B. The effect of wind on energy consumption in buildings. Energy Build. 1977, 1, 77–84. [Google Scholar] [CrossRef]
- Desmarais, G.; Derome, D.; Fazio, P. Mapping of air leakage in exterior wall assemblies. J. Build. Phys. 2000, 24, 132–154. [Google Scholar] [CrossRef]
- Torres-Rivas, A.; Palumbo, M.; Haddad, A.; Cabeza, L.F.; Jiménez, L.; Boer, D. Multi-objective optimisation of bio-based thermal insulation materials in building envelopes considering condensation risk. Appl. Energy 2018, 224, 602–614. [Google Scholar] [CrossRef]
- Qu, M.-L.; Tian, S.-Q.; Fan, L.-W.; Yu, Z.-T.; Ge, J. An experimental investigation and fractal modeling on the effective thermal conductivity of novel autoclaved aerated concrete (AAC)-based composites with silica aerogels (SA). Appl. Therm. Eng. 2020, 179, 115770. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Z.; Liu, Y.; Wang, D.; Ma, C.; Liu, J. Comprehensive correction of thermal conductivity of moist porous building materials with static moisture distribution and moisture transfer. Energy 2019, 176, 103–118. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, C.; Liu, Y.; Wang, D.; Liu, J. Effect of moisture migration and phase change on effective thermal conductivity of porous building materials. Int. J. Heat Mass Transf. 2018, 125, 330–342. [Google Scholar] [CrossRef]
- Lewry, A.J.; Crewdson, L.F.E. Approaches to testing the durability of materials used in the construction and maintenance of buildings. Constr. Build. Mater. 1994, 8, 211–222. [Google Scholar] [CrossRef]
- Zach, J.; Slávik, R.; Novák, V. Investigation of the process of heat transfer in the structure of thermal insulation materials based on natural fibres. Proc. Eng. 2016, 151, 352–359. [Google Scholar] [CrossRef] [Green Version]
- Brambilla, A.; Sangiorgio, A. Mould growth in energy efficient buildings: Causes, health implications and strategies to mitigate the risk. Ren. Sustain. Energy Rev. 2020, 132, 110093. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Meklin, T.; Vepsalainen, A.; Nevalainen, A. Fungi and actinobacteria in moisture-damaged building materials—Concentrations and diversity. Int. Biodeter. Biodegradat. 2002, 49, 27–37. [Google Scholar] [CrossRef]
- Pasanen, A.-L.; Kasanen, J.-P.; Rautiala, S.; Ikäheimo, M.; Rantamäki, J.; Kääriäinen, H.; Kalliokoski, P. Fungal growth and survival in building materials under fluctuating moisture and temperature conditions. Int. Biodeter. Biodegradat. 2000, 46, 117–127. [Google Scholar] [CrossRef]
- Garbacz, M.; Malec, A.; Duda-Saternus, S.; Suchorab, Z.; Guz, Ł.; Łagód, G. Methods for early detection of microbiological infestation of buildings based on gas sensor technologies. Chemosensors 2020, 8, 7. [Google Scholar] [CrossRef] [Green Version]
- ISO. Building Components and Building Elements. Thermal Resistance and Thermal Transmittance. Calculation Methods; European Committee for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Deseyve, C.; Bednar, T. Wind induced airflow through lightweight pitched roof construction: Test roof element—Measurements and model validation. In Proceedings of the 8th Symposium on Building Physics in the Nordic Countries, Copenhagen, Denmark, 16–18 June 2008. [Google Scholar]
- Miszczuk, A. Influence of air tightness of the building on its energy-efficiency in single-family buildings in Poland. MATEC Web Conf. 2017, 117, 00120. [Google Scholar] [CrossRef]
- Ambrose, M.; Syme, M. Air tightness of new Australian residential buildings. Proc. Eng. 2017, 180, 33–40. [Google Scholar] [CrossRef]
- Hui-Xing, L.; Ran, Z.; Guo-Hui, F.; Kai-Liang, H.; Chi-Hong, C. The test and analysis of air tightness for zero energy building in cold region. Proc. Eng. 2016, 146, 239–243. [Google Scholar] [CrossRef] [Green Version]
- Šadauskienė, J.; Paukštys, V.; Šeduikytė, L.; Banionis, K. Impact of air tightness on the evaluation of building energy performance in Lithuania. Energies 2014, 7, 4972–4987. [Google Scholar] [CrossRef] [Green Version]
- Timusk, J.; Seskus, A.L.; Ary, N. The control of wind cooling of wood frame building enclosures. J. Therm. Insulat. 1991, 15, 8–19. [Google Scholar] [CrossRef]
- Uvsløkk, S. The importance of wind barriers for insulated timber frame constructions. J. Therm. Insulat. Build. Envel. 1996, 20, 40–62. [Google Scholar] [CrossRef]
- Straube, J.; VanStraaten, R.; Trainor, T.; Habellion, A. Wind washing effects on mineral wool insulated sheathings. In Proceedings of the ASHRAE Thermal Performance of the Exterior Envelopes of Whole Buildings XIII International Conference, Clearwater Beach, FL, USA, 4–8 December 2016. [Google Scholar]
- Doggett, M.S.; Brunjes, R.F. Simulation of convective heat loss through mineral wool in a rainscreen FAÇADE. In Proceedings of the Presentation to Minnesota Building Enclosure Council, Minneapolis, MN, USA, 24 May 2016. [Google Scholar]
- Janssens, A.; Hens, H. Effects of wind on the transmission heat loss in duo-pitched insulated roofs: A field study. Energy Build. 2007, 39, 1047–1054. [Google Scholar] [CrossRef]
- Huifen, Z.; Fuhua, Y.; Qian, Z. Research on the impact of wind angles on the residential building energy consumption. Math. Problems Eng. 2014, 794650, 15. [Google Scholar] [CrossRef]
- Shuang-Ying, W.; De-Lei, L.; Lan, X.; Zu-Guo, S. Experimental study on the effect of wind on heat losses from a fully open cylindrical cavity with only bottom wall heated. Int. J. Green Energy 2015, 12, 1244–1254. [Google Scholar] [CrossRef]
- Yoon, S.; Hoyano, A.; Gonaikawa, K. Wind pressure effecs on transfer of heat and moisture across a breathing wall. Study on properties of natural ventilation, thermal insulation and vapor transmission in a breathing wall Part 1. J. Arch. Plan. 2000, 65, 67–74. [Google Scholar] [CrossRef] [Green Version]
- Paepcke, A.; Nicolai, A. Performance analysis of coupled quasi-steady state air flow calculation and dynamic simulation of hygrothermal transport inside porous materials. Energy Proc. 2017, 132, 759–764. [Google Scholar] [CrossRef]
- Janssen, H.; Vereecken, E.; Holúbek, M. A confrontation of two concepts for the description of the over-capillary moisture range: Air entrapment versus low capillarity. Energy Proc. 2015, 78, 1490–1494. [Google Scholar] [CrossRef] [Green Version]
- Suchorab, Z.; Widomski, M.K.; Łagód, G.; Barnat-Hunek, D.; Majerek, D. A noninvasive TDR sensor to measure the moisture content of rigid porous materials. Sensors 2018, 11, 3935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kosiński, P.; Brzyski, P.; Szewczyk, A.; Motacki, W. Thermal properties of raw hemp fiber as a loose-fill insulation material. J. Nat. Fib. 2018, 15, 717–730. [Google Scholar] [CrossRef]
- Kosiński, P.; Brzyski, P.; Duliasz, B. Moisture and wetting properties of thermal insulation materials based on hemp fiber, cellulose and mineral wool in a loose state. J. Nat. Fib. 2020, 17, 199–213. [Google Scholar] [CrossRef]
- Engineering ToolBox. Wind Velocity and Wind Load. 2011. Available online: https://www.engineeringtoolbox.com/wind-load-d_1775.html (accessed on 24 August 2020).
- Available online: https://archiwum.miir.gov.pl/strony/zadania/budownictwo/charakterystyka-energetyczna-budynkow/dane-do-obliczen-energetycznych-budynkow-1/ (accessed on 24 August 2020).
- Kosiński, P.; Wójcik, R.; Semen, B. Experimental study on the deterioration of thermal insulation performance due to wind washing of the cavity insulation in leaky walls. Sci. Technol. Built Environ. 2019, 25, 1164–1177. [Google Scholar] [CrossRef]
- Wójcik, R.; Kosiński, P. Seeming air tightness of construction partitions. Energy Proc. 2015, 78, 1519–1524. [Google Scholar] [CrossRef] [Green Version]


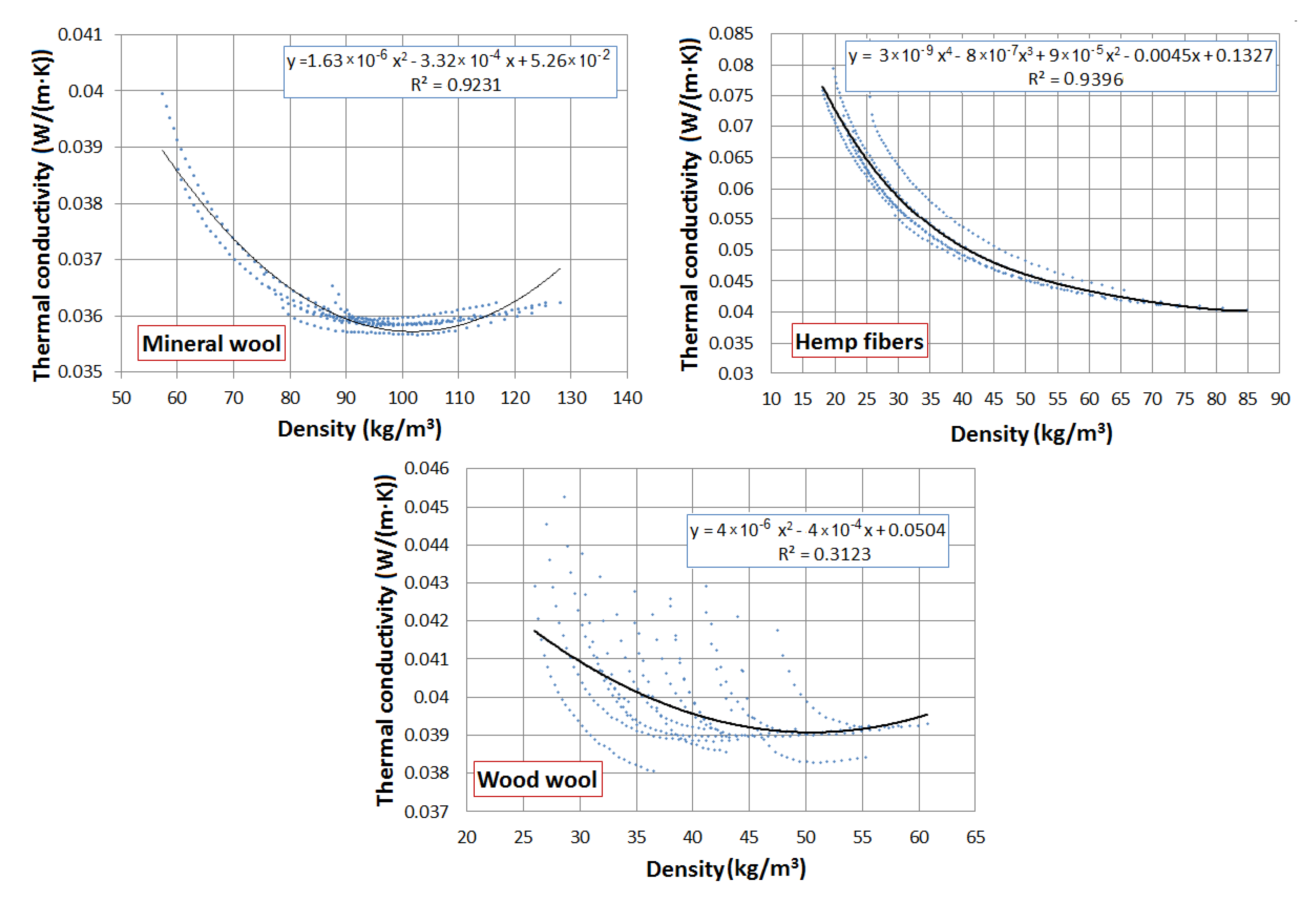
| Density (kg/m3) | Thermal Conductivity λ (W/(mK)) | Air Permeability k (m2) |
|---|---|---|
| mineral wool | ||
| 80 | 3.64 × 10−2 | 14.84 × 10−10 |
| 102 | 3.57 × 10−2 | 6.84 × 10−10 |
| 120 | 3.62 × 10−2 | 4.17 × 10−10 |
| wood wool | ||
| 30 | 4.09 × 10−2 | 1480.07 × 10−10 |
| 51 | 3.90 × 10−2 | 16.91 × 10−10 |
| 60 | 3.94 × 10−2 | 4.98 × 10−10 |
| hemp fibers | ||
| 25 | 6.49 × 10−2 | 781.31 × 10−10 |
| 45 | 4.79 × 10−2 | 286.60 × 10−10 |
| 68 | 4.12 × 10−2 | 141.16 × 10−10 |
| Gypsum board | 13.00 × 10−2 | - |
| OSB (oriented strand board) | 20.00 × 10−2 | - |
| Pressure Difference (Pa) | Air Flow (m3/h) | |||
|---|---|---|---|---|
| Without Material | Hemp Fibers | Wood Wool | Mineral Wool | |
| 5 | 41.13 | 2.33–4.45 | 0.08–(0.27)–10.62 | 0.07–0.24 |
| 10 | 58.16 | 4.66–8.91 | 0.16–(0.54)–21.23 | 0.13–0.48 |
| 15 | 71.23 | 6.70–13.37 | 0.24–(0.81)–31.85 | 0.20–0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosiński, P.; Brzyski, P.; Suchorab, Z.; Łagód, G. Heat Losses Caused by the Temporary Influence of Wind in Timber Frame Walls Insulated with Fibrous Materials. Materials 2020, 13, 5514. https://doi.org/10.3390/ma13235514
Kosiński P, Brzyski P, Suchorab Z, Łagód G. Heat Losses Caused by the Temporary Influence of Wind in Timber Frame Walls Insulated with Fibrous Materials. Materials. 2020; 13(23):5514. https://doi.org/10.3390/ma13235514
Chicago/Turabian StyleKosiński, Piotr, Przemysław Brzyski, Zbigniew Suchorab, and Grzegorz Łagód. 2020. "Heat Losses Caused by the Temporary Influence of Wind in Timber Frame Walls Insulated with Fibrous Materials" Materials 13, no. 23: 5514. https://doi.org/10.3390/ma13235514
APA StyleKosiński, P., Brzyski, P., Suchorab, Z., & Łagód, G. (2020). Heat Losses Caused by the Temporary Influence of Wind in Timber Frame Walls Insulated with Fibrous Materials. Materials, 13(23), 5514. https://doi.org/10.3390/ma13235514