Temperature-Related Properties of Solid Birch Wood under Quasi-Static and Dynamic Bending
Abstract
:1. Introduction
2. Materials and Methods
2.1. Wood Specie, Quality, and Test Matrix
2.2. Conditioning of the Samples
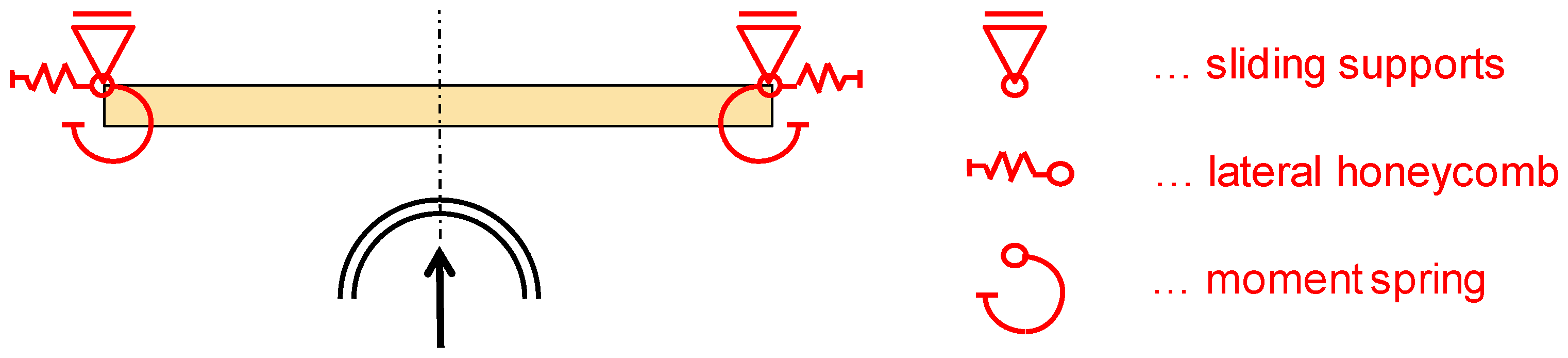
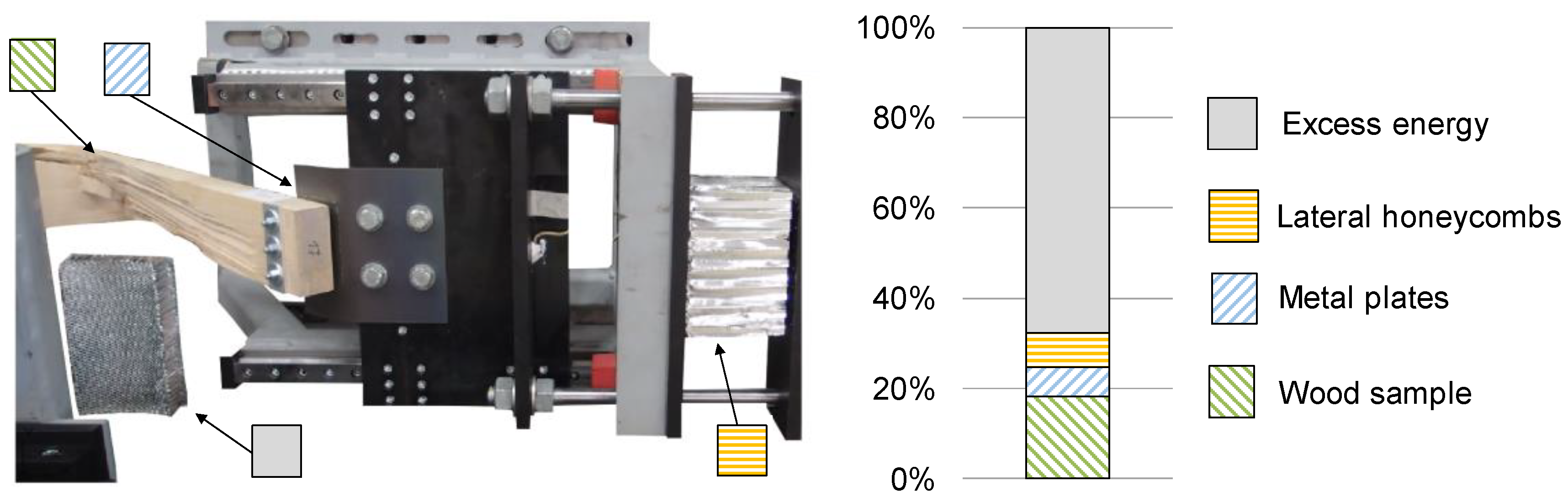
2.3. Test Facility
3. Results
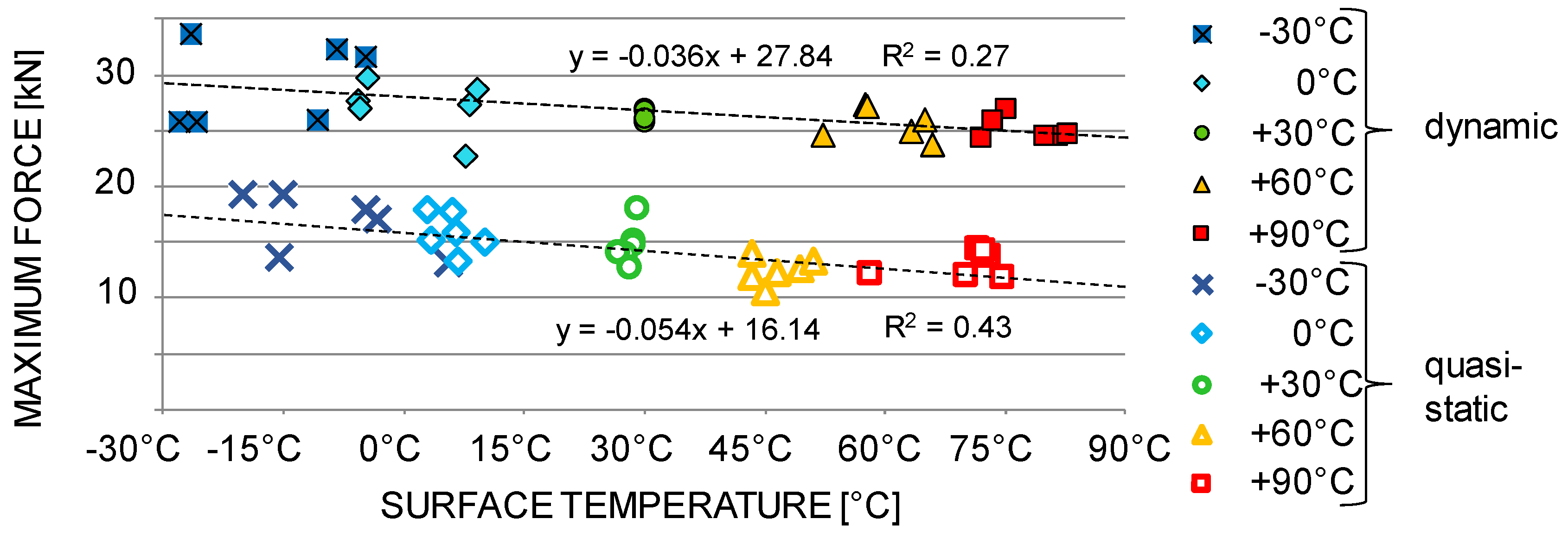
3.1. Density, Fiber Deviation, and Climatic Conditions
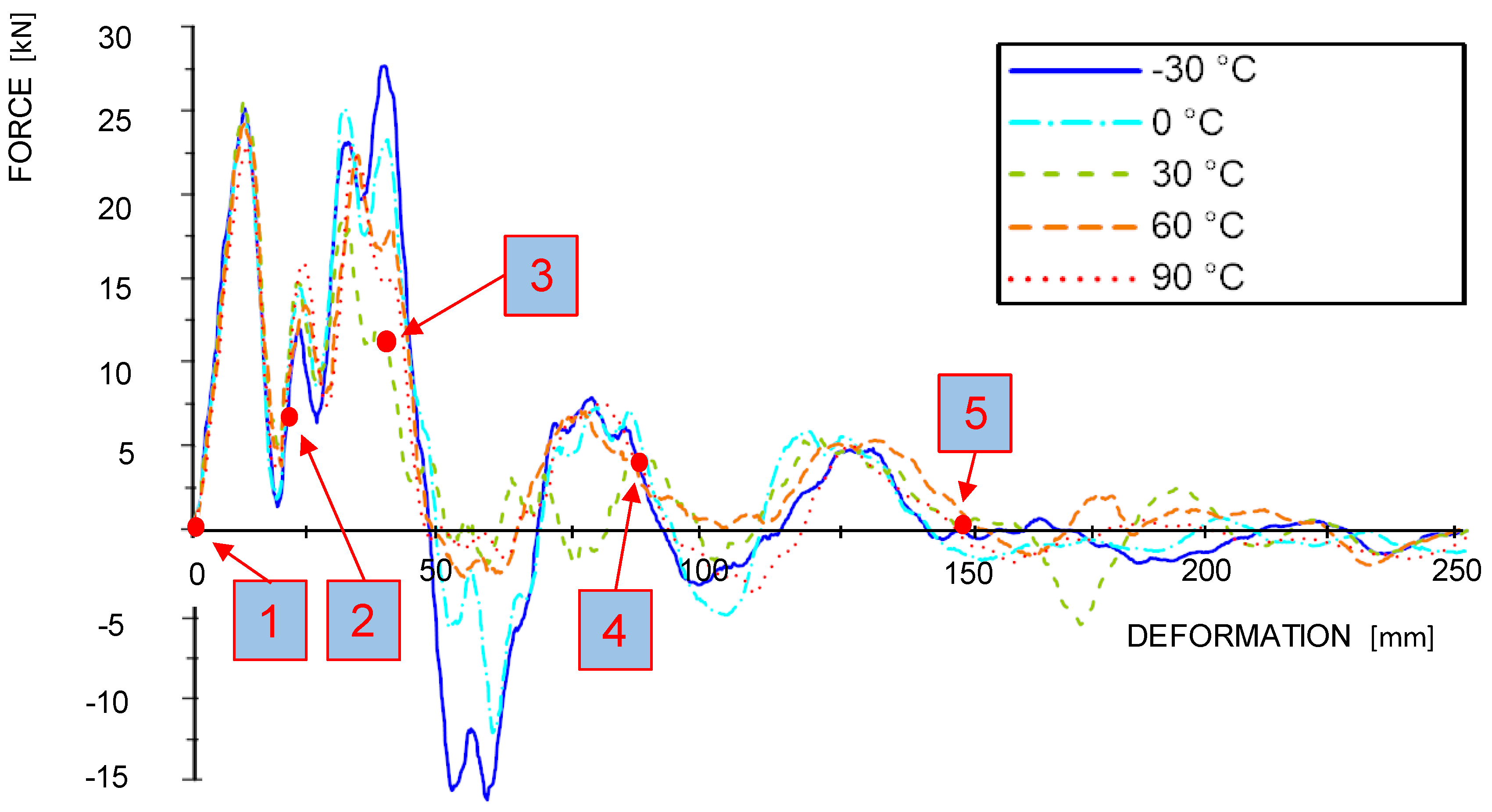
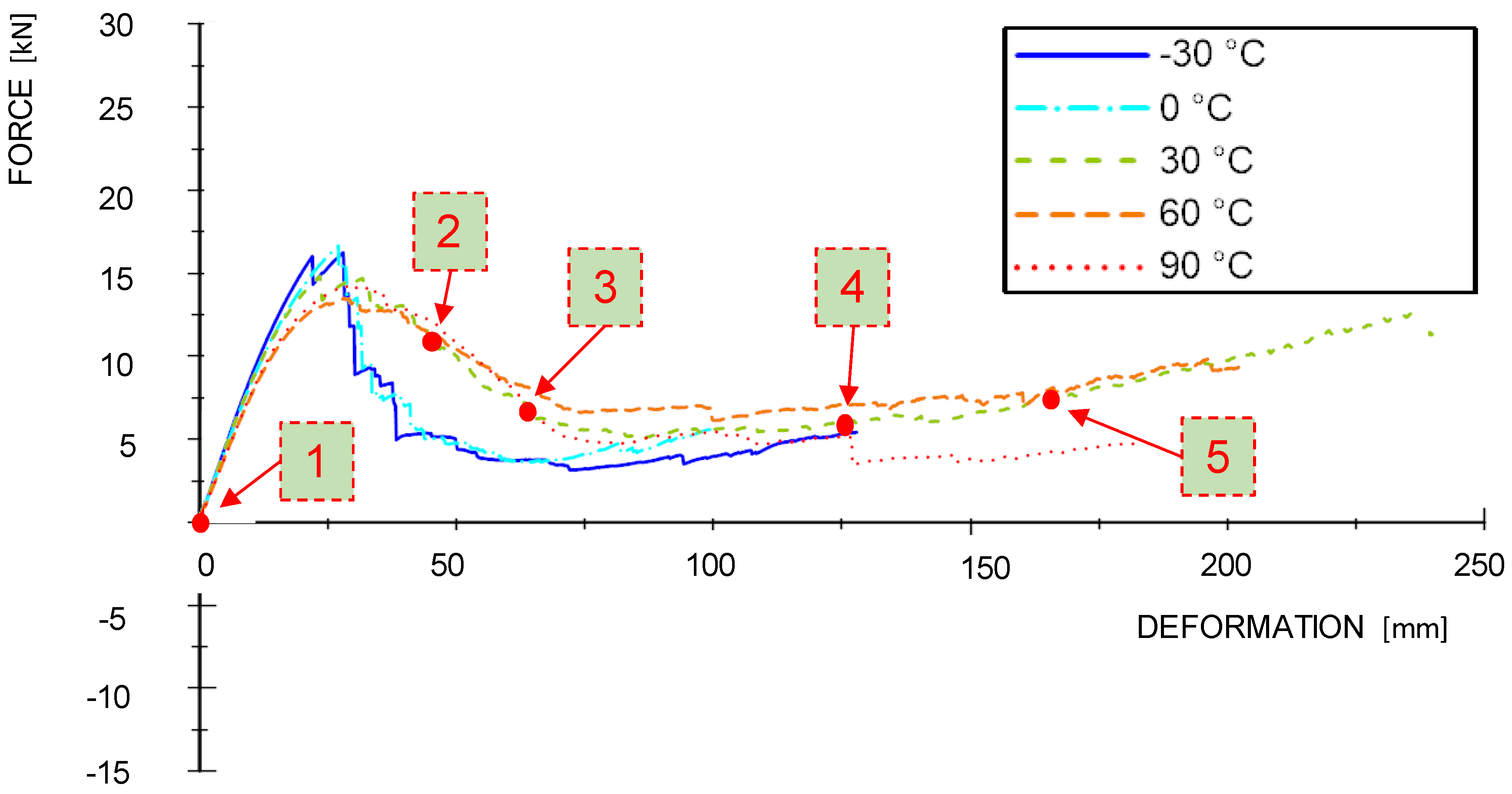
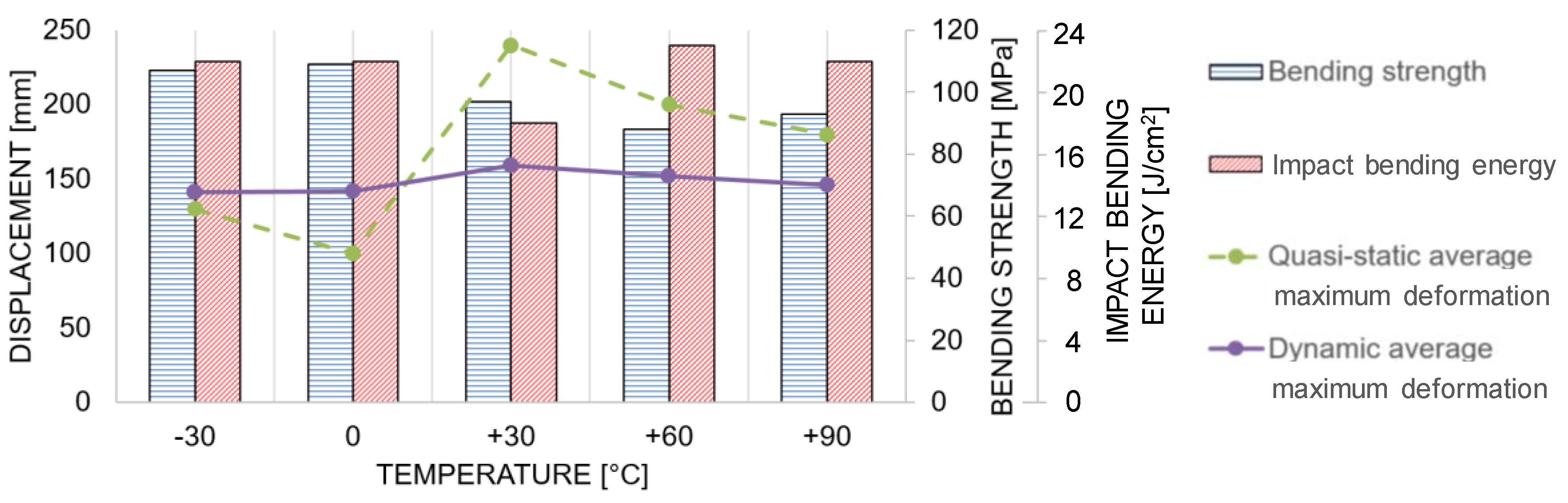
3.2. Force-Deformation Behavior
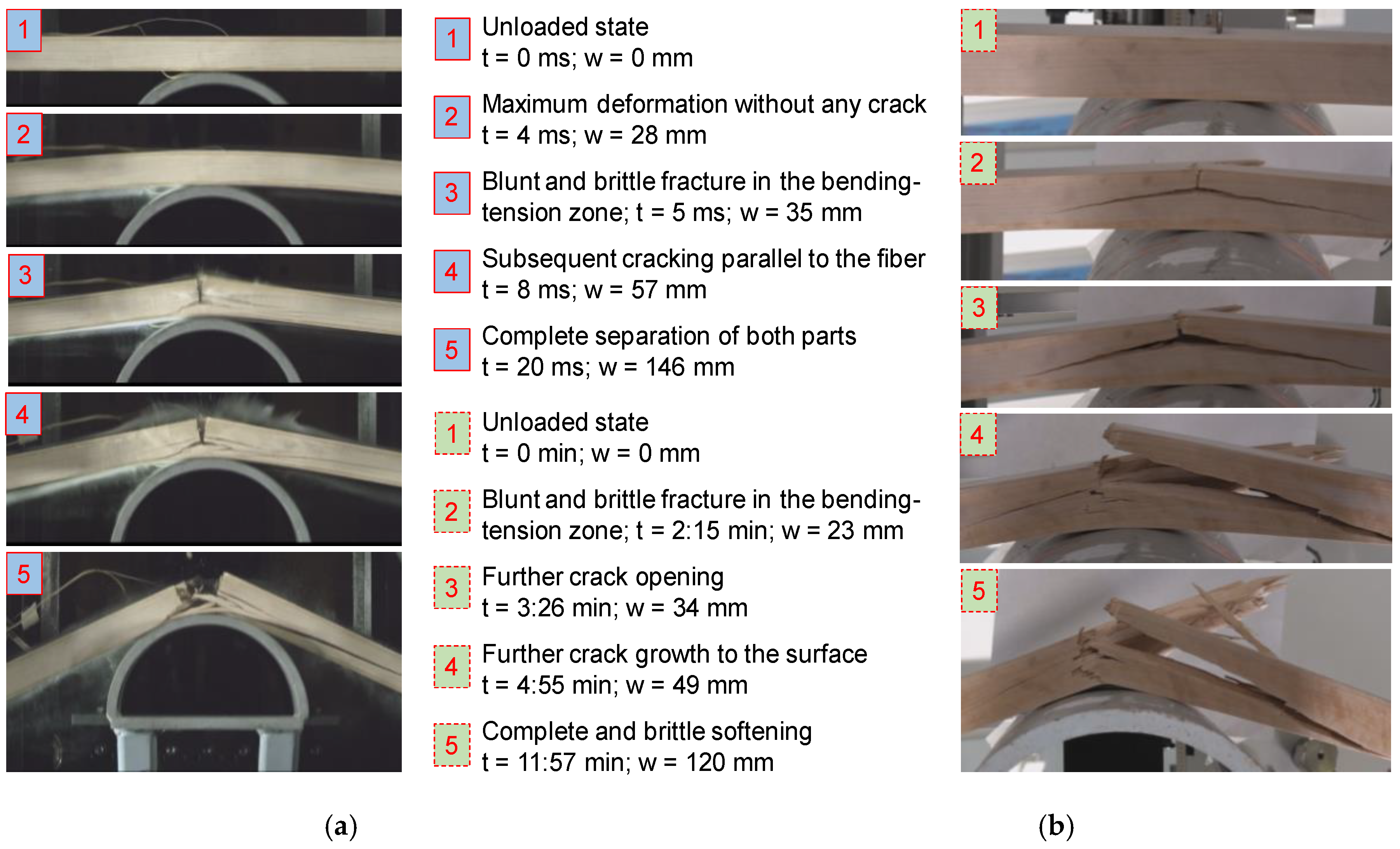
3.3. Failure Sequence and Fracture Characteristics
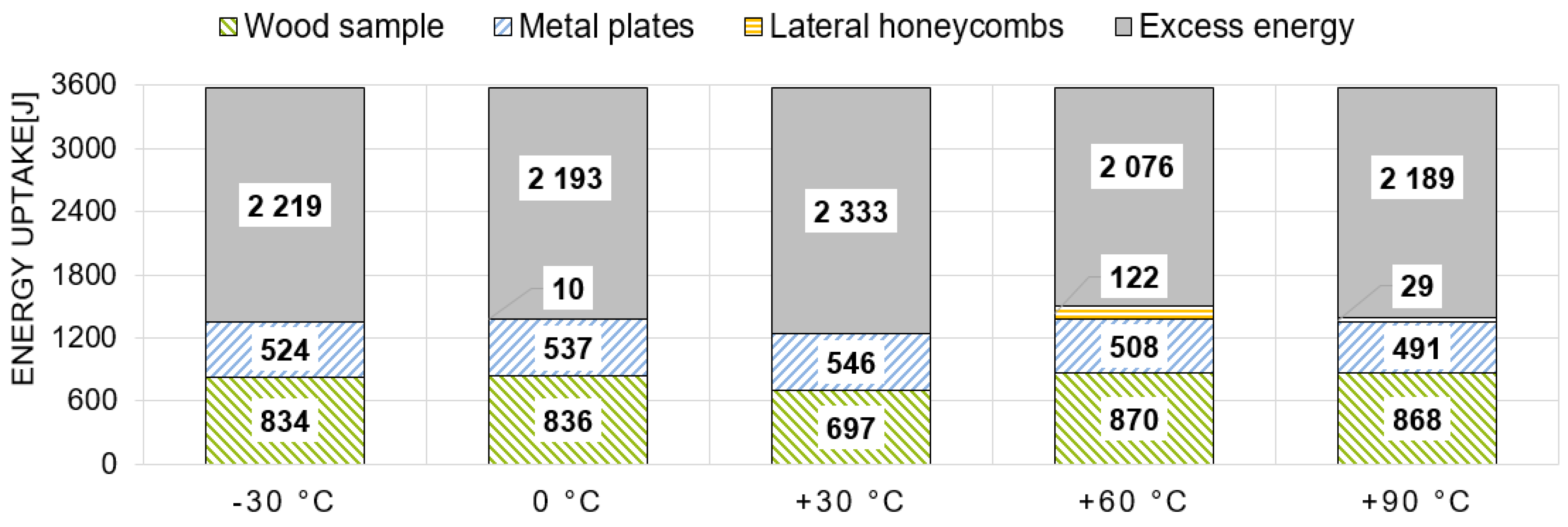
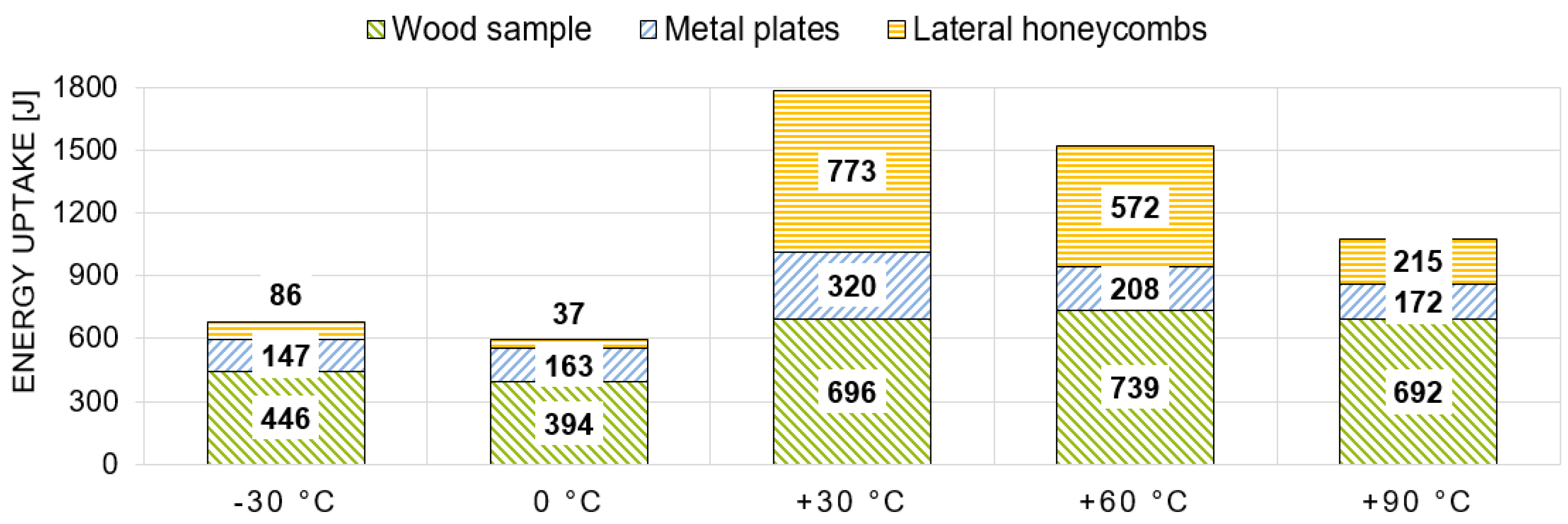
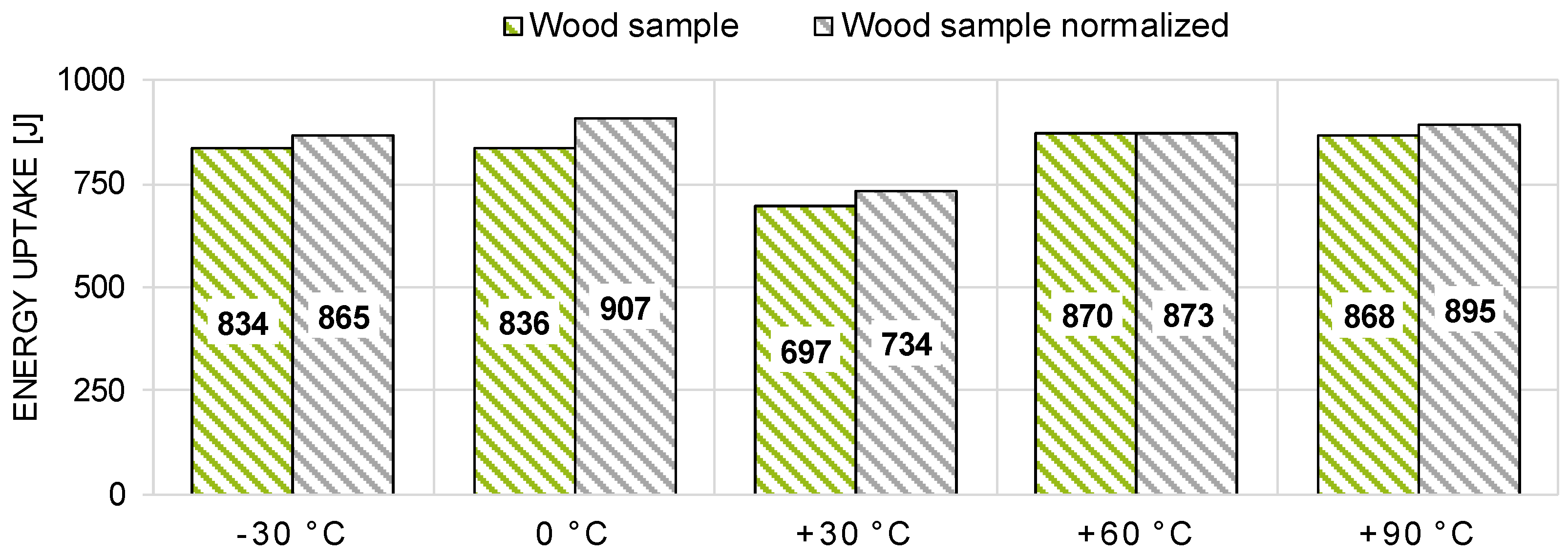
3.4. Energy-Absorbing Capabilities
4. Discussion
4.1. Density, Fiber Deviation, and Climatic Conditions
4.2. Force-Deformation Behavior
4.3. Failure Sequence and Fracture Characteristics
4.4. Energy-Absorbing Capabilities
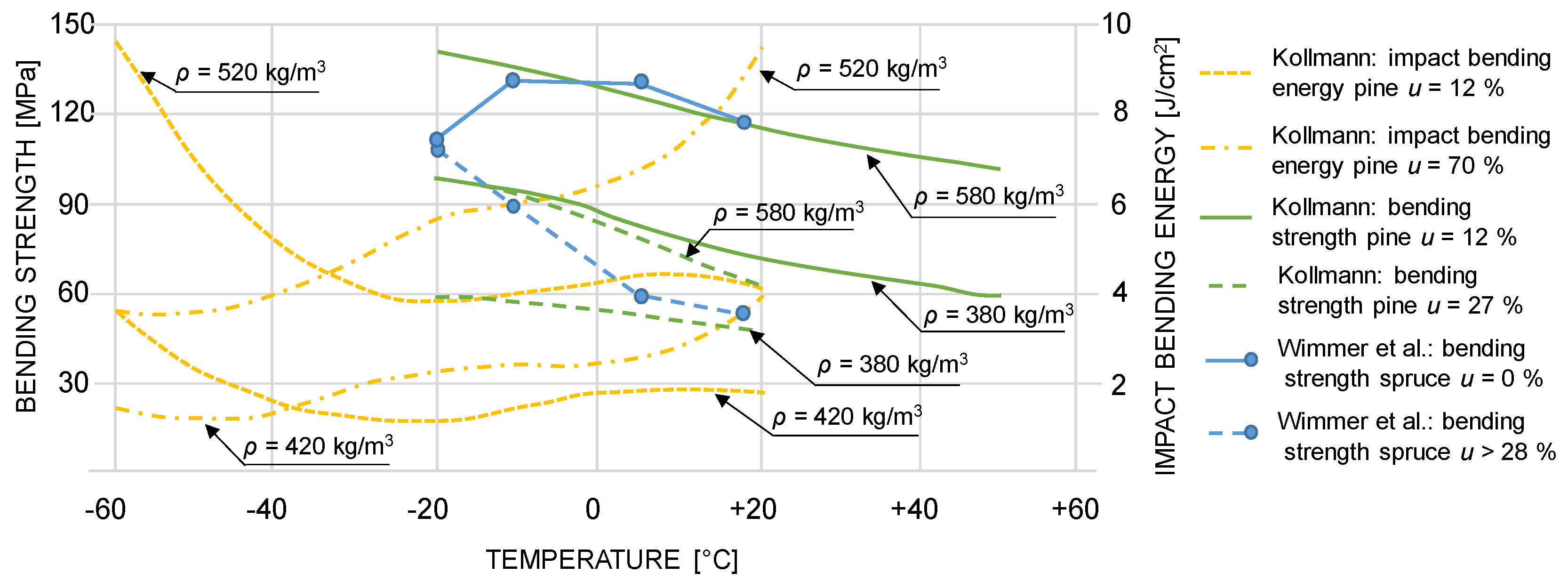
4.5. Comparison of Bending Strength and Impact Bending Energy Values
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Müller, C. Untersuchung von Holzwerkstoffen Unter Schlagbelastung zur Beurteilung der Werkstoffeignung für den Maschinenbau. Ph.D. Thesis, Chemnitz University of Technology, Chemnitz, Germany, October 2015. (In German). [Google Scholar]
- Müller, U.; Jost, T.; Kurzböck, C.; Stadlmann, A.; Kirschbichler, S.; Baumann, G.; Feist, F. Crash Simulation of wood and composite for future automotive engineering. Wood Mater. Sci. Eng. 2018. [Google Scholar] [CrossRef]
- ÖNORM EN 1991-1-7—2014-09: Eurocode 1: Actions on Structures—Part 1–7: General Actions–Accidental Actions (Consolidated Version); Austrian Standards International: Vienna, Austria, 2014.
- ÖNORM EN 1991-2—2012-03: Eurocode 1: Actions on Structures—Part 2: Traffic Loads on Bridges (Consolidated Version); Austrian Standards International: Vienna, Austria, 2012.
- ÖNORM EN 1991-3—2013-12: Eurocode 1: Actions on Structures—Part 3: Actions Induced by Cranes and Machinery (Consolidated Version); Austrian Standards International: Vienna, Austria, 2013.
- Goubel, C.; Massenzio, M.; Ronel, S. Wood-steel structure for vehicle restraint systems. In Proceedings of the 8th European LS-DYNA Users Conference in Strasbourg, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Murray, Y.D. Manual for LS-Dyna Wood Material Model 143; report FHWA-HRT-04-097, U.S.; Department of Transportation, Federal Highway Administration, 6300 Georgetown Pike: McLean, VA, USA, 2007. [Google Scholar]
- Shenoy, M.M.; Smith, L.V.; Axtell, J.T. Performance assessment of wood, metal and composite baseball bats. Compos. Struct. 2001, 52, 397–404. [Google Scholar] [CrossRef]
- O’Brien, M. Finite Element Analysis of Wood and Composite Structured Hockey Sticks. University of Massachusetts at Amherst, Professor Ian Grosse, 605 Finite Element Analysis, ASME. 2003. Available online: http://www-unix.ecs.umass.edu/mie/labs/mda/fea/fealib/obrien/obrienReport.pdf (accessed on 27 November 2020).
- Ruggiero, E.; Sherwood, J.; Drane, P.; Kretschmann, D. An investigation of bat durability by wood species. 9th Conference of the International Sports Engineering Association. Procedia Eng. 2012, 34, 427–432. [Google Scholar] [CrossRef] [Green Version]
- Drane, P.; Sherwood, J.; Colosimo, R.; Kretschmann, D. A study of wood baseball bat breakage, 9th Conference of the International Sports Engineering Association. Procedia Eng. 2012, 34, 616–621. [Google Scholar] [CrossRef] [Green Version]
- Manin, L.; Poggi, M.; Havard, N. Vibrations of table tennis racket composite wood blades: modelling and experiments, 9th Conference of the International Sports Engineering Association. Procedia Eng. 2012, 34, 694–699. [Google Scholar] [CrossRef]
- Ruggiero, E.; Sherwood, J.; Drane, P.; Duffy, M.; Kretschmann, D. Finite element modeling of wood bat profiles for durability, The 2014 conference of the International Sports Engineering Association. Procedia Eng. 2014, 72, 527–532. [Google Scholar] [CrossRef] [Green Version]
- Wimmer, R.; Felber, G.; Teischinger, A. Biegemechanische Eigenschaften von Fichte in Abhängigkeit von Feuchtigkeit und Temperatur. Holztechnologie 2011, 52, 41–45. (In German) [Google Scholar]
- Kollmann, F. Technologie des Holzes und der Holzwerkstoffe; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1982; pp. 333–336, 478–483, 804–808, 849–850. ISBN 3-540-11778-4. (In German) [Google Scholar]
- Kretschmann, D.E.; Green, D.W. Modeling moisture content-mechanical property relationships for clear southern pine. Wood Fiber Sci. 1996, 28, 320–337. [Google Scholar]
- Bucar, D.G.; Merhar, M. Impact and dynamic bending strength determination of Norway Spruce by impact pendulum deceleration. BioResources 2015, 10, 4740–4750. [Google Scholar]
- Tukiainen, P.; Hughes, M. The effect of temperature and moisture content on the fracture behavior of spruce and birch. Holzforschung 2015. [Google Scholar] [CrossRef]
- Gerhards, C.C. Effect of moisture content and temperature on the mechanical properties of wood: an analysis of immediate effects. Wood Fiber 1982, 14, 4–36. Available online: http://wfs.swst.org/index.php/wfs/article/viewFile/501/501 (accessed on 27 November 2020).
- Heräjärvi, H. Static bending properties of Finnish brich wood. Wood Sci. Technol. 2004, 37, 523–530. [Google Scholar] [CrossRef]
- Falconer, J.; Rivas, B. De Havilland Mosquito Owners’Workshop Manual; Haynes Publishing Group: Somerset, UK, 2013; ISBN-13: 978-0-85733-360-5. [Google Scholar]
- ISO 3129–2019 11. Wood—Sampling Methods and General Requirements for Physical and Mechanical Testing of Small Clear Wood Specimens; International Organization of Standardization: Geneva, Switzerland, 2019.
- Wagenführ, R. Holzatlas; Hanser: München, Germany, 2006; ISBN-13: 978-3-446-40649-0. (In German) [Google Scholar]
- Grabner, M. Werkholz: Eigenschaften und Historische Nutzung 60 Mitteleuropäischer Baum- und Straucharten; Verlag Dr. Kessel: Remangen-Oberwinter, Germany, 2017; ISBN-13: 978-3945941249. (In German) [Google Scholar]
- Sell, J. Eigenschaften und Kenngrössen von Holzarten; Baufachverlag: Zürich, Switzerland, 1997; pp. 35–41, ISBN-13: 978-3855652235. (In German) [Google Scholar]
- Kretschmann, D.E. Wood Handbook: Mechanical Properties of Wood; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1999; pp. 4–5. [Google Scholar]
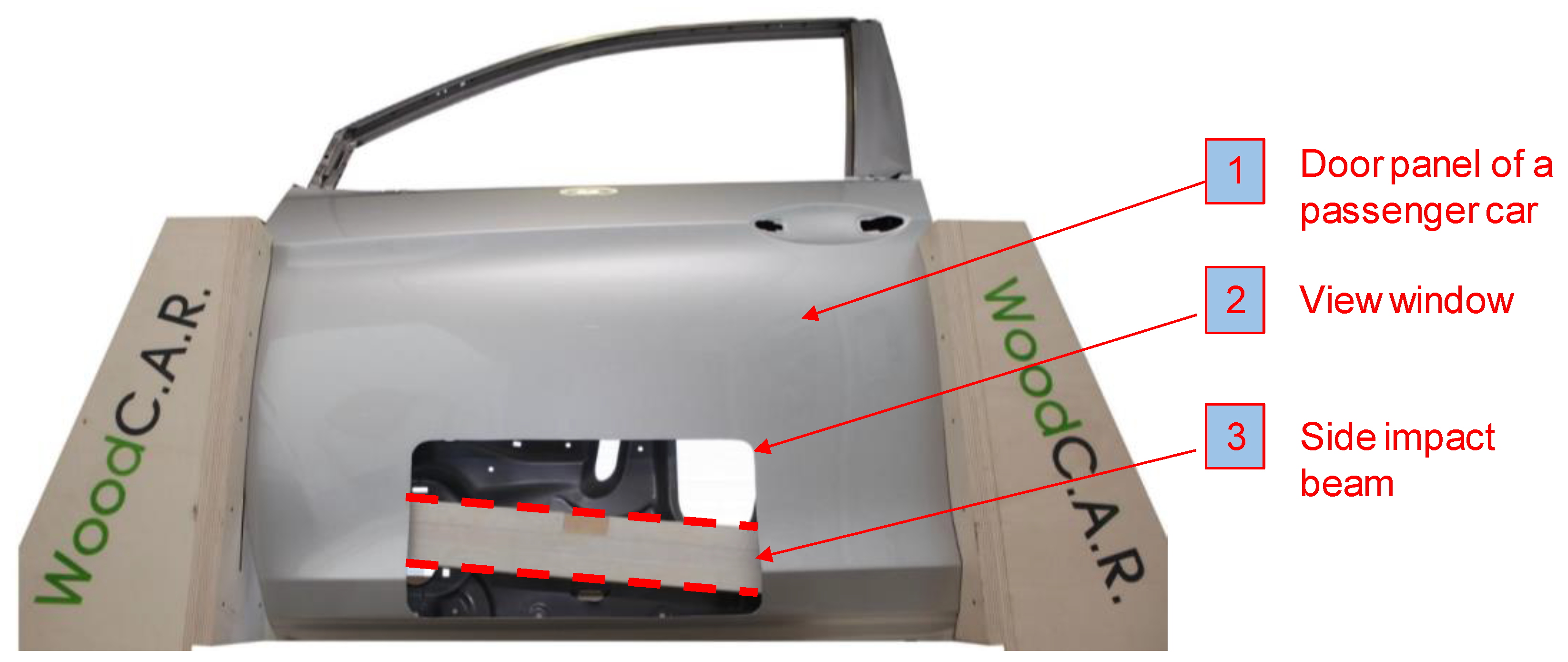
- Shaharuzaman, M.A.; Sapuan, S.M.; Mansor, M.R.; Zuhri, M.Y.M. Passenger car’s side door impact beam: A review. J. Eng. Technol. 2018, 9, 1–22. [Google Scholar]
- Baumann, G.; Stadlmann, A.; Kurzböck, C.; Feist, F. Crashsichere Holzverbundwerkstoffe in Leichtbaukarosserien der Zukunft. Automob. Z. ATZ 2019, 121, 54–59. [Google Scholar] [CrossRef]
- Simlinger, T. Experimentelle und Numerische Untersuchungen von Seitenaufprallträgern in Holzhybridbauweise. Master′s Thesis, Graz University of Technology, Graz, Austria, 2020. (In German). [Google Scholar]
- Klee, J. Experimentelle Untersuchung Eines Seitenaufprallträgers in Holzhybridbauweise. Bachelor Thesis, Graz University of Technology, Graz, Austria, 2019. (In German). [Google Scholar]
- ISO 13061–2–2014 10 01. Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 2: Determination of Density for Physical and Mechanical Tests; International Organization of Standardization: Geneva, Switzerland, 2014.
- ISO 554–1976 08. Standard Atmospheres for Conditioning and/or Testing–Specifications; International Organization of Standardization: Geneva, Switzerland, 1976.
- Götz, S.; Kraft, J. Mathematische Formelsammlung; ÖBV & HPT Verlags GmbH & Co. KG: Vienna, Austria, 2017; p. 16, ISBN-13: 978-3-209-10079-1. (In German) [Google Scholar]
- FMVSS 214. Laboratory Test Procedure for FMVSS 214; U.S. Department of Transportation, National Highway traffic safety administration, Office of Vehicle Safety Compliance: Washington, DC, USA, 1992.
- Missanjo, E.; Matsumura, J. Wood Density and mechanical properties of Pinus kesiya Royle ex Gordon in Malawi. Forests 2016, 7, 135. [Google Scholar] [CrossRef] [Green Version]
- ISO 13061–10–2017 10. Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 10: Determination of Impact Bending Strength; International Organization of Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Wilson, E.; Mohammadi, M.S.; Nairn, J.A. Crack propagation fracture toughness of several wood species. Adv. Civil Eng. Mater. 2013, 2, 20120045. [Google Scholar] [CrossRef]
- Reiterer, A.; Sinn, G.; Stanzl-Tschegg, S.E. Fracture characteristics of different wood species under mode I loading perpendicular to the grain. Mater. Sci. Eng. 2002, A332, 29–36. [Google Scholar] [CrossRef]
- Kim, K.Y. A note on the Hankinson formula. Wood Fiber Sci. 1986, 18, 345–348. [Google Scholar]
- Zhao, L.; Jiang, J.; Lu, J.; Zhan, T. Flexural property of wood in low temperature environment. Cold Reg. Sci. Technol. 2015, 116, 65–69. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, C.; Hu, S.; Yun, H.; Jiang, G.; Zhang, S. Effects of temperature on the bending performance of wood-based panels. BioResources 2012, 7, 3597–3606. [Google Scholar]
- Salmen, N.L.; Fellers, C. The Fundamentals of Energy Consumption during Viscoelastic and Plastic Deformation of Wood; Swedish Forest Products Research Laboratory: Stockholm, Sweden, 1982. [Google Scholar]
- Gilbertson, C.G.; Bulleit, W.M. Load duration effects in wood at high strain rates. Am. Soc. Civil Eng. 2013, 25, 1647–1654. [Google Scholar] [CrossRef]
- Bröker, F.W.; Salamon, S. Instrumentierung eines Pendelschlagwerkes für die Holzprüfung. Holz als Roh-und Werkst. 1989, 47, 93–97. (In German) [Google Scholar] [CrossRef]
- Kraemer, O.J. Aufbau und Verleimung von Flugzeugsperrholz, Luftfahrtforschung; Band. 11, Heft 2; Zentrale für technisch-wissenschaftliches Berichtswesen über Luftfahrtforschung (Hrsg.) Verlag: Berlin/Verlag Oldenburg, Germany, 1934; p. 33. (In German) [Google Scholar]
- Boatright, S.W.J.; Garrett, G. The effect of microstructure and stress state on the fracture behaviour of wood. J. Mat. Sci. 1983, 18, 2181–2199. [Google Scholar] [CrossRef]
- Ashby, M.F.; Easterling, K.E.; Harryson, R.; Maiti, K. The fracture and toughness of woods. Proc. R. Soc. London A 1985, A398, 261–280. [Google Scholar]
- DeBaise, G.R. Morphology of wood shear fracture. J. Mater. 1972, 7, 568–572. [Google Scholar]
- Koran, Z. Electron microscopy of radial traceid of black spruce separated by tensile failure at various temperatures. Tappi 1967, 50, 60–67. [Google Scholar]
- Conrad, M.P.C.; Smith, G.D.; Fernhund, G. Fracture of Solid Wood: A Review of Structure and Properties at Different Length Scales. Wood Fiber Sci. 2003, 35, 570–584. [Google Scholar]
- Côté, A.; Hanna, R.B. Ultrasound characteristics of wood fracture surfaces. Wood Fiber Sci. 1983, 15, 135–163. [Google Scholar]
- Blicblau, A.S.; Cook, D.J. Aspects of wood fracture toughness at various testing speeds. Civil Eng. Trans. 1986, 28, 153–158. [Google Scholar]
- Johnson, J.A. Crack initiation in wood plates. Wood Sci. 1973, 6, 151–158. [Google Scholar]
- Nadeau, J.S.; Bennett, R.; Fuller, E.R. An explanation for the rate-of-loading and the duration-of-load effects in wood in terms of fracture mechanics. J. Mater. Sci. 1982, 17, 2831–2840. [Google Scholar] [CrossRef]
- Schniewind, A.P.; Centeno, J.C. Fracture toughness and duration of load factor I. Six principal systems of crackpropagation and the duration factor for cracks propa-gating parallel to grain. Wood Fiber 1973, 5, 152–159. [Google Scholar]
- Mindness, S. The fracture of wood in tension parallel to the grain. Can. J. Civil Eng. 1977, 4, 412–416. [Google Scholar] [CrossRef]
- Vasic, S.; Stanzl-Tschegg, S. Experimental and numerical investigation of wood fracture mechanisms at different humidity levels. Holzforschung 2007, 61, 367–374. [Google Scholar] [CrossRef]
- Leicester, R.H. Application of Linear Fracture Mechanics to Timber Engineering. In Proceedings of the Structural Integrity and Fractural International Conference (SIF’04), Brisbane, Australia, 26–29 September 2004. [Google Scholar]
- Barrett, J.D.; Foschi, R.O. Mode II stress-intensity factors for cracked wood beams. Eng. Fract. Mech. 1977, 9, 371–378. [Google Scholar] [CrossRef]
- ISO 13061–3–2014 12 01. Physical and Mechanical Properties of Wood—Test Methods for Small clear Wood Specimens—Part 3: Determination of Ultimate Strength in Static Bending; International Organization of Standardization: Geneva, Switzerland, 2014.





| Temperature | −30 °C | 0 °C | +30 °C | +60 °C | +90 °C |
|---|---|---|---|---|---|
| Dynamic | n = 6 | n = 6 | n = 6 | n = 6 | n = 6 |
| Quasi-static | n = 6 | n = 6 | n = 6 | n = 6 | n = 6 |
| Temperature-Level | n (-) | Tmean (°C) | σT (°C) | umean (%) | CV (u) (%) | ρ12,mean (kg/m3) | CV (ρ12) (%) | θmean[°] | CV (θ) (%) |
| Dynamic | |||||||||
| −30 °C | 6 | −17 | 10.4 | 9.4 | 17.0 | 592 | 9.0 | 2.6 | 60.2 |
| 0 °C | 6 | +2 | 9.1 | 9.3 | 15.1 | 574 | 4.9 | 5.1 | 50.9 |
| +30 °C | 6 | +30 | - | 9.5 | 13.7 | 586 | 3.9 | 3.6 | 50.8 |
| +60 °C | 6 | +60 | 5.4 | 6.5 | 41.5 | 605 | 10.7 | 5.1 | 104.1 |
| +90 °C | 6 | +77 | 4.6 | 3.6 | 19.4 | 594 | 9.8 | 5.9 | 35.8 |
| n (-) | Tstart (°C) | σT (°C) | ΔT (°C) | σΔT (°C) | umean (%) | CV (u) (%) | ρ12,mean (kg/m3) | CV (ρ12) (%) | |
| Quasi-static | |||||||||
| −30 °C | 6 | −27 | 7.6 | +25.1 | 7.5 | 10.1 | 7.9 | 599 | 10.9 |
| 0 °C | 6 | −1 | 1.1 | +9.9 | 1.8 | 9.8 | 13.3 | 625 | 5.0 |
| +30 °C | 6 | +32 | 1.7 | −5.4 | 1.1 | 9.3 | 8.6 | 649 | 9.9 |
| +60 °C | 6 | +61 | 1.0 | −23.3 | 2.3 | 8.1 | 4.9 | 600 | 5.0 |
| +90 °C | 6 | +89 | 4.8 | −32.6 | 6.3 | 5.2 | 13.5 | 637 | 7.8 |
| Author | Sell [25] | Wagenführ [23] | Grabner [24] | Kretschmann [26] |
|---|---|---|---|---|
| Quasi-static bending strength (MPa) | 120 to 144 * | 76 to 155 ** | 112 *** | 114 **** |
| Impact bending energy (J/cm2) | 7.5 to 10 * | 4.5 to 13 ** | 4 *** | 14.1–17.5 **** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baumann, G.; Brandner, R.; Müller, U.; Kumpenza, C.; Stadlmann, A.; Feist, F. Temperature-Related Properties of Solid Birch Wood under Quasi-Static and Dynamic Bending. Materials 2020, 13, 5518. https://doi.org/10.3390/ma13235518
Baumann G, Brandner R, Müller U, Kumpenza C, Stadlmann A, Feist F. Temperature-Related Properties of Solid Birch Wood under Quasi-Static and Dynamic Bending. Materials. 2020; 13(23):5518. https://doi.org/10.3390/ma13235518
Chicago/Turabian StyleBaumann, Georg, Reinhard Brandner, Ulrich Müller, Cedou Kumpenza, Alexander Stadlmann, and Florian Feist. 2020. "Temperature-Related Properties of Solid Birch Wood under Quasi-Static and Dynamic Bending" Materials 13, no. 23: 5518. https://doi.org/10.3390/ma13235518
APA StyleBaumann, G., Brandner, R., Müller, U., Kumpenza, C., Stadlmann, A., & Feist, F. (2020). Temperature-Related Properties of Solid Birch Wood under Quasi-Static and Dynamic Bending. Materials, 13(23), 5518. https://doi.org/10.3390/ma13235518






