Effective and Apparent Diffusion Coefficients of Chloride Ions and Chloride Binding Kinetics Parameters in Mortars: Non-Stationary Diffusion–Reaction Model and the Inverse Problem
Abstract
1. Introduction
Selected Methods Used for Determination of Chloride Diffusion Coefficients
2. Materials and Methods
2.1. Characterization of the Samples and Storage and Sampling Conditions
2.2. Non-Stationary Diffusion Measurements
3. Modeling of Chloride Transport
3.1. Binding of Chlorides in a Mortar
- The adsorbed ions must cover all of the adsorption sites at all times and must form no more than a monolayer on these sites;
- The adsorption sites must be uniform and localized. The adsorbed ions, regardless of species, must not interact with one another;
- The ion exchange process must be the replacement of a single ion by another single ion.
- The adsorption sites may be grouped into classes, each of which is characterized by the number of sites it contains and by the relative affinity it possesses for the exchanging species.
- For each class of sites, exchange is described by the competitive Langmuir equation (all assumptions for the Langmuir isotherm must be met).
3.2. Diffusion–Reaction Model of Chloride Transport in Cementitious Materials
3.3. The Inverse Problem for the Diffusion–Reaction Model
4. Results
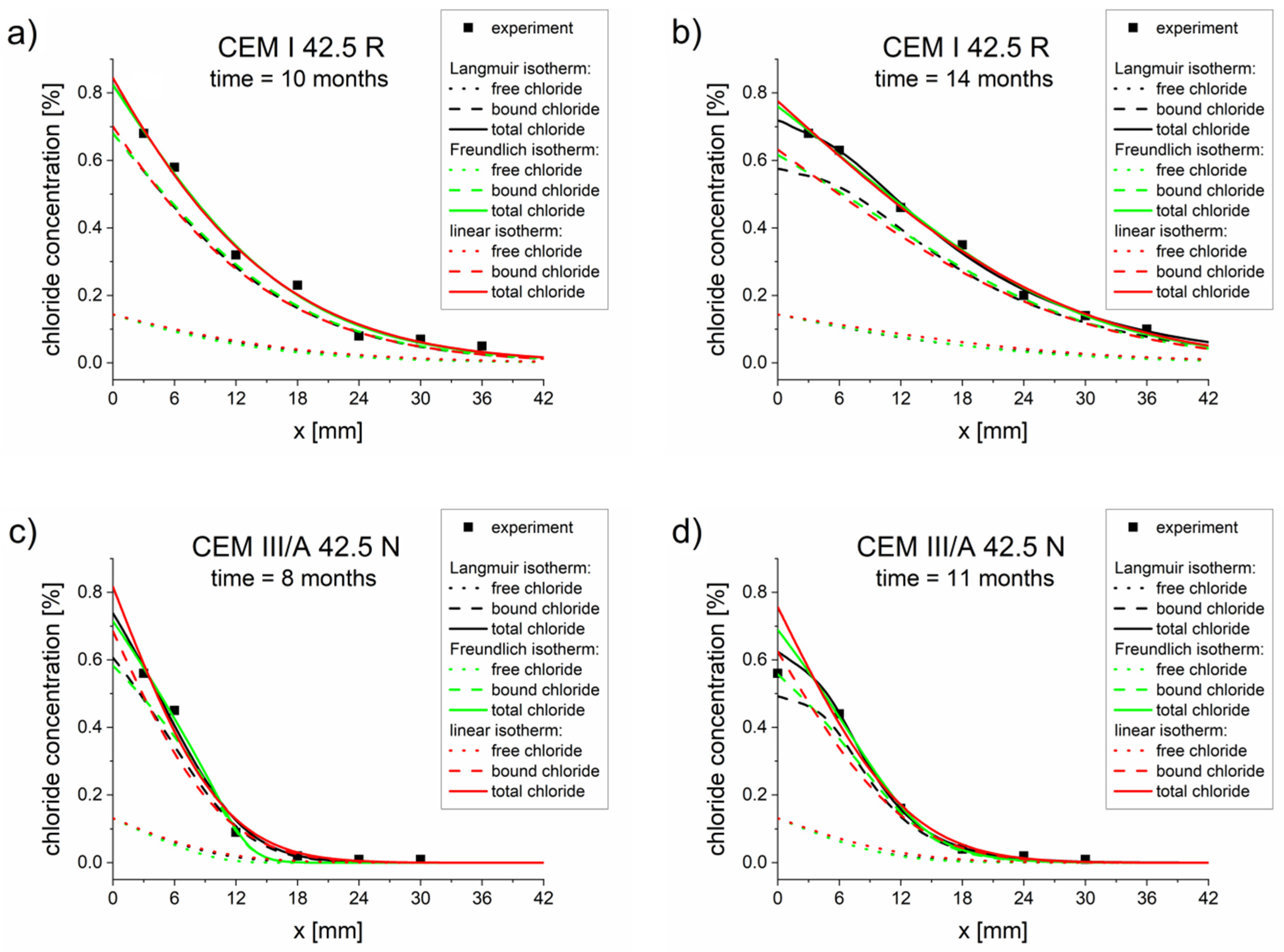
4.1. Optimization for a Single Measurement
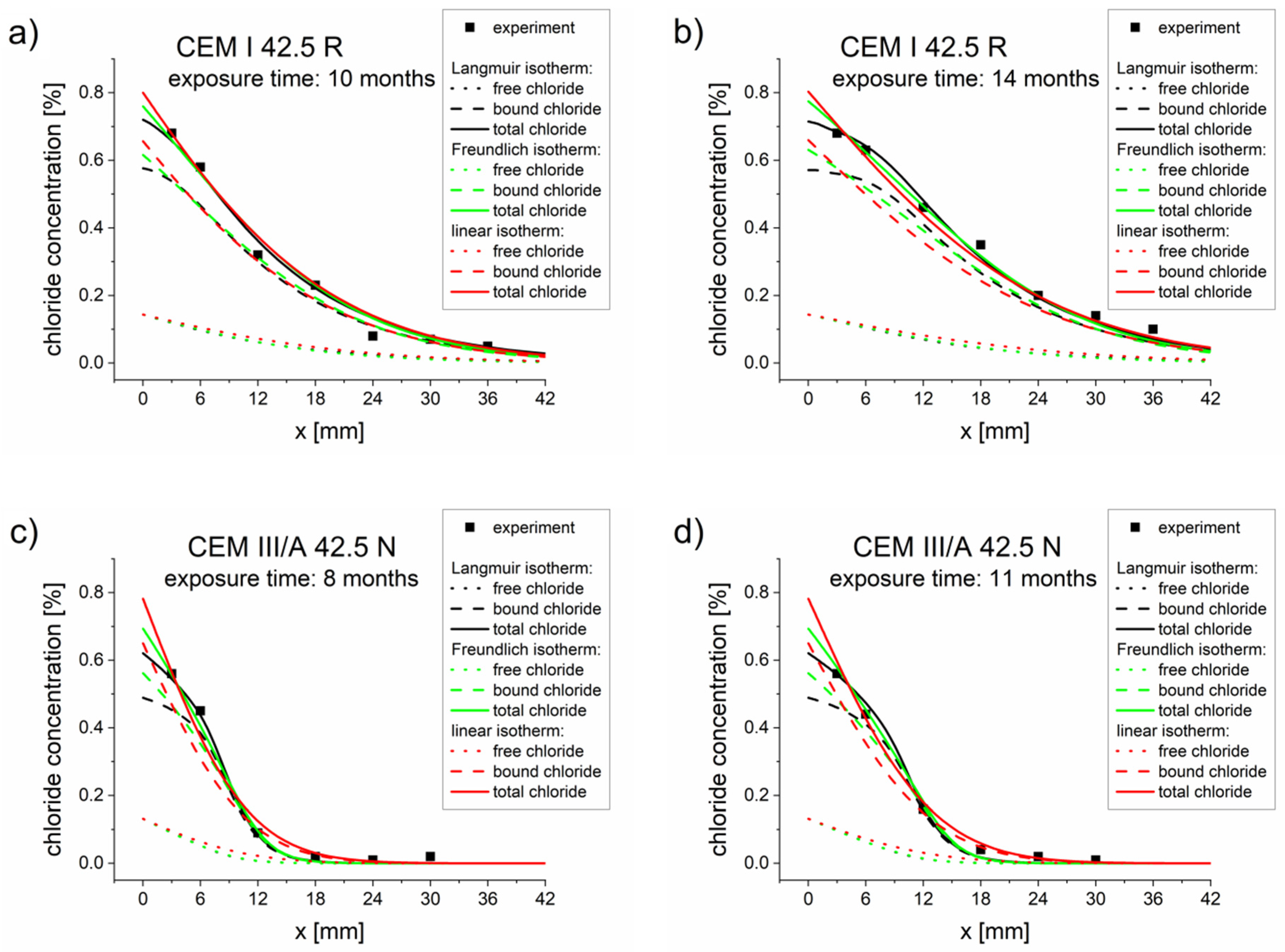
4.2. Optimization Based on Two Measurements
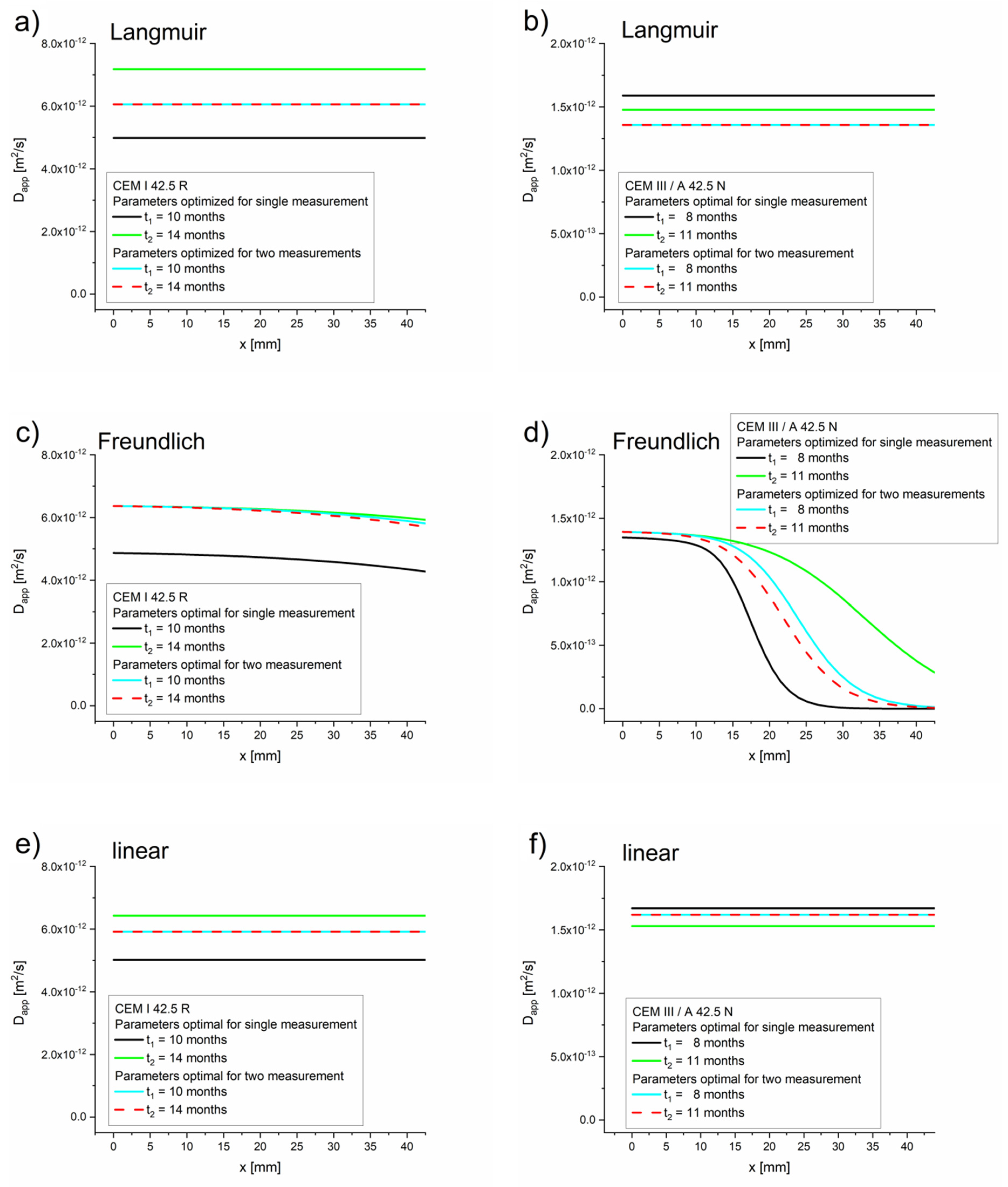
4.3. Apparent and Effective Diffusion Coefficients
5. Discussion
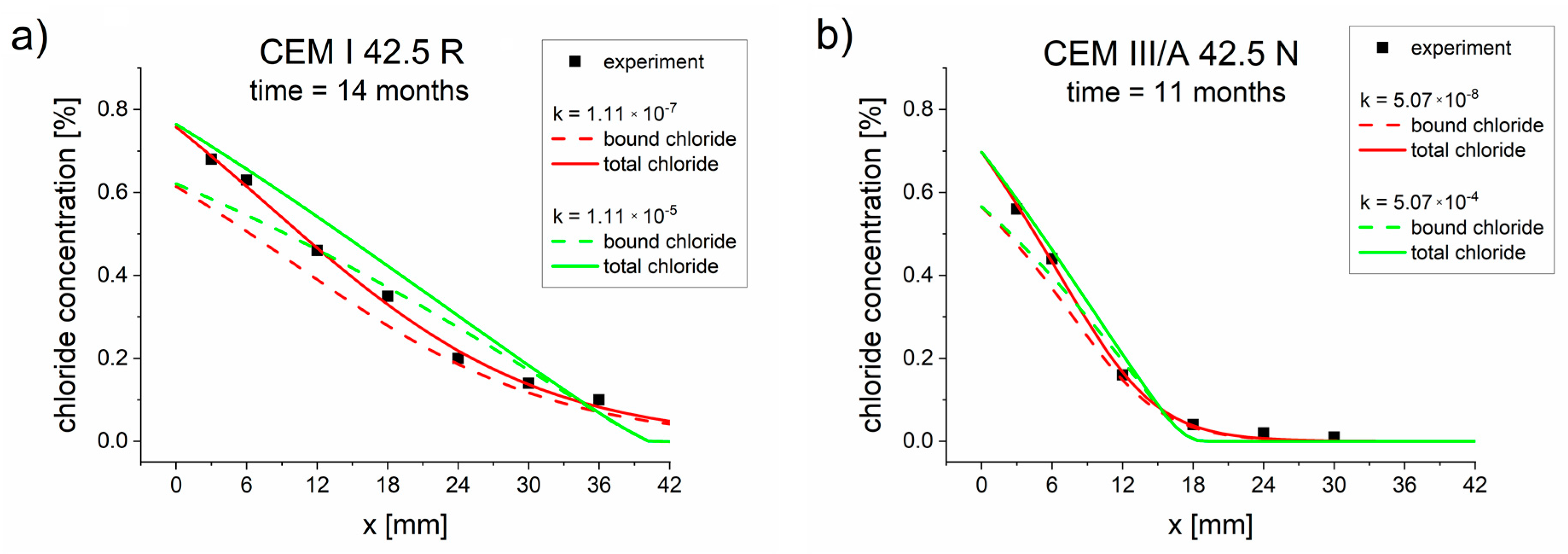
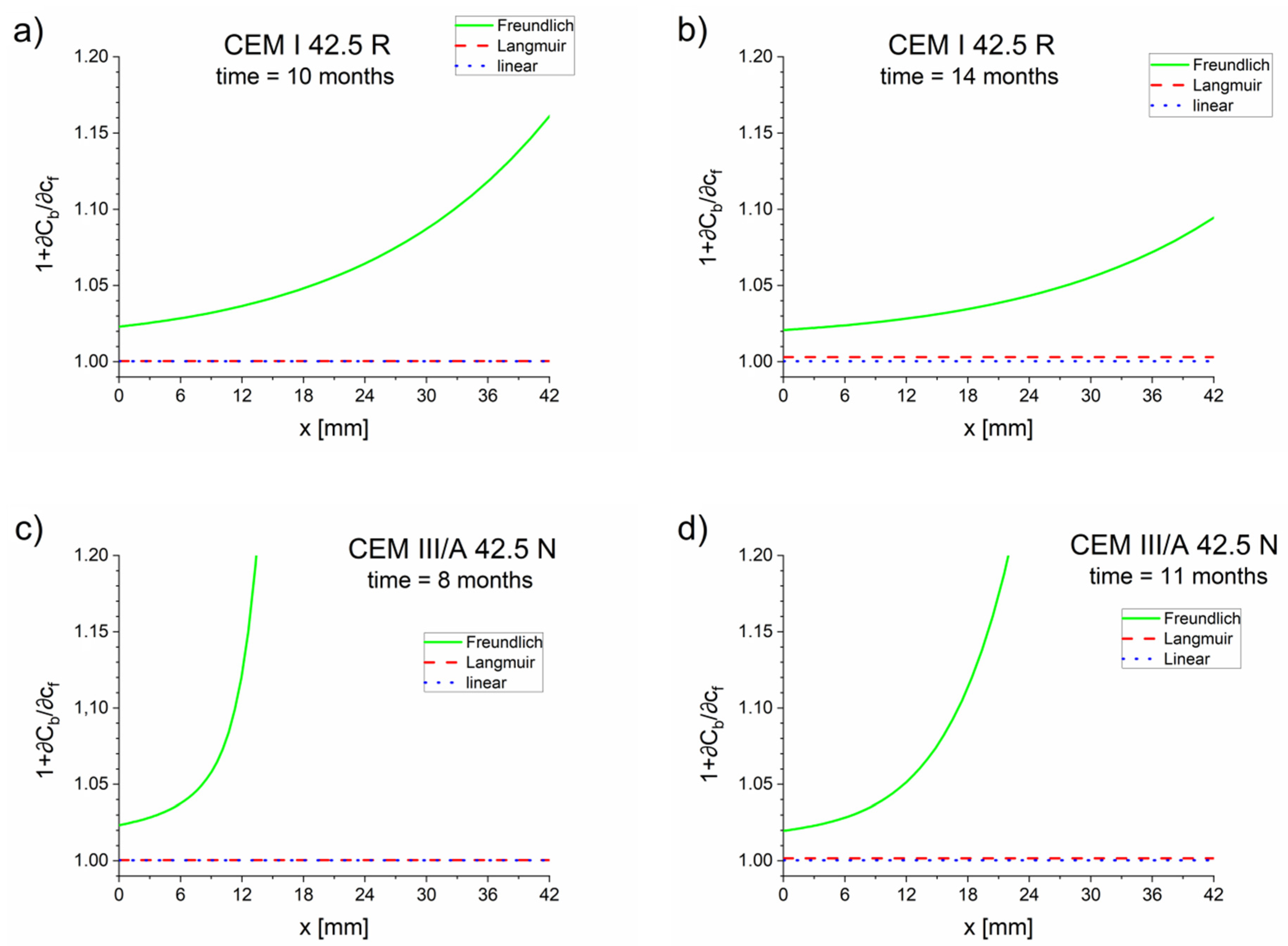
5.1. Application of Binding Isotherms
5.2. Influence of Porosity
5.3. Further Extensions of the Model
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Simplified Chloride Diffusion Model
Appendix B. Comments Concerning the So-Called Apparent Diffusion Coefficient
References
- BS EN 206: 2013. Concrete—Specification, Performance, Production and Conformity; British Standard Institution: London, UK, 2013.
- CEN-EN 197-1. Cement Part 1: Composition, Specifications and Conformity Criteria for Common Cements; European Committee for Standardization (CEN): Brussels, Belgium, 2011.
- Poole, A.B. Introduction to alkali-aggregate reaction and concrete. In The Alkali-silica Reaction in Concrete; Swamy, R.N., Ed.; Blackie and Sons Ltd.: Glasgow, UK, 1992; pp. 1–29. [Google Scholar]
- Fernandes, I.; Broekmans, M.A.T.M. Alkali–Silica Reactions: An Overview. Part I. Metallogr. Microstruct. Anal. 2013, 2, 257–267. [Google Scholar] [CrossRef]
- Neville, A.M.; Brooks, J.J. Concrete Technology, 2nd ed.; Pearson Education Limited: Harlow, UK, 2010; pp. 1–442. [Google Scholar]
- Kurdowski, W. Cement and Concrete Chemistry; Springer: Dotrecht, The Netherlands, 2014; pp. 1–700. [Google Scholar]
- AASHTO T259–80. Standard Method of Test for Resistance of Concrete to Chloride ion Penetration; AASHTO T: Washington, DC, USA, 1980; pp. 259–280. [Google Scholar]
- NT BUILD-443. Concrete Hardened: Accelerated Chloride Penetration; Nordtest: Espoo, Finland, 1995; pp. 1–5.
- ASTM International. C1556-11a Standard Test Method for Determining the Apparent Chloride Diffusion Coefficient of Cementitious Mixtures by Bulk Diffusion; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- McGrath, P.F.; Hooton, R.D. Re-evaluation of the AASHTO T259 90-day salt ponding test. Cem. Concr. Res. 1999, 29, 1239–1248. [Google Scholar] [CrossRef]
- Yang, C.C. A comparison of transport properties for concrete using the ponding test and the accelerated chloride migration test. Mater. Struct. 2005, 38, 313–320. [Google Scholar] [CrossRef]
- Climent, M.A.; De Vera, G.; López, J.F.; Viqueira, E.; Andrade, C. A test method for measuring chloride diffusion coefficients through nonsaturated concrete: Part I. The instantaneous plane source diffusion case. Cem. Concr. Res. 2002, 32, 1113–1123. [Google Scholar] [CrossRef]
- Guimarães, A.T.C.; Climent, M.A.; de Vera, G.; Vicente, F.J.; Rodrigues, F.T.; Andrade, C. Determination of chloride diffusivity through partially saturated Portland cement concrete by a simplified procedure. Constr. Build. Mater. 2011, 25, 785–790. [Google Scholar] [CrossRef]
- Szyszkiewicz, K.; Jasielec, J.J.; Królikowska, A.; Filipek, R. Determination of Chloride Diffusion Coefficient in Cement-Based Materials–A Review of Experimental and Modeling Methods: Part I—Diffusion Methods. Cement Wapno Beton 2017, 1, 52–66. [Google Scholar]
- Jasielec, J.J.; Szyszkiewicz, K.; Królikowska, A.; Filipek, R. Determination of Chloride Diffusion Coefficient in Cement-Based Materials—A Review of Experimental and Modeling Methods: Part II—Migration Methods. Cement Wapno Beton 2017, 2, 154–167. [Google Scholar]
- Szyszkiewicz, K.; Jasielec, J.J.; Królikowska, A.; Filipek, R. Determination of Chloride Diffusion Coefficient in Cement-Based Materials – A Review of Experimental and Modeling Methods: Part III—EIS-based Methods. Cement Wapno Beton 2017, 3, 219–229. [Google Scholar]
- Patel, R.A.; Phung, Q.T.; Seetharam, S.C.; Perko, J.; Jaques, D.; Maes, N.; De Schutter, G.; Ye, G.; Van Breugel, K. Diffusivity of Saturated Ordinary Portland Cement-based Materials: A Critical Review of Experimental and Analytical Modelling Approaches. Cem. Concr. Res. 2016, 90, 52–72. [Google Scholar] [CrossRef]
- Florea, M.V.A.; Brouwers, H.J.H. Chloride binding related to hydration products Part I: Ordinary portland cement. Cem. Concr. Res. 2012, 42, 282–290. [Google Scholar] [CrossRef]
- Reiterman, P.; Keppert, M. Effect of various de-icers containing chloride ions on scaling resistance and chloride penetration depth of highway concrete. Roads Bridges Drogi Mosty 2020, 19, 51–64. [Google Scholar]
- Pruckner, F.; Gjørv, O. Effect of CaCl2 and NaCl additions on concrete corrosivity. Cem. Concr. Res. 2004, 34, 1209–1217. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, L.; Wang, W.; Jiang, Y. Influence of CaCl2 and NaCl from different sources on chloride threshold value for the corrosion of steel reinforcement in concrete. Constr. Build. Mat. 2011, 25, 663–669. [Google Scholar] [CrossRef]
- Farnam, Y.; Wiese, A.; Bentz, D.; Davis, J.; Weiss, J. Damage development in cementitious materials exposed to magnesium chloride de-icing salt. Constr. Build. Mat. 2015, 93, 384–392. [Google Scholar] [CrossRef]
- Peterson, K.; Julio-Betancourt, G.; Sutter, L.; Hooton, R.D.; Johnston, D. Observations of chloride ingress and calcium oxychloride formation in laboratory concrete and mortar at 5 °C. Cem. Concr. Res. 2013, 45, 79–90. [Google Scholar] [CrossRef]
- Brown, P.; Bothe, J. The system CaO-Al2O3-CaCl2-H2O at 23 ± 2 °C and the mechanisms of chloride binding in concrete. Cem. Concr. Res. 2004, 34, 1549–1553. [Google Scholar] [CrossRef]
- Martin-Perez, B.; Zibara, H.; Hooton, R.D.; Thomas, M.D.A. A study of the effect of chloride binding on service life predictions. Cem. Concr. Res. 2000, 30, 1215–1223. [Google Scholar] [CrossRef]
- Justnes, H. A review of chloride binding in cementitious systems. Nord. Concr. Res. 1998, 21, 1–6. [Google Scholar]
- Isgor, O.B.; Razaqpur, A.G. Finite element modeling of coupled heat transfer, moisture transport and carbonation processes in concrete structures. Cem. Concr. Compos. 2004, 26, 57–73. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Modeling the transport of ions in unsaturated cement-based materials. Comput. Struct. 2007, 85, 1740–1756. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Multiionic approaches to model chloride binding in cementious materials. In Proceedings of the 2nd International Symposium on Advances in Concrete through Science and Engineering, Quebec City, QC, Canada, 11–13 September 2006. [Google Scholar]
- Suryavanshi, A.K.; Scantlebury, J.D.; Lyon, S.B. Mechanism of Friedel’s salt formation in cement rich in tri-calcium aluminate. Cem. Concr. Res. 1996, 26, 717–727. [Google Scholar] [CrossRef]
- Brown, P.W.; Badger, S. The distribution of bound sulfates and chlorides in concrete subjected to mixed NaCl, MgSO4, Na2SO4 attack. Cem. Concr. Res. 2000, 30, 1535–1542. [Google Scholar] [CrossRef]
- Mohammed, T.U.; Hamada, H.; Yamaji, T. Concrete after 30 years of exposure—Part I: Mineralogy, microstructure and interfaces. ACI Mater. J. 2004, 101, 3–12. [Google Scholar]
- Nielsen, E.P.; Herfort, D.; Geiker, M.R. Binding of chloride and alkalis in portland cement systems. Cem. Concr. Res. 2005, 35, 117–123. [Google Scholar] [CrossRef]
- Barberon, F.; Baroghel-Bouny, V.; Zanni, H.; Bresson, B.; d’Espinose de la Caillerie, J.-B.; Malosse, L.; Zehong, G. Interactions between chloride and cement-paste materials. Magn. Reson. Imaging 2005, 23, 267–272. [Google Scholar] [CrossRef]
- Azad, V.J.; Li, C.; Verba, C.; Ideker, J.H.; Isgor, O.B. A COMSOL-GEMS Interface for modeling coupled reactive-transport geochemical processes. Comput. Geosci. 2016, 92, 79–89. [Google Scholar] [CrossRef]
- Azad, V.J.; Isgor, O.B. Modeling chloride ingress in concrete with thermodynamically calculated chemical binding. Int. J. Adv. Eng. Sci. Appl. Math. 2017, 9, 97–108. [Google Scholar] [CrossRef]
- Tran, V.Q.; Soive, A.; Baroghel-Bouny, V. Modelisation of chloride reactive transport in concrete including thermodynamic equilibrium, kinetic control and surface complexation. Cem. Concr. Res. 2018, 110, 70–85. [Google Scholar] [CrossRef]
- Isgor, O.B.; Weiss, W.J. A nearly self-sufficient framework for modelling reactive-transport processes in concrete. Mater. Struct. 2019, 52, 3. [Google Scholar] [CrossRef]
- CEN-EN 196-1, Methods of Testing Cement—Part 1: Determination of Strength; European Committee for Standardization (CEN): Brussels, Belgium, 2016.
- CEN-EN 196-2, Method of Testing Cement—Part 2: Chemical Analysis of Cement; European Committee for Standardization (CEN): Brussels, Belgium, 2013.
- Bishnoi, S.; Scrivener, K.L. µic: A new platform for modelling the hydration of cements. Cem. Concr. Res. 2009, 39, 266–274. [Google Scholar] [CrossRef]
- Tang, L.; Nilsson, L.O. Chloride binding capacity and binding isotherms of OPC pastes and mortars. Cem. Concr. Res. 1992, 23, 247–253. [Google Scholar]
- Sandberg, P. Studies of chloride binding in concrete exposed in marine environment. Cem. Concr. Res. 1999, 29, 473–477. [Google Scholar] [CrossRef]
- Loser, R.; Lothenbach, B.; Leemann, A.; Tuchschmid, M. Chloride resistance of concrete and its binding capacity—Comparison between experimental results and thermodynamic modelling. Cem. Concr. Compos. 2010, 32, 34–42. [Google Scholar] [CrossRef]
- Tang, L. Chloride Transport in Concrete—Measurement and Prediction. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1996. [Google Scholar]
- Arya, C.; Buenfeld, N.R.; Newman, J.B. Assessment of simple methods of determining the free chloride ion content of cement paste. Cem. Concr. Res. 1987, 17, 907–918. [Google Scholar] [CrossRef]
- Zibara, H. Binding of External Chlorides by Cement Pastes. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2001. [Google Scholar]
- Yuan, Q.; Shi, C.; De Schutter, G.; Audenaert, K.; Deng, D. Chloride binding of cement-based materials subjected to external chloride environment—A review. Constr. Build. Mater. 2009, 23, 1–13. [Google Scholar] [CrossRef]
- Kammerer, J.; Carle, R.; Kammerer, D.R. Adsorption and Ion Exchange: Basic Principles and Their Application in Food Processing. J. Agric. Food Chem. 2011, 59, 22–42. [Google Scholar] [CrossRef]
- Sposito, G. Derivation of the Langmuir Equation for Ion Exchange Reactions in Soils. Soil Sci. Soc Am. J. 1979, 43, 197–198. [Google Scholar] [CrossRef]
- Sergi, W.; Yu, S.W.; Page, C.L. Diffusion of chloride and hydroxyl ions in cementitious materials exposed to a saline environment. Mag. Concr. Res. 1992, 44, 63–69. [Google Scholar] [CrossRef]
- Truc, O. Prediction of Chloride Penetration into Saturated Concrete—Multi-species Approach. Ph.D. Thesis, Department of Building Materials, Chalmers University of Technology, Goteborg, Sweden, 2000. [Google Scholar]
- Spiesz, P.; Ballari, M.M.; Brouwers, H.J.H. RCM: A new model accounting for the non-linear chloride binding isotherm and the non-equilibrium conditions between the free-and bound-chloride concentrations. Constr. Build. Mater. 2012, 27, 293–304. [Google Scholar] [CrossRef]
- Sposito, G. Derivation of the Freundlich Equation for Ion Exchange Reactions in Soils. Soil Sci. Soc. Am. J. 1980, 44, 652–654. [Google Scholar] [CrossRef]
- Tuutti, K. Analysis of pore solution squeezed out of cement and mortar. Nordic Concr. Res. 1982, 1, 1–16. [Google Scholar]
- Mohammed, T.U.; Hamada, H. Relationship between free chloride and total chloride contents in concrete. Cem. Concr. Res. 2003, 33, 1487–1490. [Google Scholar] [CrossRef]
- Wright, S.J. Coordinate descent algorithms. Math. Program. 2015, 151, 3–34. [Google Scholar] [CrossRef]
- Shackelford, C.D.; Daniel, D.E. Diffusion in Saturated Soil. I: Background. J. Geotech. Eng. ASCE 1991, 117, 467–484. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on the plane surfaces of glass, mica, and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Boyd, G.E.; Schubert, J.; Adamson, A.W. The exchange adsorption of ions from aqueous solutions by organic zeolites. I. Ion-exchange equilibria. J. Am. Chem. Soc. 1947, 69, 2818–2829. [Google Scholar] [CrossRef]
- Mindess, S.; Young, J.F.; Darwin, D. Concrete, 2nd ed.; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 2003. [Google Scholar]
- Muller, A.C.A.; Scrivener, K.L. A reassessment of mercury intrusion porosimetry by comparison with 1H NMR relaxometry. Cem. Concr. Res. 2017, 100, 350–360. [Google Scholar] [CrossRef]
- Abell, A.B.; Willis, K.L.; Lange, D.A. Mercury intrusion porosimetry and image analysis of cement-based materials. J. Colloid Interface Sci. 1999, 211, 39–44. [Google Scholar] [CrossRef]
- Katrin, R.; Dirk, H. Characterization of mineral building materials by mercury intrusion porosimetry. Part. Part. Syst. Char. 2006, 23, 20–28. [Google Scholar]
- Guedes, M.; Evangelista, L.; de Brito, J.; Ferro, A.C. Microstructural characterization of concrete prepared with recycled aggregates. Microsc. Microanal. 2013, 19, 1222–1230. [Google Scholar] [CrossRef]
- Rübner, K.; Prinz, C.; Adolphs, J.; Hempel, S.; Schnelld, A. Microstructural characterisation of lightweight granules made from masonry rubble. Microporous Mesoporous Mater. 2015, 209, 113–121. [Google Scholar] [CrossRef]
- Wenzel, O.; Schwotzer, M.; Müller, E.; Chakravadhanula, V.S.K.; Scherer, T.; Gerdes, A. Investigating the pore structure of the calcium silicate hydrate phase. Mater. Char. 2017, 133, 133–137. [Google Scholar] [CrossRef]
- Kumar, R.; Bhattacharjee, B. Porosity, pore size distribution and in situ strength of concrete. Cem. Concr. Res. 2003, 33, 155–164. [Google Scholar] [CrossRef]
- Bonen, D. The nanostructure of the cement paste and its porosity. In Proceedings of the 2nd International Symposium on Advances in Concrete through Science and Engineering, Quebec City, QC, Canada, 11–13 September 2006; Marchand, J., Bissonnette, B., Gagné, R., Jolin, M., Paradis, F., Eds.; RILEM Publications SARL: Paris, France, 2006. [Google Scholar]
- Diamond, S. The microstructure of cement paste and concrete-a visual primer. Cem. Concr. Compos. 2004, 26, 919–933. [Google Scholar] [CrossRef]
- Diamond, S.; Leeman, M.E. Pore size distributions in hardened cement pastes by SEM image analysis. In MRS Symposium Proc. V. 137, Microstructure of Cement Based Systems; Materials Research Society: Pittsburgh, PA, USA, 1989; pp. 217–226. [Google Scholar]
- Ye, G. The Microstructure and Permeability of Cementitious Materials. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 2003. [Google Scholar]
- Diamond, S. Physical and chemical characteristics of cement composites. In Durability of Concrete and Cement Composites, 1st ed.; Page, C.L., Page, M.M., Eds.; Woodhead Publishing: Cambridge, UK, 2007; pp. 10–44. [Google Scholar]
- Muller, A.C.A.; Scrivener, K.L.; Gajewicz, A.M.; McDonald, P.J. Densification of C–S–H measured by 1H NMR relaxometry. J. Phys. Chem. C 2013, 117, 403–412. [Google Scholar] [CrossRef]
- Muller, A.C.A.; Scrivener, K.L.; Gajewicz, A.M.; McDonald, P.J. Use of bench-top NMR to measure the density, composition and desorption isotherm of C–S–H in cement paste. Microporous Mesoporous Mater. 2013, 178, 99–103. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete, (CBI); Report Fo 4.82; Swedish Cement and Concrete Research Institute: Stockholm, Swedish, 1982. [Google Scholar]
- Crank, J. Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Johannesson, B.; Yamada, K.; Nilsson, L.-O.; Hosokawa, Y. Multi-species ionic diffusion in concrete with account to interaction between ions in the pore solution and the cement hydrates. Mater. Struct. 2007, 40, 651–665. [Google Scholar] [CrossRef]
- Spiesz, P.; Brouwers, H.J.H. The apparent and effective chloride migration coefficients obtained in migration tests. Cem. Concr. Res. 2013, 48, 116–127. [Google Scholar] [CrossRef]
- Tang, L. Concentration dependence of diffusion and migration of chloride ions Part 1. Theoretical considerations. Cem. Concr. Res. 1999, 29, 1463–1468. [Google Scholar] [CrossRef]

| Type of Cement | Sand | Cement | Water |
|---|---|---|---|
| CEM I 42.5 R | 1470 | 490 | 245 |
| CEM III/A 42.5 N | 1410 | 470 | 235 |
| Type of Cement | Bending Strength // Compression Strength (MPa) | Absorption (%) | Test Results from Mercury Porosimetry | |||||
|---|---|---|---|---|---|---|---|---|
| Maturation Time | Maturation Time | Porosity (%) | Cumulative Pore Volume (mm3/g) | Density (kg/m3) | ||||
| 2 Days | 28 Days | 90 Days | 28 Days | 90 Days | ||||
| CEM I 42.5 R | 6.2 // 38.9 | 7.5 // 48.4 | 7.6 // 54.1 | 8.0 | 9.0 | 16.8 | 79.1 | 2130 |
| CEM III/A 42.5 N | 3.5 // 14.5 | 7.2 // 55.4 | 8.1 // 59.0 | 6.4 | 6.4 | 15.5 | 72.3 | 2140 |
| Time (Months) | Series | Chloride Content Measured (% of Sample Mass) at Depths of: | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 mm | 6 mm | 12 mm | 18 mm | 24 mm | 30 mm | 36 mm | ||
| 10 | A series | 0.69 | 0.59 | 0.29 | 0.21 | 0.06 | 0.05 | 0.05 |
| B series | 0.67 | 0.57 | 0.35 | 0.24 | 0.10 | 0.08 | 0.04 | |
| Average | 0.68 | 0.58 | 0.32 | 0.23 | 0.08 | 0.07 | 0.05 | |
| 14 | A series | 0.67 | 0.62 | 0.46 | 0.35 | 0.20 | 0.13 | 0.10 |
| B series | 0.68 | 0.64 | 0.46 | 0.34 | 0.20 | 0.14 | 0.10 | |
| Average | 0.68 | 0.63 | 0.46 | 0.35 | 0.20 | 0.14 | 0.10 | |
| Time (Months) | Series | Chloride Content Measured (% of Sample Mass) at Depths of: | |||||
|---|---|---|---|---|---|---|---|
| 3 mm | 6 mm | 12 mm | 18 mm | 24 mm | 30 mm | ||
| 8 | A series | 0.56 | 0.44 | 0.07 | 0.01 | 0.01 | 0.00 |
| B series | 0.55 | 0.45 | 0.11 | 0.02 | 0.01 | 0.01 | |
| Average | 0.56 | 0.45 | 0.09 | 0.02 | 0.01 | 0.01 | |
| 11 | A series | 0.54 | 0.42 | 0.16 | 0.03 | 0.01 | 0.01 |
| B series | 0.57 | 0.45 | 0.15 | 0.05 | 0.02 | 0.00 | |
| Average | 0.56 | 0.44 | 0.16 | 0.04 | 0.02 | 0.01 | |
| Type of Cement | Time of Measurement (Months) | Deff (m2/s) | k (s−1) | Kb (m3/kg) | Β (m3/kg) | Goal Function |
|---|---|---|---|---|---|---|
| CEM I 42.5 R | t1 = 10 | 4.99 × 10−12 | 9.09 × 10−8 | 5.69 × 10−4 | 0.02 | 3.44 × 10−7 |
| t2 = 14 | 7.20 × 10−12 | 3.38 × 10−8 | 3.16 × 10−3 | 0.46 | 1.14 × 10−7 | |
| t1 and t2 | 6.08 × 10−12 | 4.10 × 10−8 | 3.30 × 10−3 | 0.48 | 4.48 × 10−7 | |
| CEM III/A 42.5 N | t1 = 8 | 1.59 × 10−12 | 9.98 × 10−7 | 5.69 × 10−4 | 0.03 | 3.70 × 10−7 |
| t2 = 11 | 1.48 × 10−12 | 7.75 × 10−8 | 1.67 × 10−3 | 0.26 | 1.47 × 10−8 | |
| t1 and t2 | 1.36 × 10−12 | 4.14 × 10−7 | 1.66 × 10−3 | 0.26 | 1.62 × 10−7 |
| Type of Cement | Time of Measurement (Months) | Deff (m2/s) | k (s−1) | Kb (m3η/kgη) | (–) | Goal Function |
|---|---|---|---|---|---|---|
| CEM I 42.5 R | t1 = 10 | 4.98 × 10−12 | 5.16 × 10−8 | 1.83 × 10−3 | 0.51 | 3.48 × 10−7 |
| t2 = 14 | 6.50 × 10−12 | 5.07 × 10−8 | 1.58 × 10−3 | 0.50 | 1.34 × 10−7 | |
| t1 and t2 | 5.66 × 10−12 | 5.70 × 10−8 | 1.61 × 10−3 | 0.50 | 5.00 × 10−7 | |
| CEM III/A 42.5 N | t1 = 8 | 1.38 × 10−12 | 8.41 × 10−7 | 1.55 × 10−3 | 0.48 | 1.47 × 10−7 |
| t2 = 11 | 1.42 × 10−12 | 1.11 × 10−7 | 1.43 × 10−3 | 0.50 | 4.40 × 10−8 | |
| t1 and t2 | 1.35 × 10−12 | 3.34 × 10−7 | 1.52 × 10−3 | 0.48 | 2.36 × 10−7 |
| Type of Cement | Time of Measurement (Months) | Deff (m2/s) | k (s−1) | Kb (m3/kg) | Goal Function |
|---|---|---|---|---|---|
| CEM I 42.5 R | t1 = 10 | 5.02 × 10−12 | 1.26 × 10−7 | 4.26 × 10−4 | 3.56 × 10−7 |
| t2 = 14 | 6.43 × 10−12 | 9.38 × 10−7 | 3.77 × 10−4 | 1.60 × 10−7 | |
| t1 and t2 | 5.92 × 10−12 | 1.63 × 10−7 | 3.93 × 10−4 | 5.76 × 10−7 | |
| CEM III/A 42.5 N | t1 = 8 | 1.67 × 10−12 | 9.88 × 10−7 | 4.06 × 10−4 | 6.39 × 10−7 |
| t2 = 11 | 1.53 × 10−12 | 9.63 × 10−7 | 3.70 × 10−4 | 1.50 × 10−7 | |
| t1 and t2 | 1.62 × 10−12 | 7.30 × 10−7 | 3.85 × 10−4 | 4.96 × 10−7 |
| Type of Cement | Porosity (%) | Deff (m2/s) | k (s-1) | Kb (m3/kg) | β (m3/kg) | Goal Function |
|---|---|---|---|---|---|---|
| CEM I 42.5 R | 16.8 | 6.08 × 10−12 | 4.10 × 10−8 | 3.30 × 10−3 | 0.48 | 4.48 × 10−7 |
| 33.6 | 6.01 × 10−12 | 3.28 × 10−8 | 2.76 × 10−3 | 0.47 | 4.42 × 10−7 | |
| 50.4 | 5.89 × 10−12 | 2.41 × 10−8 | 2.03 × 10−3 | 0.43 | 4.69 × 10−7 | |
| 67.2 | 5.68 × 10−12 | 1.51 × 10−8 | 1.30 × 10−3 | 0.42 | 5.24 × 10−7 | |
| CEM III/A 42.5 N | 15.5 | 1.36 × 10−12 | 4.14 × 10−7 | 1.66 × 10−3 | 0.26 | 1.62 × 10−7 |
| 31.0 | 1.40 × 10−12 | 2.43 × 10−7 | 1.46 × 10−3 | 0.26 | 1.40 × 10−7 | |
| 46.5 | 1.46 × 10−12 | 1.54 × 10−7 | 1.21 × 10−3 | 0.26 | 1.81 × 10−7 | |
| 62 | 1.47 × 10−12 | 9.68 × 10−8 | 1.19 × 10−3 | 0.36 | 2.23 × 10−7 |
| Type of Cement | Porosity (%) | Deff (m2/s) | k (s−1) | Kb (m3η/kgη) | (–) | Goal Function |
|---|---|---|---|---|---|---|
| CEM I 42.5 R | 16.8 | 5.66 × 10−12 | 5.70 × 10−8 | 1.61 × 10−3 | 0.50 | 5.00 × 10−7 |
| 33.6 | 5.70 × 10−12 | 4.25 × 10−8 | 1.48 × 10−3 | 0.48 | 5.01 × 10−7 | |
| 50.4 | 5.69 × 10−12 | 3.03 × 10−8 | 1.17 × 10−3 | 0.48 | 5.21 × 10−7 | |
| 67.2 | 5.60 × 10−12 | 1.80 × 10−8 | 8.39 × 10−3 | 0.45 | 5.58 × 10−7 | |
| CEM III/A 42.5 N | 15.5 | 1.35 × 10−12 | 3.34 × 10−7 | 1.52 × 10−3 | 0.48 | 2.36 × 10−7 |
| 31.0 | 1.42 × 10−12 | 1.76 × 10−7 | 1.47 × 10−3 | 0.44 | 2.49 × 10−7 | |
| 46.5 | 1.38 × 10−12 | 9.54 × 10−7 | 9.80 × 10−4 | 0.52 | 3.53 × 10−7 | |
| 62 | 1.46 × 10−12 | 5.85 × 10−8 | 1.92 × 10−3 | 0.14 | 1.92 × 10−7 |
| Type of Cement | Porosity (%) | Deff (m2/s) | k (s−1) | Kb (m3/kg) | Goal Function |
|---|---|---|---|---|---|
| CEM I 42.5 R | 16.8 | 5.92 × 10−12 | 1.63 × 10−7 | 3.93 × 10−4 | 5.76 × 10−7 |
| 33.6 | 5.76 × 10−12 | 1.37 × 10−7 | 3.34 × 10−4 | 5.86 × 10−7 | |
| 50.4 | 5.46 × 10−12 | 7.12 × 10−7 | 2.52 × 10−4 | 6.47 × 10−7 | |
| 67.2 | 5.65 × 10−12 | 3.51 × 10−8 | 1.82 × 10−4 | 6.09 × 10−7 | |
| CEM III/A 42.5 N | 15.5 | 1.62 × 10−12 | 7.30 × 10−7 | 3.85 × 10−4 | 4.96 × 10−7 |
| 31.0 | 1.60 × 10−12 | 9.99 × 10−7 | 3.32 × 10−4 | 4.74 × 10−7 | |
| 46.5 | 1.56 × 10−12 | 9.99 × 10−7 | 2.72 × 10−4 | 4.69 × 10−7 | |
| 62 | 1.58 × 10−12 | 9.98 × 10−7 | 1.95 × 10−4 | 4.72 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasielec, J.J.; Stec, J.; Szyszkiewicz-Warzecha, K.; Łagosz, A.; Deja, J.; Lewenstam, A.; Filipek, R. Effective and Apparent Diffusion Coefficients of Chloride Ions and Chloride Binding Kinetics Parameters in Mortars: Non-Stationary Diffusion–Reaction Model and the Inverse Problem. Materials 2020, 13, 5522. https://doi.org/10.3390/ma13235522
Jasielec JJ, Stec J, Szyszkiewicz-Warzecha K, Łagosz A, Deja J, Lewenstam A, Filipek R. Effective and Apparent Diffusion Coefficients of Chloride Ions and Chloride Binding Kinetics Parameters in Mortars: Non-Stationary Diffusion–Reaction Model and the Inverse Problem. Materials. 2020; 13(23):5522. https://doi.org/10.3390/ma13235522
Chicago/Turabian StyleJasielec, Jerzy J., Jakub Stec, Krzysztof Szyszkiewicz-Warzecha, Artur Łagosz, Jan Deja, Andrzej Lewenstam, and Robert Filipek. 2020. "Effective and Apparent Diffusion Coefficients of Chloride Ions and Chloride Binding Kinetics Parameters in Mortars: Non-Stationary Diffusion–Reaction Model and the Inverse Problem" Materials 13, no. 23: 5522. https://doi.org/10.3390/ma13235522
APA StyleJasielec, J. J., Stec, J., Szyszkiewicz-Warzecha, K., Łagosz, A., Deja, J., Lewenstam, A., & Filipek, R. (2020). Effective and Apparent Diffusion Coefficients of Chloride Ions and Chloride Binding Kinetics Parameters in Mortars: Non-Stationary Diffusion–Reaction Model and the Inverse Problem. Materials, 13(23), 5522. https://doi.org/10.3390/ma13235522









