Bending Performance of Steel Fiber Reinforced Concrete Beams Based on Composite-Recycled Aggregate and Matched with 500 MPa Rebars
Abstract
:1. Introduction
2. Research Significance
3. Experimental Work
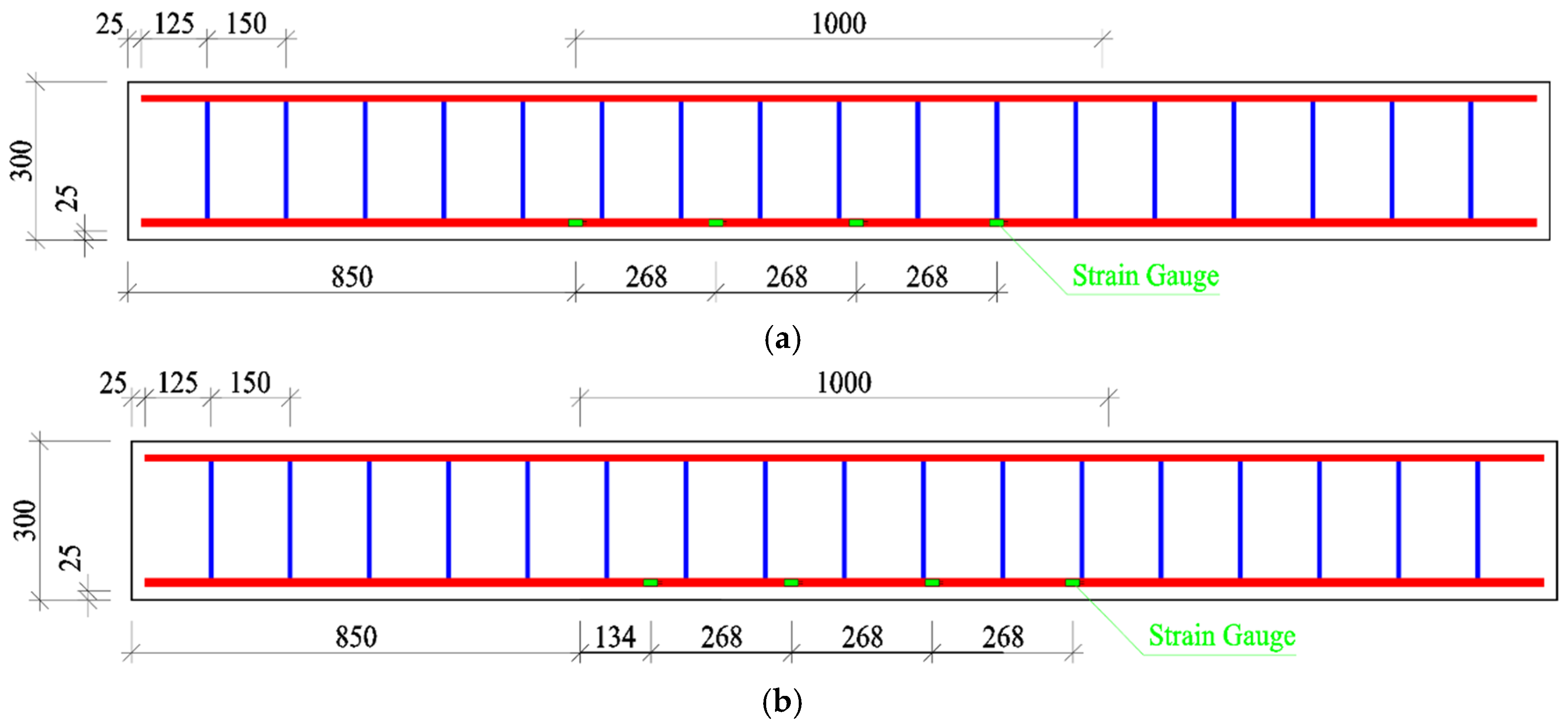
3.1. Design of the Test Beams
3.2. Preparation of SFR-CRAC
3.3. Fabrication of the Test Beams
3.4. Test Methods
4. Test Results
4.1. Strain at Mid-Span Cross-Section
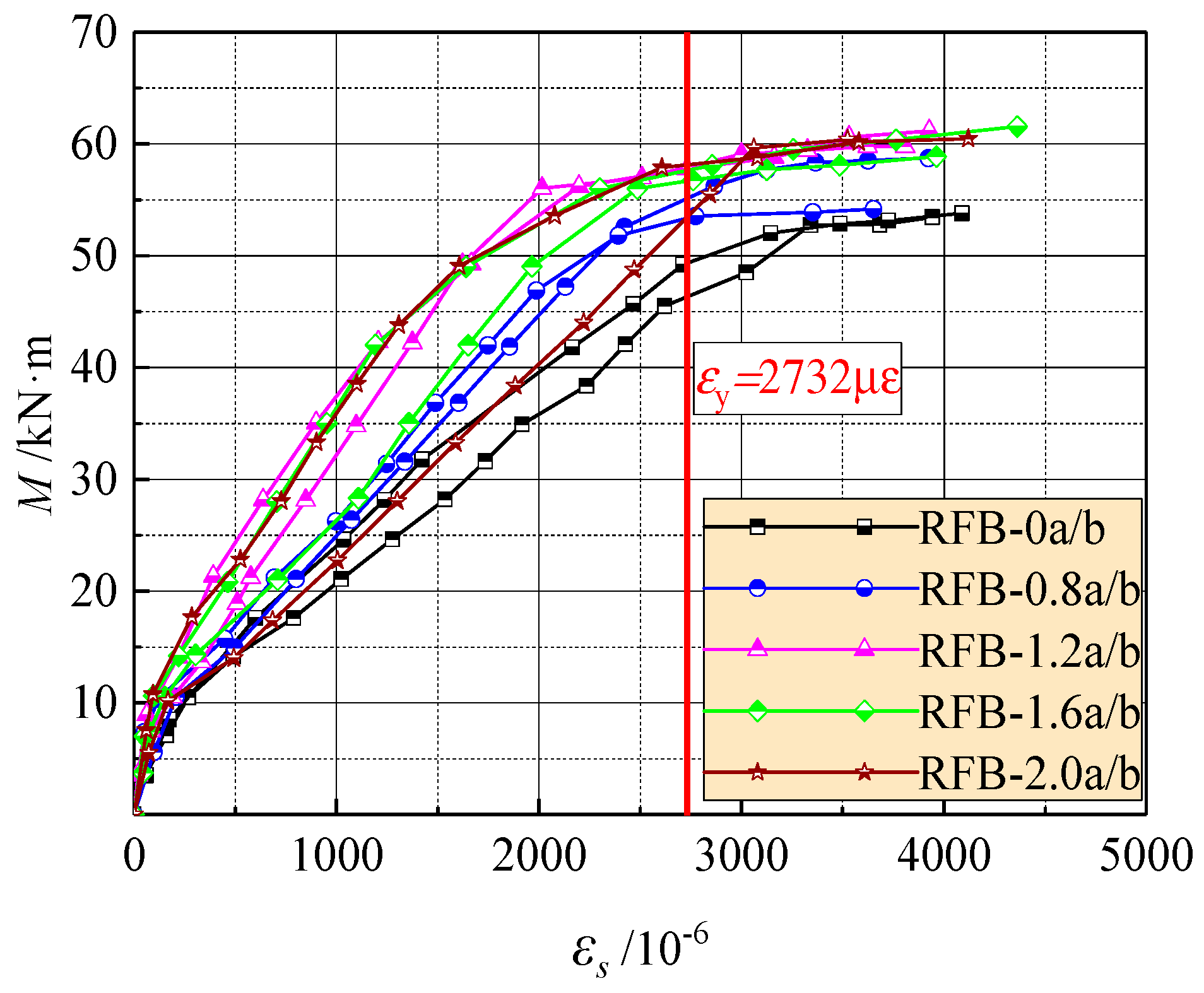
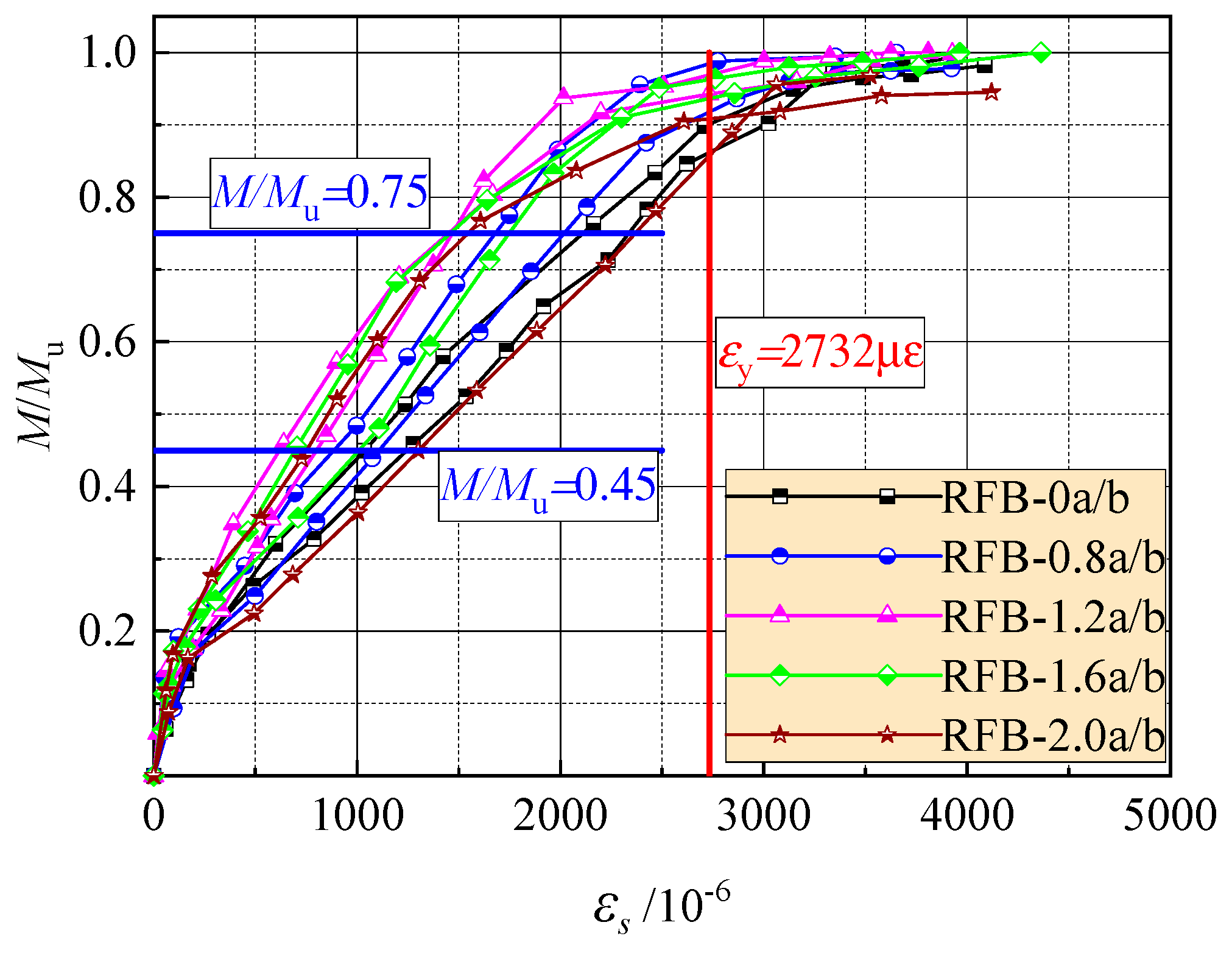
4.2. Tensile Strain of Longitudinal Rebars
4.3. Crack Distribution and Failure Pattern
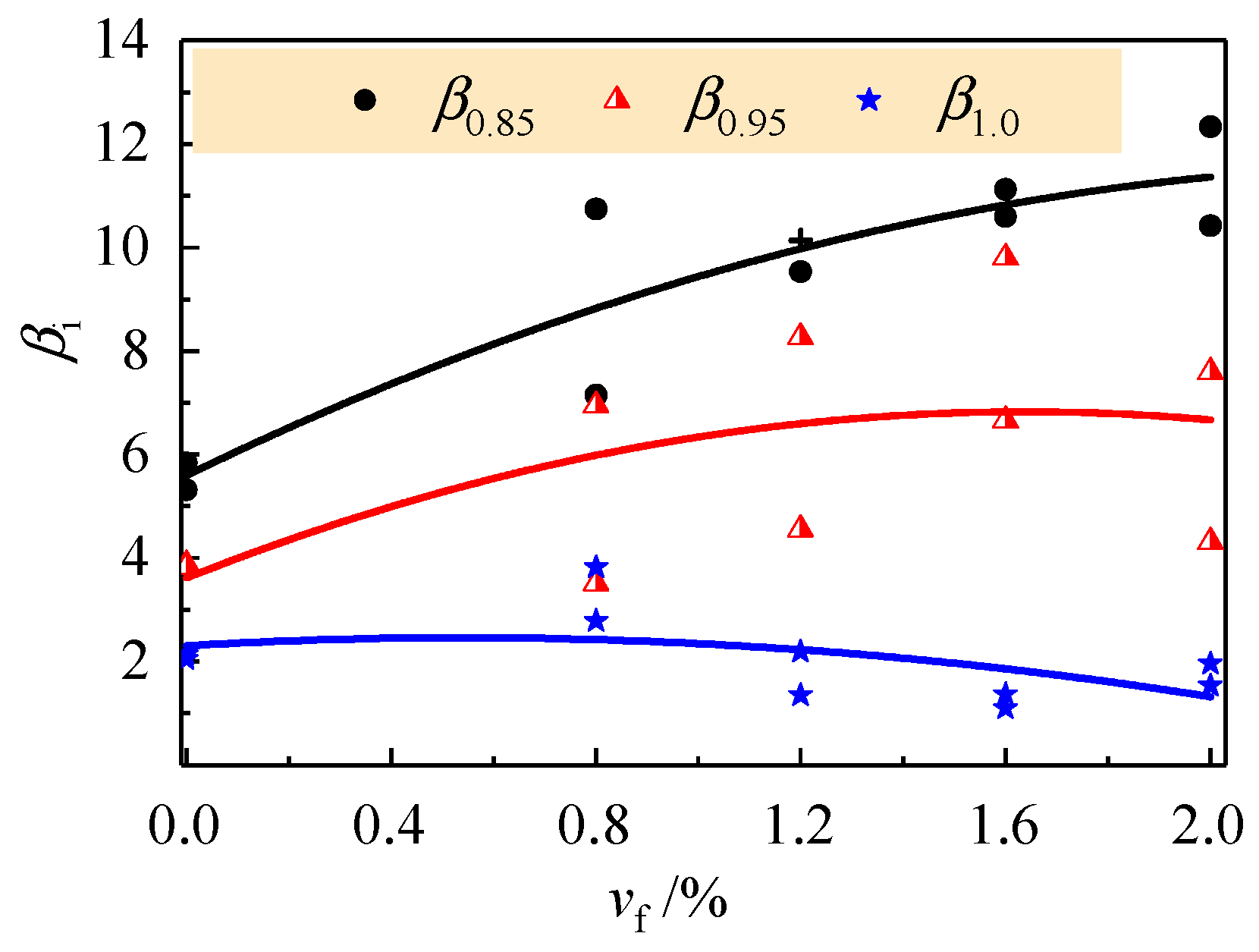
4.4. Mid-span Deflection and Flexural Ductility
5. Discussion
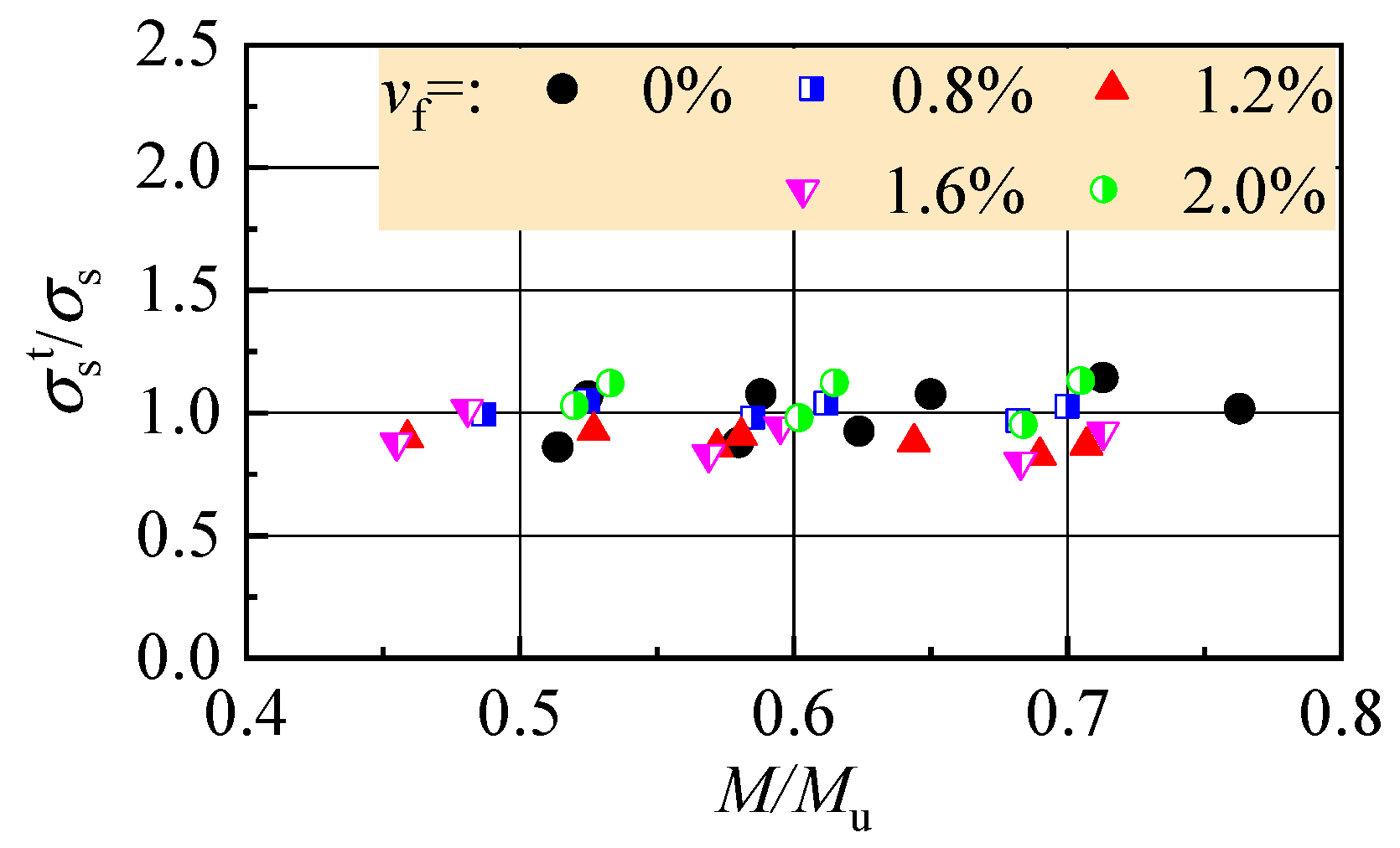
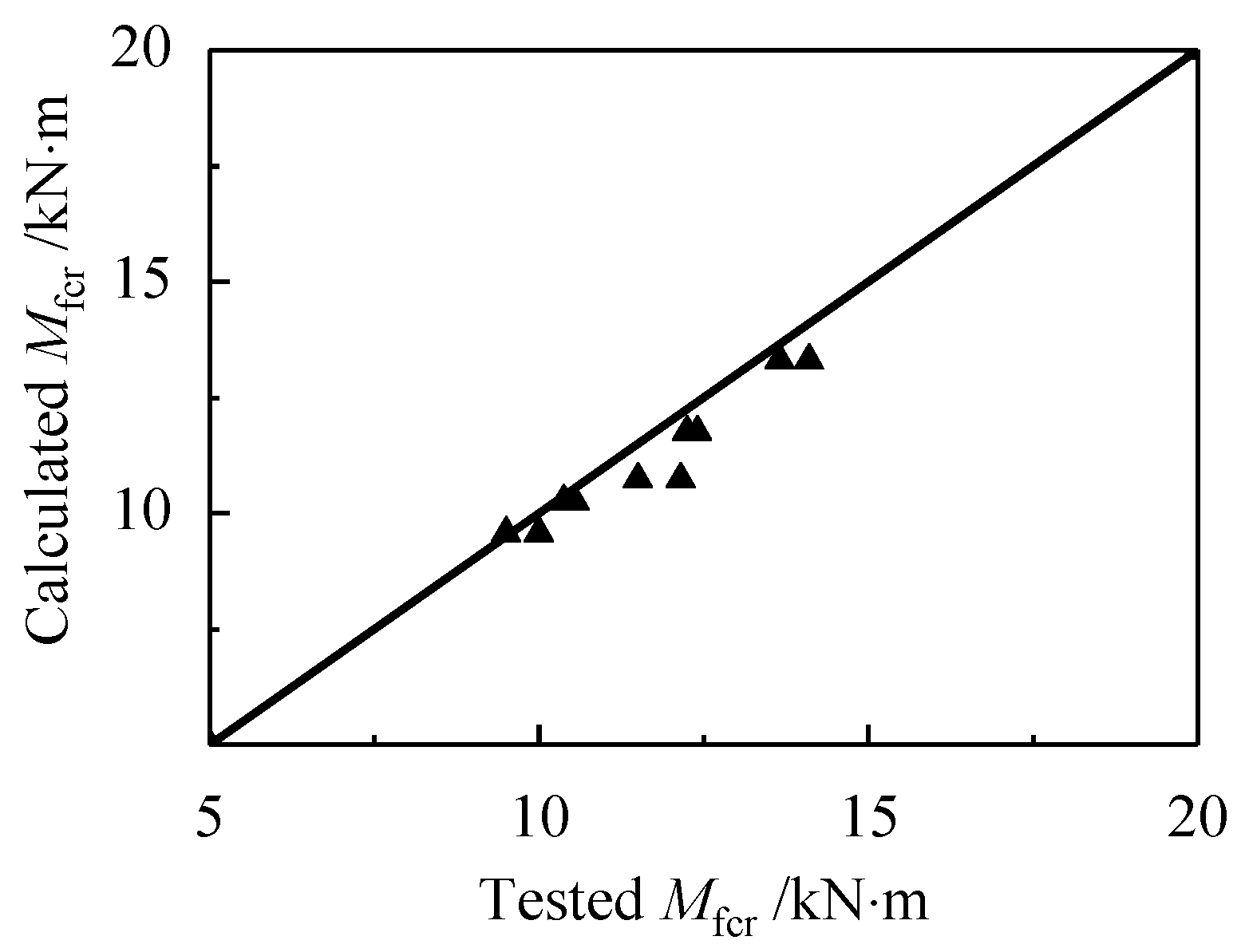
5.1. Cracking Resistance
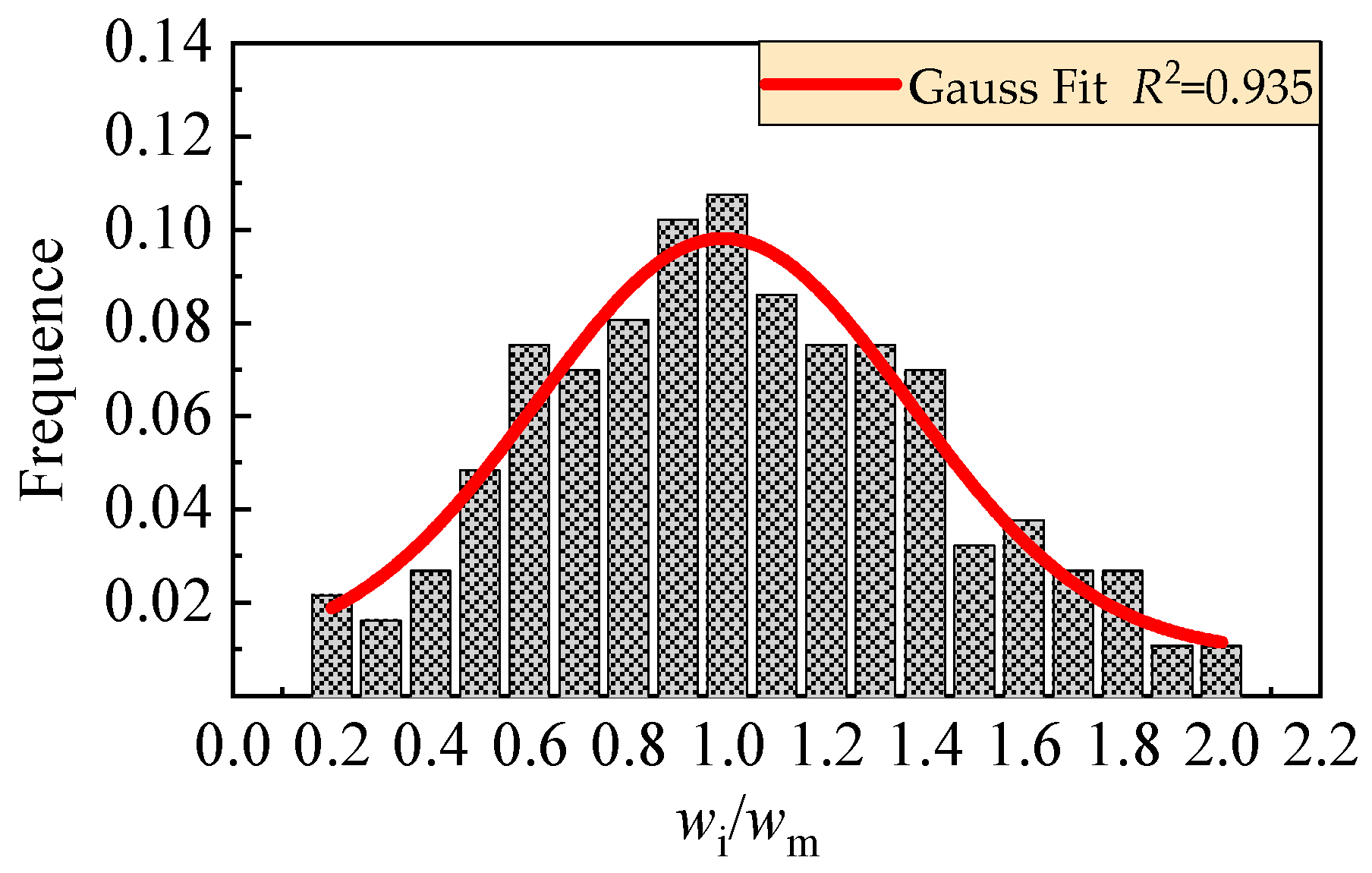
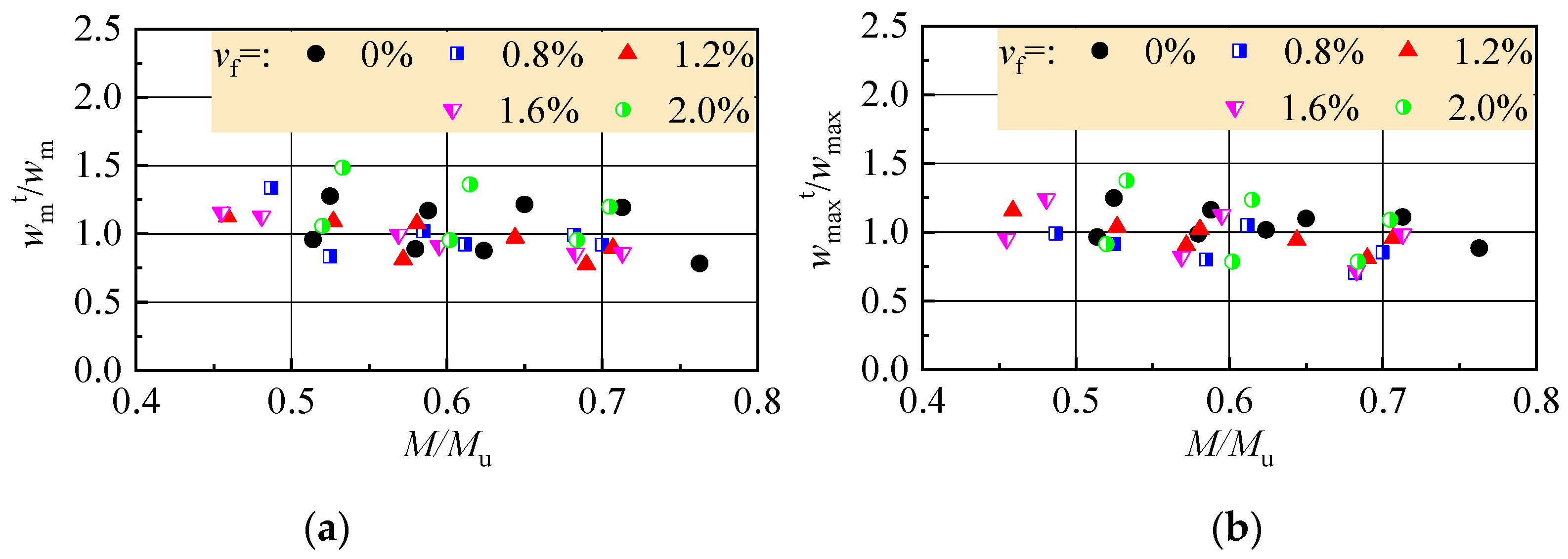
5.2. Crack Width
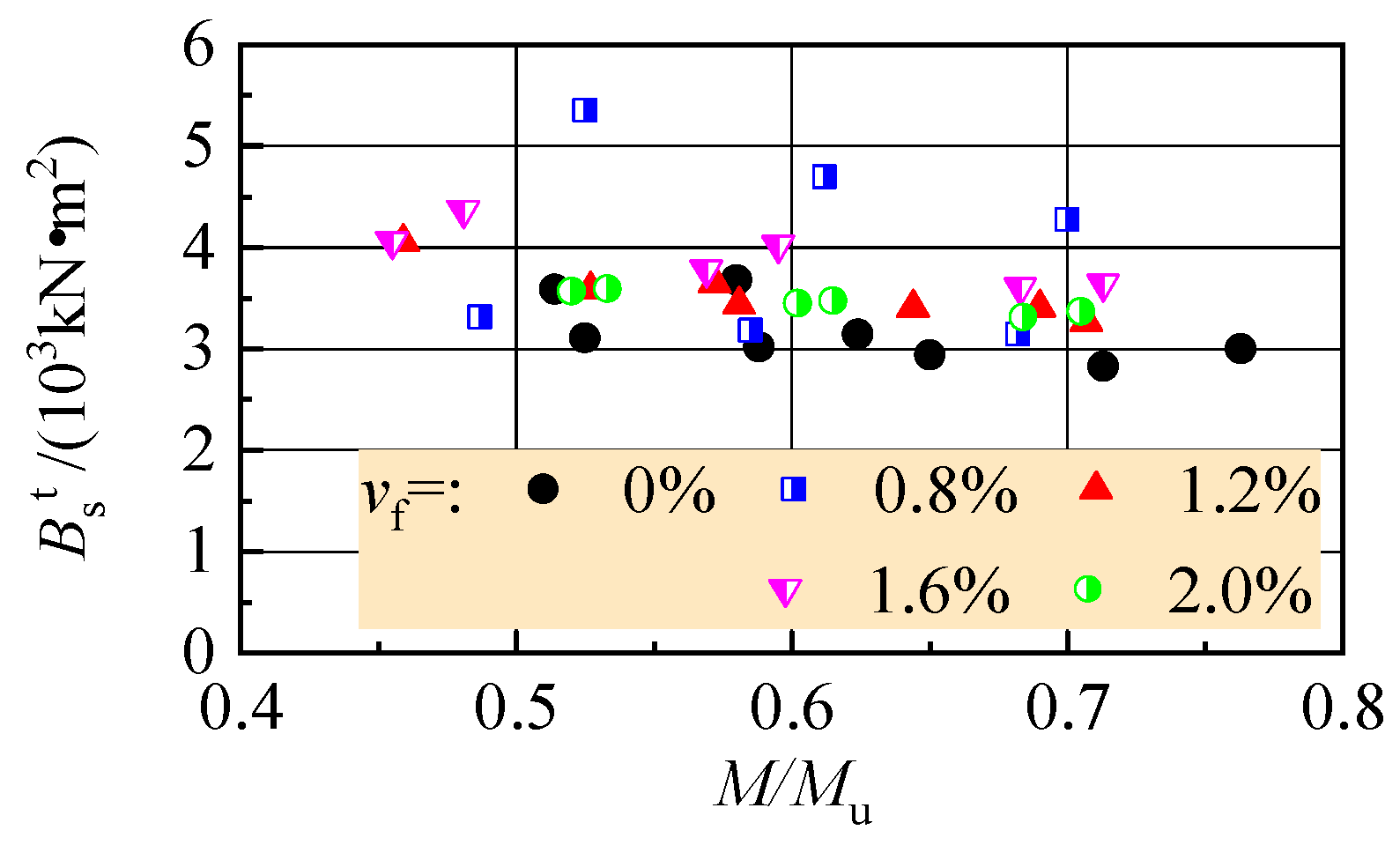
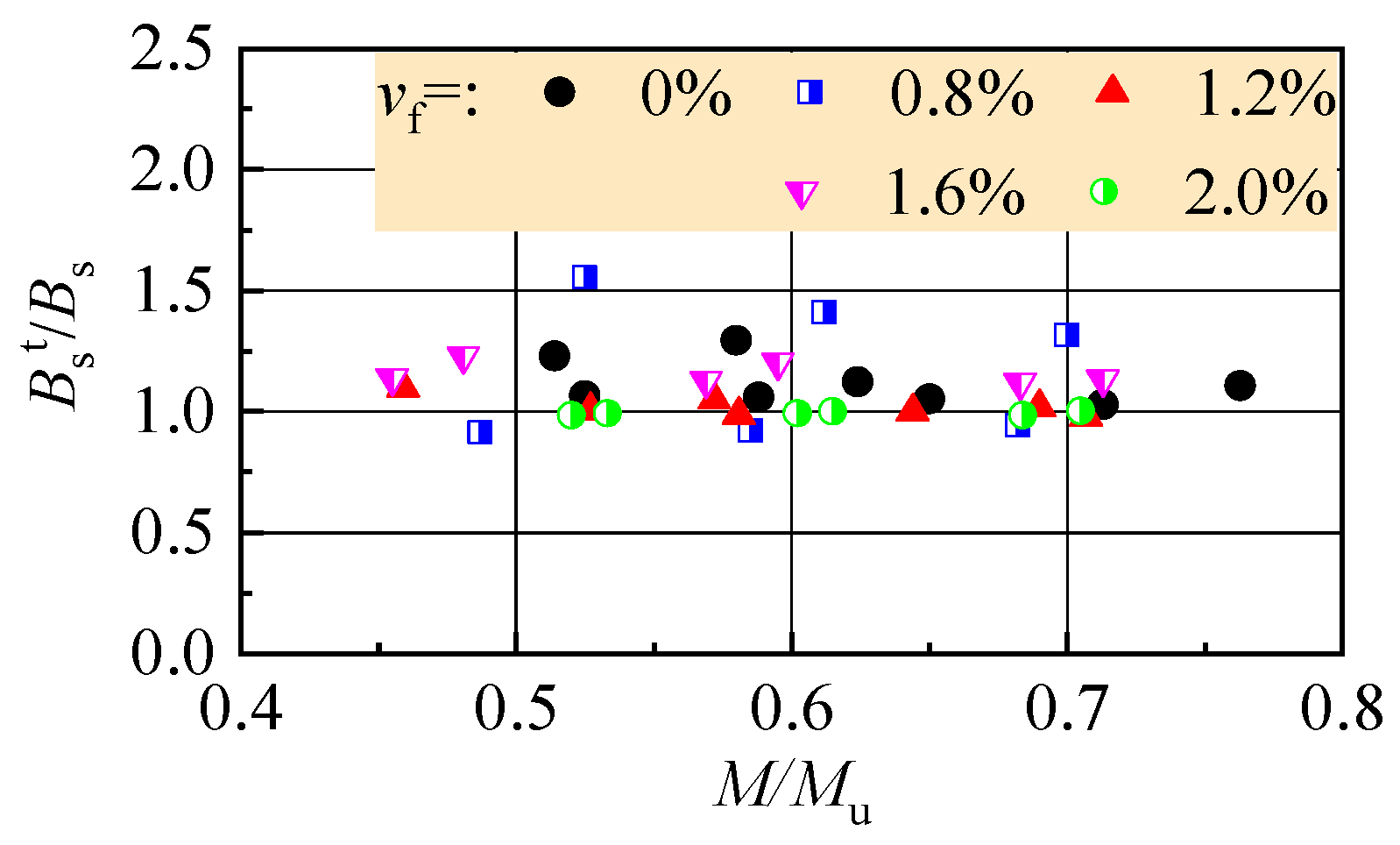
5.3. Flexural Stiffness
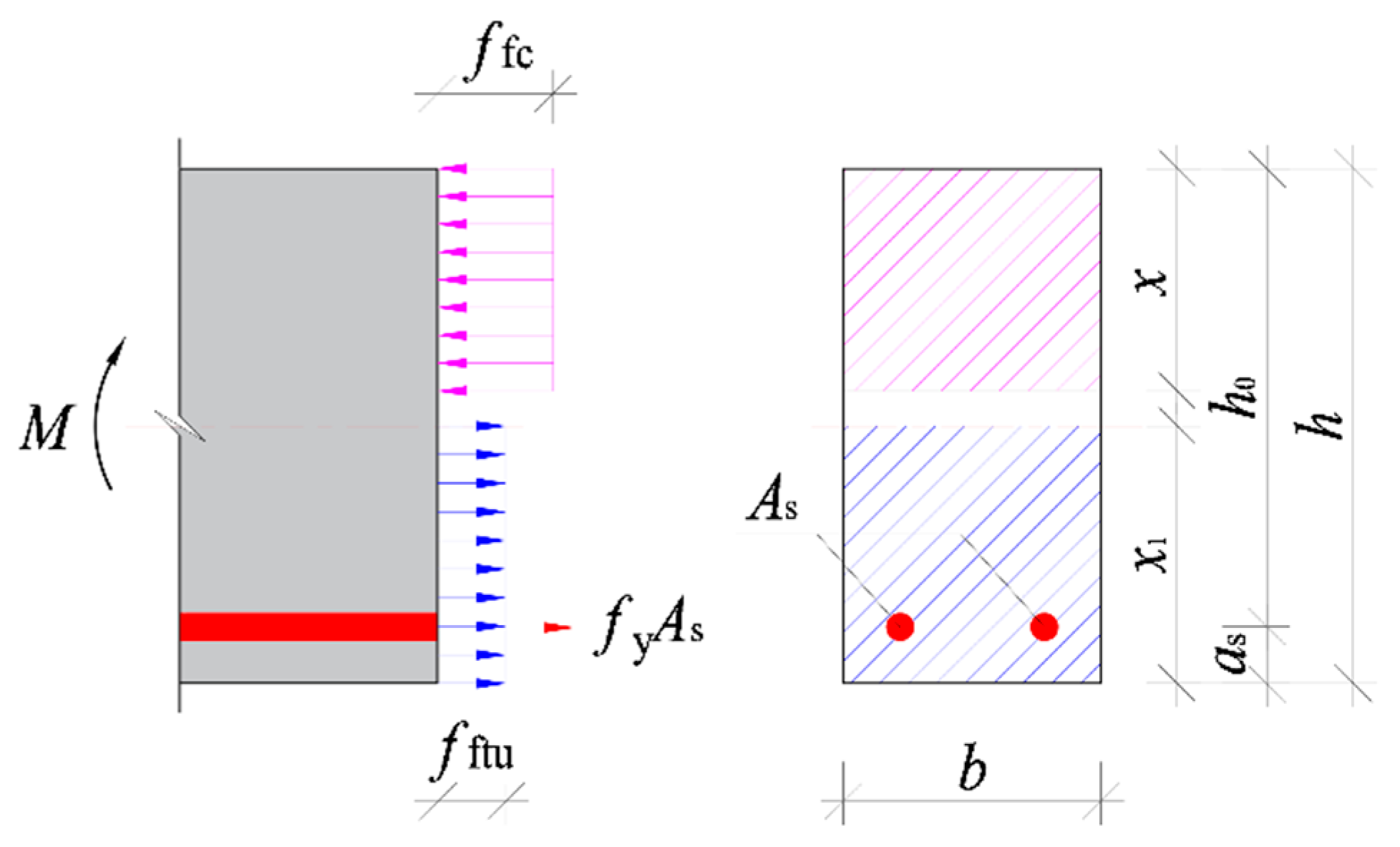
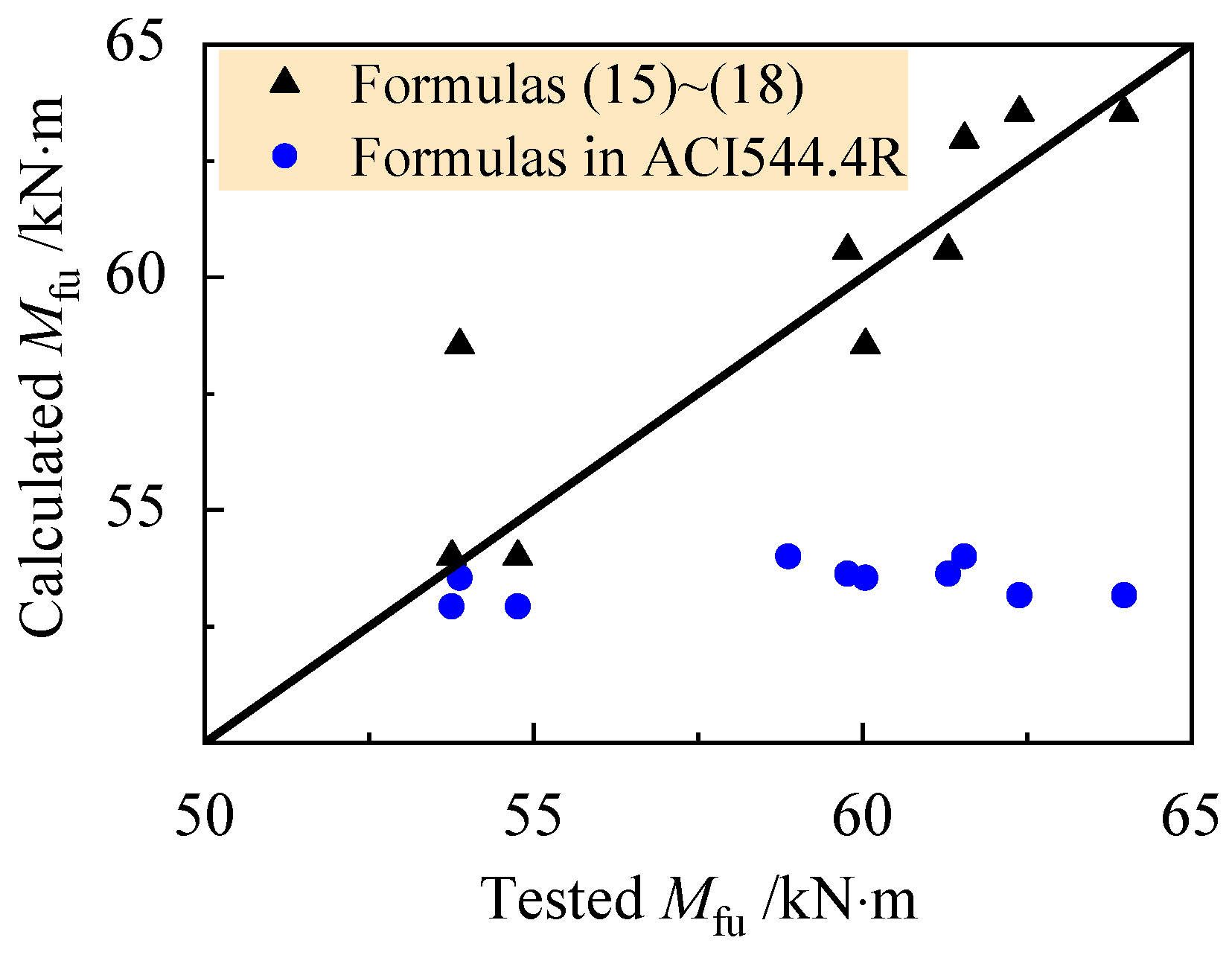
5.4. Flexural Capacity
6. Conclusions
- (1)
- Steel fiber reinforced composite-recycled aggregate concrete (SFR-CRAC) prepared in this study has good workability to produce the reinforced SFR-CRAC beams.
- (2)
- Similar to conventional reinforced concrete beams, the assumption of plane cross-section is valid to build the calculation models of cracking resistance, crack width, flexural stiffness, and flexural capacity of the reinforced SFR-CRAC beams.
- (3)
- The same enhancement of steel fibers on the cracking resistance of reinforced SFR-CRAC beams and the tensile strength of SFR-CRAC. The cracking moment of reinforced SFR-CRAC beams can be predicted by using the tensile strength of SFR-CRAC. The reduced crack spacing and good crack distribution pattern of reinforced SFR-CRAC benefit to minimize the crack width. This also improves the strain distribution pattern and reduces the tensile stress of longitudinal tensile rebars at cracked sections. Therefore, the 500 MPa longitudinal tensile rebars work at a high stress level with the premise of matching the limit crack width specified in the standard for reinforced SFR-CRAC beams at normal serviceability state. The flexural stiffness of reinforced SFR-CRAC beams at normal serviceability also increased with the improvement of crack distribution.
- (4)
- Designed with the rational longitudinal reinforcement ratio, the reinforced SFR-CRAC beams fail in the typical mode of the yield of 500 MPa longitudinal rebars followed by the fast widening of main cracks and the crushed SFR-CRAC in the compression zone. Good flexural ductility presents on the reinforced SFR-CRAC beams matched with 500 MPa longitudinal rebars, especially at the post-peak loading levels.
- (5)
- Considering the improvements by steel fibers and linked with those of conventional reinforced concrete beams, formulas for predicting the cracking moment, crack width, flexural stiffness, and ultimate moment of SFR-CRAC beams are proposed for the reference of design.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lotfi, S.; Eggimann, M.; Wagner, E.; Mróz, R.; Deja, J. Performance of recycled aggregate concrete based on a new concrete recycling technology. Constr. Build. Mater. 2015, 95, 243–256. [Google Scholar] [CrossRef]
- Liang, Y.-C.; Ye, Z.-M.; Vernerey, F.; Xi, Y. Development of Processing Methods to Improve Strength of Concrete with 100% Recycled Coarse Aggregate. J. Mater. Civ. Eng. 2015, 27, 04014163. [Google Scholar] [CrossRef] [Green Version]
- Katz, A. Treatments for the Improvement of Recycled Aggregate. J. Mater. Civ. Eng. 2004, 16, 597–603. [Google Scholar] [CrossRef]
- Qiu, J.; Tng, D.Q.S.; Yang, E. Surface treatment of recycled concrete aggregates through microbial carbonate precipitation. Constr. Build. Mater. 2014, 57, 144–150. [Google Scholar] [CrossRef]
- Elhakam, A.A.; Mohamed, A.E.; Awad, E. Influence of self-healing, mixing method and adding silica fume on mechanical properties of recycled aggregates concrete. Constr. Build. Mater. 2012, 35, 421–427. [Google Scholar] [CrossRef]
- Butler, L.; West, J.S.; Tighe, S.L. Effect of recycled concrete coarse aggregate from multiple sources on the hardened properties of concrete with equivalent compressive strength. Constr. Build. Mater. 2013, 47, 1292–1301. [Google Scholar] [CrossRef]
- Zhao, S.; Guo, Q.; Li, G.X.; Su, Y.F. Basic Mechanical Properties of Concrete with Machine-Made Sand and Recycled Coarse Aggregate. Appl. Mech. Mater. 2013, 357, 1102–1105. [Google Scholar] [CrossRef]
- Corinaldesi, V.; Moriconi, G. Influence of mineral additions on the performance of 100% recycled aggregate concrete. Constr. Build. Mater. 2009, 23, 2869–2876. [Google Scholar] [CrossRef]
- Ostrowski, K.; Stefaniuk, D.; Sadowski, Ł.; Krzywiński, K.; Gicala, M.; Różańska, M. Potential use of granite waste sourced from rock processing for the application as coarse aggregate in high-performance self-compacting concrete. Constr. Build. Mater. 2020, 238, 117794. [Google Scholar] [CrossRef]
- Brand, A.S.; Roesler, J.R.; Salas, A. Initial moisture and mixing effects on higher quality recycled coarse aggregate concrete. Constr. Build. Mater. 2012, 79, 565–573. [Google Scholar] [CrossRef]
- Wijayasundara, M.; Mendis, P.; Crawford, R.H. Integrated assessment of the use of recycled concrete aggregate replacing natural aggregate in structural concrete. J. Clean. Prod. 2017, 174, 591–604. [Google Scholar] [CrossRef]
- Li, C.Y.; Nie, P.; Li, F.L. Study on mechanical properties and water permeability of recycled aggregate porous concrete. Adv. Mater. Res. 2012, 366, 36–39. [Google Scholar] [CrossRef]
- Li, F.L.; Li, J.; Chen, S.; Zhao, W.J. Experiment of basic mechanical properties of concrete mixed with composite aggregate. Adv. Mater. Res. 2011, 168–170, 2178–2181. [Google Scholar] [CrossRef]
- Ding, X.X.; Li, C.Y.; Xu, Y.Y.; Li, F.L.; Zhao, S.B. Experimental study on long-term compressive strength development of concrete with manufactured sand. Constr. Build. Mater. 2016, 108, 67–73. [Google Scholar] [CrossRef]
- Zhao, S.; Ding, X.; Zhao, M.; Li, C.; Pei, S. Experimental study on tensile strength development of concrete with manufactured sand. Constr. Build. Mater. 2017, 138, 247–253. [Google Scholar] [CrossRef]
- Li, C.Y.; Wang, F.; Deng, X.S.; Li, Y.Z.; Zhao, S.B. Experimental study on strength development of recycled-aggregate concrete with large particle natural aggregate. Materials 2019, 12, 1891. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.L.; Ding, X.X.; Li, J.; Law, D. Numerical Analysis of Mix Proportion of Self-Compacting Concrete Compared to Ordinary Concrete. Key Eng. Mater. 2018, 789, 69–75. [Google Scholar] [CrossRef]
- Ding, X.X.; Zhao, M.L.; Zhou, S.Y.; Fu, Y.; Li, C.Y. Statistical analysis and preliminary study on the mix proportion design of self-compacting steel fiber reinforced concrete. Materials 2019, 12, 637. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.X.; Li, C.Y.; Han, B.; Lu, Y.Z.; Zhao, S.B. Effects of different deformed steel-fibers on preparation and fundamental properties of self-compacting SFRC. Constr. Build. Mater. 2018, 168, 471–481. [Google Scholar] [CrossRef]
- Li, C.Y.; Shang, P.R.; Li, F.L.; Feng, M.; Zhao, S.B. Shrinkage and mechanical properties of self-compacting SFRC with calcium sulfoaluminate expansive agent. Materials 2020, 13, 588. [Google Scholar] [CrossRef] [Green Version]
- Li, C.Y.; Geng, H.B.; Deng, C.H.; Li, B.C.; Zhao, S.B. Experimental investigation on columns of steel fiber reinforced concrete with recycled aggregates under large eccentric compression load. Materials 2019, 3, 445. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, D.D.; Geng, H.B.; Li, Q.; Li, B.C.; Ma, K. Study on large eccentric compression resistance of steel fiber recycled concrete columns. Hans J. Civ. Eng. 2018, 3, 313–320. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Code for Design of Concrete Structures; China Building Industry Press: Beijing, China, 2010; GB50010-2010. (In Chinese) [Google Scholar]
- Xu, J.J.; Chen, Z.P.; Xue, J.Y.; Chen, Y.L.; Liu, Z.Q. A review of experimental results of steel reinforced recycled aggregate concrete members and structures in China (2010–2016). Procedia Eng. 2017, 210, 109–119. [Google Scholar] [CrossRef]
- Li, C.Y.; Zhao, S.B.; Chen, H.; Gao, D.Y. Experimental study on flexural capacity of reinforced SFRFLC superposed beams. J. Build. Struct. 2015, 2, 257–264. [Google Scholar]
- Zhao, M.S.; Su, J.Z.; Shang, P.R.; Zhao, S.B. Experimental study and theoretical prediction of flexural behaviors of reinforced SFRELC beams. Constr. Build. Mater. 2019, 208, 454–463. [Google Scholar] [CrossRef]
- China Association for Engineering Construction Standardization. Technical Specification for Steel Fiber Reinforced Concrete Structures; China Plan Press: Beijing, China, 2004; CECS38:2004. (In Chinese) [Google Scholar]
- ACI Committee 544. Design Considerations for Steel Fiber Reinforced Concrete; American Concrete Institute: Farmington Hill, MI, USA, 2009; ACI 544.4R-2009. [Google Scholar]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Design Standard for Steel Fiber Reinforced Concrete Structures; China Standard Press: Beijing, China, 2020; JGJ/T465-2019. [Google Scholar]
- Ostrowski, K.; Sadowski, Ł.; Stefaniuk, D.; Wałach, D.; Gawenda, T.; Oleksik, K.; Usydus, I. The Effect of the Morphology of Coarse Aggregate on the Properties of Self-Compacting High-Performance Fibre-Reinforced Concrete. Materials 2018, 11, 1372. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Standard for Technical Requirements and Test Method of Sand and Crushed Stone (or Gravel) for Ordinary Concrete; China Building Industry Press: Beijing, China, 2006; JGJ 52-2006.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Recycled Coarse Aggregate for Concrete; Standard Press of China: Beijing, China, 2011; GB/T 25177-2010.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Recycled Fine Aggregate for Concrete and Mortar; Standard Press of China: Beijing, China, 2011; GB/T 25176-2010.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Steel Fiber Reinforced Concrete; China Standard Press: Beijing, China, 2015; JG/T472-2015.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Specification for Mix Proportion Design of Ordinary Concrete; China Building Industry Press: Beijing, China, 2011; JGJ 55-2011.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Standard of Test Methods of Concrete Structures; China Building Industry Press: Beijing, China, 2012; GB/T50152-2012.
- Li, X.K.; Li, C.Y.; Zhao, M.L.; Yang, H.; Zhou, S.Y. Testing and prediction of shear performance for steel fiber reinforced expanded-shale lightweight concrete beams without web reinforcements. Materials 2019, 12, 1594. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.B. Design Principle of Concrete Structures, 2nd ed.; Tongji University Press: Shanghai, China, 2013. [Google Scholar]
- Zhao, S.B.; Guan, J.F.; Li, X.K. Simulation Testing and Optimal Design of Reinforced Concrete Structures; China Water Power Press: Beijing, China, 2011. [Google Scholar]
- Zhao, S.B.; Guan, J.F.; Zhang, X.P.; Cheng, X.T. Experimental study and statistical analysis of crack patterns of reinforced concrete beams. Eng. Mech. 2008, 12, 141–146. [Google Scholar]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Code for Durability Design of Concrete Structures; China Building Industry Press: Beijing, China, 2008; GB50476-2008.
- European Committee for Standardization. Design of Structures for Earthquake Resistance; Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004; Eurocode 8. EN 1998-1. [Google Scholar]

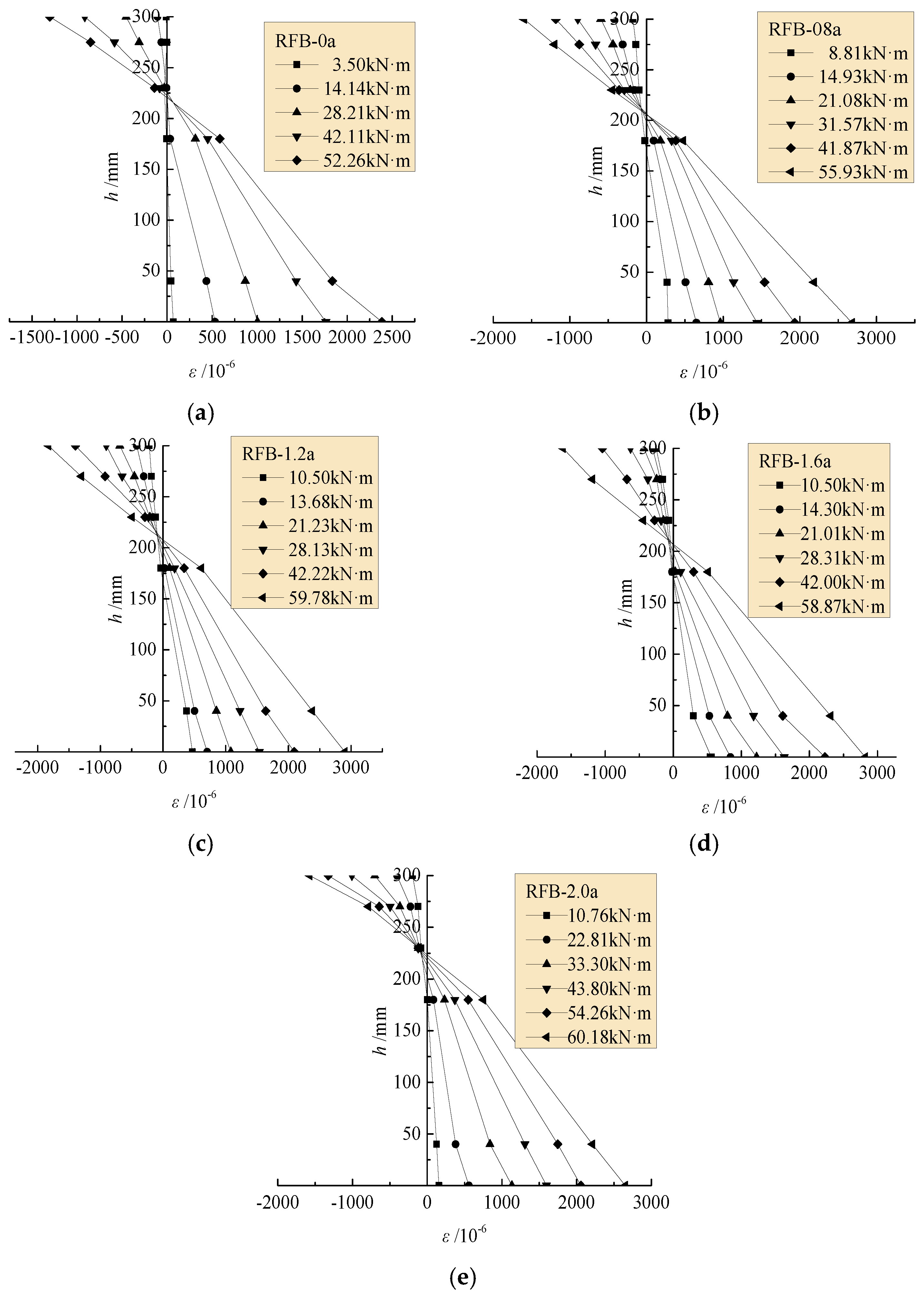



| Identifier | Particle Size (mm) | Bulk Density (kg/m3) | Closed Compact Density (kg/m3) | Particle Density (kg/m3) | Water Absorption of 24 h (%) | Crushed Index (%) |
|---|---|---|---|---|---|---|
| Coarse RA | 5–16 | 1293.3 | 1445.5 | 2673.8 | 5.10 | 14.30 |
| Fine RA | 0–5 | 1330 | 1470 | 2395.73 | 9.45 | — |
| NA | 16–25 | 1417 | 1592 | 2721.9 | 0.47 | 12.80 |
| Identifier | vf (%) | Dosage of Aggregates (kg/m3) | Additive (%) | Additional Water (kg/m3) | Basic Mechanical Properties (MPa) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fine RA | Coarse FA | NA | fcu | ffc | fft | Ec | ||||
| RFB-0a/b | 0 | 709.1 | 587.5 | 391.7 | 0.3 | 41.8 | 36.2 | 27.7 | 2.41 | 2.08 × 104 |
| RFB-0.8a/b | 0.8 | 725.6 | 563.5 | 375.7 | 0.3 | 41.8 | 39.3 | 30.2 | 2.68 | 2.61 × 104 |
| RFB-1.2a/b | 1.2 | 733.8 | 551.5 | 367.7 | 0.4 | 41.8 | 39.9 | 30.6 | 2.84 | 2.85 × 104 |
| RFB-1.6a/b | 1.6 | 742.0 | 539.5 | 359.6 | 0.5 | 41.8 | 36.8 | 32.4 | 3.01 | 2.29 × 104 |
| RFB-2.0a/b | 2.0 | 750.3 | 527.5 | 351.6 | 0.6 | 41.8 | 38.4 | 28.5 | 3.46 | 2.53 × 104 |
| Identifier | vf (%) | Mcr (kN·m) | Mu (kN·m) | M/Mu | M (kN·m) | σs (MPa) | wm (mm) | wmax (mm) | af (mm) |
|---|---|---|---|---|---|---|---|---|---|
| RFB-0a | 0.0 | 10.00 | 53.76 | 0.525 | 28.21 | 322.56 | 0.16 | 0.26 | 5.57 |
| 0.588 | 31.61 | 364.35 | 0.17 | 0.28 | 6.43 | ||||
| 0.650 | 34.93 | 402.57 | 0.20 | 0.30 | 7.29 | ||||
| 0.713 | 38.36 | 469.35 | 0.22 | 0.34 | 8.32 | ||||
| RFB-0b | 0.0 | 9.50 | 54.76 | 0.514 | 28.14 | 259.56 | 0.12 | 0.20 | 4.81 |
| 0.580 | 31.78 | 298.83 | 0.13 | 0.24 | 5.30 | ||||
| 0.624 | 34.16 | 338.76 | 0.14 | 0.27 | 6.66 | ||||
| 0.763 | 41.79 | 454.44 | 0.16 | 0.30 | 8.55 | ||||
| RFB-0.8a | 0.8 | 10.54 | 60.04 | 0.525 | 31.50 | 280.83 | 0.09 | 0.16 | 3.61 |
| 0.612 | 36.75 | 336.76 | 0.13 | 0.24 | 4.80 | ||||
| 0.700 | 42.00 | 389.53 | 0.16 | 0.24 | 6.03 | ||||
| RFB-0.8b | 0.8 | 10.38 | 53.88 | 0.487 | 26.25 | 209.37 | 0.10 | 0.12 | 4.86 |
| 0.585 | 31.50 | 261.87 | 0.11 | 0.14 | 6.07 | ||||
| 0.682 | 36.75 | 312.48 | 0.14 | 0.16 | 7.17 | ||||
| RFB-1.2a | 1.2 | 11.50 | 59.77 | 0.527 | 31.50 | 243.96 | 0.11 | 0.17 | 5.39 |
| 0.581 | 34.75 | 270.56 | 0.13 | 0.20 | 6.20 | ||||
| 0.644 | 38.50 | 297.90 | 0.14 | 0.22 | 6.94 | ||||
| 0.707 | 42.25 | 328.71 | 0.15 | 0.26 | 7.93 | ||||
| RFB-1.2b | 1.2 | 12.15 | 61.30 | 0.459 | 28.14 | 203.96 | 0.09 | 0.15 | 4.26 |
| 0.572 | 35.05 | 258.94 | 0.10 | 0.18 | 5.89 | ||||
| 0.690 | 42.29 | 313.29 | 0.13 | 0.22 | 7.62 | ||||
| RFB-1.6a | 1.6 | 12.40 | 58.87 | 0.481 | 28.31 | 232.52 | 0.09 | 0.16 | 3.98 |
| 0.595 | 35.03 | 285.01 | 0.11 | 0.22 | 5.34 | ||||
| 0.713 | 42.00 | 346.67 | 0.14 | 0.26 | 7.07 | ||||
| RFB-1.6b | 1.6 | 12.25 | 61.55 | 0.455 | 28.00 | 198.02 | 0.09 | 0.12 | 4.23 |
| 0.569 | 35.00 | 250.16 | 0.12 | 0.16 | 5.68 | ||||
| 0.683 | 42.01 | 300.30 | 0.14 | 0.19 | 7.15 | ||||
| RFB-2.0a | 2.0 | 13.65 | 63.98 | 0.520 | 33.30 | 279.31 | 0.10 | 0.14 | 5.73 |
| 0.602 | 38.54 | 321.08 | 0.12 | 0.16 | 6.86 | ||||
| 0.684 | 43.80 | 364.71 | 0.15 | 0.20 | 8.11 | ||||
| RFB-2.0b | 2.0 | 14.10 | 62.39 | 0.533 | 33.25 | 303.60 | 0.14 | 0.21 | 5.68 |
| 0.615 | 38.37 | 365.40 | 0.17 | 0.25 | 6.78 | ||||
| 0.705 | 44.01 | 436.39 | 0.19 | 0.28 | 8.02 |
| Identifier | RFB-0a/b | RFB-0.8a/b | RFB-1.2a,b | RFB-1.6a,b | RFB-2.0a,b | |
|---|---|---|---|---|---|---|
| Maximum (mm) | 167, 161 | 161, 173 | 182, 164 | 142, 170 | 155, 160 | |
| Minimum (mm) | 94, 123 | 104, 85 | 93, 71 | 88. 88 | 85, 85 | |
| Average (mm) | tested | 118, 128 | 132, 110 | 111, 112 | 115, 110 | 110, 115 |
| Calculated | 119 | 115 | 113 | 111 | 109 | |
| Tested/Calculated | 0.990, 1.074 | 1.144, 0.954 | 0.978, 0.987 | 1.031, 0.986 | 1.003, 1.049 | |
| Identifier | δy (mm) | δ0.85 (mm) | δ0.95 (mm) | δ1.0 (mm) | β0.85 | β0.95 | β1.0 |
|---|---|---|---|---|---|---|---|
| RFB-0a | 10.46 | 55.50 | 40.56 | 21.40 | 5.31 | 3.88 | 2.05 |
| RFB-0b | 10.77 | 62.90 | 41.40 | 23.00 | 5.84 | 3.84 | 2.13 |
| RFB-0.8a | 9.34 | 100.30 | 64.90 | 35.70 | 10.74 | 6.95 | 3.82 |
| RFB-0.8b | 11.25 | 80.45 | 39.50 | 31.30 | 7.15 | 3.51 | 2.78 |
| RFB-1.2a | 12.50 | 126.80 | 103.35 | 27.35 | 10.14 | 8.27 | 2.19 |
| RFB-1.2b | 13.00 | 123.90 | 59.30 | 17.50 | 9.53 | 4.56 | 1.35 |
| RFB-1.6a | 11.73 | 130.50 | 115.00 | 16.05 | 11.12 | 9.80 | 1.37 |
| RFB-1.6b | 11.00 | 116.60 | 73.30 | 12.08 | 10.60 | 6.66 | 1.10 |
| RFB-2.0a | 11.46 | 119.46 | 49.35 | 17.60 | 10.42 | 4.31 | 1.53 |
| RFB-2.0b | 10.15 | 125.10 | 77.10 | 19.87 | 12.33 | 7.60 | 1.96 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Pei, S.; Fan, K.; Geng, H.; Li, F. Bending Performance of Steel Fiber Reinforced Concrete Beams Based on Composite-Recycled Aggregate and Matched with 500 MPa Rebars. Materials 2020, 13, 930. https://doi.org/10.3390/ma13040930
Li X, Pei S, Fan K, Geng H, Li F. Bending Performance of Steel Fiber Reinforced Concrete Beams Based on Composite-Recycled Aggregate and Matched with 500 MPa Rebars. Materials. 2020; 13(4):930. https://doi.org/10.3390/ma13040930
Chicago/Turabian StyleLi, Xiaoke, Songwei Pei, Kunpeng Fan, Haibin Geng, and Fenglan Li. 2020. "Bending Performance of Steel Fiber Reinforced Concrete Beams Based on Composite-Recycled Aggregate and Matched with 500 MPa Rebars" Materials 13, no. 4: 930. https://doi.org/10.3390/ma13040930
APA StyleLi, X., Pei, S., Fan, K., Geng, H., & Li, F. (2020). Bending Performance of Steel Fiber Reinforced Concrete Beams Based on Composite-Recycled Aggregate and Matched with 500 MPa Rebars. Materials, 13(4), 930. https://doi.org/10.3390/ma13040930





