Influence of Effective Laser Energy on the Structure and Mechanical Properties of Laser Melting Deposited Ti6Al4V Alloy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results and Discussion
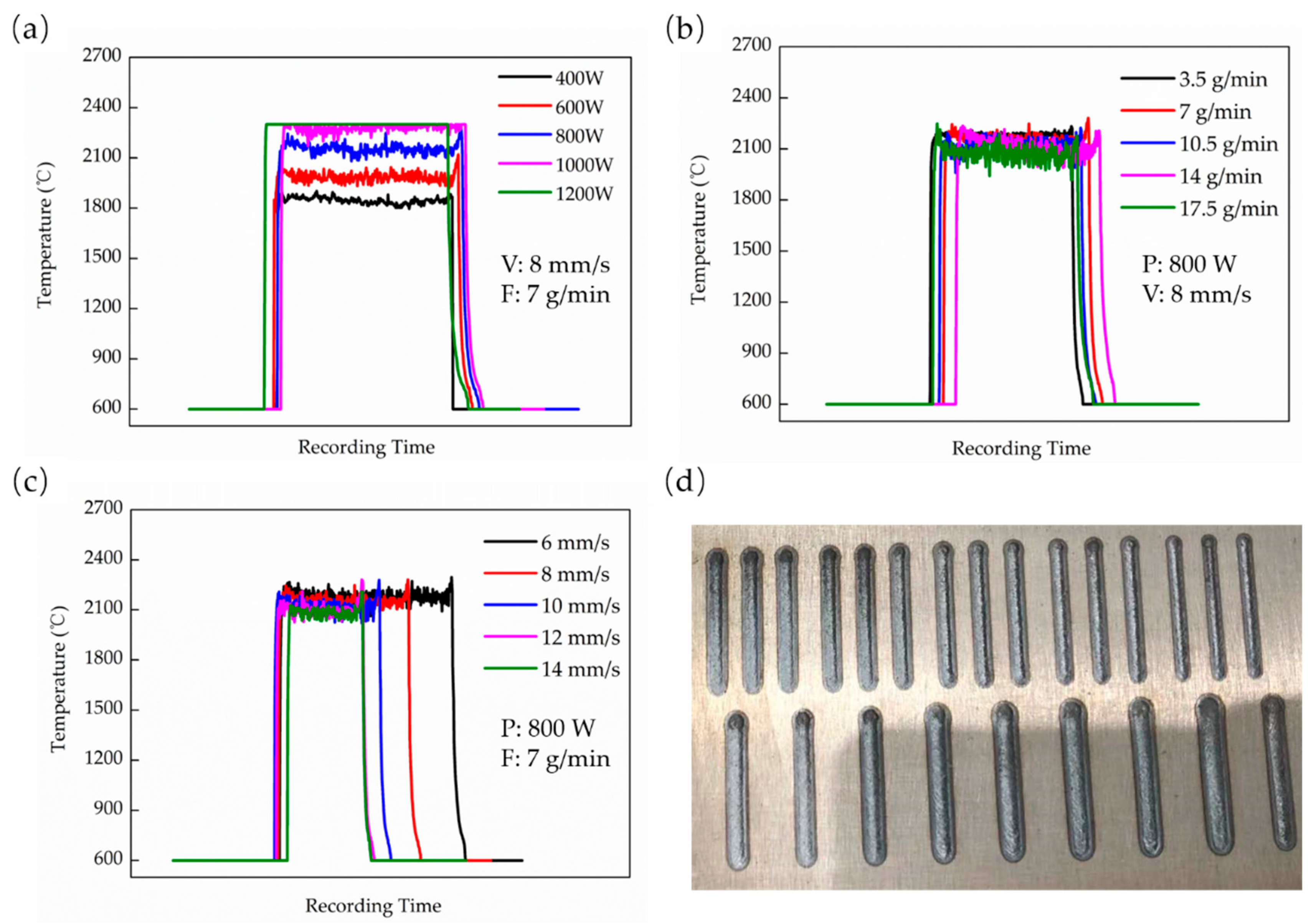
3.1. The Effective Laser Energy
3.2. Meso-Structures and Micro-Structures
3.2.1. Meso-Structure
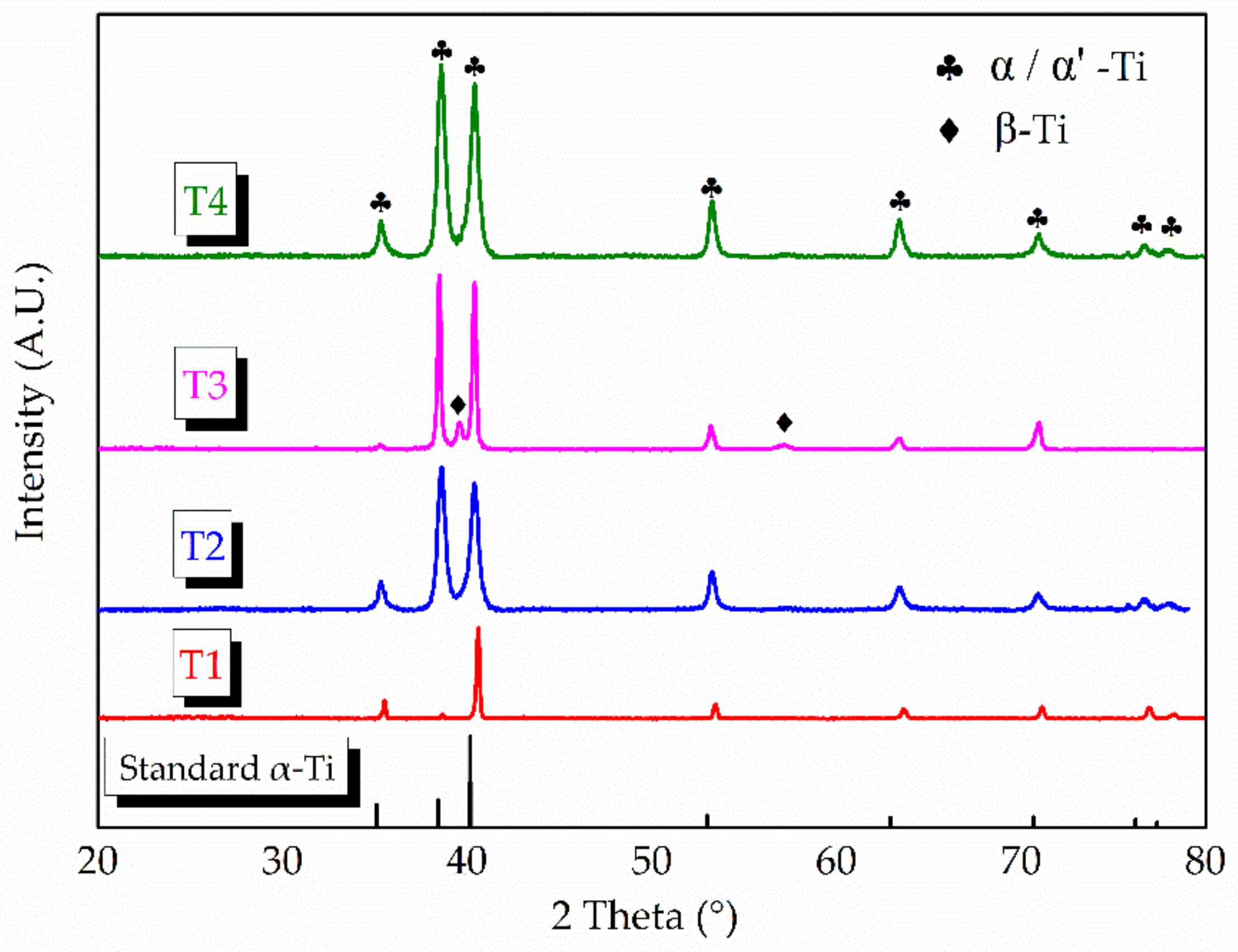
3.2.2. Micro-Structure
3.2.3. Structures Forming Mechanism
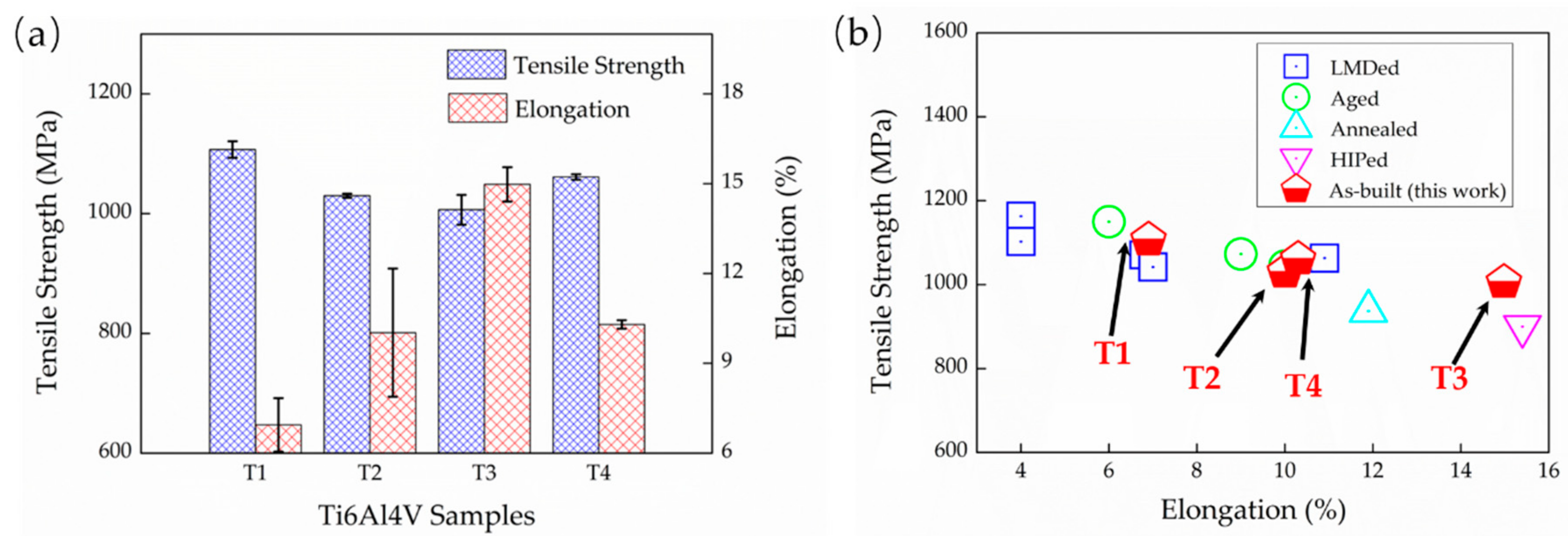
3.3. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ford, S.L.N. Additive Manufacturing Technology: Potential Implications for U.S. Manufacturing Competitiveness. J. Int. Commer. Econ. 2014, 6, 40. [Google Scholar]
- Kobryn, P.A.; Moore, E.H.; Semiatin, S.L. The Effect of Laser Power and Traverse Speed on Microstructure, Porosity, and Build Height in Laser-Deposited Ti-6Al-4V. Scr. Mater. 2000, 43, 299–305. [Google Scholar] [CrossRef]
- Kobryn, P.A.; Semiatin, S.L. The Laser Additive Manufacture of Ti-6Al-4V. Jom 2001, 53, 40–42. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive Manufacturing of Ti6Al4V Alloy: A Review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Zheng, H.; Tang, K.; Ding, L.; Li, H.; Gong, S. Microstructure and Mechanical Properties of LMD-SLM Hybrid Forming Ti6Al4V Alloy. Mater. Sci. Eng. A 2016, 660, 24–33. [Google Scholar] [CrossRef]
- Bian, L.; Thompson, S.M.; Shamsaei, N. Mechanical Properties and Microstructural Features of Direct Laser-Deposited Ti-6Al-4V. Jom 2015, 67, 629–638. [Google Scholar] [CrossRef]
- Marshall, G.J.; Young, W.J.; Thompson, S.M.; Shamsaei, N.; Daniewicz, S.R.; Shao, S. Understanding the Microstructure Formation of Ti-6Al-4V During Direct Laser Deposition via In-Situ Thermal Monitoring. Jom 2016, 68, 778–790. [Google Scholar] [CrossRef]
- Han, J.; Yang, J.; Yu, H.; Yin, J.; Gao, M.; Wang, Z.; Zeng, X. Microstructure and Mechanical Property of Selective Laser Melted Ti6Al4V Dependence on Laser Energy Density. Rapid Prototyp. J. 2017, 23, 217–226. [Google Scholar] [CrossRef]
- Mierzejewska, A. Effect of Laser Energy Density, Internal Porosity and Heat Treatment on Mechanical Behavior of Biomedical Ti6Al4V Alloy Obtained with DMLS Technology. Materials 2019, 12, 2331. [Google Scholar] [CrossRef] [Green Version]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Humbeeck, J.V.; Kruth, J. A Study of the Microstructural Evolution during Selective Laser Melting of Ti-6Al-4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Xu, W.; Sun, S.; Elambasseril, J.; Liu, Q.; Brandt, M.; Qian, M. Ti-6Al-4V Additively Manufactured by Selective Laser Melting with Superior Mechanical Properties. Jom 2015, 67, 668–673. [Google Scholar] [CrossRef]
- Cao, S.; Chen, Z.; Lim, C.V.S.; Yang, K.; Jia, Q.; Jarvis, T.; Tomus, D.; Wu, X. Defect, Microstructure, and Mechanical Property of Ti-6Al-4V Alloy Fabricated by High-Power Selective Laser Melting. Jom 2017, 69, 2684–2692. [Google Scholar] [CrossRef]
- Laquai, R.; Müller, B.R.; Kasperovich, G.; Haubrich, J.; Requena, G.; Bruno, G. X-Ray Refraction Distinguishes Unprocessed Powder from Empty Pores in Selective Laser Melting Ti-6Al-4V. Mater. Res. Lett. 2018, 6, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, J.P.; Santos, T.G.; Miranda, R.M. Revisiting Fundamental Welding Concepts to Improve Additive Manufacturing: From Theory to Practice. Prog. Mater. Sci. 2020, 107, 100590. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Scudino, S.; Maity, T.; Das, J.; Eckert, J. Is the Energy Density a Reliable Parameter for Materials Synthesis by Selective Laser Melting? Mater. Res. Lett. 2017, 5, 386–390. [Google Scholar] [CrossRef] [Green Version]
- Gong, H.; Rafi, K.; Gu, H.; Janaki Ram, G.D.; Starr, T.; Stucker, B. Influence of Defects on Mechanical Properties of Ti-6Al-4V Components Produced by Selective Laser Melting and Electron Beam Melting. Mater. Des. 2015, 86, 545–554. [Google Scholar] [CrossRef]
- Kumar, P.; Prakash, O.; Ramamurty, U. Micro-and Meso-Structures and their Influence on Mechanical Properties of Selectively Laser Melted Ti-6Al-4V. Acta Mater. 2018, 154, 246–260. [Google Scholar] [CrossRef]
- Lia, F.; Park, J.Z.; Keist, J.S.; Joshi, S.; Martukanitz, R.P. Thermal and Microstructural Analysis of Laser-Based Directed Energy Deposition for Ti-6Al-4V and Inconel 625 Deposits. Mater. Sci. Eng. A 2018, 717, 1–10. [Google Scholar] [CrossRef]
- Wu, X.; Liang, J.; Mei, J.; Mitchell, C.; Goodwin, P.S.; Voice, W. Microstructures of Laser-Deposited Ti-6Al-4V. Mater. Des. 2004, 25, 137–144. [Google Scholar] [CrossRef]
- Yu, J.; Rombouts, M.; Maes, G.; Motmans, F. Material Properties of Ti6Al4V Parts Produced by Laser Metal Deposition. Phys. Procedia 2012, 39, 416–424. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, T.; Manvatkar, V.; De, A.; Debroy, T. Dimensionless Numbers in Additive Manufacturing. J. Appl. Phys. 2017, 121, 2017. [Google Scholar] [CrossRef] [Green Version]
- Sterling, A.J.; Torries, B.; Shamsaei, N.; Thompson, S.M.; Seely, D.W. Fatigue Behavior and Failure Mechanisms of Direct Laser Deposited Ti-6Al-4V. Mater. Sci. Eng. A 2016, 655, 100–112. [Google Scholar] [CrossRef]
- Neikter, M.; Åkerfeldt, P.; Pederson, R.; Antti, M.L.; Sandell, V. Microstructural Characterization and Comparison of Ti-6Al-4V Manufactured with Different Additive Manufacturing Processes. Mater. Charact. 2018, 143, 68–75. [Google Scholar] [CrossRef]
- Qiu, C.; Ravi, G.A.; Dance, C.; Ranson, A.; Dilworth, S.; Attallah, M.M. Fabrication of Large Ti-6Al-4V Structures by Direct Laser Deposition. J. Alloy Compd. 2015, 629, 351–361. [Google Scholar] [CrossRef]
- Qiu, C.; Adkins, N.J.E.; Attallah, M.M. Microstructure and Tensile Properties of Selectively Laser-Melted and of HIPed Laser-Melted Ti-6Al-4V. Mater. Sci. Eng. A 2013, 578, 230–239. [Google Scholar] [CrossRef]
- Sabban, R.; Bahl, S.; Chatterjee, K.; Suwas, S. Globularization Using Heat Treatment in Additively Manufactured Ti-6Al-4V for High Strength and Toughness. Acta Mater. 2019, 162, 239–254. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, J.; Guo, S.; Tan, H.; Lin, X.; Huang, W. Influence of α/β Interface Phase on the Tensile Properties of Laser Cladding Deposited Ti-6Al-4V Titanium Alloy. J. Mater. Sci. Technol. 2017, 33, 675–681. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Ramirez, D.A.; Martinez, E.; Hernandez, J.; Amato, K.N.; Shindo, P.W.; Medina, F.R.; Wicker, R.B. Metal Fabrication by Additive Manufacturing Using Laser and Electron Beam Melting Technologies. J. Mater. Sci. Technol. 2012, 28, 1–14. [Google Scholar] [CrossRef]
- Simonelli, M.; Tse, Y.Y.; Tuck, C. Effect of the Build Orientation on the Mechanical Properties and Fracture Modes of SLM Ti-6Al-4V. Mater. Sci. Eng. A 2014, 616, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Lui, E.W.; Pateras, A.; Qian, M.; Brandt, M. In Situ Tailoring Microstructure in Additively Manufactured Ti-6Al-4V for Superior Mechanical Performance. Acta Mater. 2017, 125, 390–400. [Google Scholar] [CrossRef]
- Qazi, J.I.; Rahim, J.; SAM Fores, F.H.; Senkov, O.N.; Genc, A. Phase Transformations in Ti-6Al-4V-xH Alloys. Metall. Mater. Trans. A 2001, 32, 2453–2463. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Viswanathan, G.B.; Denkenberger, R.; Furrer, D.; Fraser, H.L. The Role of Crystallographic and Geometrical Relationships Between α and β Phases in an α/β Titanium Alloy. Acta Mater. 2003, 51, 4679–4691. [Google Scholar] [CrossRef]
- Sridharan, N.; Chaudhary, A.; Nandwana, P.; Babu, S.S. Texture Evolution during Laser Direct Metal Deposition of Ti-6Al-4V. Jom 2016, 68, 772–777. [Google Scholar] [CrossRef]
- Verhaeghe, F.; Craeghs, T.; Heulens, J.; Pandelaers, L. A Pragmatic Model for Selective Laser Melting with Evaporation. Acta Mater. 2009, 57, 6006–6012. [Google Scholar] [CrossRef]
- El Cheikh, H.; Courant, B.; Branchu, S.; Hascoët, J.; Guillén, R. Analysis and Prediction of Single Laser Tracks Geometrical Characteristics in Coaxial Laser Cladding Process. Opt. Lasers Eng. 2012, 50, 413–422. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Lin, X.; Chen, J.; Huang, W. Heat-Treated Microstructure and Mechanical Properties of Laser Solid Forming Ti-6Al-4V Alloy. Rare Met. 2009, 28, 537–544. [Google Scholar] [CrossRef]
- Barriobero-Vila, P.; Gussone, J.; Haubrich, J.; Sandlöbes, S.; Da Silva, J.; Cloetens, P.; Schell, N.; Requena, G. Inducing Stable α + β Microstructures During Selective Laser Melting of Ti-6Al-4V Using Intensified Intrinsic Heat Treatments. Materials 2017, 10, 268. [Google Scholar] [CrossRef]













| Element | Ti | Al | V | Fe | O | N | C |
|---|---|---|---|---|---|---|---|
| wt.% | Bal. | 6.53 | 4.13 | 0.25 | 0.08 | 0.04 | 0.01 |
| Parameter | Single Track | Ti6Al4V Bulk |
|---|---|---|
| Laser power/P (kW) | 0.2–1 | 1–2 |
| Scanning speed/V (mm/s) | 6–14 | 8–12 |
| Powder feed rate/F (g/min) | 3.5–14 | 7–14 |
| Beam diameter/d (mm) | 3 | 3 |
| Layer thickness/ΔZ (mm) | - | 0.6–1.5 |
| Nomenclature | P (W) | V (mm/s) | F (g/min) | ΔZ (mm) | Ee |
|---|---|---|---|---|---|
| T1 | 1000 | 8 | 14 | 1.58 | 2.07 × 105 |
| T2 | 1500 | 10 | 7 | 0.60 | 5.46 × 105 |
| T3 | 2000 | 12 | 10.50 | 0.63 | 7.98 × 105 |
| T4 | 2000 | 8 | 10.50 | 1.11 | 9.13 × 105 |
| Spot | Elements (wt.%) | |||
|---|---|---|---|---|
| Ti | Al | V | Fe | |
| 1 | 89.93 | 6.70 | 3.02 | 0.33 |
| 2 | 90.39 | 5.90 | 3.53 | 0.16 |
| 3 | 90.34 | 6.02 | 3.49 | 0.13 |
| 4 | 77.68 | 5.31 | 15.69 | 1.31 |
| 5 | 91.57 | 6.46 | 1.62 | 0.33 |
| 6 | 62.65 | 3.98 | 31.87 | 1.48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, D.; Li, X.; Zhang, M.; Wang, M.; Zhang, Z.; Qu, S. Influence of Effective Laser Energy on the Structure and Mechanical Properties of Laser Melting Deposited Ti6Al4V Alloy. Materials 2020, 13, 962. https://doi.org/10.3390/ma13040962
Fu D, Li X, Zhang M, Wang M, Zhang Z, Qu S. Influence of Effective Laser Energy on the Structure and Mechanical Properties of Laser Melting Deposited Ti6Al4V Alloy. Materials. 2020; 13(4):962. https://doi.org/10.3390/ma13040962
Chicago/Turabian StyleFu, Daojian, Xiaoqiang Li, Minai Zhang, Min Wang, Zhen Zhang, and Shengguan Qu. 2020. "Influence of Effective Laser Energy on the Structure and Mechanical Properties of Laser Melting Deposited Ti6Al4V Alloy" Materials 13, no. 4: 962. https://doi.org/10.3390/ma13040962
APA StyleFu, D., Li, X., Zhang, M., Wang, M., Zhang, Z., & Qu, S. (2020). Influence of Effective Laser Energy on the Structure and Mechanical Properties of Laser Melting Deposited Ti6Al4V Alloy. Materials, 13(4), 962. https://doi.org/10.3390/ma13040962






