Structural Properties and Water Uptake of SrTi1−xFexO3−x/2−δ
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis Protocol
2.2. Structural and Microstructural Characterization
2.3. Thermogravimetric Analysis
3. Results
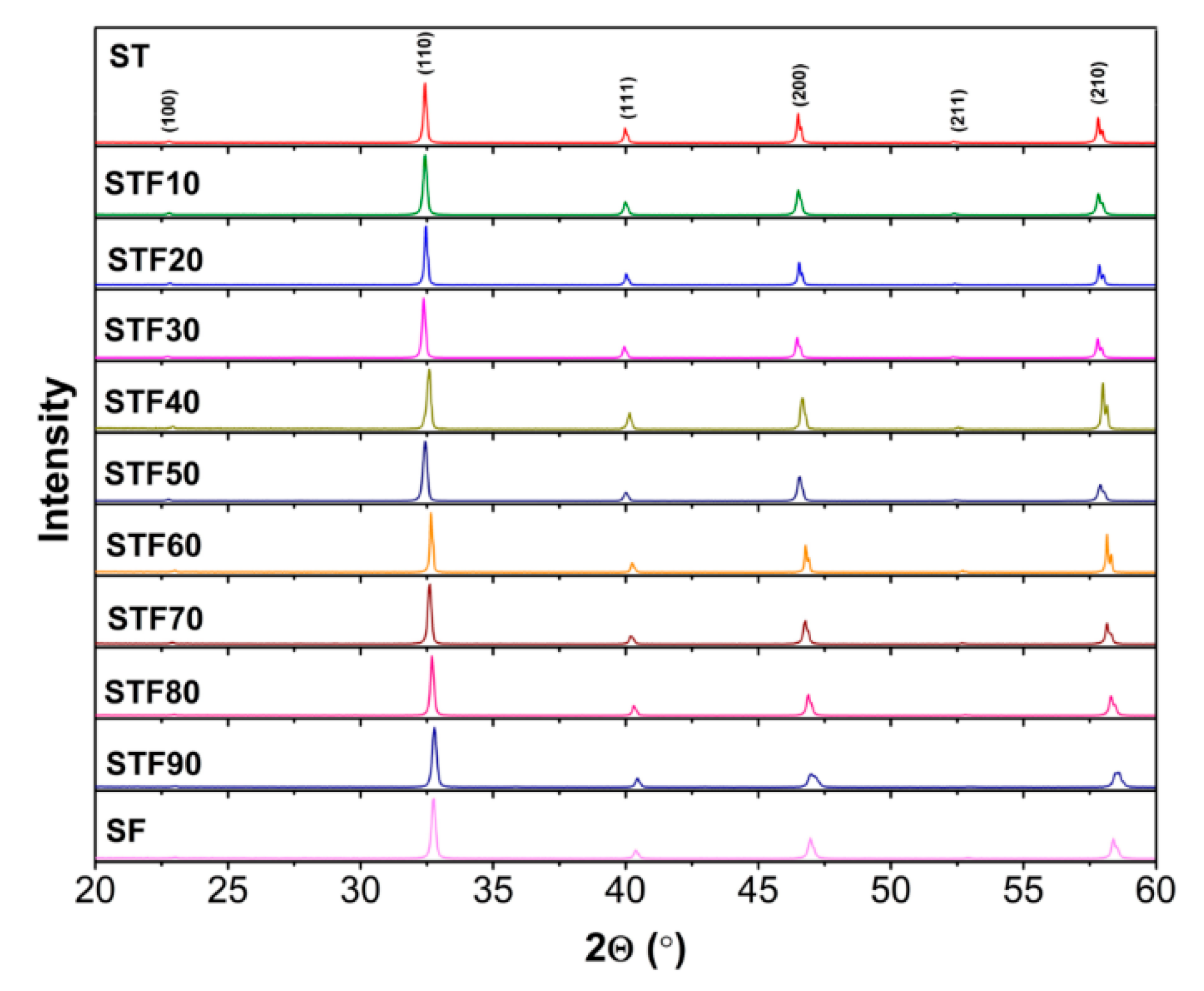
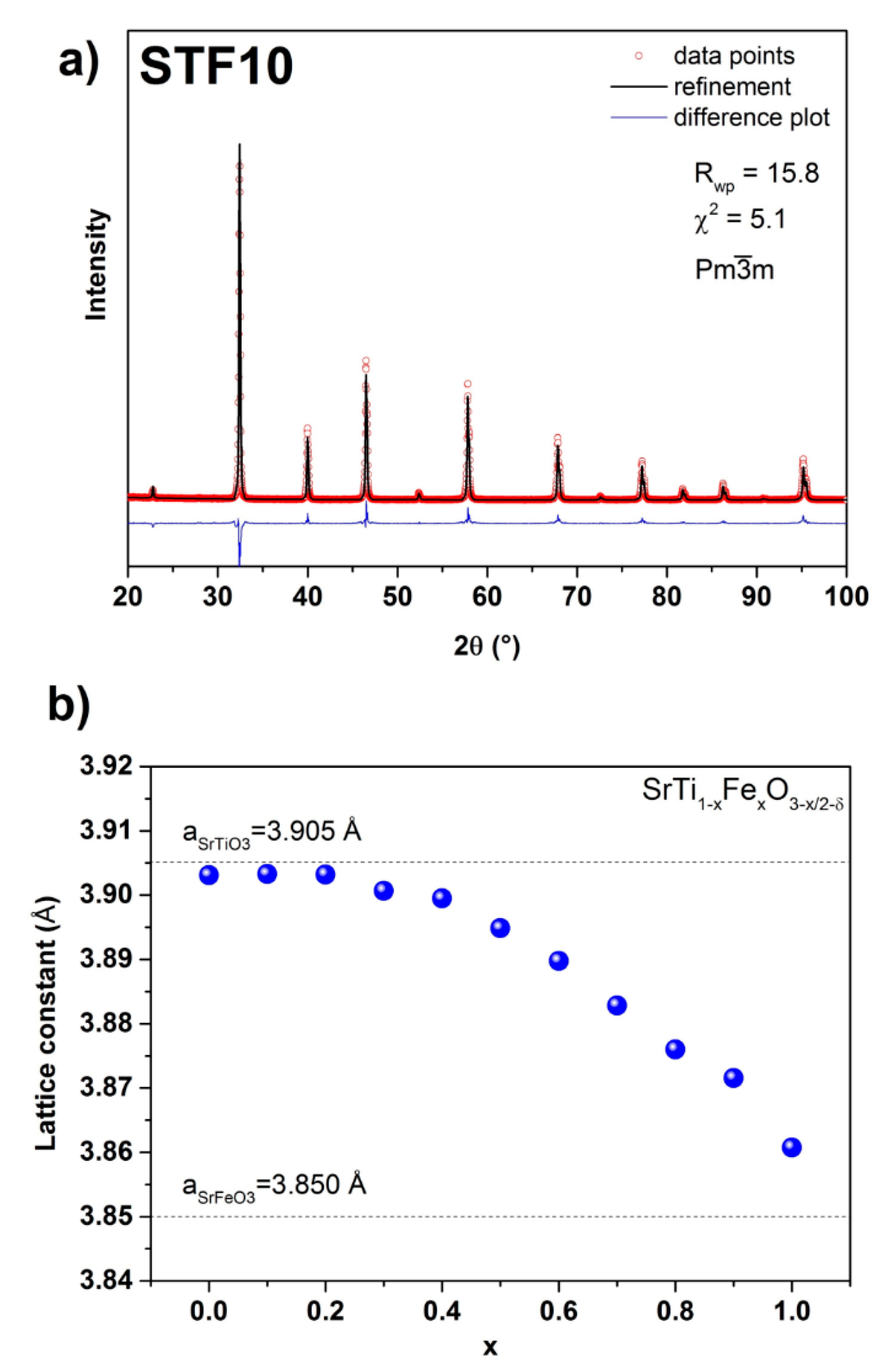
3.1. Structure and Microstructure of SrTi1−xFexO3−x/2−δ
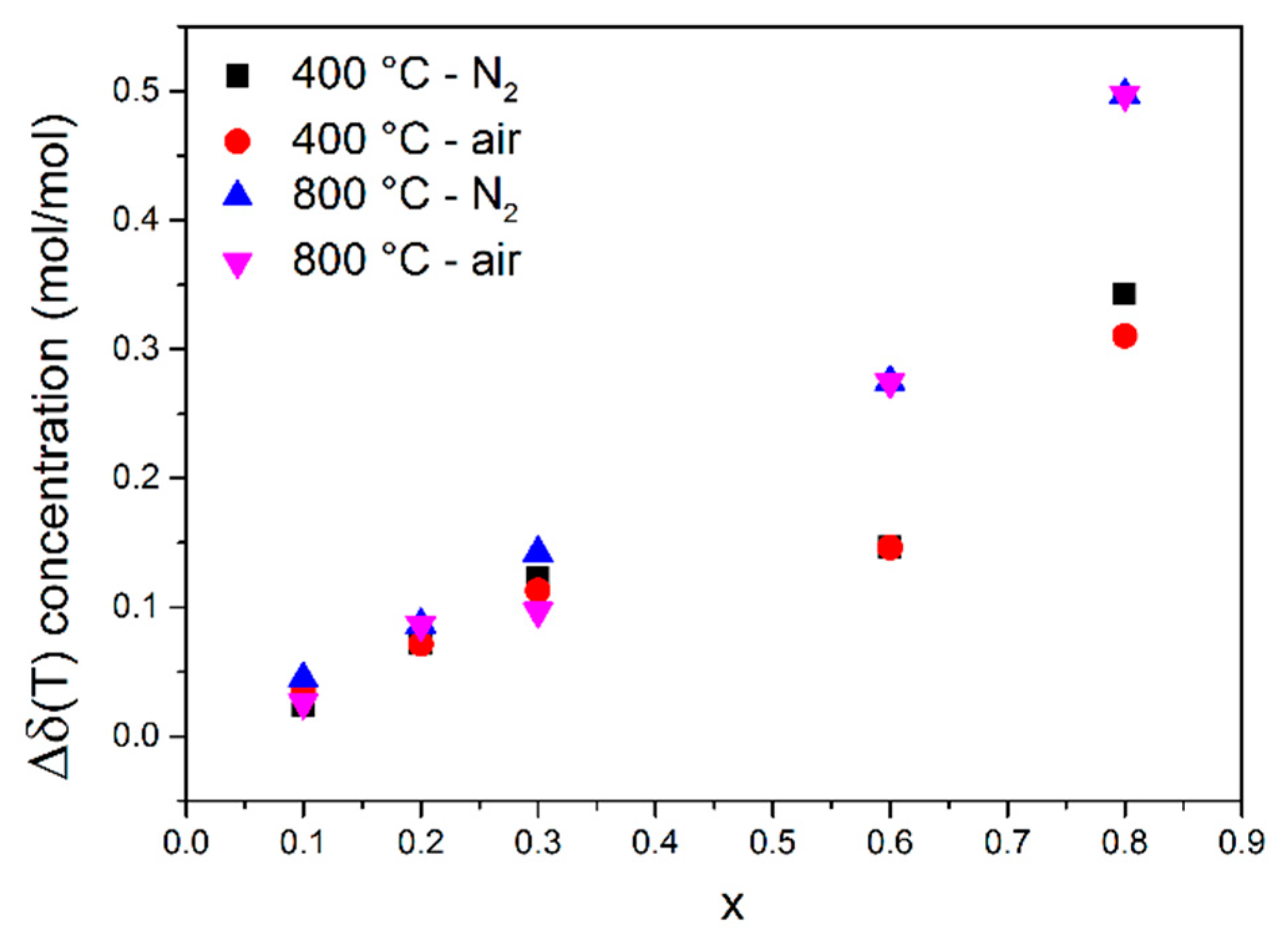
3.2. Oxygen Nonstoichiometry
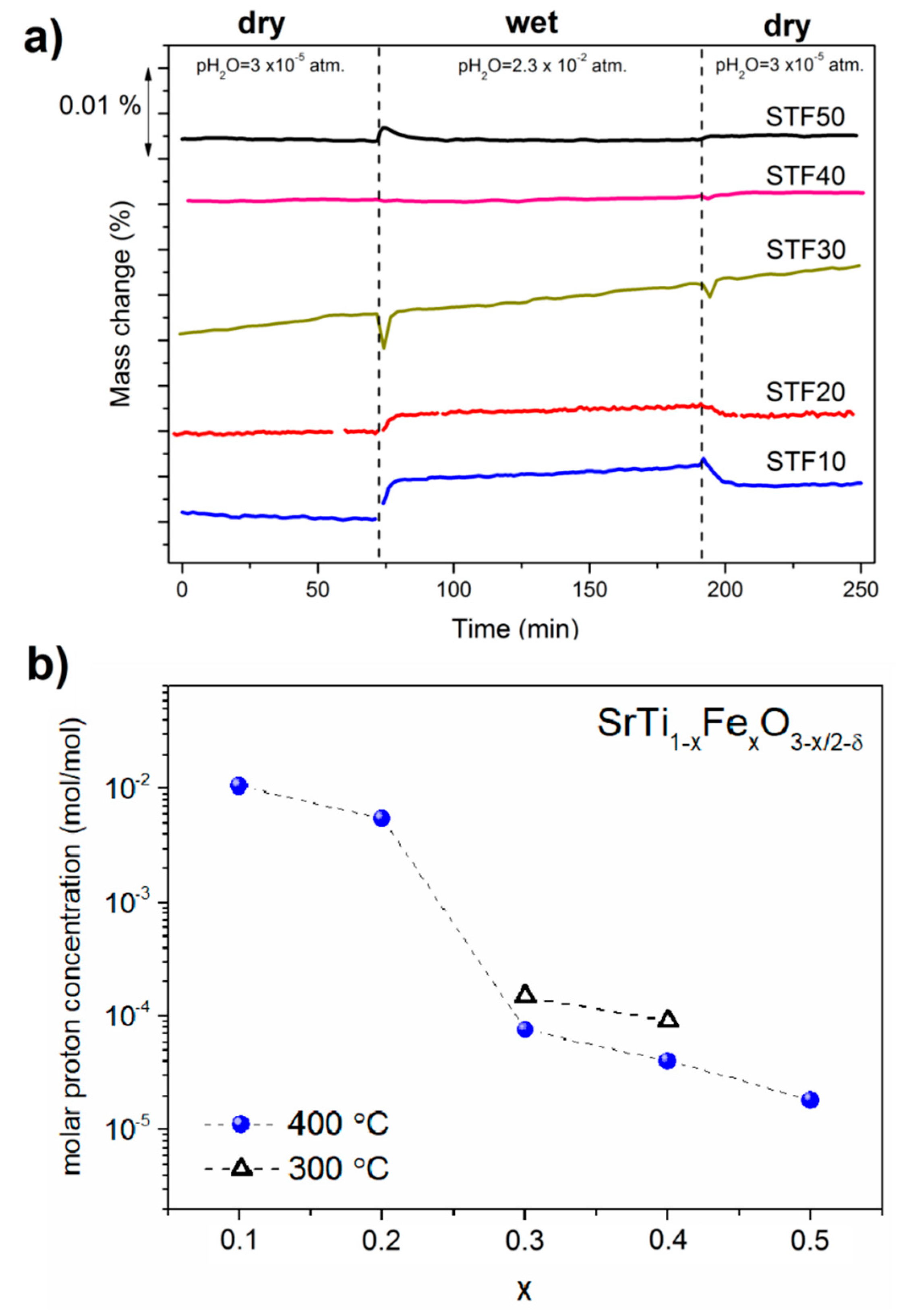
3.3. Water Uptake and Proton Concentration Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Skinner, S.J.; Kilner, J.A. Oxygen ion conductors. Mater. Today 2003, 6, 30–37. [Google Scholar] [CrossRef]
- Boivin, J.C.; Mairesse, G. Recent Material Developments in Fast Oxide Ion Conductors. Chem. Mater. 1998, 10, 2870–2888. [Google Scholar] [CrossRef]
- Rahman, I.Z.; Raza, M.A.; Rahman, M.A. Perovskite Based Anode Materials for Solid Oxide Fuel Cell Application: A Review. Adv. Mater. Res. 2012, 445, 497–502. [Google Scholar] [CrossRef]
- Moure, C.; Peña, O. Recent Advances in Perovskites: Processing and Properties. Prog. Solid State Chem. 2015, 43, 123–148. [Google Scholar] [CrossRef]
- Balachandran, U.; Eror, N.G. Electrical conductivity in strontium titanate. J. Solid State Chem. 1981, 39, 351–359. [Google Scholar] [CrossRef]
- Hui, S.; Petric, A. Electrical conductivity of yttrium-doped SrTiO3: Influence of transition metal additives. Mater. Res. Bull. 2002, 37, 1215–1231. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Zhou, X.; Xu, N.; Xie, Z.; Chen, N. Electrical conductivity and structural stability of La-doped SrTiO3 with A-site deficiency as anode materials for solid oxide fuel cells. Int. J. Hydrogen Energy 2010, 35, 7913–7918. [Google Scholar] [CrossRef]
- Kamecki, B.; Miruszewski, T.; Karczewski, J. Structural and electrical transport properties of Pr-doped SrTi0.93Co0.07O3−δ a novel SOEC fuel electrode materials. J. Electroceram. 2019, 42, 31–40. [Google Scholar] [CrossRef] [Green Version]
- Bochentyn, B.; Karczewski, J.; Miruszewski, T.; Krupa, A.; Gazda, M.; Jasinski, P.; Kusz, B. Donor-substituted SrTi1+xO3−δ anodes for SOFC. Solid State Ion. 2012, 225, 118–123. [Google Scholar] [CrossRef]
- Blennow, P.; Hagen, A.; Hansen, K.K.; Wallenberg, L.R.; Mogensen, M. Defect and electrical transport properties of Nb-doped SrTiO3. Solid State Ion. 2008, 179, 2047–2058. [Google Scholar] [CrossRef]
- Tufte, O.N.; Chapman, P.W. Electron Mobility in Semiconducting Strontium Titanate. Phys. Rev. 1967, 155, 796–802. [Google Scholar] [CrossRef]
- Rothschild, A.; Menesklou, W.; Tuller, H.L.; Ivers-Tiffée, E. Electronic structure, defect chemistry, and transport properties of SrTi1−xFexO3−y solid solutions. Chem. Mater. 2006, 18, 3651–3659. [Google Scholar] [CrossRef]
- Rothschild, A.; Litzelman, S.J.; Tuller, H.L.; Menesklou, W.; Schneider, T.; Ivers-Tiffée, E. Temperature-independent resistive oxygen sensors based on SrTi1−xFexO3−δ solid solutions. Sens. Actuators B Chem. 2005, 108, 223–230. [Google Scholar] [CrossRef]
- Steinsvik, S.; Bugge, R.; Gjønnes, J.; Taftø, J.; Norby, T. The defect structure of SrTi1−xFexO3−y (x = 0–0.8) investigated by electrical conductivity measurements and electron energy loss spectroscopy (EELS). J. Phys. Chem. Solids 1997, 58, 969–976. [Google Scholar] [CrossRef]
- Maldonado, F.; Maza, L.; Stashans, A. Electronic properties of Cr-, B-doped and codoped SrTiO3. J. Phys. Chem. Solids 2017, 100, 1–8. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Gao, F.; Chen, N.; Xu, N. La and Sc co-doped SrTiO3 as novel anode materials for solid oxide fuel cells. Electrochem. Commun. 2008, 10, 1567–1570. [Google Scholar] [CrossRef]
- Shin, C.J.; Yoo, H.I. Al-doped SrTiO3: Part II, unusual thermodynamic factor and chemical diffusivity. Solid State Ion. 2007, 178, 1089–1094. [Google Scholar] [CrossRef]
- Echeverri, E.; Arnache, O. Structural and impedance analysis of Co-doped SrTiO3 perovskite. J. Phys. Conf. Ser. 2016, 687, 012040. [Google Scholar] [CrossRef] [Green Version]
- Yoo, K.B.; Park, B.H.; Choi, G.M. Stability and performance of SOFC with SrTiO3-based anode in CH4 fuel. Solid State Ion. 2012, 225, 104–107. [Google Scholar] [CrossRef]
- Vashuk, V.V.; Kokhanovskii, L.V.; Yushkevich, I.I. Electrical conductivity and oxygen stoichiometry of SrFeO3-δ. Inorg. Mater. 2000, 36, 79–83. [Google Scholar] [CrossRef]
- Hodges, J.P.; Short, S.; Jorgensen, J.D.; Xiong, X.; Dabrowski, B.; Mini, S.M.; Kimball, C.W. Evolution of Oxygen-Vacancy Ordered Crystal Structures in the Perovskite Series SrnFenO3n−1 (n=2, 4, 8, and ∞), and the Relationship to Electronic and Magnetic Properties. J. Solid State Chem. 2000, 151, 190–209. [Google Scholar] [CrossRef]
- Bocquet, A.E.; Fujimori, A.; Mizokawa, T.; Saitoh, T.; Namatame, H.; Suga, S.; Kimizuka, N.; Takeda, Y.; Takano, M. Electronic structure of SrFe4+O3 and related Fe perovskite oxides. Phys. Rev. B 1992, 45, 1561–1570. [Google Scholar] [CrossRef] [PubMed]
- Patrakeev, M.V.; Leonidov, I.A.; Kozhevnikov, V.L.; Kharton, V.V. Ion–electron transport in strontium ferrites: Relationships with structural features and stability. Solid State Sci. 2004, 6, 907–913. [Google Scholar] [CrossRef]
- Simner, S.P.; Shelton, J.P.; Anderson, M.D.; Stevenson, J.W. Interaction between La(Sr)FeO3 SOFC cathode and YSZ electrolyte. Solid State Ion. 2003, 161, 11–18. [Google Scholar] [CrossRef]
- Brixner, L.H. Preparation and properties of the SrTi1−xFexO3−x2/Ox2 system. Mater. Res. Bull. 1968, 3, 299–308. [Google Scholar] [CrossRef]
- Jung, W. Environmental Science Activity of SrTi1−xFexO3 Surfaces. Energy Environ. Sci. 2012, 5, 7979–7988. [Google Scholar] [CrossRef]
- Widerøe, M.; Münch, W.; Larring, Y.; Norby, T. Proton and apparent hydride ion conduction in Al-substituted SrTiO3. Solid State Ion. 2002, 154–155, 669–677. [Google Scholar] [CrossRef]
- Muñoz-García, A.B.; Pavone, M. First-Principles Design of New Electrodes for Proton-Conducting Solid-Oxide Electrochemical Cells: A-Site Doped Sr2Fe1.5Mo0.5O6-δ Perovskite. Chem. Mater. 2016, 28, 490–500. [Google Scholar] [CrossRef]
- Ricote, S.; Almansoori, A.; Sanders, M.; Tong, J.; Duan, C.; Nikodemski, S.; Hayre, R.O.; Shang, M. Readily processed protonic ceramic fuel cells with high performance at low temperatures. Science 2015, 349, 1321–1326. [Google Scholar] [CrossRef]
- Poetzsch, D.; Merkle, R.; Maier, J. Proton uptake in the H+-SOFC cathode material Ba0.5Sr0.5Fe0.8Zn0.2O3-δ: Transition from hydration to hydrogenation with increasing oxygen partial pressure. Faraday Discuss. 2015, 182, 129–143. [Google Scholar] [CrossRef]
- Yu, J.H.; Lee, J.S.; Maier, J. Water incorporation in oxides: A moving boundary problem. Solid State Ion. 2010, 181, 154–162. [Google Scholar] [CrossRef]
- Skubida, W.; Niemczyk, A.; Zheng, K.; Liu, X.; Świeczek, K. Crystal Structure, Hydration, and Two-Fold/Single-Fold Diffusion Kinetics in Proton-Conducting Ba0.9La0.1Zr0.25Sn0.25In0.5O3−a Oxide. Crystals 2018, 8, 136. [Google Scholar] [CrossRef] [Green Version]
- Poetzsch, D.; Merkle, R.; Maier, J. Stoichiometry variation in materials with three mobile carriers-Thermodynamics and transport kinetics exemplifi ed for protons, oxygen vacancies, and holes. Adv. Funct. Mater. 2015, 25, 1542–1557. [Google Scholar] [CrossRef]
- Zohourian, R.; Merkle, R.; Raimondi, G.; Maier, J. Mixed-Conducting Perovskites as Cathode Materials for Protonic Ceramic Fuel Cells: Understanding the Trends in Proton Uptake. Adv. Funct. Mater. 2018, 28, 1801241. [Google Scholar] [CrossRef]
- Fan, L.; Su, P.C. Layer-structured LiNi0.8Co0.2O2: A new triple (H+/O2-/e-) conducting cathode for low temperature proton conducting solid oxide fuel cells. J. Power Sources 2016, 306, 369–377. [Google Scholar] [CrossRef]
- Strandbakke, R.; Cherepanov, V.A.; Zuev, A.Y.; Tsvetkov, D.S.; Argirusis, C.; Sourkouni, G.; Prünte, S.; Norby, T. Gd-and Pr-based double perovskite cobaltites as oxygen electrodes for proton ceramic fuel cells and electrolyser cells. Solid State Ion. 2015, 278, 120–132. [Google Scholar] [CrossRef]
- Han, D.; Okumura, Y.; Nose, Y.; Uda, T. Synthesis of La1−XSrxSc1−yFeyO3−δ (LSSF) and measurement of water content in LSSF, LSCF and LSC hydrated in wet artificial air at 300 °C. Solid State Ion. 2010, 181, 1601–1606. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Babilo, P.; Haile, S.M. Defect Chemistry of Yttrium-Doped Barium Zirconate: A Thermodynamic Analysis of Water Uptake. Chem. Mater. 2008, 20, 6352–6357. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter. 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Falcón, H.; Barbero, J.A.; Alonso, J.A.; Martínez-Lope, M.J.; Fierro, J.L.G. SrFeO3-δ perovskite oxides: Chemical features and performance for methane combustion. Chem. Mater. 2002, 14, 2325–2333. [Google Scholar] [CrossRef]
- Vračar, M.; Kuzmin, A.; Merkle, R.; Purans, J.; Kotomin, E.A.; Maier, J.; Mathon, O. Jahn-Teller distortion around Fe4+ in Sr (FexTi1−x) O3−δ from x-ray absorption spectroscopy, x-ray diffraction, and vibrational spectroscopy. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 76, 174107. [Google Scholar] [CrossRef]
- Ghaffari, M.; Liu, T.; Huang, H.; Tan, O.K.; Shannon, M. Investigation of local structure effect and X-ray absorption characteristics (EXAFS) of Fe (Ti) K-edge on photocatalyst properties of SrTi(1−x)FexO(3−δ). Mater. Chem. Phys. 2012, 136, 347–357. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomie Distances in Halides and Chaleogenides. Acta Cryst. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Kuhn, M.; Kim, J.J.; Bishop, S.R.; Tuller, H.L. Oxygen nonstoichiometry and defect chemistry of perovskite-structured BaxSr1−xTi1−yFeyO3−y/2+δ solid solutions. Chem. Mater. 2013, 25, 2970–2975. [Google Scholar] [CrossRef]
- Holt, A.; Norby, T.; Glenne, R. Defects and transport in SrFe1−xCOxO3−δ. Ionics (Kiel) 1999, 5, 434–443. [Google Scholar] [CrossRef]
- Pasierb, P.; Komornicki, S.; Rekas, M. Comparison of the chemical diffusion of undoped and Nb-doped SrTiO3. J. Phys. Chem. Solids 1999, 60, 1835–1844. [Google Scholar] [CrossRef]
- Park, C.Y.; Jacobson, A.J. Electrical Conductivity and Oxygen Nonstoichiometry of La0.2Sr0.8Fe0.55Ti0.45O3−δ. J. Electrochem. Soc. 2005, 152, J65. [Google Scholar] [CrossRef]
- Stevenson, J.W. Electrochemical Properties of Mixed Conducting Perovskites La1−xMxCo1−yFeyO3−δ (M = Sr, Ba, Ca). J. Electrochem. Soc. 2006, 143, 2722. [Google Scholar] [CrossRef]
- Sendilkumar, A.; Raju, K.C.J.; Babu, P.D.; Srinath, S. Positive temperature coefficient of resistance of tetragonal Ti4+ doped nano SrFeO3−d. J. Alloys Compd. 2013, 561, 174–179. [Google Scholar] [CrossRef]
- de Ligny, D.; Richet, P. High-temperature heat capacity and thermal expansion of and perovskites of SrTiO3 and SrZrO3 perovskites. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 53, 3013–3022. [Google Scholar] [CrossRef]
- Crawford, J.; Jacobs, P. Point Defect Energies for Strontium Titanate: A Pair-Potentials Study. J. Solid State Chem. 1999, 144, 423–429. [Google Scholar] [CrossRef]
- Zohourian, R.; Merkle, R.; Maier, J. Proton uptake into the protonic cathode material BaCo0.4Fe0.4Zr0.2O3-δ and comparison to protonic electrolyte materials. Solid State Ion. 2017, 299, 64–69. [Google Scholar] [CrossRef]
- Zohourian, R. Mixed-Conducting Perovskites as Cathodes in Protonic Ceramic Fuel Cells: Defect Chemistry and Transport Properties. Ph.D. Thesis, Max Planck Institute for Solid State Research, Stuttgart, Germany, 2018. [Google Scholar]
- Yang, L.; Liu, Z.; Wang, S.; Choi, Y.; Zuo, C.; Liu, M. A mixed proton, oxygen ion, and electron conducting cathode for SOFCs based on oxide proton conductors. J. Power Sources 2010, 195, 471–474. [Google Scholar] [CrossRef]
- Norby, T. Proton Conductivity in Perovskite Oxides. In Perovskite Oxide Solid Oxide Fuel Cells; Ishihara, T., Ed.; Springer: Boston, MA, USA, 2009; pp. 217–241. [Google Scholar] [CrossRef]
- Norby, T.; Larring, Y. Concentration and transport of protons in oxides. Curr. Opin. Solid State Mater. Sci. 1997, 2, 593–599. [Google Scholar] [CrossRef]
- Mielewczyk-Gryń, A.; Wachowski, S.; Prześniak-Welenc, M.; Dzierzgowski, K.; Regoutz, A.; Payne, D.J.; Gazda, M. Water uptake analysis of acceptor-doped lanthanum orthoniobates. J. Therm. Anal. Calorim. 2019, 6, 225–232. [Google Scholar] [CrossRef] [Green Version]
- Norby, T.; Widerøe, M.; Glöckner, R.; Larring, Y. Hydrogen in oxides. Dalt. Trans. 2004, 3012–3018. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
- van Benthem, K.; Elsasser, C.; French, R.H. Bulk electronic structure of Experiment and theory. J. Appl. Phys. 2011, 90, 6156–6164. [Google Scholar] [CrossRef] [Green Version]
- Miruszewski, T.; Gdaniec, P.; Rosiński, W.; Karczewski, J.; Bochentyn, B.; Kusz, B. Structure and electrical properties of Y, Fe-based perovskite mixed conducting composites fabricated by a modi fi ed polymer precursor method. Solid State Sci. 2017, 70, 41–46. [Google Scholar] [CrossRef]



| Sample | Sintering Temperature (°C) | Density (g cm−3) | Relative Density (%) |
|---|---|---|---|
| SrTiO3 (ST) | 1400 | 4.57 | 89 |
| SrTi0.9Fe0.1O2.95 (STF10) | 1400 | 4.49 | 87 |
| SrTi0.8Fe0.2O2.9 (STF20) | 1400 | 4.81 | 92 |
| SrTi0.7Fe0.3O2.85 (STF30) | 1400 | 4.78 | 92 |
| SrTi0.6Fe0.4O2.8 (STF40) | 1300 | 3.53 | 67 |
| SrTi0.5Fe0.5O2.75 (STF50) | 1200 | 4.16 | 79 |
| SrTi0.4Fe0.6O2.7 (STF60) | 1200 | 4.45 | 84 |
| SrTi0.3Fe0.7O2.65 (STF70) | 1200 | 4.70 | 88 |
| SrTi0.2Fe0.8O2.6 (STF80) | 1200 | 4.12 | 76 |
| SrTi0.1Fe0.9O2.55 (STF90) | 1200 | 4.71 | 86 |
| SrFeO3 (SF) | 1200 | 4.70 | 85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miruszewski, T.; Dzierzgowski, K.; Winiarz, P.; Wachowski, S.; Mielewczyk-Gryń, A.; Gazda, M. Structural Properties and Water Uptake of SrTi1−xFexO3−x/2−δ. Materials 2020, 13, 965. https://doi.org/10.3390/ma13040965
Miruszewski T, Dzierzgowski K, Winiarz P, Wachowski S, Mielewczyk-Gryń A, Gazda M. Structural Properties and Water Uptake of SrTi1−xFexO3−x/2−δ. Materials. 2020; 13(4):965. https://doi.org/10.3390/ma13040965
Chicago/Turabian StyleMiruszewski, Tadeusz, Kacper Dzierzgowski, Piotr Winiarz, Sebastian Wachowski, Aleksandra Mielewczyk-Gryń, and Maria Gazda. 2020. "Structural Properties and Water Uptake of SrTi1−xFexO3−x/2−δ" Materials 13, no. 4: 965. https://doi.org/10.3390/ma13040965
APA StyleMiruszewski, T., Dzierzgowski, K., Winiarz, P., Wachowski, S., Mielewczyk-Gryń, A., & Gazda, M. (2020). Structural Properties and Water Uptake of SrTi1−xFexO3−x/2−δ. Materials, 13(4), 965. https://doi.org/10.3390/ma13040965







