Experimental Study on the Shear Behavior of GFRP–Concrete Composite Beam Connections
Abstract
:1. Introduction
2. Specimen Fabrication and Test Setup
2.1. Test Specimens and Materials
2.2. Specimen Fabrication
2.3. Test Setup, Loading Procedure, and Instrumentation
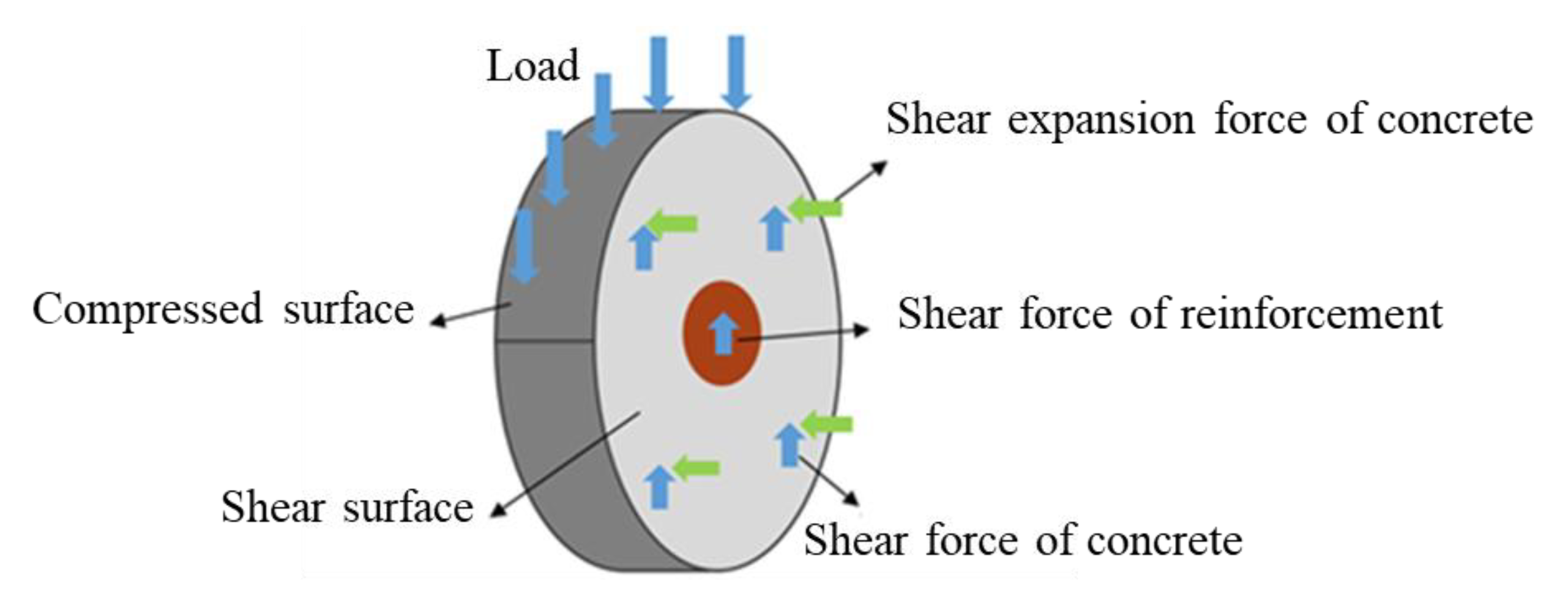
3. Push-Out Test Results and Discussion
3.1. Failure Modes
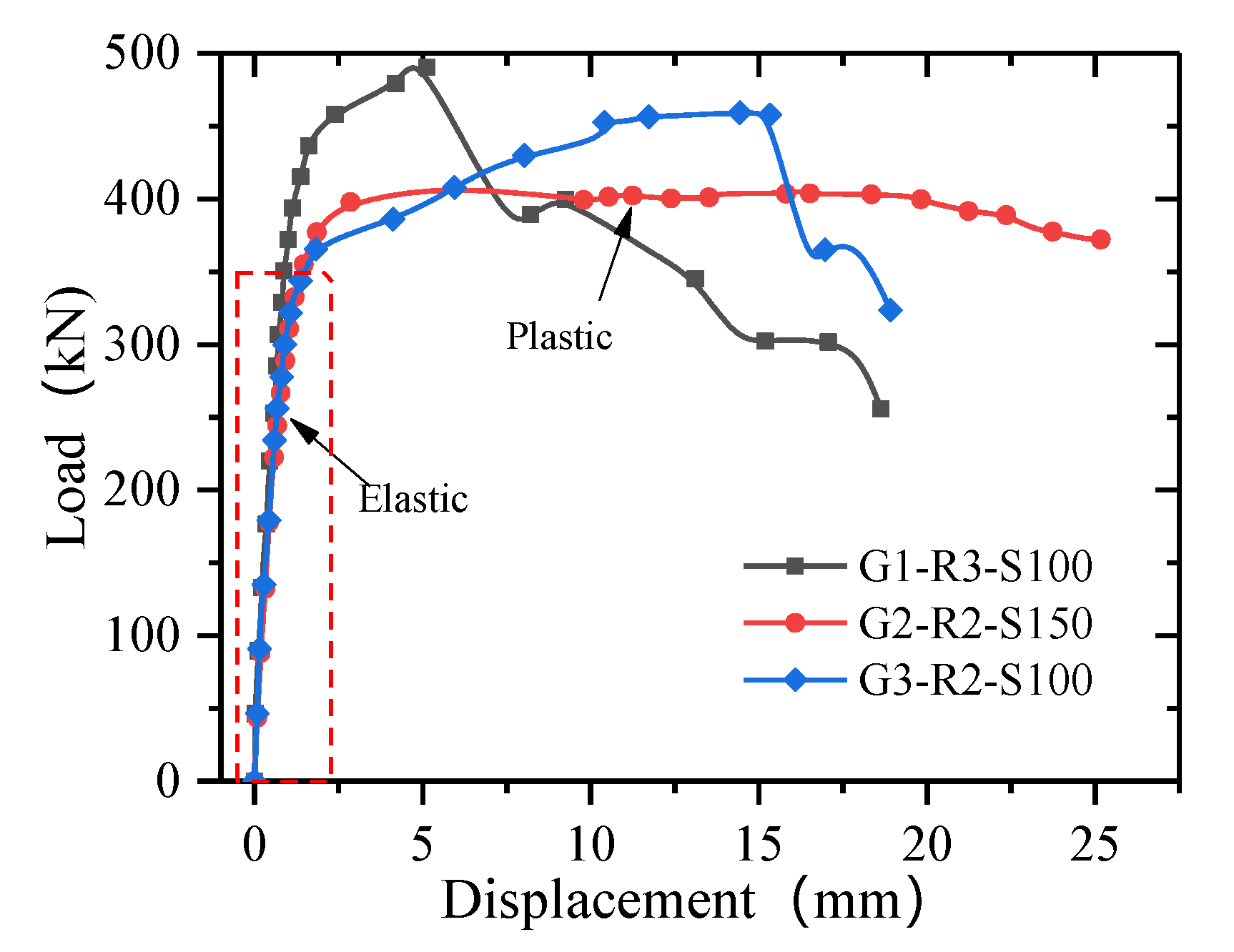
3.2. Load–Slip Relationships
3.2.1. Bolt Connectors
3.2.2. T-Type Perforated Plates
3.2.3. Slot-Type Perforated Plate
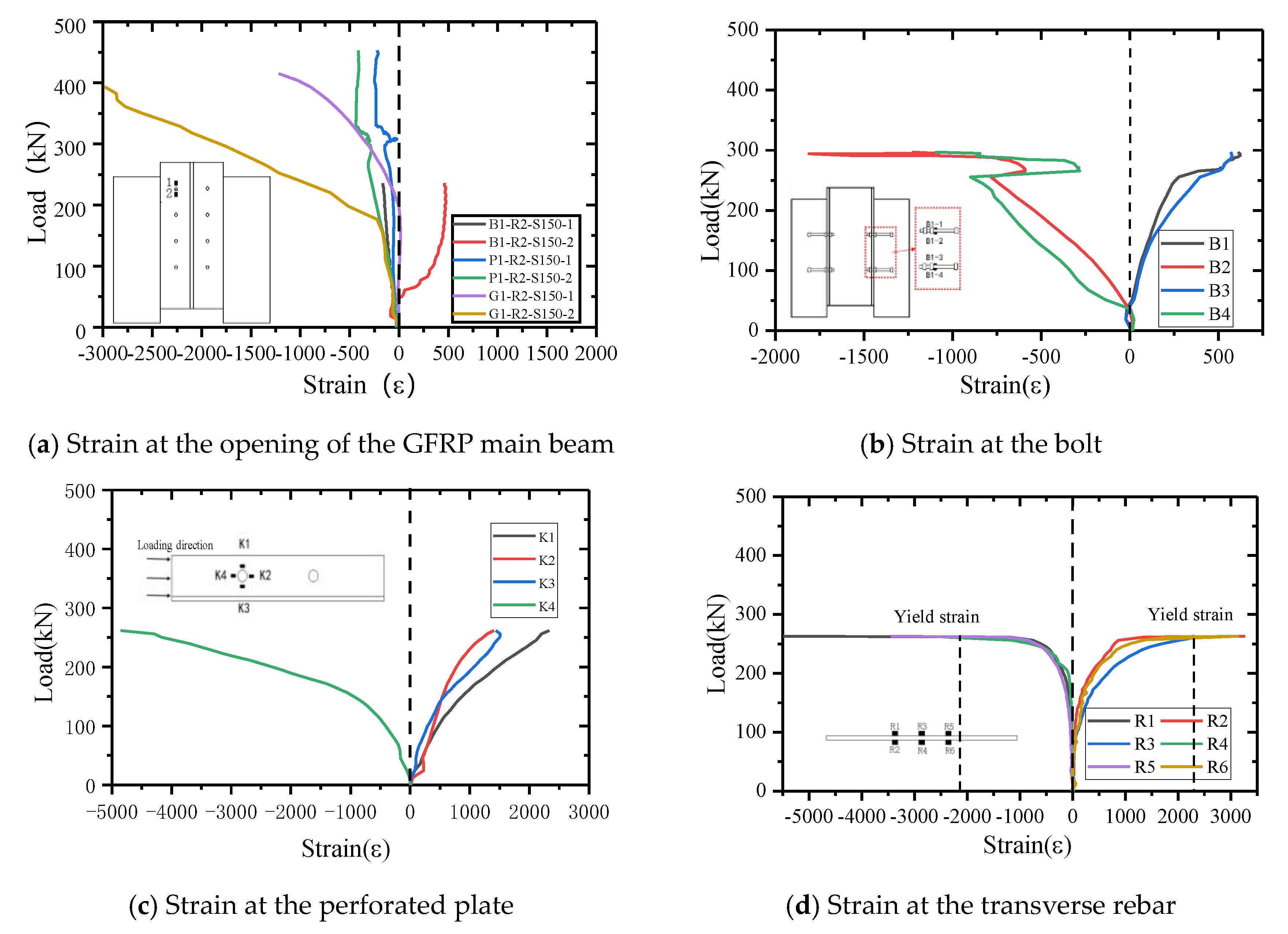
3.3. Load Versus Longitudinal Strain Curves
4. Calculation of the Bearing Capacity and Rigidity of the Interface Connections
4.1. Ultimate Shear Capacity of a Single Connection
4.2. Shear Stiffness
4.3. Shear Capacity of Connectors
4.3.1. Bolt Connectors
4.3.2. Perforated Plate
- (1)
- Code for design of steel and concrete composite bridge (GB 50917-2013) [28]where (N) is the design value of shear capacity of single hole of PBL connector (N); is the diameter of predrilled hole (mm); is the diameter of Transverse rebar (mm); is design value of concrete axial tensile strength (MPa); is design value of shear strength of reinforcement, , is design value of tensile strength of reinforcement (MPa); and, is the coefficient of improvement, taking 6.1.
- (2)
- Specifications for Design and Construction of Highway Steel-concrete Composite Bridge(JTG/T D64-01) [29]where is design value of shear capacity of single hole of PBL connector (N); is the diameter of predrilled hole (mm); is the diameter of transverse rebar (mm); is axial compressive strength of concrete (MPa); and, is design value of tensile strength of reinforcement (MPa).
5. Conclusions
- (1)
- The failure mode of the bolt specimen is a severing of the bolt bar after the concrete around the bolt is crushed; the specimen undergoes brittle failure. There are two failure modes for the T-shaped perforated plate with transverse rebar: one is the severing of the concrete tenon and transverse rebar, the other is peeling off of the interface between the GFRP beam and the concrete; all of the specimens undergo ductile failure. The failure mode of the T-shaped perforated plate without transverse rebar is a severing of the concrete tenon; the specimen undergoes brittle failure. There are two failure modes for the slot-type perforated plate: one is a severing of the concrete tenon and transverse rebar, the other is damage to the bond layer between the opening plate and GFRP beam; and, the specimens undergo ductile failure.
- (2)
- The load–slip curve for the bolt specimen is small at the initial stage of loading; when the ultimate load is reached, the load changes abruptly, and the sliding deformation ability becomes poor. The load–slip curve for the T-shaped perforated plate specimen exhibits an elastic stage and plastic stage, and the plastic stage retains good sliding deformation ability after reaching the ultimate load. The load–slip curve for the slotted perforated plate specimen is the same as that for the T-shaped perforated plate specimen. The difference is that there are two contact surfaces between the perforated steel bar and the opening. After one side is damaged, the other side retains some bearing capacity, which causes the load–slip curve to exhibit a platform for a period after the sudden drop.
- (3)
- The ultimate bearing capacity of a single connection is the lowest for the bolt connection; the T-shaped perforated plate is 1.7 times greater and the slot-shaped perforated plate is 2.7 times greater. The ductility coefficient and shear rigidity of the T-shaped perforated plate are the highest, followed by the slotted perforated plate, and the bolt has the lowest values.
Author Contributions
Funding
Conflicts of Interest
References
- Feng, P.; Cheng, S. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. J. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- Feng, P.; Wang, J. Effects of corrosive environments on properties of pultruded GFRP plates. J. Compos. Part B Eng. 2014, 67, 427–433. [Google Scholar] [CrossRef]
- Nguyen, H.; Mutsuyoshib, W. Hybrid FRP-UHPFRC composite girders: Part 1—Experimental and numerical approach. J. Compos. Struct. 2015, 125, 631–652. [Google Scholar] [CrossRef]
- Nguyen, H.; Zatarc, W. Hybrid FRP-UHPFRC composite girders: Part 2—Analytical approach. J. Compos. Struct. 2015, 125, 653–671. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, S. Experimental study on shear connectors of FRP concrete composite beams. J. Highw. Transp. Res. Dev. 2014, 10, 207–210. [Google Scholar]
- Japan Society of Civil Engineers. Design Manual of Steel-Concrete Composite Structure; Japan Society of Civil Engineers: Tokyo, Japan, 1989. (In Japanese) [Google Scholar]
- Liu, Y.Q.; Zeng, M.G. Application and research of shear connectors in bridge structures. J. Harbin Inst. Technol. 2003, 35, 272–275. [Google Scholar]
- Ribeiro, M.; Tavares, C. Static flexural performance of GFRP-polymer concrete hybrid beams. Key Eng. Mater. 2002, 230–232, 148–151. [Google Scholar] [CrossRef]
- Meshgin, P.; Choi, K. Experimental and analytical investigations of creep of epoxy adhesive at the concrete—FRP interfaces. Int. J. Adhes. Adhes. 2009, 29, 56–66. [Google Scholar] [CrossRef]
- Nordin, H.; TaLjsten, B. Testing of hybrid FRP composite beams in bending. J. Compos. Part B Eng. 2004, 35, 27–33. [Google Scholar] [CrossRef]
- Fam, A.; Skutezky, T. Composite T-beams using reduced-scale rectangular FRP tubes and concrete slabs. J. Compos. Constr. 2006, 10, 172–181. [Google Scholar] [CrossRef]
- Canning, L.; Hollaway, L.; Thorne, A. An investigation of the composite action of an FRP/concrete prismatic beam. J. Constr. Bulid. Mater. 1999, 13, 417–426. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, Q. Experimental testing of a smart FRP-concrete composite bridge superstructure. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; International Society for Optics and Photonics: Bellingham, WA, USA, 2010. [Google Scholar]
- Feng, P.; Lu, X. Application of Fiber Reinforced Polymer in Construction: Experiment, Theory and Methodology; China Architecture & Building Press: Beijing, China, 2011. [Google Scholar]
- Wang, J.; Li, S. Calculation and experiments on ultimate bearing capacity of FRP-concrete composite beams based on single layer failure criteria. J. Southeast Univ. Nat. Sci. Ed. 2013, 43, 952–956. [Google Scholar]
- Zou, X.; Feng, P. Perforated FRP ribs for shear connecting of FRP-concrete hybrid beams/decks. J. Compos. Struct. 2016, 152, 267–276. [Google Scholar] [CrossRef]
- Zou, X.; Feng, P. Bolted shear connection of FRP-concrete hybrid beams. J. Compos. Constr. 2018, 22, 04018012. [Google Scholar] [CrossRef]
- Zou, X.; Chen, J. High shear strength post-forming FRP profiles: Manufacture and testing. China Civ. Eng. J. 2016, 2016, 40–47. [Google Scholar]
- European Committee for Standardization. Eurocode 4, Design of Composite Steel and Concrete Structures—Part 1.1 (EC 4): EN 1994-1-1; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- AQSIQ. Standard for Test Method of Mechanical Properties on Ordinary Concrete (GB·T50081-2002); General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2003.
- AQSIQ. Pultruded Fiber Reinforced Polymer Composites Structural Profiles (GB/T 31539-2015); General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2016.
- Japan Steel Construction Association. Japan Steel Construction Association. A Study on the Pushing Test Method of Spiders with Spiders; Japan Steel Construction Association: Tokyo, Japan, 1996. (In Japanese) [Google Scholar]
- AISC. American Institute of Steel Construction in Specification for Structural Steel Buildings; AISC: Chicago, IL, USA, 2011. [Google Scholar]
- American Concrete Institute. Building Code Requirements for Structural Concrete and Commentary; ACI: Farmington Hills, MI, USA, 2011. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 5th ed.; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Nguyen, H.; Mutsuyoshi, H. Push-out tests for shear connections between UHPFRC slabs and FRP girder. Compos. Struct. 2014, 118, 528–547. [Google Scholar] [CrossRef]
- Correia, J.R.; Branco, F.A. Flexural behavior of GFRP-concrete hybrid beams with interconnection slip. Compos. Struct. 2007, 77, 66–78. [Google Scholar] [CrossRef]
- MOHURD. Code for Design of Steel and Concrete Composite Bridge (GB 50917-2013); Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2013.
- CCCC Highway Construction. Specifications for Design and Construction of Highway Steel-Concrete Composite Bridge (JTG/T D64-01); CCCC Highway Construction Co., Ltd.: Beijing, China, 2015. [Google Scholar]
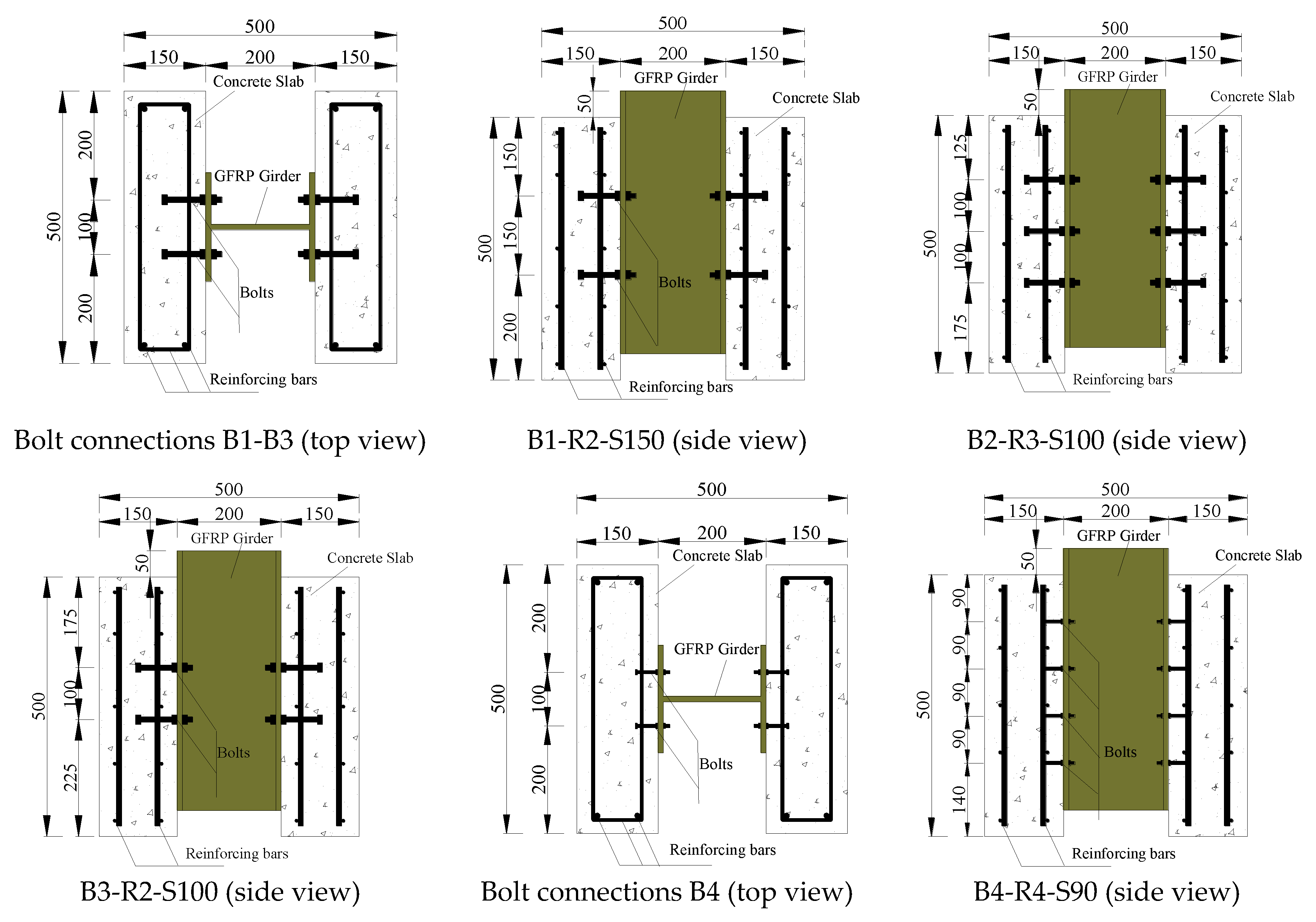





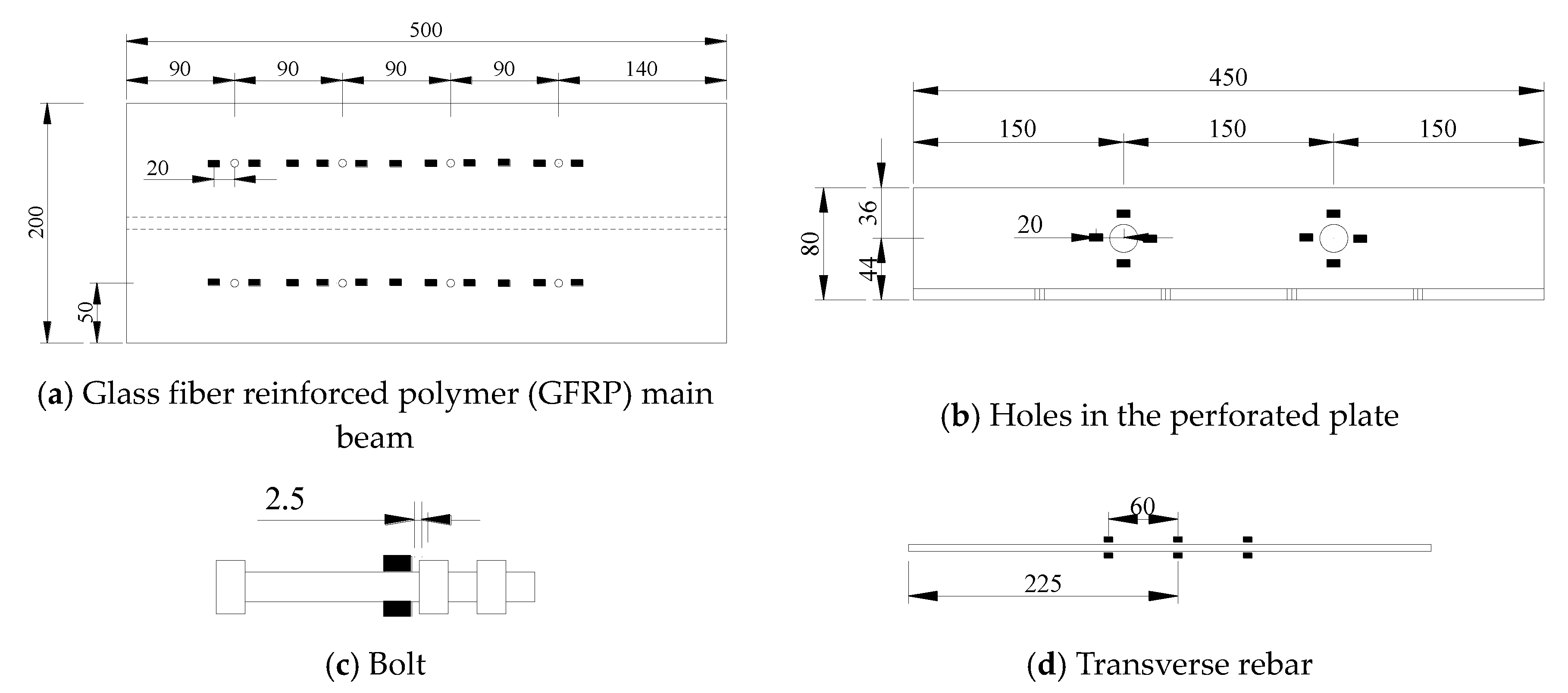





| Specimen | Connection Type | Bolt Diameter (mm) | Connection Bolts Diameter (mm) | Bolt Grade | Predrilled In The Perforated Plate | Connection Spacing | Parameter |
|---|---|---|---|---|---|---|---|
| B1-R2-S150 | Bolt | 10 | / | 8.8 | / | 2@150 mm | Spacing |
| B2-R3-S100 | 10 | 8.8 | 3@100 mm | Row | |||
| B3-R2-S100 | 10 | 8.8 | 2@100 mm | - | |||
| B4-R4-S90 | 6 | 12.9 | 4@90 mm | Bolt grade | |||
| P1-R2-S150 | T-type perforated plate | / | 6 | 12.9 | 20 | 2@150 mm | Spacing |
| P2-R3-S100 | 3@100 mm | Row | |||||
| P3-R2-S100-NR | 2@100 mm | Transverse rebar | |||||
| P4-R2-S100 | 2@100 mm | - | |||||
| G1-R3-S100 | Slot-type perforated plate | / | 6 | 12.9 | 20 | 3@100 mm | Row |
| G2-R2-S150 | 2@150 mm | Spacing | |||||
| G3-R2-S100 | 2@100 mm | - |
| Specimen Name | Connection Type | Ultimate Shear Capacity of a Single Connection (kN) |
|---|---|---|
| B1-R2-S150 | Bolt | 37 |
| B2-R3-S100 | 36 | |
| B3-R2-S100 | 37 | |
| B4-R4-S90 | 15 | |
| P1-R2-S150 | T-type perforated plate | 70 |
| P2-R3-S100 | 58 | |
| P3-R2-S100-NR | 44 | |
| P4-R2-S100 | 63 | |
| G1-R3-S100 | Slot-type perforated plate | 82 |
| G2-R2-S150 | 115 | |
| G3-R2-S100 | 101 |
| Specimen Name | D | ||||||
|---|---|---|---|---|---|---|---|
| B1-R2-S150 | 297.1 | 6.2 | 1.8 | 0.76 | 3.4 | 1155 | 130..3 |
| B2-R3-S100 | 435.4 | 5.2 | 1.8 | 0.39 | 2.9 | 169.3 | 372.1 |
| B3-R2-S100 | 292.9 | 6.2 | 2.2 | 0.85 | 2.8 | 93.2 | 114.9 |
| B4-R4-S90 | 232.1 | 2.7 | 1.7 | 0.95 | 1.6 | 95.6 | 81.4 |
| P1-R2-S150 | 278.9 | 18.5 | 0.6 | 0.21 | 30.8 | 325.4 | 442.7 |
| P2-R3-S100 | 346.7 | 22.0 | 0.7 | 0.16 | 31.4 | 346.7 | 722.3 |
| P3-R2-S100-NR | 174.6 | 0.9 | 0.2 | 0.06 | 4.5 | 611.1 | 825.5 |
| P4-R2-S100 | 253.3 | 14.8 | 0.5 | 0.14 | 29.6 | 354.9 | 603.1 |
| G1-R3-S100 | 491.5 | 18.6 | 0.8 | 0.30 | 23.3 | 430.1 | 546.1 |
| G2-R2-S150 | 459.3 | 16.7 | 1.1 | 0.34 | 15.2 | 292.3 | 450.30 |
| G3-R2-S100 | 409.7 | 16.1 | 0.9 | 0.33 | 17.9 | 315.3 | 413.8 |
| Specimen Source | Specimen Name | Bolt Grade | (MPa) | (mm) | (kN) | ||
|---|---|---|---|---|---|---|---|
| Present study | B1-R2-S150 | 8 | 8.8 | 800 | 10 | 297 | 0.59 |
| B2-R3-S100 | 12 | 8.8 | 800 | 10 | 435 | 0.58 | |
| B3-R2-S100 | 8 | 8.8 | 800 | 10 | 292 | 0.58 | |
| B4-R4-S90 | 16 | 12.9 | 1200 | 10 | 232 | 0.43 | |
| Nguyen [26] | H-16C1-50-35 | 4 | / | 520 | 16 | 389 | 0.93 |
| H-16C1-E-50-35 | 4 | / | 520 | 16 | 459 | 1.10 | |
| H-16C2-E-50-35 | 4 | / | 520 | 16 | 454 | 1.08 | |
| H-16C1-E-35-30 | 4 | / | 520 | 16 | 443 | 1.06 | |
| H-16C1-E-35-20 | 4 | / | 520 | 16 | 385 | 0.92 | |
| G-16C2-E-35-30 | 4 | / | 520 | 16 | 412 | 0.98 | |
| H-10C1-100-50 | 4 | / | 520 | 10 | 125 | 0.76 | |
| Correia [27] | SCS1 | 4 | / | 800 | 8 | 68 | 0.42 |
| SCS2 | 4 | / | 800 | 10 | 157 | 0.63 | |
| Zou [17] | OSB-NC1 | 8 | M4.8 | 400 | 12 | 225 | 0.62 |
| OSB-NC2 | 12 | M4.8 | 400 | 12 | 347 | 0.64 | |
| HSB-NC3 | 8 | M6.8 | 600 | 12 | 325 | 0.60 | |
| HSB-UHPC3 | 4 | M6.8 | 400 | 12 | 355 | 0.65 |
| Standard | Specimen Name | ||||
|---|---|---|---|---|---|
| GB 50917-2013 [28] | P1-R2-S150 | 274 | 68.5 | 39.1 | 1.75 |
| P2-R3-S100 | 347 | 57.8 | 39.1 | 1.48 | |
| P4-R2-S100 | 250 | 62.5 | 39.1 | 1.60 | |
| G1-R3-S100 | 491.5 | 82 | 78.2 | 1.05 | |
| G2-R2-S150 | 459.3 | 114.8 | 78.2 | 1.47 | |
| G3-R2-S100 | 409.7 | 102.4 | 78.2 | 1.31 | |
| JTG/TD64-01 [29] | P1-R2-S150 | 274 | 68.5 | 56.7 | 1.21 |
| P2-R3-S100 | 347 | 57.8 | 56.7 | 1.02 | |
| P4-R2-S100 | 250 | 62.5 | 56.7 | 1.10 | |
| G1-R3-S100 | 491.5 | 82 | 113.4 | 0.72 | |
| G2-R2-S150 | 459.3 | 114.8 | 113.4 | 1.01 | |
| G3-R2-S100 | 409.7 | 102.4 | 113.4 | 0.90 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, J.; Cao, L.; Han, J. Experimental Study on the Shear Behavior of GFRP–Concrete Composite Beam Connections. Materials 2020, 13, 1067. https://doi.org/10.3390/ma13051067
Di J, Cao L, Han J. Experimental Study on the Shear Behavior of GFRP–Concrete Composite Beam Connections. Materials. 2020; 13(5):1067. https://doi.org/10.3390/ma13051067
Chicago/Turabian StyleDi, Jin, Lu Cao, and Jiahao Han. 2020. "Experimental Study on the Shear Behavior of GFRP–Concrete Composite Beam Connections" Materials 13, no. 5: 1067. https://doi.org/10.3390/ma13051067




