Mechanism of Continuous Melting and Secondary Contact Melting in Resistance Heating Metal Wire Additive Manufacturing
Abstract
:1. Introduction
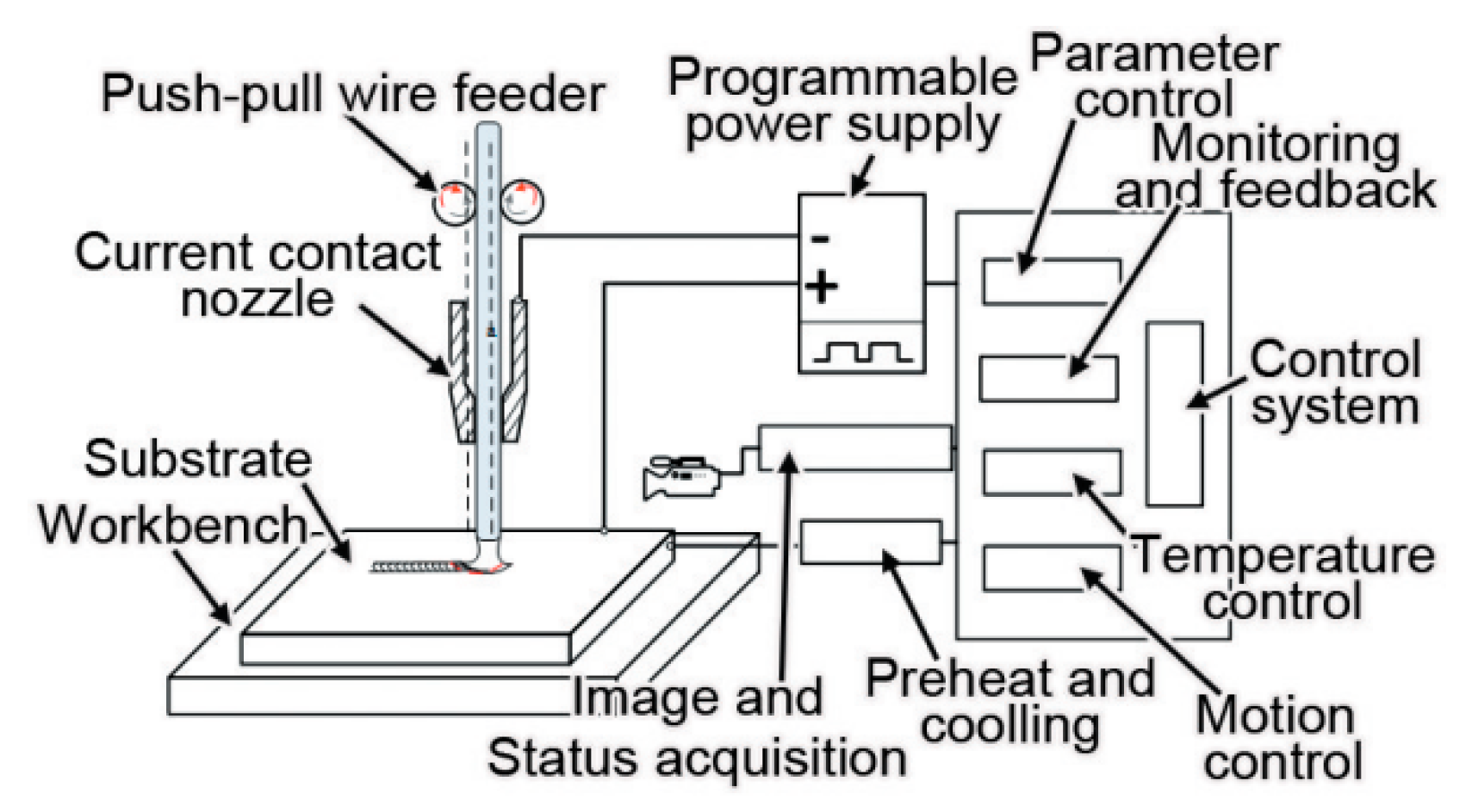
2. Resistance Heating Wire Additive Manufacturing Principle
3. Materials and Experimental Procedure
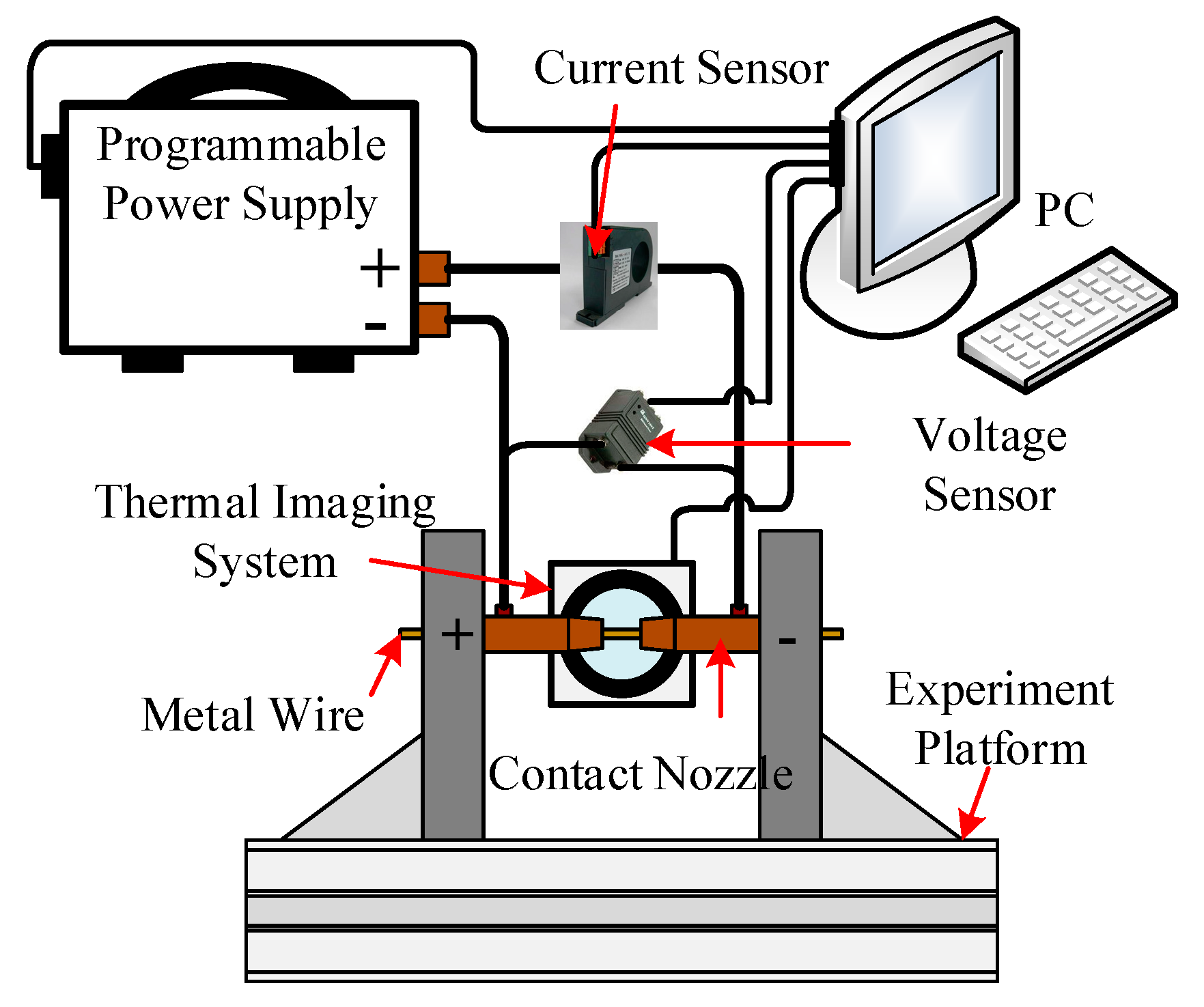
3.1. Experimental System
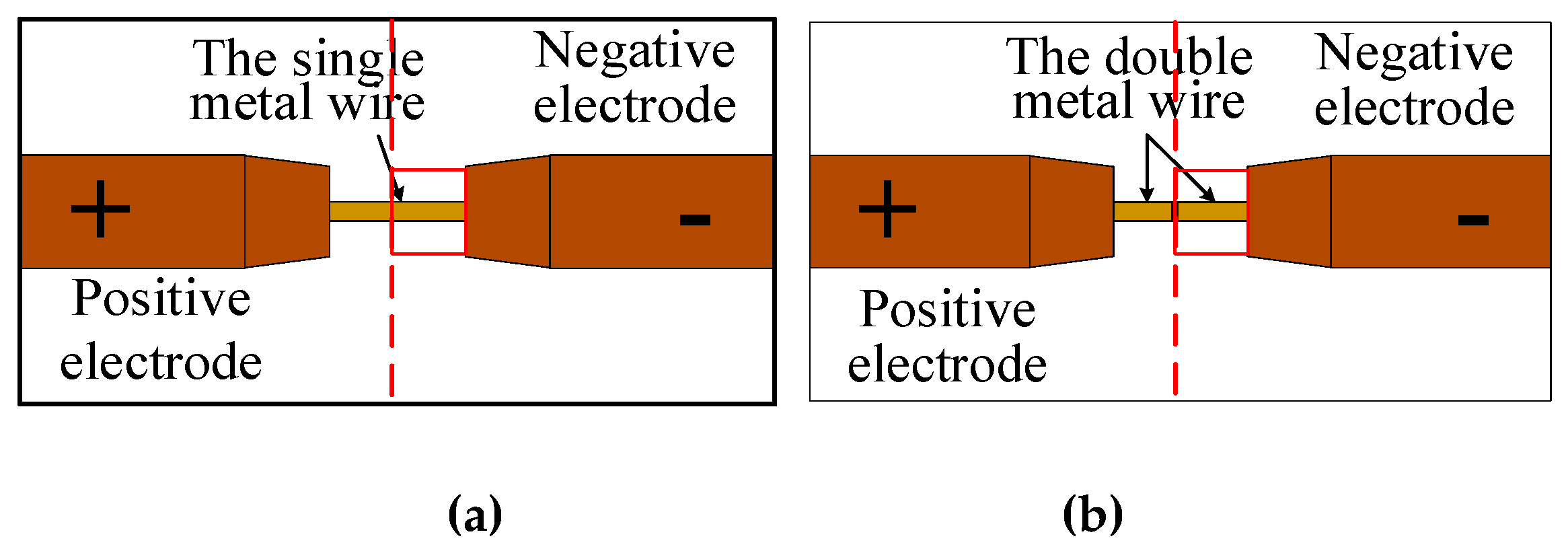
3.2. Experimental Principle
3.3. Materials and Experimental Method
4. Results and Discussion
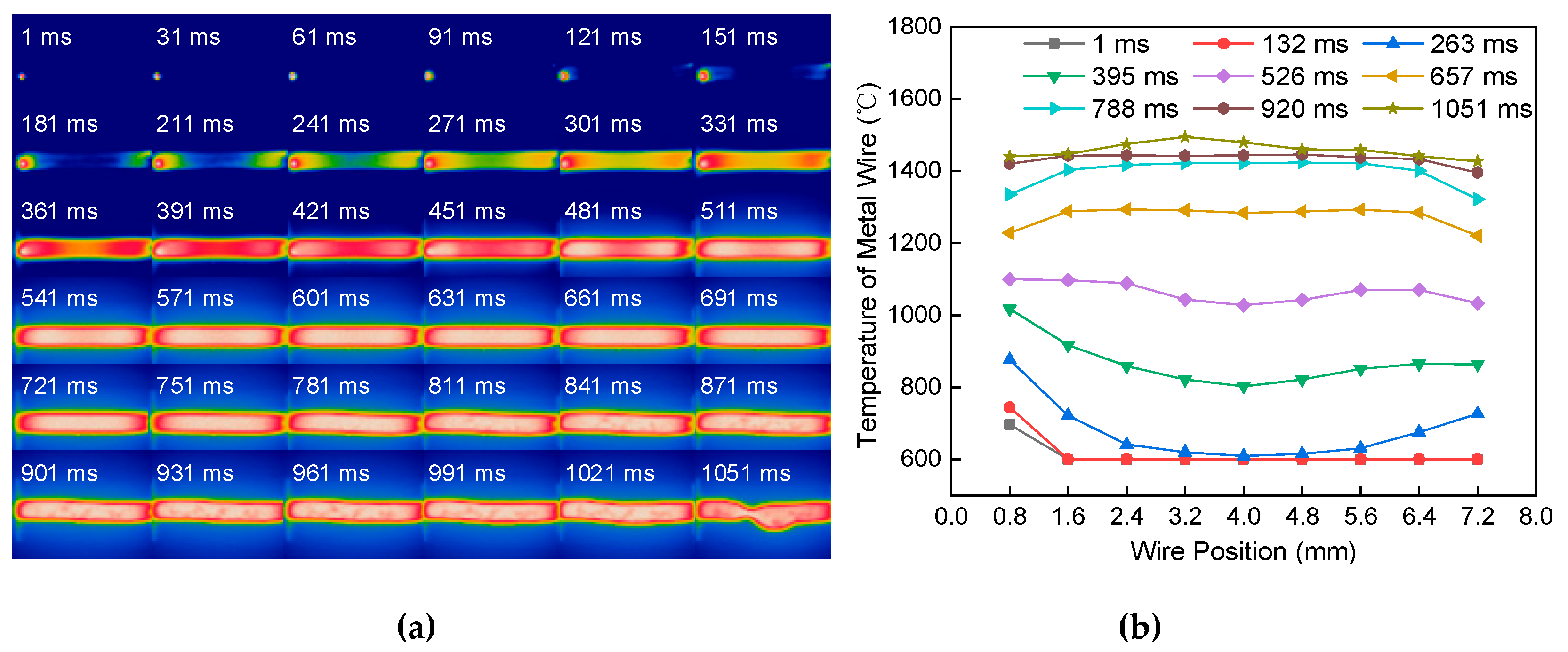
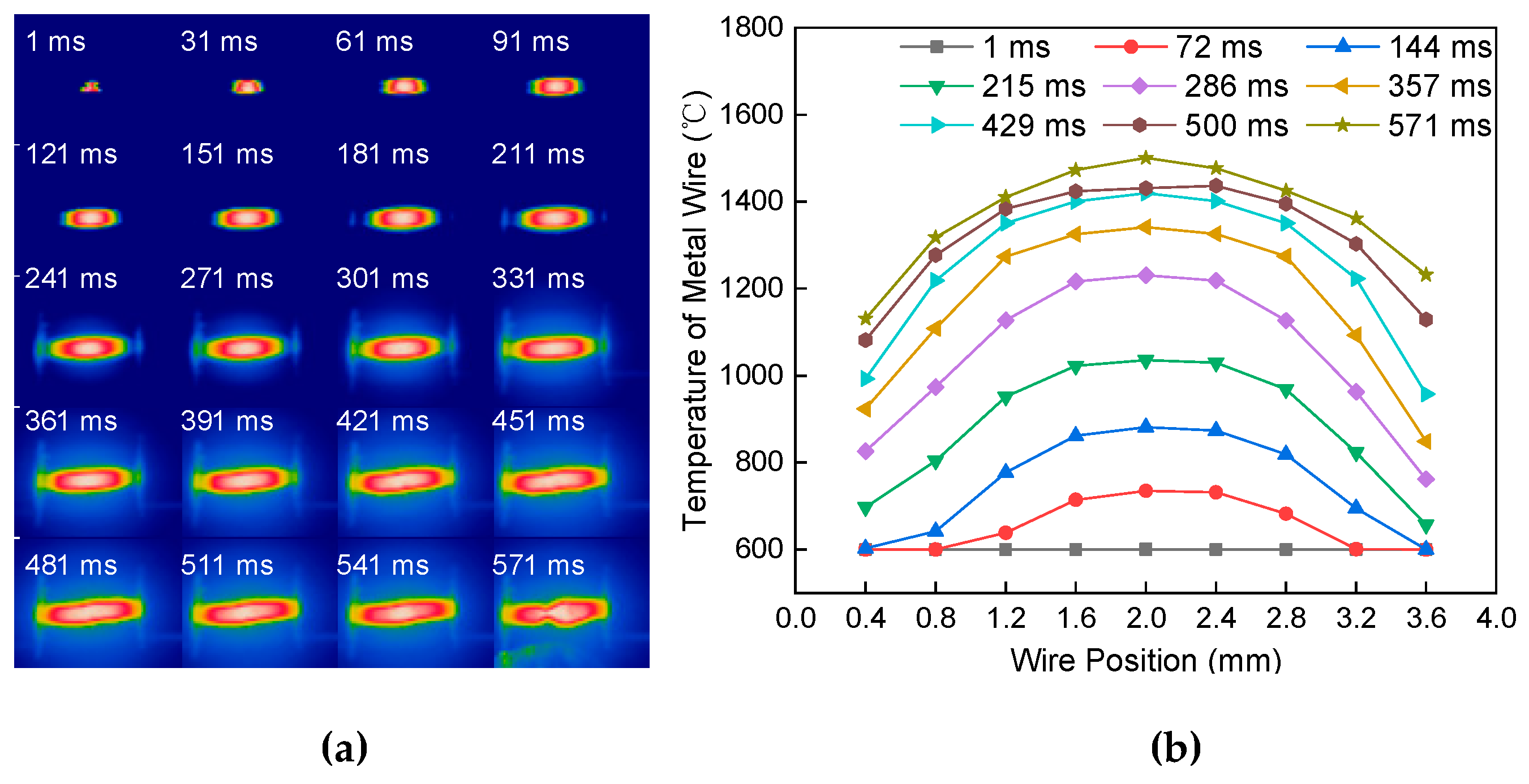
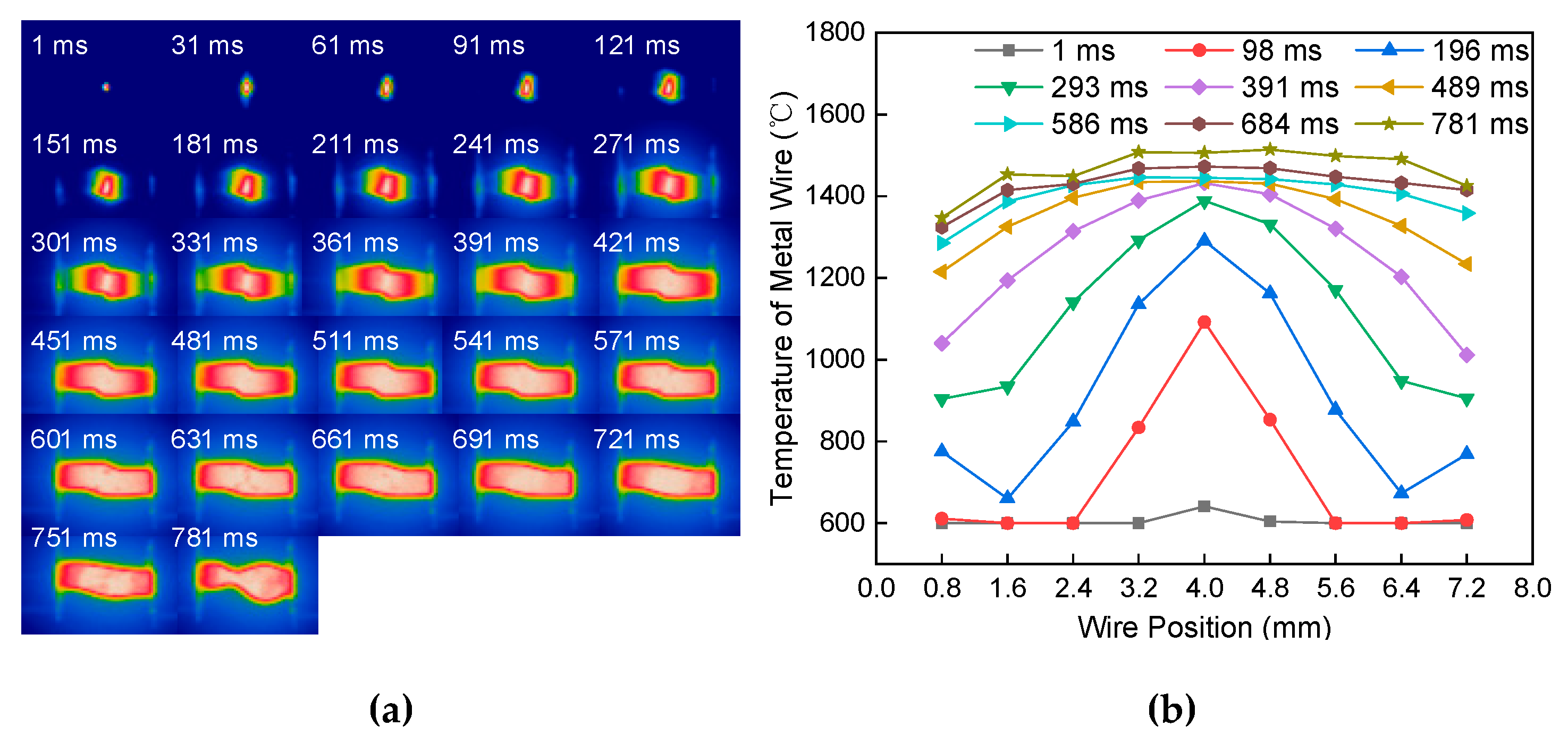
4.1. Temperature Field Distribution of Metal Wire
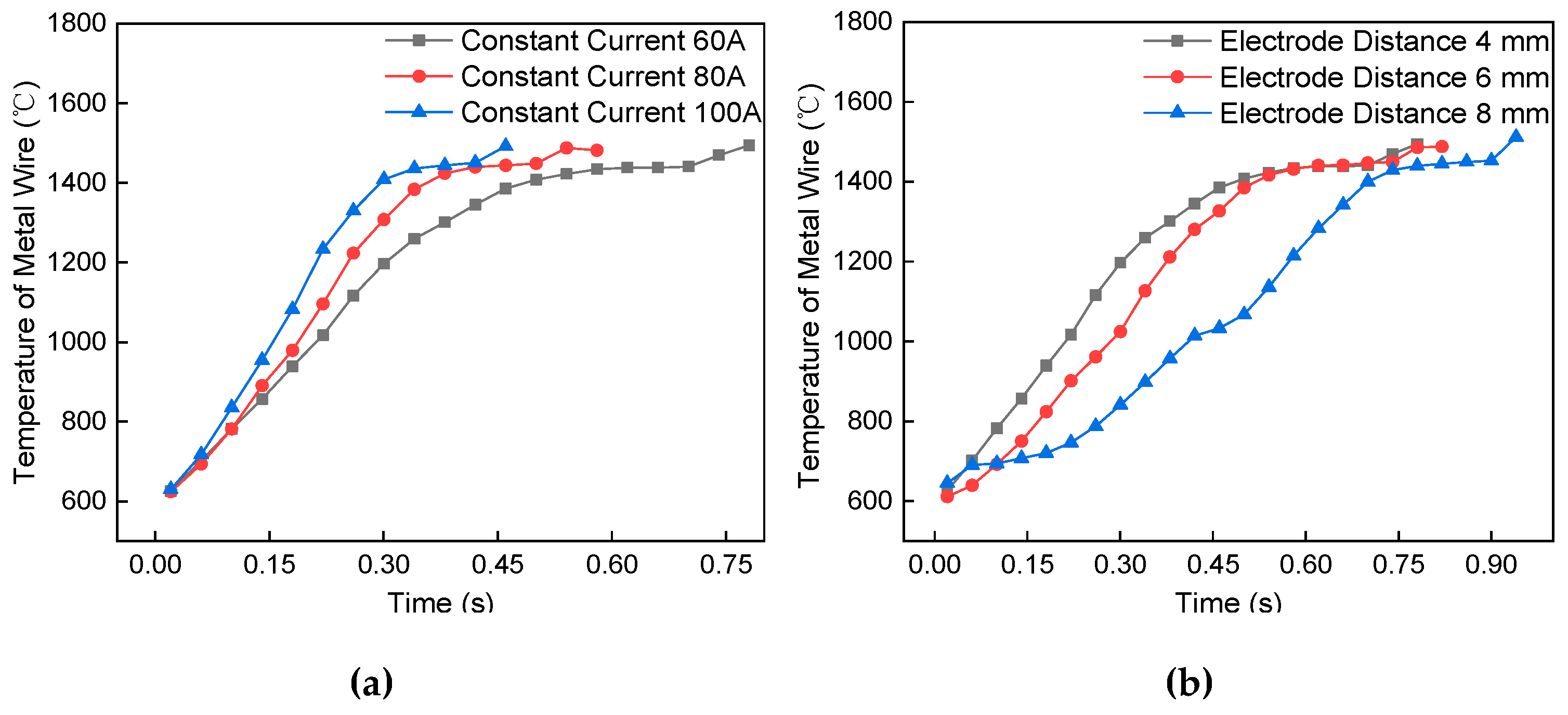
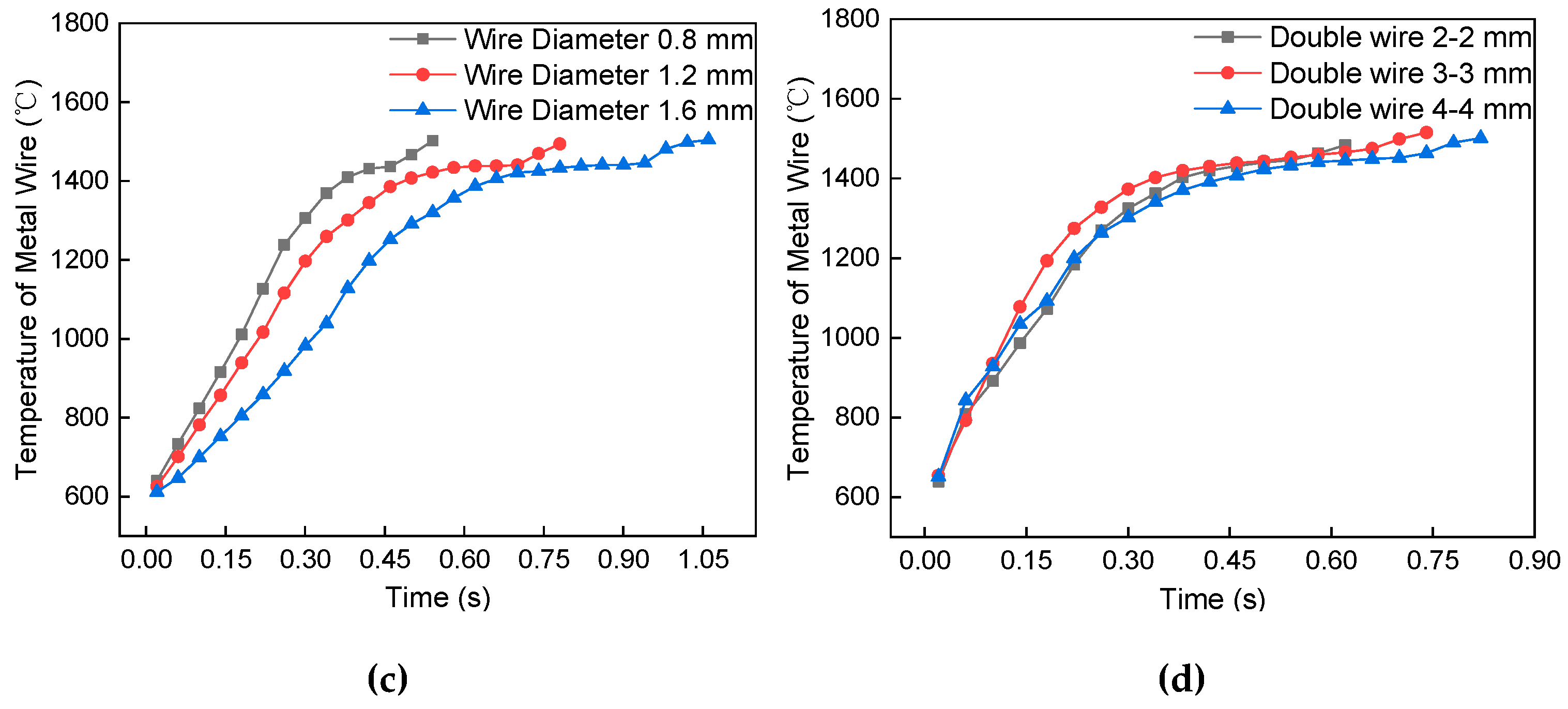
4.2. Factors Affecting Wire Temperature
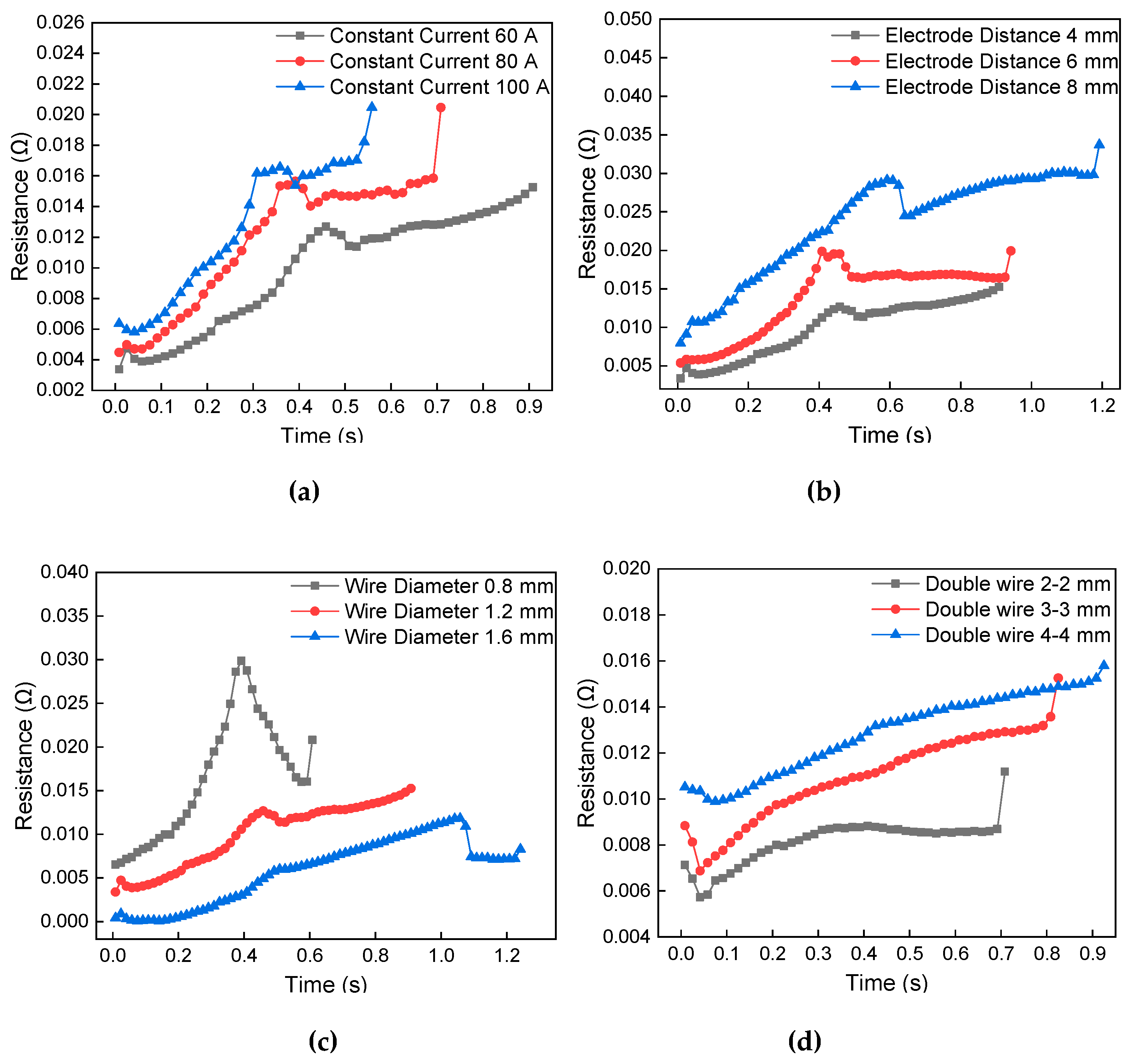
4.3. Evolution of Electric Resistance
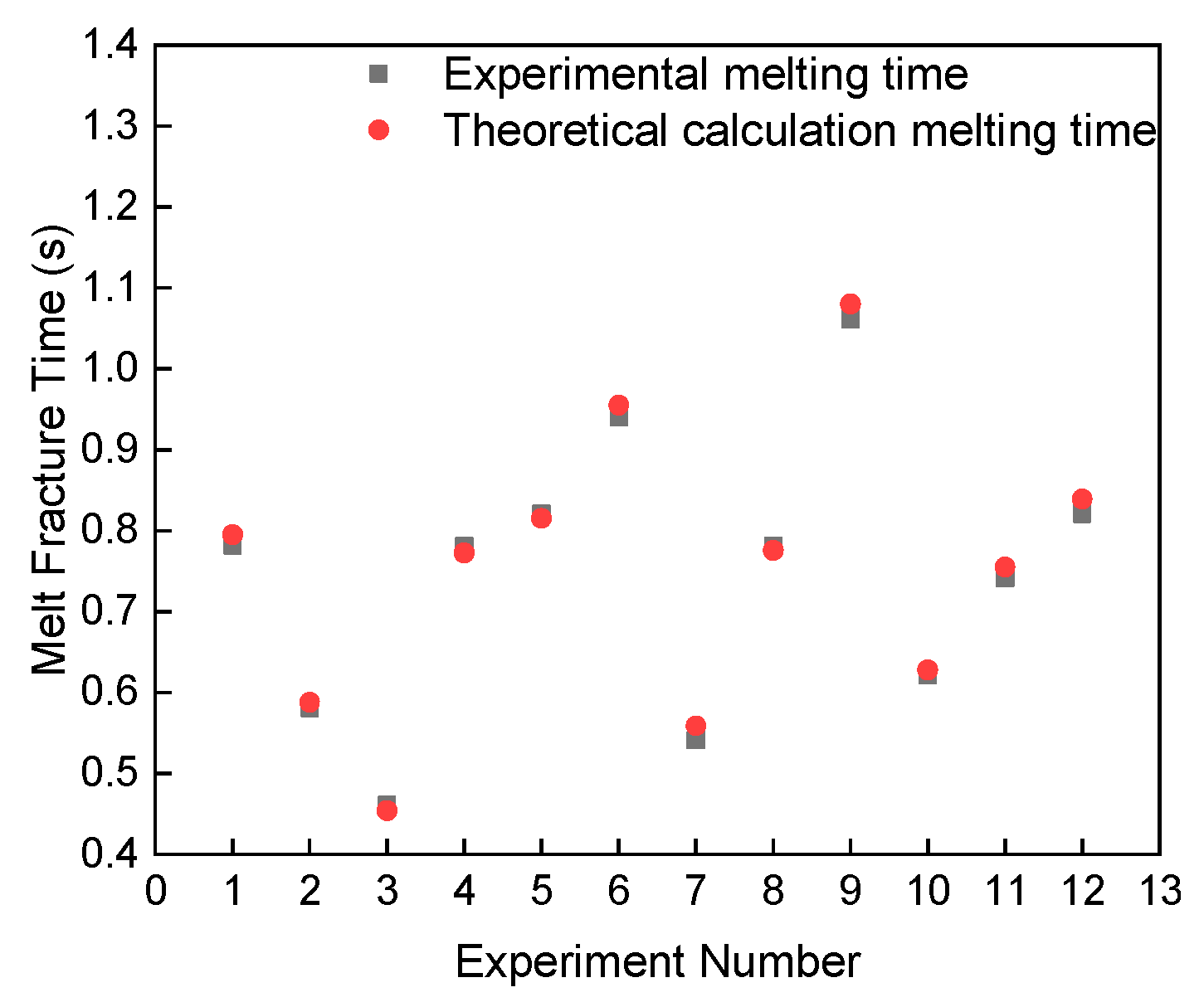
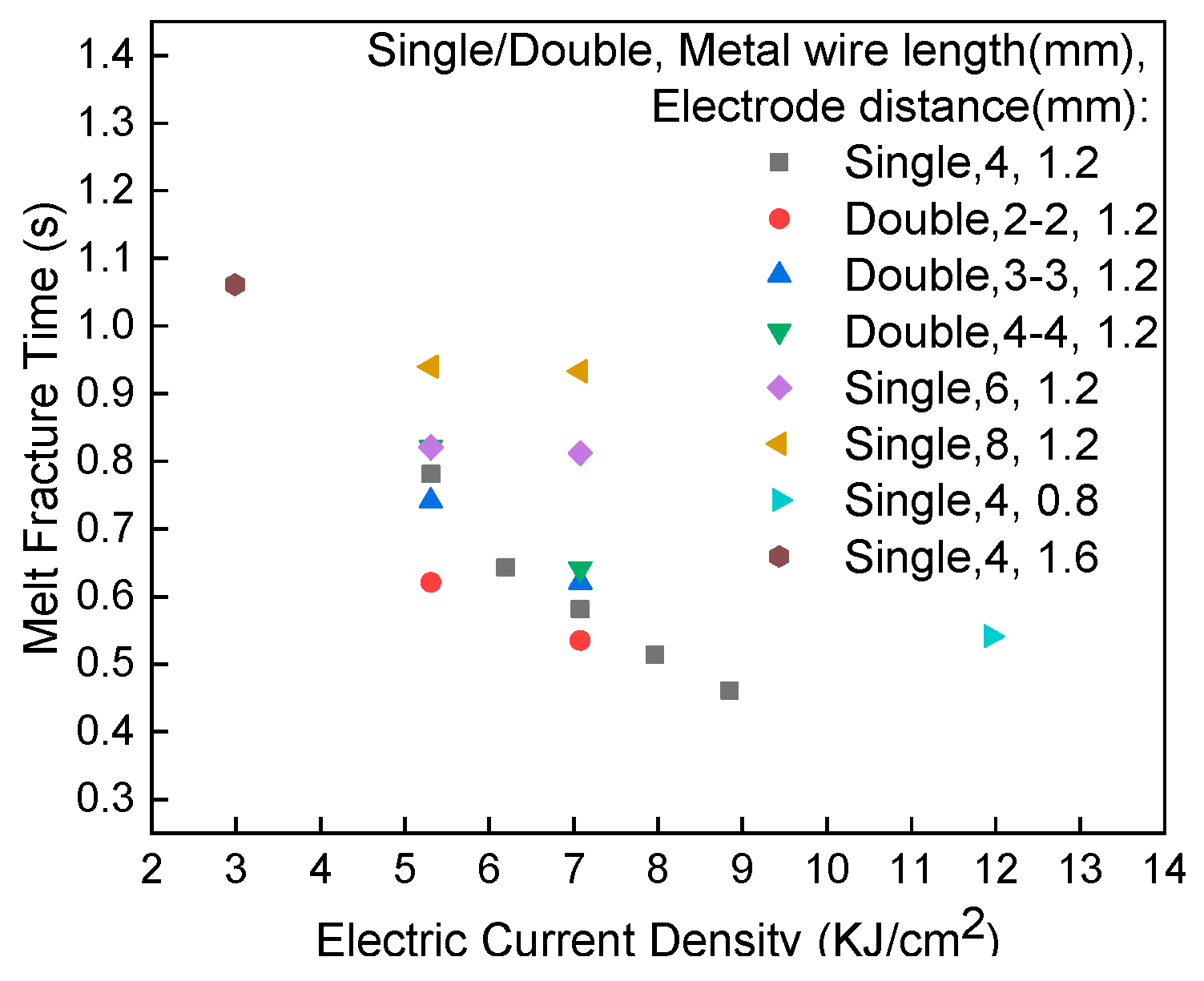
4.4. Melt Fracture Time
4.5. Distinct Region of the Melted Wire
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fateri, M.; Kaouk, A.; Cowley, A.; Siarov, S.; Palou, M.V.; González, F.G.; Marchant, R.; Cristoforetti, S.; Sperl, M. Feasibility study on additive manufacturing of recyclable objects for space applications. Addit. Manuf. 2018, 24, 400–404. [Google Scholar] [CrossRef]
- Evans, W.T.; Neely, K.E.; Strauss, A.M.; Cook, G.E. Weldability of an iron meteorite by friction stir spot welding: A contribution to in-space manufacturing. Acta Astronaut. 2017, 140, 452–458. [Google Scholar] [CrossRef]
- Ceruti, A.; Marzocca, P.; Liverani, A.; Bil, C. Maintenance in Aeronautics in an Industry 4.0 Context: The Role of Augmented Reality and Additive Manufacturing. J. Comput. Des. Eng. 2019, 6, 516–526. [Google Scholar] [CrossRef]
- Pereira, T.; Kennedy, J.V.; Potgieter, J.A. comparison of traditional manufacturing vs additive manufacturing, the best method for the job. Procedia Manuf. 2019, 30, 11–18. [Google Scholar] [CrossRef]
- Al-Meslemi, Y.; Anwer, N.; Mathieu, L. Environmental Performance and Key Characteristics in Additive Manufacturing: A Literature Review. Procedia CIRP 2018, 69, 148–153. [Google Scholar] [CrossRef]
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar] [CrossRef]
- Mawale, M.B.; Kuthe, A.M.; Dahake, S.W. Additive layered manufacturing: State-of-the-art applications in product innovation. Concurr. Eng. 2016, 24, 94–102. [Google Scholar] [CrossRef]
- Williams, H.; Butler-Jones, E. Additive Manufacturing Standards for Space Resource Utilization. Addit. Manuf. 2019, 28, 676–681. [Google Scholar] [CrossRef]
- Goulas, A.; Binner, J.G.P.; Harris, R.A.; Friel, R.J. Assessing extraterrestrial regolith material simulants for in-situ resource utilisation based 3D printing. Appl. Mater. Today 2017, 6, 54–61. [Google Scholar] [CrossRef]
- Pinkerton, A.J. Lasers in additive manufacturing. Opt. Laser Technol. 2016, 78, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Konyashin, I.; Hinners, H.; Ries, B.; Kirchner, A.; Klöden, B.; Kieback, B.; Nilen, R.W.N.; Sidorenko, D. Additive manufacturing of WC-13% Co by selective electron beam melting: Achievements and challenges. Int. J. Refract. Met. Hard Mater. 2019, 84, 105028. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, M.; Chen, C.; Zeng, X. Spectral diagnosis of wire arc additive manufacturing of Al alloys. Addit. Manuf. 2019, 30, 100869. [Google Scholar] [CrossRef]
- Li, M.; Lu, T.; Dai, J.; Jia, X.; Gu, X.; Dai, T. Microstructure and mechanical properties of 308L stainless steel fabricated by laminar plasma additive manufacturing. Mater. Sci. Eng. A 2020, 770, 138523. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, C.; Jiang, F.; Yan, Z.; Zhang, P. Study on Heat Generation Mechanism and Melting Behavior of Droplet Transition in Resistive Heating Metal Wires. Acta Metall Sin 2018, 54, 1297–1310. [Google Scholar]
- Lu, S.; Li, J.; Cheng, M.; Li, Q.; Li, F.; Lv, Z.; Zhang, Y.; Lu, C.; Li, S. Joule heating-A significant factor in electrocaloric effect. Ceram. Int. 2019, 45, 16992–16998. [Google Scholar] [CrossRef]
- Jung, H.W.; Kim, S.J.; Kim, Y.J.; Kim, J.Y.; Lee, J.Y.; Park, J.H. Finite element analysis of vertical micro-probe considering Joule-heating effect. Int. J. Fatigue 2017, 101, 96–105. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Park, J.H.; Rashidi, M.M.; Chen, J.M. Effects of thermal boundary conditions on the joule heating of electrolyte in a microchannel. J. Hydrodyn. 2016, 28, 850–862. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, H.; Luo, Z.; Li, Y.; Bi, J.; Guo, J.; Gao, F. Temperature field and microstructure characterization of AA6061/H70 dissimilar thermo-compensated resistance spot welds having different joint configurations. J. Manuf. Process. 2017, 28, 336–342. [Google Scholar] [CrossRef]
- Zhou, K.; Shi, T.; Cai, L. Online measuring the electrical resistivity of molten nugget of stainless steel in resistance spot welding. J. Manuf. Process. 2017, 28, 109–115. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Wan, R.; Yang, Z.; Xie, X. Study on the thermo-effect of nugget growing in single-phase AC resistance spot welding based on the calculation of dynamic resistance. Measurement 2016, 78, 18–28. [Google Scholar] [CrossRef]
- Wang, X.; Yu, J.; Zhao, R.; Zhu, B.; Gao, N.; Xiang, B.; Yu, Y.; Zhang, K.; Huang, Z.; Zu, F. Effects of melting time and temperature on the microstructure and thermoelectric properties of p-type Bi0. 3Sb1. 7Te3 alloy. J. Phys. Chem. Solids 2019, 124, 281–288. [Google Scholar] [CrossRef]
- Kołodziej, A.; Łojewska, J.; Jaroszyński, M.; Gancarczyk, A.; Jodłowski, P. Heat transfer and flow resistance for stacked wire gauzes: Experiments and modelling. Int. J. Heat Fluid Flow 2012, 33, 101–108. [Google Scholar] [CrossRef]
- Hayat, T.; Shah, F.; Alsaedi, A.; Ahmad, B. Entropy optimized dissipative flow of effective Prandtl number with melting heat transport and Joule heating. Int. Commun. Heat Mass Transf. 2020, 111, 104454. [Google Scholar] [CrossRef]
- Gies, S.; Tekkaya, A.E. Analytical prediction of Joule heat losses in electromagnetic forming coils. J. Mater. Process. Technol. 2017, 246, 102–115. [Google Scholar] [CrossRef]
- Chi, X.; Yu, B.; Jiang, X. Parameter estimation for the time fractional heat conduction model based on experimental heat flux data. Appl. Math. Lett. 2020, 102, 106094. [Google Scholar] [CrossRef]
- Venkatadri, K.; Bég, O.A.; Rajarajeswari, P.; Prasad, V.R. Numerical simulation of thermal radiation influence on natural convection in a trapezoidal enclosure: Heat flow visualization through energy flux vectors. Int. J. Mech. Sci. 2019, 171, 105391. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, M.; Yang, F. The effect of an electric current on the nanoindentation behavior of tin. Acta Mater. 2012, 60, 3773–3782. [Google Scholar] [CrossRef]







| Experimental Scheme | Current (A) | Current Waveform | Single/Double Metal Wire | Heating Length (mm) | Wire Diameter (mm) |
|---|---|---|---|---|---|
| 1-1 | 60 | Constant current | Single | 4.0 | 1.2 |
| 1-2 | 80 | Constant current | Single | 4.0 | 1.2 |
| 1-3 | 100 | Constant current | Single | 4.0 | 1.2 |
| 2-1 | 60 | Constant current | Single | 4.0 | 1.2 |
| 2-2 | 60 | Constant current | Single | 6.0 | 1.2 |
| 2-3 | 60 | Constant current | Single | 8.0 | 1.2 |
| 3-1 | 60 | Constant current | Single | 4.0 | 0.8 |
| 3-2 | 60 | Constant current | Single | 4.0 | 1.2 |
| 3-3 | 60 | Constant current | Single | 4.0 | 1.6 |
| 4-1 | 60 | Constant current | Double | 2.0 and 2.0 | 1.2 |
| 4-2 | 60 | Constant current | Double | 3.0 and 3.0 | 1.2 |
| 4-3 | 60 | Constant current | Double | 4.0 and 4.0 | 1.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, C.; Chen, S.; Jiang, F.; Xu, B.; Dong, S. Mechanism of Continuous Melting and Secondary Contact Melting in Resistance Heating Metal Wire Additive Manufacturing. Materials 2020, 13, 1069. https://doi.org/10.3390/ma13051069
Yuan C, Chen S, Jiang F, Xu B, Dong S. Mechanism of Continuous Melting and Secondary Contact Melting in Resistance Heating Metal Wire Additive Manufacturing. Materials. 2020; 13(5):1069. https://doi.org/10.3390/ma13051069
Chicago/Turabian StyleYuan, Chengwei, Shujun Chen, Fan Jiang, Bin Xu, and Shanwen Dong. 2020. "Mechanism of Continuous Melting and Secondary Contact Melting in Resistance Heating Metal Wire Additive Manufacturing" Materials 13, no. 5: 1069. https://doi.org/10.3390/ma13051069
APA StyleYuan, C., Chen, S., Jiang, F., Xu, B., & Dong, S. (2020). Mechanism of Continuous Melting and Secondary Contact Melting in Resistance Heating Metal Wire Additive Manufacturing. Materials, 13(5), 1069. https://doi.org/10.3390/ma13051069





