Modal Performance of Two-Fiber Orthogonal Gradient Composite Laminates Embedded with SMA
Abstract
:1. Introduction
2. Formulation
3. Results and Discussion
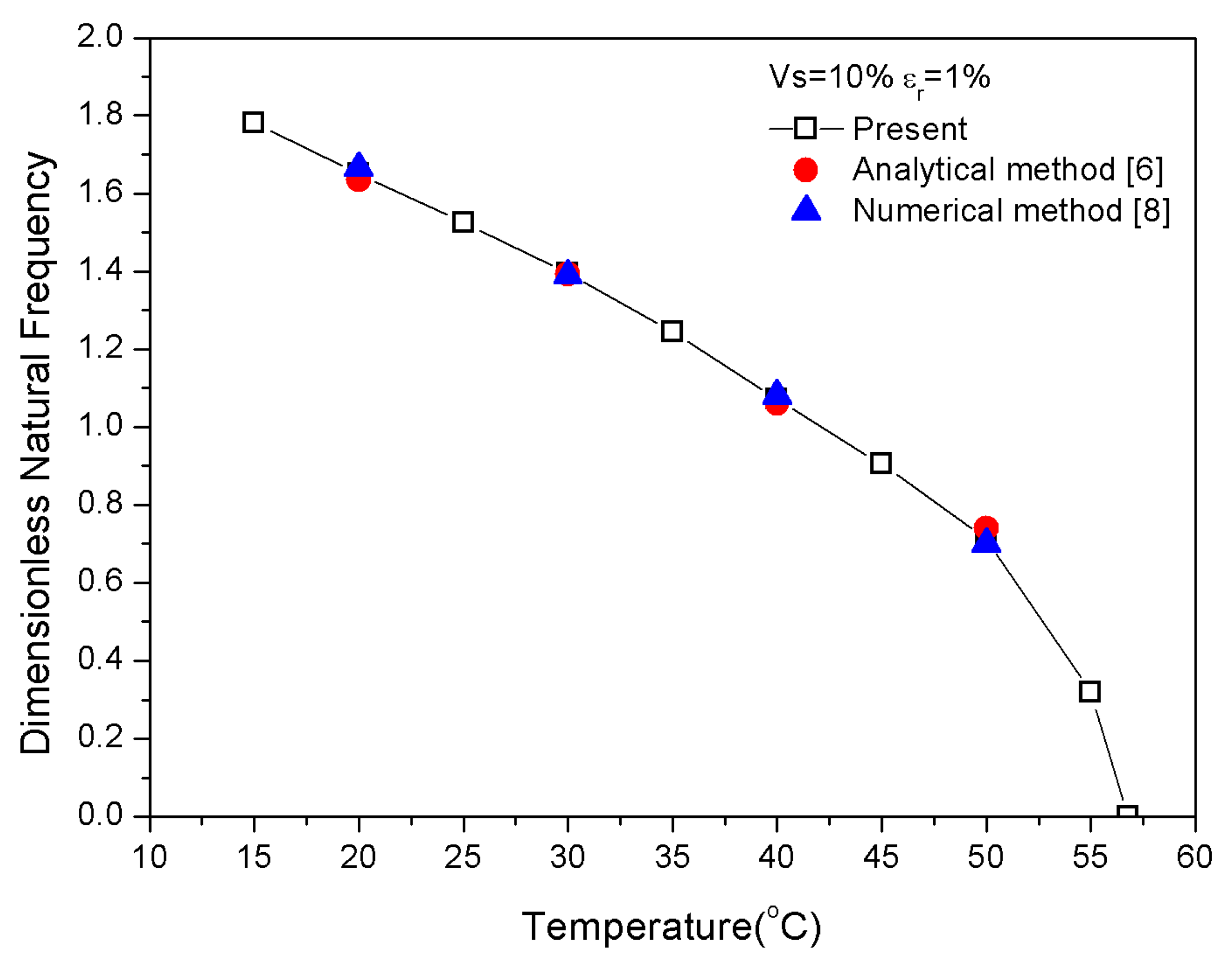
3.1. Materials and Verification
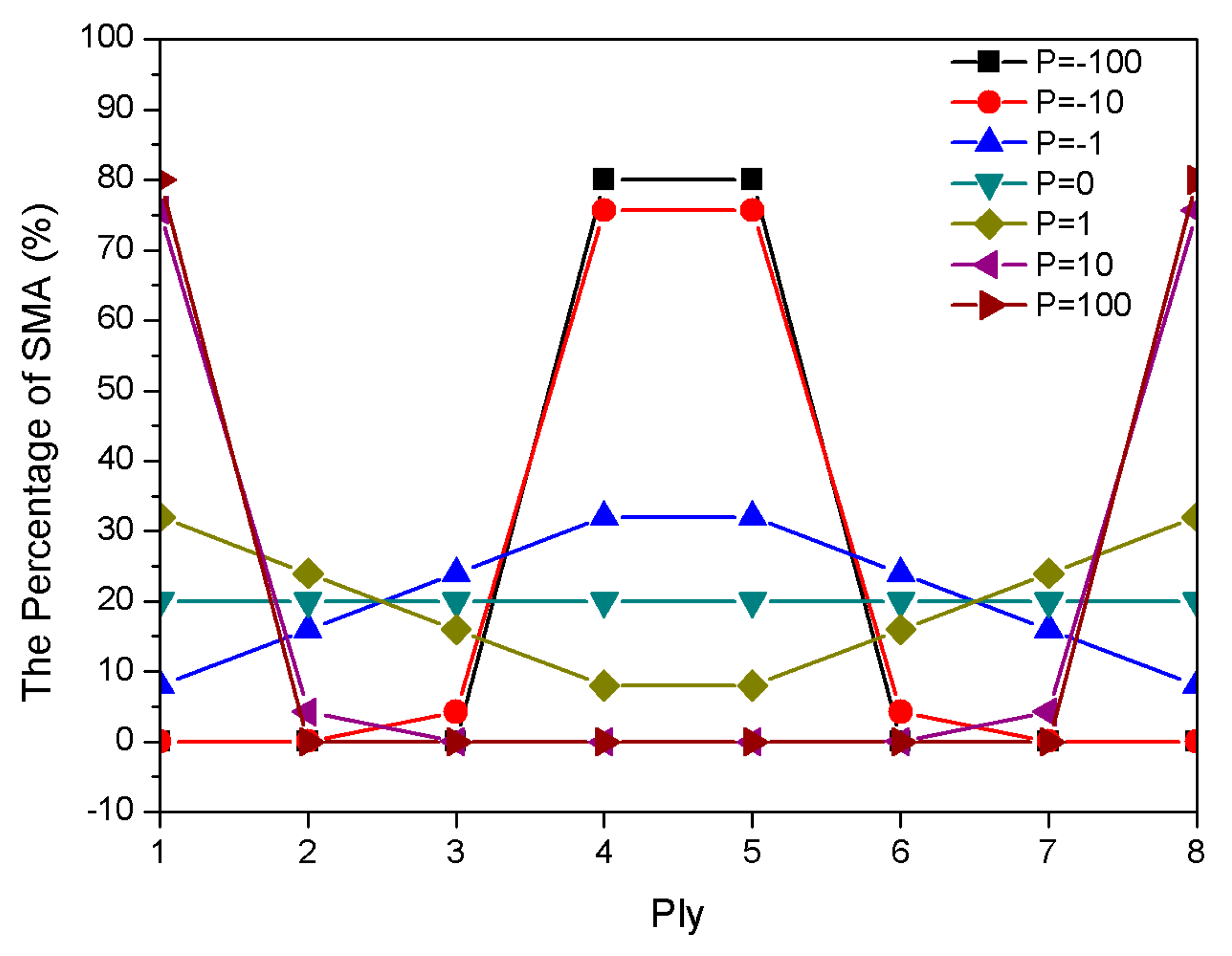
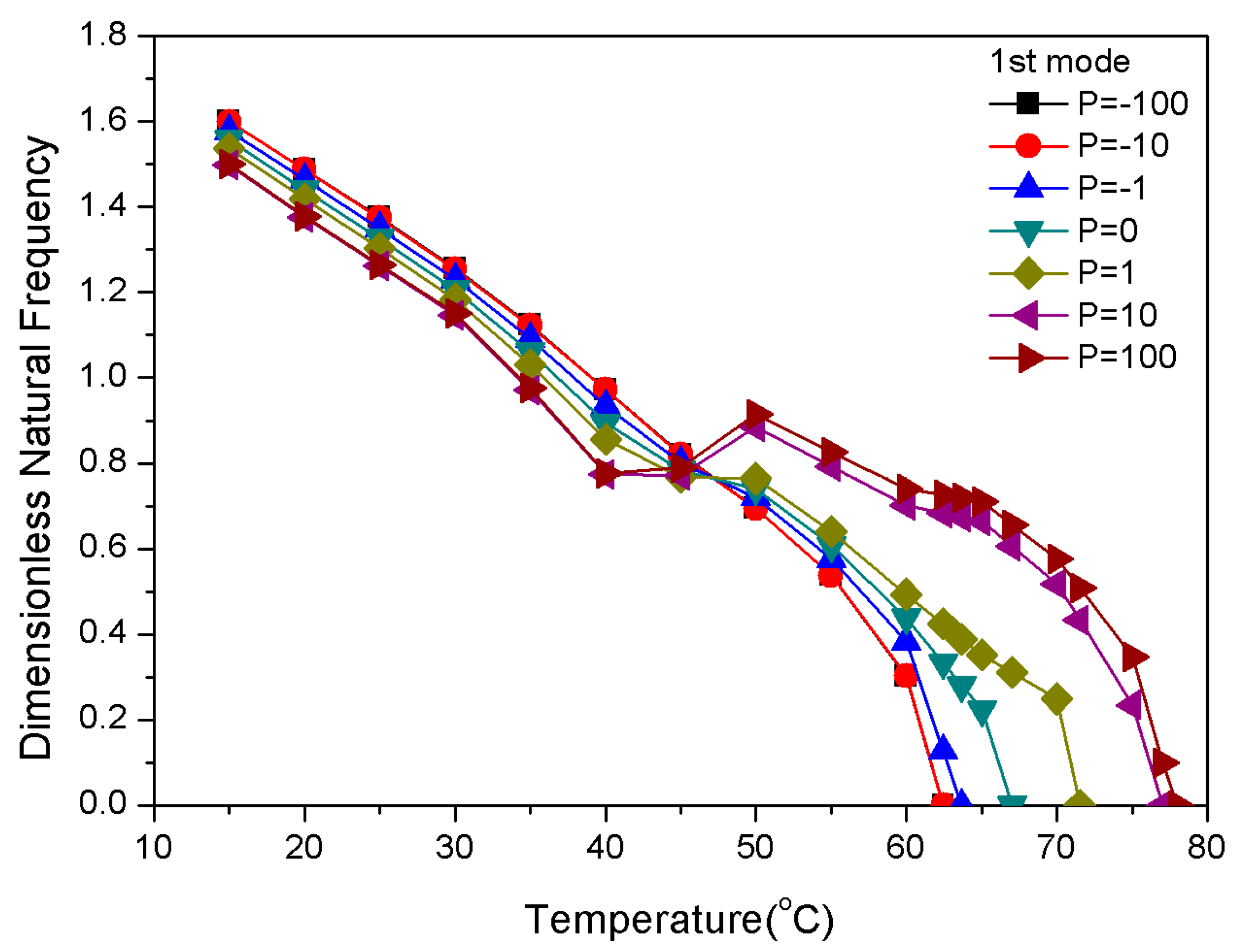
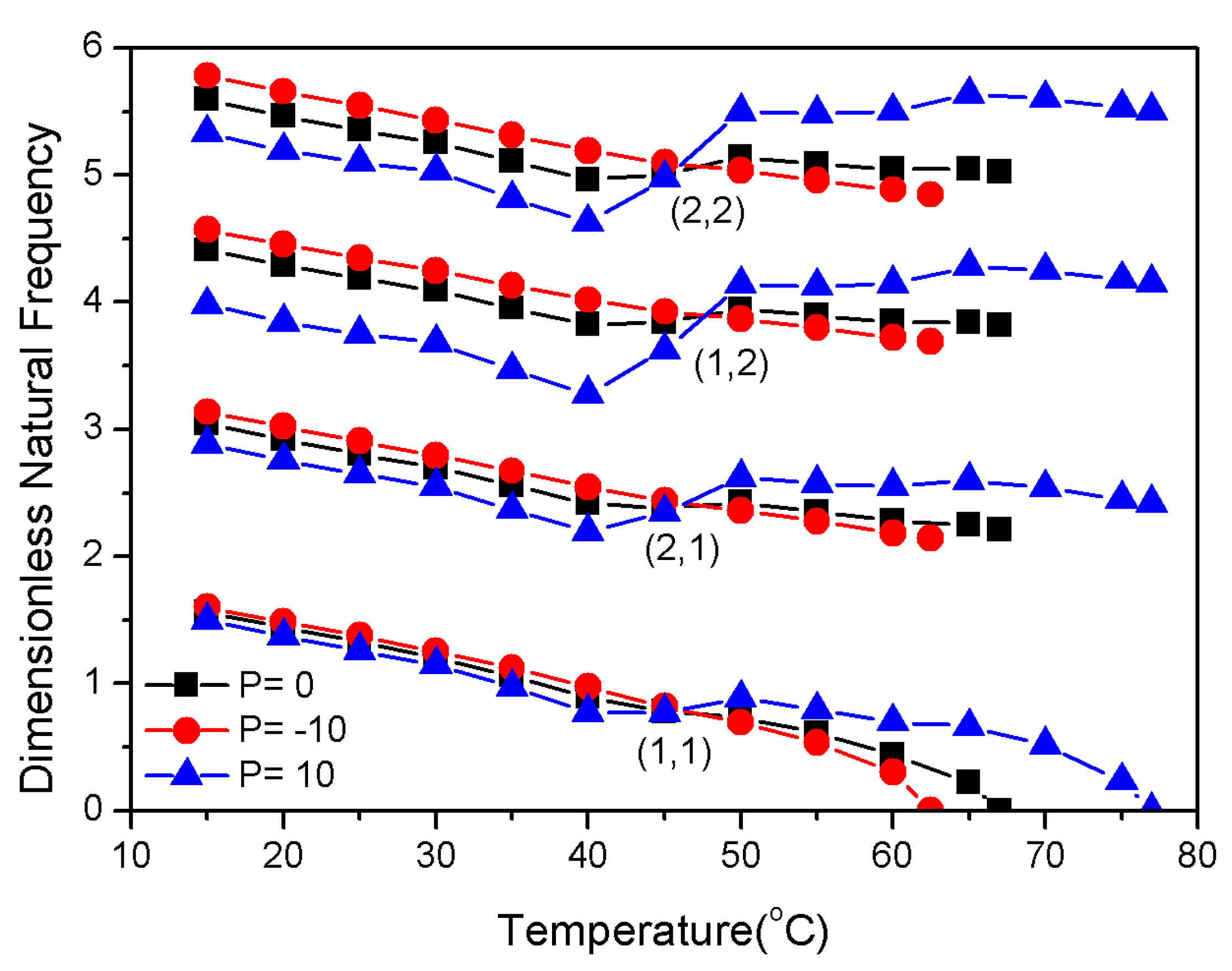
3.2. Influence of Physical Parameter P (Gradient Index) on Frequency
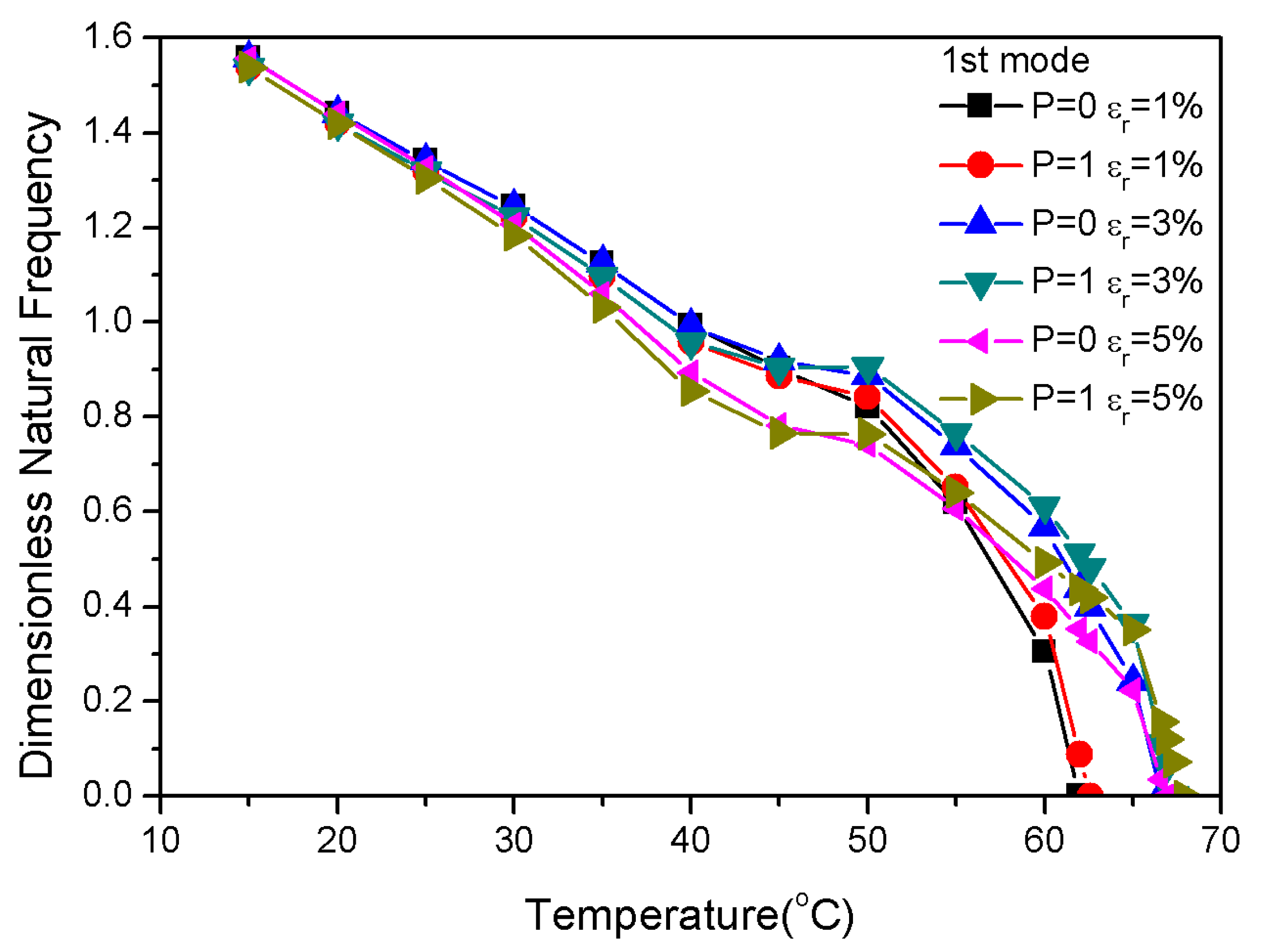
3.3. Influence of Pre-Strain Value on Frequency
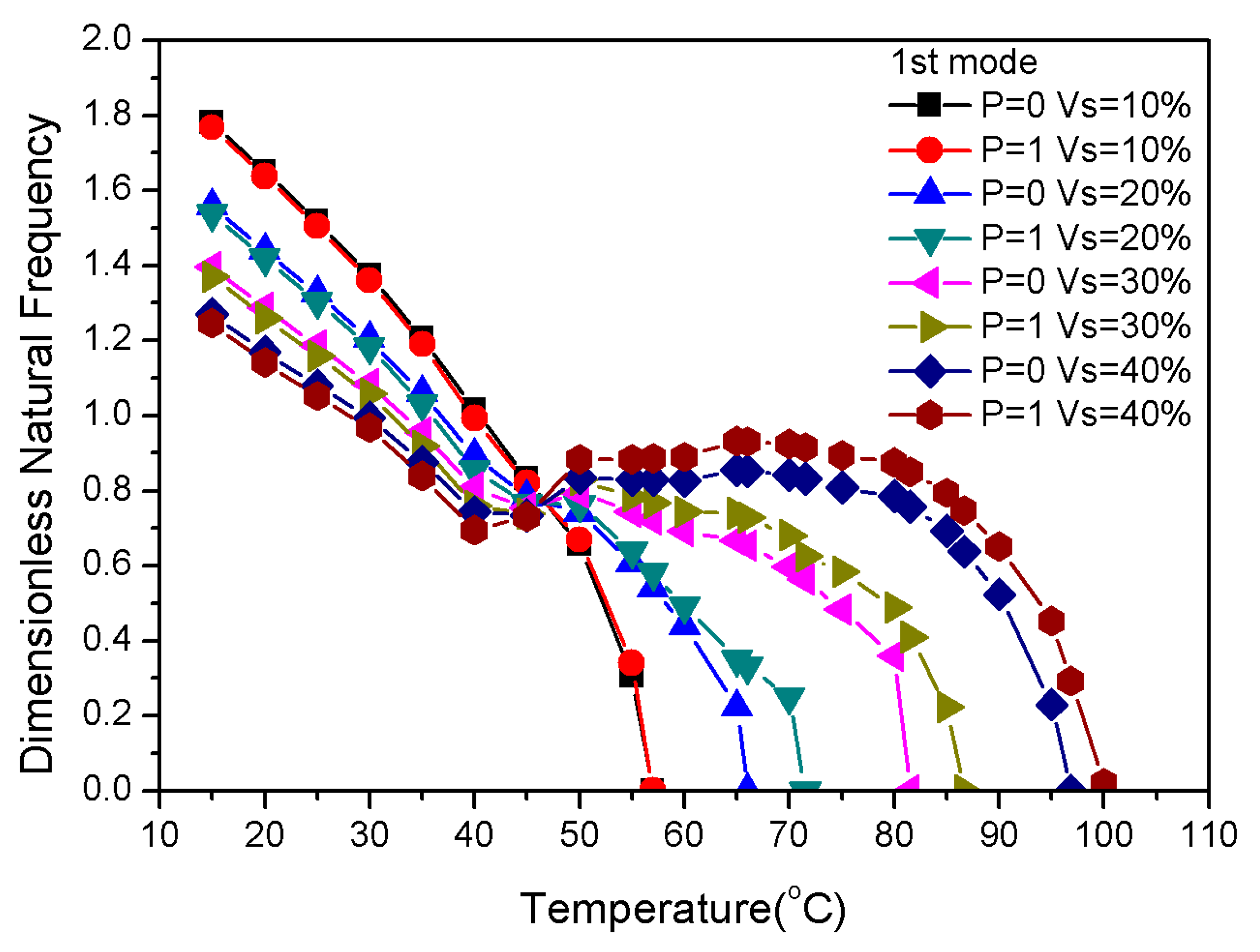
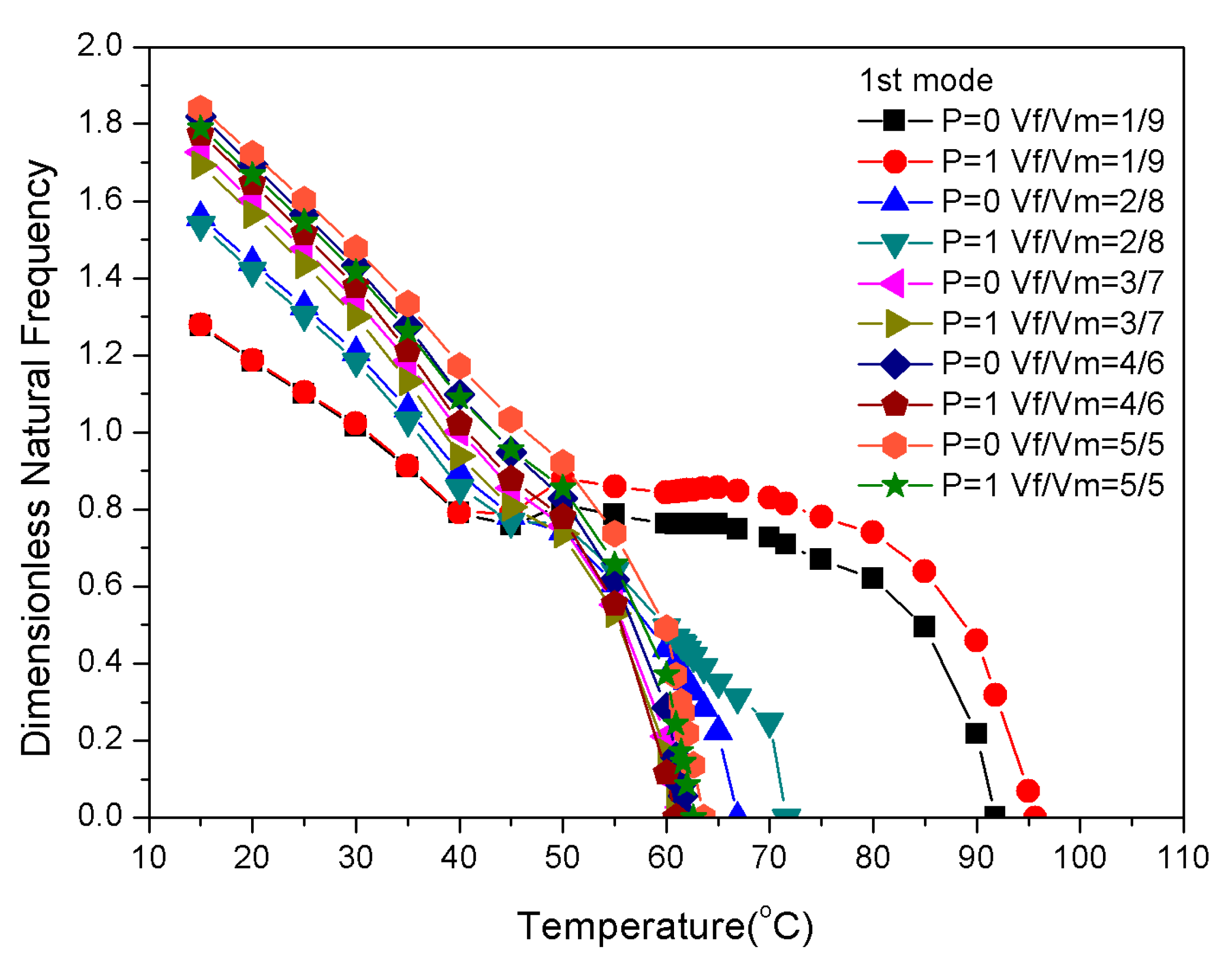
3.4. Influence of Component Volume Fraction of Materials on Frequency
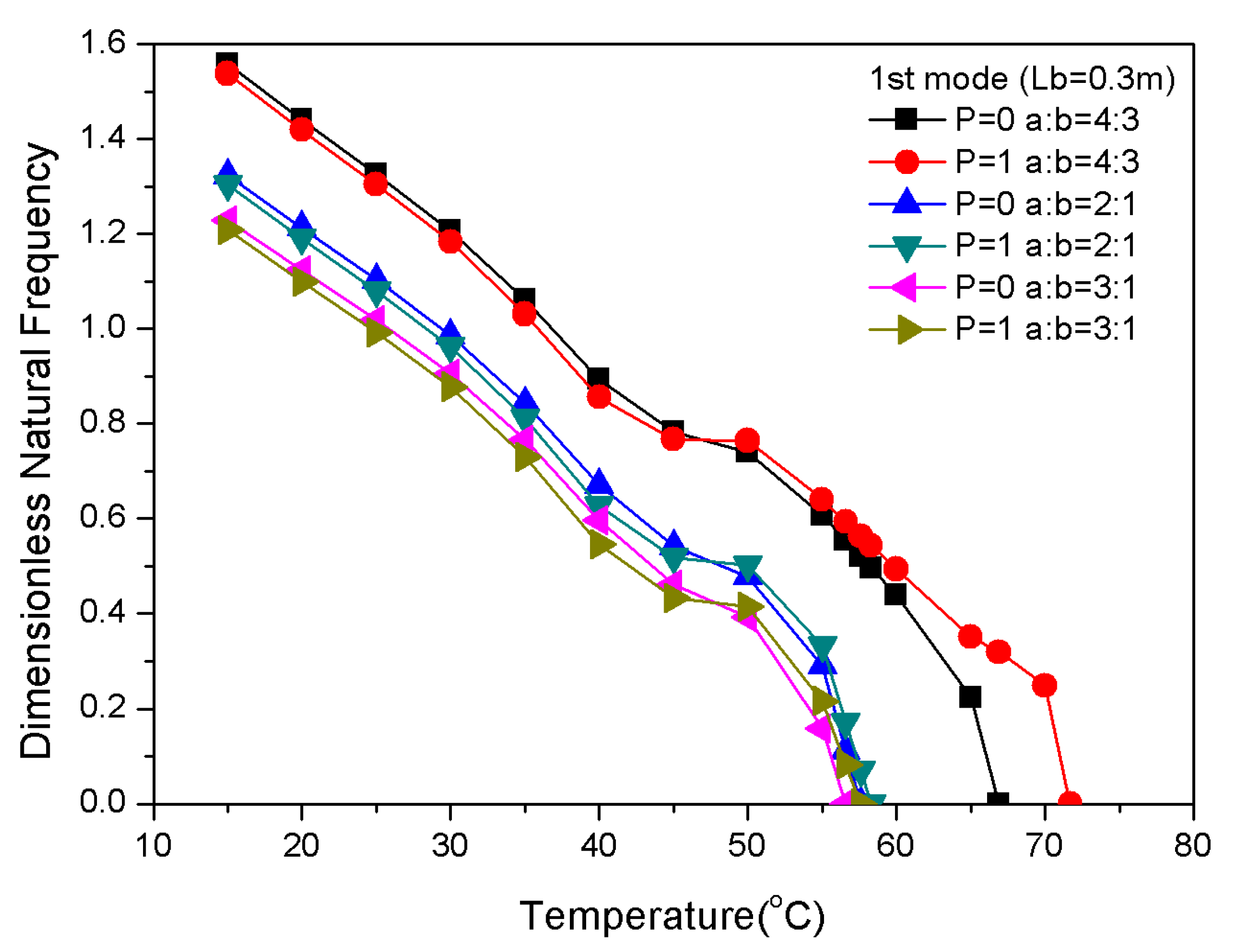
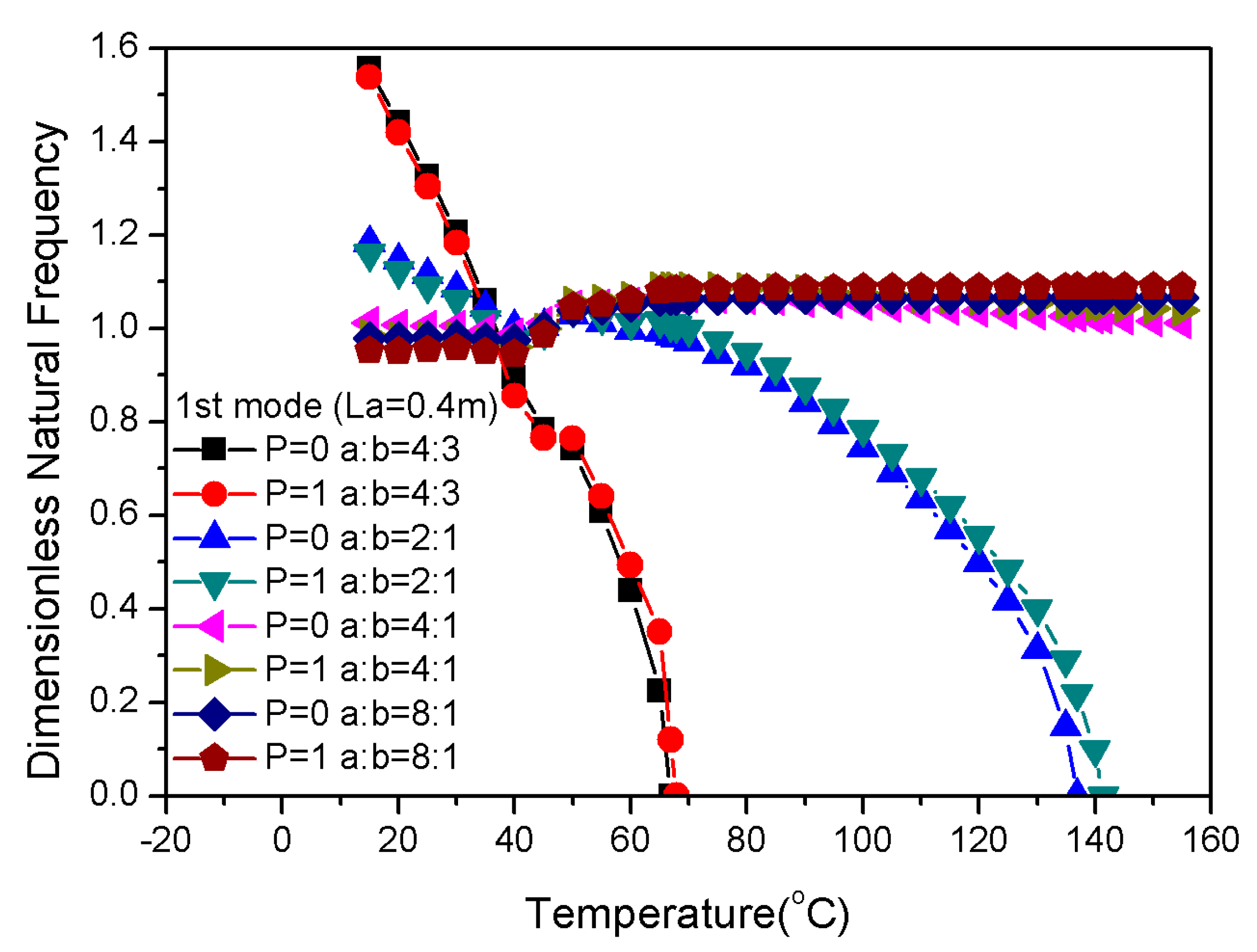
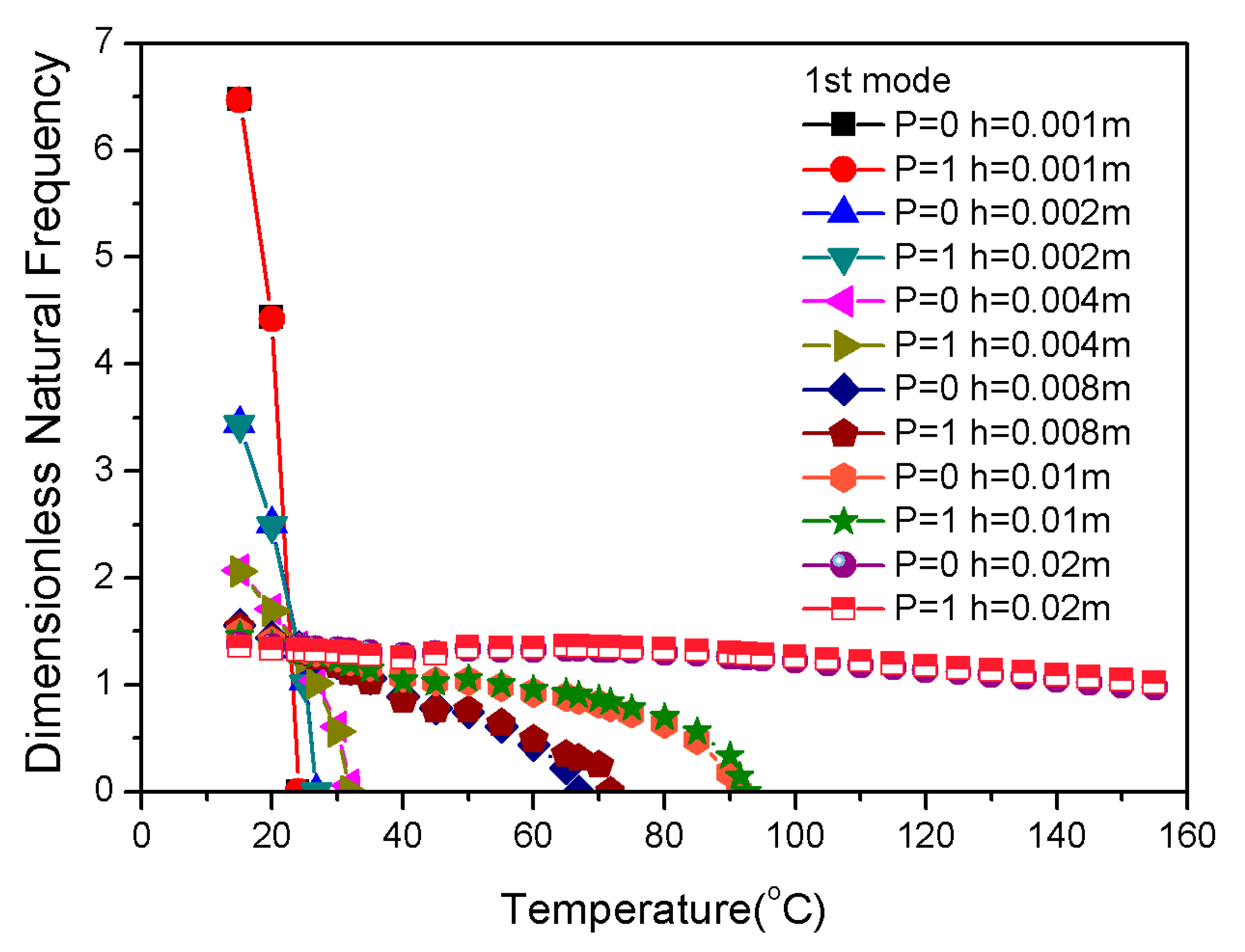
3.5. Influence of Geometrical Properties on Frequency
4. Conclusions
- (1)
- The natural frequency and critical buckling temperature of positive gradient distribution in SMA fibers in composite laminates are higher than those of uniform and negative gradient distributions. Therefore, the positive gradient distribution of SMA fibers is much better for embedding and improves the efficiency of pre-strain to produce recovery stress.
- (2)
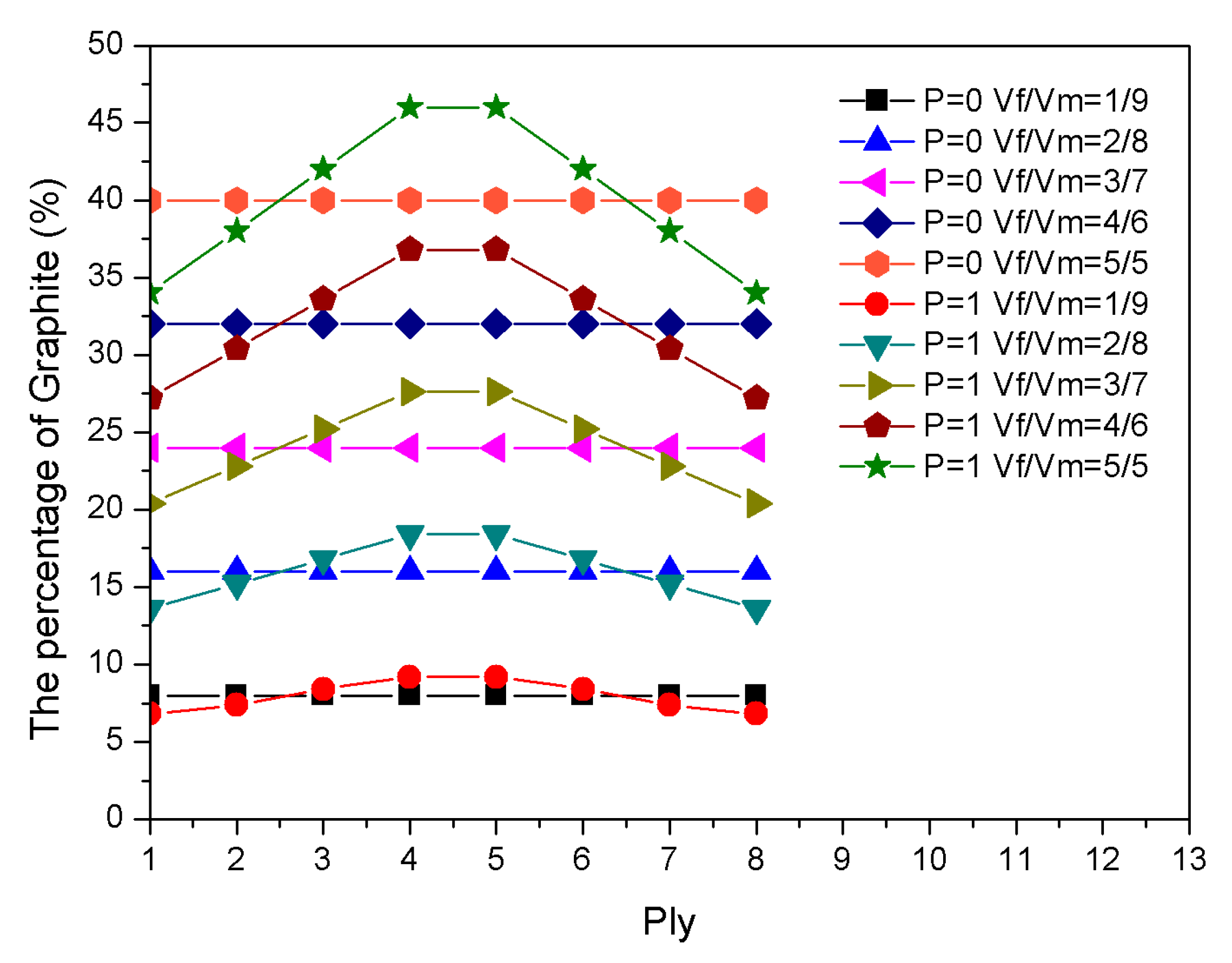
- The large modulus of elasticity of graphite affects thermal stress, while the pre-strain and distribution of nitinol affect in-plane recovery stress. The natural frequency and critical buckling temperature of composite laminates can be effectively adjusted by controlling the internal force of the composite laminate with the proportion and content of graphite and SMAs.
- (3)
- When the SMA volume fraction is constant, the reduction of the width or the increase of the thickness of composite laminates can effectively increase the natural frequency and the critical buckling temperature.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rogers, C.A. Active vibration and structural acoustic control of shape memory alloy hybrid composites: Experimental results. J. Acoust. Soc. Am. 1990, 88, 2803. [Google Scholar] [CrossRef] [Green Version]
- Rogers, C.; Barker, D. Experimental studies of active strain energy tuning of adaptive composites. In Proceedings of the 31st Structures, Structural Dynamics and Materials Conference, Long Beach, CA, USA, 2 April 1990. [Google Scholar] [CrossRef]
- Rogers, C.; Liang, C.; Jia, J. Structural modification of simply-supported laminated plates using embedded shape memory alloy fibers. Comput. Struct. 1991, 38, 569–580. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Krawczuk, M.; Zak, A. Natural frequencies of a multilayer composite plate with shape memory alloy wires. Finite Elem. Anal. Des. 1999, 32, 71–83. [Google Scholar] [CrossRef]
- Malekzadeh, K.; Mozafari, A.; Ghasemi, F.A. Free vibration response of a multilayer smart hybrid composite plate with embedded SMA wires. Lat. Am. J. Solids Struct. 2014, 11, 279–298. [Google Scholar] [CrossRef] [Green Version]
- Mahabadi, R.K.; Shakeri, M.; Daneshpazhooh, M. Free Vibration of Laminated Composite Plate with Shape Memory Alloy Fibers. Lat. Am. J. Solids Struct. 2016, 13, 314–330. [Google Scholar] [CrossRef] [Green Version]
- Shiau, L.-C.; Wu, T.-Y. Free Vibration of Buckled Laminated Plates by Finite Element Method. J. Vib. Acoust. 1997, 119, 635–640. [Google Scholar] [CrossRef]
- Park, J.-S.; Kim, J.-H.; Moon, S.-H. Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers. Compos. Struct. 2004, 63, 179–188. [Google Scholar] [CrossRef]
- Roh, J.-H.; Oh, I.-K.; Yang, S.-M.; Han, J.-H.; Lee, I. Thermal post-buckling analysis of shape memory alloy hybrid composite shell panels. Smart Mater. Struct. 2004, 13, 1337–1344. [Google Scholar] [CrossRef]
- Kuo, S.-Y.; Shiau, L.-C.; Chen, K.-H. Buckling analysis of shape memory alloy reinforced composite laminates. Compos. Struct. 2009, 90, 188–195. [Google Scholar] [CrossRef]
- Kumar, C.N.; Singh, B.N. Thermal buckling analysis of SMA fiber-reinforced composite plates. J. Aerosp Eng. 2009, 22, 4342. [Google Scholar] [CrossRef]
- Li, S.-R.; Yu, W.-S.; Batra, R. Free Vibration of Thermally Pre/Post-Buckled Circular Thin Plates Embedded with Shape Memory Alloy Fibers. J. Therm. Stress. 2010, 33, 79–96. [Google Scholar] [CrossRef] [Green Version]
- Shiau, L.-C.; Kuo, S.-Y.; Chang, S.-Y. Free vibration of buckled SMA reinforced composite laminates. Compos. Struct. 2011, 93, 2678–2684. [Google Scholar] [CrossRef]
- Kuo, S.-Y.; Shiau, L.-C.; Lai, C.-H. Flutter of buckled shape memory alloy reinforced laminates. Smart Mater. Struct. 2012, 21, 35020. [Google Scholar] [CrossRef]
- Asadi, H.; Kiani, Y.; Aghdam, M.; Shakeri, M. Enhanced thermal buckling of laminated composite cylindrical shells with shape memory alloy. J. Compos. Mater. 2015, 50, 243–256. [Google Scholar] [CrossRef]
- Miyazaki, E.; Watanabe, Y. Development of Shape Memory Alloy Fiber Reinforced Smart FGMs. Mater. Sci. Forum 2003, 423, 107–112. [Google Scholar] [CrossRef]
- Xue, L. Theoretical Analysis of Functionally Graded Shape Memory Alloy Beam Subjected to Pure Bending. Chin. J. Mech. Eng. 2012, 48, 40. [Google Scholar] [CrossRef]
- Shariat, B.S.; Meng, Q.; Mahmud, A.S.; Wu, Z.; Bakhtiari, S.; Zhang, J.; Motazedian, F.; Yang, H.W.; Rio, G.; Nam, T.-H.; et al. Functionally graded shape memory alloys: Design, fabrication and experimental evaluation. Mater. Des. 2017, 124, 225–237. [Google Scholar] [CrossRef]
- Viet, N.; Zaki, W.; Umer, R. Analytical model of functionally graded material/shape memory alloy composite cantilever beam under bending. Compos. Struct. 2018, 203, 764–776. [Google Scholar] [CrossRef]
- Shariat, B.S.; Liu, Y.N.; Bakhtiari, S. Modelling and experimental investigation of geometrically graded shape memory alloys with parallel design configure ration. J. Alloy Compd. 2019, 791, 711–721. [Google Scholar] [CrossRef]
- Birman, V. Stability of functionally graded shape memory alloy sandwich panels. Smart Mater. Struct. 1997, 6, 278–286. [Google Scholar] [CrossRef]
- Sepiani, H.; Ebrahimi, F.; Karimipour, H. A mathematical model for smart functionally graded beam integrated with shape memory alloy actuators. J. Mech. Sci. Technol. 2009, 23, 3179–3190. [Google Scholar] [CrossRef]
- Asadi, H.; Akbarzadeh, A.; Wang, Q. Nonlinear thermo-inertial instability of functionally graded shape memory alloy sandwich plates. Compos. Struct. 2015, 120, 496–508. [Google Scholar] [CrossRef]
- Babaee, A.; Sadighi, M.; Nikbakht, A.; Alimirzaei, S. Generalized differential quadrature nonlinear buckling analysis of smart SMA/FG laminated beam resting on nonlinear elastic medium under thermal loading. J. Therm. Stress. 2018, 41, 583–607. [Google Scholar] [CrossRef]


| SMA | Graphite | Epoxy | |||
|---|---|---|---|---|---|
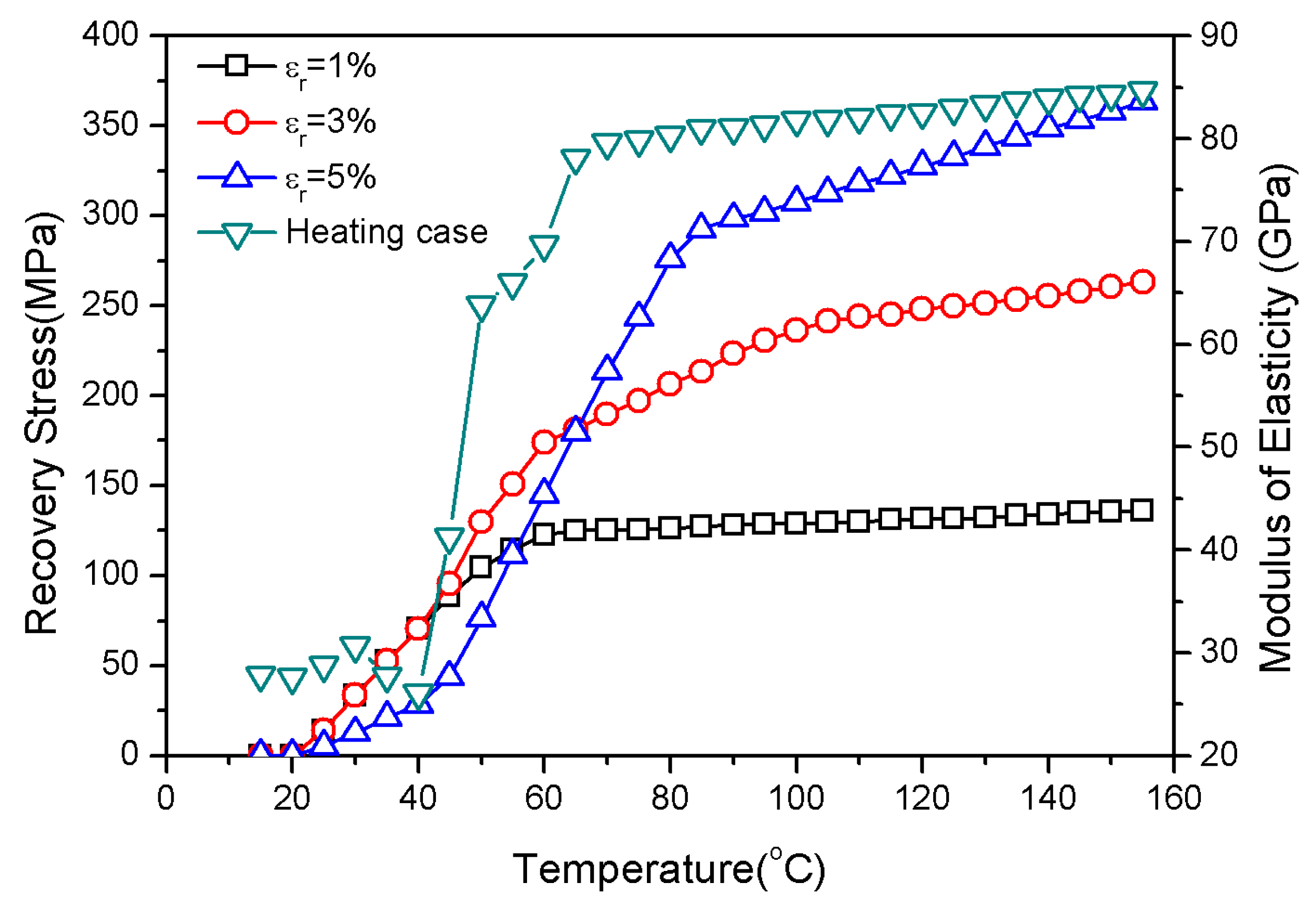
| (GPa) | From Figure 2 | (GPa) | 275.6 | (GPa) | 3.43 |
| (MPa) | From Figure 2 | (GPa) | 114.8 | (GPa) | 1.27 |
| 0.3 | 0.2 | 0.35 | |||
| (kg·m3) | 6450 | (kg·m3) | 1900 | (kg·m3) | 1250 |
| (1/°C) | 10.26 × 10−6 | (1/°C) | 24.40 × 10−6 | (1/°C) | 64.80 × 10−6 |
| Dimensionless Natural Frequency (ω) | |||||
|---|---|---|---|---|---|
| T = 30 °C | Present | Malekzadeh [5] | Mahabadi [6] | Park [8] | |
| = 1% | Vs = 5% | 1.497 | 1.496 | 1.488 | - |
| Vs = 10% | 1.395 | 1.393 | 1.392 | 1.389 | |
| Vs = 15% | 1.312 | - | 1.307 | 1.303 | |
| Vs = 15% | = 3% | 1.310 | 1.308 | 1.303 | 1.300 |
| = 5% | 1.283 | - | 1.279 | - | |
| P | ϖ (T = 30 °C) | ϖ (T = 45 °C) | ϖ (T = 60 °C) | Tcr (°C) |
|---|---|---|---|---|
| −100 | 1.255 | 0.820 | 0.302 | 62.5 |
| −10 | 1.254 | 0.820 | 0.303 | 62.5 |
| −1 | 1.230 | 0.802 | 0.383 | 63.7 |
| 0 | 1.206 | 0.783 | 0.439 | 67.0 |
| 1 | 1.184 | 0.767 | 0.493 | 71.5 |
| 10 | 1.145 | 0.773 | 0.702 | 77.0 |
| 100 | 1.151 | 0.789 | 0.741 | 78.0 |
| Vf/Vm | P = 0 Tcr (°C) | P = 1 Tcr (°C) |
|---|---|---|
| 1/9 | 91.8 | 95.7 |
| 2/8 | 66.9 | 71.6 |
| 3/7 | 61.6 | 61.4 |
| 4/6 | 62.0 | 60.9 |
| 5/5 | 63.6 | 62.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhang, Z.; Li, C.; Mao, K.; Huang, Q. Modal Performance of Two-Fiber Orthogonal Gradient Composite Laminates Embedded with SMA. Materials 2020, 13, 1102. https://doi.org/10.3390/ma13051102
Huang Y, Zhang Z, Li C, Mao K, Huang Q. Modal Performance of Two-Fiber Orthogonal Gradient Composite Laminates Embedded with SMA. Materials. 2020; 13(5):1102. https://doi.org/10.3390/ma13051102
Chicago/Turabian StyleHuang, Yizhe, Zhifu Zhang, Chaopeng Li, Kuanmin Mao, and Qibai Huang. 2020. "Modal Performance of Two-Fiber Orthogonal Gradient Composite Laminates Embedded with SMA" Materials 13, no. 5: 1102. https://doi.org/10.3390/ma13051102
APA StyleHuang, Y., Zhang, Z., Li, C., Mao, K., & Huang, Q. (2020). Modal Performance of Two-Fiber Orthogonal Gradient Composite Laminates Embedded with SMA. Materials, 13(5), 1102. https://doi.org/10.3390/ma13051102





