Analyzing Uncertainty of an Ankle Joint Model with Genetic Algorithm
Abstract
:1. Introduction
Aim of the Study
2. Materials and Methods
2.1. Overview of the Proposed Approach
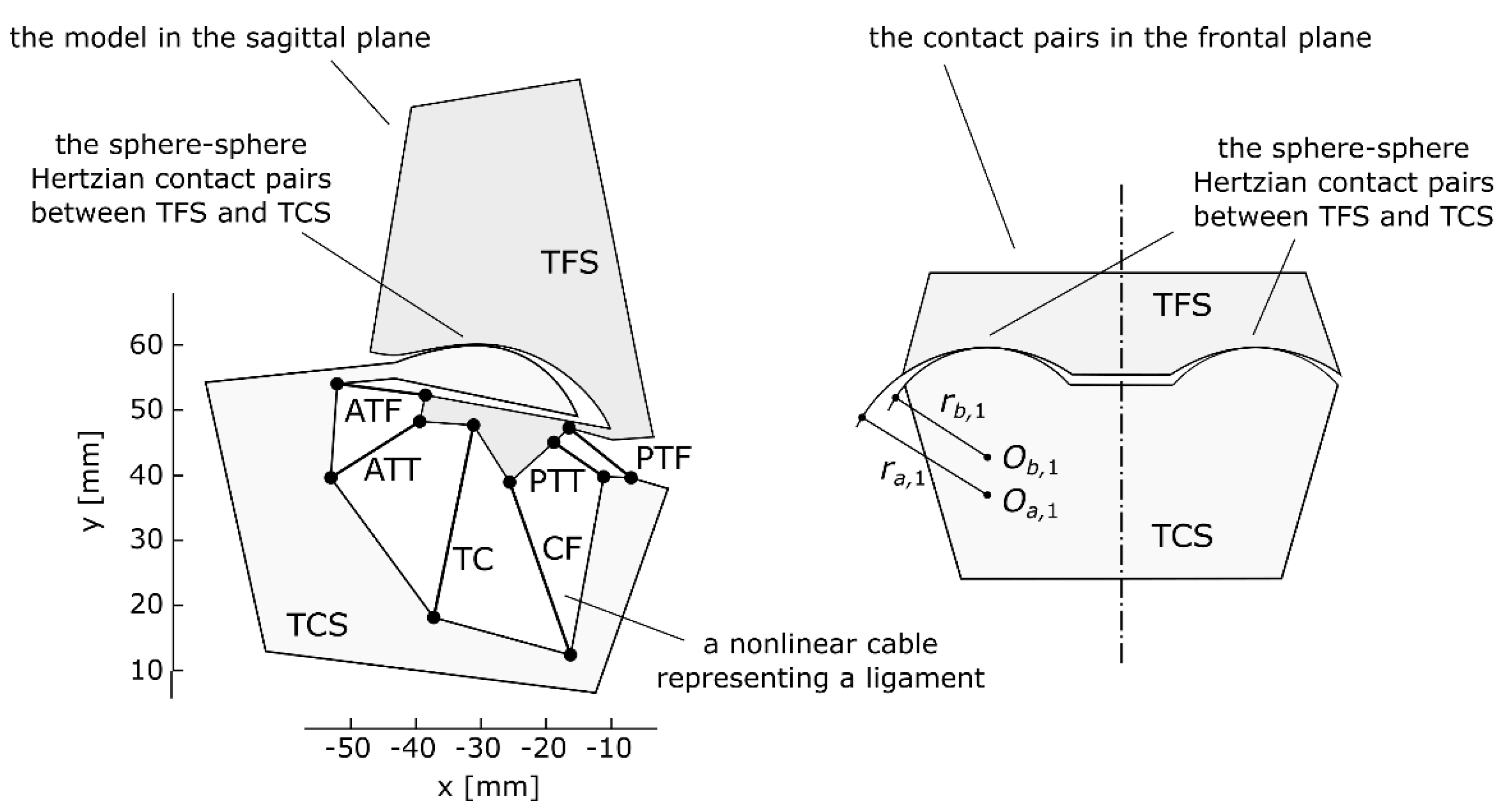
2.2. Ankle Model Assumed to Verify the Procedure
2.3. Encoding the Adversarial Structures
2.4. Objective Function
2.5. Optimization Procedure
2.6. Generating the Initial Population for the Algorithm
3. Results
3.1. Optimization Process
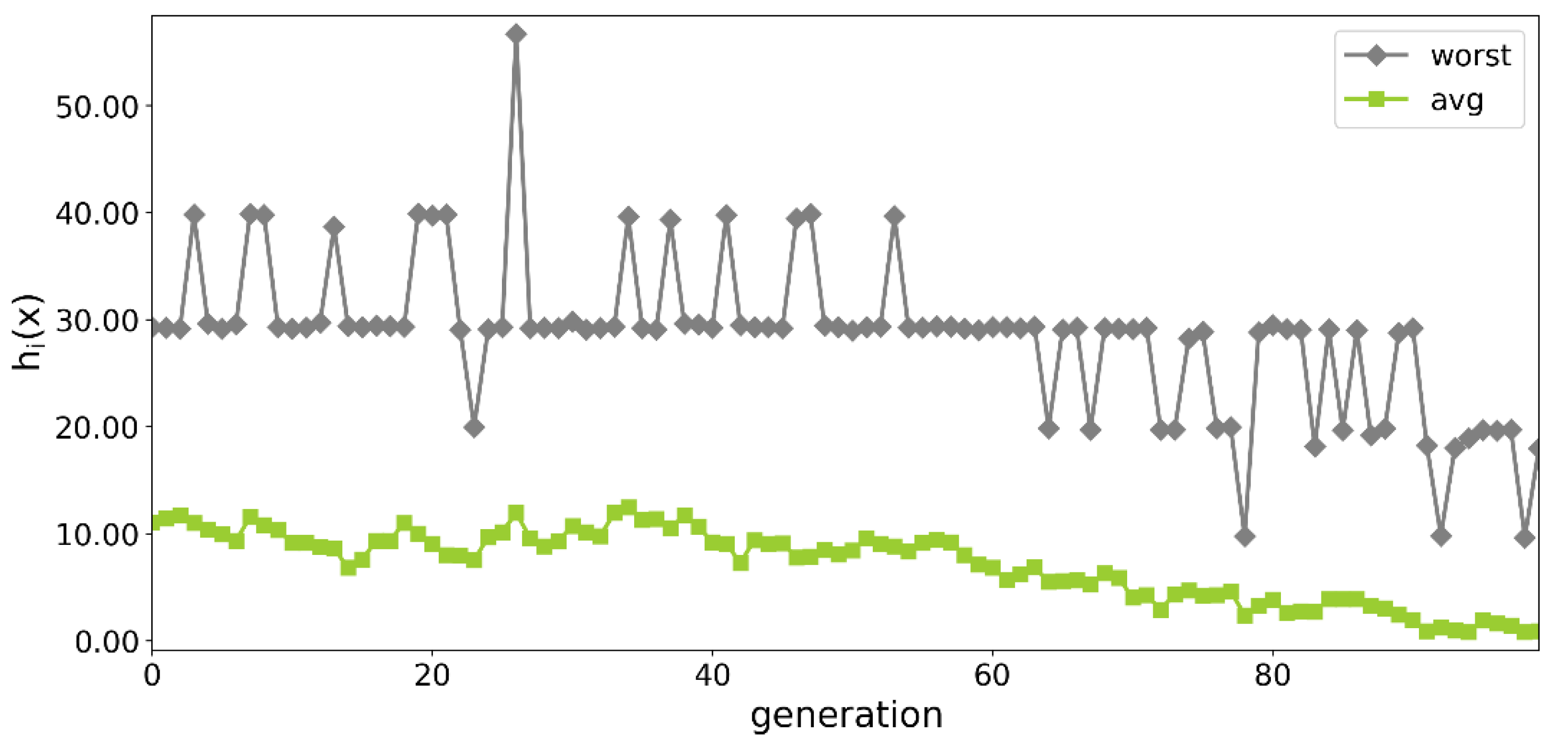
3.1.1. Initial Runs of the Optimization
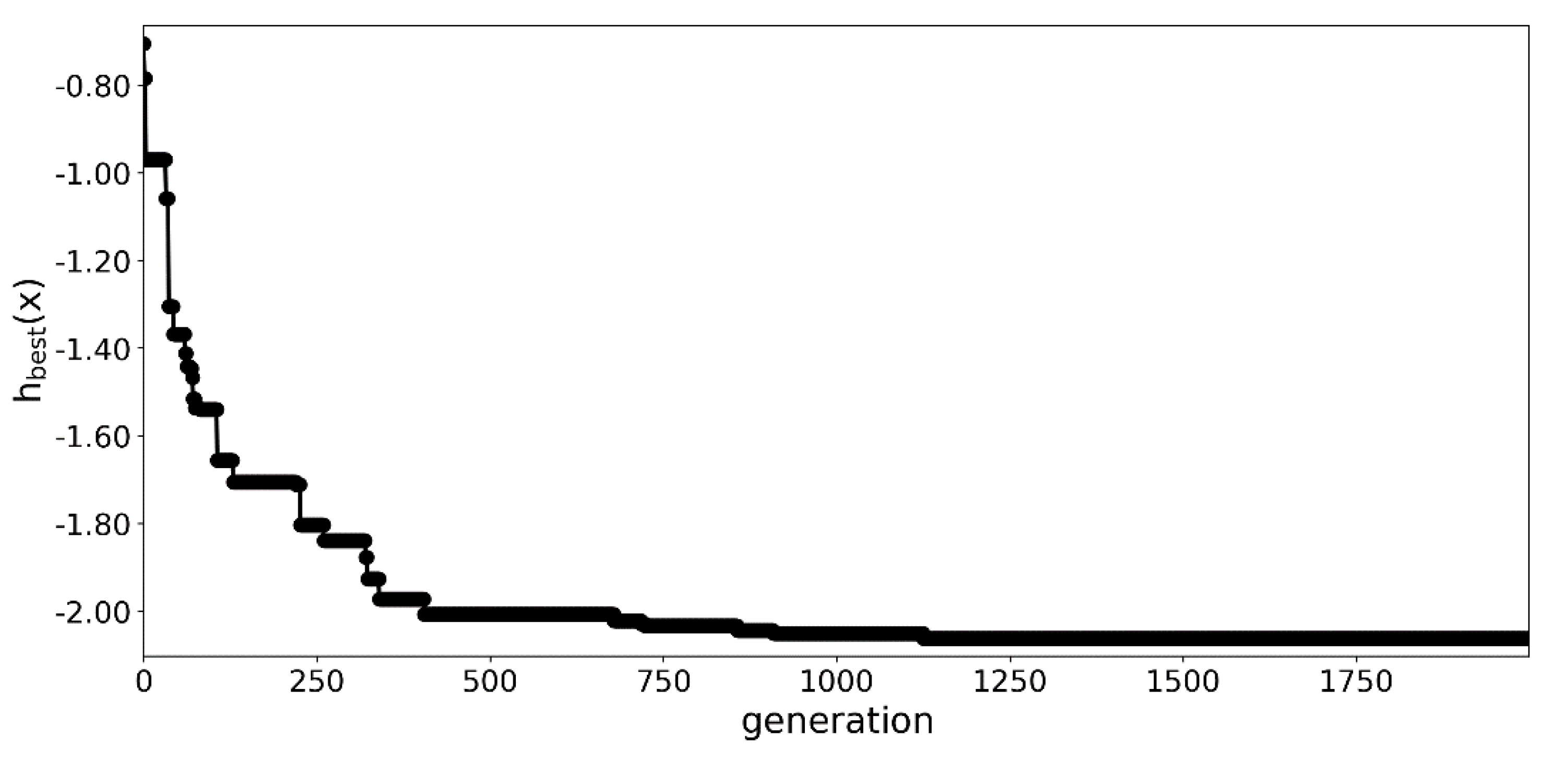
3.1.2. An Extended Run with 2000 Generations
3.1.3. Computing the Baseline
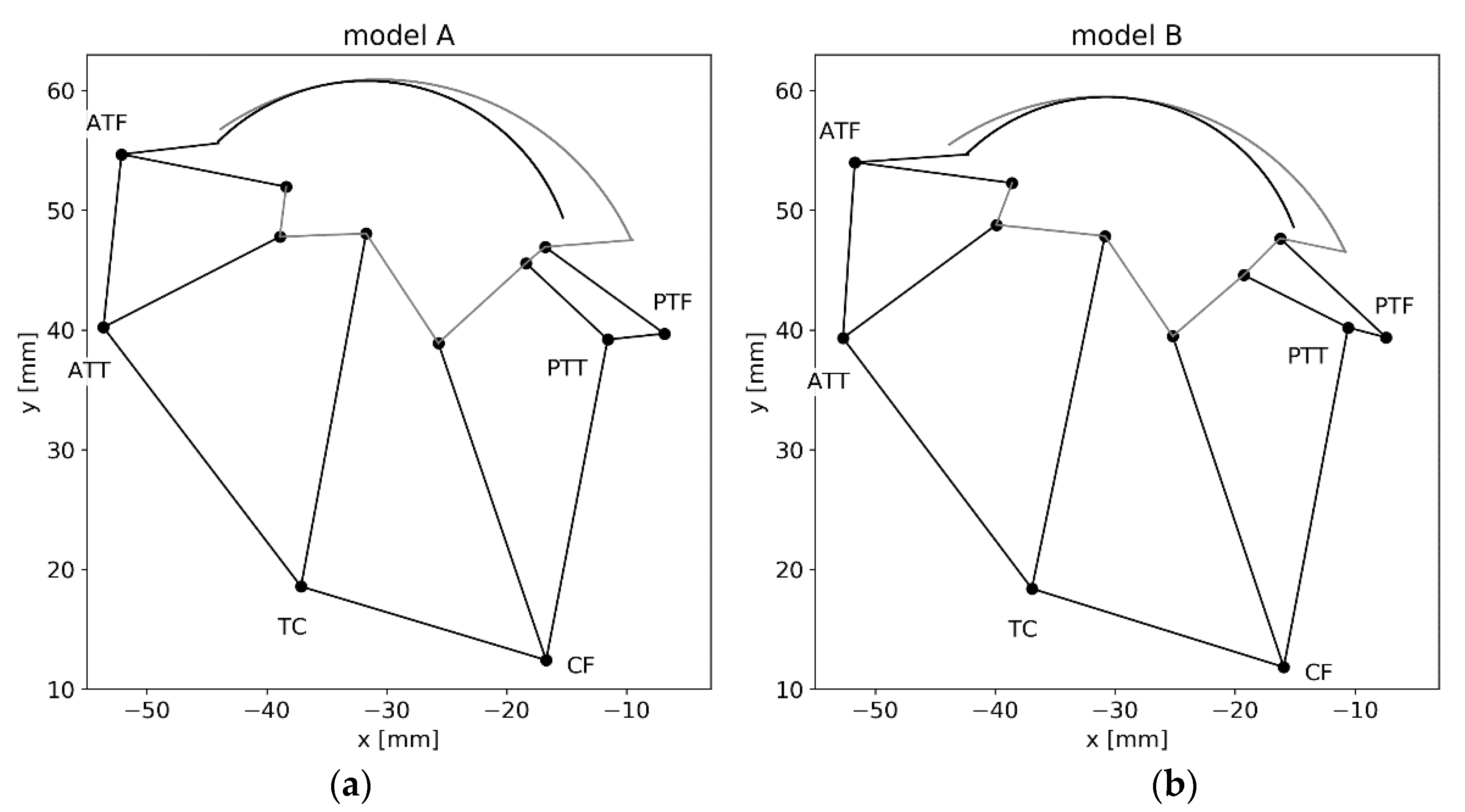
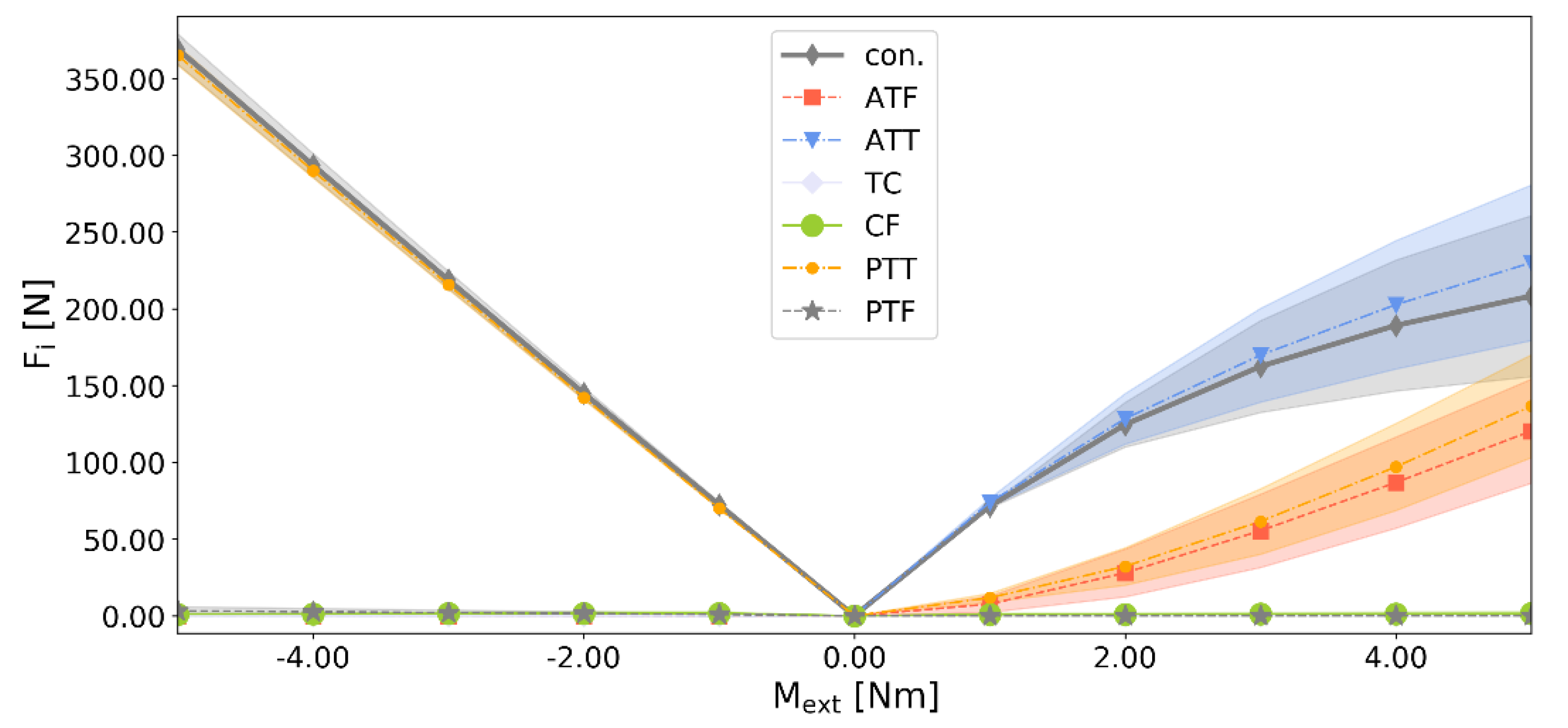
3.2. Analyzing the Uncertainty of the Ankle Model
4. Discussion
4.1. Optimization Procedure
4.2. Effect of Uncertainties on the Ankle Model
5. Conclusions
Funding
Conflicts of Interest
References
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232–238. [Google Scholar] [CrossRef] [Green Version]
- Polzer, H.; Kanz, K.G.; Prall, W.C.; Haasters, F.; Ockert, B.; Mutschler, W.; Grote, S. Diagnosis and treatment of acute ankle injuries: Development of an evidence-based algorithm. Orthop. Rev. (Pavia) 2011, 4, 5. [Google Scholar] [CrossRef] [Green Version]
- Cook, D.; Julias, M.; Nauman, E. Biological variability in biomechanical engineering research: Significance and meta-analysis of current modeling practices. J. Biomech. 2014, 47, 1241–1250. [Google Scholar] [CrossRef]
- Leardini, A.; O’Connor, J.J.; Catani, F.; Giannini, S. A geometric model of the human ankle joint. J. Biomech. 1999, 32, 585–591. [Google Scholar] [CrossRef]
- Wei, F.; Hunley, S.C.; Powell, J.W.; Haut, R.C. Development and validation of a computational model to study the effect of foot constraint on ankle injury due to external rotation. Ann. Biomed. Eng. 2011, 39, 756–765. [Google Scholar] [CrossRef]
- Wei, F.; Braman, J.E.; Weaver, B.T.; Haut, R.C. Determination of dynamic ankle ligament strains from a computational model driven by motion analysis based kinematic data. J. Biomech. 2011, 44, 2636–2641. [Google Scholar] [CrossRef] [PubMed]
- Button, K.D.; Wei, F.; Meyer, E.G.; Haut, R.C. Specimen-specific computational models of ankle sprains produced in a laboratory setting. J. Biomech. Eng. 2013, 135, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Jamwal, P.K.; Hussain, S.; Tsoi, Y.H.; Ghayesh, M.H.; Xie, S.Q. Musculoskeletal modelling of human ankle complex: Estimation of ankle joint moments. Clin. Biomech. 2017, 44, 75–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klekiel, T.; Będziński, R. Finite Element Analysis of Large Deformation of Articular Cartilage in Upper Ankle Joint of Occupant in Military Vehicles during Explosion. Arch. Metall. Mater. 2015, 60, 2115–2121. [Google Scholar] [CrossRef] [Green Version]
- Liacouras, P.C.; Wayne, J.S. Computational Modeling to Predict Mechanical Function of Joints: Application to the Lower Leg with Simulation of Two Cadaver Studies. J. Biomech. Eng. 2007, 129, 811. [Google Scholar] [CrossRef]
- Forlani, M.; Sancisi, N.; Parenti-Castelli, V. A Three-Dimensional Ankle Kinetostatic Model to Simulate Loaded and Unloaded Joint Motion. J. Biomech. Eng. 2015, 137, 061005. [Google Scholar] [CrossRef] [PubMed]
- Gregorio, R.; Parenti-Castelli, V.; O’Connor, J.J.; Leardini, A. Mathematical models of passive motion at the human ankle joint by equivalent spatial parallel mechanisms. Med. Biol. Eng. Comput. 2007, 45, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Iaquinto, J.M.; Wayne, J.S. Computational model of the lower leg and foot/ankle complex: Application to arch stability. J. Biomech. Eng. 2010, 132, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Sellers, W.I.; Crompton, R.H. Using sensitivity analysis to validate the predictions of a biomechanical model of bite forces. Ann. Anat. 2004, 186, 89–95. [Google Scholar] [CrossRef]
- Hutchinson, J.R. Biomechanical Modeling and Sensitivity Analysis of Bipedal Running Ability. I. Extant Taxa. J. Morphol. 2004, 262, 421–440. [Google Scholar] [CrossRef]
- Wang, Q.A.; Zhu, Y.; Wang, Q.A.; Li, W.; Cai, X. Analytic uncertainty and sensitivity analysis of models with input correlations. Physica A 2017, 494, 140–162. [Google Scholar]
- Muc, A. Layout optimization of doubly-curved laminated composite. Eng. Comput. 1996, 13, 263–282. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Szepietowska, K.; Magnain, B.; Lubowiecka, I.; Florentin, E. Sensitivity analysis based on non-intrusive regression-based polynomial chaos expansion for surgical mesh modelling. Struct. Multidiscip. Optim. 2018, 57, 1391–1409. [Google Scholar] [CrossRef]
- Jacquelin, E.; Brizard, D.; Dumas, R. A screening method to analyse the sensitivity of a lower limb multibody kinematic model. Comput. Methods Biomech. Biomed. Engin. 2019, 22, 925–935. [Google Scholar] [CrossRef]
- Fishman, G.S. Monte Carlo; Springer: New York, NY, USA, 1996. [Google Scholar]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. Methods Comparison of Three Variables in the of Values Input a from Computer Code Output Selecting of Analysis for. Technometrics 1979, 21, 239–245. [Google Scholar]
- El Habachi, A.; Moissenet, F.; Duprey, S.; Cheze, L.; Dumas, R. Global sensitivity analysis of the joint kinematics during gait to the parameters of a lower limb multi-body model. Med. Biol. Eng. Comput. 2015, 53, 655–667. [Google Scholar] [CrossRef] [PubMed]
- Skelboe, S. True Worst-Case Analysis of Linear Electrical Circuits by Interval Arithmetic. IEEE Trans. Circuits Syst. 1979, 26, 874–879. [Google Scholar] [CrossRef]
- Femia, N.; Spagnuolo, G. True Worst-Case Circuit Tolerance Analysis Using Genetic Algorithms and Affine Arithmetic. IEEE Trans. Circuits Syst. 2000, 47, 1285–1296. [Google Scholar]
- Borucka, A.; Ciszkiewicz, A. A Planar Model of an Ankle Joint with Optimized Material Parameters and Hertzian Contact Pairs. Materials 2019, 12, 2621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gudavalli, M.R.; Triano, J.J. An analytical model of lumbar motion segment in flexion. J. Manip. Physiol. Ther. 1999, 22, 201–208. [Google Scholar] [CrossRef]
- Machado, M.; Flores, P.; Claro, J.C.P.; Ambrósio, J.; Silva, M.; Completo, A.; Lankarani, H.M. Development of a planar multibody model of the human knee joint. Nonlinear Dyn. 2009, 60, 459–478. [Google Scholar] [CrossRef]
- Ciszkiewicz, A.; Milewski, G. Structural and Material Optimization for Automatic Synthesis of Spine-Segment Mechanisms for Humanoid Robots with Custom Stiffness Profiles. Materials 2019, 12, 1982. [Google Scholar] [CrossRef] [Green Version]
- Ciszkiewicz, A.; Milewski, G. Ligament-based spine-segment mechanisms. Bull. Polish Acad. Sci. Tech. Sci. 2018, 66, 705–712. [Google Scholar]
- Machado, M.; Flores, P.; Ambrosio, J.; Completo, A. Influence of the contact model on the dynamic response of the human knee joint. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2011, 225, 344–358. [Google Scholar] [CrossRef] [Green Version]
- Funk, J.R.; Hall, G.W.; Crandall, J.R.; Pilkey, W.D. Linear and Quasi-Linear Viscoelastic Characterization of Ankle Ligaments. J. Biomech. Eng. 2002, 122, 15. [Google Scholar] [CrossRef]
- Sancisi, N.; Parenti-Castelli, V. A 1-Dof parallel spherical wrist for the modelling of the knee passive motion. Mech. Mach. Theory 2010, 45, 658–665. [Google Scholar] [CrossRef]
- van der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Herrera, F.; Lozano, M.; Verdegay, J.L. Tackling Real-Coded Genetic Algorithms: Operators and Tools for Behavioural Analysis. Artif. Intell. Rev. 1998, 12, 265–319. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989; ISBN 0201157675. [Google Scholar]
- Muc, A.; Muc-Wierzgoń, M. An evolution strategy in structural optimization problems for plates and shells. Compos. Struct. 2012, 94, 1461–1470. [Google Scholar] [CrossRef]
- Ciszkiewicz, A.; Lorkowski, J.; Milewski, G. A novel planning solution for semi-autonomous aspiration of Baker’s cysts. Int. J. Med. Robot. 2018, 14, e1882. [Google Scholar] [CrossRef]
- Muc, A.; Gurba, W. Genetic algorithms and finite element analysis in optimization of composite structures. Compos. Struct. 2001, 54, 275–281. [Google Scholar] [CrossRef]
- Maciazek, M.; Pasko, M. Optimum allocation of active power filters in large supply systems. Bull. Polish Acad. Sci. Tech. Sci. 2016, 64, 37–44. [Google Scholar]
- Bukala, J.; Malachowski, J.; Szafranski, T. Numerical optimization and design study of small wind turbine mast structure. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 5562–5567. [Google Scholar]
- Baker, J.E. Reducing Bias and Inefficiency in the Selection Algorithm. In Proceedings of the Second International Conference on Genetic algoRithms, Cambridge, MA, USA, 28–31 July 1987; pp. 14–21. [Google Scholar]
- Eshelman, L.J.; Schaffer, J.D. Real-Coded Genetic Algorithms and Interval-Schemata. Found. Genet. Algorithms 1993, 2, 187–202. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: New York, NY, USA, 1992; ISBN 3540606769. [Google Scholar]



| Baseline | Optimization after 100 gen. | Optimization after 2000 gen. | |
|---|---|---|---|
| Value of the objective h(x) (obtained using Equation (2)) | −0.23 | −1.30 | −2.06 |
| ΔθA (deg) | ΔθB (deg) | Avg1 (deg) | abs_diff1 (deg) | rel_diff1 (%) | |
|---|---|---|---|---|---|
| Mext = 5.00 Nm | 41.21 | 31.35 | 36.28 | 9.86 | 27.18 |
| Mext = −5.00 Nm | −19.79 | −29.23 | −24.51 | 9.44 | 38.52 |
| range of motion | 61.00 | 60.58 | 60.79 | 0.42 | 0.69 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciszkiewicz, A. Analyzing Uncertainty of an Ankle Joint Model with Genetic Algorithm. Materials 2020, 13, 1175. https://doi.org/10.3390/ma13051175
Ciszkiewicz A. Analyzing Uncertainty of an Ankle Joint Model with Genetic Algorithm. Materials. 2020; 13(5):1175. https://doi.org/10.3390/ma13051175
Chicago/Turabian StyleCiszkiewicz, Adam. 2020. "Analyzing Uncertainty of an Ankle Joint Model with Genetic Algorithm" Materials 13, no. 5: 1175. https://doi.org/10.3390/ma13051175
APA StyleCiszkiewicz, A. (2020). Analyzing Uncertainty of an Ankle Joint Model with Genetic Algorithm. Materials, 13(5), 1175. https://doi.org/10.3390/ma13051175





