Discrete Element Simulation and Validation of a Mixing Process of Granular Materials
Abstract
:1. Introduction
2. Materials and Methods
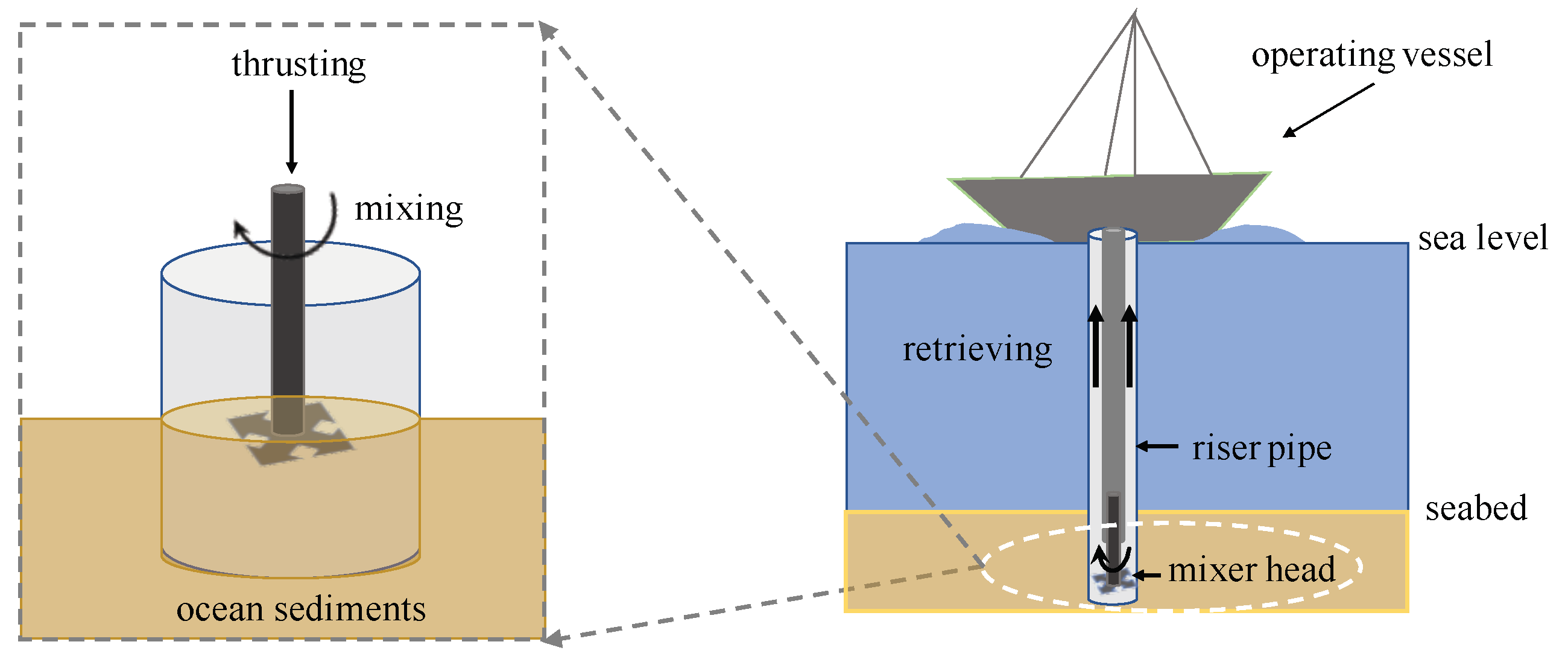
2.1. Experimental Setup
2.2. DEM Simulation
2.2.1. Discrete Element Method
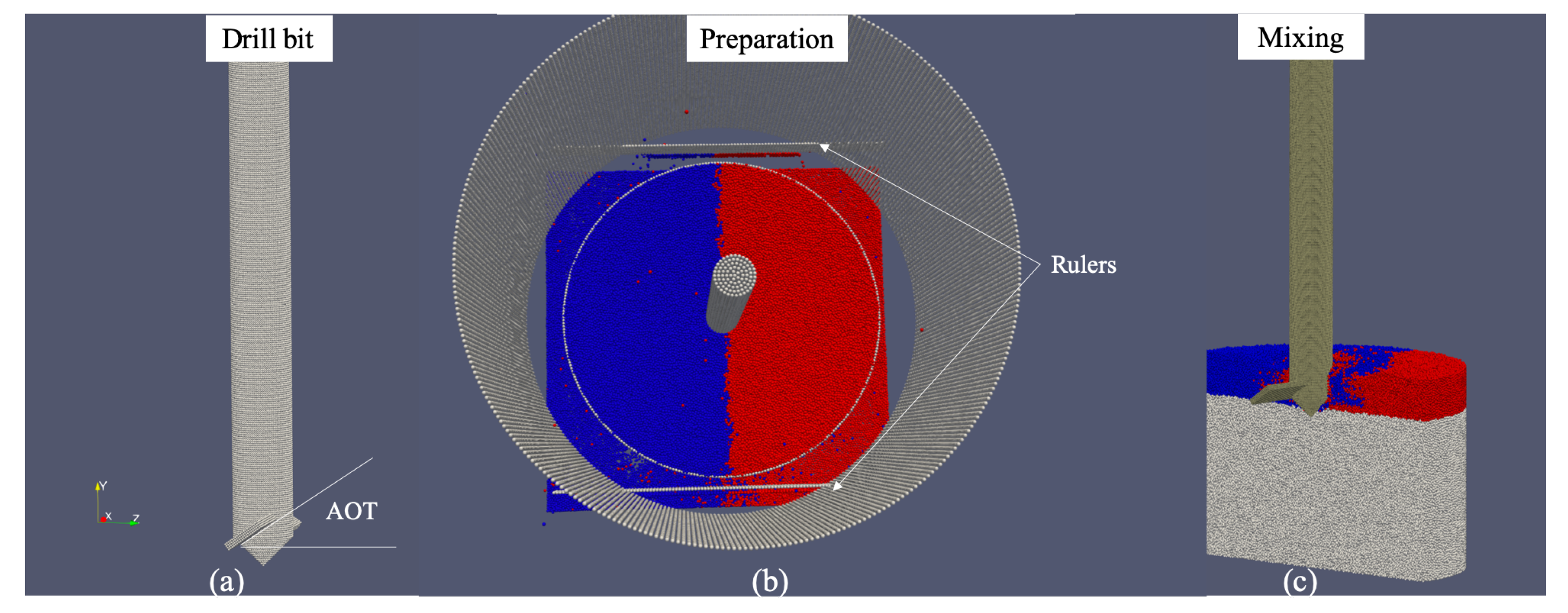
2.2.2. Simulation Setup
3. Results
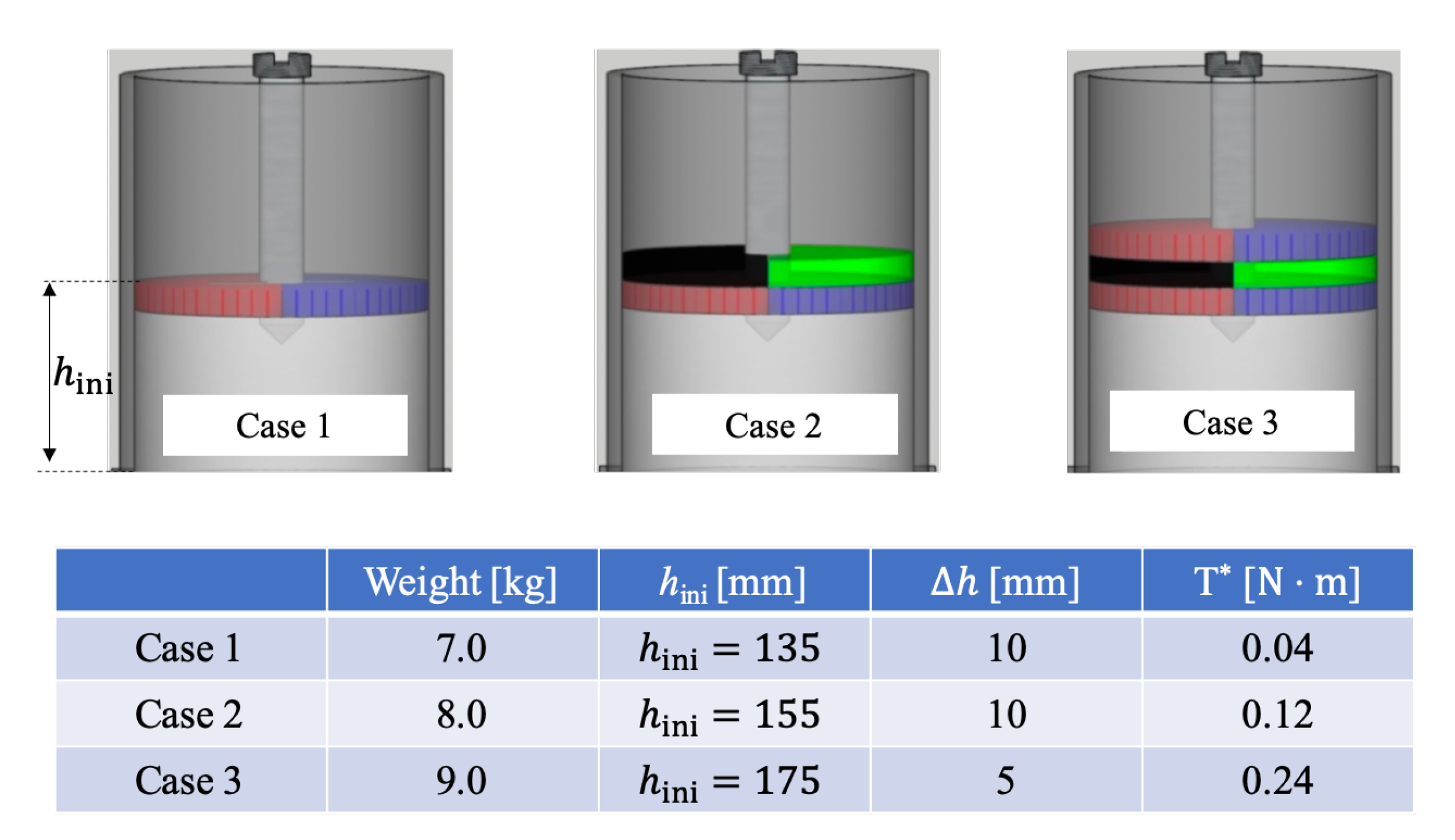
3.1. Summary of the Experiment Results
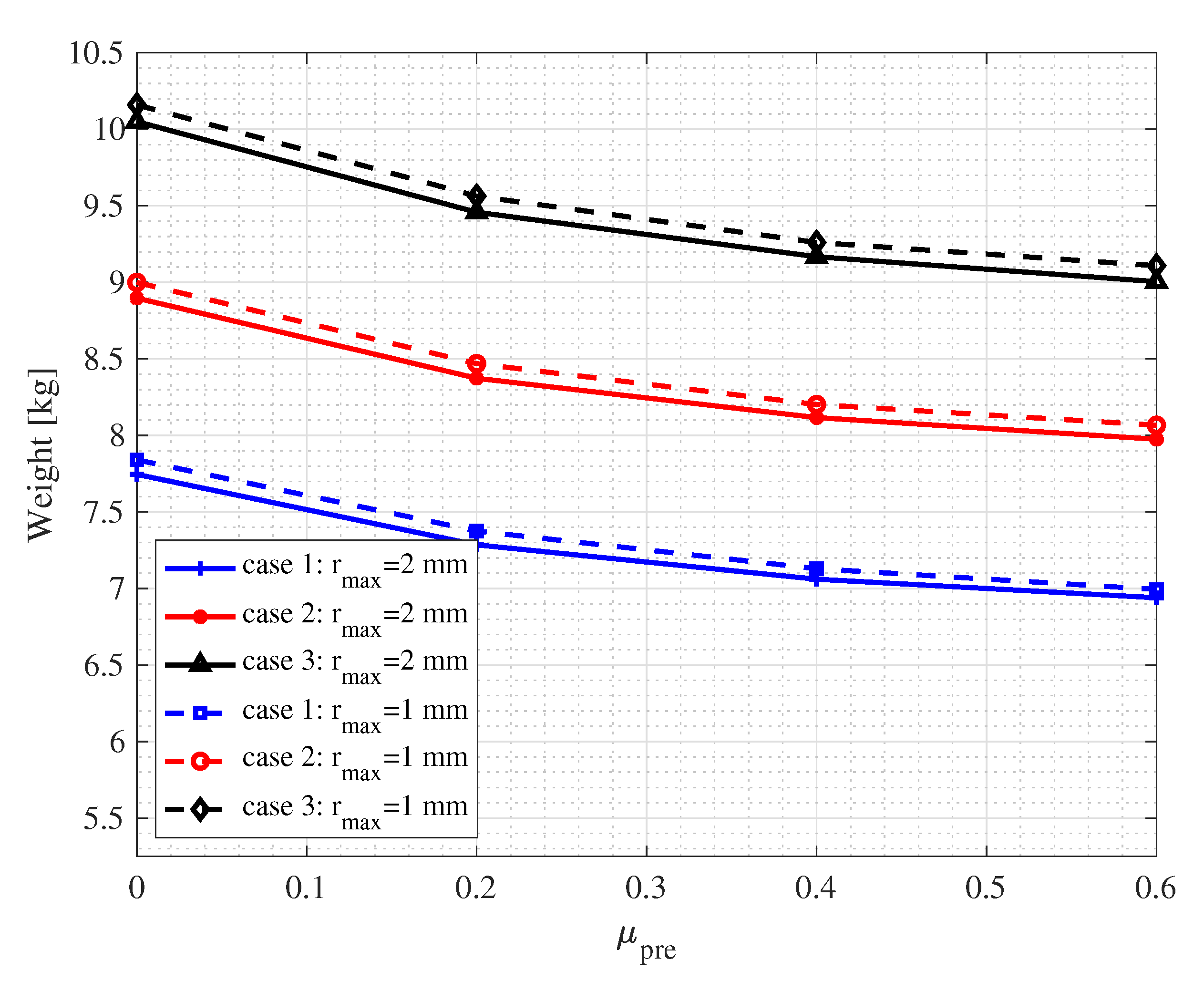
3.2. Calibration of Packing Density
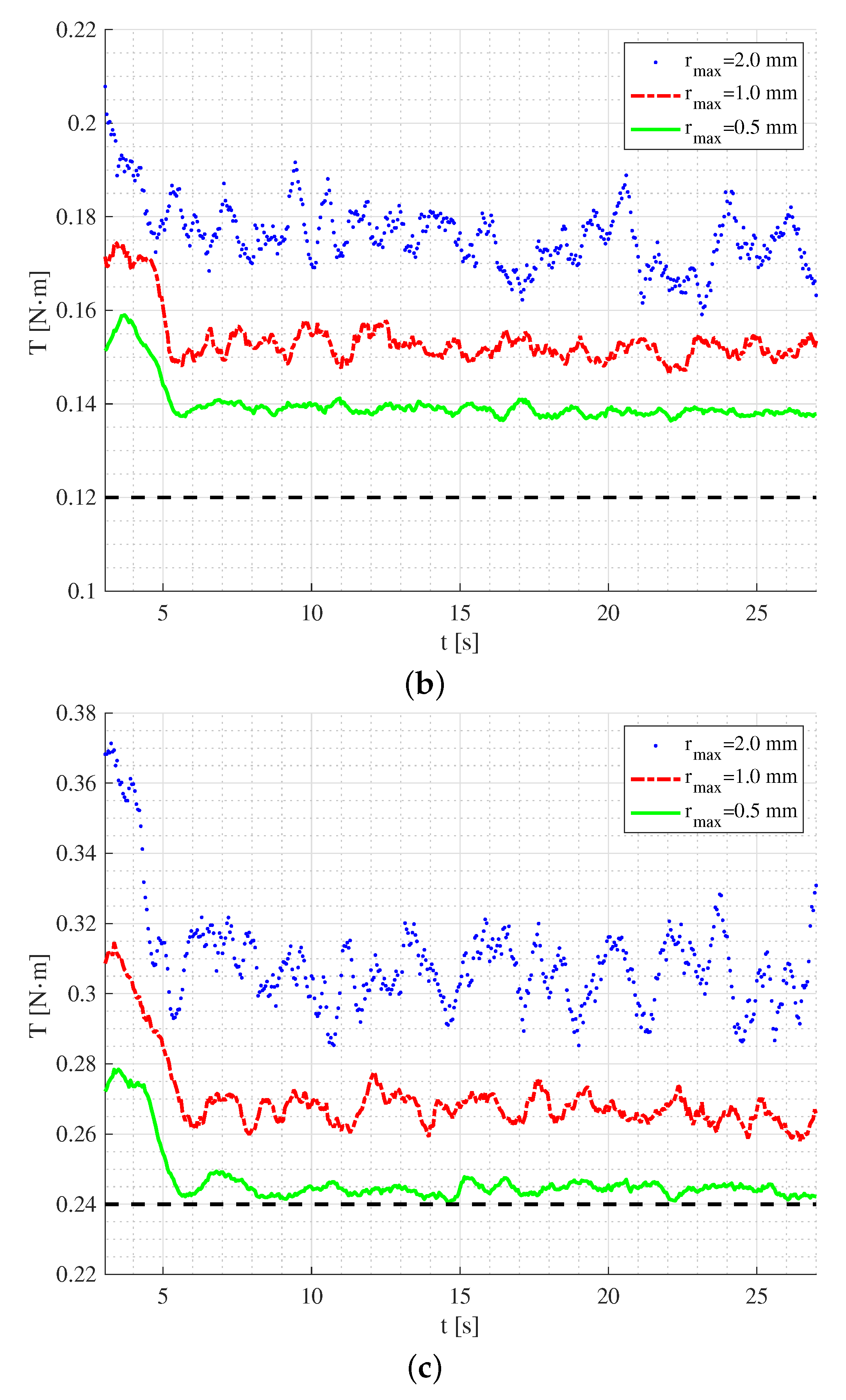
3.3. Quantitative Comparison: Torque
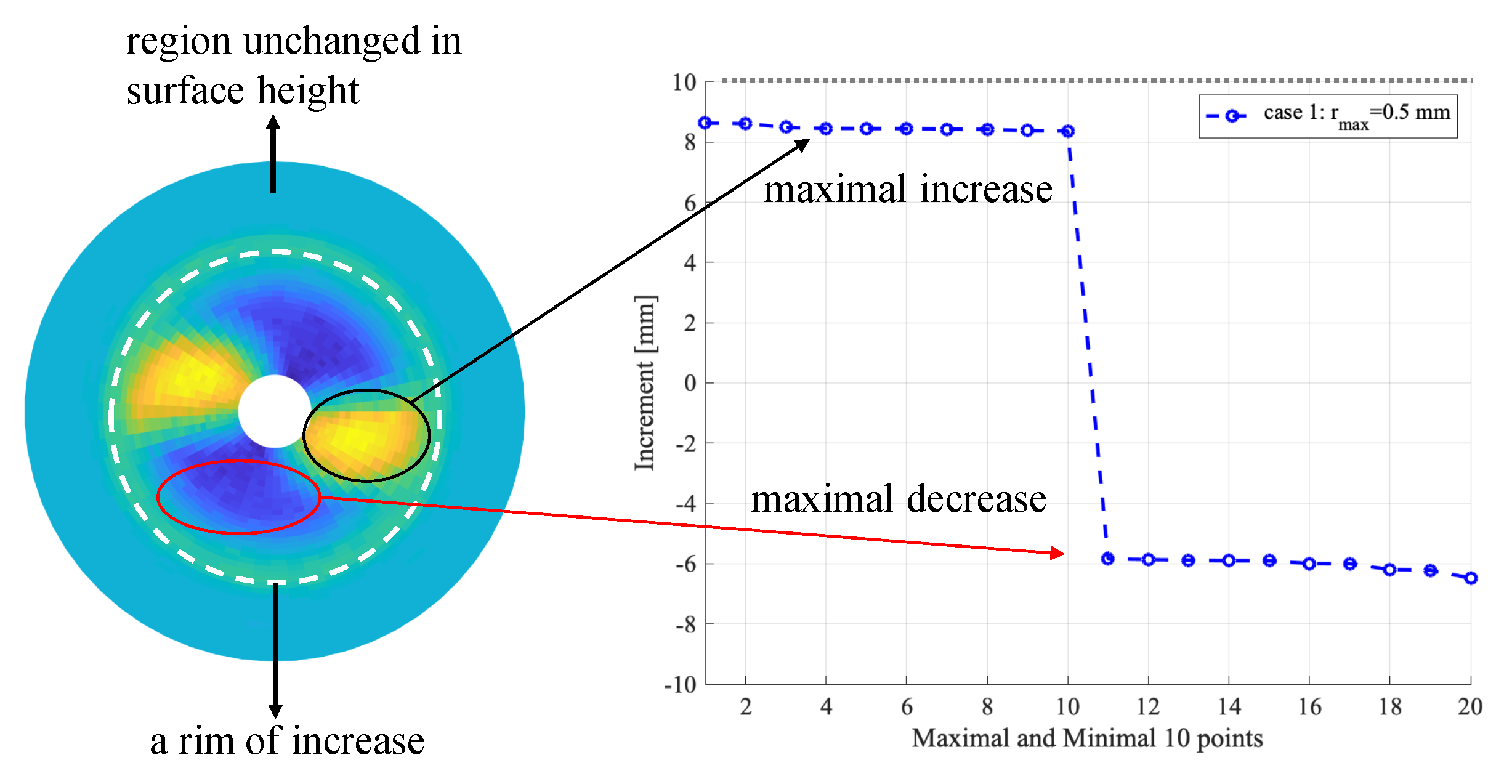
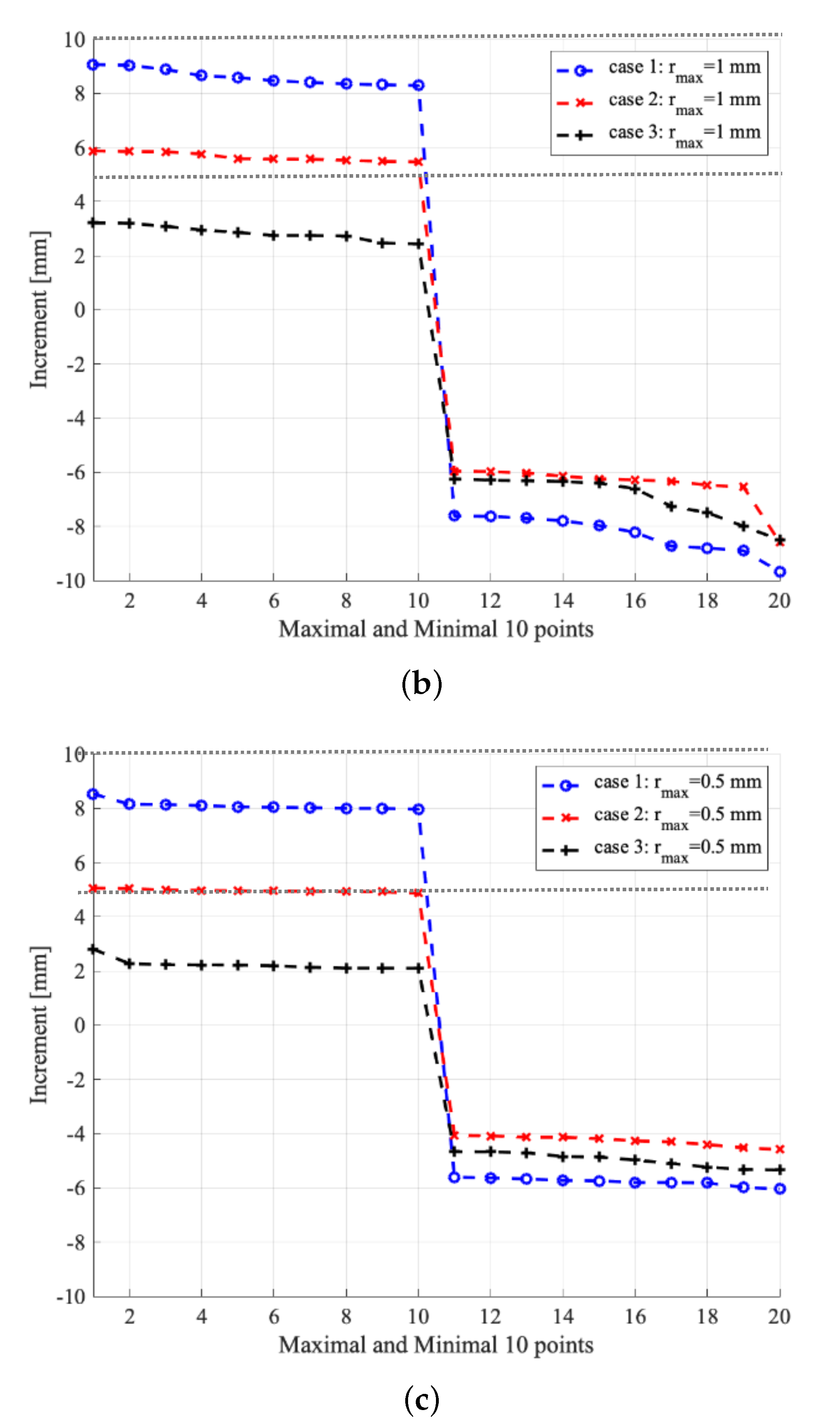
3.4. Quantitative Comparison: Increase of Surface Height
3.5. Qualitative Comparison: Surface Mixing Pattern
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DEM | Discrete Element Method |
| EOM | Equation of Motion |
| RPM | Revolutions per Minute |
| AOA | Angle of Attack |
References
- Litster, J.; Ennis, B. The Science and Engineering of Granulation Processes; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Parikh, D. Handbook of Pharmaceutical Granulation Technology, 2nd ed.; Drugs and the Pharmaceutical Sciences; Taylor & Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Chandratilleke, G.; Yu, A.; Stewart, R.; Bridgwater, J. Effects of blade rake angle and gap on particle mixing in a cylindrical mixer. Powder Technol. 2009, 193, 303–311. [Google Scholar] [CrossRef]
- Remy, B. Granular Flow, Segregation In addition, Agglomeration in Bladed Mixers. Ph.D. Thesis, Rutgers The State University of New Jersey, New Brunswick, NJ, USA, 2010. [Google Scholar]
- Radl, S.; Kalvoda, E.; Glasser, B.J.; Khinast, J.G. Mixing characteristics of wet granular matter in a bladed mixer. Powder Technol. 2010, 200, 171–189. [Google Scholar] [CrossRef]
- Halidan, M. Particle Mixing Study in Different Mixers. Ph.D. Thesis, The University of New South Wales, Sydney, Australia, 2014. [Google Scholar]
- Pantaleev, S.; Yordanova, S.; Janda, A.; Marigo, M.; Ooi, J.Y. An experimentally validated DEM study of powder mixing in a paddle blade mixer. Powder Technol. 2017, 311, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Chandratilleke, G.; Dong, K.; Shen, Y. DEM study of the effect of blade-support spokes on mixing performance in a ribbon mixer. Powder Technol. 2018, 326, 123–136. [Google Scholar] [CrossRef]
- Mero, J. The Mineral Resources of the Sea; Elsevier Science: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Glasby, G.P. Lessons Learned from Deep-Sea Mining. Science 2000, 289, 551–553. [Google Scholar] [CrossRef]
- Miller, K.A.; Thompson, K.F.; Johnston, P.; Santillo, D. An Overview of Seabed Mining Including the Current State of Development, Environmental Impacts, and Knowledge Gaps. Front. Mar. Sci. 2018, 4, 418. [Google Scholar] [CrossRef]
- Takaya, Y.; Yasukawa, K.; Kawasaki, T.; Fujinaga, K.; Ohta, J.; Usui, Y.; Nakamura, K.; Kimura, J.-I.; Chang, Q.; Hamada, M.; et al. The tremendous potential of deep-sea mud as a source of rare-earth elements. Sci. Rep. 2018, 8, 5763. [Google Scholar] [CrossRef] [Green Version]
- Litster, J.; Hapgood, K.; Michaels, J.; Sims, A.; Roberts, M.; Kameneni, S. Scale-up of mixer granulators for effective liquid distribution. Powder Technol. 2002, 124, 272–280. [Google Scholar] [CrossRef]
- Cavinato, M.; Artoni, R.; Bresciani, M.; Canu, P.; Santomaso, A.C. Scale-up effects on flow patterns in the high shear mixing of cohesive powders. Chem. Eng. Sci. 2013, 102, 1–9. [Google Scholar] [CrossRef]
- Saito, Y.; Ingram, A.; Fan, X.; Seville, J.P.K. Three-Dimensional Visualization of Powder Motion in a High Shear Mixer. Mater. Trans. 2011, 52, 1693–1696. [Google Scholar] [CrossRef] [Green Version]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Muguruma, Y.; Tanaka, T.; Tsuji, Y. Numerical simulation of particulate flow with liquid bridge between particles (simulation of centrifugal tumbling granulator). Powder Technol. 2000, 109, 49–57. [Google Scholar] [CrossRef]
- Luding, S. Cohesive, frictional powders: Contact models for tension. Granular Matter 2008, 10, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Trulsson, M.; Andreotti, B.; Claudin, P. Transition from the Viscous to Inertial Regime in Dense Suspensions. Phys. Rev. Lett. 2012, 109, 118305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seto, R.; Mari, R.; Morris, J.F.; Denn, M.M. Discontinuous Shear Thickening of Frictional Hard-Sphere Suspensions. Phys. Rev. Lett. 2013, 111, 218301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ness, C.; Sun, J. Flow regime transitions in dense non-Brownian suspensions: Rheology, microstructural characterization, and constitutive modeling. Phys. Rev. E 2015, 91, 012201. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.; Strack, O. A Discrete Numerical Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Matuttis, H.; Chen, J. Understanding the Discrete Element Method: Simulation of Non-Spherical Particles for Granular and Multi-Body Systems; Wiley: Singapore, 2014. [Google Scholar]
- Furuichi, M.; Nishiura, D. Iterative load-balancing method with multigrid level relaxation for particle simulation with short-range interactions. Comput. Phys. Commun. 2017, 219, 135–148. [Google Scholar] [CrossRef]
- Furuichi, M.; Nishiura, D.; Kuwano, O.; Bauville, A.; Hori, T.; Sakaguchi, H. Arcuate stress state in accretionary prisms from real-scale numerical sandbox experiments. Sci. Rep. 2018, 8, 8685. [Google Scholar] [CrossRef]
- El Shourbagy, S.A.M.; Morita, S.; Matuttis, H.G. Simulation of the Dependence of the Bulk-Stress–Strain Relations of Granular Materials on the Particle Shape. J. Phys. Soc. Jpn. 2006, 75, 104602. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Evans, T.M.; Zhou, X. Three-dimensional Voronoi analysis of monodisperse ellipsoids during triaxial shear. Powder Technol. 2018, 323, 323–336. [Google Scholar] [CrossRef]
- Marinack, M.C., Jr.; Musgrave, R.E.; Higgs, C.F., III. Experimental Investigations on the Coefficient of Restitution of Single Particles. Tribol. Trans. 2013, 56, 572–580. [Google Scholar] [CrossRef]





| Parameters and Settings | Values |
|---|---|
| Container (inner) diameter | 205 mm |
| Shaft diameter | 30 mm |
| Blade diameter | 100 mm |
| Blade thickness | 4 mm |
| Blade width | 20 mm |
| mixer head tip to container bottom | 100 mm |
| Maximal diameter of color sand | 0.85 mm |
| Mass-median diameter of color sand | 0.5487 mm |
| Density of sand grain | 2700 kg/m |
| Minimal and maximal bulk density of color sand | {1332, 1651} kg/m |
| Parameters and Settings | Values |
|---|---|
| Particle density | 2700 |
| Young’s modulus E | 10 |
| Poisson’s ratio | 0.2 |
| Coefficient of friction for particles | 0.6 (0.0 to 0.6 for sample preparation) |
| Coefficient of friction for wall | 0.6 |
| Coefficient of restitution e | 0.2 |
| Coefficient of rolling friction | 0.05 |
| Maximal particle radius | {2, 1, 0.5} mm |
| Mass-median diameter of particles | {3.692, 1.847, 0.923} mm |
| Number of particles | Case 1: {133392, 1128223, 9473830} |
| Case 2: {151212, 1280155, 10756606} | |
| Case 3: {169032, 1432087, 12039382} |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Furuichi, M.; Nishiura, D. Discrete Element Simulation and Validation of a Mixing Process of Granular Materials. Materials 2020, 13, 1208. https://doi.org/10.3390/ma13051208
Chen J, Furuichi M, Nishiura D. Discrete Element Simulation and Validation of a Mixing Process of Granular Materials. Materials. 2020; 13(5):1208. https://doi.org/10.3390/ma13051208
Chicago/Turabian StyleChen, Jian, Mikito Furuichi, and Daisuke Nishiura. 2020. "Discrete Element Simulation and Validation of a Mixing Process of Granular Materials" Materials 13, no. 5: 1208. https://doi.org/10.3390/ma13051208
APA StyleChen, J., Furuichi, M., & Nishiura, D. (2020). Discrete Element Simulation and Validation of a Mixing Process of Granular Materials. Materials, 13(5), 1208. https://doi.org/10.3390/ma13051208





