Deformation and Failure of MXene Nanosheets
Abstract
:1. Introduction
2. Modeling Methods
2.1. FE Model of Nanoindentation
2.2. FE Model of Pure MXene Film
3. Results
3.1. FE Simulation of Nanoindentation
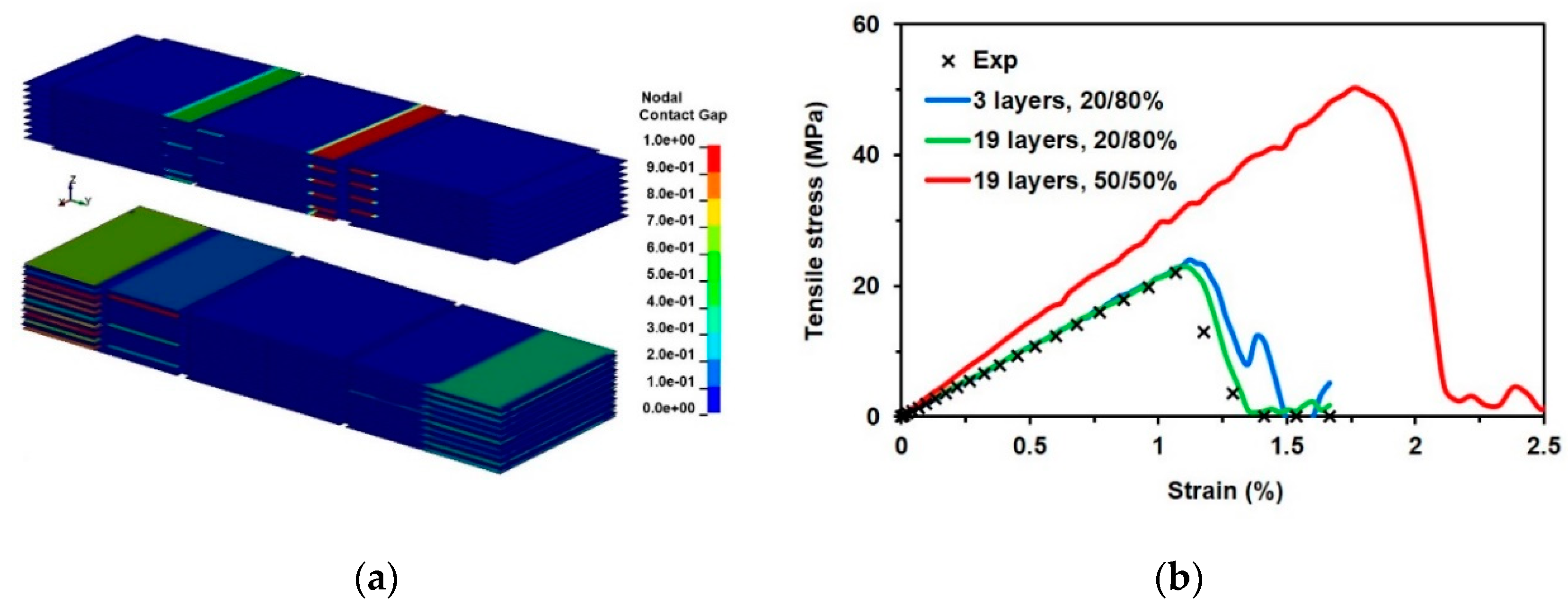
3.2. FE Simulation of Pure MXene Film
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Naguib, M.; Kurtoglu, M.; Presser, V.; Lu, J.; Niu, J.; Heon, M.; Hultman, L.; Gogotsi, Y.; Barsoum, M.W. Two-dimensional nanocrystals produced by exfoliation of Ti3AlC2. Adv. Mater. 2011, 23, 4248–4253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th anniversary article: MXenes: A new family of two-dimensional materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [CrossRef] [PubMed]
- Ronchi, R.M.; Arantes, J.T.; Santos, S.F. Synthesis, structure, properties and applications of MXenes: Current status and perspectives. Ceram. Int. 2019, 45, 18167–18188. [Google Scholar] [CrossRef]
- Ling, Z.; Ren, C.E.; Zhao, M.-Q.; Yang, J.; Giammarco, J.M.; Qiu, J.; Barsoum, M.W.; Gogotsi, Y. Flexible and conductive MXene films and nanocomposites with high capacitance. Proc. Natl. Acad. Sci. USA 2014, 111, 16676–16681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anasori, B.; Lukatskaya, M.R.; Gogotsi, Y. 2D metal carbides and nitrides (MXenes) for energy storage. Nat. Rev. Mater. 2017, 2, 1609. [Google Scholar] [CrossRef]
- Ghidiu, M.; Lukatskaya, M.; Zhao, M.; Gogotsi, Y.; Barsoum, M. Conductive two-dimensional titanium carbide ‘clay’ with high volumetric capacitance. Nature 2015, 516, 78–81. [Google Scholar] [CrossRef]
- Borysiuk, V.N.; Mochalin, V.N.; Gogotsi, Y. Molecular dynamic study of the mechanical properties of two-dimensional titanium carbides Tin+1Cn(MXenes). Nanotechnology 2015, 26, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Lipatov, A.; Lu, H.; Alhabeb, M.; Anasori, B.; Gruverman, A.; Gogotsi, Y.; Sinitskii1, A. Elastic properties of 2D Ti3C2Tx MXene monolayers and bilayers. Sci. Adv. 2018, 4, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Borysiuk, V.N.; Mochalin, V.N.; Gogotsi, Y. Bending rigidity of two-dimensional titanium carbide (MXene) nanoribbons: A molecular dynamics study. Comput. Mater. Sci. 2018, 143, 418–424. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, J.; Si, C.; Sun, Z. Flexible two-dimensional Tin + 1Cn (n = 1, 2 and 3) and their functionalised MXenes predicted by density functional theories. Phys. Chem. 2015, 17, 15348–15354. [Google Scholar]
- Zhao, M.Q.; Ren, C.E.; Ling, Z.; Lukatskaya, M.R.; Zhang, C.; Van Aken, K.L.; Barsoum, M.W.; Gogotsi, Y. Flexible MXene/carbon nanotube composite paper with high volumetric capacitance. Adv. Mater. 2015, 27, 339–345. [Google Scholar] [CrossRef]
- Kilikevičius, S.; Kvietkaitė, S.; Žukienė, K.; Omastová, M.; Aniskevich, A.; Zeleniakienė, D. Numerical investigation of the mechanical properties of a novel hybrid polymer composite reinforced with graphene and MXene nanosheets. Comput. Mater. Sci. 2020, 174, 109497. [Google Scholar] [CrossRef]
- Monastyreckis, G.; Mishnaevsky, L., Jr.; Hatter, C.B.; Aniskevich, A.; Gogotsi, Y.; Zeleniakiene, D. Micromechanical modeling of MXene-polymer composites. Carbon 2020, 162, 402–409. [Google Scholar] [CrossRef]
- Shearer, C.J.; Slattery, A.D.; Stapleton, A.J.; Shapter, J.G.; Gibson, C.T. Accurate thickness measurement of graphene. Nanotechnology 2016, 27, 125704. [Google Scholar] [CrossRef]
- Fu, Z.H.; Zhang, Q.F.; Legut, D.; Si, C.; Germann, T.C.; Lookman, T.; Du, S.Y.; Francisco, J.S.; Zhang, R.F. Stabilization and strengthening effects of functional groups in two-dimensional titanium carbide. Phys. Chem. 2016, 94, 104103. [Google Scholar] [CrossRef]
- Jang, J.; Suhr, J.; Gibson, R.F. Combined numerical/experimental investigation of particle diameter and interphase effects on coefficient of thermal expansion and Young’s modulus of SiO2/epoxy nanocomposites. Polym. Compos. 2012, 33, 1415–1423. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, Z.H.; Legut, D.; Germannd, T.C.; Zhang, R.F. Stacking stability and sliding mechanism in weakly bonded 2D transition metal carbides by van der Waals force. RSC Adv. 2017, 7, 55912–55919. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.; Zhu, Y. Measuring graphene adhesion using atomic force microscopy with a microsphere tip. Nanoscale 2015, 7, 10760–10766. [Google Scholar] [CrossRef] [PubMed]
- Burnham, N.A.; Dominguez, D.D.; Mowery, R.L.; Colton, R.J. Probing the surface forces of monolayer films with an atomic-force microscope. Phys. Rev. Lett. 1990, 64, 1931–1934. [Google Scholar] [CrossRef] [PubMed]
- Cappella, B.; Kappl, M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar]
- Li, Y.; Huang, S.; Wei, C.; Wu, C.; Mochalin, V.N. Adhesion of two-dimensional titanium carbides (MXenes) and graphene to silicon. Nat. Commun. 2019, 10, 3014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mashtalir, O.; Naguib, M.; Mochalin, V.N.; Dall’Agnese, Y.; Heon, M.; Barsoum, M.W.; Gogotsi, Y. Intercalation and delamination of layered carbides and carbonitrides. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Jastrzębska, A.M.; Karwowska, E.; Wojciechowski, T.; Ziemkowska, W.; Rozmysłowska, A.; Chlubny, L.; Olszyna, A. The atomic structure of Ti2C and Ti3C2 MXenes is responsible for their antibacterial activity toward E. coli bacteria. J. Mater. Eng. Perform. 2019, 28, 1272–1277. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J.; Wu, Y.; Huang, H.; Li, G.; Zhang, X.; Wang, Z. Applied Surface Science Surface modified MXene Ti3C2 multilayers by aryl diazonium salts leading to large-scale delamination. Appl. Surf. Sci. 2016, 384, 287–293. [Google Scholar] [CrossRef]
- Chen, L.; Shi, X.; Yu, N.; Zhang, X.; Du, X. Measurement and analysis of thermal conductivity of Ti3C2Tx MXene films. Materials 2018, 11, 1701. [Google Scholar] [CrossRef] [Green Version]
- LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2014; Volume II, pp. 1–1265.



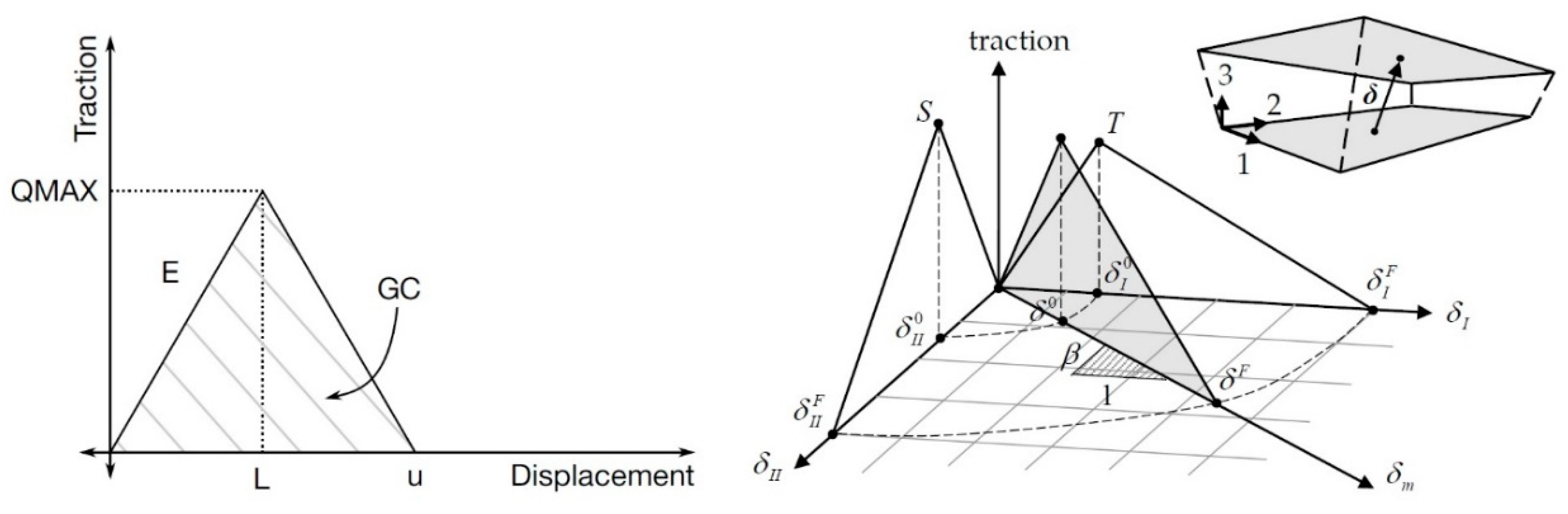





| Material | Density, ρ, g/cm3 | Elastic Modulus, E, GPa | Poisson’s Ratio, ν | Tensile Strength, σu, GPa |
|---|---|---|---|---|
| Ti3C2Tz | 3.19 [8] | 333 [8] | 0.227 [15] | 17.3 [8] |
| SiO2 [16] | 2.65 | 70.0 | 0.17 | - |
| Diamond nanoindenter | 3.50 | 1000 | 0.20 | - |
| Normal Failure Stress, nfls (T), MPa | Shear Failure Stress, sfls (S), Mpa | Normal Energy Release Rates, eraten (GIC) mJ/m2 | Shear Energy Release Rates, erates (GIIC) mJ/m2 | Ratio of Tangential Stiffness to Normal Stiffness, ct2cn | Normal Stiffness, Cn €, MPa/μm |
|---|---|---|---|---|---|
| 2 ÷ 4 | 2 ÷ 4 | 30 ÷ 60 | 30 ÷ 60 | 1 | 200–350 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeleniakiene, D.; Monastyreckis, G.; Aniskevich, A.; Griskevicius, P. Deformation and Failure of MXene Nanosheets. Materials 2020, 13, 1253. https://doi.org/10.3390/ma13051253
Zeleniakiene D, Monastyreckis G, Aniskevich A, Griskevicius P. Deformation and Failure of MXene Nanosheets. Materials. 2020; 13(5):1253. https://doi.org/10.3390/ma13051253
Chicago/Turabian StyleZeleniakiene, Daiva, Gediminas Monastyreckis, Andrey Aniskevich, and Paulius Griskevicius. 2020. "Deformation and Failure of MXene Nanosheets" Materials 13, no. 5: 1253. https://doi.org/10.3390/ma13051253
APA StyleZeleniakiene, D., Monastyreckis, G., Aniskevich, A., & Griskevicius, P. (2020). Deformation and Failure of MXene Nanosheets. Materials, 13(5), 1253. https://doi.org/10.3390/ma13051253







