Advances in Atomic Layer Deposition (ALD) Nanolaminate Synthesis of Thermoelectric Films in Porous Templates for Improved Seebeck Coefficient
Abstract
:1. Introduction
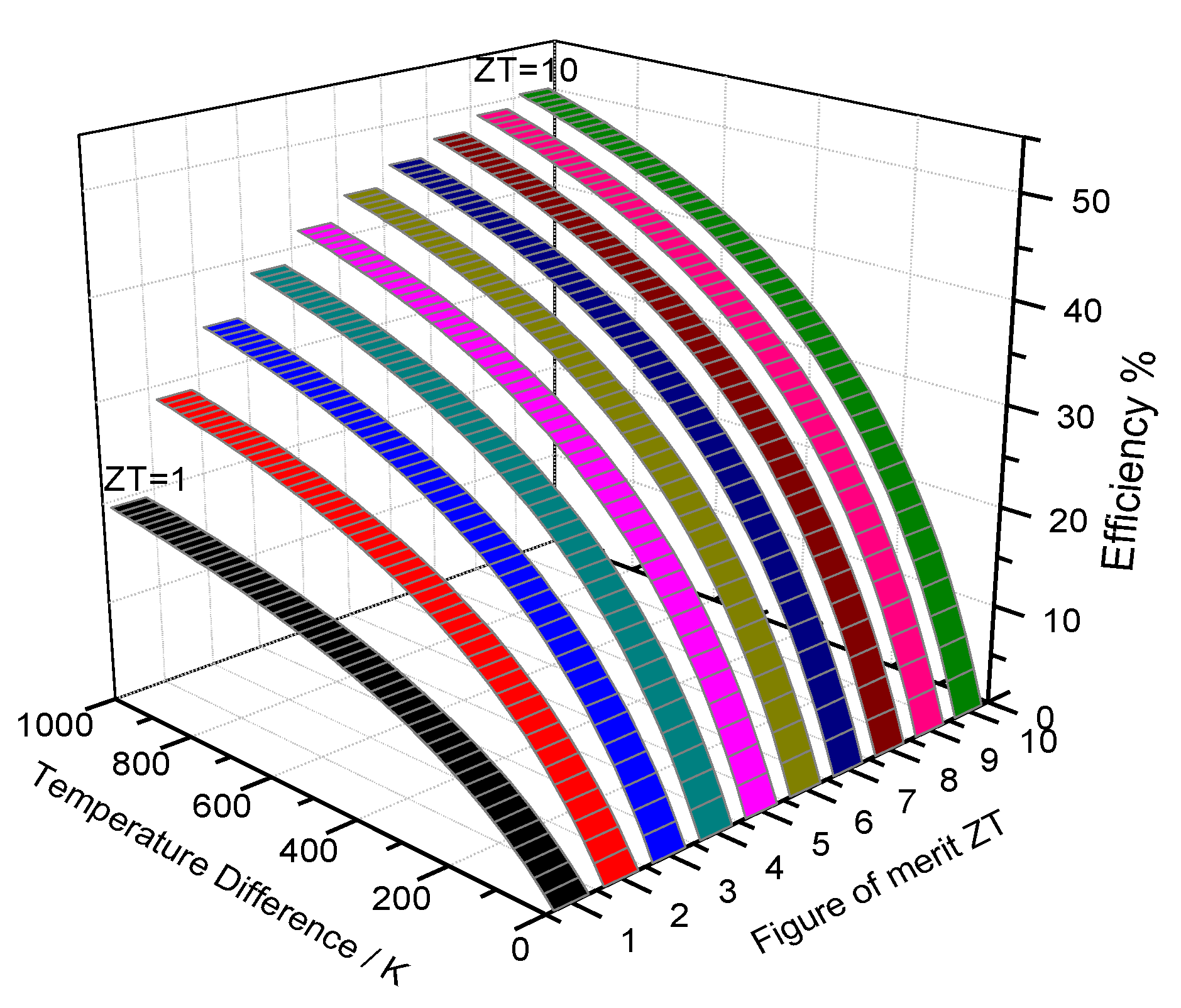
1.1. Introduction to Thermoelectrics
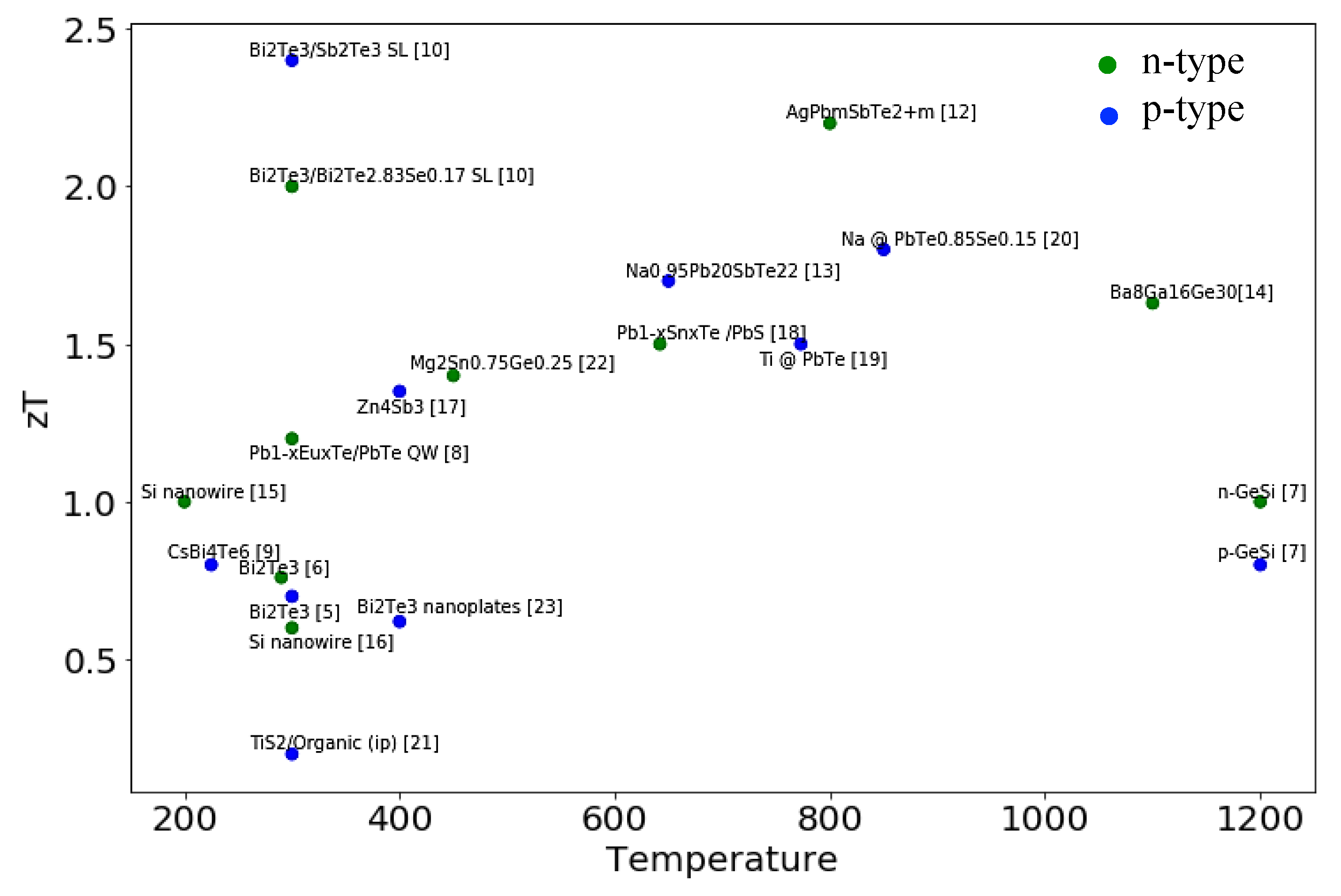
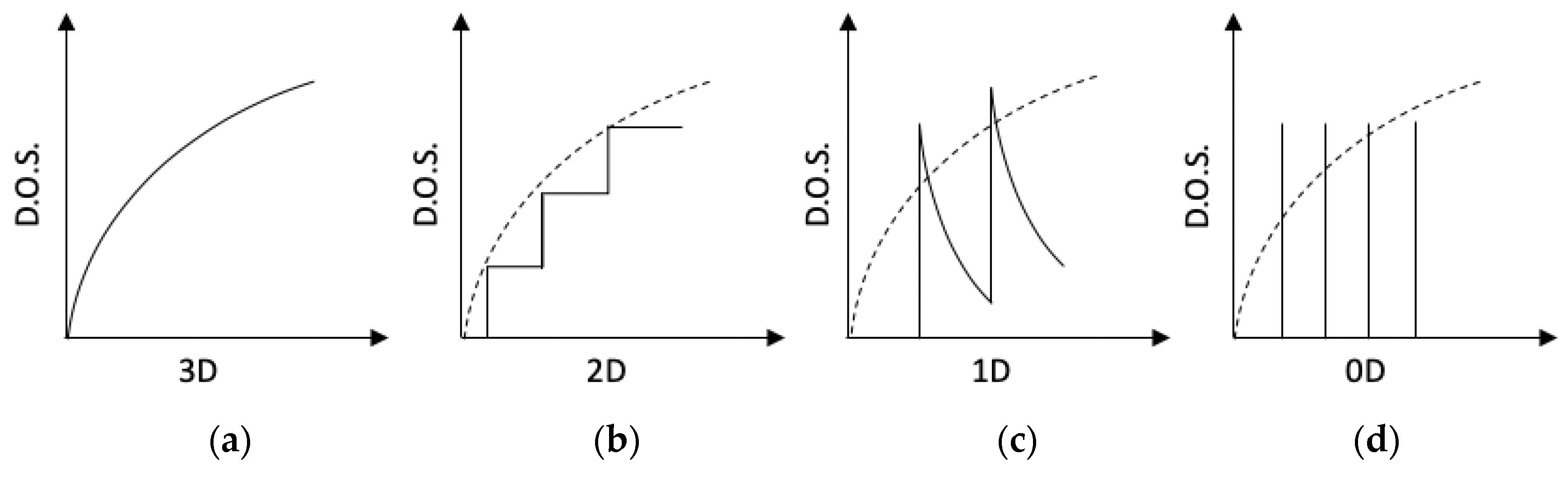
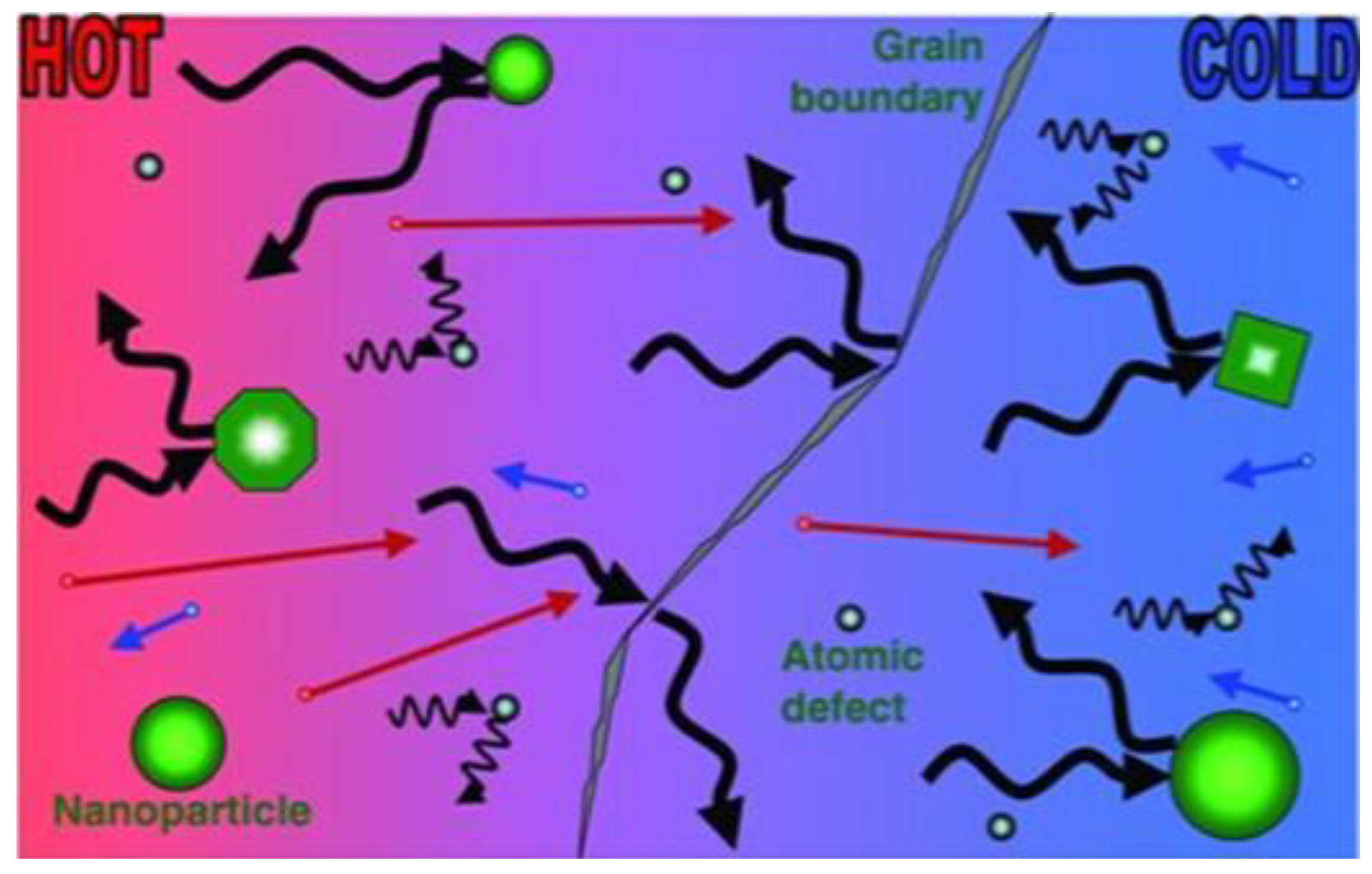
1.2. Approaches for Thermoelectrics Improvement
2. Atomic Layer Deposition Technique
3. Nanostructured Thermoelectrical Materials in zT Improvement
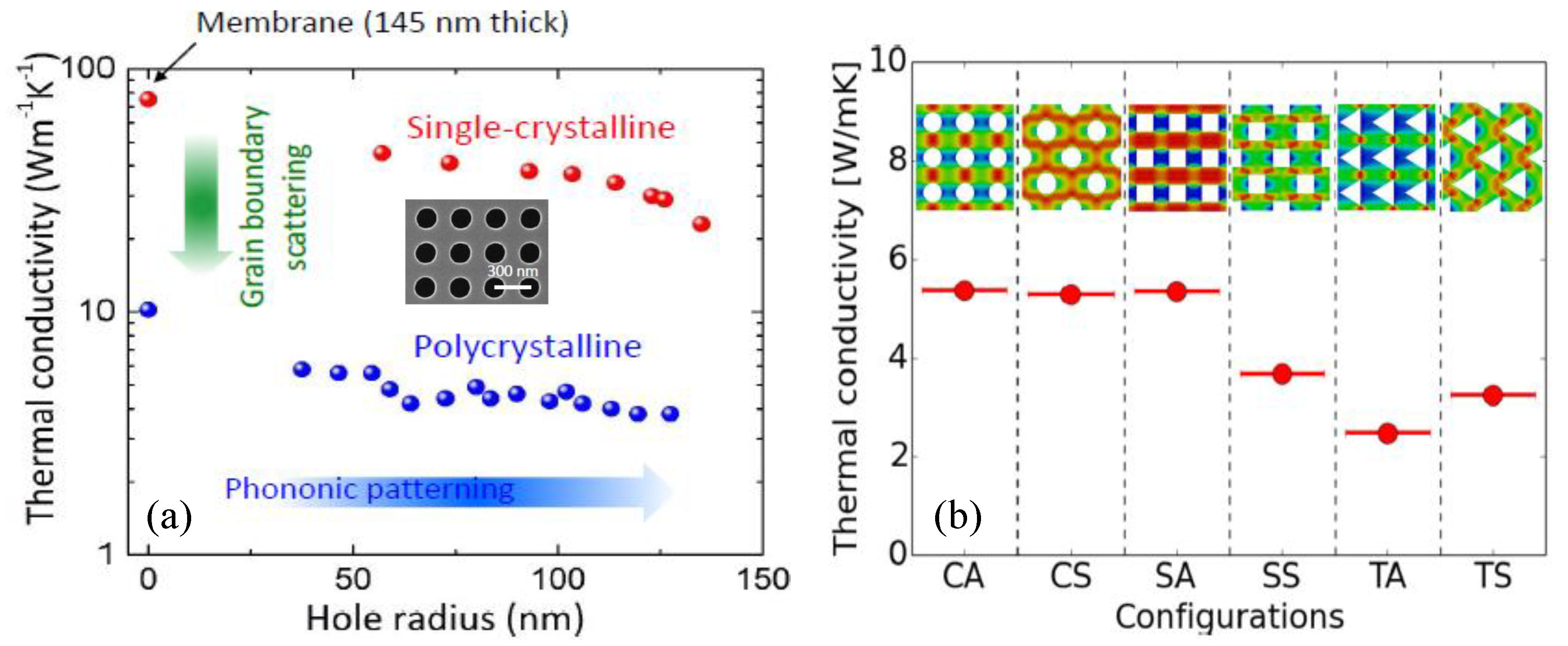
3.1. Phononic Crystal
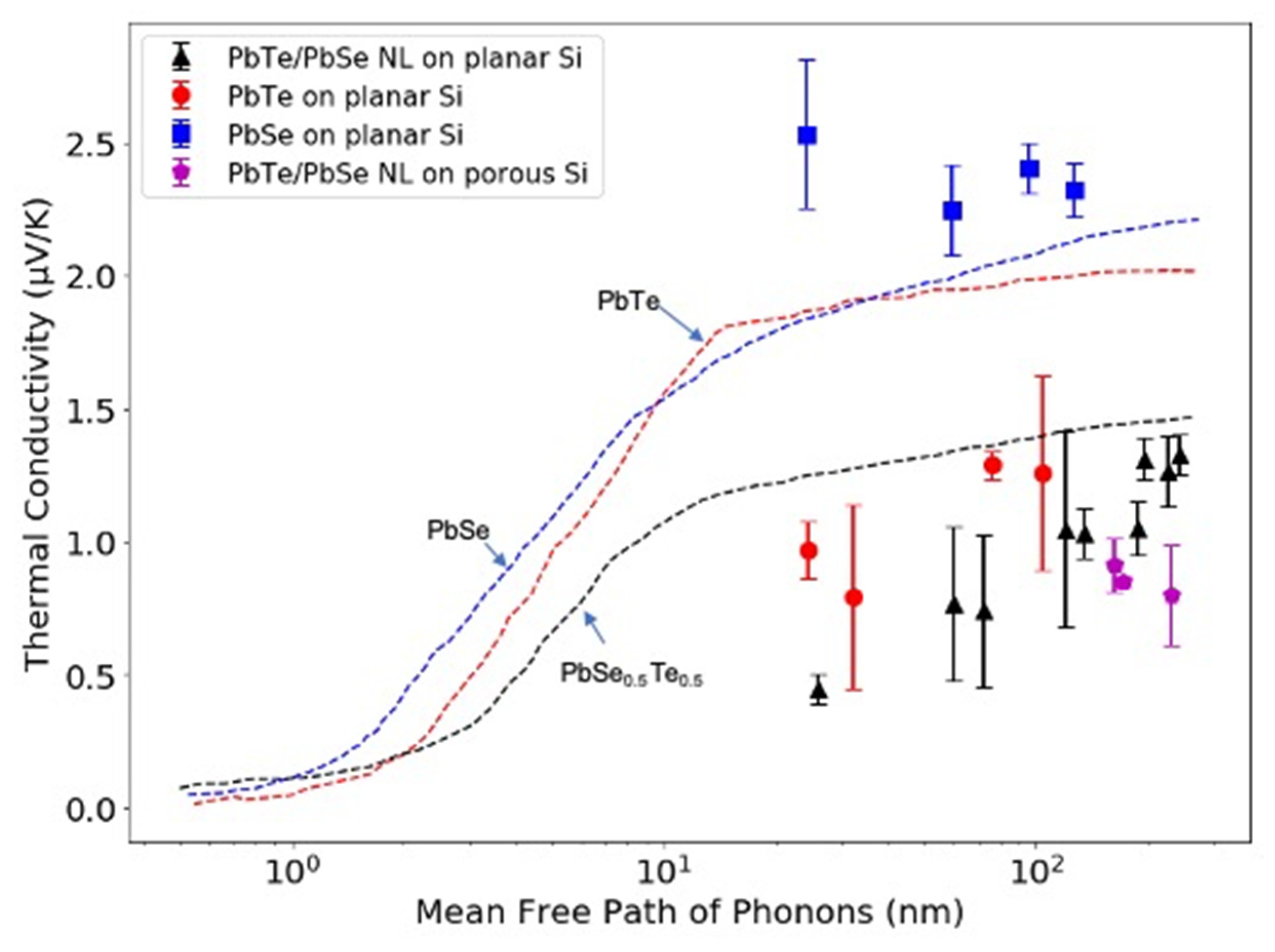
3.2. Lead Chalcogenide Based ALD Nanolaminate on Porous Templates
3.3. ZnO-Based ALD Themoelectric Nanolaminates
3.4. Hybrid Organic-Inorganic Superlattice Structures
4. Concluding Remarks and Future Outlook
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Chen, X.; Lin, P.; Zhang, K.; Baumgart, H.; Geist, B.; Kochergin, V. Seebeck Coefficient Enhancement of ALD PbTe/PbSe Nanolaminate Structures Deposited inside Porous Silicon Templates. ECS J. Solid State Sci. Technol. 2016, 5, P503–P508. [Google Scholar] [CrossRef] [Green Version]
- Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 1995; 701p. [Google Scholar]
- Vaqueiro, P.; Powell, A.V. Recent developments in nanostructured materials for high-performance thermoelectrics. J. Mater. Chem. 2010, 20, 9577–9584. [Google Scholar] [CrossRef] [Green Version]
- Jonson, M.; Mahan, G. Mott’s formula for the thermopower and the Wiedemann-Franz law. Phys. Rev. B 1980, 21, 4223. [Google Scholar] [CrossRef]
- Goldsmid, H.; Douglas, R. The use of semiconductors in thermoelectric refrigeration. Br. J. Appl. Phys. 1954, 5, 386. [Google Scholar] [CrossRef]
- Goldsmid, H.; Sheard, A.; Wright, D. The performance of bismuth telluride thermojunctions. Br. J. Appl. Phys. 1958, 9, 365. [Google Scholar] [CrossRef]
- Dismukes, J.; Ekstrom, L.; Steigmeier, E.; Kudman, I.; Beers, D. Thermal and electrical properties of heavily doped Ge-Si alloys up to 1300 K. J. Appl. Phys. 1964, 35, 2899–2907. [Google Scholar] [CrossRef]
- Harman, T.; Spears, D.; Manfra, M. High thermoelectric figures of merit in PbTe quantum wells. J. Electron. Mater. 1996, 25, 1121. [Google Scholar] [CrossRef]
- Chung, D.-Y.; Hogan, T.; Brazis, P.; Rocci-Lane, M.; Kannewurf, C.; Bastea, M.; Uher, C.; Kanatzidis, M.G. CsBi4Te6: A high-performance thermoelectric material for low-temperature applications. Science 2000, 287, 1024–1027. [Google Scholar] [CrossRef] [Green Version]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef]
- Harman, T.; Taylor, P.; Walsh, M.; LaForge, B. Quantum dot superlattice thermoelectric materials and devices. Science 2002, 297, 2229–2232. [Google Scholar] [CrossRef] [Green Version]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.; Kanatzidis, M.G. Cubic AgPbmSbTe2+ m: Bulk thermoelectric materials with high figure of merit. Science 2004, 303, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Poudeu, P.F.; D’Angelo, J.; Downey, A.D.; Short, J.L.; Hogan, T.P.; Kanatzidis, M.G. High Thermoelectric Figure of Merit and Nanostructuring in Bulk p-type Na1−xPbmSbyTem+2. Angew. Chem. Int. Ed. 2006, 45, 3835–3839. [Google Scholar] [CrossRef] [PubMed]
- Saramat, A.; Svensson, G.; Palmqvist, A.; Stiewe, C.; Müller, E.; Platzek, D.; Williams, S.; Rowe, D.; Bryan, J.; Stucky, G. Large thermoelectric figure of merit at high temperature in Czochralski-grown clathrate Ba 8 Ga 16 Ge 30. J. Appl. Phys. 2006, 99, 023708. [Google Scholar] [CrossRef] [Green Version]
- Boukai, A.I.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.-K.; Goddard Iii, W.A.; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Hochbaum, A.I.; Chen, R.; Delgado, R.D.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef]
- Snyder, G.J.; Christensen, M.; Nishibori, E.; Caillat, T.; Iversen, B.B. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties. Nat. Mater. 2004, 3, 458–463. [Google Scholar] [CrossRef]
- Androulakis, J.; Lin, C.-H.; Kong, H.-J.; Uher, C.; Wu, C.-I.; Hogan, T.; Cook, B.A.; Caillat, T.; Paraskevopoulos, K.M.; Kanatzidis, M.G. Spinodal decomposition and nucleation and growth as a means to bulk nanostructured thermoelectrics: Enhanced performance in Pb1-x Sn x Te-PbS. J. Am. Chem. Soc. 2007, 129, 9780–9788. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [Green Version]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, L.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef]
- Niemelä, J.-P.; Karttunen, A.; Karppinen, M. Inorganic–organic superlattice thin films for thermoelectrics. J. Mater. Chem. C 2015, 3, 10349–10361. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Kim, H.S.; Chen, S.; Jie, Q.; Lv, B.; Yao, M.; Ren, Z.; Opeil, C.P.; Wilson, S.; Chu, C.-W. n-type thermoelectric material Mg2Sn0. 75Ge0. 25 for high power generation. Proc. Natl. Acad. Sci. USA 2015, 112, 3269–3274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, J.S.; Choi, M.K.; Han, M.-K.; Park, K.; Kim, J.-Y.; Lim, S.J.; Oh, M.; Kuk, Y.; Park, C.; Kim, S.-J. n-type nanostructured thermoelectric materials prepared from chemically synthesized ultrathin Bi2Te3 nanoplates. Nano Lett. 2012, 12, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Rowe, D.M. Thermoelectrics Handbook: Macro to Nano; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Slack, G.A. Design concepts for improved thermoelectric materials. In MRS Online Proceedings Library Archive; Cambridge University Press: Cambridge, UK, 1997; Volume 478. [Google Scholar]
- Tong, X.C. Advanced Materials for Thermal Management of Electronic Packaging; Springer Science & Business Media: Berlin, Germany, 2011; Volume 30. [Google Scholar]
- Tritt, T.M. Thermoelectric phenomena, materials, and applications. Annu. Rev. Mater. Res. 2011, 41, 433–448. [Google Scholar] [CrossRef]
- Uher, C. Materials Aspect of Thermoelectricity; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Wang, S.; Salvador, J.R.; Yang, J.; Wei, P.; Duan, B.; Yang, J. High-performance n-type Yb x Co 4 Sb 12: From partially filled skutterudites towards composite thermoelectrics. NPG Asia Mater. 2016, 8, e285. [Google Scholar] [CrossRef] [Green Version]
- Sales, B.C.; Chakoumakos, B.; Jin, R.; Thompson, J.; Mandrus, D. Structural, magnetic, thermal, and transport properties of X 8 Ga 16 Ge 30 (X= E u, S r, Ba) single crystals. Phys. Rev. B 2001, 63, 245113. [Google Scholar] [CrossRef]
- Suekuni, K.; Avila, M.; Umeo, K.; Fukuoka, H.; Yamanaka, S.; Nakagawa, T.; Takabatake, T. Simultaneous structure and carrier tuning of dimorphic clathrate Ba 8 Ga 16 Sn 30. Phys. Rev. B 2008, 77, 235119. [Google Scholar] [CrossRef]
- Takabatake, T. Nano-cage structured materials: Clathrates. In Thermoelectric Nanomaterials; Springer: Berlin, Germany, 2013; pp. 33–49. [Google Scholar]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef]
- Toberer, E.S.; May, A.F.; Snyder, G.J. Zintl chemistry for designing high efficiency thermoelectric materials. Chem. Mater. 2009, 22, 624–634. [Google Scholar] [CrossRef]
- Slack, G.A. The thermal conductivity of nonmetallic crystals. Solid State Phys. 1979, 34, 1–71. [Google Scholar]
- Kim, W.; Wang, R.; Majumdar, A. Nanostructuring expands thermal limits. Nano Today 2007, 2, 40–47. [Google Scholar] [CrossRef]
- Liu, C.-J.; Liu, G.-J.; Liu, Y.-L.; Chen, L.-R. Thermoelectric properties of compacted Bi2-xSbxTe3 nanoplatelets with nominal composition of x= 1.5. In AIP Conference Proceedings; American Institute of Physics: College Park, MA, USA, 2012; pp. 103–106. [Google Scholar]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dresselhaus, M.S.; Chen, G.; Tang, M.Y.; Yang, R.; Lee, H.; Wang, D.; Ren, Z.; Fleurial, J.P.; Gogna, P. New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and old concepts in thermoelectric materials. Angew. Chem. Int. Edit. 2009, 48, 8616–8639. [Google Scholar] [CrossRef] [PubMed]
- Vineis, C.J.; Shakouri, A.; Majumdar, A.; Kanatzidis, M.G. Nanostructured thermoelectrics: Big efficiency gains from small features. Adv. Mater. 2010, 22, 3970–3980. [Google Scholar] [CrossRef] [PubMed]
- Harman, T.; Taylor, P.; Spears, D.; Walsh, M. PbTe-based quantum-dot thermoelectric materials with high ZT. In Proceedings of the Eighteenth International Conference on Thermoelectrics. Proceedings, ICT’99 (Cat. No. 99TH8407), Baltimore, MD, USA, 29 August–2 September 1999; IEEE: Piscataway, NJ, USA, 2002; pp. 280–284. [Google Scholar]
- Caylor, J.; Coonley, K.; Stuart, J.; Colpitts, T.; Venkatasubramanian, R. Enhanced thermoelectric performance in PbTe-based superlattice structures from reduction of lattice thermal conductivity. Appl. Phys. Lett. 2005, 87, 023105. [Google Scholar] [CrossRef]
- Hsieh, T.-Y.; Lin, H.; Hsieh, T.-J.; Huang, J.-C. Thermal conductivity modeling of periodic porous silicon with aligned cylindrical pores. J. Appl. Phys. 2012, 111, 124329. [Google Scholar] [CrossRef]
- Dauscher, A.; Dinescu, M.; Boffoué, O.; Jacquot, A.; Lenoir, B. Temperature-dependant growth of PbTe pulsed laser deposited films on various substrates. Thin Solid Films 2006, 497, 170–176. [Google Scholar] [CrossRef]
- Trindade, T.; Brien, P.O. Lead (II) dithiocarbamato complexes as precursors for the LP-MOCVD of lead sulfide. Chem. Vap. Depos. 1997, 3, 75–77. [Google Scholar] [CrossRef]
- Jdanov, A.; Pelleg, J.; Dashevsky, Z.; Shneck, R. Growth and characterization of PbTe films by magnetron sputtering. Mater. Sci. Eng. B 2004, 106, 89–94. [Google Scholar] [CrossRef]
- Wu, H.; Cao, C.; Si, J.; Xu, T.; Zhang, H.; Wu, H.; Chen, J.; Shen, W.; Dai, N. Observation of phonon modes in epitaxial PbTe films grown by molecular beam epitaxy. J. Appl. Phys. 2007, 101, 103505. [Google Scholar] [CrossRef]
- Banga, D.; Kim, Y.-G.; Stickney, J. PbSe∕ PbTe Superlattice Formation via E-ALD. J. Electrochem. Soc. 2011, 158, D99–D106. [Google Scholar] [CrossRef]
- Lin, P.; Chen, X.; Zhang, K.; Baumgart, H. Improved Gas Sensing Performance of ALD AZO 3-D Coated ZnO Nanorods. ECS J. Solid State Sci. Technol. 2018, 7, Q246–Q252. [Google Scholar] [CrossRef]
- Gu, D.; Baumgart, H.; Abdel-Fattah, T.M.; Namkoong, G. Synthesis of nested coaxial multiple-walled nanotubes by atomic layer deposition. Acs Nano 2010, 4, 753–758. [Google Scholar] [CrossRef] [PubMed]
- Gu, D.; Baumgart, H.; Tapily, K.; Shrestha, P.; Namkoong, G.; Ao, X.; Müller, F. Precise control of highly ordered arrays of nested semiconductor/metal nanotubes. Nano Res. 2011, 4, 164–170. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-M.; Kong, D.-L.; Chen, Q.; Xue, J.-M. Surface engineering of synthetic nanopores by atomic layer deposition and their applications. Front. Mater. Sci. 2013, 7, 335–349. [Google Scholar] [CrossRef] [Green Version]
- George, S.M. Atomic layer deposition: An overview. Chem. Rev. 2010, 110, 111–131. [Google Scholar] [CrossRef]
- Puurunen, R.L. Surface chemistry of atomic layer deposition: A case study for the trimethylaluminum/water process. J. Appl. Phys. 2005, 97, 9. [Google Scholar] [CrossRef]
- Mackus, A.J.; Schneider, J.R.; MacIsaac, C.; Baker, J.G.; Bent, S.F. Synthesis of doped, ternary, and quaternary materials by atomic layer deposition: A review. Chem. Mater. 2018, 31, 1142–1183. [Google Scholar] [CrossRef]
- Sønsteby, H.H.; Fjellvåg, H.; Nilsen, O. Functional perovskites by atomic layer deposition–an overview. Adv. Mater. Interfaces 2017, 4, 1600903. [Google Scholar] [CrossRef]
- Nakagawa, J.; Kage, Y.; Hori, T.; Shiomi, J.; Nomura, M. Crystal structure dependent thermal conductivity in two-dimensional phononic crystal nanostructures. Appl. Phys. Lett. 2015, 107, 023104. [Google Scholar] [CrossRef] [Green Version]
- Nomura, M.; Kage, Y.; Nakagawa, J.; Hori, T.; Shiomi, J.M.J.; Moser, D.; Paul, O. Multiscale phonon blocking in Si phononic crystal nanostructures. arXiv 2015, arXiv:1502.02789. [Google Scholar]
- Majumdar, A. Thermoelectricity in semiconductor nanostructures. Science 2004, 303, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-H.; Galli, G.A.; Grossman, J.C. Nanoporous Si as an efficient thermoelectric material. Nano Lett. 2008, 8, 3750–3754. [Google Scholar] [CrossRef]
- Hopkins, P.E.; Rakich, P.T.; Olsson, R.H.; El-Kady, I.F.; Phinney, L.M. Origin of reduction in phonon thermal conductivity of microporous solids. Appl. Phys. Lett. 2009, 95, 161902. [Google Scholar] [CrossRef]
- Nomura, M.; Kage, Y.; Nakagawa, J.; Hori, T.; Maire, J.; Shiomi, J.; Anufriev, R.; Moser, D.; Paul, O. Impeded thermal transport in Si multiscale hierarchical architectures with phononic crystal nanostructures. Phys. Rev. B 2015, 91, 205422. [Google Scholar] [CrossRef]
- Nomura, M.; Kage, Y.; Müller, D.; Moser, D.; Paul, O. Electrical and thermal properties of polycrystalline Si thin films with phononic crystal nanopatterning for thermoelectric applications. Appl. Phys. Lett. 2015, 106, 223106. [Google Scholar] [CrossRef]
- Song, D.; Chen, G. Thermal conductivity of periodic microporous silicon films. Appl. Phys. Lett. 2004, 84, 687–689. [Google Scholar] [CrossRef]
- Romano, G.; Di Carlo, A.; Grossman, J.C. Mesoscale modeling of phononic thermal conductivity of porous Si: Interplay between porosity, morphology and surface roughness. J. Comput. Electron. 2012, 11, 8–13. [Google Scholar] [CrossRef]
- Romano, G.; Grossman, J.C. Toward phonon-boundary engineering in nanoporous materials. Appl. Phys. Lett. 2014, 105, 033116. [Google Scholar] [CrossRef] [Green Version]
- Geist, B.L.; Zaynetdinov, M.; Myers, K.; Zhang, K.; Chen, X.; Pillai, A.R.; Baumgart, H.; Robinson, H.D.; Kochergin, V. Fabrication and Characterization of Nanostructured Thermoelectric Materials and Devices. In Proceedings of MRS Proceedings; Cambridge University Press: Cambridge, UK, 2015; p. mrsf14-1735-cc14-35. [Google Scholar]
- Vaidyanathan, R.; Cox, S.M.; Happek, U.; Banga, D.; Mathe, M.K.; Stickney, J.L. Preliminary studies in the electrodeposition of PbSe/PbTe superlattice thin films via electrochemical atomic layer deposition (ALD). Langmuir 2006, 22, 10590–10595. [Google Scholar] [CrossRef]
- Zhang, K.; Pillai, A.R.; Bollenbach, K.; Nminibapiel, D.; Cao, W.; Baumgart, H.; Scherer, T.; Chakravadhanula, V.; Kübel, C.; Kochergin, V. Atomic layer deposition of nanolaminate structures of alternating PbTe and PbSe thermoelectric films. ECS J. Solid State Sci. Technol. 2014, 3, P207. [Google Scholar] [CrossRef] [Green Version]
- Robinson, H.D.; Sneh, O.; Kochergin, V. Nanostructured Telluride Films on Macroporous Silicon for High Efficiency Thermoelectric Devices. In MRS Online Proceedings Library Archive; Cambridge University Press: Cambridge, UK, 2011; Volume 1314. [Google Scholar]
- Zhang, K.; Pillai, A.D.R.; Nminibapiel, D.; Tangirala, M.; Chakravadhanula, V.S.; Kübel, C.; Baumgart, H.; Kochergin, V. ALD growth of PbTe and PbSe superlattices for thermoelectric applications. ECS Trans. 2013, 58, 131–139. [Google Scholar] [CrossRef]
- Chen, X. Enhancement of Thermoelectric Properties of ALD Synthesized PbTe and PbSe by Phonon Engineering; Old Dominion University: Norfolk, Virginia, 2017. [Google Scholar]
- Vineis, C.; Harman, T.; Calawa, S.; Walsh, M.; Reeder, R.; Singh, R.; Shakouri, A. Carrier concentration and temperature dependence of the electronic transport properties of epitaxial PbTe and PbTe/PbSe nanodot superlattices. Phys. Rev. B 2008, 77, 235202. [Google Scholar] [CrossRef]
- Streetman, B.G.; Banerjee, S. Solid State Electronic Devices; Prentice Hall: Upper Saddle River, NJ, USA, 2000; Volume 5. [Google Scholar]
- Wan, B.; Hu, C.; Xi, Y.; Xu, J.; He, X. Room-temperature synthesis and seebeck effect of lead chalcogenide nanocubes. Solid State Sci. 2010, 12, 123–127. [Google Scholar] [CrossRef]
- Tian, Z.; Garg, J.; Esfarjani, K.; Shiga, T.; Shiomi, J.; Chen, G. Phonon conduction in PbSe, PbTe, and PbTe 1− x Se x from first-principles calculations. Phys. Rev. B 2012, 85, 184303. [Google Scholar] [CrossRef] [Green Version]
- DeCoster, M.E.; Chen, X.; Zhang, K.; Rost, C.M.; Hoglund, E.R.; Howe, J.M.; Beechem, T.E.; Baumgart, H.; Hopkins, P.E. Thermal Conductivity and Phonon Scattering Processes of ALD Grown PbTe–PbSe Thermoelectric Thin Films. Adv. Funct. Mater. 2019, 29, 1904073. [Google Scholar] [CrossRef]
- Lee, W.-Y.; Park, N.-W.; Kang, S.-Y.; Kim, G.-S.; Koh, J.-H.; Saitoh, E.; Lee, S.-K. Enhanced Cross-Plane Thermoelectric Figure of Merit Observed in Al2O3/ZnO Superlattice Film by Hole Carrier Blocking and Phonon Scattering. J. Phys. Chem. C 2019. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Liu, F.; He, D.; He, J.; Luo, J.; Xiao, Y.; Pan, F. Effective atomic interface engineering in Bi2Te2. 7Se0. 3 thermoelectric material by atomic-layer-deposition approach. Nano Energy 2018, 49, 257–266. [Google Scholar] [CrossRef]
- Meng, C.; Liu, C.; Fan, S. A promising approach to enhanced thermoelectric properties using carbon nanotube networks. Adv. Mater. 2010, 22, 535–539. [Google Scholar] [CrossRef]
- Luo, J.; Billep, D.; Waechtler, T.; Otto, T.; Toader, M.; Gordan, O.; Sheremet, E.; Martin, J.; Hietschold, M.; Zahn, D.R. Enhancement of the thermoelectric properties of PEDOT: PSS thin films by post-treatment. J. Mater. Chem. A 2013, 1, 7576–7583. [Google Scholar] [CrossRef]
- Talin, A.A.; Centrone, A.; Ford, A.C.; Foster, M.E.; Stavila, V.; Haney, P.; Kinney, R.A.; Szalai, V.; El Gabaly, F.; Yoon, H.P. Tunable electrical conductivity in metal-organic framework thin-film devices. Science 2014, 343, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wang, Z.; Hassan, Z.M.; Lin, P.; Zhang, K.; Baumgart, H.; Redel, E. Seebeck Coefficient Measurements of Polycrystalline and Highly Ordered Metal-Organic Framework Thin Films. ECS J. Solid State Sci. Technol. 2017, 6, P150–P153. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Wang, Z.; Lin, P.; Zhang, K.; Baumgart, H.; Redel, E.; Wöll, C. Thermoelectric Properties of Highly Ordered Metal-Organic Framework Films. ECS Trans. 2016, 75, 119–126. [Google Scholar] [CrossRef]
- Wan, C.; Gu, X.; Dang, F.; Itoh, T.; Wang, Y.; Sasaki, H.; Kondo, M.; Koga, K.; Yabuki, K.; Snyder, G.J. Flexible n-type thermoelectric materials by organic intercalation of layered transition metal dichalcogenide TiS 2. Nat. Mater. 2015, 14, 622. [Google Scholar] [CrossRef] [PubMed]
- Karttunen, A.J.; Sarnes, L.; Townsend, R.; Mikkonen, J.; Karppinen, M. Flexible thermoelectric ZnO–organic superlattices on cotton textile substrates by ALD/MLD. Adv. Electron. Mater. 2017, 3, 1600459. [Google Scholar] [CrossRef] [Green Version]
- Tynell, T.; Giri, A.; Gaskins, J.; Hopkins, P.E.; Mele, P.; Miyazaki, K.; Karppinen, M. Efficiently suppressed thermal conductivity in ZnO thin films via periodic introduction of organic layers. J. Mater. Chem. A 2014, 2, 12150–12152. [Google Scholar] [CrossRef] [Green Version]
- Niemelä, J.-P.; Giri, A.; Hopkins, P.E.; Karppinen, M. Ultra-low thermal conductivity in TiO 2: C superlattices. J. Mater. Chem. A 2015, 3, 11527–11532. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.T.; Choi, S.Y.; Shin, E.H.; Moon, K.S.; Koo, H.Y.; Lee, G.-G.; Ha, G.H. The influence of CNTs on the thermoelectric properties of a CNT/Bi2Te3 composite. Carbon 2013, 52, 541–549. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Baumgart, H. Advances in Atomic Layer Deposition (ALD) Nanolaminate Synthesis of Thermoelectric Films in Porous Templates for Improved Seebeck Coefficient. Materials 2020, 13, 1283. https://doi.org/10.3390/ma13061283
Chen X, Baumgart H. Advances in Atomic Layer Deposition (ALD) Nanolaminate Synthesis of Thermoelectric Films in Porous Templates for Improved Seebeck Coefficient. Materials. 2020; 13(6):1283. https://doi.org/10.3390/ma13061283
Chicago/Turabian StyleChen, Xin, and Helmut Baumgart. 2020. "Advances in Atomic Layer Deposition (ALD) Nanolaminate Synthesis of Thermoelectric Films in Porous Templates for Improved Seebeck Coefficient" Materials 13, no. 6: 1283. https://doi.org/10.3390/ma13061283
APA StyleChen, X., & Baumgart, H. (2020). Advances in Atomic Layer Deposition (ALD) Nanolaminate Synthesis of Thermoelectric Films in Porous Templates for Improved Seebeck Coefficient. Materials, 13(6), 1283. https://doi.org/10.3390/ma13061283




