Effects of Feed per Tooth and Radial Depth of Cut on Amplitude Parameters and Power Spectral Density of a Machined Surface
Abstract
:1. Introduction
2. Simulation Model of 3D Surface in End Milling
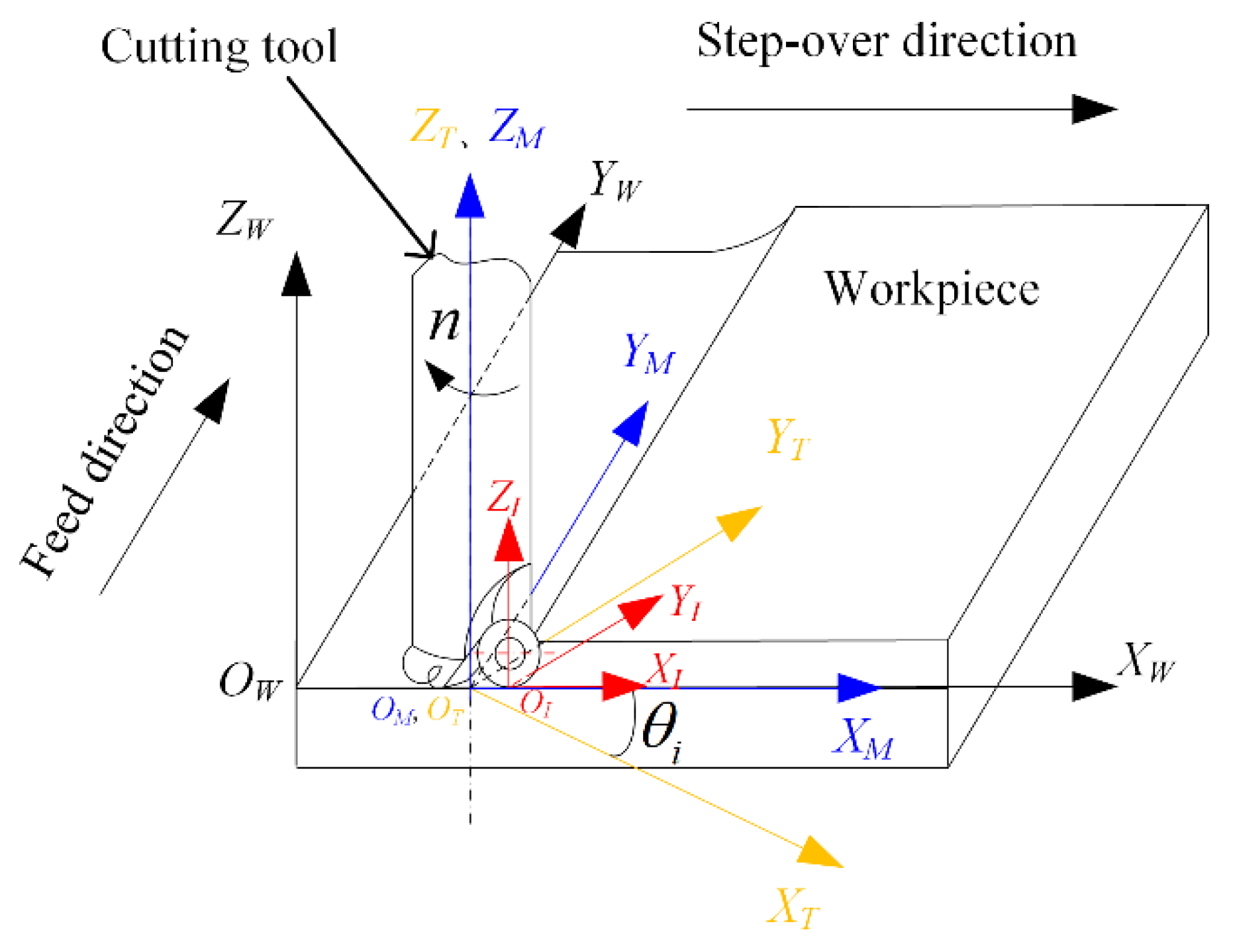
2.1. Modelling of Cutting Tool Insert Trajectory
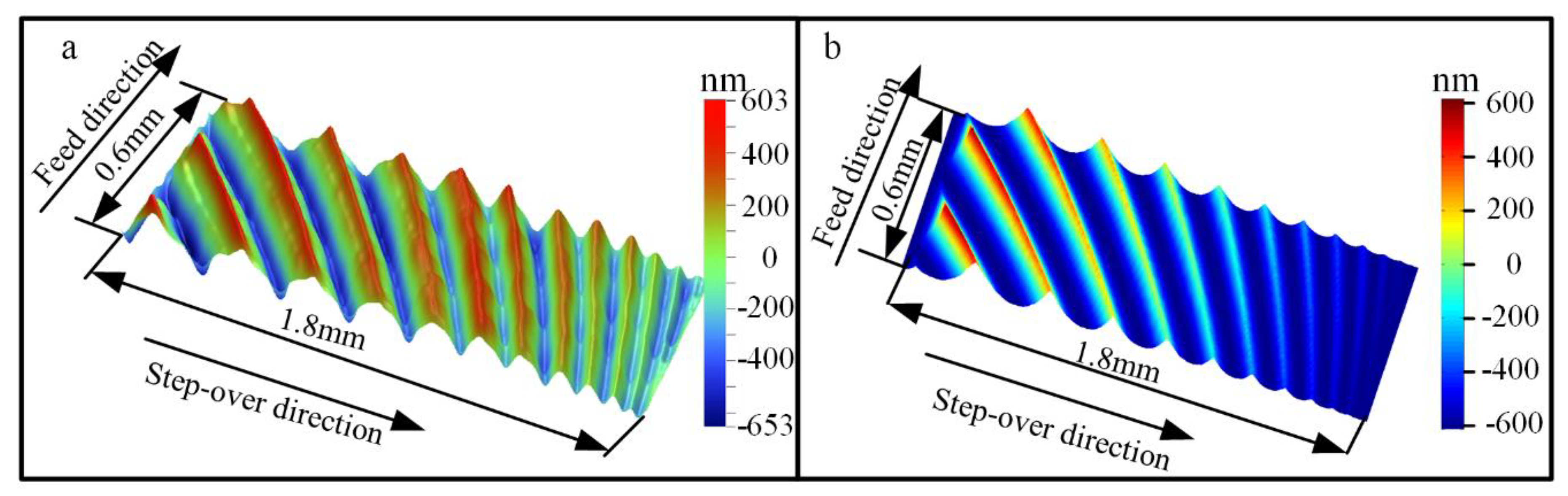
2.2. Experimental Verification of the Model
3. Results and Discussion
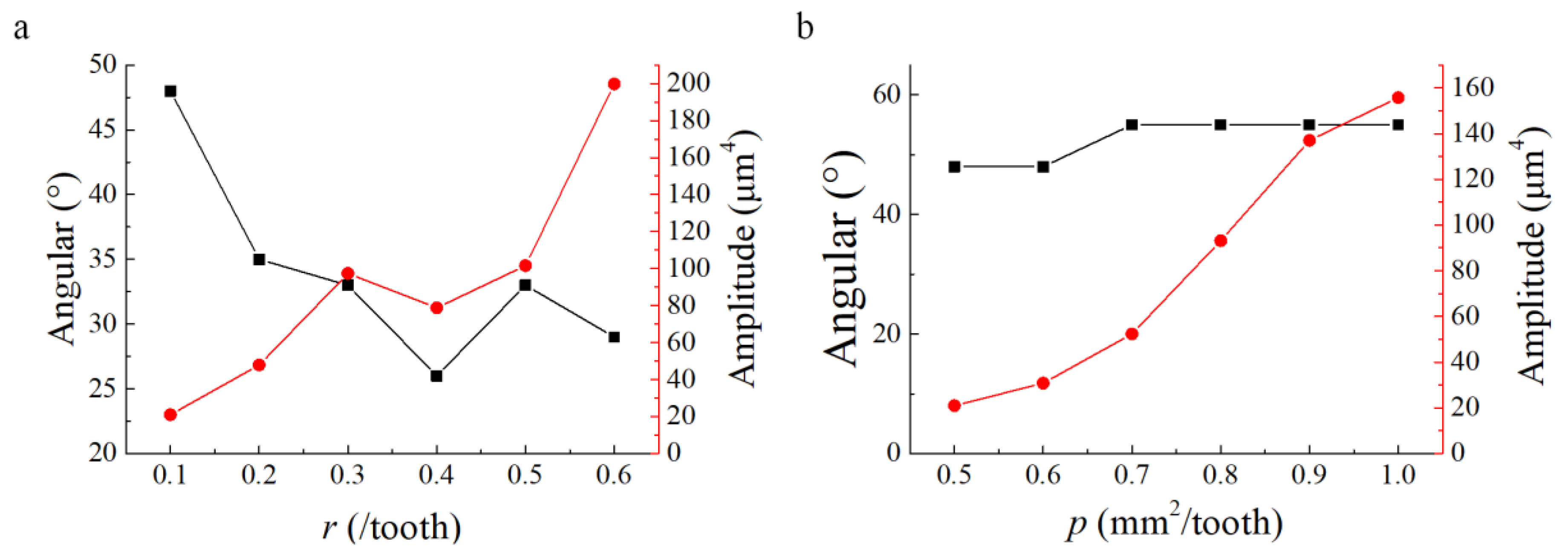
3.1. Influence of p and r on Amplitude Parameters
3.2. Research on PSD Based on the Simulation Model
3.2.1. PSD of the Machined Surface
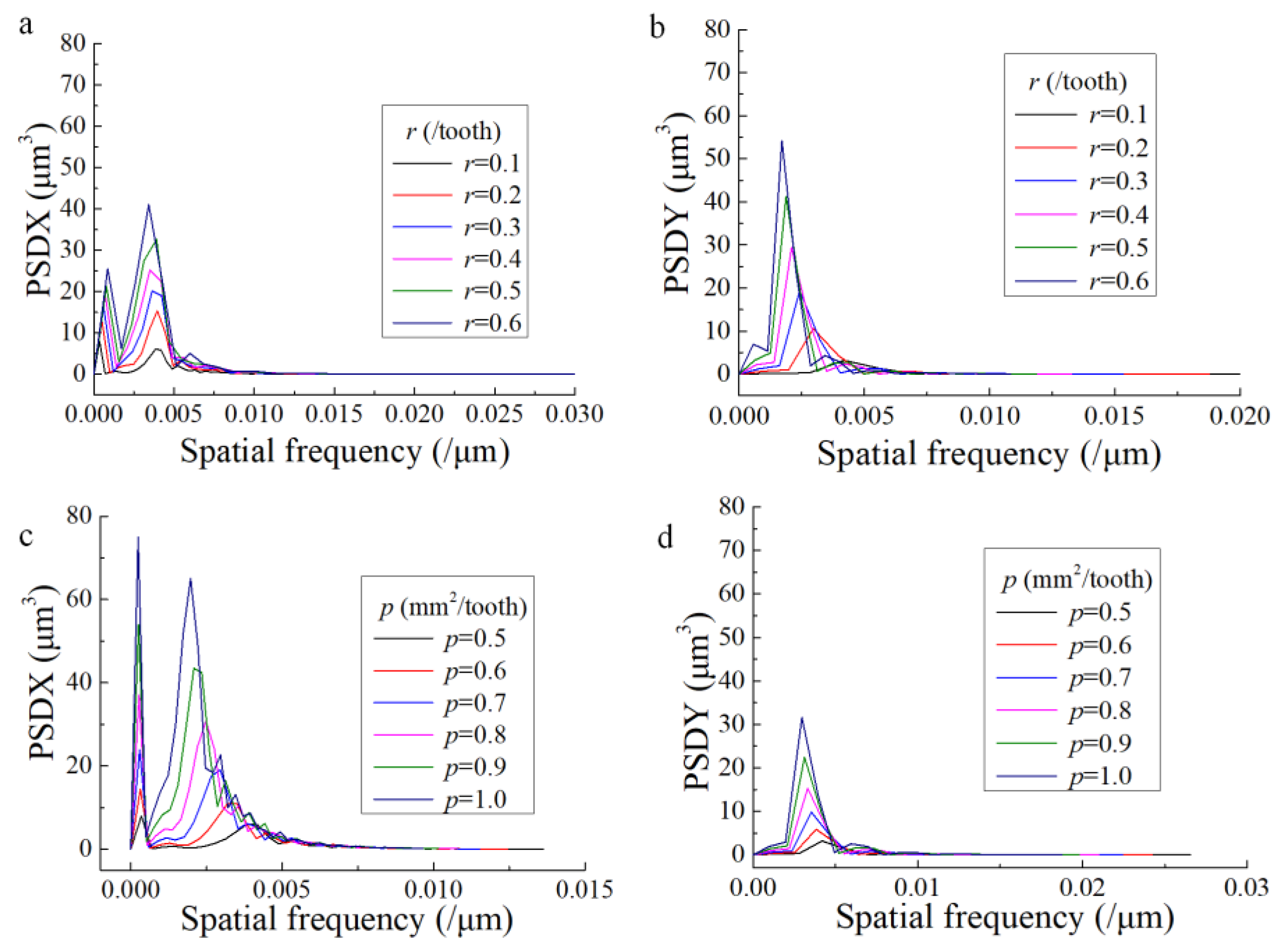
3.2.2. Influence of p and r on 1D PSD
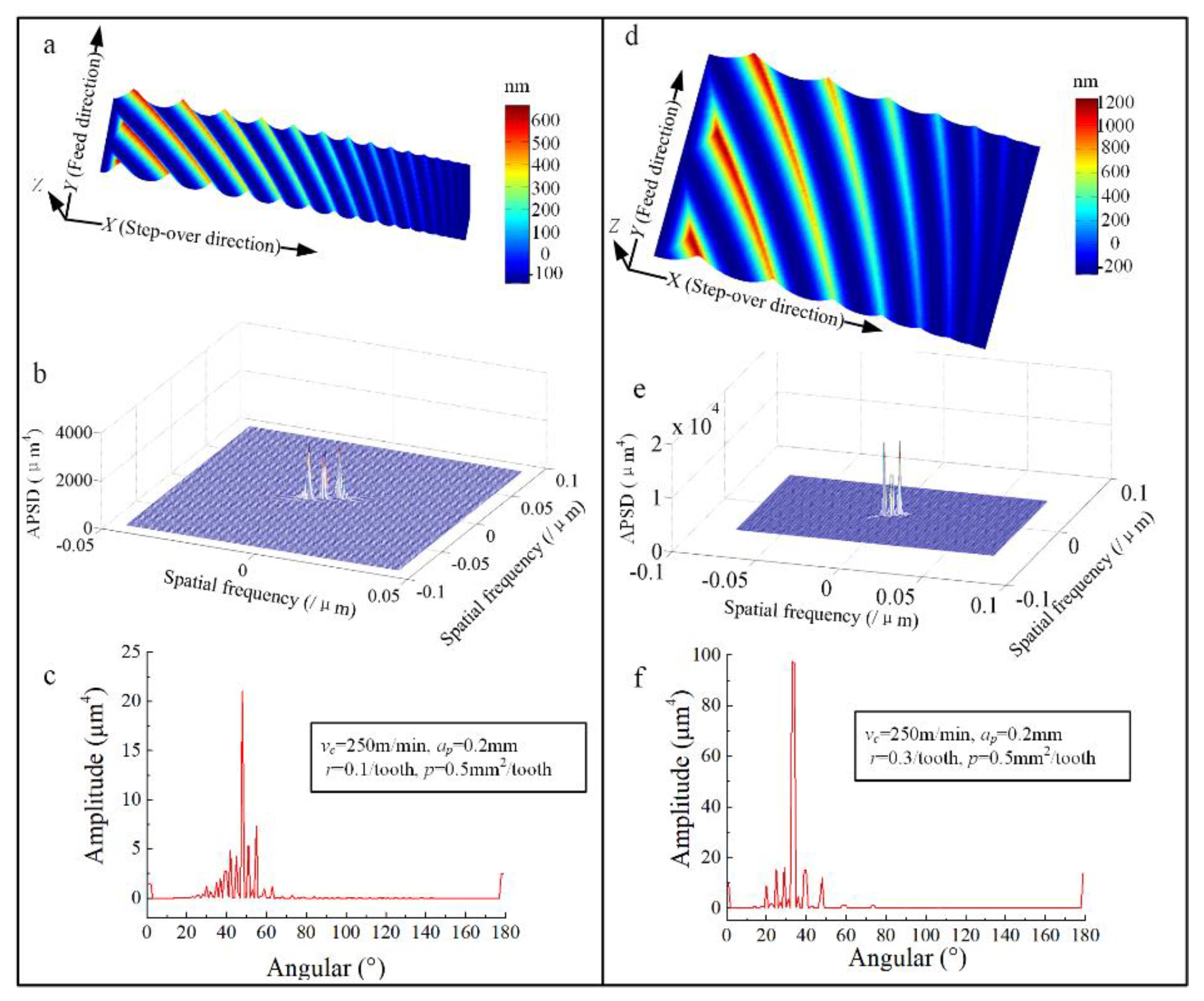
3.2.3. Research on APSD and the Angular Spectrum of the Milled Surface
4. Conclusions
- Sba and Sq have a monotonous tendency to increase with the increase of r and p. The exponential models of Sba and Sq versus r and p were fitted.
- The effects of p and r on the 1D PSD profile along the feed direction and step-over direction were researched. The result shows that the PSD amplitude is higher with higher values of both p and r along the feed and step-over directions. fz affects the peaks of the 1D PSD along both directions whereas ae affects the peak of the 1D PSD along the step-over direction.
- The angular spectrum of the surface was calculated by the APSD. It can be found that the number of the angle spectrum peaks for the specific machined surface approximately equals the number of residual ridges on the surface topography. The research on the effect of p and r on the angular spectrum reveals that r is the dominant factor influencing the direction of surface energy spectrum distribution.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krolczyk, G.M.; Maruda, R.W.; Krolczyk, J.B.; Nieslony, P.; Wojciechowski, S.; Legutko, S. Parametric and nonparametric description of the surface topography in the dry and MQCL cutting conditions. Measurement 2018, 121, 225–239. [Google Scholar] [CrossRef]
- Menezes, P.L.; Kishore; Kailas, S.V. Effect of surface roughness parameters and surface texture on friction and transfer layer formation in tin–steel tribo-system. J. Mater. Process. Technol. 2008, 208, 372–382. [Google Scholar] [CrossRef]
- Singh, R.; Melkote, S.N.; Hashimoto, F. Frictional response of precision finished surfaces in pure sliding. Wear 2005, 258, 1500–1509. [Google Scholar] [CrossRef]
- Suraratchai, M.; Limido, J.; Mabru, C.; Chieragatti, R. Modelling the influence of machined surface roughness on the fatigue life of aluminium alloy. Int. J. Fatigue 2008, 30, 2119–2126. [Google Scholar] [CrossRef] [Green Version]
- Guillemot, N.; Lartigue, C.; Billardon, R.; Mawussi, B.K. Prediction of the endurance limit taking account of the microgeometry after finishing milling. IJIDeM 2010, 4, 239–249. [Google Scholar] [CrossRef]
- Novovic, D.; Dewes, R.C.; Aspinwall, D.K.; Voice, W.; Bowen, P. The effect of machined topography and integrity on fatigue life. Int. J. Mach. Tools Manuf. 2004, 44, 125–134. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Vivancos-Calvet, J.; González-Rojas, H. Influence of feed, eccentricity and helix angle on topography obtained in side milling processes. Int. J. Mach. Tools Manuf. 2011, 51, 889–897. [Google Scholar] [CrossRef]
- Ryu, S.H.; Choi, D.K.; Chu, C.N. Roughness and texture generation on end milled surfaces. Int. J. Mach. Tools Manuf. 2006, 46, 404–412. [Google Scholar] [CrossRef]
- Shaghayegh, S.; Hossein, S.M.; Hamed, H. The influence of tool path strategies on cutting force and surface texture during ball end milling of low curvature convex surfaces. Sci. World J. 2014, 2014, 1–14. [Google Scholar]
- Lavernhe, S.; Quinsat, Y.; Lartigue, C. Model for the prediction of 3D surface topography in 5-axis milling. Int. J. Adv. Manuf. Technol. 2010, 51, 915–924. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhao, J.; Zhang, W. Influence of milling modes and tool postures on the milled surface for multi-axis finish ball-end milling. Int. J. Adv. Manuf. Technol. 2015, 77, 2035–2050. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Prediction of surface roughness in hard turning under high pressure coolant using Artificial Neural Network. Measurement 2016, 92, 464–474. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Modeling of Surface Roughness Using RSM, FL and SA in Dry Hard Turning. Arab. J. Sci. Eng. 2018, 43, 1125–1136. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Z. Surface topography analysis and cutting parameters optimization for peripheral milling titanium alloy Ti–6Al–4V. Int. J. Refract. Met. Hard Mater. 2015, 51, 192–200. [Google Scholar] [CrossRef]
- Tangjitsitcharoen, S.; Thesniyom, P.; Ratanakuakangwan, S. Prediction of surface roughness in ball-end milling process by utilizing dynamic cutting force ratio. J. Intell. Manuf. 2017, 28, 13–21. [Google Scholar] [CrossRef]
- Twardowski, P.; Wojciechowski, S.; Wieczorowski, M.; Mathia, T. Surface roughness analysis of hardened steel after high-speed milling. Scanning 2011, 33, 386–395. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, S.; Shi, W. Modeling of surface topography based on relationship between feed per tooth and radial depth of cut in ball-end milling of AISI H13 steel. Int. J. Adv. Manuf. Technol. 2018, 95, 4199–4209. [Google Scholar] [CrossRef]
- Lawson, J.K.; Wolfe, C.R.; Manes, K.R.; Trertholme, J.B.; Aikens, D.M.; English, R.E., Jr. Specification of optical components using the power spectral density function. Proc. SPIE 2536, Opt. Manuf. Test. 1995, 2536, 38–50. [Google Scholar]
- Alcock, S.G.; Ludbrook, G.D.; Owen, T.; Dockree, R. Using the power spectral density method to characterise the surface topography of optical surfaces. Proc. SPIE 7801, Adv. Metrol. X-Ray EUV Opt. III 2010, 7801, 1–8. [Google Scholar]
- Michalski, J. Surface topography of the cylindrical gear tooth flanks after machining. Int. J. Adv. Manuf. Technol. 2009, 43, 513–528. [Google Scholar] [CrossRef]
- Jacobs, T.D.B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- Krolczyk, G.M.; Maruda, R.W.; Nieslony, P.; Wieczorowski, M. Surface morphology analysis of duplex stainless steel (DSS) in clean production using the power spectral density. Measurement 2016, 94, 464–470. [Google Scholar] [CrossRef]
- Kubiak, K.J.; Bigerelle, M.; Mathia, T.G.; Dubois, A.; Dubar, L. Dynamic evolution of interface roughness during friction and wear processes. Scanning 2014, 36, 30–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mishra, V.; Khan, G.S.; Chattopadhyay, K.D.; Nand, K.; Sarepaka, R.G.V. Effects of tool overhang on selection of machining parameters and surface finish during diamond turning. Measurement 2014, 55, 353–361. [Google Scholar] [CrossRef]
- Khan, G.S.; Sarepaka, R.G.V.; Chattopadhyay, K.D.; Jain, P.K.; Bajpai, R.P. Characterization of nanoscale roughness in single point diamond turned optical surfaces using power spectral density analysis. Indian J. Eng. Mater. Sci. 2004, 11, 25–30. [Google Scholar]
- Duparré, A.; Ferre-Borrull, J.; Gliech, S.; Notni, G.; Steinert, J.; Bennett, J.M. Surface Characterization Techniques for Determining the Root-Mean-Square Roughness and Power Spectral Densities of Optical Components. Appl. Opt. 2002, 41, 154–41171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, Z.; Kirk, T.B. Two-dimensional fast Fourier transform and power spectrum for wear particle analysis. Tribol. Int. 1997, 30, 583–590. [Google Scholar] [CrossRef]
- Dong, W.P.; Stout, K.J. Two-dimensional fast Fourier transform and power spectrum for surface roughness in three dimensions. Proc. Inst. Mech. Eng., Part. B 1995, 209, 381–391. [Google Scholar] [CrossRef]
- Wu, J.P.; Kirk, T.B.; Peng, Z.; Miller, K.; Zheng, M.H. Utilization of two-dimensional fast Fourier transform and power spectral analysis for assessment of early degeneration of articular cartilage. J. Musculoskelet. Res. 2005, 9, 119–131. [Google Scholar] [CrossRef]
- Cheung, C.F.; Lee, W.B. Characterisation of nanosurface generation in single-point diamond turning. Int. J. Mach. Tools Manuf. 2001, 41, 851–875. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, S.; Li, Z.; Li, J. Tool path planning and milling surface simulation for vehicle rear bumper mold. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]

| No. | vc (m/min) | fz (mm/tooth) | ae (mm) | ap (mm) |
|---|---|---|---|---|
| 1 | 250 | 0.3 | 1.8 | 0.2 |
| 2 | 190 | 0.25 | 1.8 | 0.5 |
| 3 | 220 | 0.35 | 0.6 | 0.8 |
| 4 | 160 | 0.35 | 1.2 | 1.4 |
| No. | Surface Roughness | Experimental Result (μm) | Simulated Result (μm) | Error (%) 1 |
|---|---|---|---|---|
| 1 | Sba | 0.215 | 0.194 | 9.77 |
| Sq | 0.255 | 0.248 | 2.75 | |
| 2 | Sba | 0.154 | 0.134 | 12.99 |
| Sq | 0.183 | 0.171 | 6.56 | |
| 3 | Sba | 0.101 | 0.0904 | 10.5 |
| Sq | 0.124 | 0.116 | 6.45 | |
| 4 | Sba | 0.186 | 0.180 | 3.23 |
| Sq | 0.240 | 0.231 | 3.75 |
| p | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|
| r | |||||||
| 0.1 | 0.127 | 0.165 | 0.205 | 0.247 | 0.291 | 0.337 | |
| 0.2 | 0.194 | 0.253 | 0.314 | 0.38 | 0.449 | 0.521 | |
| 0.3 | 0.237 | 0.307 | 0.389 | 0.465 | 0.551 | 0.647 | |
| 0.4 | 0.273 | 0.353 | 0.44 | 0.537 | 0.64 | 0.739 | |
| 0.5 | 0.304 | 0.392 | 0.51 | 0.588 | 0.719 | 0.814 | |
| 0.6 | 0.338 | 0.434 | 0.538 | 0.643 | 0.791 | 0.879 | |
| p | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|
| r | |||||||
| 0.1 | 0.162 | 0.21 | 0.26 | 0.314 | 0.369 | 0.426 | |
| 0.2 | 0.248 | 0.322 | 0.4 | 0.483 | 0.571 | 0.662 | |
| 0.3 | 0.303 | 0.393 | 0.496 | 0.594 | 0.702 | 0.823 | |
| 0.4 | 0.349 | 0.452 | 0.562 | 0.687 | 0.815 | 0.942 | |
| 0.5 | 0.389 | 0.502 | 0.653 | 0.752 | 0.917 | 1 | |
| 0.6 | 0.432 | 0.553 | 0.687 | 0.82 | 1 | 1.1 | |
| Model | Degree of Freedom | Sum of Squares | Mean Square | F Value | P |
|---|---|---|---|---|---|
| Regression | 2 | 7.8912 | 3.9456 | 7201.76 | 0.000 |
| Residual | 33 | 0.0181 | 0.0005 | ||
| Total | 35 | 7.9092 | R2: 0.998, R2(Adj.): 0.998 | ||
| Model | Degree of Freedom | Sum of Squares | Mean Square | F Value | P |
|---|---|---|---|---|---|
| Regression | 2 | 7.8022 | 3.9011 | 5719.82 | 0.000 |
| Residual | 33 | 0.0225 | 0.0007 | ||
| Total | 35 | 7.8247 | R2: 0.997, R2(Adj.): 0.997 | ||
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| r (/tooth) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| p (mm2/tooth) | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| No. | R (/tooth) | P (mm2/tooth) | fz (mm/tooth) | ae (mm) | Xp1 (mm) | Xp2 (mm) | Yp (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.5 | 0.224 | 2.236 | 2.862 | 0.26 | 0.239 |
| 2 | 0.2 | 0.5 | 0.316 | 1.581 | 2.024 | 0.253 | 0.337 |
| 3 | 0.3 | 0.5 | 0.387 | 1.291 | 1.653 | 0.275 | 0.413 |
| 4 | 0.4 | 0.5 | 0.447 | 1.118 | 1.431 | 0.286 | 0.477 |
| 5 | 0.5 | 0.5 | 0.500 | 1.000 | 1.28 | 0.256 | 0.533 |
| 6 | 0.6 | 0.5 | 0.548 | 0.913 | 1.169 | 0.292 | 0.584 |
| 7 | 0.1 | 0.6 | 0.245 | 2.449 | 3.135 | 0.285 | 0.261 |
| 8 | 0.1 | 0.7 | 0.265 | 2.646 | 3.387 | 0.339 | 0.282 |
| 9 | 0.1 | 0.8 | 0.283 | 2.828 | 3.62 | 0.402 | 0.302 |
| 10 | 0.1 | 0.9 | 0.300 | 3.000 | 3.84 | 0.48 | 0.32 |
| 11 | 0.1 | 1 | 0.316 | 3.162 | 4.048 | 0.506 | 0.337 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, S. Effects of Feed per Tooth and Radial Depth of Cut on Amplitude Parameters and Power Spectral Density of a Machined Surface. Materials 2020, 13, 1323. https://doi.org/10.3390/ma13061323
Zhang Q, Zhang S. Effects of Feed per Tooth and Radial Depth of Cut on Amplitude Parameters and Power Spectral Density of a Machined Surface. Materials. 2020; 13(6):1323. https://doi.org/10.3390/ma13061323
Chicago/Turabian StyleZhang, Qing, and Song Zhang. 2020. "Effects of Feed per Tooth and Radial Depth of Cut on Amplitude Parameters and Power Spectral Density of a Machined Surface" Materials 13, no. 6: 1323. https://doi.org/10.3390/ma13061323





