Experimental Study on Basic Mechanical Properties of Basalt Fiber Reinforced Concrete
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Specimens Preparing
2.2. Loading Test
3. Results
3.1. Failure Mode
3.1.1. Compressing Failure Mode
3.1.2. Tensile Failure Mode
3.1.3. Bending Failure Mode
3.2. Performance Parameters of Compressing and Bending
3.2.1. Compressive Strength and Bending Strength
3.2.2. Evaluation of Compressive Toughness
3.2.3. Evaluation of Bending Toughness
3.2.4. Bend-Press Ratio
3.3. Tensile Performance Parameters
3.3.1. Tensile Strength
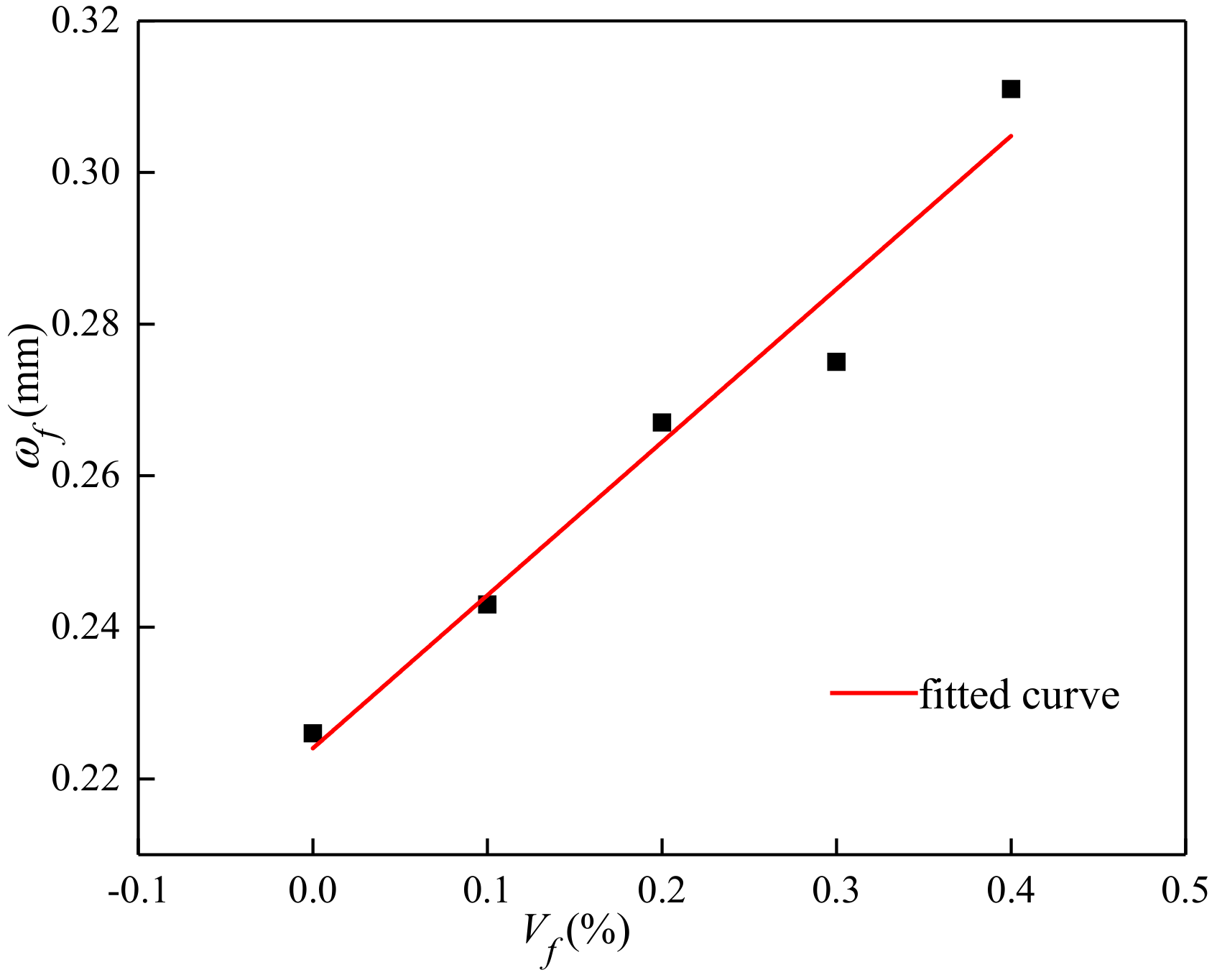
3.3.2. Crack Width
3.3.3. Maximum Crack Width
3.3.4. Fracture Energy
3.3.5. Characteristic Length
4. Discussion
5. Conclusions
- (1)
- The optimum volume fraction of basalt fibers is 0.3% and 0.4% within the scope of this study. In this case, the compressive strength, tensile strength, flexural strength, toughness index, fracture energy, flexural-compressive ratio, and reinforcement coefficient of concrete are significantly improved. With the volume fraction of basalt fiber exceeding the optimum volume fraction, the mechanical properties of basalt fiber are weakened.
- (2)
- By comparing with the tensile strength and bending strength, there was no significant improvement in compressive strength. In other words, the incorporation of basalt fiber can improve tensile strength and bending strength more than compressive strength.
- (3)
- The failure mode of concrete can be changed by the incorporation of basalt fiber from brittle failure to non-brittle failure. In addition, by observing the failure characteristics of fibers at the failure section, it can be judged that there is a good bonding behavior between basalt fiber and concrete.
- (4)
- The compressive toughness, the tensile toughness, and bending toughness of BFRC were evaluated by the advanced evaluation method of toughness, Hillerborg characteristic length, and fracture energy, respectively. It indicated that the incorporation of basalt fiber was an adoptable way to improve the toughness of concrete performance and crack resistance.
Author Contributions
Funding
Conflicts of Interest
References
- Parvez, A.; Foster, S.J. Fatigue of steel-fiber-reinforced concrete prestressed railway sleepers. Eng. Struct. 2017, 141, 241–250. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.B.; Ju, X.C. Application of ductile fiber reinforced cementitious composite in jointless concrete pavements. Compos. Part B Eng. 2013, 50, 224–231. [Google Scholar] [CrossRef]
- Li, X.; Xue, W.; Fu, C.; Yao, Z.; Liu, X. Mechanical properties of high-performance steel-fibre-reinforced concrete and its application in underground mine engineering. Materials 2019, 12, 2470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Briffaut, M.; Benboudjema, F.; D’Aloia, L. Effect of fibers on early age cracking of concrete tunnel lining. Part I: Laboratory ring test. Tunn. Undergr. Space Technol. 2016, 59, 215–220. [Google Scholar] [CrossRef]
- Mahoutian, M.; Shekarchi, M.; Libre, N.A. Application of steel fiber reinforced lightweight aggregate concrete in underground mining. J. Min. Sci. 2011, 47, 606–617. [Google Scholar] [CrossRef]
- Alsaif, A.; Koutas, L.; Bernal, S.A.; Guadagnini, M.; Pilakoutas, K. Mechanical performance of steel fiber reinforced rubberised concrete for flexible concrete pavements. Constr. Build. Mater. 2018, 172, 533–543. [Google Scholar] [CrossRef]
- Li, B.; Chi, L.Y.; Xu, L.H.; Shi, Y.C.; Li, C.N. Experimental investigation on the flexural behavior of steel-polypropylene hybrid fiber reinforced concrete. Constr. Build. Mater. 2018, 191, 80–94. [Google Scholar] [CrossRef]
- Ibrahim, I.S.; Wan Jusoh, W.A.; Mohd Sam, A.R.; Mustapa, N.A.; Muiz, S.A.R.S. The mechanical properties of steel-polypropylene fiber composites concrete. Appl. Mech. Mater. 2015, 773–774, 949–953. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.Y.; Ding, W.Q.; Qiao, Y.F. Experimental investigation on the flexural behavior of hybrid steel-pva fiber reinforced concrete containing fly ash and slag powder. Constr. Build. Mater. 2019, 228, 116706. [Google Scholar] [CrossRef]
- Shi, X.J.; Park, P.; Rew, Y.; Huang, K.J.; Sim, C.W. Constitutive behaviors of steel fiber reinforced concrete under uniaxial compression and tension. Constr. Build. Mater. 2020, 233, 117316. [Google Scholar] [CrossRef]
- Shan, L.; Zhang, L.; Xu, L. Experimental investigations on mechanical properties of hybrid steel-polypropylene fiber reinforced concrete. Appl. Mech. Mater. 2014, 638–640, 1550–1555. [Google Scholar] [CrossRef]
- Swamy, R.N.; Wagstaffe, R.L.; Oakley, D.R. Fiber reinforced cement and concrete. Mater. Struct. 1987, 20, 159. [Google Scholar] [CrossRef]
- Jiang, C.; Fan, K.; Wu, F.; Chen, D. Experimental study on the mechanical properties and microstructure of chopped basalt fiber reinforced concrete. Mater. Des. 2014, 58, 187–193. [Google Scholar] [CrossRef]
- Dias, D.P.; Thaumaturgo, C. Fracture toughness of geopolymeric concretes reinforced with basalt fibers. Cem. Concr. Compos. 2005, 27, 49–54. [Google Scholar] [CrossRef]
- Sun, X.J.; Gao, Z.; Cao, P.; Zhou, C.J.; Ling, Y.F.; Wang, X.H.; Zhao, Y.W.; Diao, M.S. Fracture performance and numerical simulation of basalt fiber concrete using three-point bending test on notched beam. Constr. Build. Mater. 2019, 225, 788–800. [Google Scholar] [CrossRef]
- Kizilkanat, A.B.; Kabay, N.; Akyüncü, V.; Chowdhury, S.; Akça, A.H. Mechanical properties and fracture behavior of basalt and glass fiber reinforced concrete: An experimental study. Constr. Build. Mater. 2015, 100, 218–224. [Google Scholar] [CrossRef]
- Torres, J.A.; Lantsoght, E.O. Influence of fiber content on shear capacity of steel fiber-reinforced concrete beams. Fibers 2019, 7, 102. [Google Scholar] [CrossRef] [Green Version]
- Romualdi, J.P.; Mandel, J.A. Tensile strength of concrete affected by uniformly distributed and closely spaced short lengths of wire reinforcement. J. Am. Concr. Inst. 1964, 61, 27–37. [Google Scholar]
- Cao, H.L.; Lang, H.J.; Meng, S.H. Experimental research on the basic structure and properties of the continuous basalt fiber. Hi-Tech Fiber Appl. 2007, 32, 8–13. [Google Scholar]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fiber and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Ergai, X.; Zhongying, L. Application prospect of basalt fiber. Fiber Compos. 2003, 19, 17–20. [Google Scholar]
- Militky, J.; Kovačič, V.; Rubnerová, J. Influence of thermal treatment on tensile failure of basalt fibers. Eng. Fract. Mech. 2002, 69, 1025–1033. [Google Scholar] [CrossRef]
- Rabinovich, F.N.; Zueva, V.N.; Makeeva, L.V. Stability of basalt fibers in a medium of hydrating cement. Glass Ceram. 2001, 58, 431–434. [Google Scholar] [CrossRef]
- Lee, J.J.; Song, J.; Kim, H. Chemical stability of basalt fiber in alkaline solution. Fibers Polym. 2014, 15, 2329–2334. [Google Scholar] [CrossRef]
- Kai, J.H.; Min, D. Stability of Basalt Fibers in Alkaline Solution and Its Effect on The Mechanical Property of Concrete. Acta Materiae Compositae Sinica 2010, 27, 150–154. [Google Scholar]
- Tang, C.; Jiang, H.; Zhang, X.; Li, G.; Cui, J. Corrosion behavior and mechanism of basalt fibers in sodium hydroxide solution. Materials 2018, 11, 1381. [Google Scholar] [CrossRef] [Green Version]
- Jalasutram, S.; Sahoo, D.R.; Matsagar, V. Experimental investigation on mechanical properties of basalt fiber-reinforced concrete. Struct. Concr. 2017, 18, 292–302. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, J.; Wang, Z. Study on Micro-structure and durability of fiber concrete. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 659–664. [Google Scholar] [CrossRef]
- Gamal, T.S.F.; Chiadighikaobi, P.C. Comparative analysis of reliability of non-destructive methods of strength control of concrete impregnated with vegetable oil: Basalt fiber for increasing the concrete strength. Mater. Today: Proc. 2019, 19, 2479–2482. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Y.; Zhang, Y.; Chen, W. Experimental research and analysis on mechanical properties of chopped basalt fiber reinforced concrete. Eng. Mech. 2014, 31, 99–102. [Google Scholar]
- Chen, F. An experimental study on mechanical properties of basalt fiber reinforced concrete. Appl. Mech. Mater. 2013, 405–408, 2767–2770. [Google Scholar] [CrossRef]
- Kabay, N. Abrasion resistance and fracture energy of concretes with basalt fiber. Constr. Build. Mater. 2014, 50, 95–101. [Google Scholar] [CrossRef]
- Pehlivanh, Z.O.; Uzun, I.; DemirI, L. Mechanical and micro structural features of autoclaved aerated concrete reinforced with autoclaved polypropylene, carbon, basalt and glass fiber. Constr. Build. Mater. 2015, 96, 428–433. [Google Scholar] [CrossRef]
- Arslan, M.E. Effects of basalt and glass chopped fibers addition on fracture energy and mechanical properties of ordinary concrete: CMOD measurement. Constr. Build. Mater. 2016, 114, 383–391. [Google Scholar] [CrossRef]
- Branston, J.; Das, S.; Kenno, S.Y.; Taylor, C. Mechanical behavior of basalt fiber reinforced concrete. Constr. Build. Mater. 2016, 124, 878–886. [Google Scholar] [CrossRef]
- Katkhuda, H.; Shatarat, N. Improving the mechanical properties of recycled concrete aggregate using chopped basalt fibers and acid treatment. Constr. Build. Mater. 2017, 140, 328–335. [Google Scholar] [CrossRef]
- Ansari, F. Stress-strain response of microcracked concrete in direct tension. Materials 1987, 84, 481–490. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]




















| Scholar | Test | Diameter | Length | Vbest |
|---|---|---|---|---|
| Wang,J. [30] | Compressive, flexural, splitting tensile | 15 μm | 30 mm | 0.1% |
| Chen,F. [31] | Compressive, splitting tensile | 17 μm | 24 mm | 0.04% |
| Kabay N. [32] | Compressive, flexural | 13–20 μm | 24 mm | 0.16% |
| Jiang,C. [13] | Compressive, flexural, splitting tensile | 20 μm | 12 mm | 0.3% |
| Kizilkanat A B. [16] | Compressive, Splitting tensile | 13–20 um | 12 mm | 0.25% |
| Pehlivanh,Z.O. [33] | Compressive, flexural | / | 8 mm | 0.304% |
| Jalasutram S. [27] | Compressive, flexural, splitting tensile | 13 μm | 12.7 mm | 0.1% |
| Arslan, M. E. [34] | Compressive, splitting tensile, flexural | 13–20 μm | 24 mm | 0.07% |
| Branston, J. [35] | Compressive, flexural | 16 μm | 36 mm | 0.46% |
| Katkhuda, H. [36] | compressive, splitting tensile, flexural | 16 μm | 18 mm | 0.3% |
| Materials | Cement | Stone | Sand | Water |
|---|---|---|---|---|
| Weight (kg/m3) | 330 | 1389.6 | 540.5 | 139 |
| Type | Diameter (µm) | Length (mm) | Density (g/cm3) | Tensile Strength (MPa) | Elasticity Modulus (GPa) | Extension at Break (%) |
|---|---|---|---|---|---|---|
| short-cut | 15 | 12 | 2.65 | 3500–4500 | 95–115 | 2.4–3.0 |
| Specimen | Vf | fc | cov | δc | I0 | I1 | ff | cov | δf | Gf | ff/fc | α |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B0 | 0 | 39.24 | 0.039 | 1.38 | 3.51 | 5.66 | 5.1 | 0.037 | 0.33 | 7.645 | 0.130 | 1 |
| B1 | 0.1 | 39.98 | 0.024 | 1.81 | 4.07 | 7.35 | 5.81 | 0.047 | 0.35 | 7.455 | 0.145 | 1.12 |
| B2 | 0.2 | 40.12 | 0.033 | 1.79 | 4.3 | 7.49 | 6.37 | 0.077 | 0.37 | 7.88 | 0.159 | 1.22 |
| B3 | 0.3 | 41.23 | 0.034 | 2.55 | 4.7 | 8.64 | 6.96 | 0.101 | 0.40 | 8.099 | 0.169 | 1.30 |
| B4 | 0.4 | 41.08 | 0.027 | 2.4 | 4.74 | 8.52 | 7.26 | 0.092 | 0.41 | 8.508 | 0.177 | 1.36 |
| B5 | 0.5 | 39.10 | 0.030 | 2.22 | 3.95 | 7.15 | 6.37 | 0.142 | 0.42 | 6.326 | 0.163 | 1.25 |
| B6 | 0.6 | 38.23 | 0.058 | 1.91 | 3.79 | 7.13 | 5.19 | 0.168 | 0.41 | 6.643 | 0.136 | 1.04 |
| Specimen | Vf | ft | cov | Et | εt | ωt | Gt | RG | Lch | RL |
|---|---|---|---|---|---|---|---|---|---|---|
| B0 | 0 | 3.48 | 0.078 | 18.3 | 181.02 | 0.226 | 162.3 | 0 | 245.25 | 0 |
| B1 | 0.1 | 3.6 | 0.091 | 18.1 | 185.43 | 0.243 | 168.45 | 3.79 | 282.31 | 15.11 |
| B2 | 0.2 | 3.88 | 0.048 | 18.7 | 198.75 | 0.267 | 197.1 | 21.44 | 293.8 | 19.79 |
| B3 | 0.3 | 4.16 | 0.077 | 19.4 | 212.32 | 0.275 | 220.8 | 36.04 | 297.03 | 21.11 |
| B4 | 0.4 | 4.21 | 0.067 | 19.1 | 223.57 | 0.311 | 232.05 | 42.98 | 300.08 | 22.36 |
| B5 | 0.5 | 3.54 | 0.118 | 19.3 | 201.02 | 0.249 | 223.35 | 37.62 | 257.99 | 5.19 |
| B6 | 0.6 | 3.36 | 0.091 | 17.9 | 184.50 | 0.229 | 182.7 | 12.57 | 231.74 | -5.51 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Jia, B.; Huang, H.; Mou, Y. Experimental Study on Basic Mechanical Properties of Basalt Fiber Reinforced Concrete. Materials 2020, 13, 1362. https://doi.org/10.3390/ma13061362
Zhou H, Jia B, Huang H, Mou Y. Experimental Study on Basic Mechanical Properties of Basalt Fiber Reinforced Concrete. Materials. 2020; 13(6):1362. https://doi.org/10.3390/ma13061362
Chicago/Turabian StyleZhou, Hao, Bin Jia, Hui Huang, and Yanling Mou. 2020. "Experimental Study on Basic Mechanical Properties of Basalt Fiber Reinforced Concrete" Materials 13, no. 6: 1362. https://doi.org/10.3390/ma13061362
APA StyleZhou, H., Jia, B., Huang, H., & Mou, Y. (2020). Experimental Study on Basic Mechanical Properties of Basalt Fiber Reinforced Concrete. Materials, 13(6), 1362. https://doi.org/10.3390/ma13061362




