Statics-Based Model-Free Damage Detection under Uncertainties Using Modal Interval Analysis
Abstract
:1. Introduction
2. Classical Interval Analysis
3. Modal Interval Analysis
4. Damage Detection Strategy
5. A Numerical Reinforced Concrete Beam
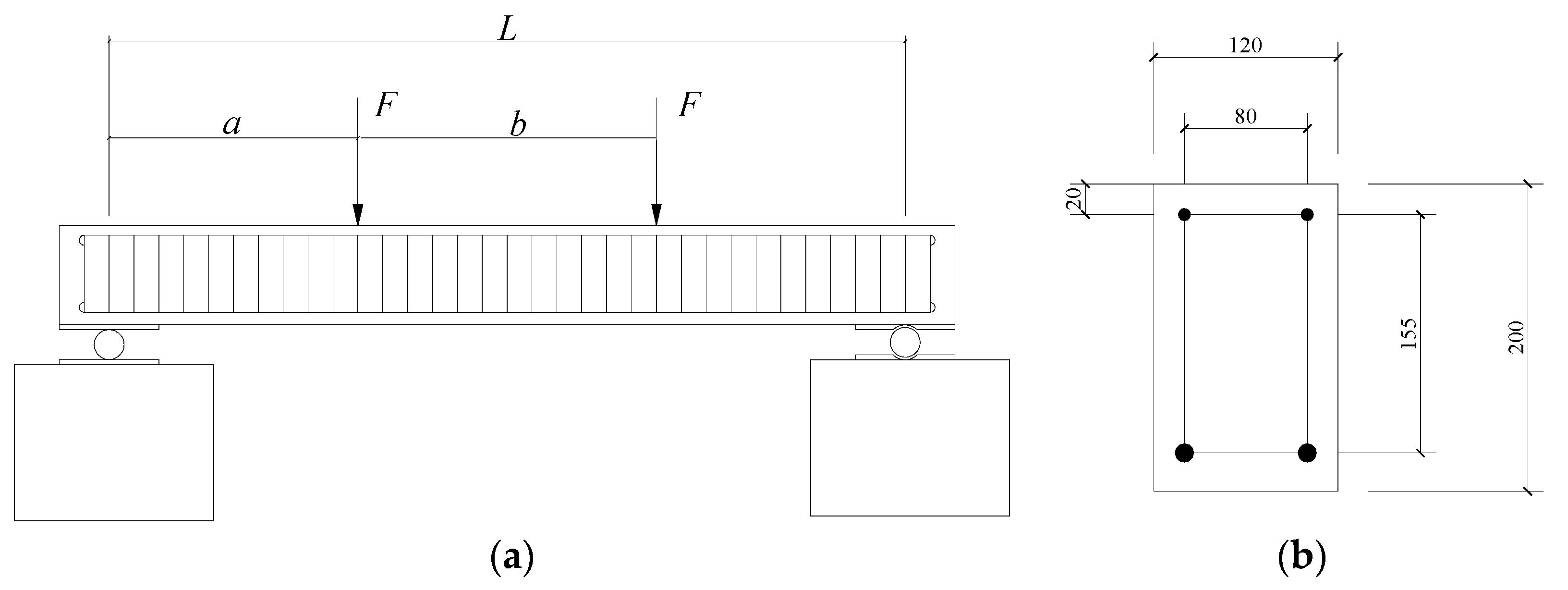
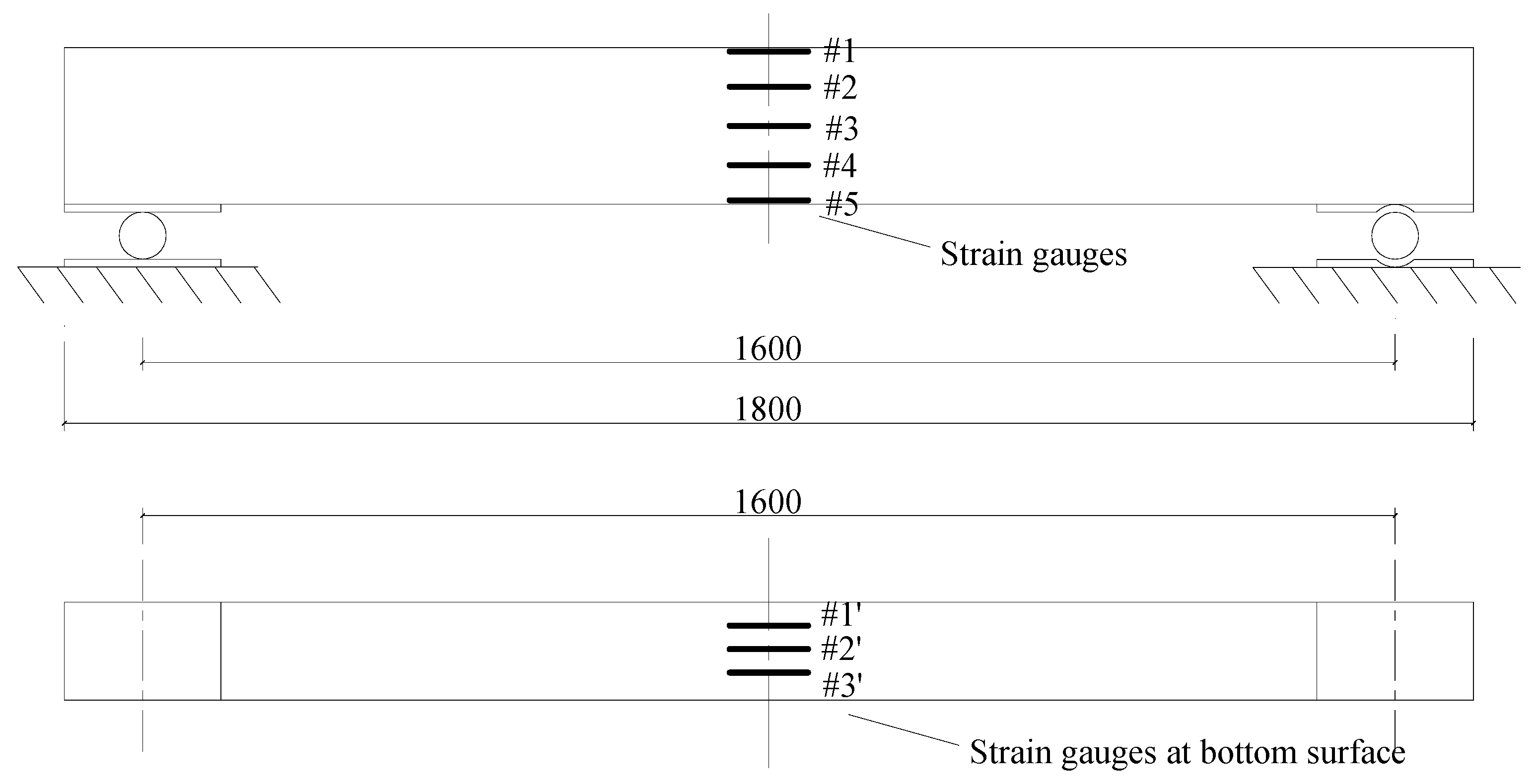
6. An Experimental Reinforced Concrete Beam
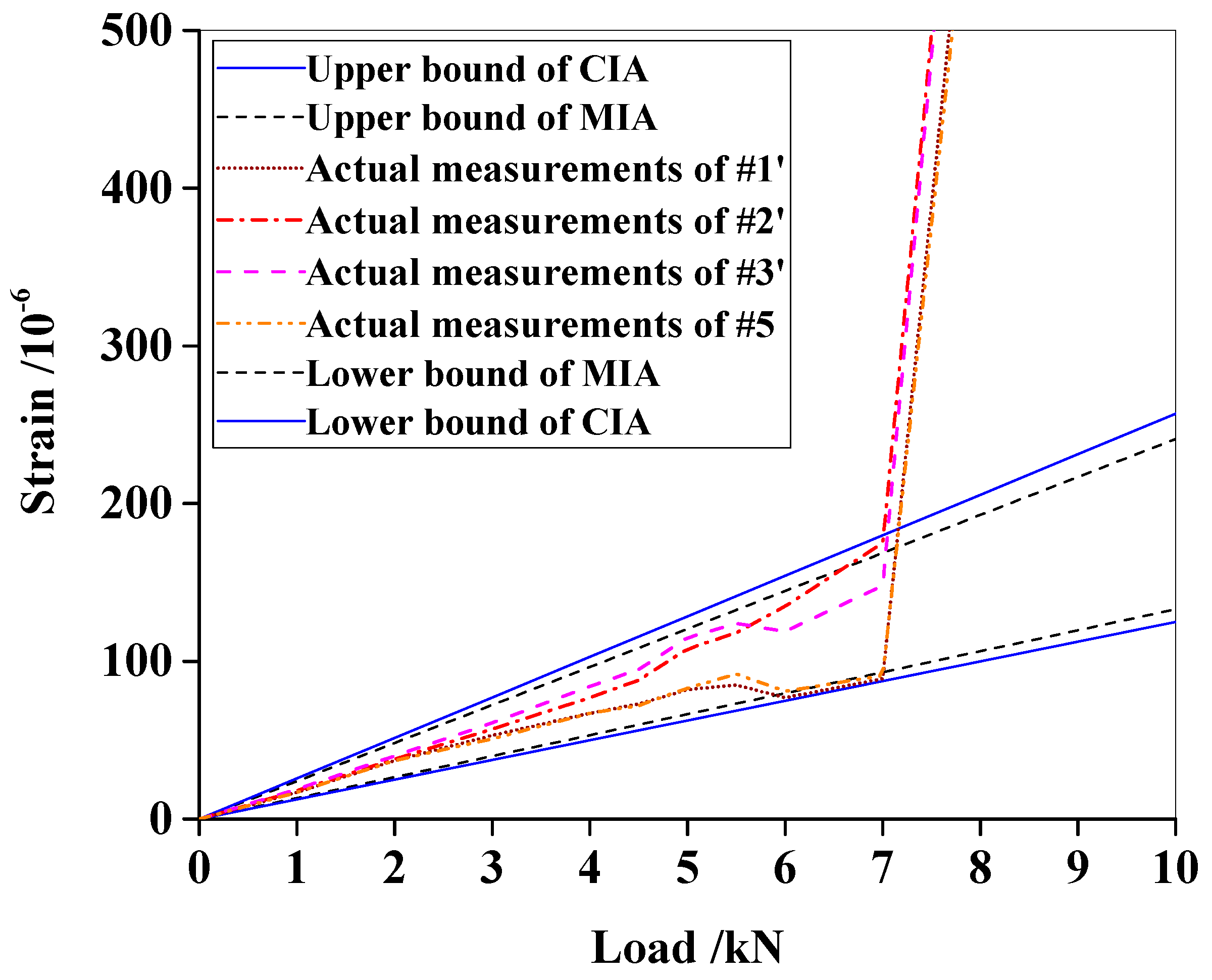
6.1. Experimental Observations and Damage Detection
6.2. Discussions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wenzel, H. Health Monitoring of Bridges; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2009. [Google Scholar]
- Xu, Y.L.; Xia, Y. Structural Health Monitoring of Long-Span Suspension Bridges; Spon Press: London, UK, 2012. [Google Scholar]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y.; Yam, L.H. Development in vibration-based structural damage detection technique. Mech. Syst. Signal Process. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Life-cycle performance of deteriorating structural systems under uncertainty: Review. J. Struct. Eng. ASCE 2016, 142, F4016001. [Google Scholar] [CrossRef]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal Process. 2015, 56–57, 123–149. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Cheng, L.; Su, Z.Q.; Guyader, J.L. Damage visualization based on local dynamic perturbation: Theory; application to characterization of multi-damage in a plane structure. J. Sound Vib. 2013, 332, 3438–3462. [Google Scholar] [CrossRef]
- Ren, W.X.; Lin, Y.Q.; Fang, S.E. Structural damage detection based on stochastic subspace identification; statistical pattern recognition: I. Theorysmart Mater. Struct. 2011, 20, 115009. [Google Scholar] [CrossRef]
- Nichols, J.M.; Moore, E.Z.; Murphy, K.D. Bayesian identification of a cracked plate using a population-based Markov Chain Monte Carlo method. Comput. Struct. 2011, 89, 1323–1332. [Google Scholar] [CrossRef]
- Chandrashekhar, M.; Ganguli, R. Damage assessment of structures with uncertainty by using mode-shape curvatures; fuzzy logic. J. Sound Vib. 2009, 326, 939–957. [Google Scholar] [CrossRef]
- Taha, R.M.M.; Lucero, J. Damage identification for structural health monitoring using fuzzy pattern recognition. Eng. Struct. 2005, 27, 1774–1783. [Google Scholar] [CrossRef]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E. Applied Interval Analysis; Springer: London, UK, 2001. [Google Scholar] [CrossRef]
- Moore, R.; Kearfott, R.; Cloud, M. Introduction to Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Fang, S.E.; Zhang, Q.H.; Ren, W.X. An interval model updating strategy using interval response surface models. Mech. Syst. Signal Process. 2015, 60–61, 909–927. [Google Scholar] [CrossRef]
- Rao, S.S.; Berke, L. Analysis of uncertain structural systems using interval analysis. AIAA J. 1997, 35, 727–735. [Google Scholar] [CrossRef]
- Gabriele, S.; Valente, C.; Brancaleoni, F. An interval uncertainty based method for damage identification. Key Eng. Mater. 2007, 347, 551–556. [Google Scholar] [CrossRef]
- Wang, X.J.; Yang, H.F.; Wang, L.; Qiu, Z.P.; Qiu, Z.P. Interval analysis method for structural damage identification based on multiple load cases. J. Appl. Mech. 2012, 79, 051010. [Google Scholar] [CrossRef]
- Zhu, F.T.; Wu, Y.J. A rapid structural damage detection method using integrated ANFIS; interval modeling technique. Appl. Soft Comput. 2014, 25, 473–484. [Google Scholar] [CrossRef]
- Garcia, O.; Vehi, J.; Matos, J.C.; Casas, J.R. Structural assessment under uncertain parameters via interval analysis. J. Comput. Appl. Math. 2008, 218, 43–52. [Google Scholar] [CrossRef] [Green Version]
- Khodaparast, H.H.; Mottershead, J.E.; Badcock, K.J. Interval model updating with irreducible uncertainty using the Kriging predictor. Mech. Syst. Signal Process. 2011, 25, 1204–1226. [Google Scholar] [CrossRef]
- Hansen, E.; Walster, G.W. Global Optimization Using Interval Analysis; Marcel Dekker, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Li, S.L.; Li, H.; Ou, J.P. Model updating for uncertain structures with interval parameters. In Proceedings of the Asia-Pacific Workshop on Structural Health Monitoring, Yokohama, Japan, 4–6 December 2006. [Google Scholar]
- Zou, Y.; Tong, L.; Steven, G.P. Vibration-based model-dependent damage (delamination) identification; health monitoring for composite structures-a review. J. Sound Vib. 2000, 230, 357–378. [Google Scholar] [CrossRef]
- Jassim, Z.A.; Ali, N.N.; Mustapha, F.; Jalil, N.A.A. A review on the vibration analysis for a damage occurrence of a cantilever beam. Eng. Fail. Anal. 2013, 31, 442–461. [Google Scholar] [CrossRef]
- Baneen, U.; Kinkaid, N.M.; Guivant, J.E.; Herszberg, I. Vibration based damage detection of a beam-type structure using noise suppression method. J. Sound Vib. 2012, 331, 1777–1788. [Google Scholar] [CrossRef]
- Viola, E.; Miniaci, M.; Fantuzzi, N.; Marzani, A. Vibration analysis of multi-stepped; multi-damaged parabolic arches using GDQ. Curved Layer. Struct. 2015, 2, 28–49. [Google Scholar] [CrossRef] [Green Version]
- Hios, J.D.; Fassois, S.D. A global statistical model based approach for vibration response-only damage detection under various temperatures: A proof-of-concept study. Mech. Syst. Signal Process. 2014, 49, 77–94. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Zak, A. Guided Waves in Structures for SHM: The Time-Domain Spectral Element Method; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Miniaci, M.; Mazzotti, M.; Radzieński, M.; Kudela, P.; Kherraz, N.; Bosia, F.; Pugno, N.M.; Ostachowicz, W. Application of a laser-based time reversal algorithm for impact localization in a stiffened aluminum plate. Front. Mater. 2019, 6, 30. [Google Scholar] [CrossRef]
- Ren, W.X.; Fang, S.E.; Deng, M.Y. Response surface based finite element model updating using structural static responses. J. Eng. Mech. ASCE 2011, 137, 248–257. [Google Scholar] [CrossRef]
- Chen, S.Z.; Wu, G.; Feng, D.C. Damage detection of highway bridges based on long-gauge strain response under stochastic traffic flow. Mech. Syst. Signal Process. 2019, 127, 551–572. [Google Scholar] [CrossRef]
- Friswell, M.I. Damage identification using inverse methods. Philos. Trans. R. Soc. 2007, 365, 393–410. [Google Scholar] [CrossRef] [PubMed]
- Gardeñes, E.; Sainz, M.; Jorba, L.; Calm, R.; Estela, R.; Mielgo, H.; Trepat, A. Model Intervals. Reliab. Comput. 2001, 7. [Google Scholar] [CrossRef]
- Sainz, M.A.; Armengol, J.; Calm, R.; Herrero, P.; Jorba, L.; Vehi, J. Modal Intervals; Springer International Publishing: Basel, Switzerland, 2014. [Google Scholar] [CrossRef]
- SL/T191-2008. Design Code for Hydraulic Concrete Structures; Water&Power Press: Beijing, China, 2009. [Google Scholar]



| Load Step | F/kN | ε by MIA | ε by CIA | εd | ||
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | |||
| 1 | 1 | 13.3 | 24.1 | 12.5 | 25.7 | 17.7 |
| 2 | 2 | 26.6 | 48.2 | 25 | 51.4 | 35.4 |
| 3 | 3 | 39.9 | 72.3 | 37.5 | 77.1 | 53.2 |
| 4 | 4 | 53.2 | 96.4 | 50 | 102.8 | 70.9 |
| 5 | 5 | 66.5 | 120.5 | 62.5 | 128.5 | 88.6 |
| 6 | 6 | 79.8 | 144.6 | 75 | 154.2 | 106.3 |
| 7 | 7 | 93.1 | 168.7 | 87.5 | 179.9 | 124.1 |
| 8 | 8 | 106.4 | 192.8 | 100 | 205.6 | 175.8 |
| 9 | 9 | 119.7 | 216.9 | 112.5 | 231.3 | 260.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, S.-E.; Huang, J.-Y. Statics-Based Model-Free Damage Detection under Uncertainties Using Modal Interval Analysis. Materials 2020, 13, 1567. https://doi.org/10.3390/ma13071567
Fang S-E, Huang J-Y. Statics-Based Model-Free Damage Detection under Uncertainties Using Modal Interval Analysis. Materials. 2020; 13(7):1567. https://doi.org/10.3390/ma13071567
Chicago/Turabian StyleFang, Sheng-En, and Ji-Yuan Huang. 2020. "Statics-Based Model-Free Damage Detection under Uncertainties Using Modal Interval Analysis" Materials 13, no. 7: 1567. https://doi.org/10.3390/ma13071567
APA StyleFang, S.-E., & Huang, J.-Y. (2020). Statics-Based Model-Free Damage Detection under Uncertainties Using Modal Interval Analysis. Materials, 13(7), 1567. https://doi.org/10.3390/ma13071567




