Analysis of a New Shape of Test Specimen for Block Shear Impact Test
Abstract
1. Introduction
- -
- Block Shear Test (BST) [16];
- -
- -
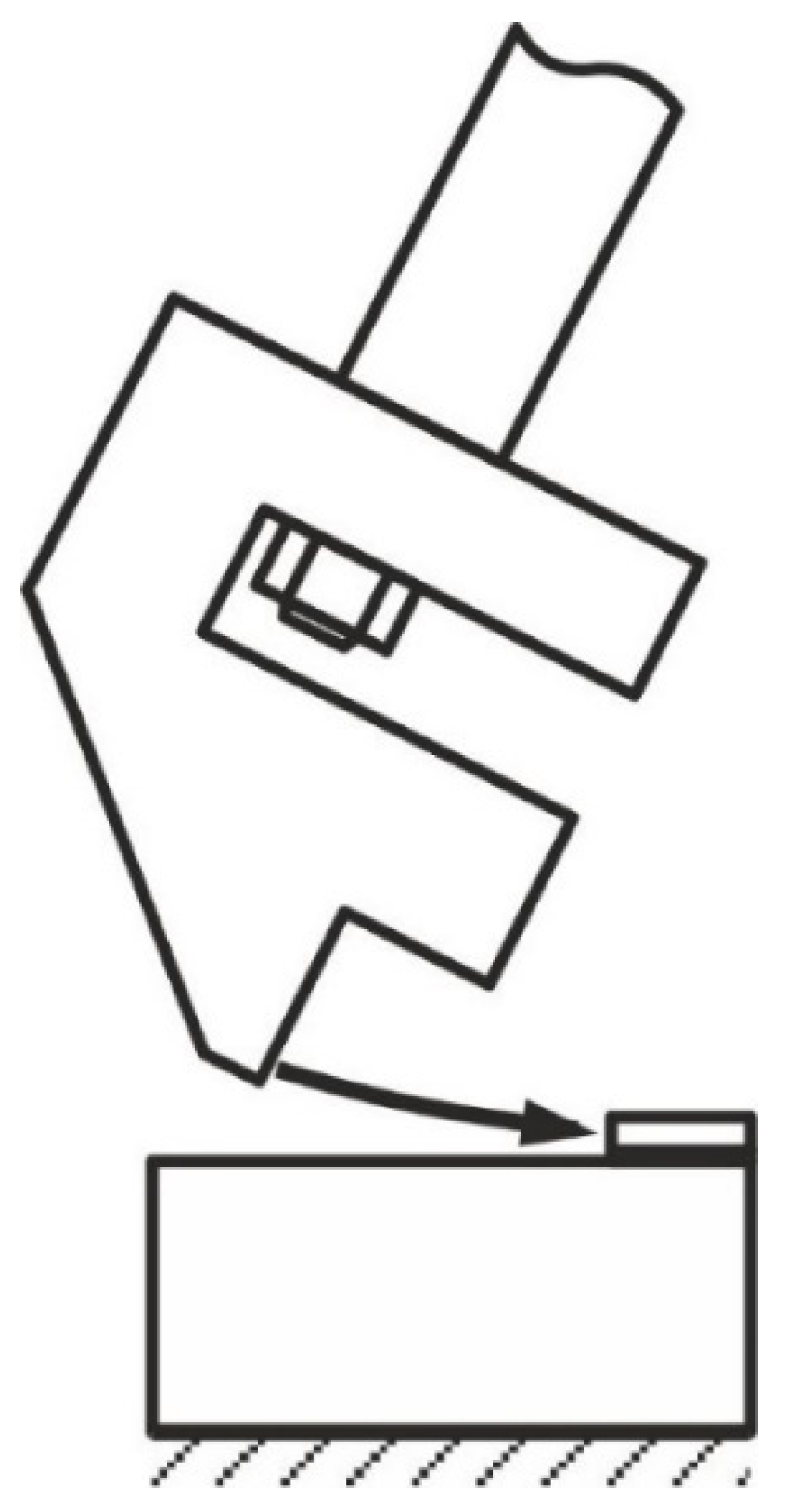
2. Research Methodology
3. Findings and Discussion of the Experimental Research
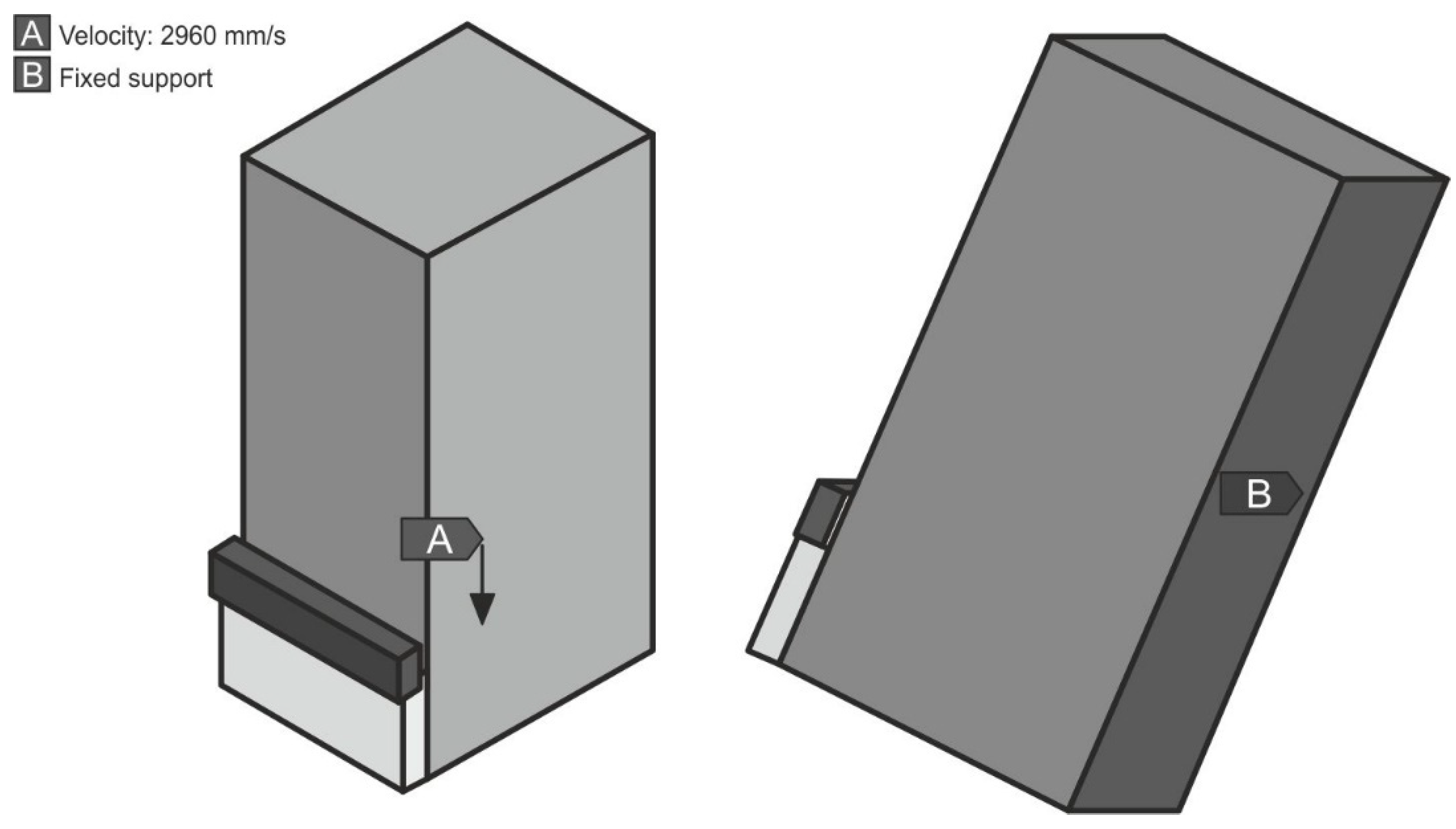
4. Assumptions for Numerical Calculations
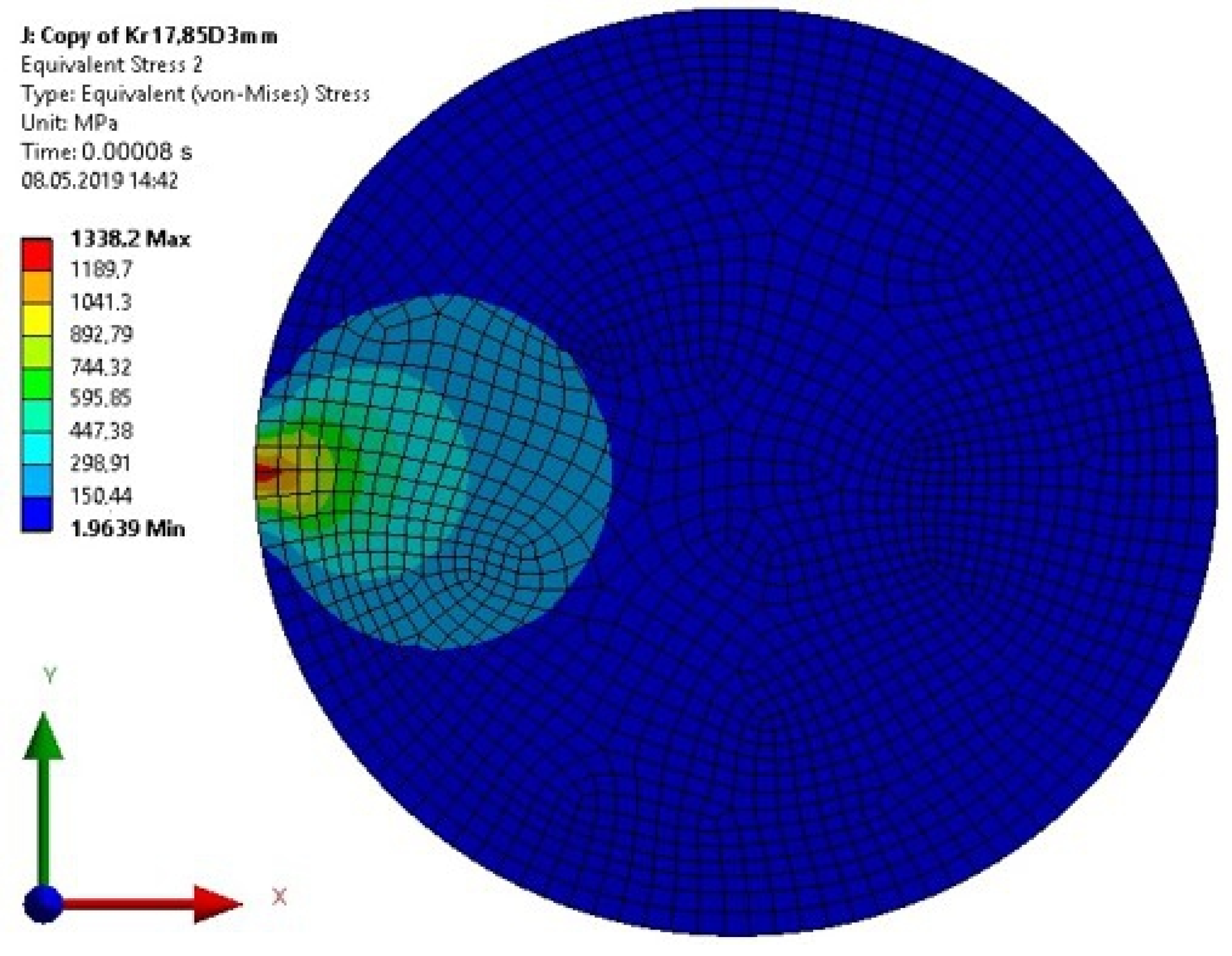
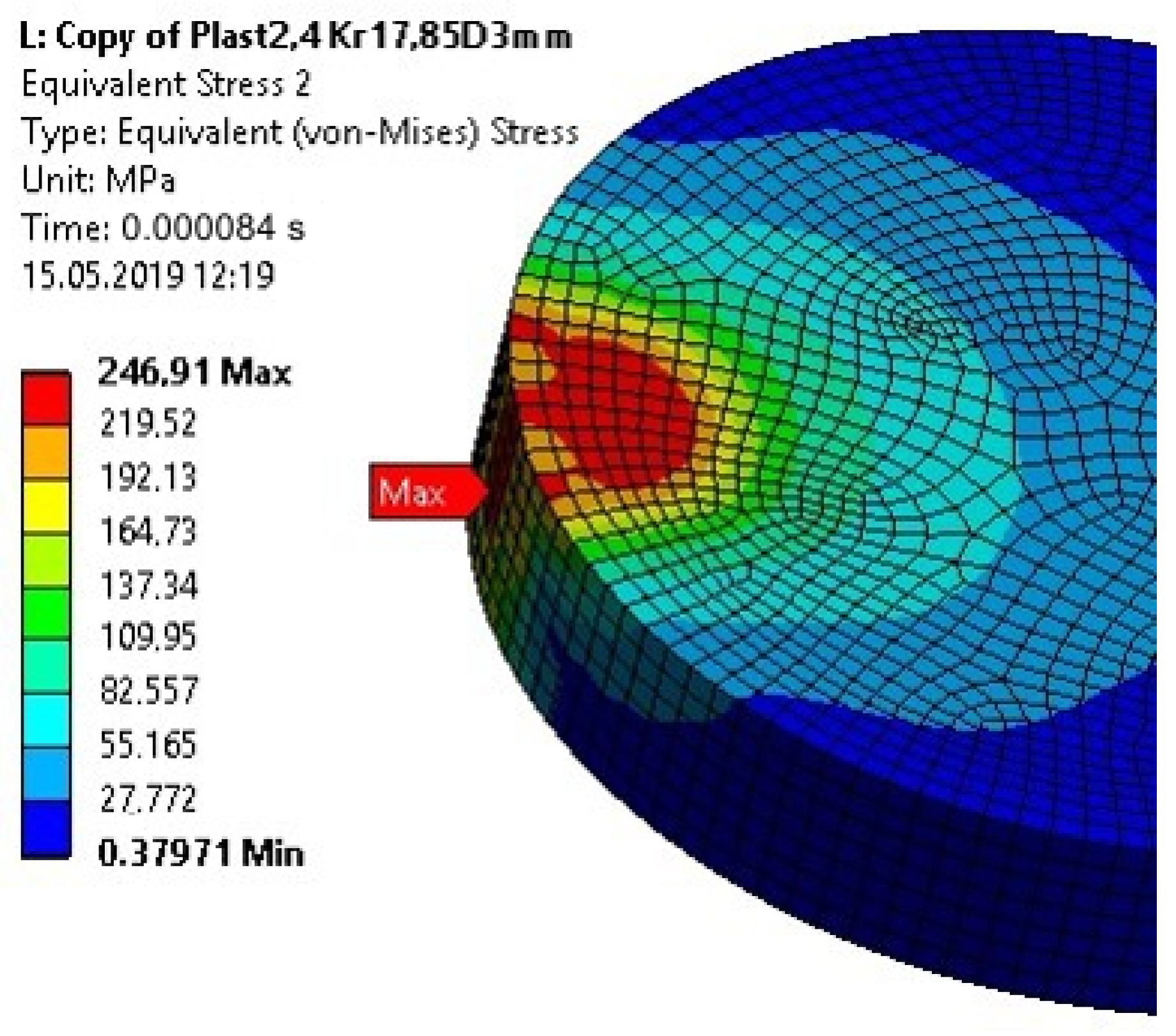
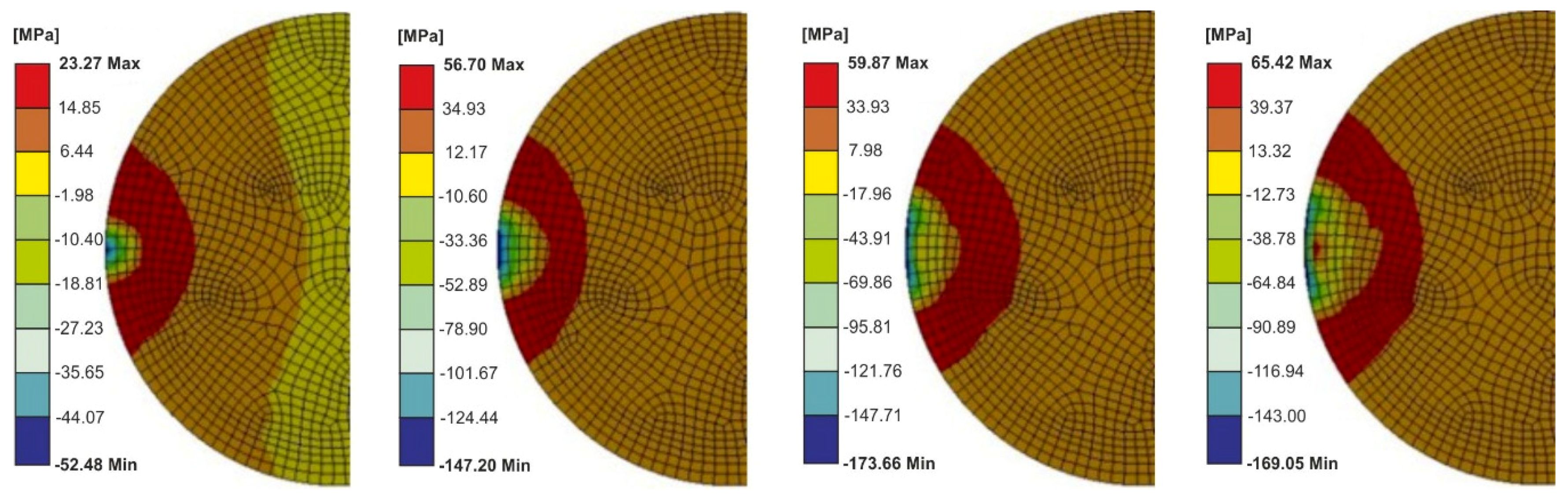
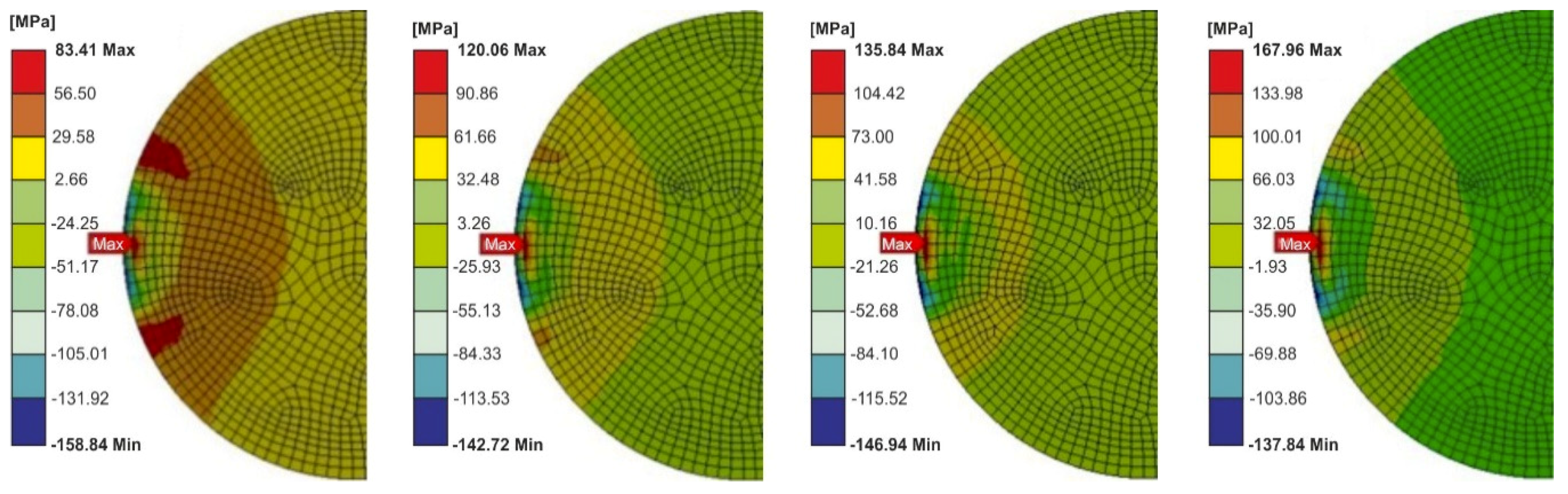
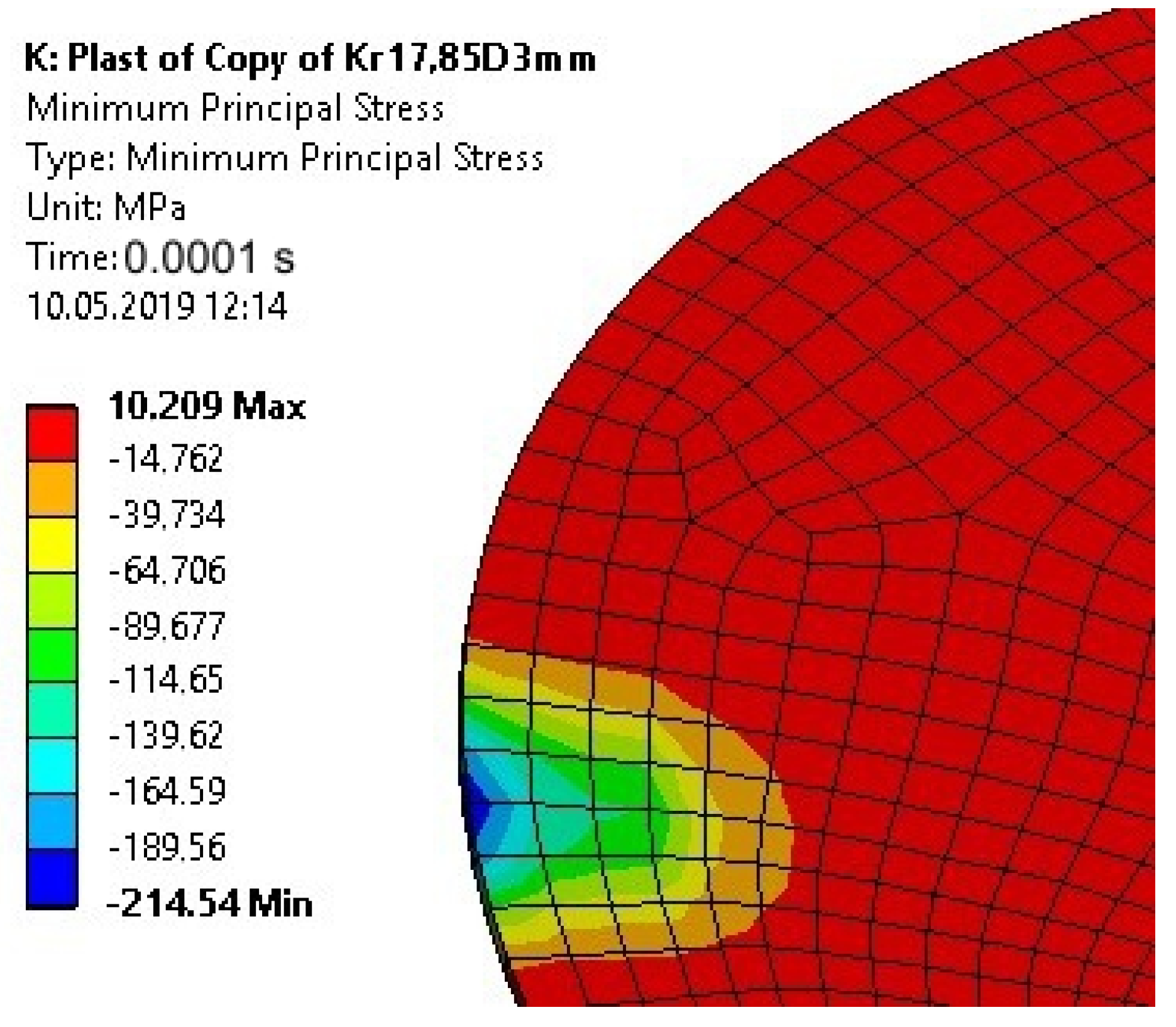
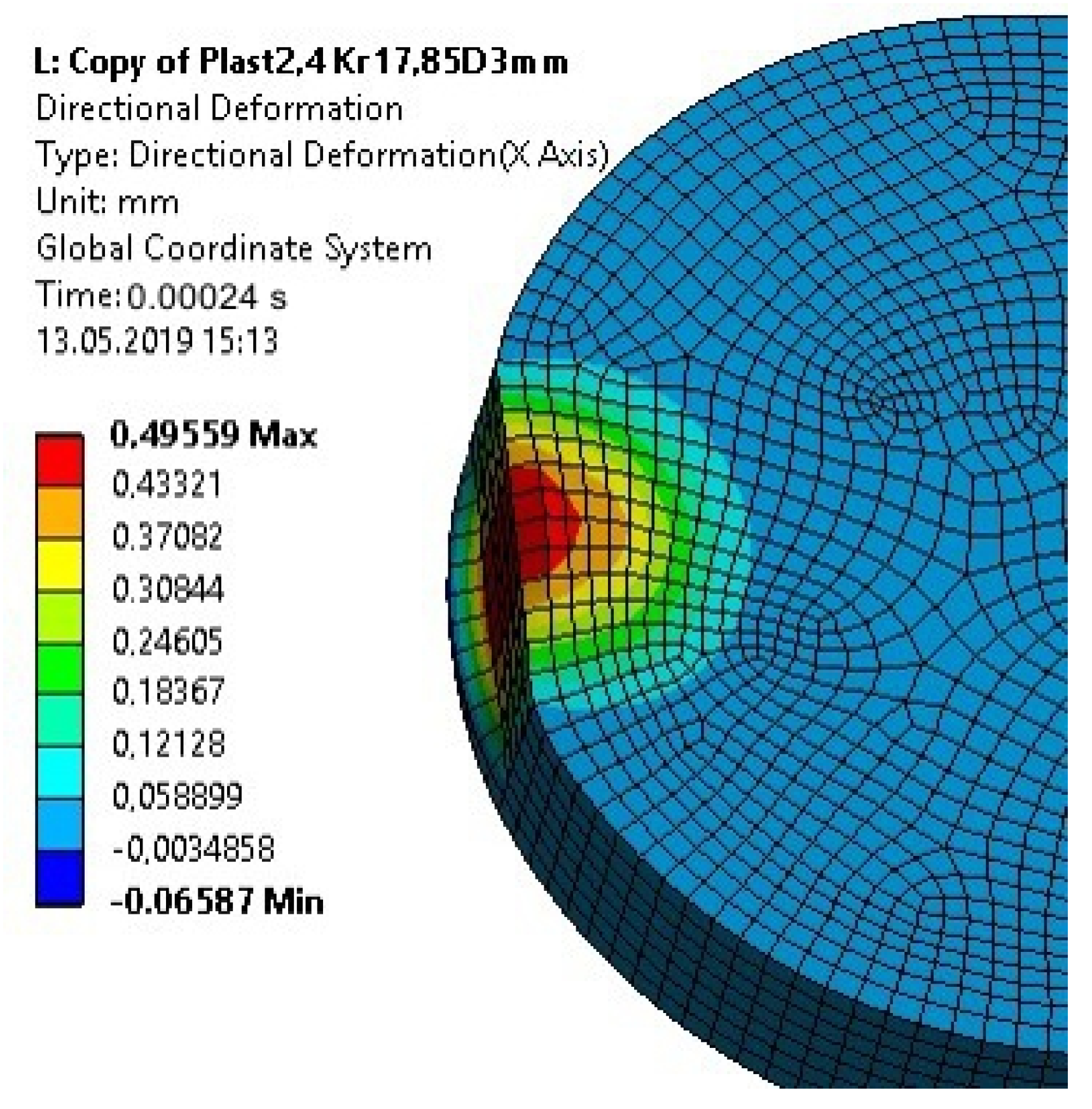
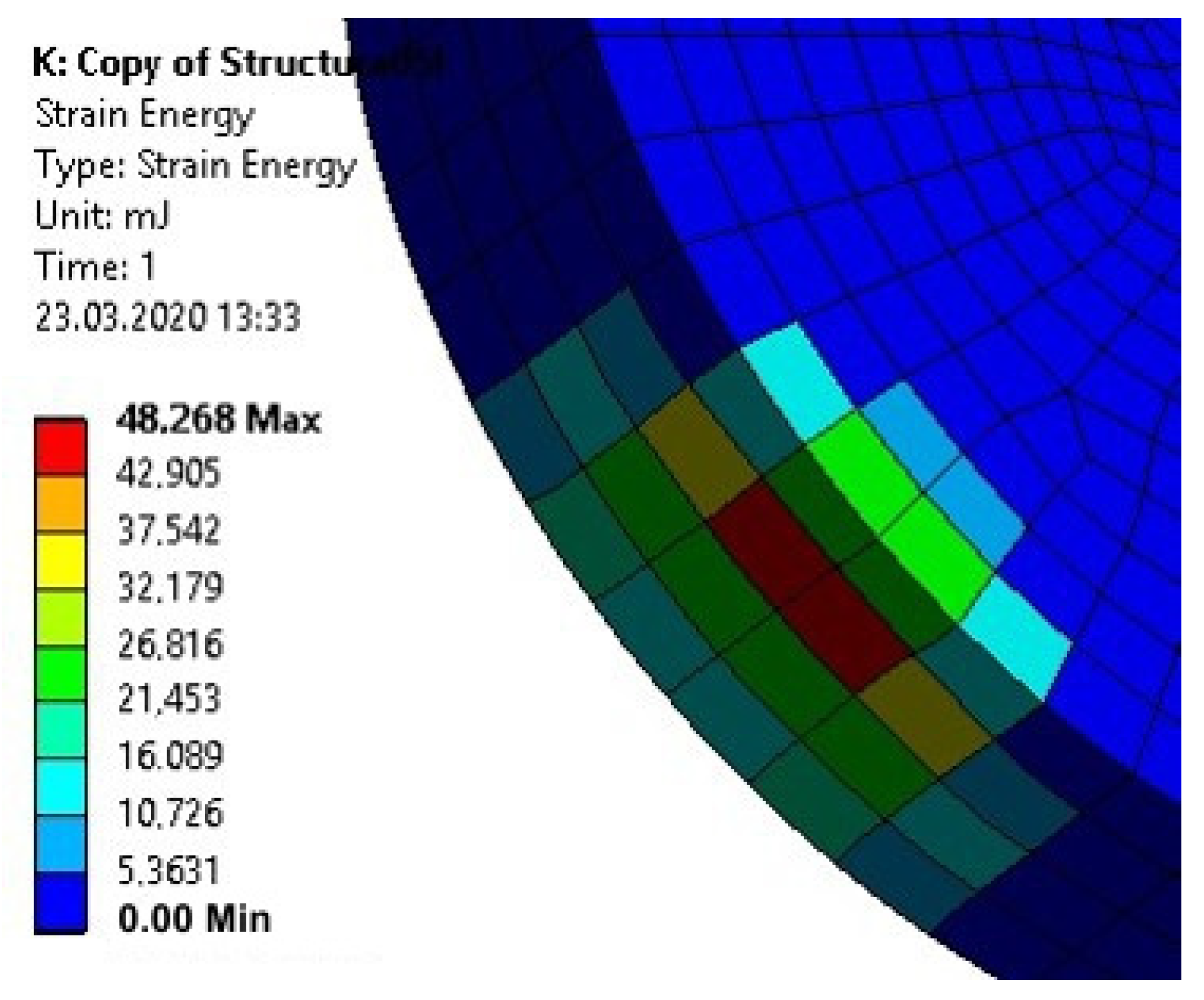
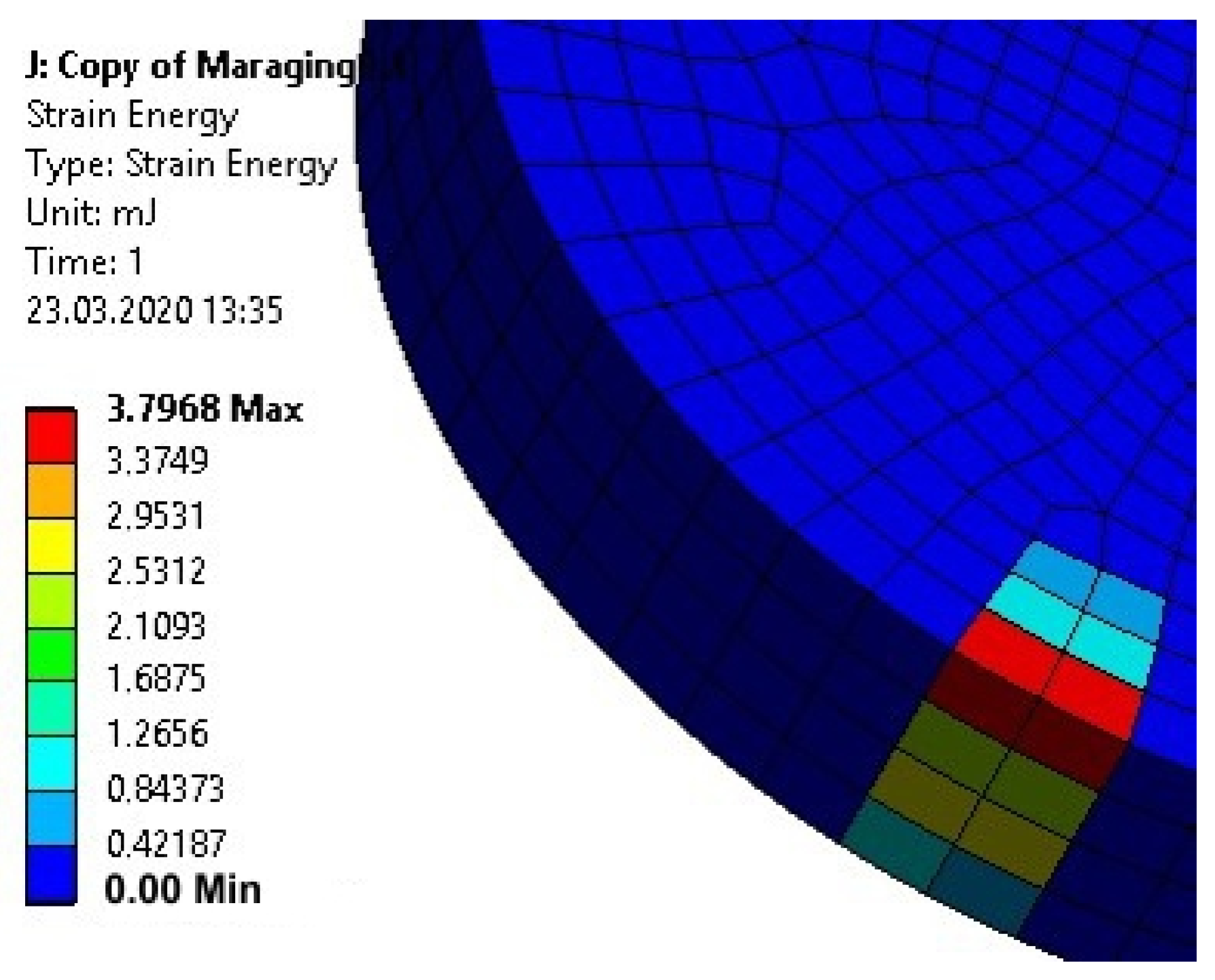
5. Analysis of the Stress State in the Dynamically Loaded Glue Connections
6. Conclusions
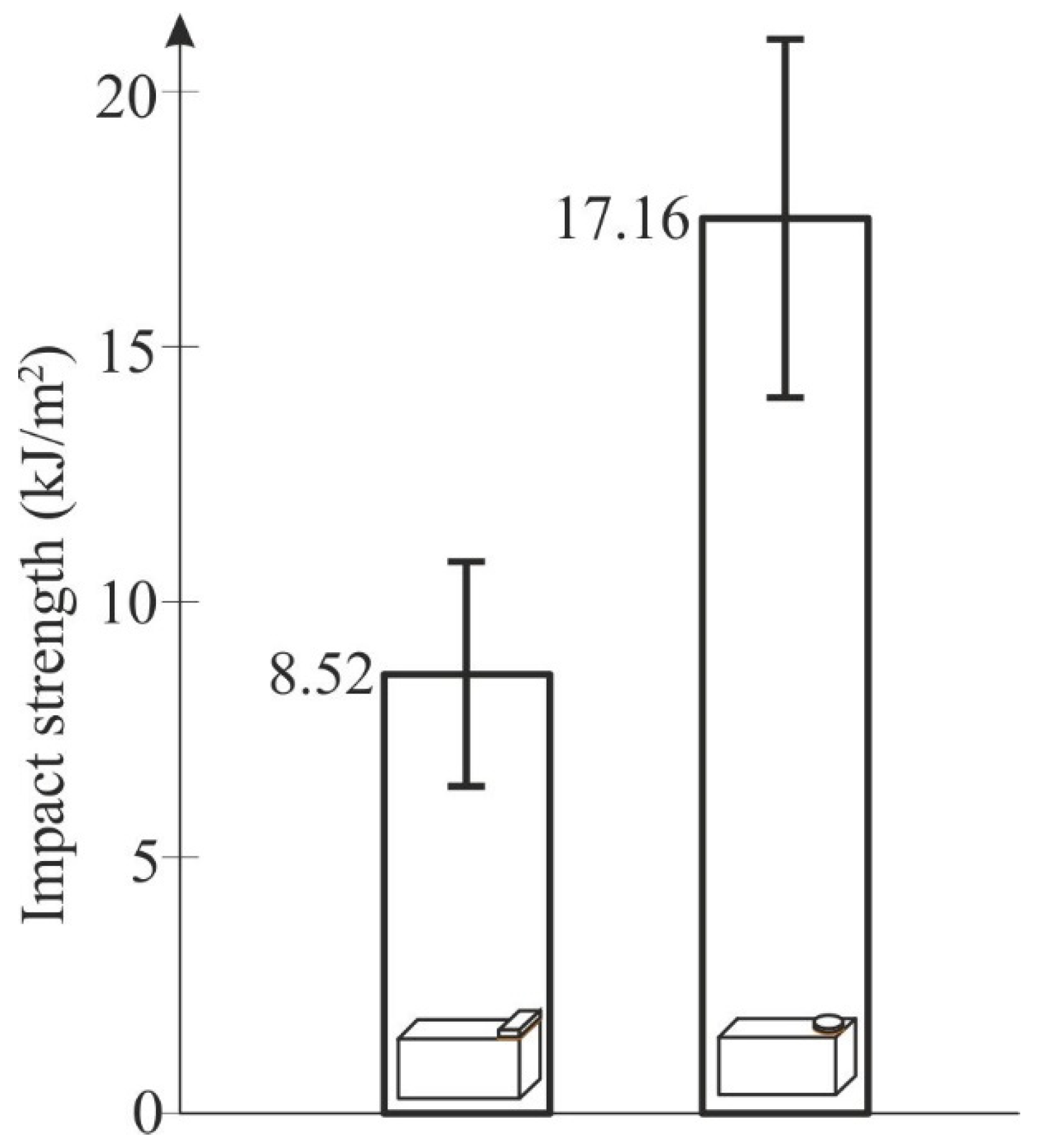
- The test findings obtained for specimens with a top cuboid or disc element cannot be used interchangeably, even though they have the same joining surface area.
- The modified specimens had higher impact strength due to the fact that part of the measured energy was associated with the plastic deformations of the upper specimen element.
- Because the level of stresses in the adhesively joined cylindrical metal elements exceeded the yield point of the carbon steel used in tests (235 MPa), they should be manufactured with a better quality steel, i.e., of increased yield point (for example, maraging steel where Re = 1500 MPa).
- The results of the numerical investigations are consistent with the results of the experimental research in qualitative terms; however, there is no such correlation in the quantitative aspect. The lack of correlation may be caused by disregarding the stiffness of the test machine, as well as too short a calculation time.
- The application of a disc-shaped top element in the specimen eliminates the problem of improper geometry of the specimen; however, the plastic deformation of this element during a test is undesirable, because it changes the stress state in the joint. The joint can then be damaged not only by applying impact load, but also because of the stresses resulting from the plastic deformation of the impacted element. The plastic deformation of the 3-mm-high disc-shaped upper element caused in the adhesive a compressive stress of high values at the edge of the joint.
- The decision on the usability of the specimens with a disc-shaped upper element requires further research, in which materials with significantly increased yield point should be used, as well as elements of different diameters and of higher height. The purpose of this future research will be to obtain the optimum dimensions and materials of the top element, whereby the effect of the stresses in the impacted element on the stress pattern in the adhesive joint will be minimized.
Author Contributions
Funding
Conflicts of Interest
References
- Sato, C. Impact behaviour of adhesively bonded joints. In Adhesive Bonding: Science, Technology and Applications; Adams, R.D., Ed.; WPL: Cambridge, MA, USA, 2005; pp. 164–188. [Google Scholar]
- Viana, G.; Machado, J.; Carbas, R.; Costa, M.; da Silva, L.F.M.; Vaz, M.; Banea, M.D. Strain rate dependence of adhesive joints for the automotive industry at low and high temperatures. J. Adhes. Sci. Technol. 2018, 32, 2162–2179. [Google Scholar] [CrossRef]
- Machado, J.J.M.; Marques, E.A.S.; Silva, M.R.G.; da Silva Lucas, F.M. Numerical study of impact behaviour of mixed adhesive single lap joints for the automotive industry. Int. J. Adhes. Adhes. 2018, 84, 92–100. [Google Scholar] [CrossRef]
- Galvez, P.; Quesada, A.; Martinez, M.A.; Abenojar, J.; Boada, M.J.L.; Diaz, V. Study of the behaviour of adhesive joints of steel with CFRP for its application in bus structures. Compos. Part B Eng. 2017, 129, 41–46. [Google Scholar] [CrossRef]
- Dost, I.; Khan, S.A.; Aziz, M. Mechanical evaluation of joining methodologies in multi material car body. Int. J. Adv. Eng. Technol. 2012, 5, 259–268. [Google Scholar]
- Moroni, F.; Pirondi, A. Technology of Rivet: Adhesive Joints. In Hybrid Adhesive Joints; da Silva, L.F.M., Pirondi, A., Ochsner, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Sadowski, T.; Golewski, P.; Zarzeka-Raczkowska, E. Damage and failure processes of hybrid joints: Adhesive bonded aluminum plates reinforced by rivets. Comput. Mater. Sci. 2011, 50, 1256–1262. [Google Scholar] [CrossRef]
- Chang, E.P. Viscoelastic Properties of Pressure-Sensitive Adhesives. J. Adhes. 1997, 60, 233–248. [Google Scholar] [CrossRef]
- Guillemenet, J.; Bistac, S.; Schultz, J. Relationship between polymer viscoelastic properties and adhesive behavior. Int. J. Adhes. Adhes. 2002, 22, 1–5. [Google Scholar] [CrossRef]
- Siviour, C.R.; Jordan, J.L. High Strain Rate Mechanics of Polymers: A Review. J. Dyn. Behav. Mater. 2016, 2, 15–32. [Google Scholar] [CrossRef]
- Godzimirski, J. (Ed.) Tworzywa adhezyjne: Zastosowanie w Naprawach Sprzętu Technicznego; WNT: Warszawa, Poland, 2010. [Google Scholar]
- Goda, Y.; Sawa, T. Study on the Effect of Strain Rate of Adhesive Material on the Stress State in Adhesive Joints. J. Adhes. 2011, 87, 766–779. [Google Scholar] [CrossRef]
- Banea, M.D.; de Sousa, F.S.M.; da Silva, L.F.M.; Campilho, R.D.S.G.; Bastos de Pereira, A.M. Effects of Temperature and Loading Rate on the Mechanical Properties of a High Temperature Epoxy Adhesive. J. Adhes. Sci. Technol. 2011, 25, 2461–2474. [Google Scholar] [CrossRef]
- Asgharifar, M.; Kong, F.; Carlson, B.; Kovacevic, R. Dynamic analysis of adhesively bonded joint under solid projectile impact. Int. J. Adhes. Adhes. 2014, 50, 17–31. [Google Scholar] [CrossRef]
- Belingardi, G.; Goglio, L.; Rossetto, M. Impact behaviour of bonded built-up beams: Experimental results. Int. J. Adhes. Adhes. 2005, 25, 173–180. [Google Scholar] [CrossRef]
- Adams, R.D.; Harris, J.A. A critical assessment of the block impact test for measuring the impact strength of adhesive bonds. Int. J. Adhes. Adhes. 1996, 16, 61–71. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Kinloch, A.J.; Taylor, A.C.; Wang, Y. The impact wedge-peel performance of structural adhesives. J. Mater. Sci. 2000, 35, 1867–1884. [Google Scholar] [CrossRef]
- Harris, J.A.; Adams, R.D. An assessment of the impact performance of bonded joints for use in high energy absorbing structures. Proc. Inst. Mech. Eng. 1985, 199, 121–131. [Google Scholar] [CrossRef]
- Casas-Rodriguez, J.P.; Ashcroft, I.A.; Silberschmidt, V.V. Damage evolution in adhesive joints to impact fatigue. J. Sound Vib. 2007, 308, 467–478. [Google Scholar] [CrossRef]
- Goglio, L.; Rosetto, M. Impact rupture of structural adhesive joints under different stress combinations. Int. J. Impact. Eng. 2008, 35, 635–643. [Google Scholar] [CrossRef]
- Karachalios, E.F.; Adams, R.D.; da Silva, L.F.M. Single lap joints loaded in tension with ductile steel adherends. Int. J. Adhes. Adhes. 2013, 43, 96–108. [Google Scholar] [CrossRef]
- Komorek, A.; Godzimirski, J. The selected aspects of the research into impact loading of adhesive joints in block samples—Comparison of different ways of applying the load. Maint. Probl. 2016, 4, 77–91. [Google Scholar]
- Komorek, A.; Godzimirski, J.; Pietras, A. Numerical Analysis of Impact Loading of Adhesive Joints. Adv. Mater. Sci. Eng. 2017, 2017, 10. [Google Scholar] [CrossRef]
- Komorek, A.; Godzimirski, J.; Pietras, A. Experimental and preliminary numerical dynamic analysis of effect of sample geometry on impact strength of adhesive joints. In Proceedings of the 7th International Conference on Mechanics and Materials in Design; FEUP-INEGI, Albufeira, Portugal, 11–15 June 2017; pp. 1013–1014. [Google Scholar]
- Eskandari, M.; Mohtadi-Bonab, M.A.; Zarei-Hanzaki, A.; Odeshi, A.G.; Szpunar, J.A. High-resolution EBSD study of adiabatic shear band and neighboring grains after dynamic impact loading of Mn-steel used in vehicle structure. J. Mater. Eng. 2016, 25, 1611–1620. [Google Scholar] [CrossRef]
- Eskandari, M.; Mohtadi-Bonab, M.A.; Zarei-Hanzaki, A.; Odeshi, A.G.; Szpunar, J.A. Microstructure and texture evolution in 21Mn–2.5 Si–1.6 Al–Ti steel subjected to dynamic impact loading. Mater. Sci. Eng. A 2015, 622, 160–167. [Google Scholar] [CrossRef]
- Taylor, A. Impact Testing of Adhesive Joints. MTS Adhes. Proj. 1996, 5, 20–23. [Google Scholar]

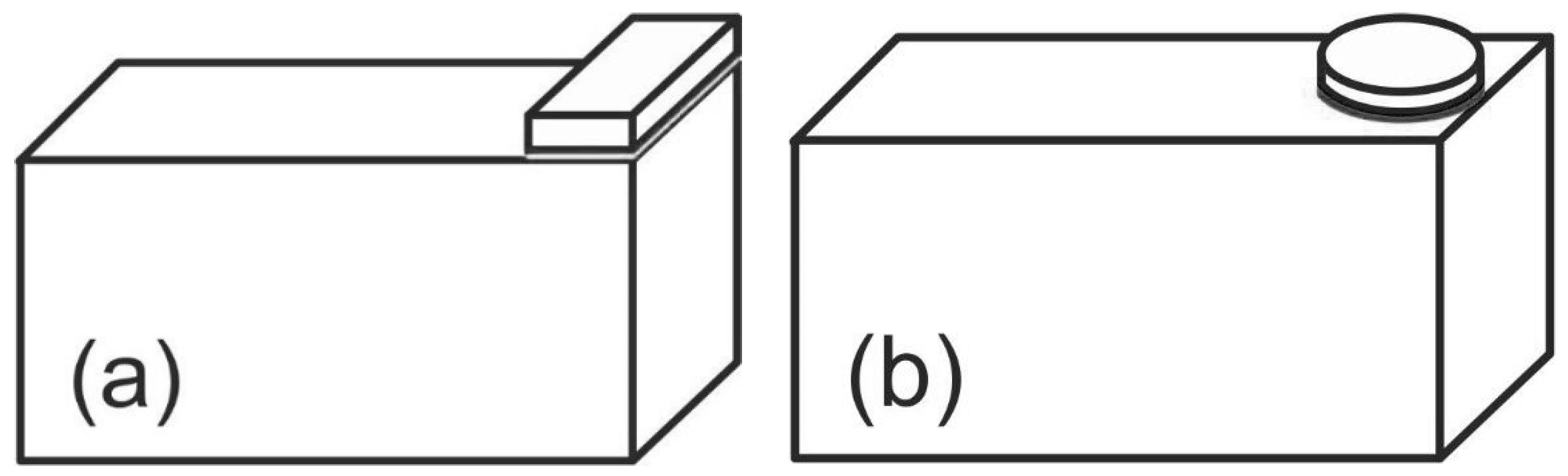


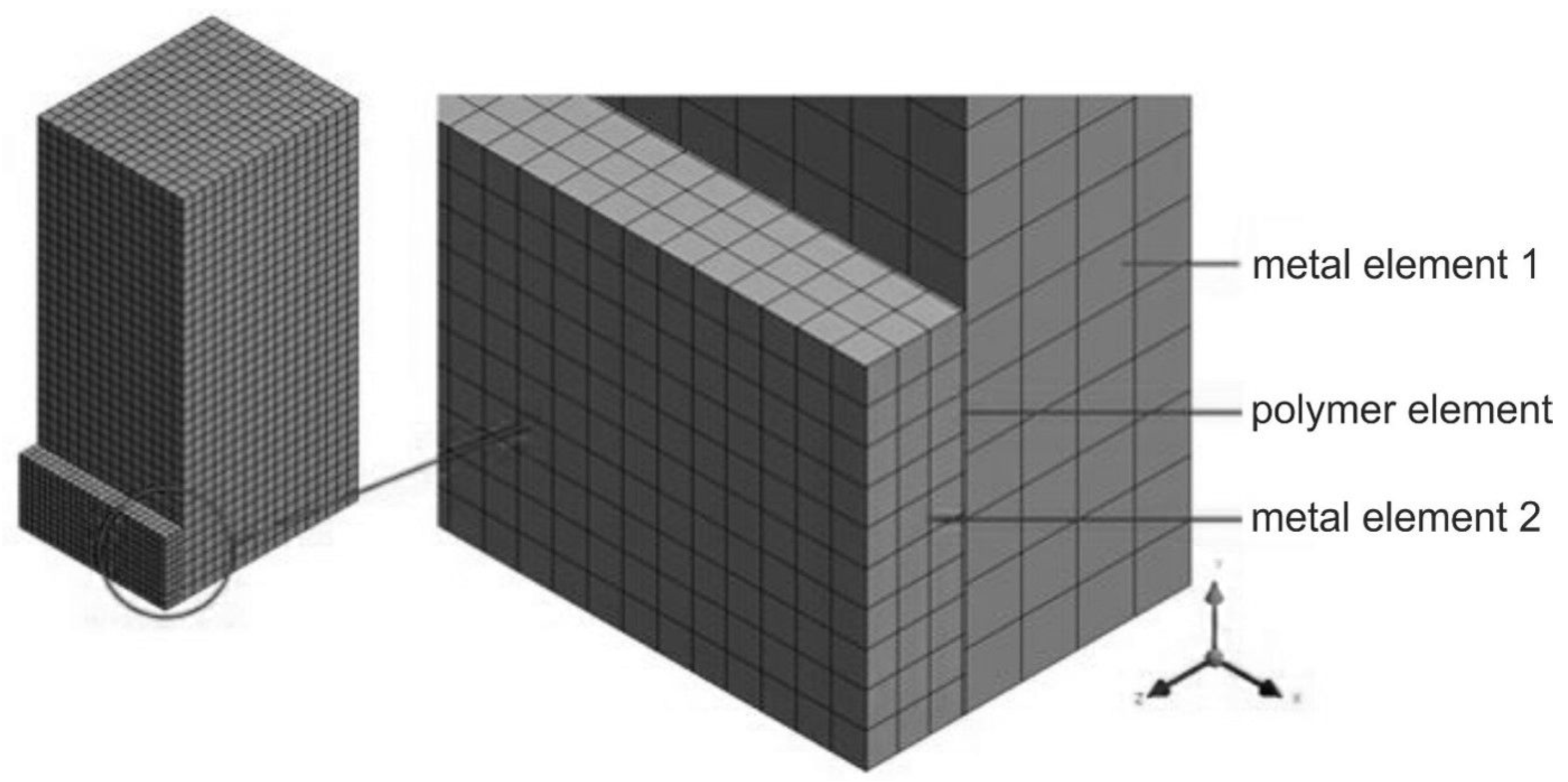
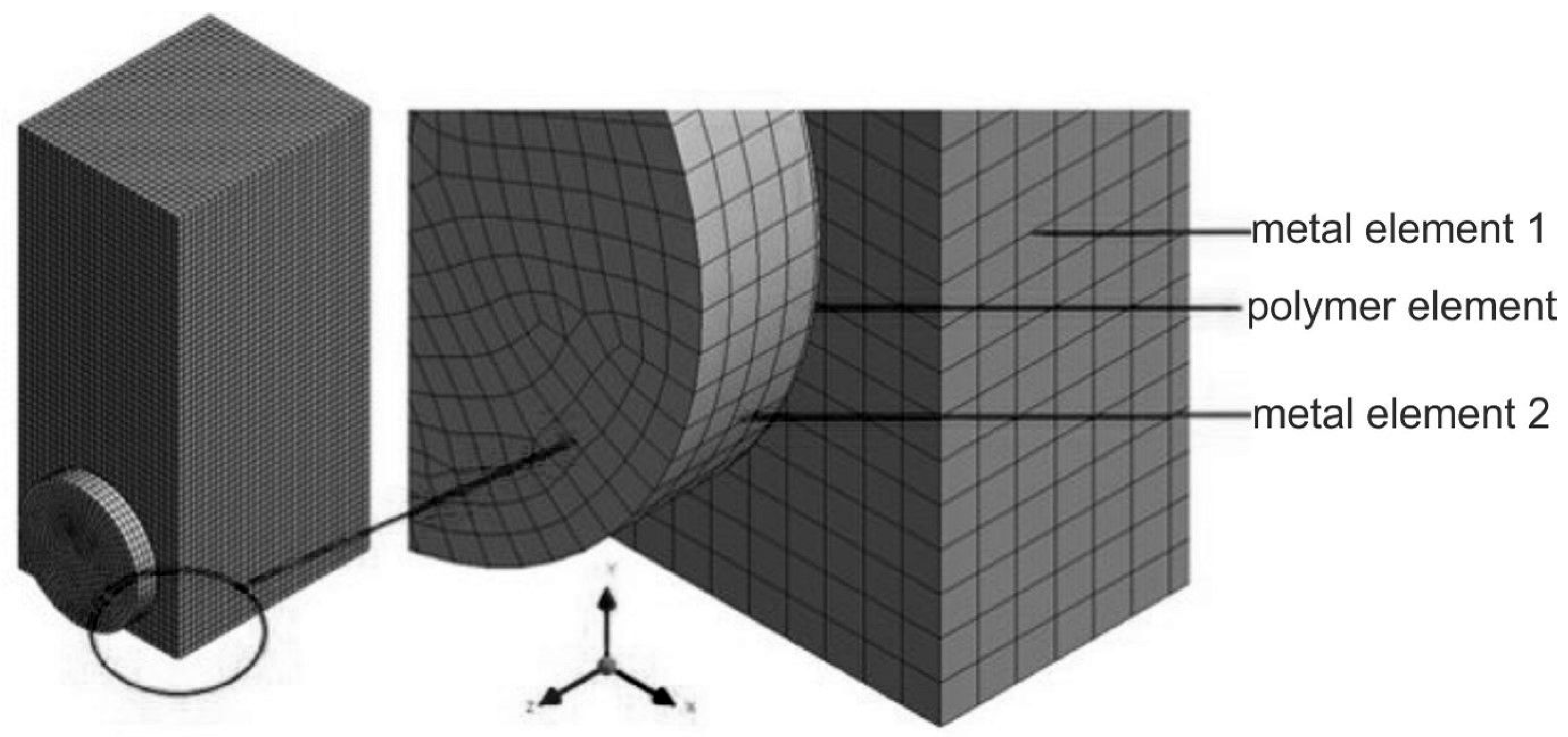

| Specimens According to ISO 9653 (Figure 3a) | Specimens with an Upper Disc-Shaped Element (Figure 3b) | ||
|---|---|---|---|
| Impact Strength of the Joint (kJ/m2) | Mean Impact Strength of the Joint (kJ/m2) | Impact Strength of the Joint (kJ/m2) | Mean Impact Strength of the Joint (kJ/m2) |
| 7.61 | 8.52 ± 2.33 | 12.87 | 17.16 ± 3.85 |
| 9.24 | 15.11 | ||
| 13.11 | 15.14 | ||
| 6.67 | 24.95 | ||
| 6.03 | 12.11 | ||
| 12.89 | 14.22 | ||
| 4.89 | 12.98 | ||
| 4.34 | 24.95 | ||
| 7.89 | 24.94 | ||
| 12.55 | 14.28 | ||
| Model No | Metal Element 1 | Polymer Element (Adhesive) | Metal Element 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height | Width | Depth | Height | Width | Depth | Diameter | Height | Width | Depth | Diameter | |
| (mm) | (mm) | (mm) | |||||||||
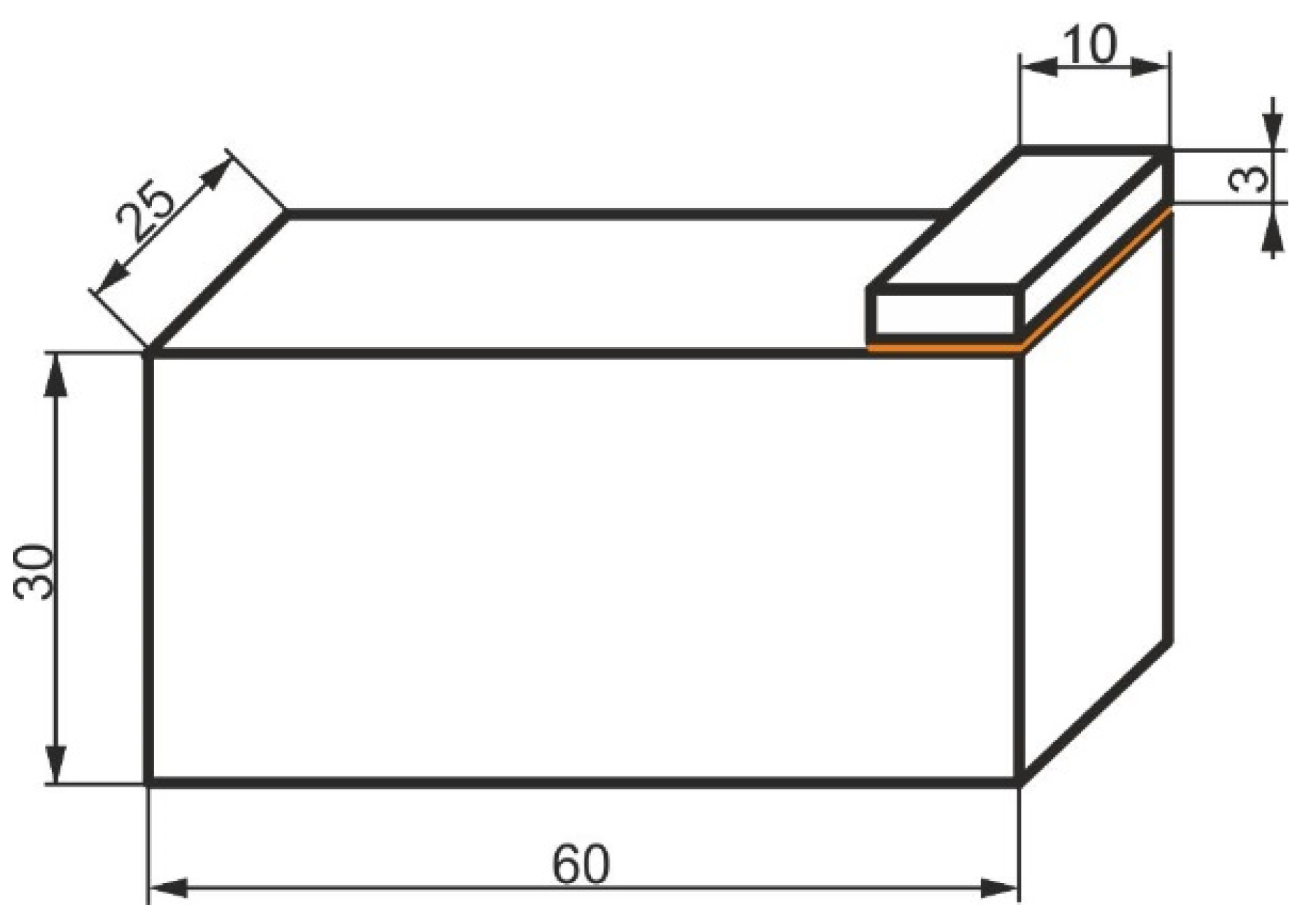
| 1 | 60 | 25 | 30 | 10 | 25 | 0.1 | - | 10 | 25 | 3 | - |
| 2 | - | - | 0.1 | 17.85 | - | - | 3 | 17.85 | |||
| Elements | Elastic Modulus | Poisson’s Ratio |
|---|---|---|
| (MPa) | - | |
| Metal 1 | 200 × 103 | 0.30 |
| Polymer | 2.7 × 103 | 0.35 |
| Metal 2 | 200 × 103 | 0.30 |
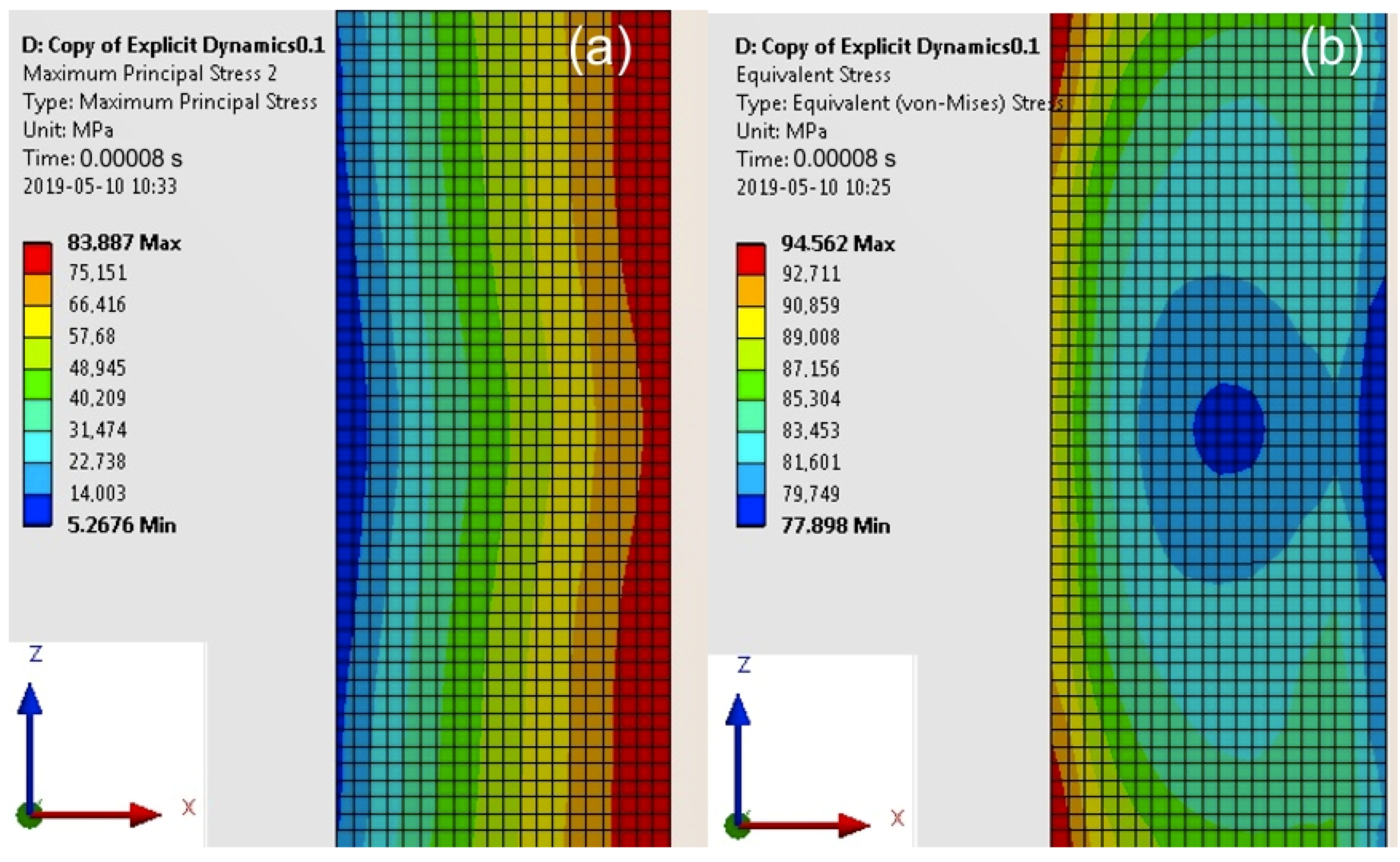
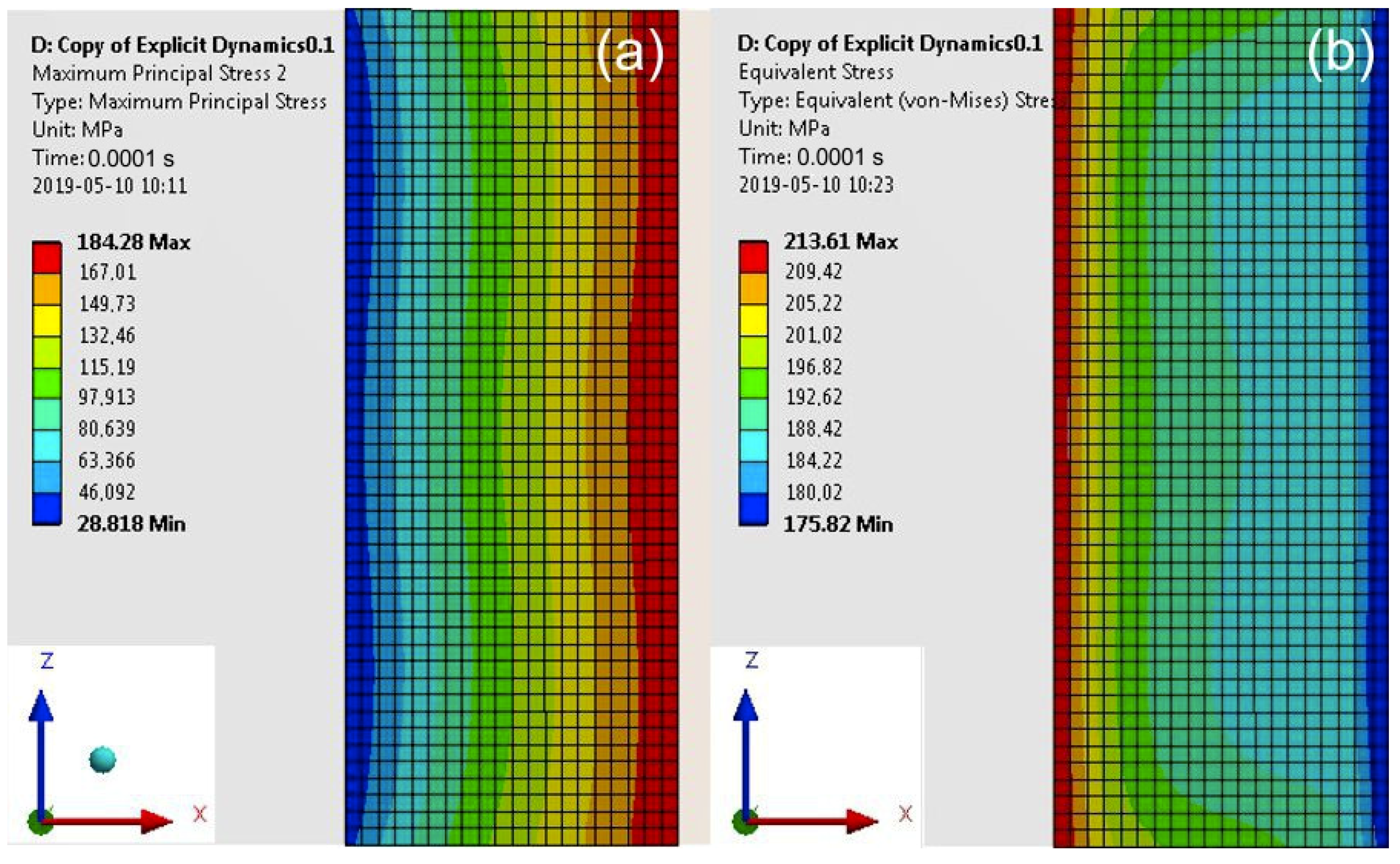
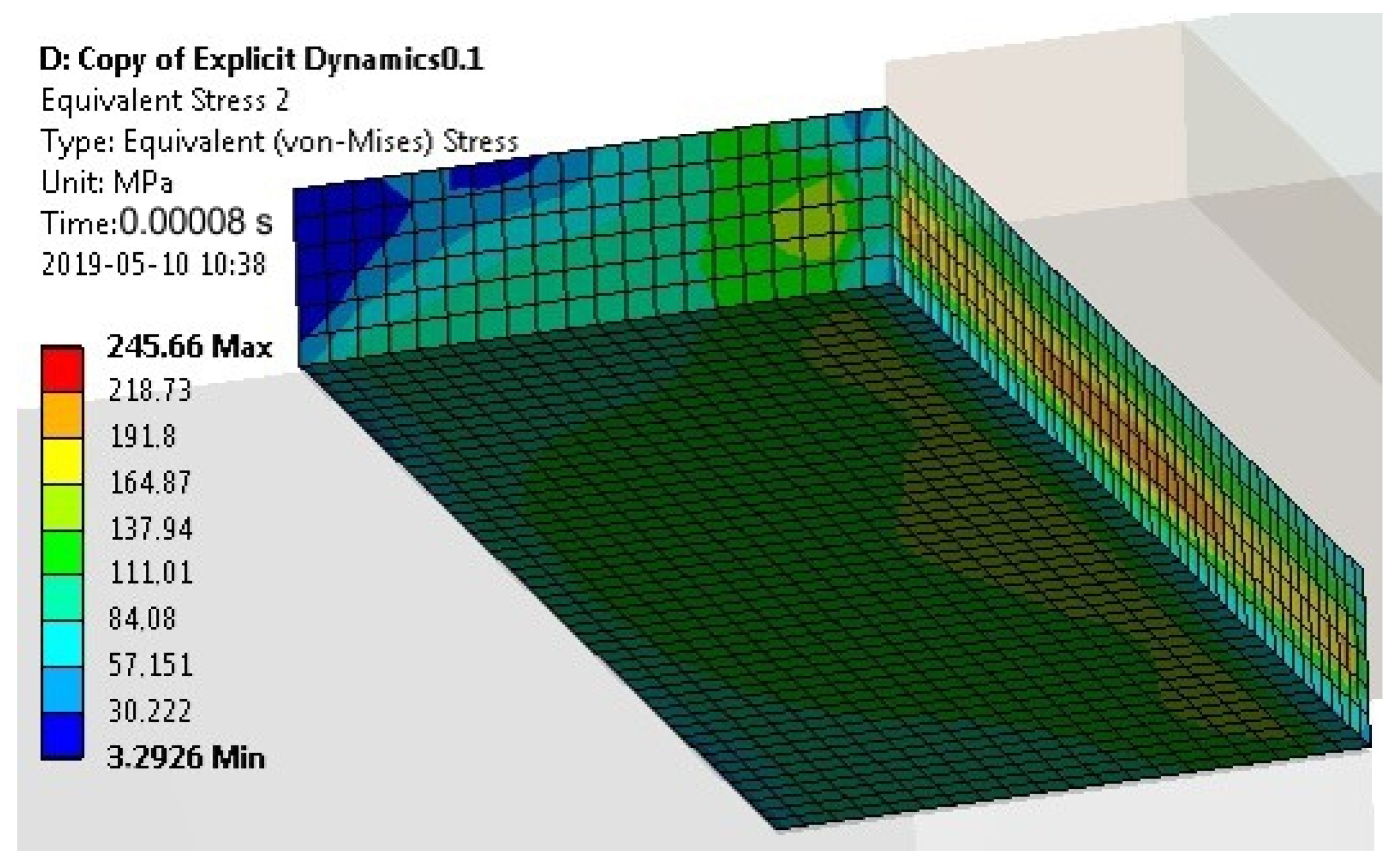
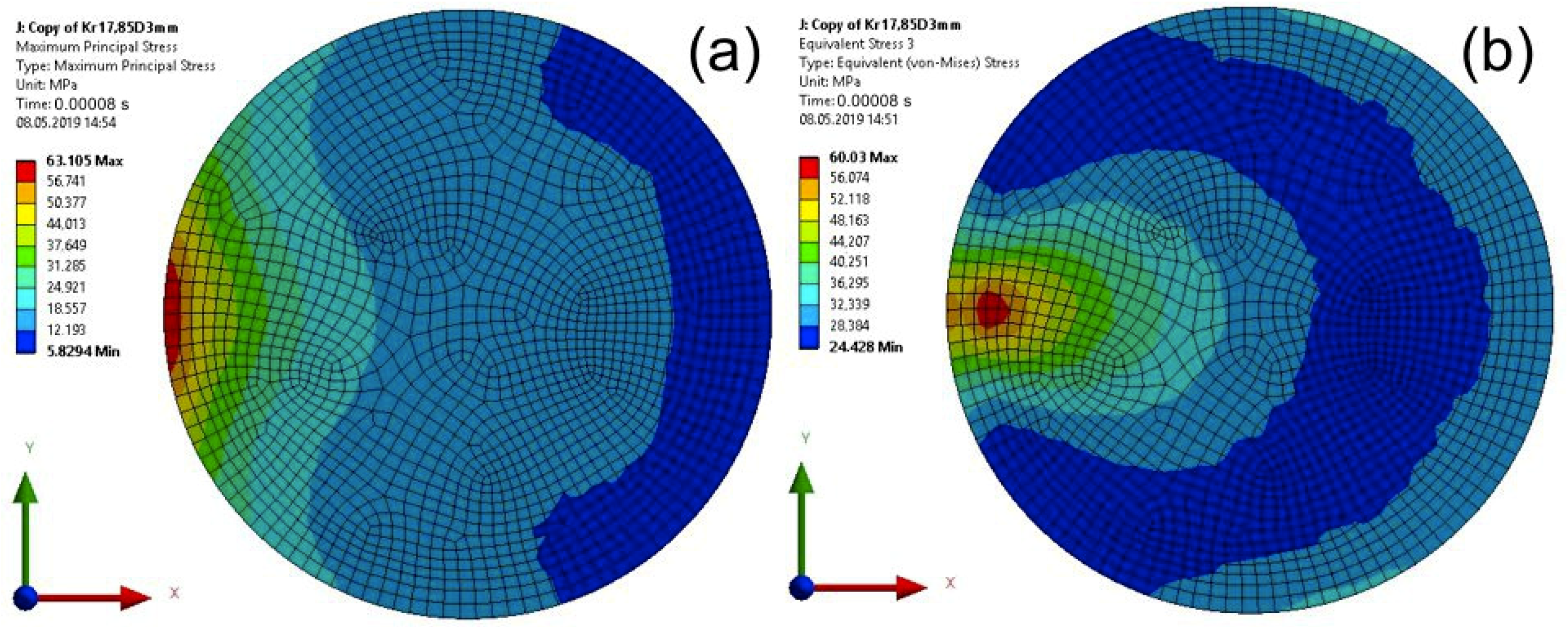
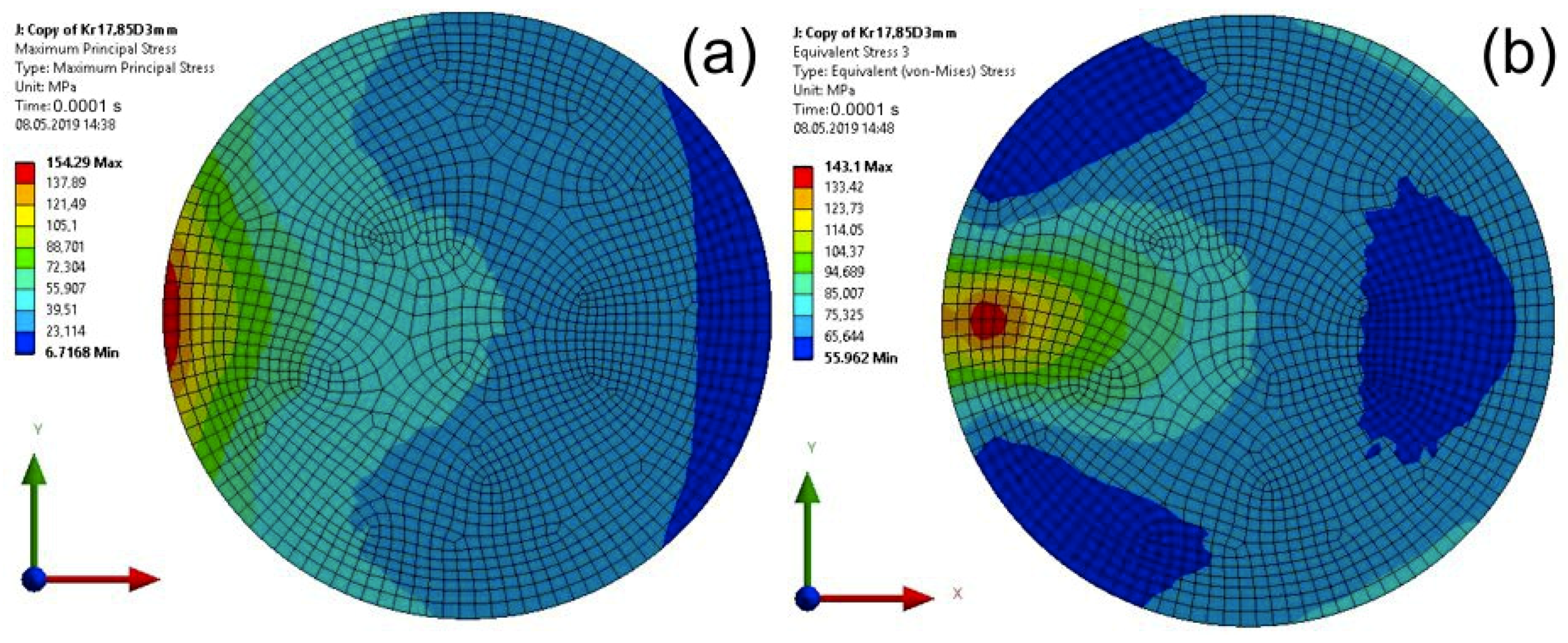
| Computation Time (s) | Max Stresses (MPa) | Model 1 (Specimen with a Cuboid Element) | Model 2 (Specimen with a Disc Element) |
|---|---|---|---|
| 0.00008 | maximum principal | 83.90 | 63.00 |
| von Mises | 94.60 | 60.03 | |
| 0.0001 | maximum principal | 184.30 | 154.30 |
| von Mises | 213.60 | 143.10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komorek, A.; Godzimirski, J.; Rośkowicz, M. Analysis of a New Shape of Test Specimen for Block Shear Impact Test. Materials 2020, 13, 1693. https://doi.org/10.3390/ma13071693
Komorek A, Godzimirski J, Rośkowicz M. Analysis of a New Shape of Test Specimen for Block Shear Impact Test. Materials. 2020; 13(7):1693. https://doi.org/10.3390/ma13071693
Chicago/Turabian StyleKomorek, Andrzej, Jan Godzimirski, and Marek Rośkowicz. 2020. "Analysis of a New Shape of Test Specimen for Block Shear Impact Test" Materials 13, no. 7: 1693. https://doi.org/10.3390/ma13071693
APA StyleKomorek, A., Godzimirski, J., & Rośkowicz, M. (2020). Analysis of a New Shape of Test Specimen for Block Shear Impact Test. Materials, 13(7), 1693. https://doi.org/10.3390/ma13071693





