Dynamic Adsorption of Sulfamethoxazole from Aqueous Solution by Lignite Activated Coke
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials, Reagents and Tests
2.2. Equipment and Conditions of Column Experiments
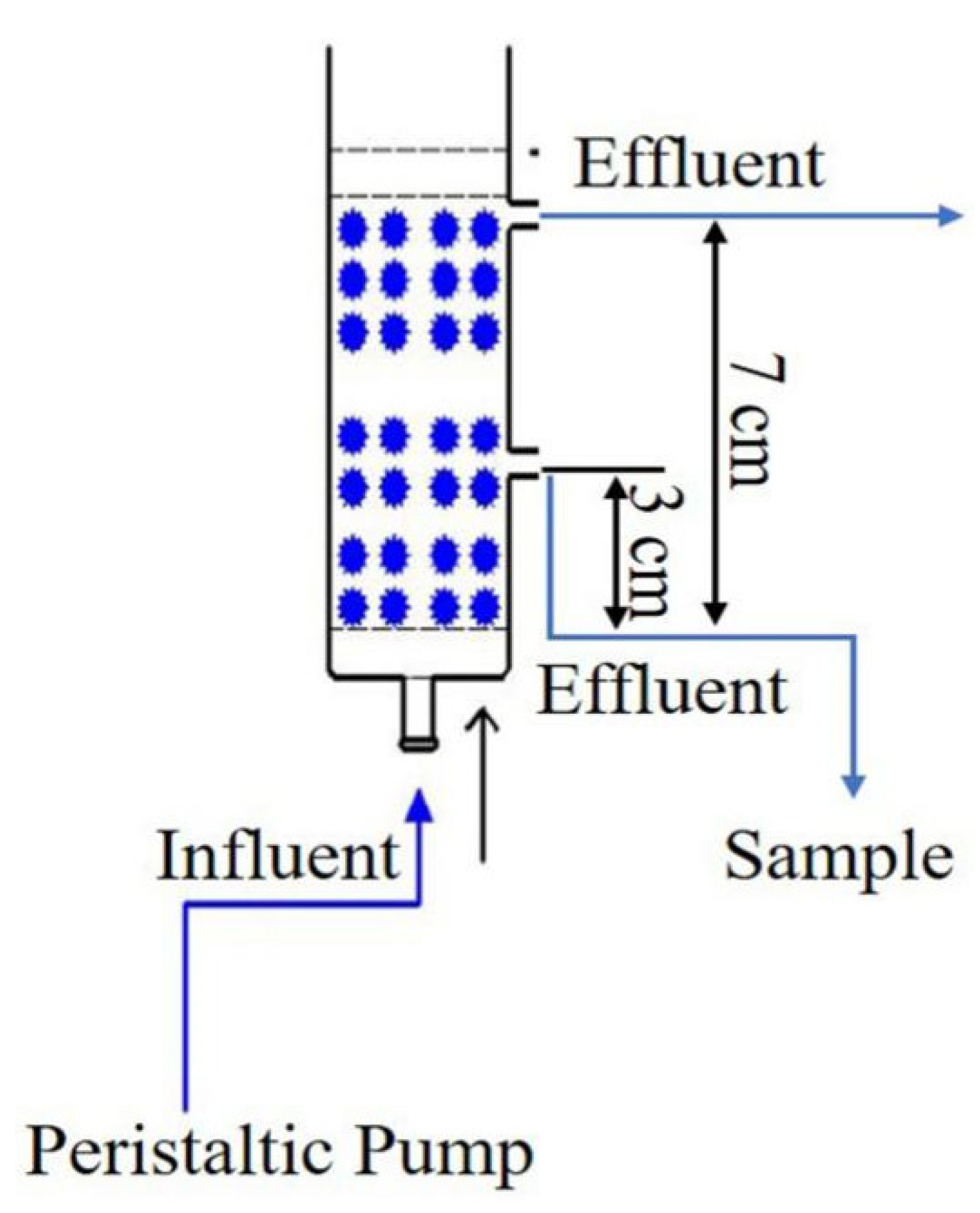
2.2.1. Column Experimental Device
2.2.2. Column Experiments
3. Results and Discussion
3.1. Adsorption Performance of Sulfamethoxazole on LACs
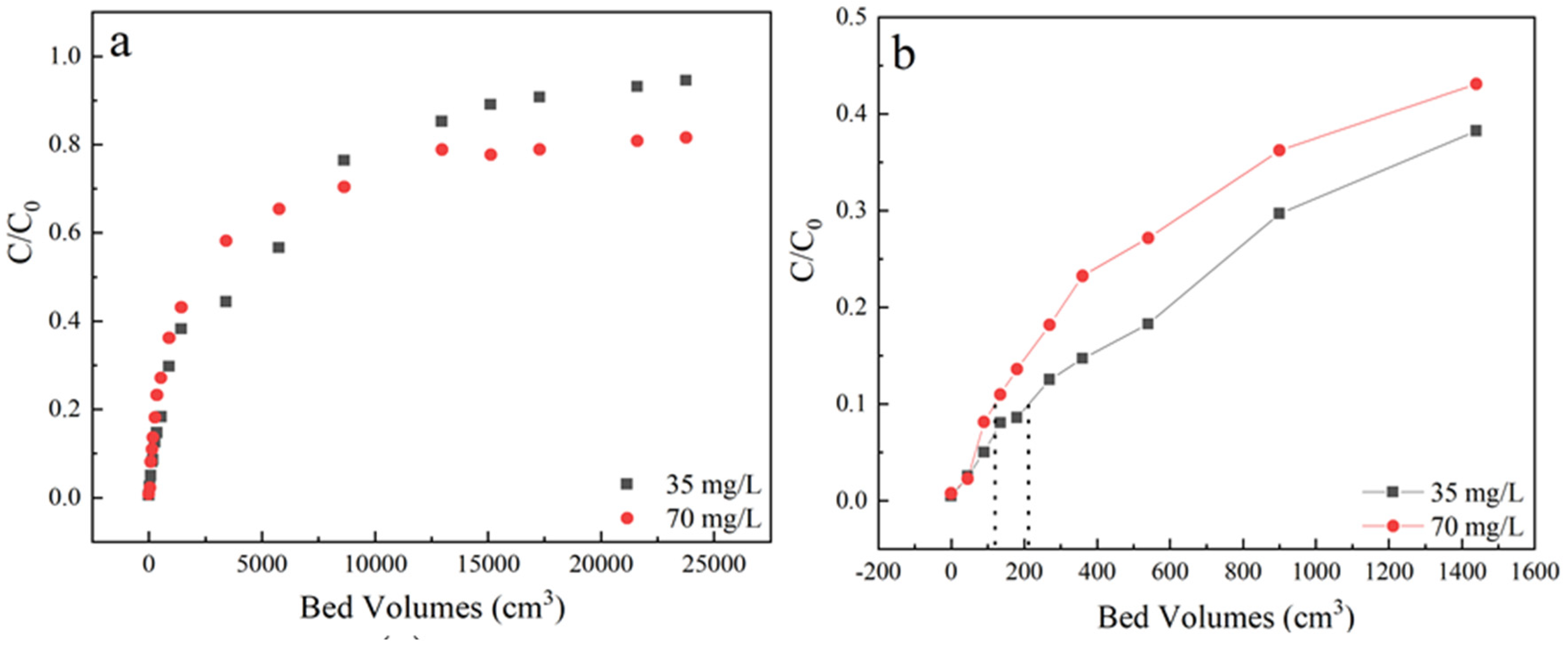
3.1.1. Effect of Initial Concentration
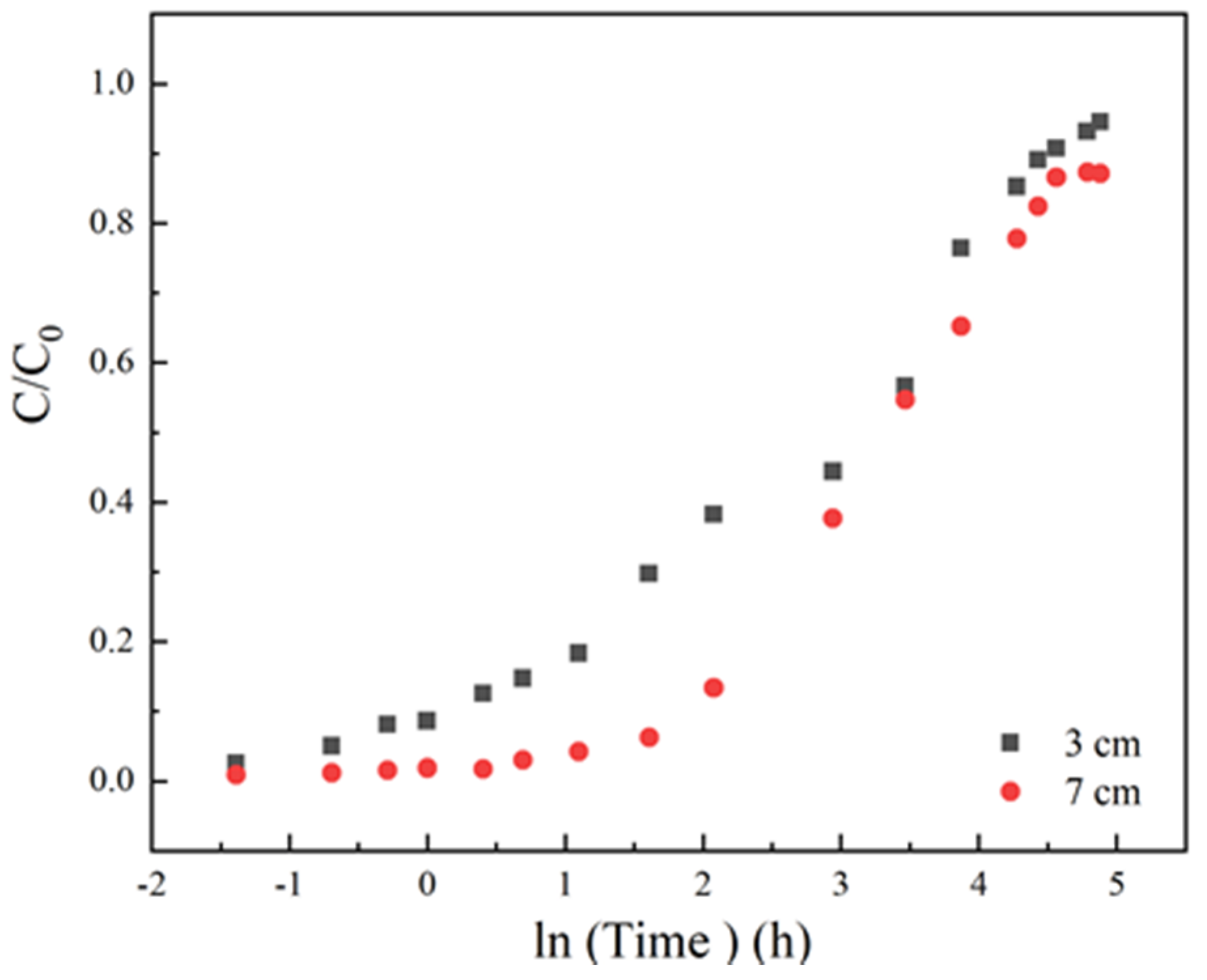
3.1.2. Effect of Column Height
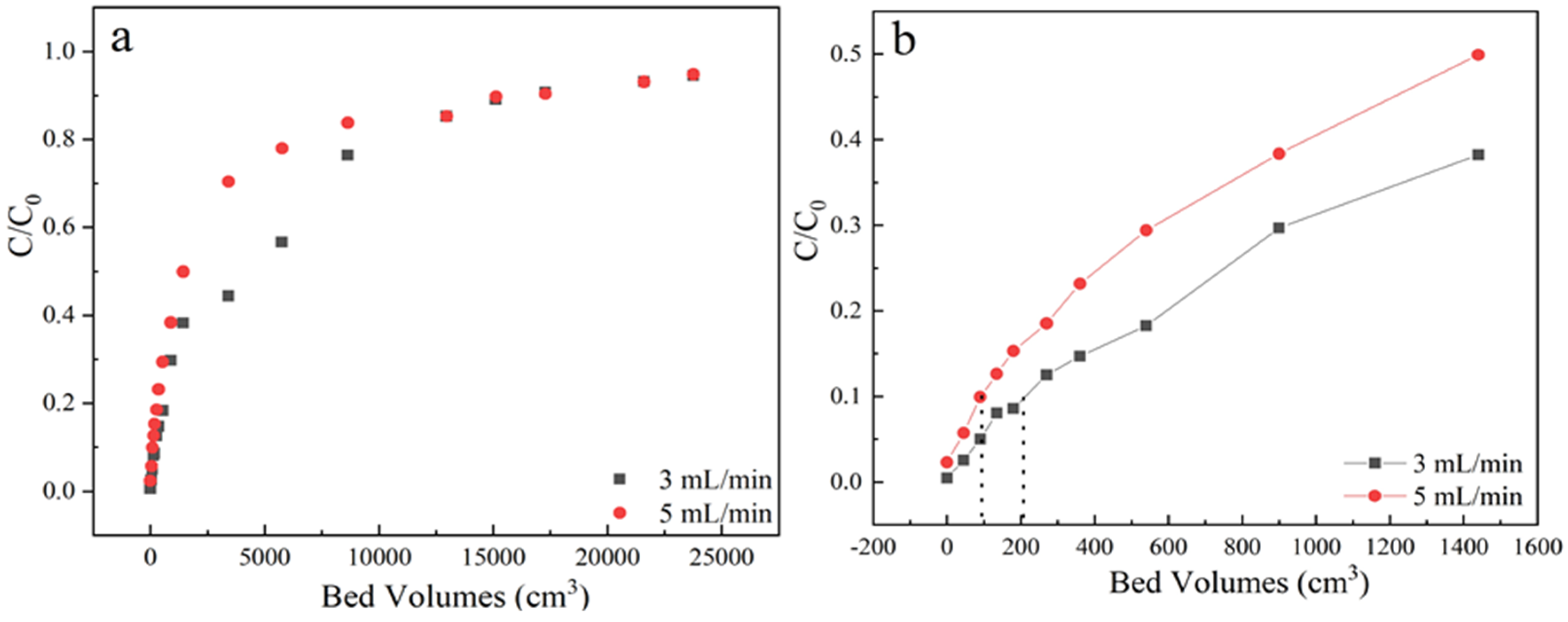
3.1.3. Effect of Flow Rate
3.1.4. Effect of pH
3.1.5. Effect of Humic Acids
3.2. Breakthrough Curves Models Analysis
3.3. Homogeneous Surface Diffusion Model (HDSM)
3.4. Evaluation of Factors Effect
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Perez-Lemus, N.; Lopez-Serna, R.; Perez-Elvira, S.I.; Barrado, E. Analytical methodologies for the determination of pharmaceuticals and personal care products (PPCPs) in sewage sludge: A critical review. Anal. Chim. Acta 2019, 1083, 19–40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.; Zhou, Y.; Shi, B.; Meng, J.; He, B.; Yang, H.; Yoon, S.J. Anthropogenic impacts on the contamination of pharmaceuticals and personal care products (PPCPs) in the coastal environments of the Yellow and Bohai seas. Environ. Int. 2020, 135, 105306. [Google Scholar] [CrossRef] [PubMed]
- Tarpani, R.R.Z.; Azapagic, A. Life cycle environmental impacts of advanced wastewater treatment techniques for removal of pharmaceuticals and personal care products (PPCPs). J. Environ. Manag. 2018, 215, 258–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, M.; Yin, H.; Wu, Q. Occurrence and health risk assessment of pharmaceutical and personal care products (PPCPs) in tap water of Shanghai. Ecotoxicol. Environ. Saf. 2019, 183, 109497. [Google Scholar] [CrossRef]
- Wang, J.; Chu, L. Irradiation treatment of pharmaceutical and personal care products (PPCPs) in water and wastewater: An overview. Radiat. Phys. Chem. 2016, 125, 56–64. [Google Scholar] [CrossRef]
- Liu, J.L.; Wong, M.H. Pharmaceuticals and personal care products (PPCPs): A review on environmental contamination in China. Environ. Int. 2013, 59, 208–224. [Google Scholar] [CrossRef]
- Yang, Y.; Ok, Y.S.; Kim, K.H.; Kwon, E.E.; Tsang, Y.F. Occurrences and removal of pharmaceuticals and personal care products (PPCPs) in drinking water and water/sewage treatment plants: A review. Sci. Total Environ. 2017, 596, 303–320. [Google Scholar] [CrossRef]
- Khan, M.; Fung, C.S.L.; Kumar, A.; He, J.; Lo, I.M.C. Unravelling mechanistic reasons for differences in performance of different Ti-and Bi-based magnetic photocatalysts in photocatalytic degradation of PPCPs. Sci. Total Environ. 2019, 686, 878–887. [Google Scholar] [CrossRef]
- Zeng, L.; Li, S.; Li, X.; Li, J.; Fan, S.; Chen, X. Visible-light-driven sonophotocatalysis and peroxymonosulfate activation over 3D Urchin-like MoS2/C nanoparticles for accelerating levofloxacin elimination: Optimization and kinetic study. Chem. Eng. J. 2019, 378, 122039. [Google Scholar] [CrossRef]
- Alkhuraiji, T.S. Advanced oxidation process based on water radiolysis to degrade and mineralize diclofenac in aqueous solutions. Sci. Total Environ. 2019, 688, 708–717. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Y.; Leiknes, T.O. Oxidation of Refractory Benzothiazoles with PMS/CuFe2O4: Kinetics and Transformation Intermediates. Environ. Sci. Technol. 2016, 50, 564–5073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, M.; Zhang, Y.; Liu, H.H.; Zhang, F.; Wang, S. Room-temperature air oxidation of organic pollutants via electrocatalysis by nanoscaled Co-CoO on graphite felt anode. Environ. Int. 2019, 131, 104977. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhong, S.; Song, Y.; Wang, B.; Zhang, F. Degradation of tetracycline hydrochloride by electro-activated persulfate oxidation. J. Electroanal. Chem. 2018, 809, 74–79. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S. Removal of pharmaceuticals and personal care products (PPCPs) from wastewater: A review. J. Environ. Manag. 2016, 182, 620–640. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Ma, T.; Zhao, S.; Rong, H. Uniform and stable immobilization of metal-organic frameworks into chitosan matrix for enhanced tetracycline removal from water. Chem. Eng. J. 2020, 382. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, Q.; Wang, C.; Yang, Z.; Xue, Q. Removal of Sulfamethoxazole, Sulfathiazole and Sulfamethazine in their Mixed Solution by UV/H2O2 Process. Int. J. Environ. Res. Public Health 2019, 16, 1797. [Google Scholar] [CrossRef] [Green Version]
- Ling, C.; Yue, C.; Yuan, R.; Qiu, J.; Liu, F.Q.; Zhu, J.J. Enhanced removal of sulfamethoxazole by an ovelcomposite of TiO2 nanocrystals in situ wrapped-Bi2O4 microrods undersimulated solar irradiation. Chem. Eng. J. 2020, 384, 123278. [Google Scholar] [CrossRef]
- Chen, C.; Liu, L.; Li, Y.; Li, W.; Zhou, L. Insight into heterogeneous catalytic degradation of sulfamethazine by peroxymonosulfate activated with CuCo2O4 derived from bimetallic oxalate. Chem. Eng. J. 2020, 384, 123257. [Google Scholar] [CrossRef]
- Cheng, M.; Liu, Y.; Huang, D.; Lai, C.; Zeng, G.; Huang, J.; Xiong, W. Prussian blue analogue derived magnetic Cu-Fe oxide as a recyclable photoFenton catalyst for the efficient removal of sulfamethazine at near neutral pH values. Chem. Eng. J. 2019, 362, 865–876. [Google Scholar] [CrossRef]
- Liu, X.; Huang, F.; Yu, Y.; Jiang, Y.; Zhao, K.; He, Y.; Zhang, Y. Determination and toxicity evaluation of the generated byproducts from sulfamethazine degradation during catalytic oxidation process. Chemosphere 2019, 226, 103–109. [Google Scholar] [CrossRef]
- Zbair, M.; Ahsaine, H.A.; Anfar, Z. Porous carbon by microwave assisted pyrolysis: An effective and low-cost adsorbent for sulfamethoxazole adsorption and optimization using response surface methodology. J. Clean Prod. 2018, 202, 571–581. [Google Scholar] [CrossRef]
- Lawal, I.A.; Lawal, M.M.; Akpotu, S.O.; Moodley, B. Theoretical and experimental adsorption studies of sulfamethoxazole and ketoprofen on synthesized ionic liquids modified CNTs. Ecotox. Environ. Safe. 2018, 161, 542–552. [Google Scholar] [CrossRef] [PubMed]
- Prasannamedha, G.; Kumar, P.S. A review on contamination and removal of sulfamethoxazole from aqueous solution using cleaner techniques: Present and future perspective. J. Clean Prod. 2020, 250, 119553. [Google Scholar] [CrossRef]
- Heo, J.; Yoon, Y.; Lee, G.; Kim, Y.; Park, C.M. Enhanced adsorption of bisphenol A and sulfamethoxazole by a novel magnetic CuZnFe2O4-biochar composite. Bioresour. Technol. 2019, 281, 179–187. [Google Scholar] [CrossRef]
- Zhang, R.; Zheng, X.; Chen, B.; Ma, J.; Niu, X.; Zhou, S. Enhanced adsorption of sulfamethoxazole from aqueous solution by Fe-impregnated graphited biochar. J. Clean Prod. 2020, 256, 120662. [Google Scholar] [CrossRef]
- Li, S.; Wang, F.; Pan, W.; Yang, X.; Gao, Q.; Sun, W.; Ni, J. Molecular insights into the effects of Cu(II) on sulfamethoxazole and 17β-estradiol adsorption by carbon nanotubes/CoFe2O4 composites. Chem. Eng. J. 2019, 373, 995–1002. [Google Scholar] [CrossRef]
- Ogunleye, D.T.; Akpotu, S.O.; Moodley, B. Adsorption of sulfamethoxazole and reactive blue 19 using graphene oxide modified with imidazolium based ionic liquid. Environ. Technol. Innov. 2020, 17, 100616. [Google Scholar] [CrossRef]
- Rostamian, R.; Behnejad, H. A comparative adsorption study of sulfamethoxazole onto graphene and graphene oxide nanosheets through equilibrium, kinetic and thermodynamic modeling. Process Saf. Environ. Protect. 2016, 102, 20–29. [Google Scholar] [CrossRef]
- Yu, K.; Ahmed, I.; Won, D.-I.; Lee, W.I.; Ahn, W.-S. Highly efficient adsorptive removal of sulfamethoxazole from aqueous solutions by porphyrinic MOF-525 and MOF-545. Chemosphere 2020, 250, 126133. [Google Scholar] [CrossRef]
- Qiu, H.; Ling, C.; Yuan, R.; Liu, F.; Li, A. Bridging effects behind the coadsorption of copper and sulfamethoxazole by a polyamine-modified resin. Chem. Eng. J. 2019, 362, 422–429. [Google Scholar] [CrossRef]
- Zheng, M.; Han, Y.; Xu, C.; Zhang, Z.; Han, H. Selective adsorption and bioavailability relevance of the cyclic organics in anaerobic pretreated coal pyrolysis wastewater by lignite activated coke. Sci. Total Environ. 2019, 653, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wu, L.; Liu, H.; Lan, H.; Qu, J. Improvement of aqueous mercury adsorption on activated coke by thiol-functionalization. Chem. Eng. J. 2013, 228, 925–934. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Liu, Q.; Wang, X.; Zhang, Z. Facile and economical synthesis of porous activated semi-cokes for highly efficient and fast removal of microcystin-LR. J. Hazard. Mater. 2015, 299, 325–332. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Du, C.; He, H.; Yang, Z.; Li, H. Effective adsorption of diclofenac sodium from neutral aqueous solution by low-cost lignite activated cokes. J. Hazard. Mater. 2020, 384, 121284. [Google Scholar] [CrossRef]
- Zhuang, S.; Liu, Y.; Wang, J. Covalent organic frameworks as efficient adsorbent for sulfamerazine removal from aqueous solution. J. Hazard. Mater. 2020, 383, 121126. [Google Scholar] [CrossRef]
- Chowdhury, S.; Saha, P.D. Batch and continuous (fixed-bed column) biosorption of Cu (II) by Tamarindus indicafruit shell. Korean J. Chem. Eng. 2013, 30, 369–378. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Hameed, B.H. Fixed-bed adsorption of reactive azo dye onto granular activated carbon prepared from waste. J. Hazard. Mater. 2010, 175, 298–303. [Google Scholar] [CrossRef]
- Chen, K.L.; Liu, L.C.; Chen, W.R. Adsorption of sulfamethoxazole and sulfapyridine antibiotics in high organic content soils. Environ. Pollut. 2017, 231 Pt 1, 1163–1171. [Google Scholar] [CrossRef]
- Bhadra, B.N.; Seo, P.W.; Jhung, S.H. Adsorption of diclofenac sodium from water using oxidized activated carbon. Chem. Eng. J. 2016, 301, 27–34. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Wang, C.; Ying, Z.; Huo, M.; Yang, W. Effective column adsorption of triclosan from pure water and wastewater treatment plant effluent by using magnetic porous reduced graphene oxide. J. Hazard. Mater. 2020, 386, 121942. [Google Scholar] [CrossRef]
- Nithya, K.; Sathish, A.; Kumar, P.S. Packed bed column optimization and modeling studies for removal of chromium ions using chemically modified Lantana camara adsorbent. Process Saf. Environ. Protect. 2020, 33, 101069. [Google Scholar] [CrossRef]
- Alardhi, S.M.; Albayati, T.M.; Alrubaye, J.M. Adsorption of the methyl green dye pollutant from aqueous solution using mesoporous materials MCM-41 in a fixed-bed column. Heliyon 2020, 6, e03253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bo, S.; Luo, J.; An, Q.; Xiao, Z.; Wang, H.; Cai, W.; Li, Z. Efficiently selective adsorption of Pb(II) with functionalized alginate-based adsorbent in batch/column systems: Mechanism and application simulation. J. Clean Prod. 2020, 250, 119585. [Google Scholar] [CrossRef]
- Weber, W.J.J.; Liu, K.T. Determination of mass transport parameters for fixed-bed. Chem. Eng. Commun. 1980, 6, 49–60. [Google Scholar] [CrossRef]
- Zheng, M.; Hu, H.; Ye, Z.; Huang, Q.; Chen, X. Adsorption desulfurization performance and adsorption-diffusion study of B2O3 modified Ag-CeOx/TiO2-SiO2. J. Hazard. Mater. 2019, 362, 424–435. [Google Scholar] [CrossRef]
- Yu, J.; Yang, F.C.; Hung, W.N.; Liu, C.L.; Yang, M.; Lin, T.F. Prediction of powdered activated carbon doses for 2-MIB removal in drinking water treatment using a simplified HSDM approach. Chemosphere 2016, 156, 374–382. [Google Scholar] [CrossRef]
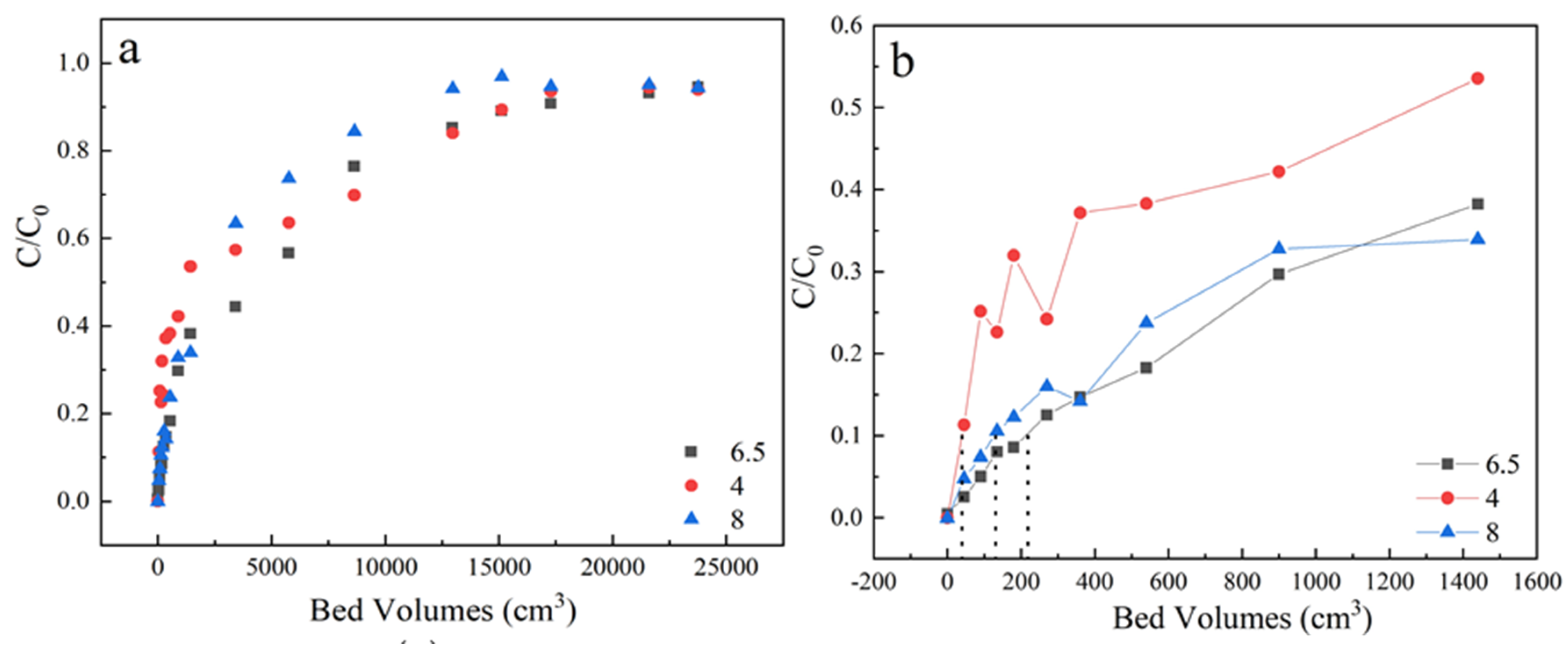

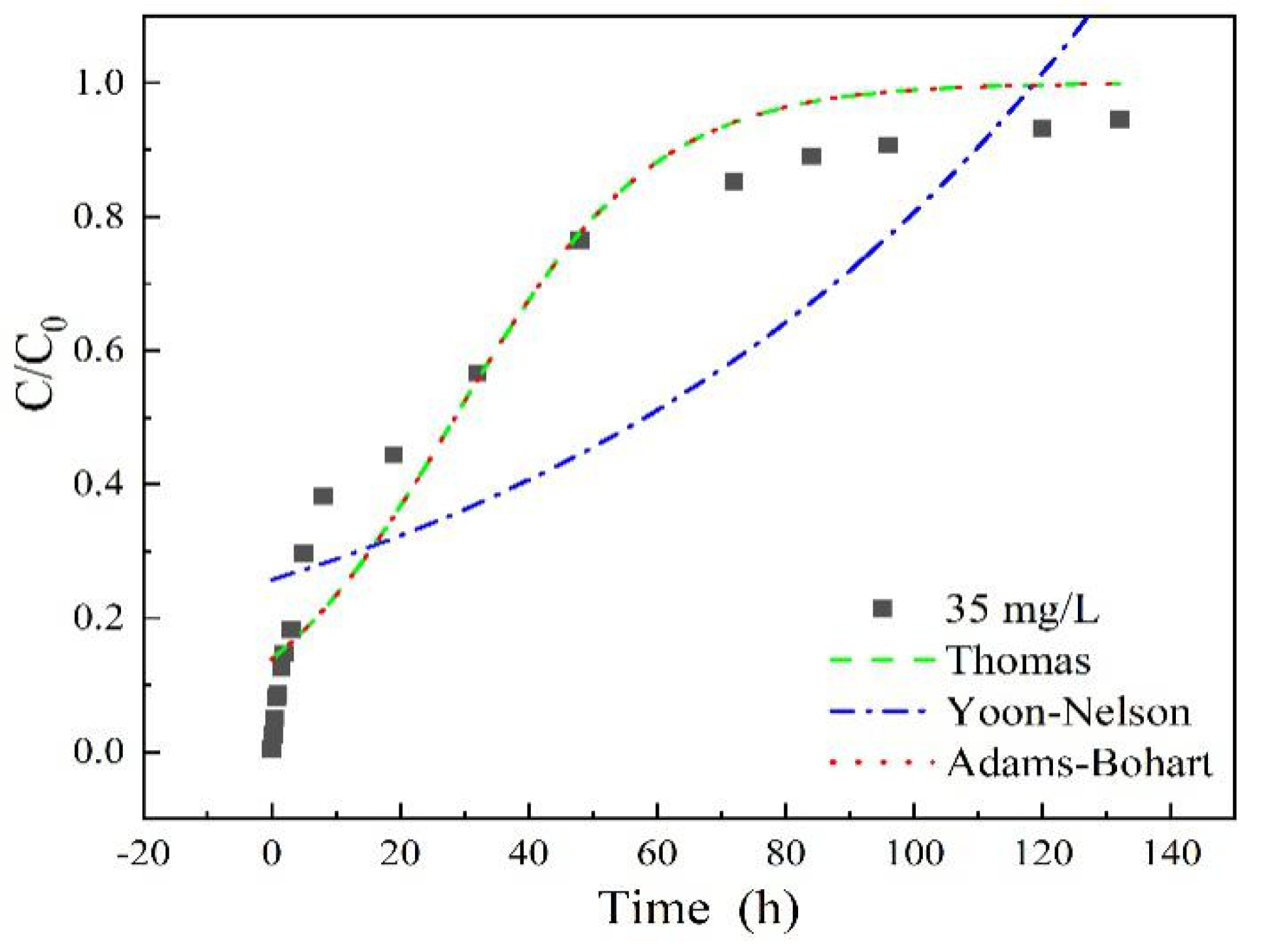
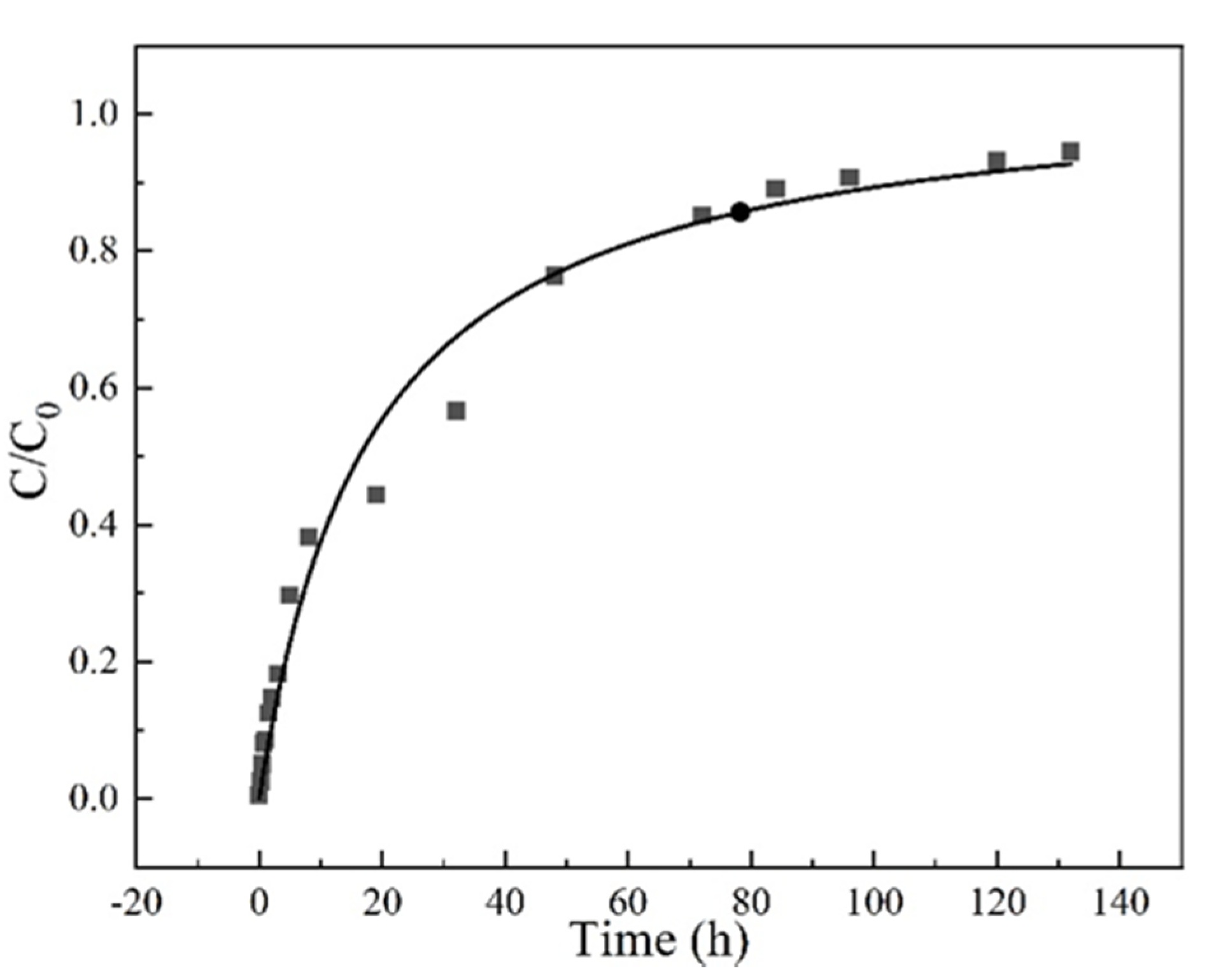
| Concentration (mg/L) | Flow Rate (mL/min) | Column Height (cm) | pH | Humic Acids (mg/L) | 10% Breakthrough Volume (cm3) | 95% Breakthrough Volume (cm3) |
|---|---|---|---|---|---|---|
| 35 | 3 | 3 | 6.5 | 0 | 210 | 23745 |
| 70 | 3 | 3 | 6.5 | 0 | 110 | 20820 |
| 35 | 3 | 3 | 6.5 | 0 | 210 | 23745 |
| 35 | 5 | 3 | 6.5 | 0 | 98 | 24000 |
| 35 | 3 | 3 | 6.5 | 0 | 210 | 23745 |
| 35 | 3 | 7 | 6.5 | 0 | 395 | 30000 |
| 35 | 3 | 3 | 4 | 0 | 15 | 20700 |
| 35 | 3 | 3 | 6.5 | 0 | 210 | 23745 |
| 35 | 3 | 3 | 8 | 0 | 115 | 12636 |
| 35 | 3 | 3 | 6.5 | 0 | 210 | 23745 |
| 35 | 3 | 3 | 6.5 | 0.1 | 680 | - |
| 35 | 3 | 3 | 6.5 | 1 | 20 | 17220 |
| 35 | 3 | 3 | 6.5 | 10 | 250 | 26190 |
| Models | Initial Concentration (mg/L) | Flow Rate (mL/min) | Column Height (cm) | |||
|---|---|---|---|---|---|---|
| 35 | 70 | 3 | 5 | 3 | 7 | |
| Thomas | ||||||
| R2 | 0.953 | 0.951 | 0.953 | 0.950 | 0.953 | 0.93 |
| qe (mg/g) | 3.04 | 11.56 | 3.04 | 4.37 | 3.04 | 3.09 |
| kT (mL/(mg·min)) | 0.039 | 0.032 | 0.039 | 0.039 | 0.039 | 0.010 |
| Yoon-Nelson | ||||||
| R2 | 0.95 | 0.90 | 0.953 | 0.91 | 0.953 | 0.93 |
| τ (h) | 25 | 12 | 25 | 12 | 38.7 | 80 |
| kY (1/min) | 0.045 | 0.039 | 0.045 | 0.078 | 0.045 | 0.038 |
| Adams-Bohart | ||||||
| R2 | 0.72 | 0.63 | 0.72 | 0.63 | 0.72 | 0.71 |
| kA (L/(mg·min)) | 0.456 | 0.375 | 0.456 | 0.377 | 0.456 | 0.54 |
| N0 (g/L) | 2.6 | 3.0 | 2.6 | 2.5 | 2.6 | 2.83 |
| Time (h) | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 | 3 | 5 |
| Ccal | 0.00 | 0.01 | 0.03 | 0.04 | 0.06 | 0.08 | 0.11 | 0.15 | 0.23 |
| Cexp | 0.00 | 0.03 | 0.05 | 0.08 | 0.09 | 0.13 | 0.15 | 0.18 | 0.30 |
| Time (h) | 8 | 19 | 32 | 48 | 72 | 84 | 96 | 120 | 132 |
| Ccal | 0.32 | 0.54 | 0.67 | 0.77 | 0.84 | 0.87 | 0.89 | 0.92 | 0.93 |
| Cexp | 0.38 | 0.44 | 0.57 | 0.76 | 0.85 | 0.89 | 0.91 | 0.93 | 0.95 |
| SSE | 0.04 | ||||||||
| Factor | Variable X | H | Δx | Δtb | ΔH | |Δtb/Δx| | |ΔH/Δx| |
|---|---|---|---|---|---|---|---|
| Initial sulfamethoxazole concentration | 35 mg/L | 2.973 | 35 | 30 | 0.009 | 0.86 | 0.003 |
| 70 mg/L | 2.982 | ||||||
| Column height | 3 cm | 2.988 | 4 | 393 | 2.59 | 98.25 | 0.6474 |
| 7 cm | 5.578 | ||||||
| Flow rate | 3 mL/min | 2.973 | 2 | 40 | 0.015 | 20 | 0.0076 |
| 5 mL/min | 2.988 | ||||||
| pH | 4 | 3.346 | 4 | 61 | 0.448 | 12.25 | 0.0073 |
| 6.5 | 2.973 | ||||||
| 8 | 3.421 | ||||||
| Humic acids | 0.1 mg/L | 3.474 | 9.9 | 220 | 0.189 | 2.22 | 0.0191 |
| 1 mg/L | 3.333 | ||||||
| 10 mg/L | 3.285 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; He, J.; Chen, K.; Shi, Z.; Li, M.; Guo, P.; Wu, L. Dynamic Adsorption of Sulfamethoxazole from Aqueous Solution by Lignite Activated Coke. Materials 2020, 13, 1785. https://doi.org/10.3390/ma13071785
Li H, He J, Chen K, Shi Z, Li M, Guo P, Wu L. Dynamic Adsorption of Sulfamethoxazole from Aqueous Solution by Lignite Activated Coke. Materials. 2020; 13(7):1785. https://doi.org/10.3390/ma13071785
Chicago/Turabian StyleLi, Haiyan, Juan He, Kaiyu Chen, Zhou Shi, Mengnan Li, Pengpeng Guo, and Liyuan Wu. 2020. "Dynamic Adsorption of Sulfamethoxazole from Aqueous Solution by Lignite Activated Coke" Materials 13, no. 7: 1785. https://doi.org/10.3390/ma13071785
APA StyleLi, H., He, J., Chen, K., Shi, Z., Li, M., Guo, P., & Wu, L. (2020). Dynamic Adsorption of Sulfamethoxazole from Aqueous Solution by Lignite Activated Coke. Materials, 13(7), 1785. https://doi.org/10.3390/ma13071785





