Next Article in Journal
Experimental Study on Freezing and Thawing Cycles of Shrinkage-Compensating Concrete with Double Expansive Agents
Next Article in Special Issue
Hot Deformation Behavior and Microstructure Evolution of Cu–Ni–Co–Si Alloys
Previous Article in Journal
In-Situ SEM Observation on Fracture Behavior of Titanium Alloys with Different Slow-Diffusing β Stabilizing Elements
Previous Article in Special Issue
Effect of Y Addition on the Microstructure and Mechanical Properties of ZM31 Alloy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 13
Issue 8
10.3390/ma13081852
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Quantum-Chemical Design of Molecular Structures of Tetra-, Penta- and Hexanuclear Metal Clusters Containing Aluminum and 3d-Element Atoms

by
Oleg V. Mikhailov
1,* and
Denis V. Chachkov
2
1
Department of Analytical Chemistry, Certification and Quality Management, Kazan National Research Technological University, K. Marx Street 68, 420015 Kazan, Russia
2
Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences – Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, 420111 Kazan, Russia
*
Author to whom correspondence should be addressed.
Materials 2020, 13(8), 1852; https://doi.org/10.3390/ma13081852
Submission received: 7 March 2020 / Revised: 11 April 2020 / Accepted: 13 April 2020 / Published: 15 April 2020
(This article belongs to the Special Issue Materials Science of Non-Ferrous Metals and Alloys)
Browse Figures
Versions Notes

Abstract

:
Various data on the structural and thermodynamic characteristics of polynuclear metal clusters containing atoms of aluminum and various d-elements with the general formula AlnMm where (n + m) is 4, 5, or 6, and which can be precursors for the formation of nanoparticles of elemental metals or intermetallic compounds, have been systematized and discussed. It has been noted that each of these metal clusters in principle is able to exist in very diverse structural isomers, differing significantly among themselves in terms of the total energy and spin multiplicity of the ground state, the number of which is determined by both the specific values of n and m, and the nature of d-elements in their compositions. The presence of very complex dynamics with respect to the changes of the individual thermodynamic characteristics of the metal clusters under consideration as well as the thermodynamic parameters of the reactions of their formation, depending on the nature of the d-element, were also ascertained. In the main, the given review is devoted to the authors’ works published over the last 10 years. Bibliography – 96 references.

1. Introduction

As is known, micro- and nanoparticles of elemental metals and their compositions, and primarily from among p- and d-elements, are now very important in modern chemistry and chemical technology. On the one hand, they are a kind of “precursor” for the production of micro- and nanoparticles of metal oxides, metal sulfides, and metal chalcogenides (which, in turn, appear to be very convenient starting materials for producing, for example, ceramic materials, catalytic and sorption systems). On the other hand, they themselves have a number of specific (and very useful) properties from an anthropogenic point of view. There is great interest in this type of nanoparticle, i.e., those that contain two or more different chemical elements in their structural units, because in this case, from purely theoretical considerations, it is very likely that they will have a number of new properties that are not observed in nanoparticles containing atoms of only one chemical element. These nanoparticles are composed of heteronuclear metal clusters with chemical metal–metal bonds formed by identical as well as different atoms. In view of the circumstance just noted, it seems to be an urgent task related to both confirming the very principal possibility of the existence of nanoparticles consisting of various metal elements and having a specific chemical composition, and if confirmed, by revealing all possible structural forms and configurations for them with using modern quantum chemical calculations.
To date, a very significant number of studies have been devoted to heteropolynuclear metal clusters with a diverse number and assortment of metal atoms in structural units—their number is measured in many hundreds, and all of them in this review paper cannot be simply cited. Most of them were devoted to heteropolynuclear metal clusters containing atoms of various 3d, 4d, and 5d elements. In particular, are related the publications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. Some such metal clusters have been applied in various fields of science and technology (see, f.e., [1,3,20,36,37]). In the works cited above [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], the objects of study were the so-called (dd)heterobimetallic metal clusters, which included atoms of two different d-elements, in particular, (Au, Fe) [9], (Pd, Ag) [12,21,43], (Au, Ag) [26], (Au, Pd) [33], (Cu, Fe) [38] and (Pt, Cu) [39]. However, of no less interest are the (pd)heterobimetallic metal clusters that include atoms of different categories of metals, namely, p- and d-elements, since theoretically it can be expected that they will demonstrate such new properties that are not inherent to metal clusters containing metal atoms of only one category. These metal clusters, however, were considered in a much smaller number of works, in particular, in [51,52,53,54,55,56,57,58,59,60,61,62,63].
Heterometallic metal clusters containing the atoms of those metals that are important in various fields of science and technology, namely aluminum and 3d elements (M), are very interesting objects from both a purely academic and practical points of view in this field. Some of them, in particular, ScnAl, YnAl, and AlnTi, were considered in [58,59,60,61,62,63]. Such metal clusters, however, contain only two types of chemical bonds, namely either M–M and Al–M, or Al–M and Al–Al. More interesting for consideration are those (pd)metal clusters that contain all three possible chemical bonds here, namely M–M, Al–M, and Al–Al. The simplest of them are tetranuclear metal clusters, where in principle, two different types of geometric bodies are possible, at the vertices of which there are M and Al atoms, namely a quadrangle and a tetrahedron, and structural variations are already quite diverse. However, much greater possibilities in terms of the diversity of molecular structures open up starting from five-atom clusters. At the present time, there is already a number of publications that have examined the structural features of this category of (pd)metal clusters consisting of four, five, and six atoms, and the quantum-chemical calculations of these metal clusters were carried out using the density functional method (DFT) combining the standard extended split-valence QZVP basis [64,65] and the OPBE functional [66,67]. To build quantum chemical models of the molecular structures of the metal clusters under examination, GAUSSIAN09 software was used [68]. Moreover, the accordance of the found stationary points to the energy minima was confirmed by calculation of the second derivatives with respect to the atomic coordinates. Further, all equilibrium structures corresponding to the minima at the potential energy surface revealed only real positive frequency values. Parameters of the molecular structures for spin multiplicities (MS) more than 1, were determined using the so-called unrestricted method (UOPBE), for MS = 1, using so-called restricted method (ROPBE). Along with this, the unrestricted method in conjunction with the GUESS = Mix option was used for the cases when MS was equal to 1. The data obtained as a result of such a procedure, were similar to those obtained using ROPBE method. The data of works [69,70,71,72] give us reason to assert that the given method allows to obtain the most accurate estimation of ratio between energies of the high-spin state and low-spin state and, at the same time, rather reliably predicts the key geometric parameters of molecular structures for various compounds of 3p- and 3d-elements. That is why the DFT OPBE/QZVP method was used by authors of the given review article in the calculation of molecular structures in all their works [73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96], where such (pd)metal clusters were considered. The given review paper will be devoted to the systematization and discussion of the main results of those calculations that are presented, namely in these publications.

2. Tetranuclear (AlM) Metal Clusters

Tetranuclear metal clusters containing aluminum atoms and d-metal atoms M can be divided into three categories depending on the number of both these atoms in the molecule, namely AlM3, Al2M2, and Al3M. Currently, information on metal clusters with such stoichiometric compositions is available only for one of the d-elements, namely for M = Fe. Such metal clusters were considered by us in the works [73,74,75,76,77,78,79,80]. In the earliest of them [73], a metal cluster of AlFe3 composition was described, for which the total number of theoretically possible isomers (4) was revealed in this work, and data on the coordinates of the iron and aluminum atoms included in its composition were presented. Similar information on the total number of isomers of this metal cluster is reported in publications [74,75]. However, a more detailed consideration of this metal cluster and its analogue with the inverse relationship between the numbers of Al and Fe atoms, namely Al3Fe, is carried out in [76,77], revealing the presence of 10 isomers of AlFe3 and seven isomers of Al3Fe. Information on their relative stability is presented in Table 1. In the same works, the parameters of the molecular structures of all these isomers were presented. According to them, in eight isomers of AlFe3, aluminum and iron atoms are located at the vertices of a distorted tetrahedron, distorted to one degree or another. In the other two, all four atoms are located in the same plane. It is characteristic that, in any of these ten isomers, all three theoretically possible Al–Fe chemical bonds are present, while three Fe–Fe bonds are present in only two isomers, and in most of them (in seven), only one such bond is realized. In this connection, we should note that, among these ten isomers, there is one in which there are no bonds between the atoms of the above d-element. At the same time, curiously, the most stable in energy terms (i.e., having the lowest total energy among all other isomers) is one of those seven isomers in which there is only one Fe–Fe bond [76,77]. According to the data presented in these publications, the ground state of this isomer is the spin quartet. The isomers closest to it in terms of total energy have a doublet and quartet ground state and are almost identical energies, which are only slightly larger than the total energy of the most stable isomer (by 11.2 and 11.3 kJ/mol, respectively). Isomers of the Al3Fe metal cluster, despite the closeness of their formal stoichiometric compositions to AlFe3 isomers, nevertheless are quite significantly different from AlFe3 isomers, not only in their total number, but also in appearance [76,77]. In six of seven isomers of Al3Fe, there are all three theoretically admissible Al–Fe chemical bonds, and only one has such a bond. As in the AlFe3 metal cluster, there are distorted tetrahedral and planar structures (4 and 3, respectively). However, here, unlike AlFe3, the most energy stable isomer contains a complete set of metal – metal bonds (three Al–Fe bonds and three Fe–Fe bonds). Molecular structures of both these isomers are shown in Figure 1. The Al–Fe chemical bond lengths in AlFe3 isomers are generally somewhat longer than those in Al3Fe, which may be connected with the absence of a complete set of Fe–Fe chemical bonds in most AlFe3 isomers [76,77].
Another theoretically possible (AlFe) tetranuclear metal cluster, namely Al2Fe2, was considered in [78,79,80]. Unlike the AlFe3 and Al3Fe metal clusters, it contains all three of the above types of chemical bonds (M–M, Al–M and Al–Al), and therefore more isomers can be expected here. Indeed, according to the data of [78,79,80], it can exist in 12 different isomers (Table 1), the most energetically favorable of which has the structure of a distorted tetrahedron with the maximum theoretically possible set of chemical bonds Al–Fe and Fe–Fe (three each of these types of bonds) (Figure 2). Outwardly, this isomer resembles the one shown in Figure 1b, but in it all four Al–Fe bonds have the same length (249.5 pm each), while in Al3Fe all these bonds are different and generally shorter (234.6, 236.7, and 250.6 pm) [79,80]. For the majority of other isomers of Al2Fe2 (seven out of 12), as well as for tetranuclear metal clusters already considered in this section (AlFe), the geometry of the distorted tetrahedron is more typical, although flat or almost coplanar structures also occupy a prominent place [78,79,80]. Isomers of Al2Fe2 with this form, however, have total energy values of more than 100 kJ/mol higher than the total energy of the most low-energy isomer. Further, the total amount of chemical bonds Al–Al, Al–Fe, and Fe–Fe in these isomers ranges from 4 to 6. The first of these bonds is absent only in one isomer, and the third, in two isomers of the metal cluster under examination. It should be noted in this connection that the lengths of the M–M, Al–M, and Al–Al bonds in various isomers of these metal clusters are in such ranges that, given the atomic radii of Al (143 pm) and Fe (126 pm), appear quite natural and predictable. In particular, in Al3Fe isomers, Al–Al bond lengths are in the range of 257–277 pm, Al–Fe bond lengths are in the range of 235–255 pm. In AlFe3 isomers, Fe–Fe bond lengths are in the range of 207–219 pm, Al–Fe bond lengths are in the range of 238–276 pm. At the same time, most of the valence (bond) angles of these same bonds, as well as the torsion (dihedral) angles, have values substantially less than 90°. The more detailed information on the structural parameters of the most energetically stable of the above metal clusters is presented in Table 2.
The images of molecular structures of all these tetranuclear metal clusters are presented in Supplementary Materials (Figures S1–S3).
In [79,80], a quantum-chemical calculation of the parameters of molecular structures of (heterotri)tetranuclear metal cluster having the composition Al2FeCo, was also carried out, for which it was found that only three isomers could be found that look very similar to each other (Figure 3).
These isomers, however, are very different from each other in total energy values as well as the spin multiplicity of the ground state. There is no doubt that (heterobi)tetranuclear metal clusters containing aluminum atoms and atoms of other d-elements are also possible, but no information has appeared in the literature on this subject yet.

3. Pentanuclear (AlM) Metal Clusters

The given type of metal clusters has been analyzed in much more detail than tetrabinuclear ones, and is currently known for all 3d elements (except for Sc), as well as for two 4d elements (Mo and Ag). It should be noted, however, that all of these metal clusters are of the same type and have the same stoichiometric composition of Al2M3. Meanwhile, pentabinuclear metal clusters with other theoretically possible sets of aluminum atoms and d-element atoms in the molecule (and namely, Al4M, Al3M2 and AlM4) have not yet been considered. The specifics of molecular structures and thermodynamic characteristics of such metal clusters having the composition indicated above, where M is a 3d element, are discussed in [74,75,81,82,83,84,85,86,87,88,89,90,91]. We should note immediately that, according to the calculation data by the DFT method, for each of these M, there is an individual set of isomers, both in assortment and in their total number (N), which varies over a very wide range—from 7 (in the case of Al2Ni3) to 25 (in the case of Al2Mn3) (Table 3). The relative total energies of these isomers also vary over a very wide range (Table 4). The most energetically advantageous among these isomers for the above M are shown in Figure 4. The molecular structure parameters of these isomers are given in Table 5. A complete assortment of molecular structures of all metal clusters considered by us can be found in the publications [74,75,81,82,83,84,85,86,87,88,89,90,91] cited above, and in the Supplemental Materials.
According to data presented in [81,83], of the 14 identified isomers of the Al2Ti3 metal cluster, only Al–Al valence bonds are realized in only seven of them, namely, Al2Ti3 (I), Al2Ti3 (II), Al2Ti3 (IV), Al2Ti3 (V), Al2Ti3 (VII), Al2Ti3 (VIII), and Al2Ti3 (X), the direct valence bonds Al–Ti and Ti–Ti, at least in the singular, each occur in all these metal clusters. The most favorable in terms of energy is the Al2Ti3 (XI) isomer with spin multiplicity MS = 5 and the geometry of the trigonal bipyramid (Figure 4a), in the “equatorial plane” of which there are three titanium atoms, the aluminum atoms are located at its vertices. The Al2Ti3 (XII) isomer with MS = 3 following the increase in total energy, has a similar structure. Four of these isomers, namely Al2Ti3 (IV), Al2Ti3 (V), Al2Ti3 (IX), and Al2Ti3 (XI), have a spin multiplicity 5, the same, namely, Al2Ti3 (I), Al2Ti3 (VI), Al2Ti3 (X), Al2Ti3 (XII), spin multiplicity 3. In the remaining six, the spin singlet turns out to be the ground state. As it may be seen, the spin state with MS = 1 for the metal cluster under consideration is predominant, although in fairness, it should be noted that the closest in energy to the Al2Ti3 (XI) isomer are the Al2Ti3 (XII) and Al2Ti3 (V) isomers with relative energies of 12.6 and 19.7 kJ/mol, respectively, exceeding the energy of Al2Ti3 (XI), having MS = 3 and 5, respectively (Table 4).
In [82,83], a quantum chemical calculation of the Al2V3 metal cluster was carried out. Information on the relative energy of its isomers is presented in Table 4. As can be seen from Table 4, in six out of 11 isomers of this metal cluster, namely in Al2V3 (I)–Al2V3 (VI), there is a direct Al–Al valence bond, while in the other five, it is absent and only V–V and V–Al bonds take place in them. Moreover, that is noteworthy, in two structures, namely Al2V3 (VIII) and Al2V3 (IX), only chemical bonds between atoms of different chemical elements (i.e., V–Al) take place, while between the same atoms there are none (which, by the way, in none of the Al2Ti3 metal clusters described above is observed). As in the case of the Al2Ti3 metal cluster, its most stable isomer, namely Al2V3 (V), has not the highest spin multiplicity (6), but a lower (though not the lowest) (4). At the same time, that is characteristic, structures with the highest spin multiplicity 6 as a whole have noticeably higher values of the total energies than structures with multiplicities 2 and 4. In addition, the Al2V3 (II) structure closest in energy to Al2V3 (V) possesses the same spin multiplicity, and its molecular structure resembles the structure of Al2V3 (V), at least in general terms. At the same time, the following three structures with increasing energy, namely, Al2V3 (III), Al2V3 (I), and Al2V3 (IV), have different values of spin multiplicity, namely, 6, 2, and 2, respectively. The most unstable is the isomer Al2V3 (IX), the total energy of which is not only much higher (almost 150 kJ/mol) compared with that for Al2V3 (V), but also all other isomers of the metal cluster under consideration, which is noteworthy, as it has the highest spin multiplicity (6) [82,83].
For the Al2Cr3 metal cluster, 20 different isomers were found (Table 3). In thirteen of them, namely, in Al2Cr3 (I), Al2Cr3 (III)–Al2Cr3 (XII), Al2Cr3 (XVI) and Al2Cr3 (XVII), there is a direct valence Al–Al bond, while in the other seven it is absent in only Cr–Cr and Cr–Al bonds are realized in them [84,85]. On the other hand, Cr–Cr bonds are present in only six isomers: Al2Cr3 (I), Al2Cr3 (V), Al2Cr3 (VI), Al2Cr3 (X), Al2Cr3 (XIII) and Al2Cr3 (XIX). Further, with the last three isomers, chromium atoms are paired together. In three structures, namely Al2Cr3 (II), Al2Cr3 (XIV), and Al2Cr3 (XV), only chemical bonds between atoms of different chemical elements (i.e., Cr–Al) take place, but there are no bonds between identical atoms (i.e., Al–Al and Cr–Cr). Information on the relative energy of these isomers is given in Table 4. As can be seen from Table 4, the most stable isomer of this metal cluster, Al2Cr3 (III), also does not have the highest spin multiplicity (7), but is somewhat lower (5). Incidentally, structures with a higher spin multiplicity 7 in general also have larger total energies than structures with a multiplicity of 5 (although smaller than structures with a multiplicity of 1 and 3) [84,85]. It is interesting that this isomer is the only one among the most stable isomers of Al2M3 in which there are no M–M bonds (Figure 4c), because in all the most stable isomers of the given composition of metal clusters formed by M atoms of the other 3d elements, at least one such a bond occurs (see Figure 4a,b,d–i).
The Al2Mn3 metal cluster is able to exist in 25 different isomers [86]. This amount is the largest among all Al2M3 metal clusters formed by 3d element atoms (Table 4). Further, only 10 of the structures, namely Al2Mn3 (I)–Al2Mn3 (VII), Al2Mn3 (IX), Al2Mn3 (XII) and Al2Mn3 (XIV) contain a covalent Al–Al bond, whereas the other 15 ones, Al2Mn3 structures contain only the Mn–Mn and Mn–Al bonds, and the Al–Al one is absent. In most of these isomers (16 of 25) there are 6 Mn-Al bonds, in six [Al2Mn3 (I)–Al2Mn3 (V), Al2Mn3 (XIV)]–5, and in three [Al2Mn3 (IX), Al2Mn3 (X) and Al2Mn3 (XIII)] by 4. Finally, in most isomers (15 of 25) there is a complete set of Mn-Mn links (by 3). In seven isomers [Al2Mn3 (VI)–Al2Mn3 (VIII), Al2Mn3 (XI)–Al2Mn3 (XIII), Al2Mn3 (XXV)], there are two such bonds and in three isomers [Al2Mn3 (I), Al2Mn3 (II) and Al2Mn3 (XXIV)]–by one [86]. The most energetically favorable Al2Mn3 (VI) isomer has the spin multiplicity of ground state MS = 6, and contains maximal number of Al–Al and Al–Mn bonds [although number of Mn–Mn in it is lesser than maximal possible number of such bonds (3)] (Figure 4d). The isomer Al2Mn3 (XX) has relative total energy only by 1.4 kJ/mol higher than total energy of Al2Mn3 (VI) isomer and the same multiplicity (6). Its geometric configuration is similar to Al2Mn3 (VI), however, unlike Al2Mn3 (VI), Al–Al bonds are absent in it [86]. The next isomer with the largest relative total energy, Al2Mn3 (XXI) (2.2 kJ/mole), is outwardly similar to Al2Mn3 (XX) but the bond lengths Al–Mn and Mn–Mn as well as a distance between Al1 and Al2 in it are bit longer than in Al2Mn3 (XX), and MS of its ground state is 4. The most low-energetic isomer of the given metal cluster having MS = 2, and namely Al2Mn3 (XIII), has relative total energy 29.3 kJ/mole and, that characteristically, has the smallest number of metal–metal bonds among all Al2Mn3 clusters under examination (only 6). Among them, 10 isomers have MS = 6, eight have MS = 4, and seven ones have MS = 2 (Table 4). As can be seen, the low-spin state is not characteristic for such metal clusters, which is quite expected from the ground state of manganese atom (3d54s2 with five unpaired electrons). It is interesting that the most high-energetic isomer of the given metal cluster, and namely Al2Mn3 (XVIII), has relative total energy, equal to 149.2 kJ/mole, has the structure of trigonal pyramid as the energetically favorable isomer Al2Mn3 (VI), and exactly the same spin multiplicity of the ground state (Table 4). Most isomers of Al2Mn3, including the most energetically favorable Al2Mn3 (VI) which is shown in Figure 4d, have molecular structures resembling a trigonal pyramid. Exceptions to this include only Al2Mn3 (I), Al2Mn3 (II), Al2Mn3 (IX), Al2Mn3 (X), Al2Mn3 (XIII), and Al2Mn3 (XXIV) [86].
The next Mn 3d elements of groups VIII, IX, and X of the periodic system of chemical elements, namely Fe, Co, and Ni, however, form a much smaller number of isomers of Al2M3 metal clusters than Mn. In the case of the first of them, iron, judging by the data presented in [87,88,89], only 8 isomers are realized, in six of which, namely Al2Fe3 (I) - Al2Fe3 (VI), there is a direct Al–Al valence bond, while in the other two structures [Al2Fe3 (VII) and Al2Fe3 (VIII)], such a bond is absent and they contain only Fe–Fe and Fe–Al bonds. The relative energies of the isomers of this metal cluster are presented in Table 4. It is noteworthy that, for clusters of this stoichiometric composition, the most energy-stable Al2Fe3 (II) structure (something like a “one-cap” tetrahedron) has multiplicity of 3 which is an intermediate between multiplicities of the high-spin and low-spin states. In the given isomer, only one M–M bond is present (Figure 4e). The Al2Fe3 (III) structure closest in energy to it with a similar geometric configuration (total energy of which is 12.8 kJ/mol higher than the total energy of the Al2Fe3 (II) structure) has spin multiplicity 5. The other two structures with MS = 3, namely Al2Fe3 (V) and Al2Fe3 (VII), have relative total energies of 24.1 and 27.1 kJ/mol higher than the structure of Al2Fe3 (II), while the two structures with MS = 5, namely, Al2Fe3 (VI) and Al2Fe3 (VIII), in terms of relative total energies (31.1 and 24.7 kJ/mol) are only slightly less stable in energy terms. The low-spin state is uncharacteristic for these clusters (Table 4), which is understandable if we take into account the presence of the iron atom in the ground state of the 3d64s2 electronic configuration with four unpaired electrons.
The Al2Co3 metal clusters are the subject of works [87,88]. The total number of isomers of this metal cluster in comparison with Al2Fe3 turns out to be somewhat larger (9). However, their structural diversity is noticeably less than that of Al2Fe3 metal clusters [87,88]. Here, the direct valence bond Al–Al is also realized in six isomers, namely, Al2Co3 (I)–Al2Co3 (III) and Al2Co3 (VII)–Al2Co3 (IX), while in the other three isomers, namely, Al2Co3 (IV)–Al2Co3 (VI), such a relationship is absent. The most stable in terms of energy among all these isomers is Al2Co3 (III) (Table 4), which represents a trigonal bipyramid, both of whose vertices are occupied by Co atoms (Figure 4f). The spin multiplicity of its ground state is 6. The closest to it in energy (28.9 kJ/mol higher) isomer of Al2Co3 (IX) also has a trigonal bipyramidal structure, but, in contrast to Al2Co3 (III), there are at the vertices of this bipyramid Al and Co atoms. It has the same spin multiplicity as Al2Co3 (III). All other isomers of the Al2Co3 metal cluster, in principle, are capable of self-existence, and have significantly higher total energies in comparison with Al2Co3 (III) and Al2Co3 (IX). The least stable among them is the trigonal bipyramidal Al2Co3 (V) with two Al atoms at the vertices of the bipyramid, and not connected by a chemical bond. As in the case of the Al2Fe3 metal cluster, the low-spin state also turns out to be uncharacteristic.
The Al2Ni3 metal cluster is represented by the smallest number of structural isomers among all other metal clusters—only seven [87,88]. The direct Al–Al valence bond in aluminum–nickel Al2Ni3 clusters, as well as in aluminum–iron and aluminum–cobalt analogous stoichiometric compositions, is realized again in six of its isomers. The only exception to this is the Al2Ni3 (VII) isomer. The relative energies of these structures are shown in Table 4. It is noteworthy that the aforementioned isomer of Al2Ni3 (VII) is also the least advantageous in terms of energy, and the absolute value of its relative energy is much larger than the same indicator for the other six isomers of Al2Ni3. As for the most advantageous structure in terms of energy, Al2Ni3 (II) outwardly resembles the Al2Co3 (III) structure, the same trigonal bipyramid with two M atoms at the vertices (Figure 4g), but with spin multiplicity of the ground state equal to 3 (as in the case of the most energetically favorable structure of the iron–aluminum cluster Al2Fe3 (II)). The isomer nearest to it in energy, namely Al2Ni3 (I) with a similar geometric configuration, has a total energy that is 48.6 kJ/mol higher than the energy of the structure Al2Ni3 (II). Despite the fact that the ground state of the nickel atom (3d84s2) is characterized by the presence of only two unpaired electrons, the low-spin state for Al2Ni3 clusters, judging by the data of [87,88], is also uncharacteristic as for aluminum–cobalt and aluminum–iron clusters of a similar stoichiometric composition. In fairness, it is worth noting that a high-spin ground state is characteristic for the Al2Ni3 metal clusters to an even lesser extent, because, as it is easily seen from the data in Table 4, the relative energies of the Al2Ni3 isomers having MS = 5, as a rule, significantly exceeds the relative energies of the isomers having MS = 3.
The next sequence number after the triad (Fe, Co, Ni) 3d element, namely Cu, forms the same number of isomers of the Al2M3 metal cluster as Fe (i.e., 8). In seven of eight of these isomers, the direct valence bond Al–Al is realized. The only exception here is the isomer of Al2Cu3 (II) [89,90,91]. Also, in 7 out of 8 isomers, with the exception of only Al2Cu3 (V), there is at least one Cu–Cu bond, and Al–Cu bonds occur in each of these isomers. The following circumstance attracts attention in that the aluminum–copper Al2Cu3 metal clusters have a very significant total number of metal–metal bonds: from seven to nine. In this connection, it is worth noting that in three of the eight Al2Cu3 isomers, the total number of metal–metal bonds is only one less than the maximum possible number of Al2Cu3 compounds, namely 10. The relative energies of all Al2Cu3 isomers are presented in Table 4. From the data presented in Table 4, it can be seen that the most stable isomer is Al2Cu3 (I); the total number of metal–metal bonds in this isomer is 9 (Figure 4h). As in the majority of metal clusters having Al2M3 stoichiometric composition and already considered above, this isomer has not the highest spin multiplicity (4), but lower (2). However, isomers with MS = 4, namely Al2Cu3 (II), Al2Cu3 (IV) and Al2Cu3 (VI) as a whole, have significantly higher total energies than isomers with MS = 2 (Table 4).
In [86], a quantum chemical calculation of the Al2Zn3 metal daster was performed and it was shown that it can exist in 14 different isomers. Relative total energies of these isomers are presented in Table 3. As may be seen from these data, in 10 out of 14 of these isomers, the direct valence bond of Al–Al occurs. The exceptions are the Al2Zn3 (X)–Al2Zn3 (XII) and Al2Zn3 (XIV) isomers. Also, in the each of them, there are at least one Zn–Zn and four Al–Zn bonds. The isomers of Al2Zn3 metal clusters under examination have a very significant total number of metal-metal bonds, from seven to nine such bonds. In addition, in eight out of 14 isomers, the total number is only one less than the maximum possible number of them in Al2M3 (10) compounds. In this indicator, Al2Zn3 is superior to any other of the number of Al2M3 metal clusters formed by 3d element atoms. However, in the most stable isomer, namely Al2Zn3 (I), the total number of metal–metal bonds is eight (Figure 4i), i.e., nine less than occurs in most isomers of the given metal cluster. Despite of the fact that, for this metal cluster, in principle, isomers with spin multiplicities of the ground state 1, 3, 5, and 7 are possible, in metal clusters discovered as a result of our quantum-chemical calculation, only two values of spin multiplicity for the ground state, namely 1 and 3, take place for Al2Zn3 isomers. The most stable of them, namely Al2Zn3 (I), has MS = 3. Interestingly, the same MS values have the next two lower-energetic isomers, namely Al2Zn3 (XIV) and Al2Zn3 (IV) having relative total energies are 3.2 and 11.0 kJ/mole, respectively. Nevertheless, the most of isomers of the cluster under examination (9 of 14) have spin singlet as ground state (Table 4). The total energy of the isomers MS = 1 as a whole is much larger than the total energy of the isomers with MS = 3. The lowest-energy of them Al2Zn3 (III) differs in energy from the isomer of Al2Zn3 (I) by 14.0, the most high-energy, Al2Zn3 (VIII), by 79.2 kJ/mole [86].
The images of molecular structures of the most stable of each of Al2M3 metal clusters under study and geometric parameters of these structures are also presented in articles [92,93] (see Figure 4 and Table 5, respectively). With respect to the most general structural features of these five-atomic metal clusters containing two Al atoms and three atoms of the 3d element M in the structural unit, it should be said that, in full accordance with theoretical expectations, for most of them, the trigonal bipyramid is most typical structure. Moreover, other geometric bodies are not uncommon here, in particular, a tetragonal pyramid and even flat polygons. Most of them are also characterized, on the one hand, by the presence of several metal–metal bonds formed by the same atom with their “neighbors,” and on the other hand, by relatively high values of the lengths of these bonds, which usually exceed 200 pm. Exceptions occur only in a few cases, in particular, in the Al2V3 metal cluster for bond lengths V1V2 in the isomers Al2V3 (I)–Al2V3 (VI), Al2V3 (X) and Al2V3 (XI), lying in the range from 171.7 pm [in the Al2V3 (VI) structure] up to 188.1 pm [in the structure of Al2V3 (I)]. On the other hand, in general, as expected, the Al–Al bonds are the longest, the M–M bonds are the shortest, while the M–Al bond lengths occupy an intermediate position between the bond lengths formed by two aluminum atoms and two atoms M. Further, the lengths of the M–M, Al–M, and Al–Al bonds in various isomers of these metal clusters are in the ranges that, taking into account the atomic radii of Al (143 pm) and M (132 pm (Ti), 134 pm (V), (Cr), 127 pm (Mn), 126 pm (Fe), 125 pm (Co), (Ni), 128 pm (Cu) and 138 pm (Zn)) seem to be quite natural and predictable. So, in Al2Ti3 isomers, the lengths of Ti–Ti bonds are in the range 210–260 pm, the lengths of Al–Ti and Al–Al bonds are in the ranges 252–270 pm and 255–280 pm, and in the Al2V3 isomers are in the ranges 170–275 pm, 250–270 pm, and 255–270 pm respectively. Most of the bond angles between the lines of these bonds and the torsion (dihedral) angles in the isomers of all Al2M3 metal clusters under consideration have values substantially less than 90°. The vast majority of such metal clusters either do not have symmetry elements at all, or have only one plane of symmetry. One of the few exceptions is the Al2V3 (IX) metal cluster isomer which has one third-order symmetry axis, three second-order symmetry axes, three symmetry planes, and a centre of symmetry [82]. It is noteworthy that, among the most stable metal clusters of each of the 3d-elements considered by us and presented in Figure 4, there is not one having a similar set of symmetry elements.
The images of molecular structures of all these pentanuclear metal clusters are presented in Supplementary Materials (Figures S4–S12).
In the articles [92,93], the thermodynamics of Al2M3 metal clusters formed by atoms of 3d elements was considered and calculation of standard thermodynamic formation parameters [ΔfH0(298 K), ΔfS0(298 K) and (ΔfG0(298 K)], as well as standard enthalpy, entropy and Gibbs energy of reactions of their formation from mono-atomic particles in the gas phase (ΔfH0298, ΔfS0298, ΔfG0298) was carried out. These parameters are presented in Table 6. As can be seen from these data, all ΔfH0(298 K), ΔfS0(298 K) and (ΔfG0(298 K) values are positive, indicating the impossibility of the formation of these metal clusters from simple substances formed by the constituent elements and existing under standard conditions (i.e., from Al (crystal) and corresponding M (crystal)). However, for the reactions of formation of Al2M3 in gas phase according to general Equation (1),
2Al (gas) + 3M (gas)→Al2M3 (gas)
another situation takes place. Each of the reactions in Equation (1) is exothermic and belong to processes whose course is due to the enthalpy factor since for any of them, the standard enthalpy is ΔH298 < 0, and ΔS298 < 0 (Table 6). In addition, heteronuclear metal clusters formed as a result of such reactions, are characterized by rather high thermal stability. In the publications [92,93], the availability of a very complex dynamics of changes in both the individual thermodynamic characteristics of the Al2M3 metal clusters under consideration and the thermodynamic parameters of these reactions of their formation depending on the nature of the 3d element was also noted. Since for each of them, ΔS298 is also negative, in the simplest version, according to the Gibbs–Helmholtz equation for the isobaric process (2)
ΔG(T) = ΔH298 – TΔS298
where ΔH298 and ΔS298 are the enthalpy and entropy changes as a result of the chemical process, referred to standard conditions, T is the process temperature in K, and ΔG(T) is the dependence of the Gibbs free energy on temperature T for reaction (1). Regardless of the nature of the 3d element M, the values of both of these parameters are negative, and this fact in turn means that the given reaction is thermodynamically resolved at relatively low temperatures and forbidden at high ones. On the contrary, the reverse reaction (1) will be allowed at sufficiently high temperatures and forbidden at low ones. The minimum temperature at which this reverse reaction begins, can be considered as the temperature of the beginning thermal decomposition of the metal cluster (Ttd) in the gas phase to individual Al and M atoms. As may be seen from the data presented in the Table 6, the ΔH298 value and, correspondingly, thermal effect of reaction (1) is very significant in all cases. Further, as it is easy to show with using Equation (2) [92,93], the temperature at which reverse reaction (1) will be possible, for almost all Al2M3 metal clusters (for with the exception of Al2Zn3 only) exceeds 1000 K (Table 7). Herewith, Al2V3 is the most stable in this respect among all the compounds under consideration, Al2Zn3 is the least stable. Upon transition from Ti to V, the temperature of the beginning of thermal decomposition increases, from V to Cr it decreases, from Cr to Ni it increases and from Ni to Zn it decreases again (Table 7). However, the dynamics of changes in the standard thermodynamic formation parameters (ΔfH0(298 K), ΔfS0(298 K) and ΔfG0(298 K)) of the Al2M3 metal clusters under consideration is of a somewhat different and more complex character. So, for ΔfH0(298 K) и (ΔfG0(298 K), the curves corresponding to it have a quite distinct “zigzag” shape, because both of these parameters when passing from Ti to V, from Cr to Mn, from Fe to Ni, and decrease from Cu to Zn, but increase from V to Cr, from Mn to Fe, and Ni to Cu. However, the dynamics of the change of ΔfS0(298 K) in the Ti–Zn series are not similar to the dynamics of change as ΔfH0(298 K) and (ΔfG0(298 K), as well as the values of the temperature of the beginning of thermal destruction Ttd [92,93]. It should be noted in this connection, that there is no correlation between the parameters of the atoms of the 3d elements that make up the Al2M3 metal clusters, which in principle can somehow be related to the thermodynamic characteristics (atomic numbers, atomic radii, ionization energies, etc.) [92,93] that are clearly visible in Figure 5 where the dependences of the thermodynamic parameters of the reaction (1) of 3d-element atomic number has been presented.
It should be noted that in the current literature there is also information on the molecular structures of some Al2M3 metal clusters, where M is a 4d element, namely Al2Mo3 and Al2Ag3, which is presented in the publications [84,85] and [90,91] cited above, respectively. However, this information is fragmentary and so far clearly insufficient for any serious generalizations.

4. Hexanuclear (AlM) Metal Clusters

Theoretically, for metal clusters of such a category, the existence of five types of metal clusters is admissible, namely Al5M, Al4M2, Al3M3, Al2M4, and AlM5, is possible. The situation here at the moment resembles that which occurs in the case of tetranuclear (AlM) metal clusters, since until now quantum-chemical calculations have been performed for only two types of such metal clusters containing the same chemical element, namely Al3Fe3 and Al2Fe4. The results of these calculations are presented in articles [74,75,94,95,96]. According to them, the first of these metal clusters can exist in 20 isomers [94,95,96], and the second in nine [95,96]. The relative total energies of all these isomers are presented in Table 8. In all isomers of the first of these metal cluster, direct Fe–Al valence bonds take place. In all of them, with the exception of only Al3Fe3 (XIII) and Al3Fe3 (XV), there are also at least one Fe–Fe and Al–Al bond. It is interesting to note in this connection that, according to the data of [94,95,96], namely the isomer of Al3Fe3 (XV), where Al–Al bonds are absent, that turns out to be the most stable in energy terms. The most important parameters of the molecular structure of this isomer are presented in Table 9, and its image in Figure 6a. However, the isomer Al3Fe3 (XIII), in which, on the contrary, there are no Fe–Fe bonds but there are Al–Al bonds, turns out to be one of the most high-energy isomers of the metal cluster under consideration (albeit not the most high-energy). Besides, the most energy-stable isomer of Al3Fe3 (XV) has a spin multiplicity of the ground state of 6, which corresponds to a high-spin state (Table 8). It is characteristic that the Al3Fe3 (XII) isomer which is nearest to it in energy, also has the same spin multiplicity, but its molecular structure differs significantly from the Al3Fe3 (XV) structure [94,95,96]. The following two structures with increasing energy, namely Al3Fe3 (V) and Al3Fe3 (XIV), have a lower spin multiplicity of 4. The most unstable isomer is Al3Fe3 (I), whose total energy is much higher (more than 150 kJ/mol) of that for the Al3Fe3 (XV) isomer and for which the spin multiplicity of the ground state is 2. Thus, it can be argued that, in general, for the isomers of Al3Fe3 metal cluster, the high-spin state is more characteristic.
The high-spin state, judging by the data of [95,96], is more characteristic in comparison with the low-spin state for Al2Fe4 clusters, too. In four of its 9 isomers, namely, Al2Fe4 (I), Al2Fe4 (II), Al2Fe4 (VIII), and Al2Fe4 (IX), there is a direct valence bond Al–Al, while in the other five isomers there is no such bond and there are only Fe–Fe and Fe–Al bonds in them. As can be seen from the data presented in Table 7, the most stable in energy terms is the isomer of Al2Fe4 (II), the image of the molecular structure of which is shown in Figure 6b, and its key parameters in Table 9. It is characteristic of the metal cluster under consideration that the most stable isomer of it also has the highest spin multiplicity, namely MS = 5. The isomers with a lower spin multiplicity equal to 3 generally have noticeably large total energies. At the same time, which is characteristic, among these isomers, there is not a single one the ground state of which would be a spin singlet. It is interesting that, according to the data of [95,96], in principle, an almost flat Al2Fe4 cluster with MS = 3 (and namely, Al2Fe4 (I) isomer) can exist, even though it is characterized by the highest total energy compared to other compounds of the same composition, and namely 165.5 kJ/mol (Table 8). In this regard, it is worth noting that, according to the data of [87,88,89], flat structures are not found among five-atom Al2Fe3 metal clusters.
The images of molecular structures of all these hexanuclear metal clusters are presented in Supplementary Materials (Figures S13 and S14).
By highlighting, among other things, the general structural motifs of the isomers of hexa-nuclear (AlFe) metal clusters considered by us, we note that for most of these isomers, as well as for pentanuclear Al2M3, on the one hand, there are several metal–metal bonds formed by one and the same atom with its “neighbors”, on the other hand, relatively high values of the lengths of these bonds, which in all cases exceed 200 pm. From the average statistical point of view, the Al–Al bonds are the longest in full accordance with theoretical expectations, the Fe–Fe bonds are the shortest, while the Fe–Al bonds lengths occupy an intermediate position between the lengths of the bonds formed by two aluminum atoms and two iron atoms. It should be noted especially that all isomers of Al3Fe3 and Al2Fe4 metal clusters are either completely asymmetric, or have only one plane of symmetry. It is also characteristic that among the isomers of both Al2Fe4 and Al3Fe3 metal clusters, there is not one with a center of symmetry in its structure, although the structures of Al2Fe4 (I) and Al2Fe4 (V) are rather close to those [94,95,96].

5. Conclusions

As can be seen from the above literature data, tetranuclear (Al2M2), pentanuclear (Al2M3), and hexa-nuclear (Al2M4, Al3M3) metal clusters, containing at least two Al atoms and at least two M atoms of any of the 3d elements, form a rather significant number of structural isomers that differ significantly from each other in their structural and geometric parameters and in the values of the total energy. Moreover, most isomers of these metal clusters either do not have symmetry elements at all or have only one plane or one axis of symmetry. In many of these isomers, each of the aluminum atoms contained in their composition is connected by chemical bonds with three neighboring atoms, while for the atoms of the 3d element M, this feature, to all appearances, takes place to a lesser extent. Judging by the thermodynamic parameters of the reactions of their formation in the gas phase, the most studied (AlM) metal clusters, namely pentanuclear Al2M3 metal clusters, are capable of independent existence, and are very stable in thermal relation (i.e., to thermal destruction). At the same time, the standard thermodynamic characteristics of compounds of a given stoichiometric composition (ΔfH0(298 K), ΔfS0(298 K) and ΔfG0(298 K)) very strongly depend on the nature of the 3d element, and the dynamics of their change in a series Ti–Zn have a very complex and, moreover, a priori unpredictable character. Judging by the data presented in the articles published on this subject, no relationship between the total number of metal–metal bonds in the metal cluster and its relative total energy is also noted.
The (pd) metal clusters considered in the given paper, in the perspective, can be used primarily for creating new composite materials and alloys based on polymetallic nanoparticles. Other possible areas of application of these and similar chemical objects include the doping of traditional alloys based on both non-ferrous and ferrous metals, metal complex catalysis, the creation of specific electrochemical systems, and semiconductor technology. The data on the specifics of the molecular structures of the metal clusters examined by us, are quite capable of serving as a starting position on the basis of which it will be possible to calculate the structures of bicomponent (aluminum + (d-metal)) nanoclusters, which are associations of these metal clusters and contain from several tens to several hundred atoms. Furthermore, since most of the elementary processes associated with the formation of many chemical compounds, including the formation of metal structures and their alloys, occur in fragments of matter of a nanometer range with the above number of atoms, in the future, it will be possible to solve the problems of their influence on the physical chemical properties of polymetallic compositions. For example, to solve the question of whether an alloy, an intermetallic compound, or a mechanical mixture are formed when aluminum and d-metal are combined. It seems highly probable that, with their application as potential so-called quantum dots, the possibilities of this technology remain far from exhausted.

Supplementary Materials

The following are available online at https://www.mdpi.com/1996-1944/13/8/1852/s1, Figure S1: Molecular structures of Al3Fe clusters, Figure S2: Molecular structures of Al2Fe2 clusters, Figure S3: Molecular structures of AlFe3 clusters, Figure S4: Molecular structures of Al2Ti3 clusters, Figure S5: Molecular structures of Al2V3 clusters, Figure S6: Molecular structures of Al2Cr3 clusters, Figure S7: Molecular structures of Al2Mn3 clusters, Figure S8: Molecular structures of Al2Fe3 clusters, Figure S9: Molecular structures of Al2Co3 clusters, Figure S10: Molecular structures of Al2Ni3 clusters, Figure S11: Molecular structures of Al2Cu3 clusters, Figure S12: Molecular structures of Al2Zn3 clusters, Figure S13: Molecular structures of Al3Fe3 clusters, Figure S14: Molecular structures of Al2Fe4 clusters.

Author Contributions

Conceptualization, O.V.M.; Methodology, O.V.M. and D.V.C.; Software, D.V.C.; Validation, O.V.M. and D.V.C.; Formal Analysis, O.V.M. and D.V.C.; Investigation, O.V.M. and D.V.C.; Resources, D.V.C.; Data Curation, D.V.C.; Writing—Original Draft Preparation, O.V.M. and D.V.C.; Writing—Review & Editing, O.V.M.; Visualization, O.V.M. and D.V.C.; Supervision, O.V.M.; Project Administration, O.V.M.; Funding Acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.

Funding

Contribution of author Chachkov D.V. was funded by the state assignment to the Federal State Institution “Scientific Research Institute for System Analysis of the Russian Academy of Sciences” No. 0065-2019-0014 for scientific research (http://www.jscc.ru).

Acknowledgments

All quantum-chemical calculations were performed at the Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences – Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” that is acknowledgement for technical support.

Conflicts of Interest

The authors declare that they have no conflict of interest, financial or otherwise.

References

  1. Maroun, F.; Ozanam, F.; Magnussen, O.M.; Behm, R.J. The role of atomic ensembles in the reactivity of bimetallic electrocatalysts. Science 2001, 293, 1811–1814. [Google Scholar] [CrossRef] [PubMed]
  2. Derosa, P.A.; Seminario, J.M.; Balbuena, P.B. Properties of Small Bimetallic Ni−Cu Clusters. J. Phys. Chem. A 2001, 105, 7917–7925. [Google Scholar] [CrossRef]
  3. Eberhardt, W. Clusters as new materials. Surf. Sci. 2002, 500, 242–270. [Google Scholar] [CrossRef]
  4. Lu, Q.L.; Zhu, L.Z.; Ma, L.; Wang, G.H. Magnetic properties of Co/Cu and Co/Pt bimetallic clusters. Chem. Phys. Lett. 2005, 407, 176–179. [Google Scholar] [CrossRef]
  5. Yuan, D.W.; Wang, Y.; Zeng, Z. Geometric, electronic, and bonding properties of Au[sub N]M (N=1–7, M=Ni, Pd, Pt) clusters. J. Chem. Phys. 2005, 122, 114310. [Google Scholar] [CrossRef]
  6. Wang, X.; Cao, Z.; Lu, X.; Lin, M.; Zhang, Q. Structure and stability of binary transition-metal clusters (NbCo)[sub n] (n ≤ 5): A relativistic density-functional study. J. Chem. Phys. 2005, 123, 064315. [Google Scholar] [CrossRef] [Green Version]
  7. Barcaro, G.; Fortunelli, A.; Rossi, G.; Nita, F.; Ferrando, R. Electronic and Structural Shell Closure in AgCu and AuCu Nanoclusters. J. Phys. Chem. B 2006, 110, 23197–23203. [Google Scholar] [CrossRef]
  8. Néel, N.; Kröger, J.; Berndt, R.; Wehling, T.O.; Lichtenstein, A.I.; Katsnelson, M.I. Controlling the kondo effectin CoCun clusters atom by atom. Phys. Rev. Lett. 2008, 101, 266803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  9. Dong, D.; Xiao-Yu, K.; Jian-Jun, G.; Ben-Xia, Z. First-principle study of AunFe (n=1–7) clusters. J. Mol. Struct. 2009, 902, 54–58. [Google Scholar]
  10. Du, J.; Shen, N.; Zhu, L.; Wang, J. Emergence of noncollinear magnetic ordering in bimetallic Co6− n Mnn clusters. J. Phys. D: Appl. Phys. 2010, 43, 015006. [Google Scholar] [CrossRef]
  11. Lv, J.; Zhang, F.Q.; Jia, J.F.; Xu, X.H.; Wu, H.S. First-principles study of structural, electronic and magnetic properties of Co13−nMn (n=1, 2, M=Mn, V and Al) clusters. J. Mol. Struct. (TheoChem) 2010, 955, 14–22. [Google Scholar] [CrossRef]
  12. Kilimis, D.A.; Papageorgiou, D.G. Density functional study of small bimetallic Ag–Pd clusters. J. Mol. Struct. 2010, 939, 112–117. [Google Scholar] [CrossRef]
  13. Lin, L.; Claes, P.; Gruene, P.; Meijer, G.; Fielicke, A.; Nguyen, M.T.; Lievens, P. Far-Infrared Spectra of Yttrium-Doped Gold Clusters AunY (n = 1-9). ChemPhysChem 2010, 11, 1932–1943. [Google Scholar] [CrossRef] [PubMed]
  14. Garbounis, D.N.; Tsipis, A.C.; Tsipis, C.A. Structural, electronic, bonding, magnetic, and optical properties of bimetallic [RunAum]0/+ (n+m ≤ 3) clusters. J. Comput. Chem. 2010, 31, 2836–2852. [Google Scholar] [CrossRef] [PubMed]
  15. Yang, A.; Fa, W.; Dong, I. Magnetic Properties of Transition-Metal-Doped Tubular Gold Clusters: M@Au24 (M = V, Cr, Mn, Fe, Co, and Ni). J. Phys. Chem. A 2010, 114, 4031–4035. [Google Scholar] [CrossRef] [PubMed]
  16. Venkataramanan, R.S.; Sahara, R.; Mizuseki, H.; Kawazoe, Y. Titanium-Doped Nickel Clusters TiNin (n = 1−12): Geometry, Electronic, Magnetic, and Hydrogen Adsorption Properties. J. Phys. Chem. A 2010, 114, 5049–5057. [Google Scholar] [CrossRef]
  17. Wang, H.Q.; Kuang, X.Y.; Li, H.F. Density functional study of structural and electronic properties of bimetallic copper-gold clusters: Comparison with pure and doped gold clusters. Phys. Chem. Chem. Phys. 2010, 12, 5156. [Google Scholar] [CrossRef]
  18. Montejano-Carrizales, J.M.; Aguilera-Granja, F.; Morán-López, J.L. Structural and magnetic properties of FemYn (m+n = 7, Y = Ru, Rh, Pd, and Pt) nanoalloys. Eur. Phys. J. D 2011, 64, 53–62. [Google Scholar] [CrossRef]
  19. Jin, X.X.; Du, J.G.; Jiang, G.; Luo, X.; Wang, X.W. Geometries and electronic properties of NbnV(0, ±1) (n = 1−6) clusters studied by density-functional theory. Eur. Phys. J. D 2011, 64, 323–329. [Google Scholar] [CrossRef]
  20. Yang, J.X.; Guo, J.J.; Die, D. Ab initio study of AunIr (n=1–8) clusters. Comput. Theor. Chem. 2011, 963, 435–438. [Google Scholar] [CrossRef]
  21. Zhao, S.; Ren, Y.; Wang, J.; Yin, W. Density functional study of NO binding on small AgnPdm (n+m≤5) clusters. Comput. Theor. Chem. 2011, 964, 298–303. [Google Scholar] [CrossRef]
  22. Ma, Q.M.; Xie, Z.; Wang, B.R.; Liu, Y.; You-Cheng Li, Y.C. Structure, stability and magnetic moments of the FenCr clusters: All-electron density functional theory investigations. Solid State Commun. 2011, 151, 806–810. [Google Scholar] [CrossRef]
  23. Aguilera-Granja, F.; Longo, R.C.; Gallego, L.J.; Vega, A. Magnetic Cooperative Effects in Small Ni–Ru Clusters. J. Phys. Chem. A 2011, 115, 13950–13955. [Google Scholar] [CrossRef] [PubMed]
  24. Nhatab, P.V.; Nguyen, M.T. Trends in structural, electronic and energetic properties of bimetallic vanadium–gold clusters AunV with n = 1-14. Phys. Chem. Chem. Phys. 2011, 13, 16254–16264. [Google Scholar] [CrossRef] [PubMed]
  25. Lv, J.; Bai, X.; Jia, J.F.; Xu, X.H.; Wu, H.S. Structural, electronic and magnetic properties of ConRh (n=1–8) clusters from density functional calculations. Phys. B Condens. Matt. 2012, 407, 14–21. [Google Scholar] [CrossRef]
  26. Hong, L.; Wang, H.; Cheng, J.; Huang, X.; Sai, L.; Zhao, J. Atomic structures and electronic properties of small Au–Ag binary clusters: Effects of size and composition. Comput. Theor. Chem. 2012, 993, 36–44. [Google Scholar] [CrossRef]
  27. Shewale, V.; Deshpande, M. Structural, electronic, and magnetic properties of NinM clusters (M=Hf, Ta, W) with n=1–12. Comput. Theor. Chem. 2012, 984, 128–136. [Google Scholar] [CrossRef]
  28. Ding, L.P.; Kuang, X.Y.; Shao, P.; Zhao, Y.R.; Li, Y.F. A comparative study on geometries, stabilities, and electronic properties between bimetallic AgnX (X = Au, Cu; n=1−8) and pure silver clusters. Chin. Phys. B 2012, 21, 043601. [Google Scholar] [CrossRef]
  29. Yao, J.; Bin Xu, B.; Wang, Y. Ground State Structures, Electronic and Magnetic Properties of ScnFe (n=2-10) Clusters. Chin. J. Chem. 2012, 30, 905–913. [Google Scholar] [CrossRef]
  30. Florez, E.; Mondragon, F.; Illas, F. Theoretical study of the structure and reactivity descriptors of CunM (M = Ni, Pd, Pt, n = 1–4) bimetallic nanoparticles supported on MgO(001). Surf. Sci. 2012, 606, 1010–1018. [Google Scholar] [CrossRef]
  31. Ju, W.; Yang, Z. Influence of spin–orbit coupling on electronic structures of TM@Au12 (TM=3d, 4d, and 5d atoms). Phys. Lett. A 2012, 376, 1300–1305. [Google Scholar] [CrossRef]
  32. Ma, L.; Wang, J.; Hao, Y.; Wang, G. Density functional theory study of FePdn (n=2–14) clusters and interactions with small molecules. Comput. Mater. Sci. 2013, 68, 166–173. [Google Scholar] [CrossRef]
  33. Liu, X.; Tian, D.; Meng, C. DFT study on stability and H2 adsorption activity of bimetallic Au79−nPdn (n=1–55) clusters. Chem. Phys. 2013, 415, 179–185. [Google Scholar] [CrossRef]
  34. Tafoughalt, M.A.; Samah, M. Structural properties and relative stability of silver-doped gold clusters AgAun-1 (n = 3–13): Density functional calculations. Comput. Theor. Chem. 2014, 1033, 23–30. [Google Scholar] [CrossRef]
  35. Wen, J.Q.; Xia, T.; Zhou, H.; Wang, J.F. A density functional theory study of small bimetallic PdnAl (n=1–8) clusters. J. Phys. Chem. Solids 2014, 75, 528–534. [Google Scholar] [CrossRef]
  36. Singh, N.B.; Sarkar, U. A density functional study of chemical, magnetic and thermodynamic properties of small palladium clusters. Mol. Simul. 2014, 40, 1255–1264. [Google Scholar] [CrossRef]
  37. Bouderbala, W.; Boudjahem, A.G.; Soltani, A. Geometries, stabilities, electronic and magnetic properties of small PdnIr (n = 1–8) clusters from first principles calculations. Mol. Phys. 2014, 112, 1789–1798. [Google Scholar] [CrossRef]
  38. Ling, W.; Dong, D.; Shi-Jian, W.; Zheng-Quan, Z. Geometrical, electronic, and magnetic properties of CunFe (n=1–12) clusters: A density functional study. J. Phys. Chem. Solids 2015, 76, 10–16. [Google Scholar] [CrossRef]
  39. Chaves, A.S.; Rondina, G.G.; Piotrowski, M.J.; Da Silva, J.L.F. Structural formation of binary PtCu clusters: A density functional theory investigation. Comput. Mater. Sci. 2015, 98, 278–286. [Google Scholar] [CrossRef]
  40. Gong, X.; Ju, W.; Li, T.; Feng, Z.; Wang, Y. Spin–orbit Splitting and Magnetism of Icosahedral M@Ag12 Clusters (M = 3d and 4d atoms). J. Clust. Sci. 2015, 26, 759–773. [Google Scholar] [CrossRef]
  41. Chachkov, D.V.; Mikhailov, O.V. Molekularnye struktury poliyadernykh metalloklasterov po dannym raschyota metodom DFT. (Geterobi)tetrayadernyi klaster Fe2Co2. Herald Technol. Univ. 2016, 19, 20–23. [Google Scholar]
  42. Die, D.; Zheng, B.X.; Zhao, L.Q.; Zhu, Q.W.; Zhao, Z.Q. Insights into the structural, electronic and magnetic properties of V-doped copper clusters: Comparison with pure copper clusters. Sci. Rep. 2016, 6, 31978. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Al-Odail, F.; Mazher, J.; Abuelela, A.M. A density functional theory study of structural, electronic and magnetic properties of small PdnAg (n = 1–8) clusters. Comput. Theor. Chem. 2017, 1125, 103–111. [Google Scholar] [CrossRef]
  44. Deng, M.; Xin, Z.; Yan, X.; Liu, J.; Yu, M. Structural, Electronic, and Magnetic Properties of Bimetallic NimNbn (m+n ≤ 8) Clusters: First Principle Study. J. Supercond. Novel Magn. 2017, 30, 251–260. [Google Scholar] [CrossRef]
  45. Zhang, G.; Zhai, Z.; Sheng, Y. Structural, electronic and magnetic properties of TinMo (n = 1-7) clusters. Eur. Phys. J. D 2017, 71, 9. [Google Scholar] [CrossRef]
  46. Zhang, J.Y.; Lv, J. Equilibrium geometries, electronic structure and magnetic properties of ConSn (n = 1–12) clusters from density functional calculations. Mod. Phys. Lett. B 2017, 31, 1750171. [Google Scholar] [CrossRef]
  47. Datta, S.; Raychaudhuri, A.K.; Saha-Dasgupta, T. First principles study of bimetallic Ni13− nAgn nano-clusters (n = 0–13): Structural, mixing, electronic, and magnetic properties. J. Chem. Phys. 2017, 146, 164301. [Google Scholar] [CrossRef] [Green Version]
  48. Singh, R.K.; Iwasa, T.; Taketsugu, T. Insights into geometries, stabilities, electronic structures, reactivity descriptors, and magnetic properties of bimetallic NimCun-m (m = 1, 2; n = 3-13) clusters: Comparison with pure copper clusters. J. Comput. Chem. 2018, 39, 1878–1889. [Google Scholar] [CrossRef] [Green Version]
  49. Ma, S.; Fei, S.; Huang, L.; Forrey, R.C.; Cheng, H. Tuning the Catalytic Activity of PdxNiy (x + y = 6) Bimetallic Clusters for Hydrogen Dissociative Chemisorption and Desorption. ACS Omega 2019, 4, 12498–12504. [Google Scholar] [CrossRef]
  50. Ranjan, P.; Chakraborty, T. Structure and electronic properties of AunPt (n = 1–8) nanoalloy clusters: The density functional theory study. J. Nanopart. Res. 2020, 22, 11. [Google Scholar] [CrossRef]
  51. Deshpande, M.D.; Roy, S.; Kanhere, D.G. Equilibrium geometries, electronic structure, and magnetic properties of NinSn clusters (n=1–12). Phys. Rev. B 2007, 76, 195423. [Google Scholar] [CrossRef]
  52. Chen, X.; Deng, K.; Liu, Y.; Tang, C.; Yuan, Y.; Tan, W.; Wang, X. The geometric, optical, and magnetic properties of the endohedral stannaspherenes M@Sn[sub 12] (M=Ti, V, Cr, Mn, Fe, Co, Ni). J. Chem. Phys. 2008, 129, 094301. [Google Scholar] [CrossRef] [PubMed]
  53. Tang, C.; Liu, M.; Zhu, W.; Deng, K. Probing the geometric, optical, and magnetic properties of 3d transition-metal endohedral Ge12M (M=Sc–Ni) clusters. Comput. Theor. Chem. 2011, 969, 56–60. [Google Scholar] [CrossRef]
  54. Rohrmann, U.; Schäfer, R. Stern-Gerlach Experiments on Fe@Sn12: Magnetic Response of a Jahn–Teller Distorted Endohedrally Doped Molecular Cage Cluster. J. Phys. Chem. C 2015, 119, 10958–10961. [Google Scholar] [CrossRef]
  55. Shewale, V.H.; Deshpande, M.D.; Kanhere, D.G. Structures, energetics and magnetic properties of (NiSn)n clusters with n = 1–6. Pramana 2009, 73, 699–710. [Google Scholar] [CrossRef]
  56. Jaiswal, S.; Kumar, V. Growth behavior and electronic structure of neutral and anion ZrGen (n = 1–21) clusters. Comput. Theor. Chem. 2016, 1075, 87–97. [Google Scholar] [CrossRef]
  57. Sosa-Hernández, E.M.; Montejano-Carrizales, J.M.; Alvarado-Leyva, P.G. Global Minimum Structures, Stability and Electronic Properties of Small NiXSnY (X+Y≤ 5) Bimetallic Clusters; a DFT Study. Eur. Phys. J. D 2016, 70, 208. [Google Scholar] [CrossRef]
  58. Zhao, G.; Zhang, J.; Jing, Q.; Luo, Y.; Wang, Y. A density functional study of Y[sub n]Al (n=1–14) clusters. J. Chem. Phys. 2007, 127, 234312. [Google Scholar] [CrossRef]
  59. Tian, F.Y.; Jing, Q.; Wang, Y.X. Structure, stability, and magnetism of ScnAl (n=1–8,12) clusters: Density-functional theory investigations. Phys. Rev. A 2008, 77, 013202. [Google Scholar] [CrossRef]
  60. Wang, M.; Qiu, G.; Huang, X.; Du, Z.; Li, Y. Study of the size-dependent properties of ScnAl (n = 1–14) clusters by density-functional theory. J. Phys. Condens. Matter. 2009, 21, 046004. [Google Scholar] [CrossRef]
  61. Du, J.; Sun, X.; Jiang, G. Structures, chemical bonding, magnetisms of small Al-doped zirconium clusters. Phys. Lett. A 2010, 374, 854–860. [Google Scholar] [CrossRef]
  62. Hua, Y.; Liu, Y.; Jiang, G.; Du, J.; Chen, J. Geometric Transition and Electronic Properties of Titanium-Doped Aluminum Clusters: AlnTi (n = 2–24). J. Phys. Chem. A 2013, 117, 2590–2597. [Google Scholar] [CrossRef] [PubMed]
  63. Rusina, G.G.; Borisova, S.D.; Chulkov, E.V. Structure and atomic vibrations in bimetallic Ni13 − nAln clusters. JETP Letters 2015, 101, 474–480. [Google Scholar] [CrossRef]
  64. Schaefer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
  65. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  66. Hoe, W.M.; Cohen, A.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
  67. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
  68. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  69. Paulsen, H.; Duelund, L.; Winkler, H.; Toftlund, H.; Trautwein, A.X. Free Energy of Spin-Crossover Complexes Calculated with Density Functional Methods. Inorg. Chem. 2001, 40, 2201–2203. [Google Scholar] [CrossRef]
  70. Swart, M.; Groenhof, A.R.; Ehlers, A.W.; Lammertsma, K. Validation of Exchange−Correlation Functionals for Spin States of Iron Complexes. J. Phys. Chem. A 2004, 108, 5479–5483. [Google Scholar] [CrossRef]
  71. Swart, M.; Ehlers, A.W.; Lammertsma, K. Performance of the OPBE exchange-correlation functional. Mol. Phys. 2004, 102, 2467–2474. [Google Scholar] [CrossRef]
  72. Swart, M. Metal–ligand bonding in metallocenes: Differentiation between spin state, electrostatic and covalent bonding. Inorg. Chim. Acta 2007, 360, 179–189. [Google Scholar] [CrossRef]
  73. Chachkov, D.V.; Mikhailov, O.V. Molekulyarnye struktury poliyadernykh metalloklasterov po dannym raschyota metodom DFT. (Geterobi)tetrayadernyi klaster AlFe3. Herald Technol. Univ. 2016, 19, 18–21. [Google Scholar]
  74. Mikhailov, O.V.; Chachkov, D.V. Models of Molecular Structures of Aluminum–Iron Clusters AlFe3, Al2Fe3, and Al2Fe4 according to Quantum-Chemical DFT Calculations. Russ. J. Inorg. Chem. 2017, 62, 336–343. [Google Scholar] [CrossRef]
  75. Mikhailov, O.V.; Chachkov, D.V. Modeli molekularnylh struktur alyuminii-zheleznykh klasterov AlFe3, Al2Fe3 i Al2Fe4 po dannym kvantovo-khimicheskogo rascheta metodom DFT. Zh. Neorg. Khim. 2017, 62, 321–329. [Google Scholar]
  76. Mikhailov, O.V.; Chachkov, D.V. Molecular Structures of Tetranuclear (Al, Fe) Metal Clusters. Glass Phys. Chem. 2018, 44, 339–345. [Google Scholar] [CrossRef]
  77. Mikhailov, O.V.; Chachkov, D.V. Molekularnye struktury tetrayadernykh (Al, Fe) metalloklasterov. Fizika i Khimiya Stekla 2018, 44, 408–415. [Google Scholar]
  78. Chachkov, D.V.; Mikhailov, O.V. Molekulyarnye struktury poliyadernykh metalloklasterov po dannym raschyota metodom DFT. (Geterotri)tetrayadernyi klaster Al2FeCo. Herald Technol. Univ. 2016, 19, 30–32. [Google Scholar]
  79. Mikhailov, O.V.; Chachkov, D.V. Quantum Chemical Calculation of Molecular Structures of Al2Fe2 and Al2FeCo Tetranuclear Metalloclusters. Glass Phys. Chem. 2017, 43, 597–604. [Google Scholar] [CrossRef]
  80. Mikhailov, O.V.; Chachkov, D.V. Kvantovo-khimicheskii raschyot molekularnykh struktur tetrayadernykh metalloklasterov Al2Fe2 i Al2FeCo. Fizika i Khimiya Stekla 2017, 43, 632–639. [Google Scholar]
  81. Chachkov, D.V.; Mikhailov, O.V. Molekulyarnye struktury poliyadernykh metalloklasterov po dannym raschyota metodom DFT. (Geterobi)pentayadernyi klaster Al2Ti3. Herald Technol. Univ. 2016, 19, 5–8. [Google Scholar]
  82. Chachkov, D.V.; Mikhailov, O.V. Molekulyarnye struktury poliyadernykh metalloklasterov po dannym raschyota metodom DFT. (Geterobi)pentayadernyi klaster Al2V3. Herald Technol. Univ. 2016, 19, 12–15. [Google Scholar]
  83. Mikhailov, O.V.; Chachkov, D.V. Molecular structure models of Al2Ti3 and Al2V3 clusters according to DFT quantum-chemical calculation. Eur. Chem. Bull. 2020, 9, 62–68. [Google Scholar] [CrossRef] [Green Version]
  84. Mikhailov, O.V.; Chachkov, D.V. Models of Molecular Structures of Al2Cr3 and Al2Mo3 Metal Clusters according to Density Functional Theory Calculations. Russ. J. Inorg. Chem. 2018, 63, 786–799. [Google Scholar] [CrossRef]
  85. Mikhailov, O.V.; Chachkov, D.V. Modeli molekularnykh struktur metalloklasterov Al2Cr3 i Al2Mo3 po dannym metoda funktsionala plotnosti. Zh. Neorg. Khim. 2018, 63, 750–763. [Google Scholar]
  86. Mikhailov, O.V.; Chachkov, D.V. Quantum-chemical calculation of molecular structures of Al2Mn3 and Al2Zn3 clusters by using DFT method. Struct. Chem. 2019, 30, 1289–1299. [Google Scholar] [CrossRef]
  87. Mikhailov, O.V.; Chachkov, D.V. Models of Molecular Structure of Heteronuclear Clusters Al2Fe3, Al2Co3, and Al2Ni3 According to the Data of Quantum-Chemical Density Functional Simulation. Russ. J. Gen. Chem. 2016, 86, 1991–1998. [Google Scholar] [CrossRef]
  88. Mikhailov, O.V.; Chachkov, D.V. Modeli molekularnykh struktur geteroyadernykh klasterov Al2Fe3, Al2Co3 и Al2Ni3 po dannym kvantovo-khimicheskogo raschyota po metody funktsionala plotnosti. Zh. Obshch. Khim. 2016, 86, 1419–1428. [Google Scholar]
  89. Mikhailov, O.V.; Chachkov, D.V. DFT calculation of molecular structures of Al2Fe3 and Al2Cu3 heterobinuclear clusters. Struct. Chem. 2018, 29, 1543–1549. [Google Scholar] [CrossRef]
  90. Chachkov, D.V.; Mikhailov, O.V. DFT Quantum Chemical Calculation of the Molecular Structures of the Metal Clusters Al2Cu3 and Al2Ag3. Russ. J. Inorg. Chem. 2019, 64, 79–87. [Google Scholar] [CrossRef]
  91. Chachkov, D.V.; Mikhailov, O.V. DFT Kvantovo-khimicheskii raschyot molekularnykh struktur metalloklasterov Al2Cu3 i Al2Ag3 metodom DFT. Zh. Neorg. Khim. 2019, 64, 63–71. [Google Scholar]
  92. Mikhailov, O.V.; Chachkov, D.V. Thermodynamics of Al2M3 Metal Clusters (M = 3d-element) in the framework of quantum-chemical modeling by DFT method. Russ. J. Inorg. Chem. 2020, 65, 646–649. [Google Scholar]
  93. Mikhailov, O.V.; Chachkov, D.V. Termodinamika metalloklasterov Al2M3 (M = 3d-element) v ramkakh kvantovo-khimicheskogo modelirovaniya metodom DFT. Zh. Neorg. Khim. 2020, 65, 598–602. [Google Scholar]
  94. Chachkov, D.V.; Mikhailov, O.V. Molekulyarnye struktury poliyadernykh metalloklasterov po dannym raschyota metodom DFT. (Geterobi)hexayadernyi klaster Al3Fe3. Herald Technol. Univ. 2016, 19, 89–93. [Google Scholar]
  95. Chachkov, D.V.; Mikhailov, O.V. Molecular Structure of Hexatomic Heteronuclear (AlFe) Metal Clusters as Determined by the DFT Quantum-Chemical Calculation. Russ. J. Gen. Chem. 2017, 87, 670–678. [Google Scholar] [CrossRef]
  96. Chachkov, D.V.; Mikhailov, O.V. Molekulyarnye struktury shestiatomnykh geteroyadernykh (AlFe) metalloklasterov po dannym po dannym kvantovo-khimicheskogo raschyota metodom DFT. Zh. Obshch. Khim. 2017, 87, 535–543. [Google Scholar]
Materials 13 01852 g001 550
Figure 1. The images of molecular structures of most stable AlFe3 (a) and Al3Fe (b) isomers [76].
Figure 1. The images of molecular structures of most stable AlFe3 (a) and Al3Fe (b) isomers [76].
Materials 13 01852 g001
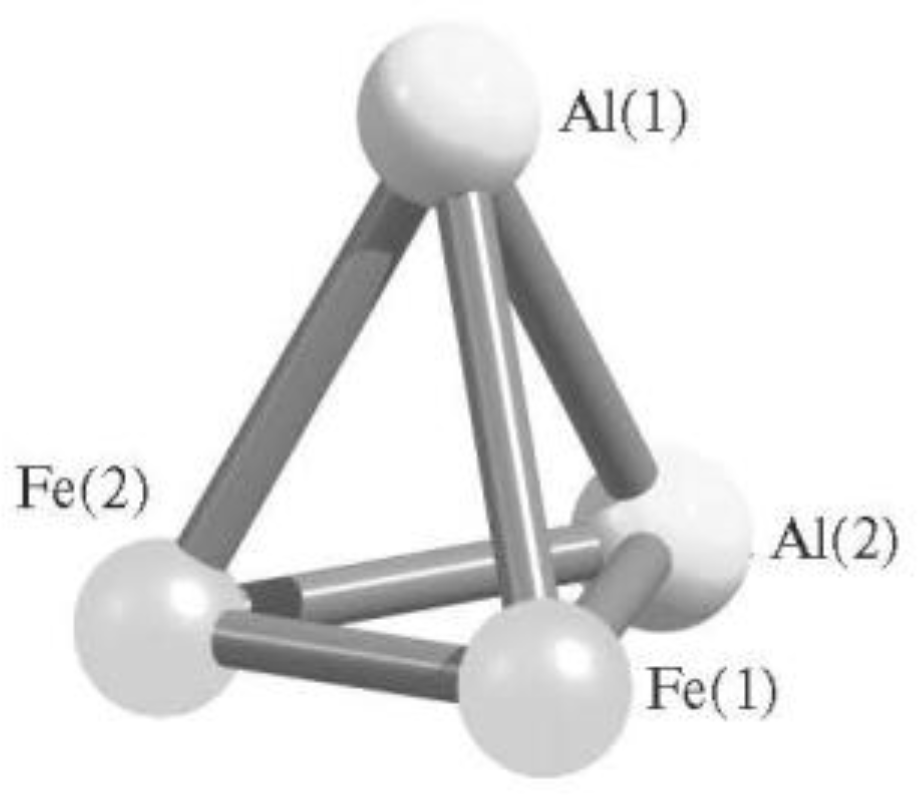
Materials 13 01852 g002 550
Figure 2. The image of molecular structure of most stable Al2Fe2 isomer [79].
Figure 2. The image of molecular structure of most stable Al2Fe2 isomer [79].
Materials 13 01852 g002
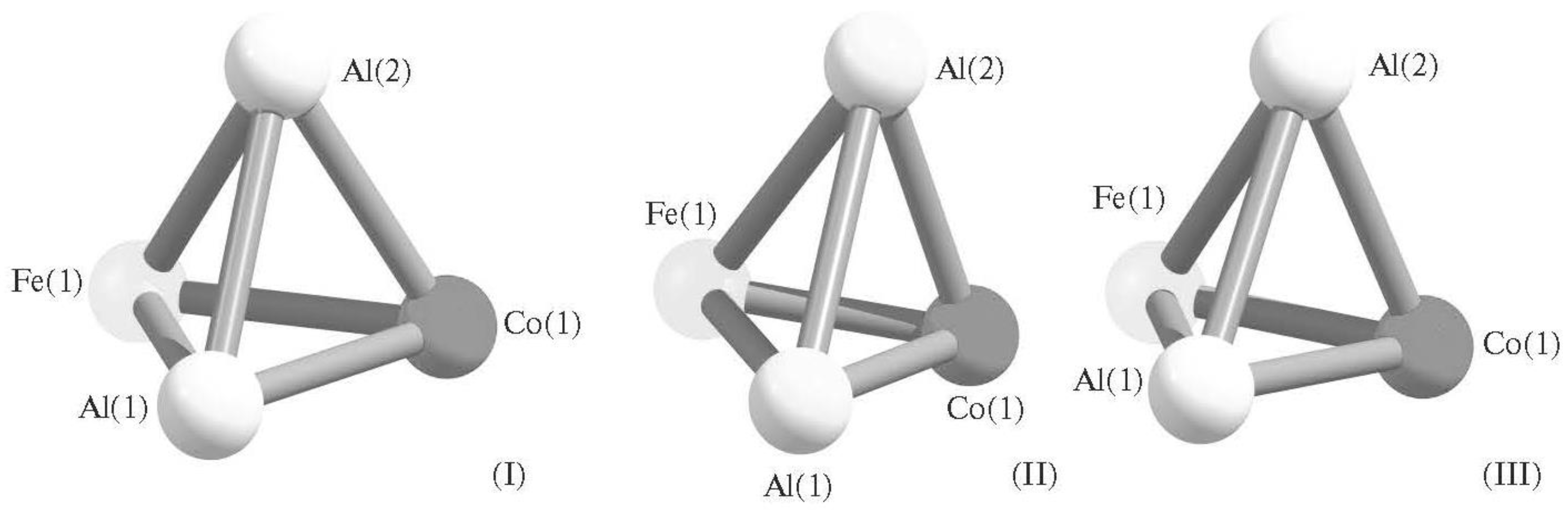
Materials 13 01852 g003 550
Figure 3. Molecular structures of three Al2FeCo isomers: (I)—with most high energy, (III) —with most low energy and (II)—with intermediate energy between (I) and (III) [79].
Figure 3. Molecular structures of three Al2FeCo isomers: (I)—with most high energy, (III) —with most low energy and (II)—with intermediate energy between (I) and (III) [79].
Materials 13 01852 g003
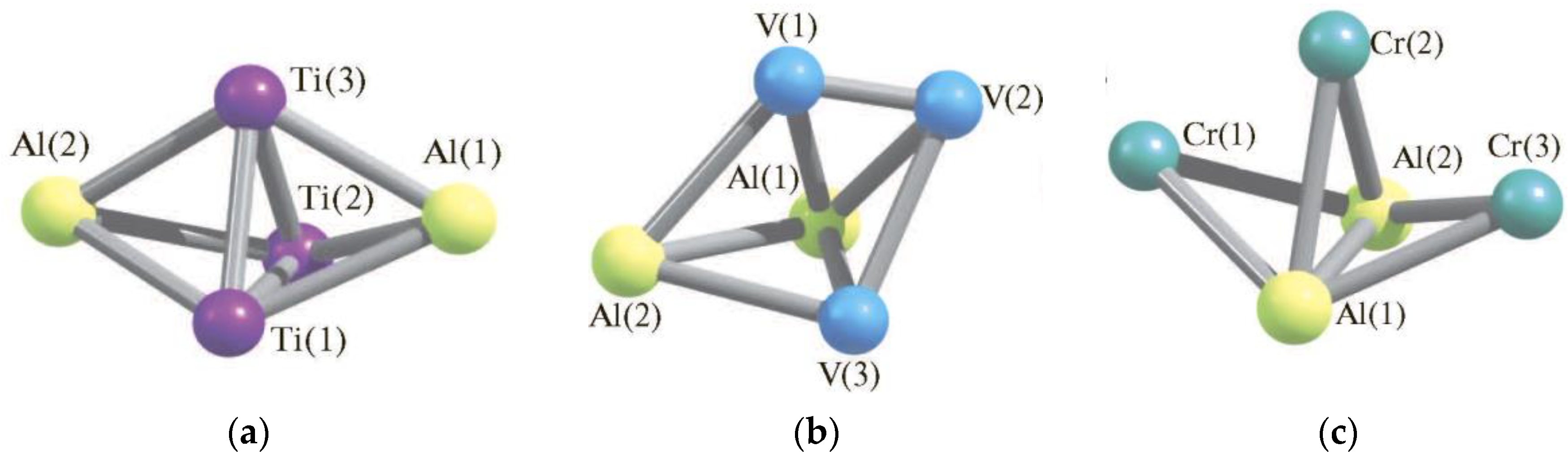
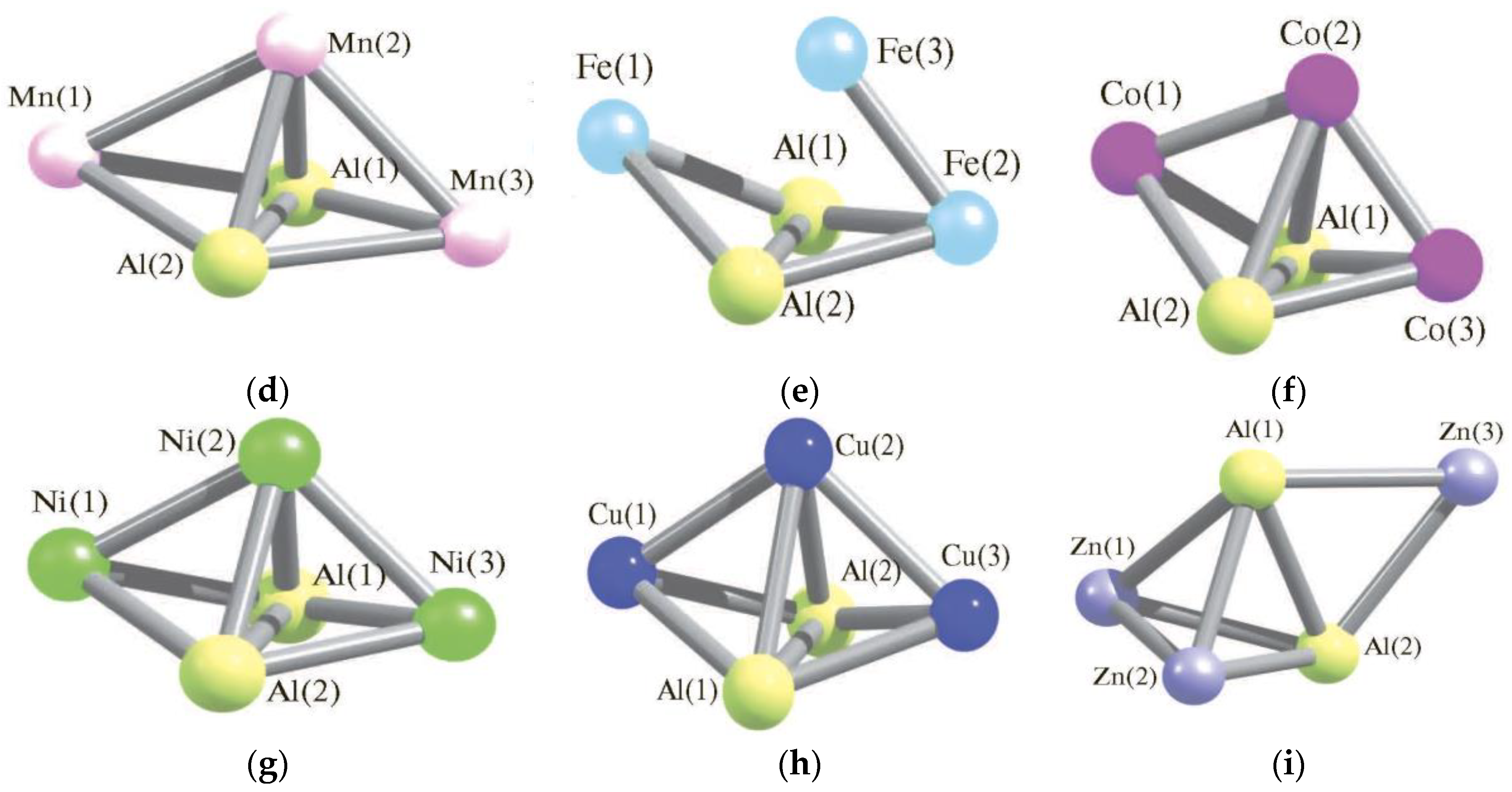
Materials 13 01852 g004a 550Materials 13 01852 g004b 550
Figure 4. The images of molecular structures of most energetic stable Al2M3 metal clusters (M—3d-element) [92,93]: (a)—Al2Ti3, (b)—Al2V3, (c)—Al2Cr3, (d)—Al2Mn3, (e)—Al2Fe3, (f)—Al2Co3, (g)—Al2Ni3, (h)—Al2Cu3, (i)—Al2Zn3.
Figure 4. The images of molecular structures of most energetic stable Al2M3 metal clusters (M—3d-element) [92,93]: (a)—Al2Ti3, (b)—Al2V3, (c)—Al2Cr3, (d)—Al2Mn3, (e)—Al2Fe3, (f)—Al2Co3, (g)—Al2Ni3, (h)—Al2Cu3, (i)—Al2Zn3.
Materials 13 01852 g004aMaterials 13 01852 g004b
Materials 13 01852 g005 550
Figure 5. The dependences of the thermodynamic parameters of the reaction (1) of 3d-element atomic number.
Figure 5. The dependences of the thermodynamic parameters of the reaction (1) of 3d-element atomic number.
Materials 13 01852 g005
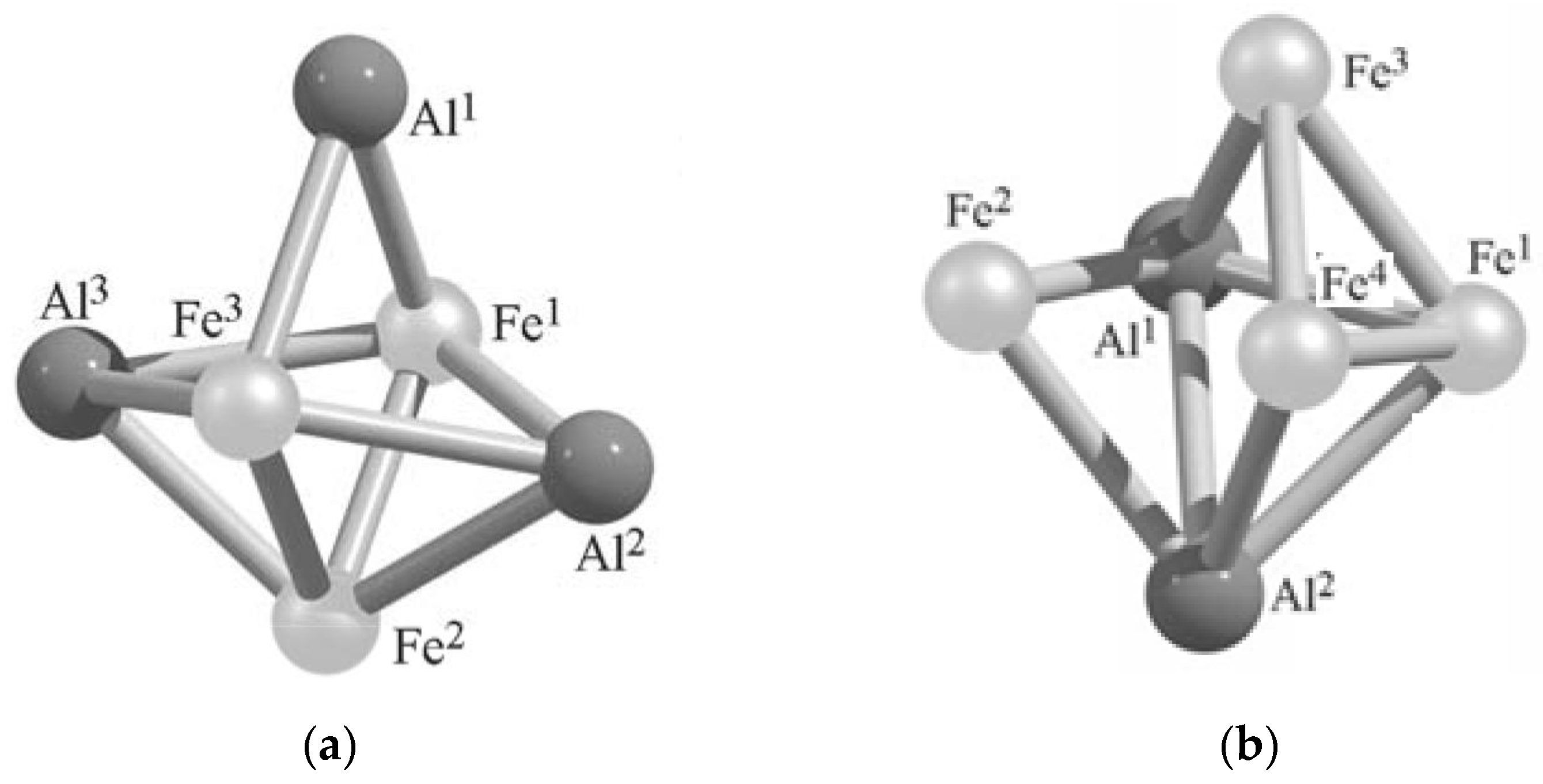
Materials 13 01852 g006 550
Figure 6. The images of molecular structures of most stable Al3Fe3 (a) and Al2Fe4 (b) isomers [95].
Figure 6. The images of molecular structures of most stable Al3Fe3 (a) and Al2Fe4 (b) isomers [95].
Materials 13 01852 g006
Table
Table 1. Relative energies and spin multiplicities of the ground states of various isomers of metal clusters Al3Fe, AlFe3 and Al2Fe2. Roman numerals in the table are the designations of these metal clusters presented in the original works.
Table 1. Relative energies and spin multiplicities of the ground states of various isomers of metal clusters Al3Fe, AlFe3 and Al2Fe2. Roman numerals in the table are the designations of these metal clusters presented in the original works.
Structure
Designation		Spin Multiplicity of
the Ground State		Relative Energy, kJ/molRef.
Al3Fe Metal Cluster
Al3Fe (I)20.0[79,80]
Al3Fe (VII)2175.1
Al3Fe (II)432.7
Al3Fe (IV)4153.3
Al3Fe (III)683.4
Al3Fe (VI)684.8
Al3Fe (V)6193.1
AlFe3 Metal Cluster
AlFe3 (II)211.2[79,80]
AlFe3 (I)2104.0
AlFe3 (VII)2122.8
AlFe3 (VIII)2198.7
AlFe3 (V)40.0
AlFe3 (III)411.3
AlFe3 (IX)4150.2
AlFe3 (VI)617.4
AlFe3 (IV)641.7
AlFe3 (X)652.6
Al2Fe2 Metal Cluster
Al2Fe2 (XII)145.1[78,79,80]
Al2Fe2 (VII)146.7
Al2Fe2 (IX)1150.3
Al2Fe2 (X)1209.8
Al2Fe2 (III)1352.5
Al2Fe2 (VI)366.5
Al2Fe2 (VIII)368.4
Al2Fe2 (IV)3137.9
Al2Fe2 (XI)3143.6
Al2Fe2 (II)3254.5
Al2Fe2 (V)50.0
Al2Fe2 (I)5152.7
Table
Table 2. Key structural parameters of most stable Al3Fe, Al2Fe2 and AlFe3 metal clusters * [76,77,78,79,80].
Table 2. Key structural parameters of most stable Al3Fe, Al2Fe2 and AlFe3 metal clusters * [76,77,78,79,80].
Al3Fe Metal ClusterAl2Fe2 Metal ClusterAlFe3 Metal Cluster
Metal-Metal Bond Lengths, pmMetal-Metal Bond Lengths, pmMetal-Metal Bond Lengths, pm
Al1Al2263.4Al1Al2260.8Al1Fe1249.1
Al1Al3263.3Al1Fe1249.5Al1Fe2249.1
Al2Al3274.3Al1Fe2249.4Al1Fe3255.5
Al1Fe1245.7Al2Fe1249.5Fe1Fe2208.6
Al2Fe1235.0Al2Fe2249.5Fe1Fe3248.7
Al3Fe1235.1Fe1Fe2199.2Fe2Fe3248.7
Bond Angles, degBond Angles, degBond Angles, deg
Al1Fe1Al266.4Fe1Al1Fe247.1Fe1Al1Fe249.5
Fe1Al1Al254.9Fe1Al2Fe247.1Al1Fe1Fe265.3
Al1Al2Fe158.7Fe1Al1Al258.5Fe1Fe2Al165.2
Al1Fe1Al366.4Fe1Al2Al158.5Fe1Al1Fe359.0
Al2Fe1Al371.4Fe2Al1Al258.5Fe2Al1Fe359.0
Al1Al2Al358.6Fe2Al2Al158.5Fe1Fe2Fe365.2
Al2Al3Al158.6Al1Fe1Al263.0Fe2Fe3Fe149.6
Al3Al1Al262.8Al1Fe2Al263.1Fe3Fe1Fe265.2
* The interatomic distances and angles within which at least one of the metal–metal bonds (Al–Al, Al–M, or M–M) is absent, are shown in this table in italics.
Table
Table 3. Total number of Al2M3 (N) metal cluster isomers for various M of 3d-elements.
Table 3. Total number of Al2M3 (N) metal cluster isomers for various M of 3d-elements.
MTiVCrMnFeCoNiCuZn
N14112025897814
Ref.[81,83][82,83][84,85][86][87,88,89][87,88][87,88][89,90,91][86]
Table
Table 4. Relative energies and spin multiplicities of the ground states of various isomers of 3d-element metal clusters having Al2M3 composition (M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn). Roman numerals in the table are the designations of these metal clusters presented in the original works.
Table 4. Relative energies and spin multiplicities of the ground states of various isomers of 3d-element metal clusters having Al2M3 composition (M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn). Roman numerals in the table are the designations of these metal clusters presented in the original works.
Structure
Designation		Spin Multiplicity of the Ground StateRelative Energy, kJ/molRef.
Al2Ti3 Metal Cluster
Al2Ti3 (XIII)121.5[81,83]
Al2Ti3 (II)124.1
Al2Ti3 (VII)144.8
Al2Ti3 (XIV)151.1
Al2Ti3 (VIII)177.5
Al2Ti3 (III)193.0
Al2Ti3 (XII)312.6
Al2Ti3 (X)337.0
Al2Ti3 (VI)337.2
Al2Ti3 (I)380.9
Al2Ti3 (XI)50.0
Al2Ti3 (V) 519.7
Al2Ti3 (IV)560.7
Al2Ti3 (IX)573.0
Al2V3 Metal Cluster
Al2V3 (I) 225.9[82,83]
Al2V3 (IV)226.7
Al2V3 (VII)230.2
Al2V3 (V)40.0
Al2V3 (II)42.4
Al2V3 (X)459.6
Al2V3 (VIII)471.3
Al2V3 (III)618.8
Al2V3 (VI)626.8
Al2V3 (XI)674.6
Al2V3 (IX)6141.0
Al2Cr3 Metal Cluster
Al2Cr3 (XVIII)1172.6[84,85]
Al2Cr3 (XVI)1186.5
Al2Cr3 (V)1197.2
Al2Cr3 (XIII)1206.8
Al2Cr3 (X)1219.0
Al2Cr3 (XIX)1266.6
Al2Cr3 (VI)1287.0
Al2Cr3 (I)1396.2
Al2Cr3 (VII)379.4
Al2Cr3 (II)392.9
Al2Cr3 (XIV)3109.3
Al2Cr3 (XI)3109.6
Al2Cr3 (III)50.0
Al2Cr3 (XVII)513.1
Al2Cr3 (VIII)519.5
Al2Cr3 (XII)539.6
Al2Cr3 (XX)573.4
Al2Cr3 (XV)586.8
Al2Cr3 (IV)722.9
Al2Cr3 (IX)739.6
Al2Mn3 Metal Cluster
Al2Mn3 (XIII)229.3[86]
Al2Mn3 (XVII)234.9
Al2Mn3 (V)247.5
Al2Mn3 (XXII)250.5
Al2Mn3 (XXV)280.8
Al2Mn3 (VIII)2124.0
Al2Mn3 (XIX)2129.4
Al2Mn3 (XXI)42.2
Al2Mn3 (XII)45.9
Al2Mn3 (IV)411.2
Al2Mn3 (XVI)427.0
Al2Mn3 (VII)429.6
Al2Mn3 (XXIV)476.1
Al2Mn3 (II)482.2
Al2Mn3 (X)4141.7
Al2Mn3 (VI)60.0
Al2Mn3 (XX)61.4
Al2Mn3 (III)619.1
Al2Mn3 (XV)628.1
Al2Mn3 (XI)636.6
Al2Mn3 (XIV)642.3
Al2Mn3 (XXIII)662.4
Al2Mn3 (IX)674.6
Al2Mn3 (I)677.2
Al2Mn3 (XVIII)6149.2
Al2Fe3 Metal Cluster
Al2Fe3(I)1273.7[87,88,89]
Al2Fe3(IV)1300.6
Al2Fe3(II)30.0
Al2Fe3(V)324.1
Al2Fe3(VII)327.1
Al2Fe3(III)512.8
Al2Fe3(VIII)524.7
Al2Fe3(VI)531.1
Al2Co3 Metal Cluster
Al2Co3(I)256.0[87,88]
Al2Co3(VII)283.6
Al2Co3(IV)292.0
Al2Co3(II)486.1
Al2Co3(VIII)486.8
Al2Co3(V)496.3
Al2Co3(III)60.0
Al2Co3(IX)628.9
Al2Co3(VI)673.3
Al2Ni3 Metal Cluster
Al2Ni3 (I)148.6[87,88]
Al2Ni3 (IV)170.8
Al2Ni3 (II)30.0
Al2Ni3 (V)373.1
Al2Ni3 (III)5102.6
Al2Ni3 (VI)5113.3
Al2Ni3 (VII)5148.4
Al2Cu3 Metal Cluster
Al2Cu3 (I)20.0[89,90,91]
Al2Cu3 (III)220.6
Al2Cu3 (V)227.0
Al2Cu3 (VII)240.1
Al2Cu3 (VIII)267.6
Al2Cu3 (IV)4136.9
Al2Cu3 (II)4144.1
Al2Cu3 (VI)4144.3
Al2Zn3 Metal Cluster
Al2Zn3 (III)114.0[86]
Al2Zn3 (II)117.7
Al2Zn3 (XII)118.9
Al2Zn3 (VI)122.1
Al2Zn3 (XIII)123.8
Al2Zn3 (XI)125.6
Al2Zn3 (V)129.6
Al2Zn3 (IX)130.5
Al2Zn3 (VIII)179.2
Al2Zn3 (I)30.0
Al2Zn3 (XIV)33.2
Al2Zn3 (IV)311.0
Al2Zn3 (VII)321.4
Al2Zn3 (X)329.6
Table
Table 5. Key structural parameters of most stable Al2M3 clusters (M—3d-element) [92,93] *.
Table 5. Key structural parameters of most stable Al2M3 clusters (M—3d-element) [92,93] *.
MTiVCrMnFeCoNiCuZn
Parameter
Metal–Metal Bond Lengths, pm
Al1Al2422.7270.2262.4276.1273.9271.5270.7271.1277.3
Al1M1254.4263.7262.6260.4244.8233.1229.0244.1267.7
Al1M2258.2265.7278.1257.6240.9252.8236.1254.2267.8
Al1M3258.2252.2262.6260.4252.3233.1229.0244.1273.7
Al2M1254.4261.0262.6260.4244.8233.1229.0244.1267.7
Al2M2258.2378.8278.1257.7240.9252.8236.1254.2247.9
Al2M3258.2254.4262.6260.4252.3233.1229.0244.1273.6
M1M3258.7265.4415.9434.8250.7341.6357.3384.1446.0
M2M3239.0253.3258.1281.6217.6215.3231.1243.1446.1
M1M2258.8171.7258.1281.6374.9215.3231.1243.1247.9
Bond Angles, deg
M1Al1M260.637.856.965.9101.052.459.658.355.2
M1Al2M260.622.956.965.8101.052.459.658.355.2
M1Al1Al233.858.560.058.056.054.453.856.358.8
M1Al2Al133.859.560.058.056.054.453.856.358.8
M2Al1Al235.690.061.957.655.457.555.057.858.8
M2Al2Al135.044.561.957.655.457.555.057.858.8
Al1M1Al2112.362.059.964.068.071.272.567.462.4
Al1M2Al2109.945.556.364.869.364.969.964.462.4
Al1M3Al2109.964.559.964.065.768.572.567.460.9
M1Al1M360.661.9104.7113.260.594.2102.6103.7110.9
M1Al2M360.662.0104.7113.260.594.2102.6103.7111.0
M1M3M262.538.636.365.9106.237.539.437.832.3
M2Al1M355.158.556.965.952.352.459.658.3110.9
M2Al2M355.141.656.9101.152.352.459.658.3111.0
M1M2M362.574.5107.339.540.0105.0101.3104.473.9
* The interatomic distances and angles within which at least one of the metal–metal bonds (Al–Al, Al–M, or M–M) is absent, are shown in this table in italics.
Table
Table 6. Standard thermodynamic parameters of formation for the most energy-stable Al2M3 metal clusters and the reactions of their formation from atoms of the chemical elements constituting them, in the gas phase [92,93].
Table 6. Standard thermodynamic parameters of formation for the most energy-stable Al2M3 metal clusters and the reactions of their formation from atoms of the chemical elements constituting them, in the gas phase [92,93].
Metal ClusterStandard Thermodynamic Parameters of Formation
ΔfH0(298 K)
kJ/mol		ΔfS0(298 K)
J/mol∙ K		ΔfG0(298 K)
kJ/mol
Al2Ti3967.4429.9883.5
Al2V3526.5438.5433.8
Al2Cr31151.1417.81067.5
Al2Mn3516.8423.1436.2
Al2Fe3823.4430.0736.5
Al2Co3817.6427.6733.9
Al2Ni3760.9430.0676.3
Al2Cu3812.2406.9737.7
Al2Zn3700.1445.1621.7
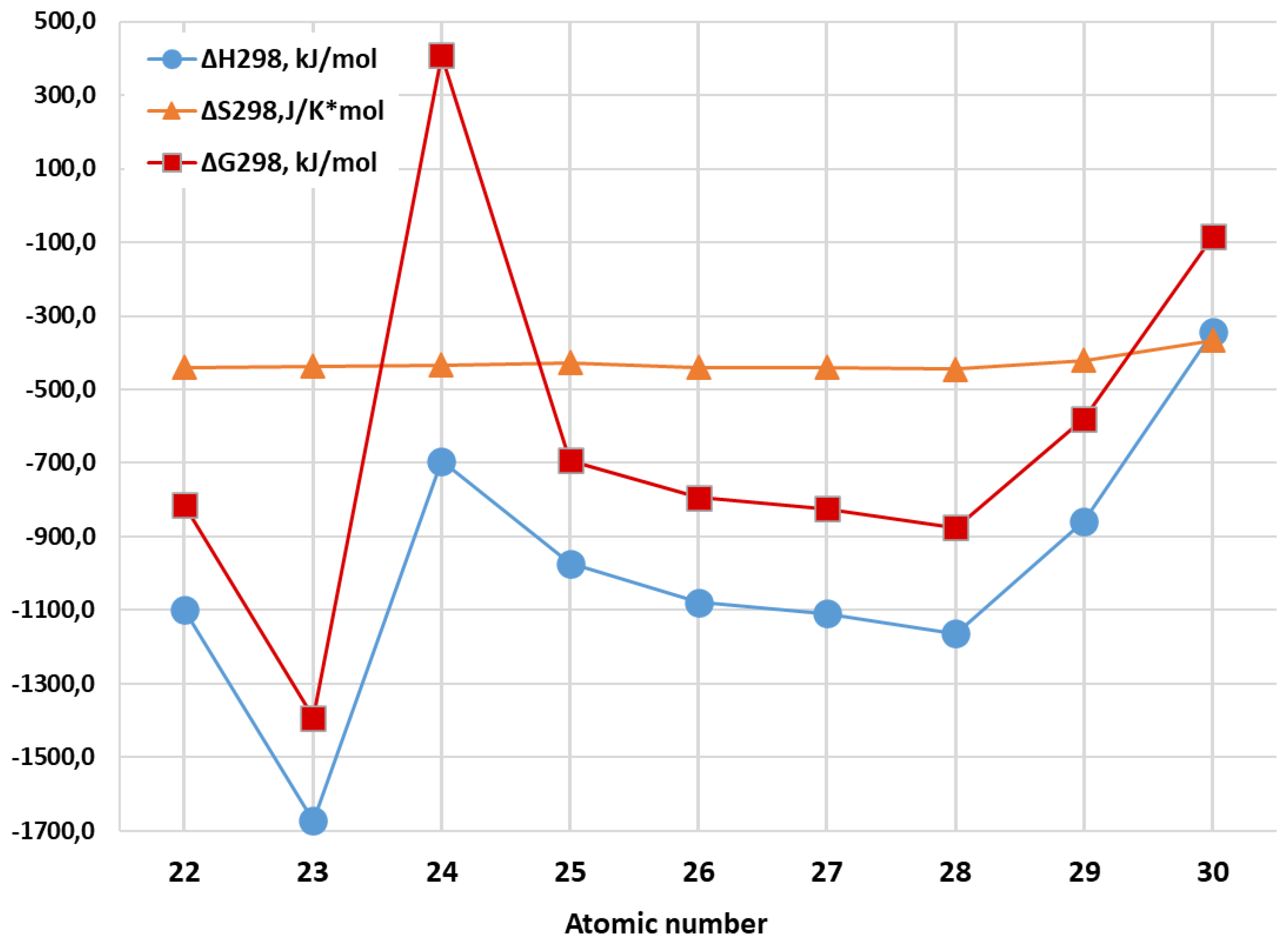
Metal ClusterStandard Thermodynamic Parameters of Reactions 2Al(gas) + 3M(gas)→Al2M3 (gas)
ΔH298, kJ/molΔS298, J/mol∙ KΔG298, kJ/mol
Al2Ti3–1098.5–439.5–813.4
Al2V3–1672.0–436.9–1392.1
Al2Cr3–694.0–433.6407.7
Al2Mn3–973.4–426.5–692.2
Al2Fe3–1078.1–440.0–793.0
Al2Co3–1109.1–439.4–824.1
Al2Ni3–1162.8–445.1–876.0
Al2Cu3–858.3–420.8–578.8
Al2Zn3–344.6–366.4–84.3
Table
Table 7. Thermal destruction onset temperatures (Ttd) for energetically most stable Al2M3 metal clusters [92,93].
Table 7. Thermal destruction onset temperatures (Ttd) for energetically most stable Al2M3 metal clusters [92,93].
Metal ClusterAtomic Number of MTtd, K
Al2Ti3222502.2
Al2V3233826.0
Al2Cr3241599.0
Al2Mn3252278.6
Al2Fe3262450.2
Al2Co3272526.4
Al2Ni3282613.0
Al2Cu3292038.7
Al2Zn330941.5
Table
Table 8. Relative energies and spin multiplicities of the ground states of various isomers of metal clusters Al3Fe3 and Al2Fe4. Roman numerals in the table are the designations of these metal clusters presented in the original works.
Table 8. Relative energies and spin multiplicities of the ground states of various isomers of metal clusters Al3Fe3 and Al2Fe4. Roman numerals in the table are the designations of these metal clusters presented in the original works.
Structure
Designation		Spin Multiplicity
of the Ground State		Relative Energy, kJ/molRef.
Al3Fe3 Metal Cluster
Al3Fe3 (IV)258.8[94,95,96]
Al3Fe3 (X)295.2
Al3Fe3 (XIX)2108.3
Al3Fe3 (VII)2134.5
Al3Fe3 (XIII)2137.2
Al3Fe3 (XVI)2153.7
Al3Fe3 (I)2158.3
Al3Fe3 (V)456.8
Al3Fe3 (XIV)456.8
Al3Fe3 (VIII)4108.9
Al3Fe3 (XI)4110.1
Al3Fe3 (II)4130.8
Al3Fe3 (XV)60.0
Al3Fe3 (XII)640.8
Al3Fe3 (IX)671.8
Al3Fe3 (VI)677.3
Al3Fe3 (III)678.1
Al3Fe3 (XX)6105.9
Al3Fe3 (XVII)6111.4
Al3Fe3 (XVIII)6155.4
Al2Fe4 Metal Cluster
Al2Fe4 (V)313.0[95,96]
Al2Fe4 (VIII)327.5
Al2Fe4 (III)380.8
Al2Fe4 (IX)3102.8
Al2Fe4 (VI)3115.7
Al2Fe4 (I)3165.5
Al2Fe4 (II)50.0
Al2Fe4 (VII)525.5
Al2Fe4 (IV)579.2
Table
Table 9. Key structural parameters of most stable Al3Fe3 and Al2Fe4 metal clusters * [94,95,96].
Table 9. Key structural parameters of most stable Al3Fe3 and Al2Fe4 metal clusters * [94,95,96].
Al3Fe3 Metal ClusterAl2Fe4 Metal Cluster
Metal–Metal Bond Lengths, pmMetal–Metal Bond Lengths, pm
Al1Al2306.2Al1Fe1242.7
Al1Al3307.1Al1Fe2249.8
Al2Al3398.9Al1Fe3243.8
Al1Fe1236.4Al1Fe4350.4
Al1Fe2370.1Al1Al2274.7
Al1Fe3236.3Al2Fe1242.7
Al2Fe1244.4Al2Fe2249.7
Al2Fe2242.1Al2Fe3350.4
Al2Fe3244.2Al2Fe4243.8
Al3Fe1244.3Fe2Fe3244.1
Al3Fe2242.1Fe1Fe4225.9
Al3Fe3244.2Fe1Fe3225.9
Fe1Fe2222.5Fe1Fe2329.1
Fe1Fe3270.9Fe2Fe4244.1
Fe2Fe3222.4Fe3Fe4230.7
Bond Angles, degBond Angles, deg
Fe2Al1Fe335.0Fe2Al1Fe359.3
Fe1Al1Fe235.0Fe1Al1Fe283.9
Fe1Al2Al335.3Fe1Al2Fe455.4
Fe2Al2Al334.5Fe2Al2Fe459.3
Al1Al2Fe284.1Al1Al2Fe256.6
Fe2Al1Al240.6Fe2Al1Al256.6
Al1Al2Al349.5Al1Al2Fe484.8
Al2Al3Fe135.3Al2Fe4Fe162.1
Al3Fe1Al2109.4Fe4Fe1Al262.6
Fe3Al1Al251.6Fe3Al1Al284.8
Fe1Al1Fe369.9Fe1Al1Fe355.4
Fe1Al1Al251.6Fe1Al1Al255.5
Al1Fe1Al279.1Al1Fe1Al268.9
Al3Fe2Fe363.3Fe4Fe2Fe356.4
* The interatomic distances and angles within which at least one of the metal–metal bonds (Al–Al, Al–Fe, or Fe–Fe) is absent, are shown in this table in italics.

Share and Cite

MDPI and ACS Style

Mikhailov, O.V.; Chachkov, D.V. Quantum-Chemical Design of Molecular Structures of Tetra-, Penta- and Hexanuclear Metal Clusters Containing Aluminum and 3d-Element Atoms. Materials 2020, 13, 1852. https://doi.org/10.3390/ma13081852

AMA Style

Mikhailov OV, Chachkov DV. Quantum-Chemical Design of Molecular Structures of Tetra-, Penta- and Hexanuclear Metal Clusters Containing Aluminum and 3d-Element Atoms. Materials. 2020; 13(8):1852. https://doi.org/10.3390/ma13081852

Chicago/Turabian Style

Mikhailov, Oleg V., and Denis V. Chachkov. 2020. "Quantum-Chemical Design of Molecular Structures of Tetra-, Penta- and Hexanuclear Metal Clusters Containing Aluminum and 3d-Element Atoms" Materials 13, no. 8: 1852. https://doi.org/10.3390/ma13081852

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop