Experimental Study on Mechanical Properties of the Sandwich Composite Structure Reinforced by Basalt Fiber and Nomex Honeycomb
Abstract
:1. Introduction
2. Experimental Program
2.1. Materials
2.2. Specimens Preparation
2.2.1. Preparation of Flatwise Compressed Specimens
2.2.2. Preparation of Bending Specimens
2.3. Experimental Equipment
2.4. Experimental Principle and Loading Program
2.4.1. Flatwise Compression Test
2.4.2. Bending Test
3. Results and Discussions
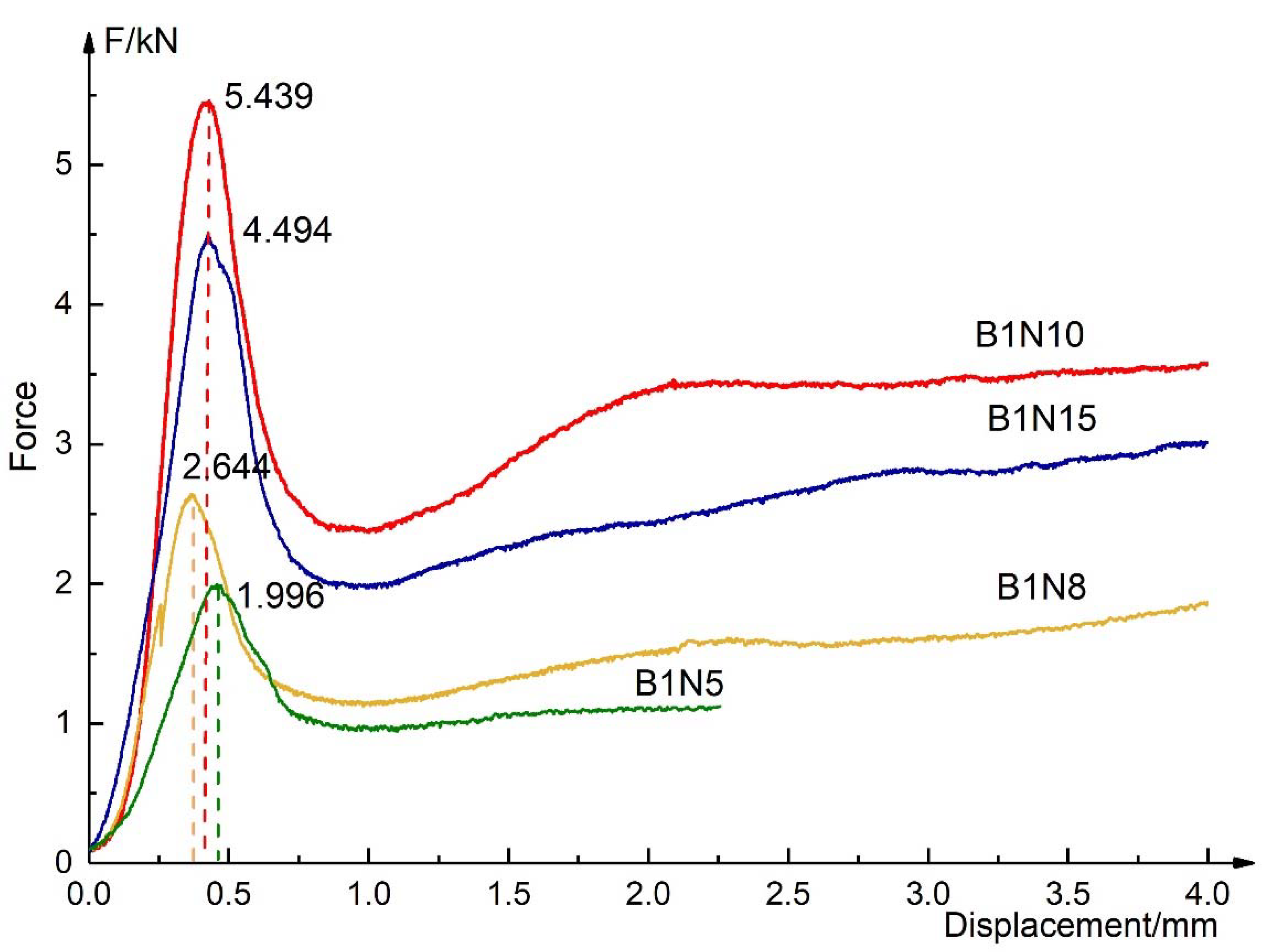
3.1. Test of Flatwise Compression Properties
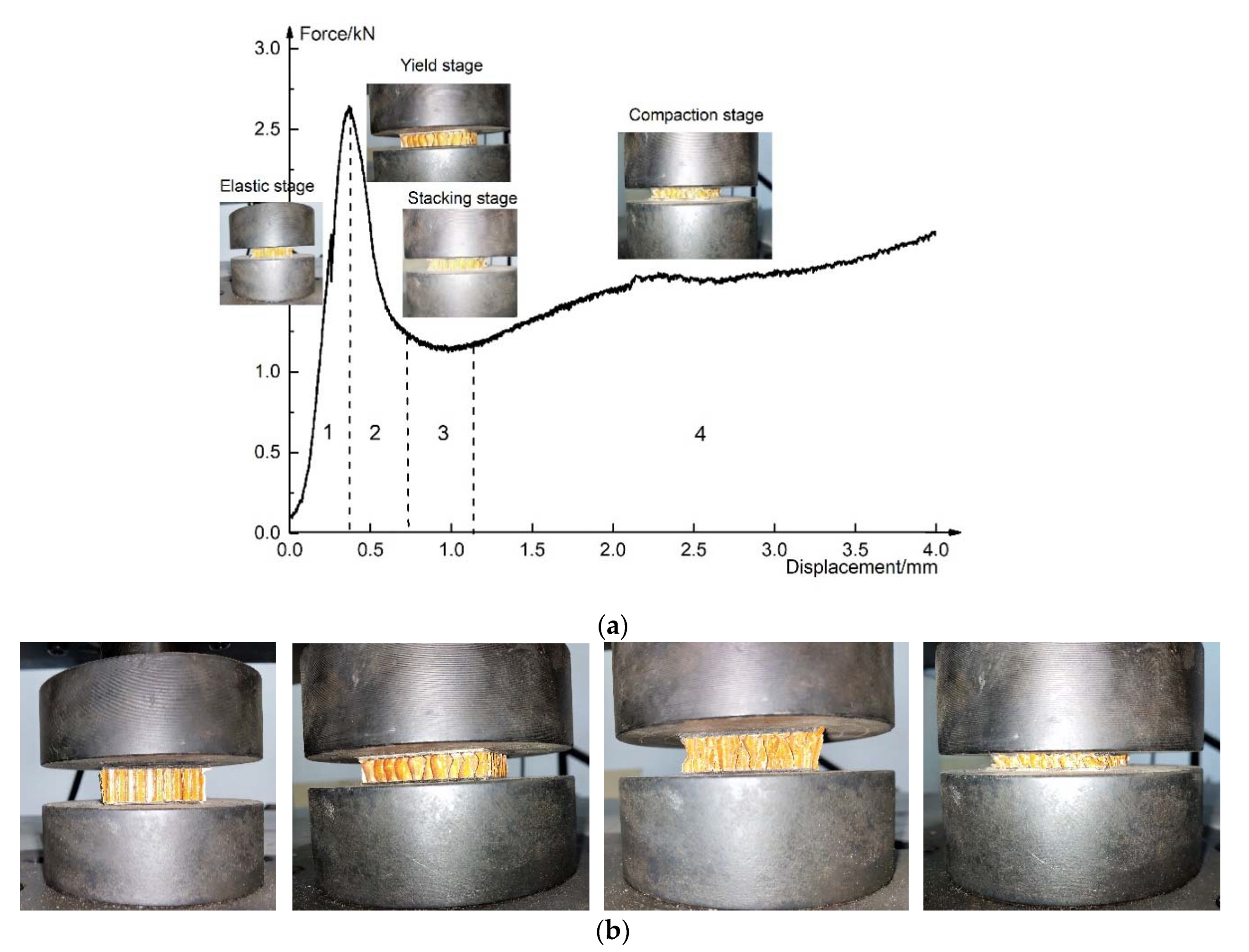
3.1.1. Failure Mode
- (1)
- The elastic stage; the honeycomb had no change almost, the specimens had no obvious deformation, and a crisp sound was heard in this stage, especially on the specimen B1N15. The sound comes from the damage of the honeycomb wall in the core layer. According to the experimental phenomenon, the damage of the honeycomb wall appeared at the later stage of the elastic stage, especially on the specimen B1N15 because of the larger height and height-thickness ratio of the honeycomb wall.
- (2)
- The yield stage; the honeycomb walls on the four sides of the specimen appeared with wrinkles at first, and the stress growth slowed down.
- (3)
- The stacking stage; the crackling sound of aramid paper extruding was heard from all of the specimens, and the honeycomb was gradually squeezed and compacted from top to bottom; at this stage, the stress began to drop.
- (4)
- The compaction stage; the honeycomb core was completely yielded, with the increase of the indenter’s displacement, the load began to rise slowly. After unloading, the upper sheet rose slowly, and the honeycomb had a spring shape. Although most of the flatwise compression bearing capacity was lost, the specimens’ shape basically remained.
3.1.2. Flatwise Compression Strength and Elastic Modulus
3.2. Test of Flexure Properties
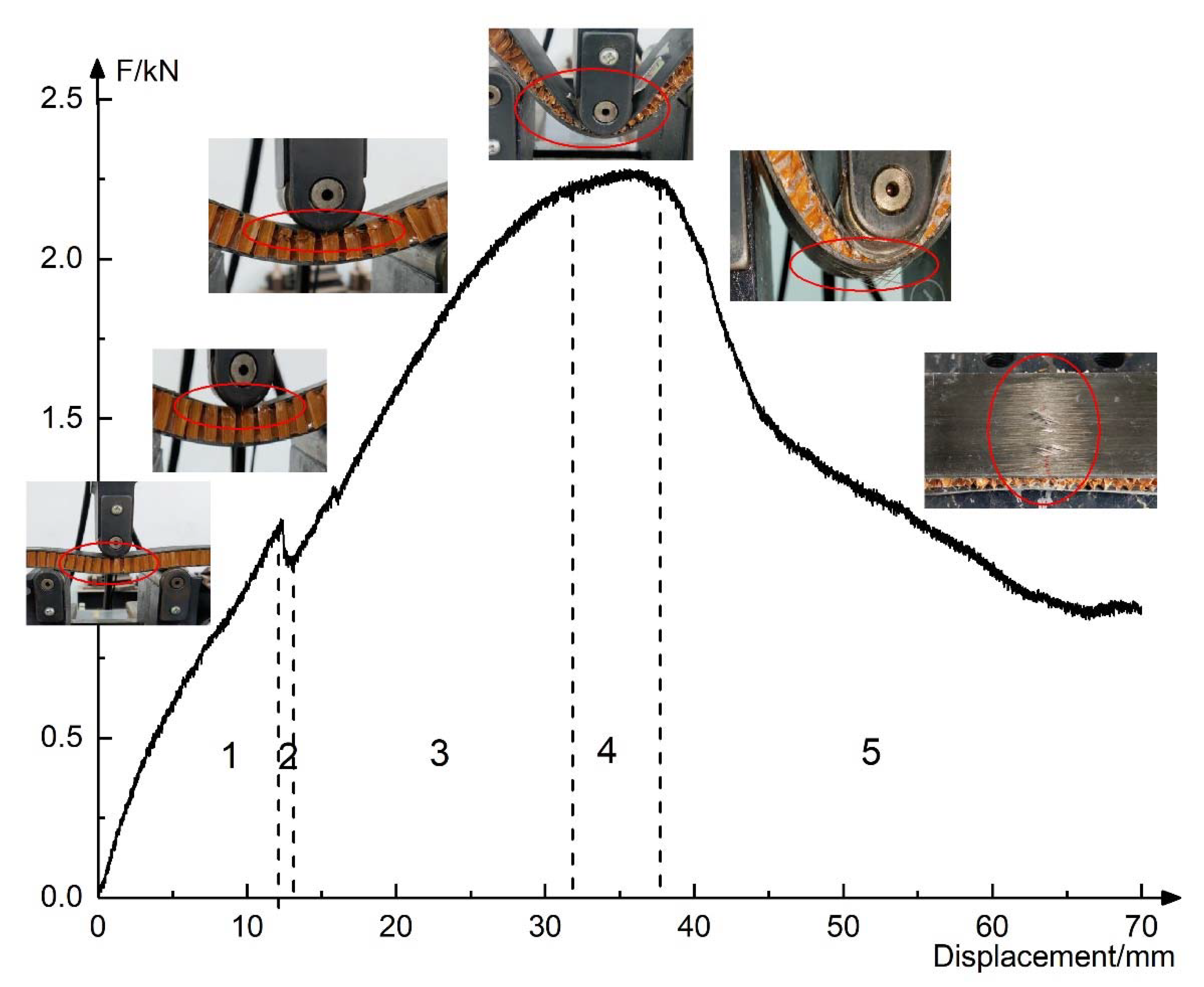
3.2.1. Failure Mode
- (1)
- The elastic stage. At this stage, the honeycomb had no obvious deformation.
- (2)
- The yielding stage. With the displacement increases, the load decreased slightly, and fold lines were found on the honeycomb wall, as shown in Figure 12, but the height and the shape of the honeycomb remains unchanged, accompanied by a slight origami sound.
- (3)
- The stacking stage. It was observed that the honeycomb walls were folded; the fold lines spread from bottom to top the middle of the specimens and spread from top to bottom at the support point, as shown in Figure 13. In this stage, the core layer and the sheet may be degummed, and the honeycomb of L-shaped specimens could be torn, resulting in a sudden drop of force, as shown in Figure 14.
- (4)
- The sheet bending resistance stage. In this stage, the honeycomb was folded into a spring shape and lost the out-plane support function to the upper and lower sheet, and then the honeycomb exits from the work and only played the role of connecting sheets.
- (5)
- The sheet broken stage. The resin of the upper sheet was layered and extruded into granules. The basalt fiber of the lower sheet was drawn out, and the crackling sound of the fiber pulling out or breaking was heard. With the increase of displacement, the force dropped sharply and then slowly. Finally, the basalt fiber sheets and the honeycomb were basically out of work, but because of the unbroken resin and the fiber in the sheets, after unloading, the specimens could still recover, and the structure remained complete and remained some strength.
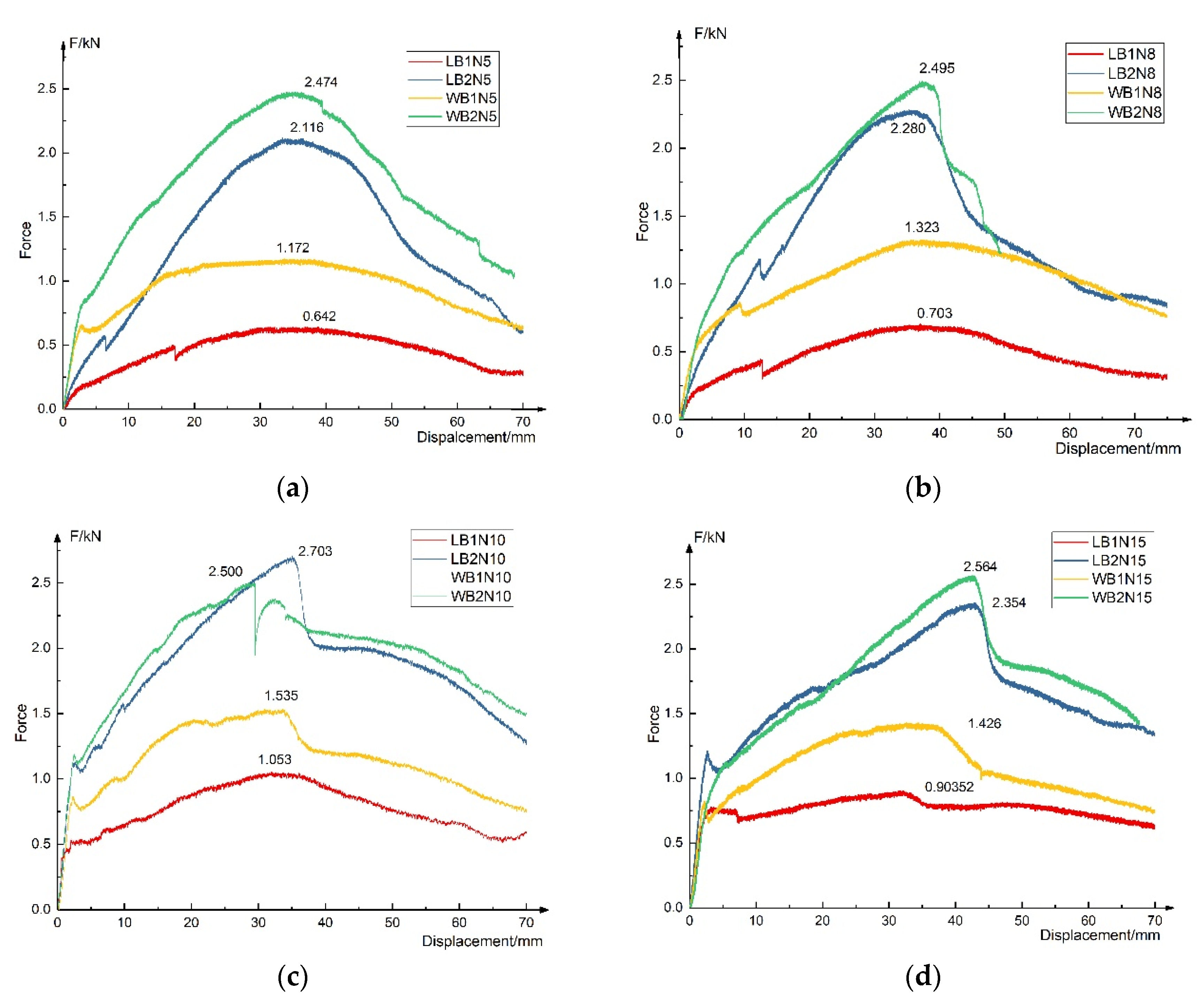
3.2.2. Shear Stress and Flexure Stiffness of the Core
- (1)
- In Equation (3), P is the mid-span load, W is the width of the specimen, h is the height of the honeycomb, and the calculation results of each specimen are shown in Figure 15.
- (a)
- In the specimens with the same direction and height, the shear stress of the core can be effectively increased by increasing the thickness of the fiber sheets.
- (b)
- In the same direction and with the same thickness of fiber sheet, the higher the honeycomb, the smaller the shear stress of honeycomb core, especially for the 15 mm high specimen, as shown in Figure 14. It can be inferred that, the higher the honeycomb, the greater the height thickness ratio of honeycomb, and the more likely the honeycomb wall will yield in the bending process, which will reduce the shear stress of honeycomb core.
- (c)
- The shear stress of the W-shaped specimen is higher than that of the L-shaped specimen with the same sheet thickness and honeycomb height beside the specimen WB2N10; the possible reason is the broken bonding layer between the sheet and core.
- (2)
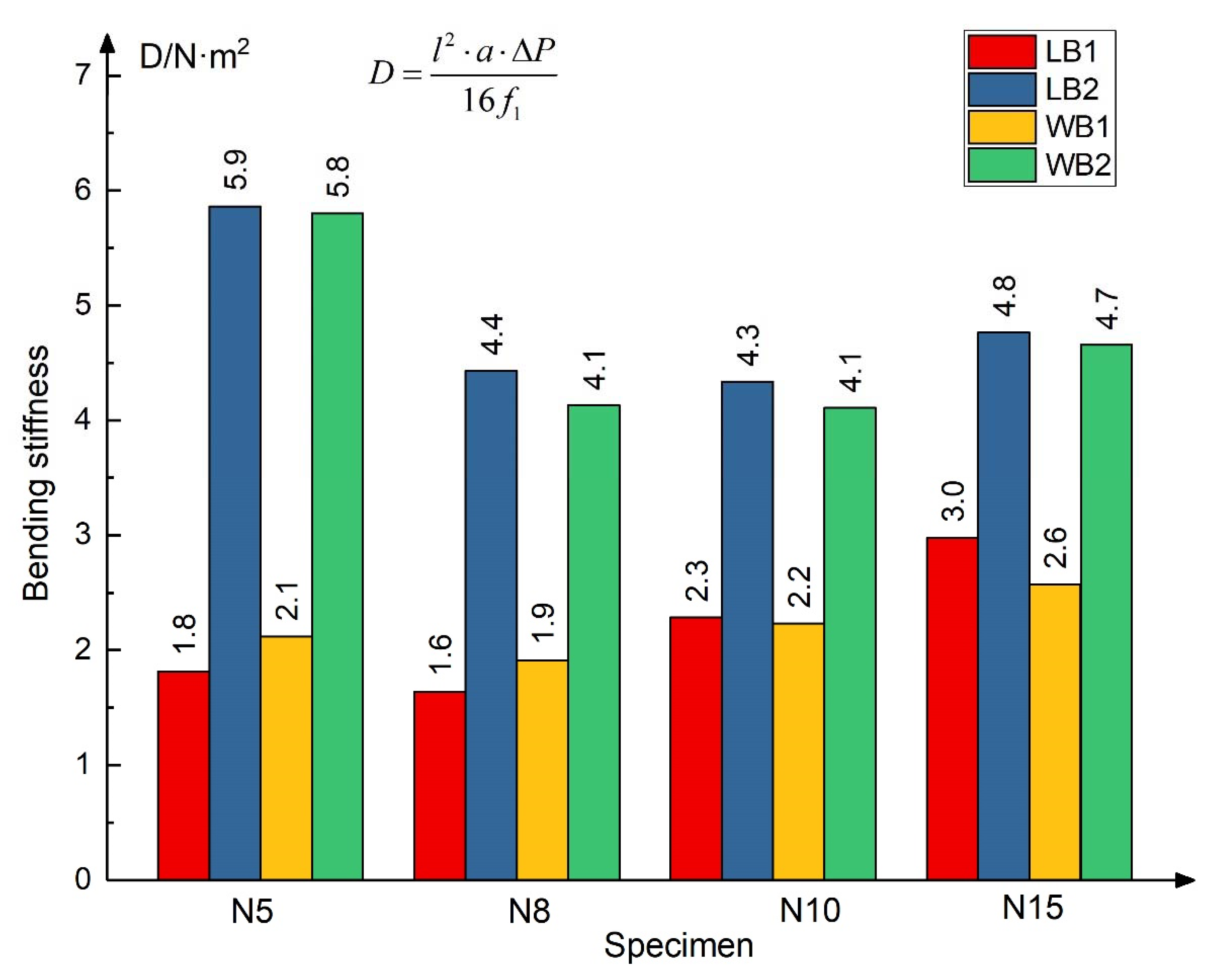
- The flexure stiffness of the structure is calculated according to Equation (4), where l is the span length, a is the overhanging length of the specimen, is the load increment value of the initial section of the curve, f1 is the deflection increment value of overhanging point (the average of the left and right points), and the calculation D of each specimen is shown in Figure 17.
- (a)
- The honeycomb direction has little influence on the flexure stiffness of the composite structure, and the difference between the flexure stiffness calculated by the specimens (red and yellow, blue and green) is within 15%. It can be considered that the L-type and W-type are at the same level; the possible reason is that the calculation of the flexure stiffness is measured in the elastic stage, and the honeycomb will not be broken at this stage.
- (b)
- The thickness increase of basalt fiber sheet can significantly improve the flexural stiffness of the structure, with a maximum increase of 323%, while changing the height of honeycomb has little effect on the flexural stiffness of the structure.
3.2.3. Influence of Basalt Fiber Sheet Thickness and Honeycomb Orientation
4. Conclusions
- (1)
- The strength of the compression specimen is greatly affected by the height of honeycomb. For the honeycomb core material with 0.05 mm thickness used in this experiment, the peak value of flat compression strength appears when the height of honeycomb is 10 mm. The high honeycomb core will lead to the premature yield of honeycomb, resulting in the drop of flat compression performance of the composite structure.
- (2)
- Three main factors affect the flexure properties: sheet thickness, honeycomb height, and honeycomb direction. Among them, the sheet thickness has the greatest influence on the flexure properties. The greater the thickness, the greater the flexure strength, the shear strength of the core, and the flexure stiffness of the structure. The influence of the honeycomb height on the flexure properties is complex. The effect on the bending strength of the structure is similar to that of the flatwise compression test, and it reaches the peak value at 10 mm, but it has a negative effect on the shear strength and flexure stiffness of the core. The flexure strength and core shear stress of the W-shaped specimen are greater than that of the L-shaped specimen and have little influence on the flexure stiffness.
- (3)
- No matter the sandwich structure under the flat pressure or bending condition, there is no shape fracture in the loading process. After unloading, the specimen can slowly recover its original shape. The fiber pulling out and fiber fracture of honeycomb crushing and basalt fiberboard can absorb the energy of loading and have good ductility.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pydah, A.; Batra, R.C. Blast loading of bumper shielded hybrid two-core Miura-ori/honeycomb core sandwich plates. Thin. Wall. Struct. 2018, 129, 45–57. [Google Scholar] [CrossRef]
- Giglio, M.; Gilioli, A.; Manes, A. Numerical investigation of a three-point bending test on sandwich panels with aluminum skins and Nomex™ honeycomb core. Comput. Mater. Sci. 2012, 56, 69–78. [Google Scholar] [CrossRef]
- Foo, C.C.; Chai, G.B.; Seah, L.K. A model to predict low-velocity impact response and damage in sandwich composites. Compos. Sci. Technol. 2008, 68, 1348–1356. [Google Scholar] [CrossRef]
- Wang, B.; Wu, L.Z.; Ma, L. Low-velocity impact characteristics and residual tensile strength of carbon fiber composite lattice core sandwich structures. Compos. Part B Eng. 2011, 42, 891–897. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, M.; Stocchi, A. Mechanical behaviors of carbon fiber composite sandwich columns with three-dimensional honeycomb cores under in-plane compression. Compos. Part B Eng. 2014, 60, 350–358. [Google Scholar] [CrossRef]
- He, W.T.; Liu, J.X.; Wang, S.Q. Low-velocity impact response and post-impact flexural behaviour of composite sandwich structures with corrugated cores. Compos. Struct. 2018, 189, 37–53. [Google Scholar] [CrossRef]
- Zaini, E.S.; Azaman, M.D.; Jamali, M.S.; Ismail, K.A. Synthesis and characterization of natural fiber reinforced polymer composites as core for honeycomb core structure: A review. J. Sandw. Struct. Mater. 2020, 22, 525–550. [Google Scholar] [CrossRef]
- Monaldo, E.; Nerilli, F.; Vairo, G. Basalt-based fiber-reinforced materials and structural applications in civil engineering. Compos. Struct. 2019, 214, 246–263. [Google Scholar] [CrossRef]
- Shen, D.; Yang, Q.; Jiao, Y.; Cui, Z.; Zhang, J. Experimental investigations on reinforced concrete shear walls strengthened with basalt fiber-reinforced polymers under cyclic load. Constr. Build. Mater. 2017, 136, 217–229. [Google Scholar] [CrossRef]
- Li, C.C.; Gao, D.Y.; Wang, Y.L.; Tang, J.Y. Effect of high temperature on the bond performance between basalt fibre reinforced polymer (BFRP) bars and concrete. Constr. Build. Mater. 2017, 141, 44–51. [Google Scholar] [CrossRef]
- Liu, H.X.; Yang, J.W.; Wang, X.Z. Bond behavior between BFRP bar and recycled aggregate concrete reinforced with basalt fiber. Constr. Build. Mater. 2017, 135, 477–483. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, L.J.; Gao, W.Y.; Zhen, B.; Lu, Z.D. Seismic retrofit of square reinforced concrete columns using basalt and carbon fiber-reinforced polymer sheets: A comparative study. Compos. Struct. 2017, 162, 294–307. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber—A review. J. Text. Inst. 2016, 107, 923–937. [Google Scholar] [CrossRef]
- Rupesh, K.M.; Rahul, K.S.; Rajesh, P.; Roopesh, S. Natural fibre reinforced composite materials: Environmentally better life cycle assessment—A case study. Mater. Today 2020. [Google Scholar] [CrossRef]
- Dhand, V.; Mittal, G.; Rhee, K.Y.; Park, S.J.; Hui, D. A short review on basalt fiber reinforced polymer composites. Compos. Part B Eng. 2015, 73, 166–180. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Singha, K.A. Short review on basalt fiber. Int. J. Text. Sci. 2012, 1, 19–28. [Google Scholar]
- Wei, B.; Cao, H.; Song, S. Environmental resistance and mechanical performance of basalt and glass fibers. Mat. Sci. Eng. A Struct. 2010, 527, 4708–4715. [Google Scholar] [CrossRef]
- Mingchao, W.; Zuoguang, Z.; Yubin, L.; Min, L.; Zhijie, S. Chemical durability and mechanical properties of alkali-proof basalt fiber and its reinforced epoxy composites. J. Reinf. Plast. Compos. 2008, 27, 393–407. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Chen, M.; Lei, L.; Wu, Z. Effect of SiO2, Al2O3 on heat resistance of basalt fiber. Thermochim. Acta 2018, 660, 56–60. [Google Scholar] [CrossRef]
- Yang, C.X.; Li, Q.M. Structural optimisation for the collapse zone of a railway vehicle. Int. J. Mech. Sci. 2020, 165, 105201. [Google Scholar] [CrossRef]
- Aminanda, Y.; Castanié, B.; Barrau, J.J. Experimental analysis and modeling of the crushing of honeycomb core. Appl. Compos. Mater. 2005, 12, 213–227. [Google Scholar] [CrossRef]
- Amélie, K.; Samuel, R.; Christophe, B. Experimental study of sandwich structures as armour against medium-velocity impacts. Int. J. Impact. Eng. 2013, 61, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.M.; Ma, J.X. Basalt fiber modified with lanthanum-ethylenediaminetetraacetic acid as potential reinforcement of cyanate matrix composites. Appl. Surf. Sci. 2019, 464, 636–643. [Google Scholar] [CrossRef]
- Elammaran, J.; Govind, A.N.; KokHeng, S. Investigation of the dielectric properties of natural fibre and conductive filler reinforced polymer composites. Mater. Today Proc. 2020, 22, 162–171. [Google Scholar] [CrossRef]
- Amor, I.B.; Rekik, H.; Kaddami, H.; Raihane, M.; Arous, M.; Kallel, A. Studies of dielectric relaxation in natural fiber-polymer composites. J. Electrostat. 2009, 67, 717–722. [Google Scholar] [CrossRef]
- Triki, A.; Guicha, M.; Hassen, M.B.; Arous, M.; Fakhfakh, Z. Studies of dielectric relaxation in natural fibres reinforced unsaturated polyester. J. Mater. Sci. 2011, 46, 3698–3707. [Google Scholar] [CrossRef]
- Al-Oqla, F.M.; Sapuan, S.M. Natural fiber reinforced polymer composites in industrial applications: Feasibility of date palm fibers for sustainable automotive industry. J. Clean. Prod. 2014, 66, 347–354. [Google Scholar] [CrossRef]
- Wu, X.R.; Yu, H.J.; Guo, L.C. Experimental and numerical investigation of static and fatigue behaviors of composites honeycomb sandwich structure. Compos. Struct. 2019, 213, 165–172. [Google Scholar] [CrossRef]
- Giglio, M.; Manes, A.; Gilioli, A. Investigations on sandwich core properties through an experimental–numerical approach. Compos. Part B Eng. 2012, 43, 361–374. [Google Scholar] [CrossRef]
- Jaafar, M.; Atlati, S.; Makich, H. A 3D FE Modeling of Machining Process of Nomex® Honeycomb Core: Influence of the Cell Structure Behaviour and Specific Tool Geometry. Procedia CIRP 2017, 58, 505–510. [Google Scholar] [CrossRef]
- Aktay, L.; Johnson, A.F.; Bernd, H. Numerical modeling of honeycomb core crush behaviour. Eng. Fract. Mech. 2008, 75, 2616–2630. [Google Scholar] [CrossRef]
- ASTM C365-03, Standard Test Method for Flatwise Compressive Properties of Sandwich Core. West Conshohocken (PA): ASTM International. 2011. Available online: https://www.astm.org/Standards/C365.htm (accessed on 1 January 2011).
- GB/T 1453-2005, Test Method for Flatwise Compression Properties of Sandwich Constructions or Cores. 2005. Available online: https://webstore.ansi.org/standards/spc/gb14532005 (accessed on 1 December 2005).
- ASTM C393/C393M-2011, Standard Test Method for Core Shear Properties of Sandwich Constructions by Beam Flexure. West Conshohocken (PA): ASTM International. 2011. Available online: http://www.sophiahightech.com/astm-c-393-testing-fixture-core-shear-properties-of-sandwich-constructions-by-beam-flexure/ (accessed on 1 January 2011).
- GB/T 1453-2005, Test Method for Flexural Properties of Sandwich Constructions. 2005. Available online: https://www.chinesestandard.net/PDF/English.aspx/GBT1456-2005 (accessed on 1 December 2005).
- Roy, R.; Park, S.J.; Kweon, J.H. Characterization of Nomex honeycomb core constituent material mechanical properties. Compos. Struct. 2014, 117, 255–266. [Google Scholar] [CrossRef]












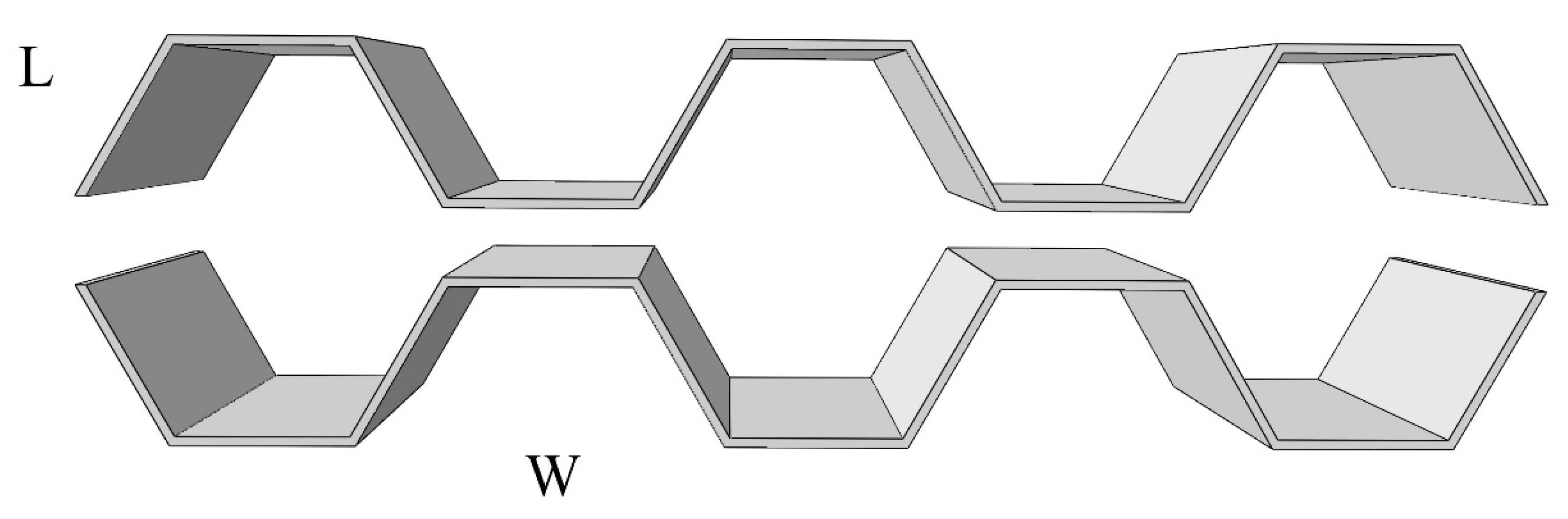
| Parameter | Basalt Fiber | Glass Fiber | Quartz Fiber | Nomex Honeycomb |
|---|---|---|---|---|
| 2.61 | 4~7 | 3.78 | 1.07 | |
| 0.005 | 0.0026~0.0068 | 0.0002 | 0.0028 |
| Properties | Basalt Plate | Basalt Fiber | Resin | Honeycomb |
|---|---|---|---|---|
| Density (g/cm3) | 1.6 | 2.80 | 1.04 | 0.048 |
| Tensile strength (MPa) | ≥1000 | 3400–4500 | 78 | – |
| Elastic modulus (GPa) | ≥50 | 88–91 | 3.65 | – |
| Elongation percentage (%) | 2.6 | 4.7 | 7.4 | – |
| Flexural strength (MPa) | – | – | 146 | – |
| Flexural modulus (GPa) | – | – | 3.35 | – |
| Compressive strength (MPa) | – | – | – | 1.5–2.5 |
| Shear strength (MPa) | – | – | – | 0.5–1.5 |
| Kind | Sheet Size L × W (mm) | Sheet Thickness s (mm) | Core Height h (mm) | Total Thickness H (mm) | Number |
|---|---|---|---|---|---|
| B1N5 | 50 × 50 | 1.2 | 5 | 7.4 | 3 |
| B1N8 | 50 × 50 | 1.2 | 8 | 10.4 | 3 |
| B1N10 | 50 × 50 | 1.2 | 10 | 12.4 | 3 |
| B1N15 | 50 × 50 | 1.2 | 15 | 17.4 | 3 |
| Type | Panel Size W × L (mm) | Sheet Thickness s (mm) | Core Height h (mm) | Total Thickness H (mm) | Number |
|---|---|---|---|---|---|
| LB1N5 | 50 × 350 | 1.2 | 5 | 7.4 | 3 |
| WB1N5 | 50 × 350 | 1.2 | 5 | 7.4 | 3 |
| LB1N10 | 50 × 350 | 1.2 | 10 | 12.4 | 3 |
| WB1N10 | 50 × 350 | 1.2 | 10 | 12.4 | 3 |
| LB1N8 | 50 × 350 | 1.2 | 8 | 10.4 | 3 |
| WB1N8 | 50 × 350 | 1.2 | 8 | 10.4 | 3 |
| LB1N15 | 50 × 350 | 1.2 | 15 | 17.4 | 3 |
| WB1N15 | 50 × 350 | 1.2 | 15 | 17.4 | 3 |
| LB2N5 | 50 × 350 | 1.4 | 5 | 7.8 | 3 |
| WB2N5 | 50 × 350 | 1.4 | 5 | 7.8 | 3 |
| LB2N10 | 50 × 350 | 1.4 | 10 | 12.8 | 3 |
| WB2N10 | 50 × 350 | 1.4 | 10 | 12.8 | 3 |
| LB2N8 | 50 × 350 | 1.4 | 8 | 10.8 | 3 |
| WB2N8 | 50 × 350 | 1.4 | 8 | 10.8 | 3 |
| LB2N15 | 50 × 350 | 1.4 | 15 | 17.8 | 3 |
| WB2N15 | 50 × 350 | 1.4 | 15 | 17.8 | 3 |
| Span L (mm) | Overhanging Length a (mm) | Width of Indenter B (mm) | Width of Supports B’ (mm) | Width of Specimen W (mm) |
|---|---|---|---|---|
| 120 | 60 | 10 | 10 | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Ma, J. Experimental Study on Mechanical Properties of the Sandwich Composite Structure Reinforced by Basalt Fiber and Nomex Honeycomb. Materials 2020, 13, 1870. https://doi.org/10.3390/ma13081870
Li Z, Ma J. Experimental Study on Mechanical Properties of the Sandwich Composite Structure Reinforced by Basalt Fiber and Nomex Honeycomb. Materials. 2020; 13(8):1870. https://doi.org/10.3390/ma13081870
Chicago/Turabian StyleLi, Zongwen, and Jianxun Ma. 2020. "Experimental Study on Mechanical Properties of the Sandwich Composite Structure Reinforced by Basalt Fiber and Nomex Honeycomb" Materials 13, no. 8: 1870. https://doi.org/10.3390/ma13081870
APA StyleLi, Z., & Ma, J. (2020). Experimental Study on Mechanical Properties of the Sandwich Composite Structure Reinforced by Basalt Fiber and Nomex Honeycomb. Materials, 13(8), 1870. https://doi.org/10.3390/ma13081870




