Magnetic Domain-Wall Induced Electric Polarization in NdCrO3 Polycrystalline Ceramic
Abstract
:1. Introduction
2. Experiment
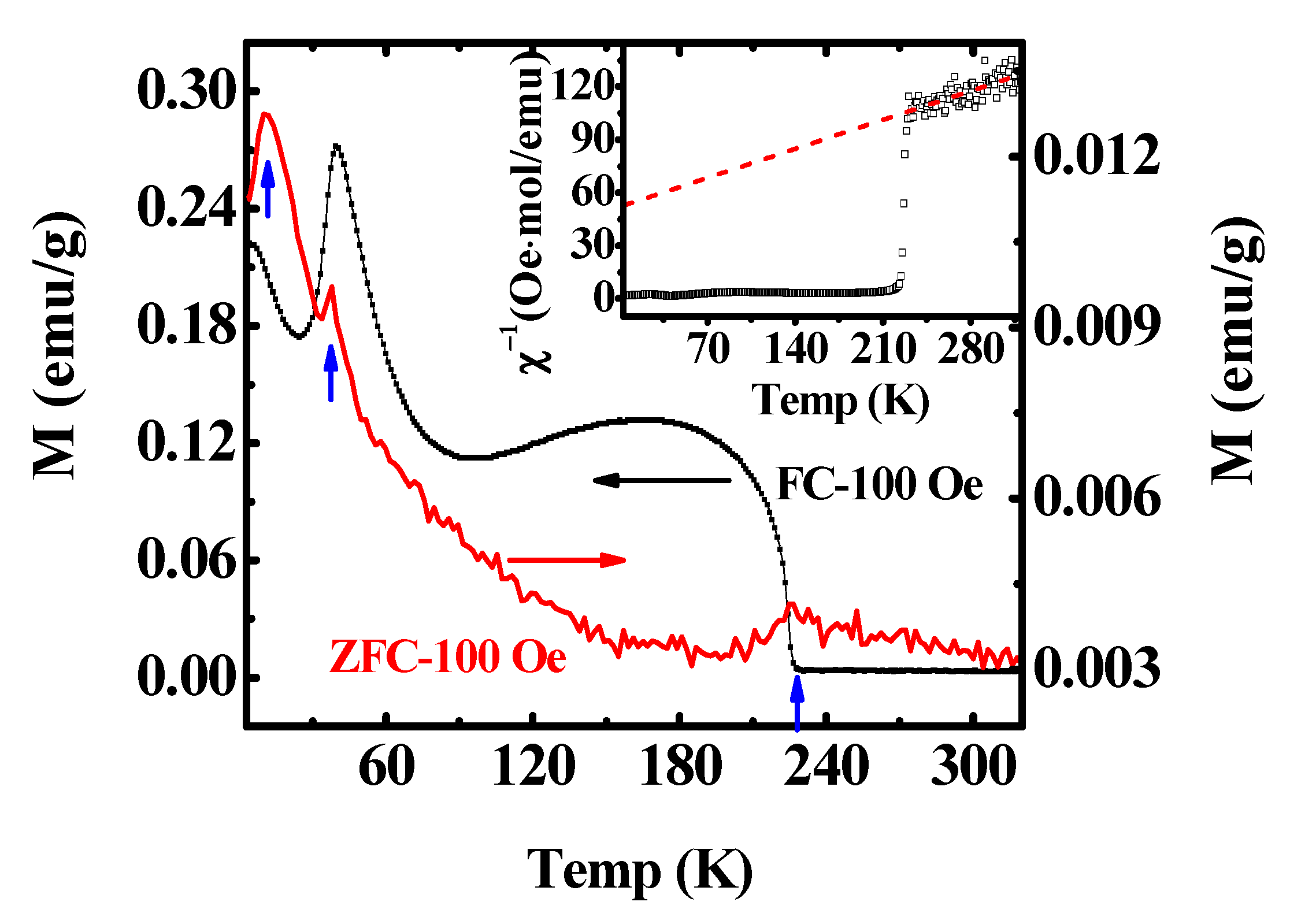
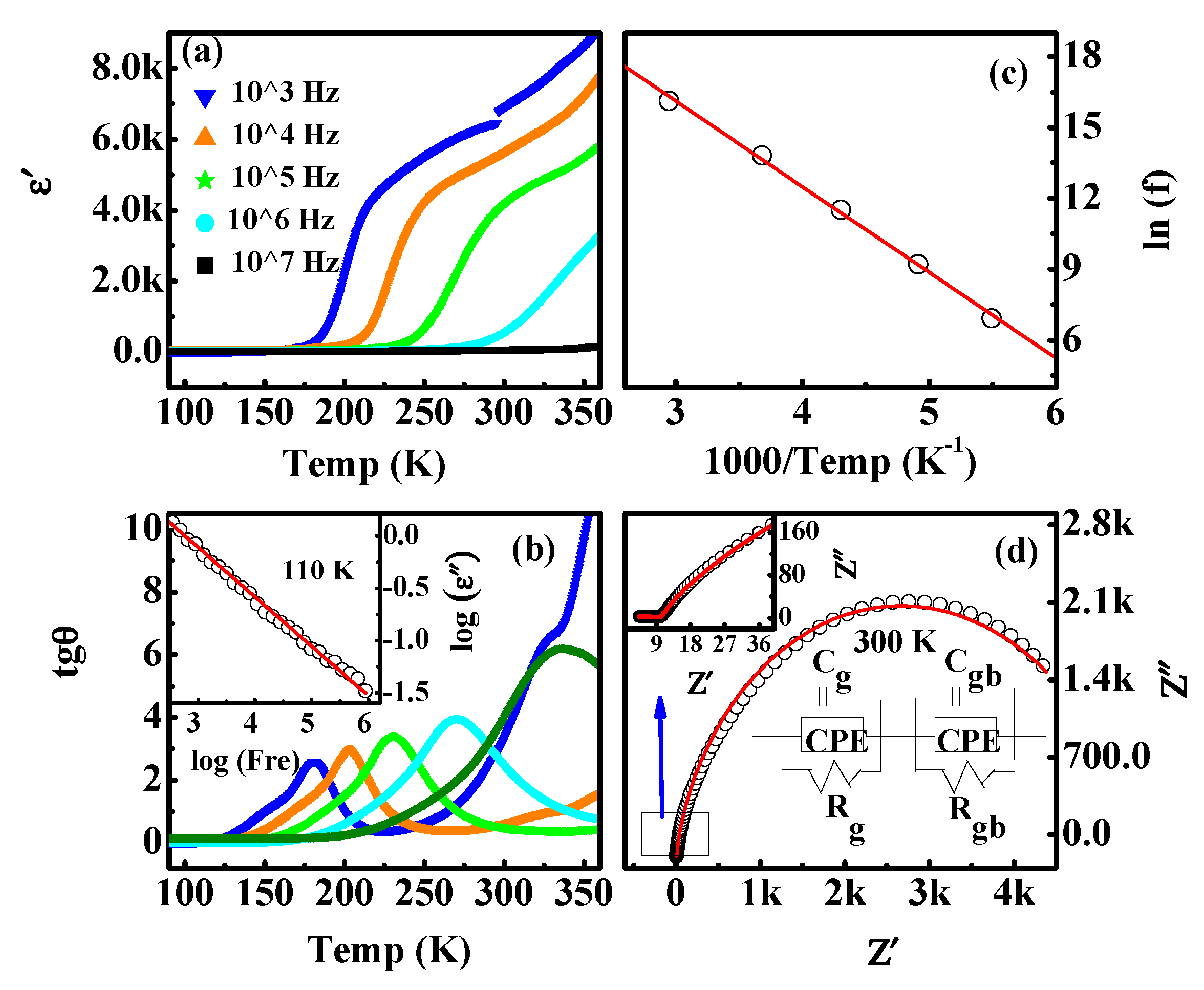
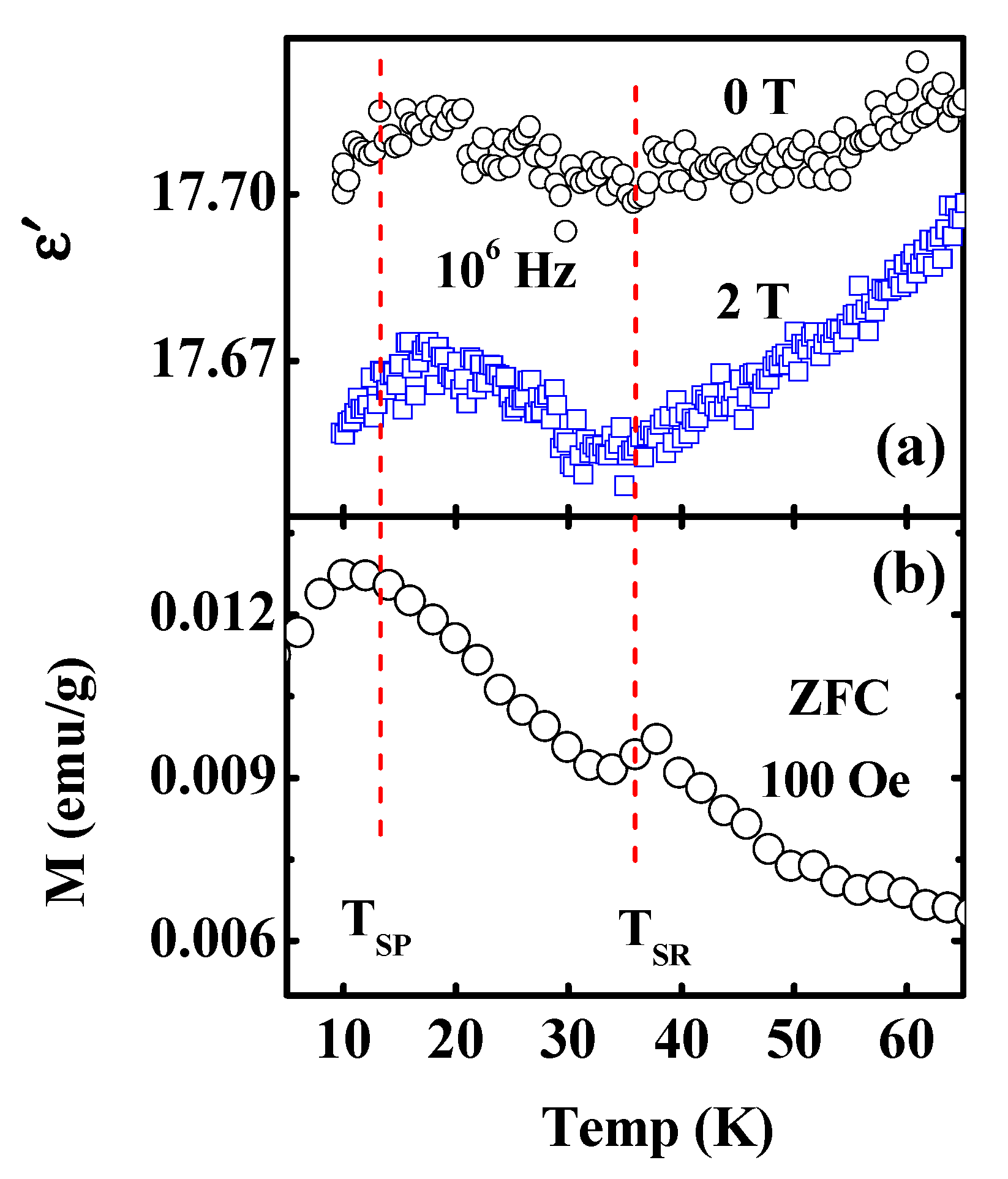
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and prospects in thin films. Nat. Mater. 2007, 6, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 2003, 299, 1719–1722. [Google Scholar] [CrossRef] [PubMed]
- Hill, N.A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 2000, 104, 6694–6709. [Google Scholar] [CrossRef]
- Arima, T.H. Ferroelectricity induced by proper-screw type magnetic order. J. Phys. Soc. Jpn. 2007, 76, 073702. [Google Scholar] [CrossRef]
- Eerenstein, W.; Mathur, N.; Scott, J.F. Multiferroic and magnetoelectric materials. Nature 2006, 442, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef] [PubMed]
- Yanez-Vilar, S.; Mun, E.; Zapf, V.; Ueland, B.; Gardner, J.S.; Thompson, J.; Singleton, J.; Sanchez-Andujar, M.; Mira, J.; Biskup, N.; et al. Multiferroic behavior in the double-perovskite LuMnCoO. Phys. Rev. B 2011, 84, 134427. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.Y.; Zhao, H.J.; Zhang, W.Q.; Chen, X.M. Magnetic domain wall induced ferroelectricity in double perovskites. Appl. Phys. Lett. 2015, 106, 152901. [Google Scholar] [CrossRef]
- Yang, Y.; Xiang, H.; Zhao, H.; Stroppa, A.; Zhang, J.; Cao, S.; Iniguez, J.; Bellaiche, L.; Ren, W. Improper ferroelectricity at antiferromagnetic domain walls of perovskite oxides. Phys. Rev. B 2017, 96, 104431. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.X.; Sun, W.; Zhang, G.B.; Cheng, Z.X.; Wang, Y.X. Magnetic domain-wall induced ferroelectric polarization in rare-earth orthoferrites AFeO3 (A= Lu, Y, Gd): First-principles calculations. J. Mater. Chem. C 2019, 7, 10059–10065. [Google Scholar] [CrossRef]
- Sahu, J.R.; Serrao, C.R.; Rao, C.N.R. Modification of the multiferroic properties of YCrO3 and LuCrO3 by Mn substitution. Solid State Commun. 2008, 145, 52–55. [Google Scholar] [CrossRef]
- Dahal, J.N.; Syed Ali, K.S.; Mishra, S.R.; Alam, J. Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn). Magnetochemistry 2018, 4, 54. [Google Scholar] [CrossRef] [Green Version]
- Rajeswaran, B.; Khomskii, D.I.; Zvezdin, A.K.; Rao, C.N.R.; Sundaresan, A. Field-induced polar order at the Néel temperature of chromium in rare-earth orthochromites: Interplay of rare-earth and Cr magnetism. Phys. Rev. B 2012, 86, 214409. [Google Scholar] [CrossRef] [Green Version]
- Preethi Meher, K.R.S.; Wahl, A.; Maignan, A.; Martin, C.; Lebedev, O.I. Observation of electric polarization reversal and magnetodielectric effect in orthochromites: A comparison between LuCrO3 andErCrO3. Phys. Rev. B 2014, 89, 144401. [Google Scholar] [CrossRef]
- Ghosh, A.; Pal, A.; Dey, K.; Majumdar, S.; Giri, S. A typical multiferroicity of HoCrO3 in bulk and film geometry. J. Mater. Chem. C 2015, 3, 4162. [Google Scholar] [CrossRef]
- Ghosh, A.; Dey, K.; Chakraborty, M.; Majumdar, S.; Giri, S. Polar octahedral rotations, cation displacement and ferroelectricity in multiferroic SmCrO3. Europhys. Lett. 2014, 107, 47012. [Google Scholar] [CrossRef]
- Gupta, P.; Poddar, P. Using Raman and dielectric spectroscopy to elucidate the spin phonon and magnetoelectric coupling in DyCrO3 nanoplatelets. RSC Adv. 2015, 5, 10094–10101. [Google Scholar] [CrossRef]
- Meher, K.R.S.P.; Martin, C.; Caignaert, V.; Damay, F.; Maignan, A. Multiferroics and magnetoelectrics: A comparison between some chromites and cobaltites. Chem. Mater. 2014, 26, 830–836. [Google Scholar] [CrossRef]
- Indra, A.; Dey, K.; Midya, A.; Mandal, P.; Gutowski, O.; Rütt, U.; Majumdar, S.; Giri, S. Erratum: Magnetoelectric coupling and exchange bias effects in multiferroic NdCrO3. J. Phys. Condens. Matter 2016, 28, 166005. [Google Scholar] [CrossRef]
- Yin, L.H.; Yang, J.; Tong, P.; Luo, X.; Park, C.B.; Shin, K.W.; Song, W.H.; Dai, J.M.; Kim, K.H.; Zhu, X.B.; et al. Role of rare earth ions in the magnetic, magnetocaloric and magnetoelectric properties of RCrO3 (R = Dy, Nd, Tb, Er) crystals. J. Mater. Chem. C 2016, 4, 11198–111204. [Google Scholar] [CrossRef]
- Shanker, J.; Buchi Suresh, M.; Narsinga Rao, G.; Suresh Babu, D. Colossal dielectric, relaxor ferroelectric, diamagnetic and weak ferromagnetic properties of NdCrO3 perovskite nanoparticles. J. Mater. Sci. 2019, 54, 5595–5604. [Google Scholar] [CrossRef]
- Hornreich, R.M.; Komet, Y.; Nolan, R.; Wanklyn, B.M.; Yaeger, I. Magneto-optical and magnetization studies in the rare-earth orthochromites. VI. NdCrO3. Phys. Rev. B 1975, 12, 5094. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, S.W.; Zhang, X.; Zhao, Z.K.; Shao, Y.P.; Yao, R.; Yang, M.M.; Gao, Y.B. Negative magnetization, dielectric and magnetodielectric properties of EuCrO3. Mater. Res. Express 2019, 6, 026101. [Google Scholar] [CrossRef]
- Du, Y.; Cheng, Z.X.; Wang, X.L.; Dou, S.X. Structure, magnetic, and thermal properties of Nd1-xLaxCrO3 (0 <= x <= 1.0). J. Appl. Phys. 2000, 108, 093914. [Google Scholar] [CrossRef] [Green Version]
- Shamir, N.; Shaked, H.; Shtrikman, S. Magnetic structure of some rare-earth orthochromites. Phys. Rev. B 1981, 24, 6642. [Google Scholar] [CrossRef]
- Lufaso, M.W.; Mugavero, S.J.; GemmillY, W.R.; Lee, Y.; Vogt, T.; ZurLoye, H.C. Pressure-and temperature-dependent X-ray diffraction studies of NdCrO3. J. Alloys Compd. 2007, 433, 91–96. [Google Scholar] [CrossRef]
- Hornreich, R. Magnetic interactions and weak ferromagnetism in the rare-earth orthochromites. J. Magn. Magn. Mater. 1978, 7, 280–285. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.W.; Zhang, X.; Zhang, L.L.; Yao, R.; Rao, G.H. Reversals of magnetization and exchange-bias in perovskite chromite YbCrO3. J. Alloys Compd. 2016, 662, 268–271. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Chandler, D. Vibrational dephasing and frequency shifts of polyatomic molecules in solution. J. Chem. Phys. 1982, 76, 2296–2314. [Google Scholar] [CrossRef]
- Bidault, O.; Goux, P.; Kchikech, M.; Belkaoumi, M.; Maglione, M. Space-charge relaxation in perovskites. Phys. Rev. B 1994, 49, 7868. [Google Scholar] [CrossRef]
- Von Hippel, A.R. Dielectrics and Waves; MIT Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Idrees, M.; Nadeem, M.; Atif, M.; Siddique, M.; Mehmood, M.; Hassan, M.M. Origin of colossal dielectric response in LaFeO3. Acta. Mater. 2011, 59, 1338–1345. [Google Scholar] [CrossRef]
- Wang, S.W.; Zhang, X.; Yao, R.; Fan, L.G.; Zhou, H.Y. High-Temperature Dielectric Relaxation Behaviors in Mn3O4 Polycrystals. Materials 2019, 12, 4026. [Google Scholar] [CrossRef] [PubMed] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Bai, Y.; Zhang, X.; Fan, L.; Zhou, H. Magnetic Domain-Wall Induced Electric Polarization in NdCrO3 Polycrystalline Ceramic. Materials 2020, 13, 1904. https://doi.org/10.3390/ma13081904
Wang S, Bai Y, Zhang X, Fan L, Zhou H. Magnetic Domain-Wall Induced Electric Polarization in NdCrO3 Polycrystalline Ceramic. Materials. 2020; 13(8):1904. https://doi.org/10.3390/ma13081904
Chicago/Turabian StyleWang, Songwei, Yang Bai, Xin Zhang, Liguo Fan, and Huaiying Zhou. 2020. "Magnetic Domain-Wall Induced Electric Polarization in NdCrO3 Polycrystalline Ceramic" Materials 13, no. 8: 1904. https://doi.org/10.3390/ma13081904
APA StyleWang, S., Bai, Y., Zhang, X., Fan, L., & Zhou, H. (2020). Magnetic Domain-Wall Induced Electric Polarization in NdCrO3 Polycrystalline Ceramic. Materials, 13(8), 1904. https://doi.org/10.3390/ma13081904



