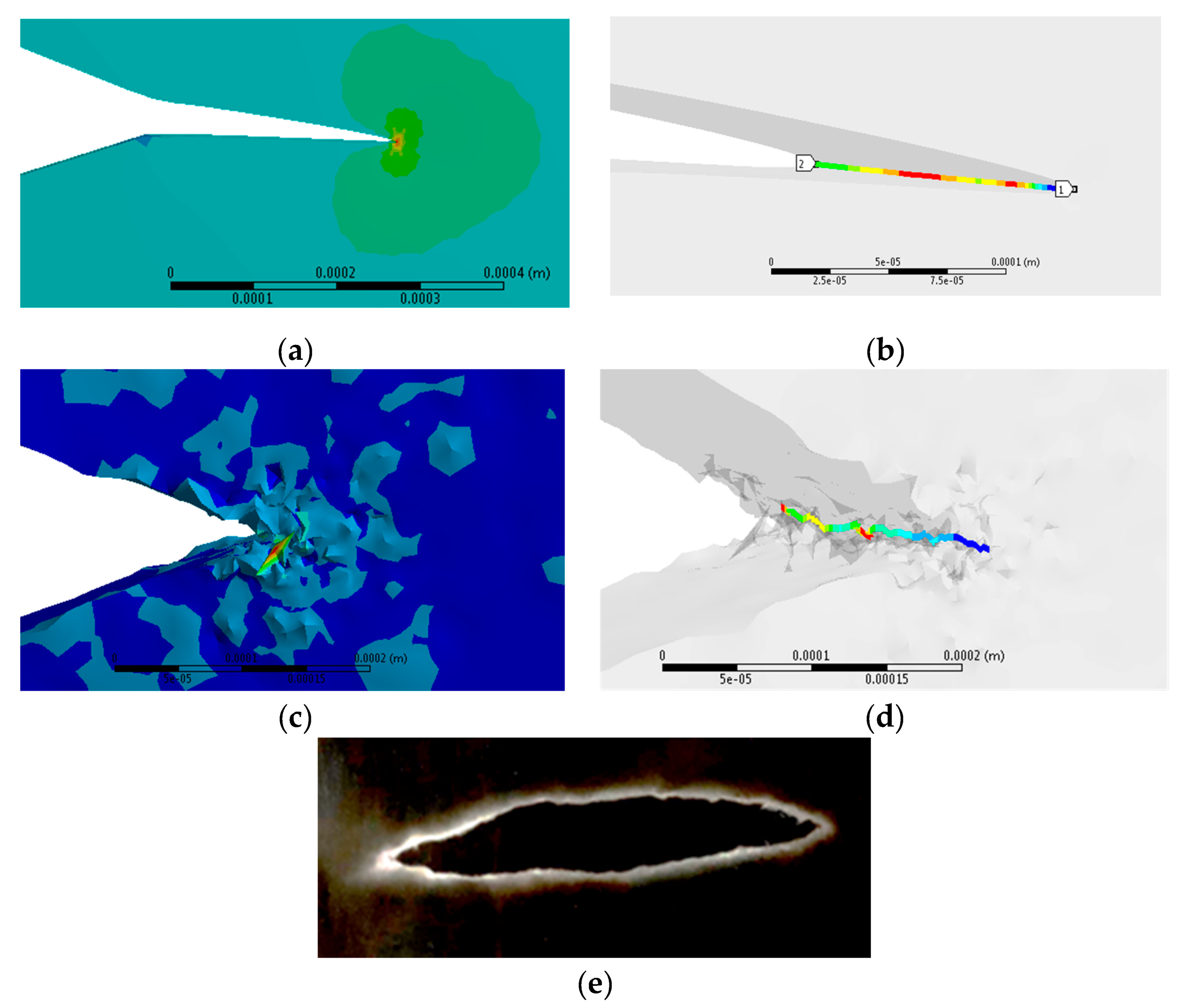
1. Introduction
In recent years, significant advances have been made in the development of new criteria that allows to explain the emergence, evolution, and propagation of cracks in materials. The fracture mechanics within the framework of linear and no-lineal mechanics is based on Griffith’s theory, which considers the extreme balance of stress applied in a crack or a defect of critical length [
1,
2,
3]. Linear fracture mechanics treats a fractured body as a structure, and all the attention is focused on the small area adjacent to the tip of the crack. We denote that this theory is applicable to materials such as glass, but metals have the property of being significantly deformed in the plastic range, and considering this plasticity is a complex problem. The objective of this work is focused on establishing the complex state of stresses that arises at the tip of the crack. High strength steels are currently used for manufacturing pipelines in order to have the best safety conditions in the transport of gases and fuels [
4,
5]. However, serious accidents may occur during its operation if there are porosities in the material, because cavities and micro discontinuities can be generated in the material structure when it is subjected to a high internal pressure. The most probable mechanism in the formation of fractures is usually due to the deceleration of the dislocations groups in the grain boundaries in combination with the diffusion of vacancies. The micro discontinuities and micro fractures will eventually produce a crack whose propagation will cause fragmentation of the body.
The analysis of defects and cracks in metal plates, as well as their causes, has been widely studied. In some cases, hydrogen diffusion can produce embrittlement and can be associated with stress-corrosion cracking [
6,
7,
8]. In other cases, hydrogen bubbles can appear; they are cavities below the surface of the material due to excessive internal pressure and can be the origin of hydrogen-induced cracking [
9,
10,
11]. Hydrogen embrittlement commonly occurs in low resistance steels with magnitudes less than 80 ksi of yield strength [
12], although there are also cases in aluminum [
9,
10,
11,
13].
The presence of cavities within the structure of a gas or oil pipe generates serious problems related to the combination of mechanical as well as physical and chemical fields. If the metal is used to withstand internal pressures as in transport pipelines, there are serious conditions for the formation and the growth of cavities due to the internal pressures. The aim of this study is to propose a new theoretical analysis of this failure by solving the Laplace’s equation, which is relevant since these cavities create a complex stress states that can induce fracture of the body [
14,
15,
16,
17,
18,
19,
20,
21]. Plastic deformation is developed in several stages and at multiple levels. However, the physical foundation of this process was established a few years ago. Three stages (I–III) in the crack growth process were previously identified. The transition from one stage to the other is a process based on the evolution of the dislocational structure of metal. This was demonstrated by test and studies carried out in situ at the HVTEM [
22]. These studies demonstrated that the dislocational structure spontaneously reorganizes itself with dramatic alterations of the physical and mechanical properties. These are self-organizing processes because the dislocations, being defects of imbalance and energy carriers, under the action of external factors, allows the system to acquire a minimum entropy during its evolution. Because of the reconfiguration of the dislocational structure, the frontal area of a propagating fracture evolves to an extraordinary and complex structure, which with the use of the numerical simulation dramatically approaches to what actually takes place. The conditions for a crack to arise and propagates depends on the state of stresses appearing at the tip of the crack, and it is precisely at this point that the contribution of this work is focused.
2. Analytical Methodology
Consider that because of the internal pressure
p, under which a pipeline operates, a cavity propagates and subsequently causes a fracture. Assuming that the cavity has a very small area compared to the diameter
Pd of the pipeline, it is possible to simplify the problem of the cavity critical balance through the analysis of the extreme equilibrium, which is when:
where
l is the length of the cavity. Additionally, we neglect the curvature of the pipeline, simplifying a problem that is originally three-dimensional. Additionally, it is assumed that the original cavity was an internal notch of circular shape with a diameter
l. In
Figure 1, the scheme of the geometry of the plate and its cavity is shown.
Without diminishing the generalities of the problem, initially it is assumed that the plane of incision of the original cavity matches with the central plane of the plate in which:
where
h is the thickness of the plate. Subsequently, when a pressure
p is applied to the incision plane, the cavity is increased. In
Figure 2a, the equivalent system 1 is shown, this means two flat plates with
h1 in thickness, fixed along the border and loaded with a uniformly distributed force
p.
3. Selection of the Differential Segment
To analyze the evolution of the cavity as the pressure increases, the solution for a circular beam subjected to bending can be used. The known solution applicable to this problem is only possible when the load does not cause plastic deformation in the plate. The theory of elastic bending for similar plates has been previously analyzed [
23,
24,
25,
26,
27]. Taking this theory for the development of the present study, we consider a load perpendicularly applied at the center of a circular cross-section, it is subsequently bended and its circular curvature is altered. This contributes to give the beam a micro-shape with a double curvature. The shape of this surface can be expressed by a radial function of the deviation as:
By the elastic property of the plate it is assumed that:
In this case the bending of the beam can be analyzed independently of its strain. When the deflection w is comparable with the thickness h1, it will be required that the solution considers the stretching of the center of the surface.
In the theory of plate bending, two hypotheses are used to simplify the problem. First, the normal Kirchhoff invariant hypothesis, which considers that the coordinate points initially located along a normal line in the center of the plane, remains in this normal line after the deformation. Second, the hypothesis of the non-deformable layers of the plate, which considers the normal stresses negligible in comparison with the bending stresses. Considering a circular plate of constant thickness with the
Z axis in the center, it is easy to see that the problem is symmetric, the deflection is only a function of the radial coordinates. If the angle of rotation of the normal is
θ, then
ω is related by:
The negative sign is due to the bending direction as shown in
Figure 3a, with the decrement of
ω,
θ increases. Now, if we consider radial sections along the plate before and after the load is applied, it is noted that as a result of the plate deflection, the
A1B1 normal, rotate a
θ angle, and the
A2B2 normal rotate at a
θ + dθ angle, as shown in
Figure 3b.
The
v-v’ segment, which is at a
z distance from the center of the plane, is extended by
. With this, the radial elongation is:
The radial elongation of point
v’ in the tangential direction is determined by comparing the length of the circumference in which it is located, before and after the application of the load. If, before deflection, this circumference was equal to
and after the loading it becomes to
, then:
For a better understanding, in
Figure 4 a differential plate element is shown having two radial sections, in which the angle between them is equal to
, and two cylindrical surfaces of
and
. Now we analyze the equilibrium of this differential element after loading, replacing the effect on the plate through the internal tension. The generalized Hook’s law for our bidimensional problem is expressed by:
where
E is the modulus of elasticity,
μ is the Poisson’s ratio,
is the normal stress in the radial direction and
is the normal stress in tangential direction. Expressing the stress from Equations (8) and (9) and considering (6) and (7), it is possible to express the stresses in the following form:
The resultant forces applied on the faces of the elementary body of the plate can be determined. The tangential stresses on the A1B1 face contribute to the resulting shear load, which is parallel to the Z axis. We represent the intensity of this force, that is, the corresponding magnitude per unit length for , giving Q in kg. Its balance will be equal to . Similarly, it can be obtained for the A2B2 face, the resultant shear forces acting on this face are .
Since the normal forces acting on the element faces are equal in magnitude but with opposite sign, the resultant of the normal forces is equal to zero. Its effect produces only bending momentums in the vertical planes of the element. We represent the momentum intensity per unit length on the faces
A1B1 and
A2B2, by
Mr and
Mt in kg cm/cm. In this case, the determination of the energy balance equation is:
Using Equations (10) and (11) we obtain:
Since the integer of Equations (14) and (15) can be expressed in terms of
, then it is possible to write:
Thus:
where
D is the bending toughness of the plate. The balance equation of the selected element of the plate can be obtained by projecting the force along the
Z axis and adding all the momentums with respect to the
Y axis, which is tangent to the arc of radius
r in the center of the plane, we obtain:
By neglecting higher order components, the Equation (21) can be expressed as:
The remaining balance equations satisfy the identities by the symmetry conditions. Setting up Equation (18) into Equation (22), under the condition that
D is constant, yields to:
Now we rearrange as follows:
Next, we integrate twice to obtain the radial distribution of the rotation angles:
The integration constants
C1 and
C2, are determined from the boundary conditions for each specific case. Equation (6) is used to determine the radial function of the deflection, and using Equation (12), the momentum diagrams can be obtained according to Equations (14) and (15). From Equations (10), (11), and (18), the functions
and
are:
Substituting the expression for the toughness of the plate:
In this case, the maximum stress values are achieved on the surfaces of the plate, when
:
4. On the Curvature of the Cavity
Considering the problem as symmetrical with respect to the center of the plane, we analyze just the lower part. Later we analyze when the convexity is formed in the upper side. It can be considered that the initial position of the plate corresponds to the diagram in
Figure 2. We can determine
Q(
r) from the equilibrium conditions for a round plate element, which was concentrically sectioned:
So, if we substitute Equations (33) and (34) into (24), and integrate twice to obtain:
In this case
, in the center of the plate where
, it follows that
For a fixed contour
, we obtain:
Finally, the Equation (36) can be rewritten as:
Using Equation (6), we can see that:
Now,
in order that:
From Equation (18) we find the expressions for
and
:
In
Figure 5, the momentum diagrams are shown, they are calculated with the use of these expressions:
The maximum stresses are reached in the fixed contour from the internal side of the cavity. We analyze the stress of the plate at the fixed support:
The equivalent stresses are:
The maximum deviation is reached in the center of the plate for
r = 0.
The stress state in the plate center is more adverse in the outside surface of the cavity, in which the tensile stresses are:
So far, we have analyzed the formation of cavities, without taking into account that the pipeline is exposed to an internal pressure
p0. In approximation with the theory of membranes, from the Laplace’s equation it is possible to calculate the
σm and
σt stresses obtained under a
p0 pressure:
where
σm is the stress in the meridional direction of the pipeline,
σt is the stress in the tangential direction,
Rm is the radius of curvature in the meridional direction, and
Rt is the radius of curvature in the tangential direction of the pipeline. For a pipeline of
Analyzing the balance of the pipeline in the axial direction, we can express:
Therefore, the selected differential element of the pipeline with a bulge or a cavity is shown in
Figure 6. In this approach there are no stresses in the normal direction to the pipeline surface.
Therefore, in the contours of the plate that form the cavity, the stresses arising from the pressure in the duct and the pressure inside the cavity must be added. Analyzing only the axial direction:
and in the tangential direction:
To analyze the axial section of the pipe, we separate the portion of the plate that limits the cavity, which is under a p pressure and we have replaced its effect by an internal stress distribution in the contour. Thus, we can analyze the axial slide of the pipeline with a cavity as a plate with a crack. It is also considered that its contour is under a uniformly distributed stress and momentum. The probability of this crack to propagate should be analyzed within the background of fracture mechanics. Even before , which is the yield strength from the elastic locations and after the increment in the yield point in the elastic-plastic range . The problem can be analyzed in the plastic range, until all the segments of the duct that surround the cavity are under a p pressure.
The behavior of the material enclosing the cavity under this pressure after its transition to a plastic state requires a special analysis. To solve this problem, we apply an approach developed by Feodosiev [
28] to describe the bending of a membrane. First, we assume that the stress is uniformly distributed in the plate thickness, and the surface of the plate acquires a spherical shape. In
Figure 7, the geometry of the plate after being subjected to the load is shown.
Considering that
is the radius of curvature of the plate after plastic bending, we get:
Since α is very small, we can assume that:
The deflection of the plate
f, is:
and the meridional and tangential stresses in the plate are:
From the Laplace’s equation
, thus:
Furthermore, using relationships based on the theory of plasticity, the axis coordinates are oriented so that
, thus:
Substituting into equation of plasticity:
Now, substituting Equation (66) into the equation for the strain intensity, we obtain:
The elongation of the plate after bending in the plastic range can be determined by the difference in the length of the
AC arc and the
AB line:
Locating Equation (68) into Equation (67’) we obtain:
To calculate the intensity of the stress
σi, considering that
σz = 0, and
σm = σt
and
Equations (71) and (69) can be used to obtain the function . To achieve this, we give a value for the deflection f, calculate εi with the Equation (69), and by using the stress–strain curve in coordinates σi–εi we determine σi. Then, using Equation (71) we calculate the pressure. Knowing the values of f and p we graph the curve. Also, it may be employed the tensile curve expressed in parabolic coordinates as .