Tests of Concrete Strength across the Thickness of Industrial Floor Using the Ultrasonic Method with Exponential Spot Heads
Abstract
:1. Introduction
2. Literature Review
- internal, which is characteristic for stocky cross-sections formed in the vertical position,
- superficial, which is observed in the case of laying floors and elements of small thickness in the horizontal position.
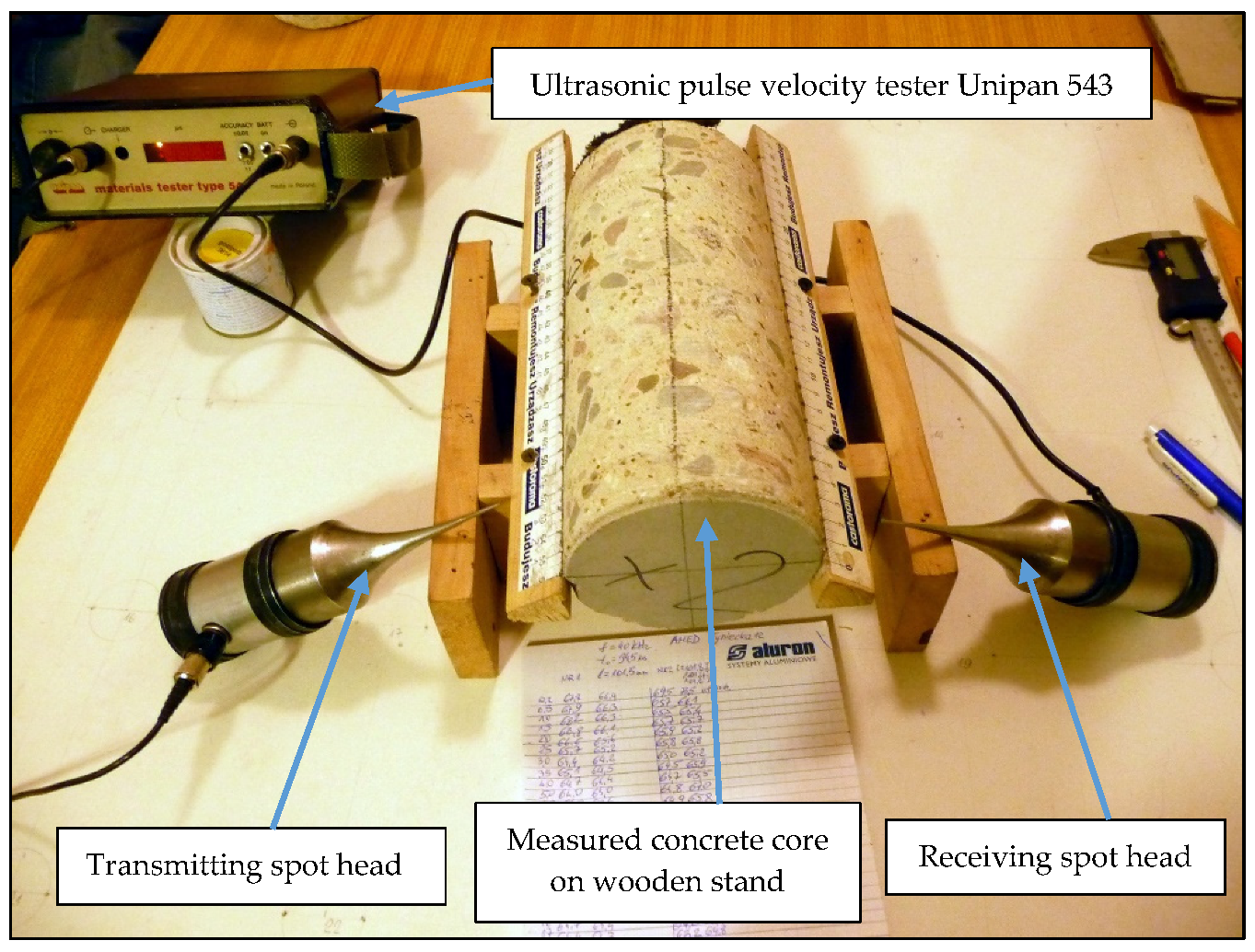
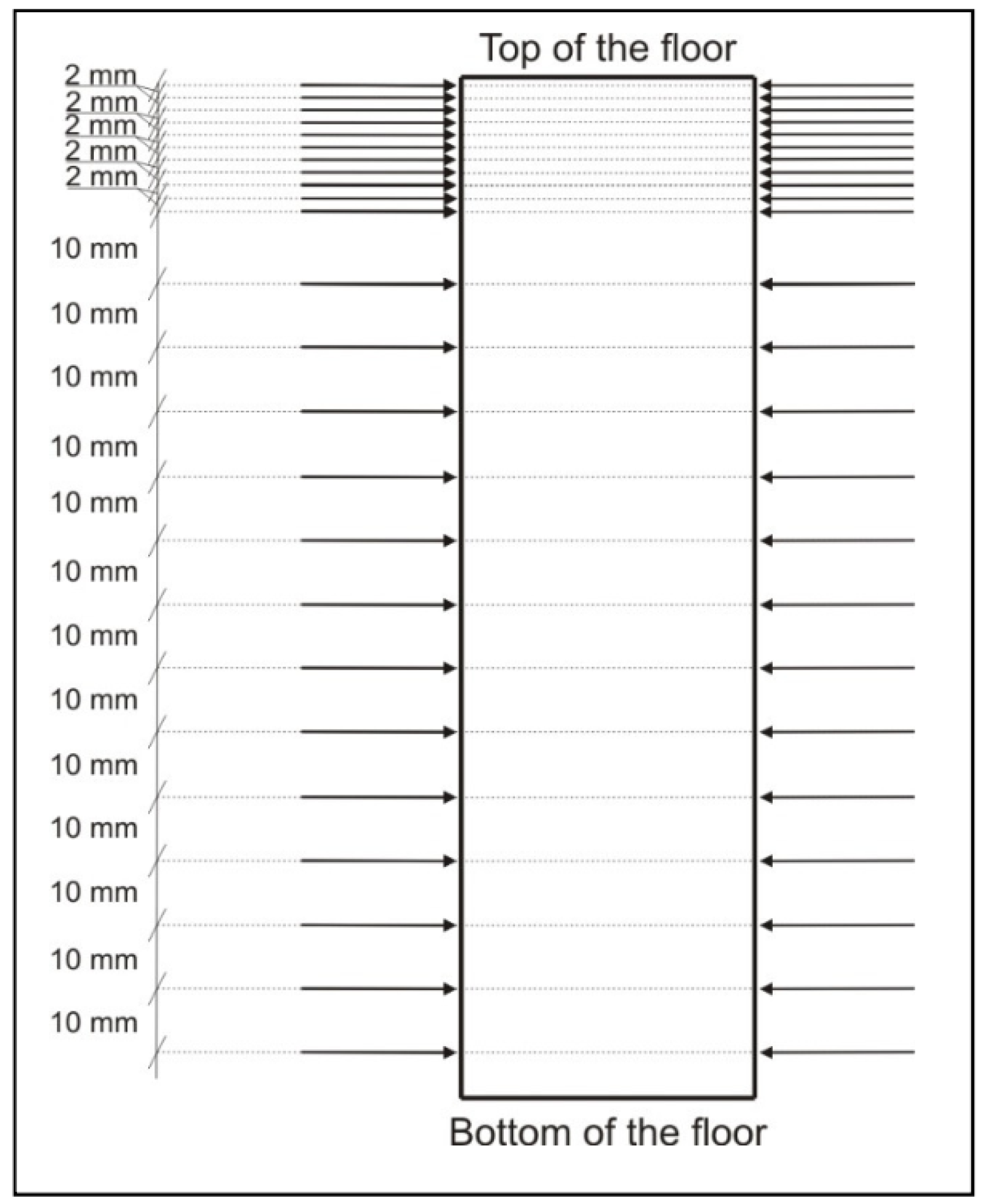
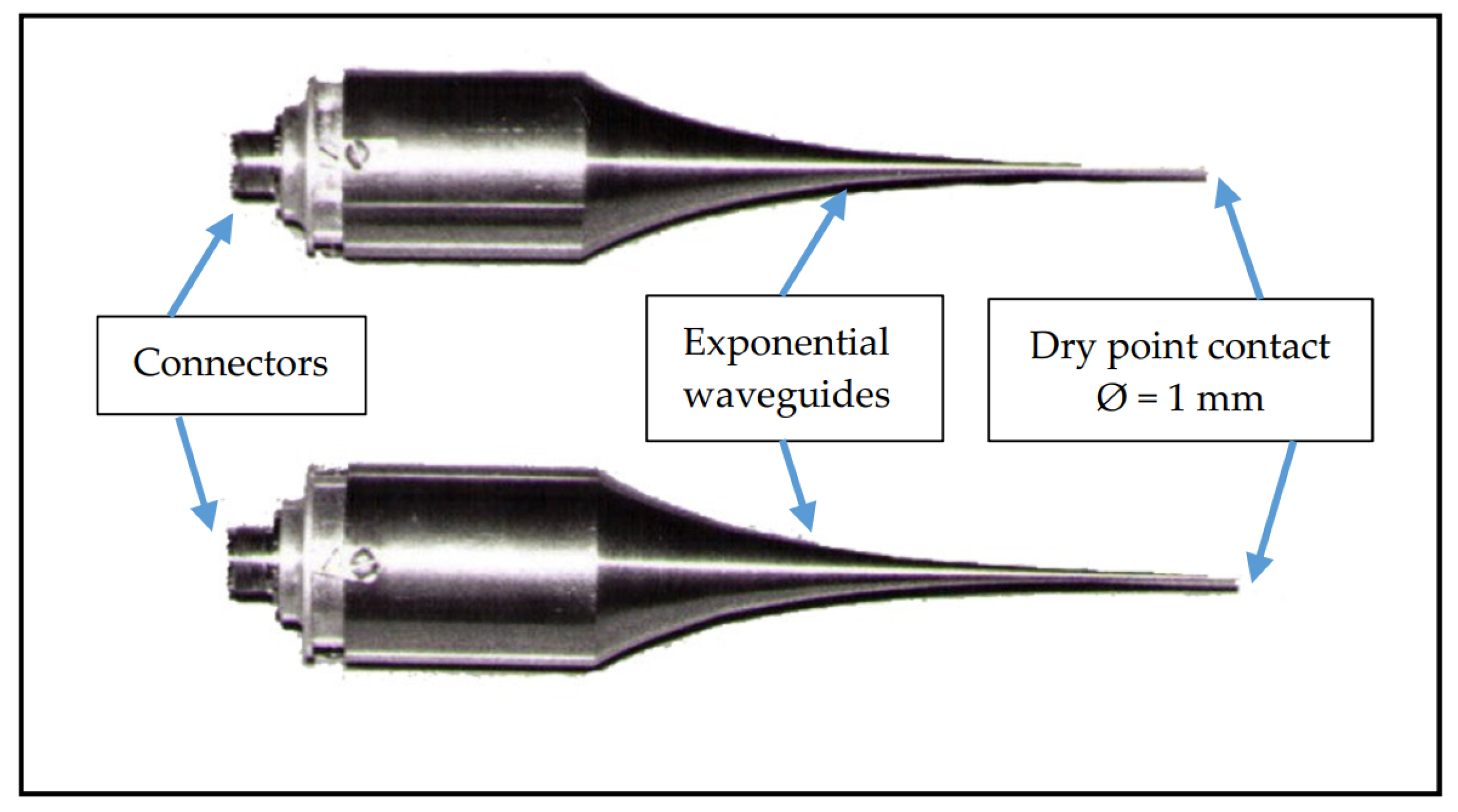
3. Materials and Test Methods
4. Results
4.1. Calibration of Ultrasound Pulse Velocity-Compression Strength Curves Based on the Strength Machine Tests
4.2. Tested Types of Strength Distributions in Cross-Section of Concrete Borehole Materials
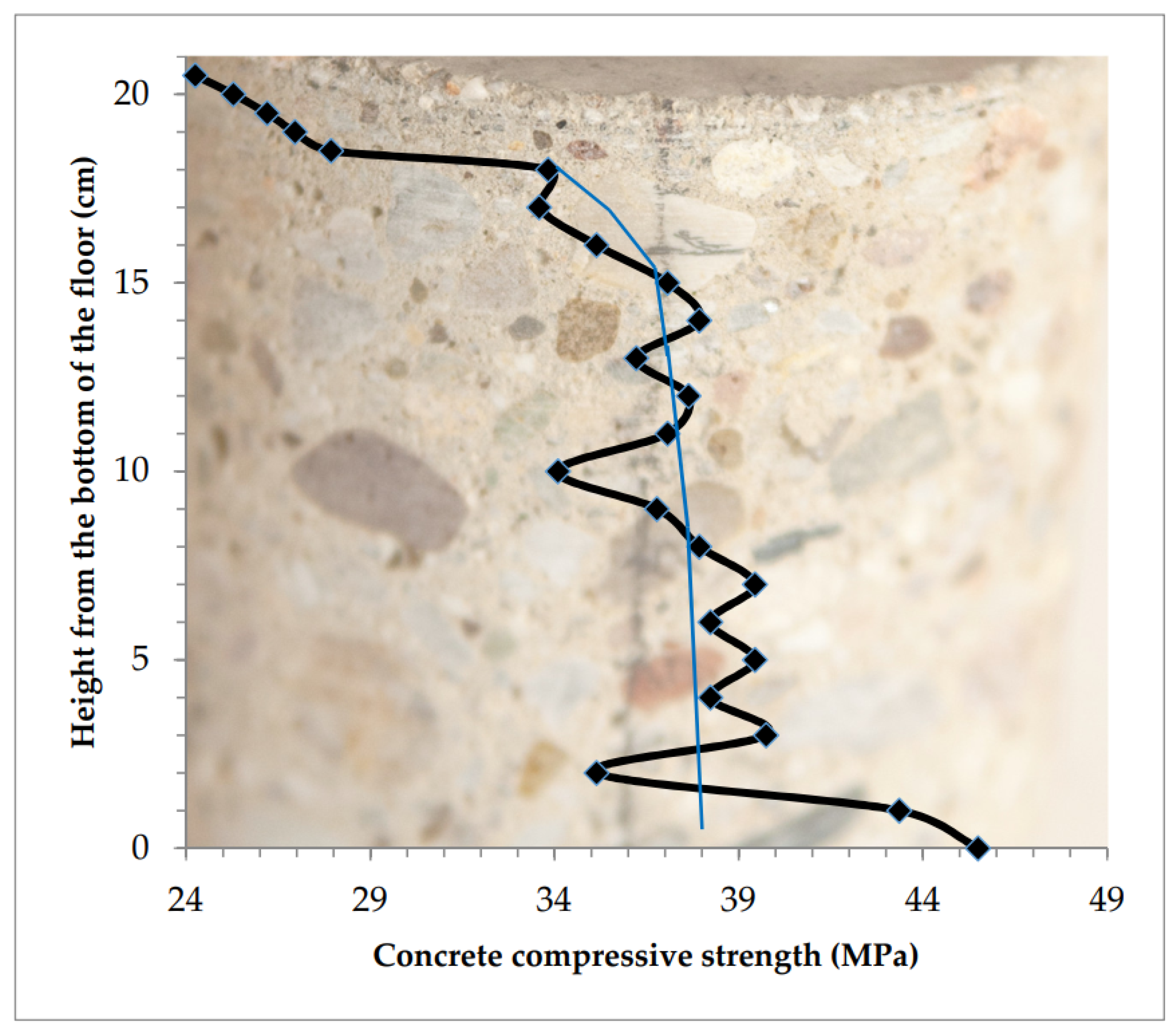
4.2.1. Concrete “Homogeneous” across Its Thickness with Superficial Weakening
4.2.2. “Homogeneous” Concrete with Weakening across the Top Layer 30–50 mm Thick
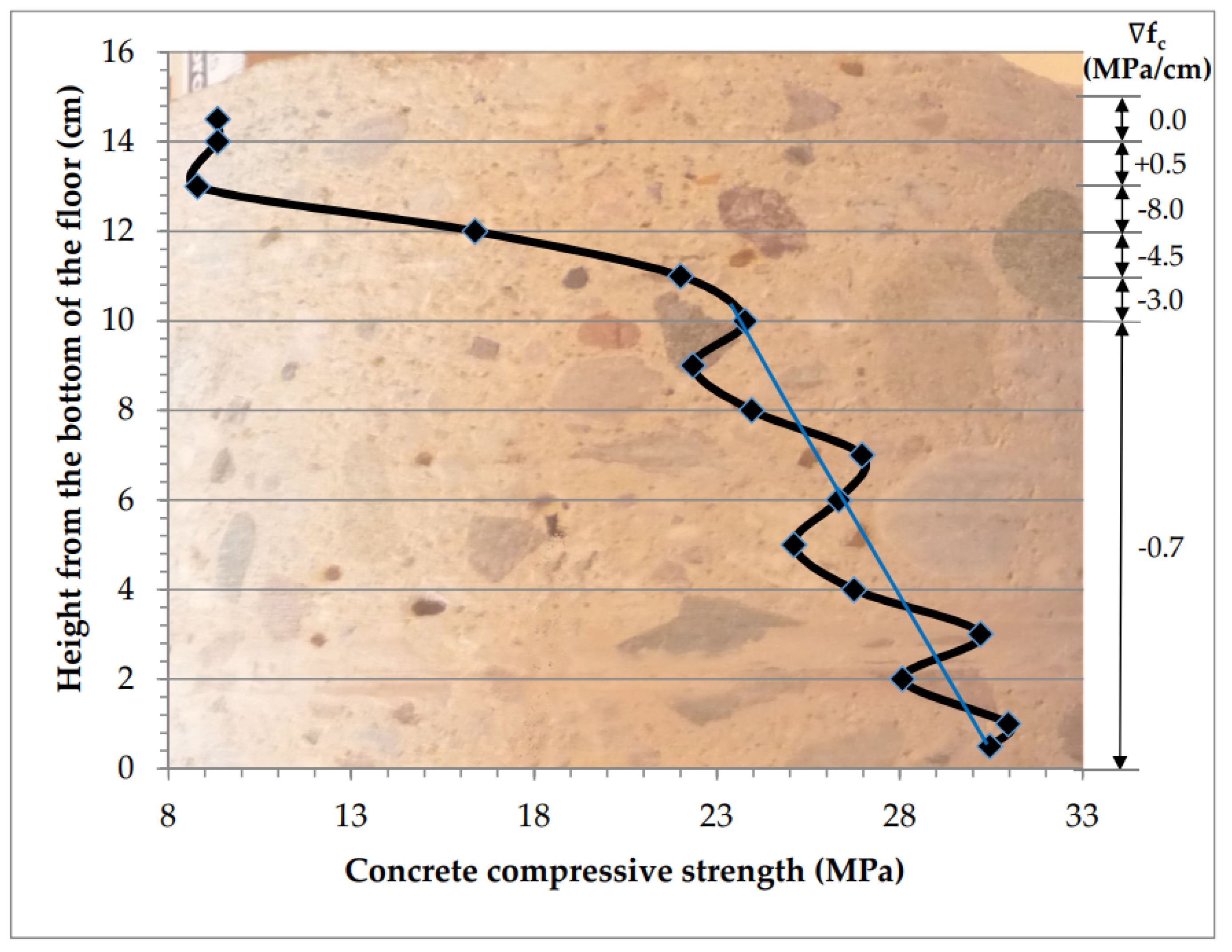
4.2.3. Concrete Strength Is Changing across Entire Section with a Quick Weakening of the Top Layer
4.2.4. Concrete Reinforced Superficially to the Expected Value Using the Mineral Powder
4.2.5. Concrete Floors under Emergency Conditions with Top Layer Hardened using Mineral Powder
- the case of strengthening the top layer with too small a quantity of mineral powder,
- the case of strengthening the floor with too weak a top layer of concrete,
- the case of excessive strengthening of the top layer of the floor.
4.3. Proposal for Evaluating Concrete Quality in the Floor Based on Its Strength Gradient and Anti-Gradient
- ∇fc,min—from the level of the beginning of a rapid decrease in strength (as above) upwards, to the zone of strengthening (increase in strength value) in the case of hardened floors or to the floor surface when there is no strengthening zone;
- ∇fc min,10 mm—on a thickness of 10 mm up from the place of onset of a rapid decrease in strength in the near-surface area (20–50 mm from the top of the floor);
- ∇fc,max—gradient of strength increase in the hardening zone, relevant to the floors treated with a surface hardening agent.
- if their minimum compressive strength measured in cross-section is considerably lower than the designed value;
- if their compressive strength in the surface zone is lower than its service load;
- if the strength gradient for the top, hardened layer exceeds the value of shear strength of concrete. Shrinkage in the place of contact between the level of concrete with increased and weakened strength leads to loosening.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guiming, W.; Yun, K.; Tao, S.; Zhonghe, S. Effect of water–binder ratio and fly ash on the homogeneity of concrete. Constr. Build. Mat. 2013, 38, 1129–1134. [Google Scholar]
- Caijun, S.; Zemei, W.; Jianfan, X.; Dehui, W.; Zhengyu, H.; Zhi, F. A review on ultra high performance concrete: Part I. Raw materials and mixture design. Constr. Build. Mat. 2015, 30, 741–751. [Google Scholar]
- Rhazi, J.; Hassaim, M.; Ballivy, G.; Hunaidi, O. Effects of concrete non-homogeneity on Rayleigh waves dispersion. Mag. Concr. Res. 2002, 54, 193–201. [Google Scholar] [CrossRef]
- Maj, M.; Ubysz, A.; Hammadeh, H.; Askifi, F. Non-Destructive Testing of Technical Conditions of RC Industrial Tall Chimneys Subjected to High Temperature. Materials 2019, 12, 2027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stawiski, B.; Kania, T. Effect of manufacturing technology on quality of slabs made of regular concrete. In Proceedings of the Conference People, Buildings and Environment, Lednice, Czech Republic, 7–9 November 2012; Hanák, T., Ed.; Institute of Structural Economics and Management, Faculty of Civil Engineering: Brno, Slovakia, 2012; Volume 2, pp. 391–400. Available online: http://www.fce.vutbr.cz/ekr/PBE/PBE2012_Proceedings.pdf (accessed on 1 March 2020).
- EN 13791. Evaluation of Concrete Compression Strength in Structures and Prefabricated Concrete Products; European Committee for Standardization: Brussels, Belgium, 2008. [Google Scholar]
- Schabowicz, K. Modern acoustic techniques for testing concrete structures accessible from one side only. Arch. Civ. Mech. Eng. 2015, 15, 1149–1159. [Google Scholar] [CrossRef]
- Schabowicz, K. Non-Destructive Testing of Materials in Civil Engineering. Materials 2019, 12, 3237. [Google Scholar] [CrossRef] [Green Version]
- Szymanowski, J.; Sadowski, Ł. The influence of the addition of tetragonal crystalline titanium oxide nanoparticles on the adhesive and functional properties of layered cementitious composites. Compos. Struct. 2019, 233, 111636. [Google Scholar] [CrossRef]
- EN 206+A1:2016-12. Concrete—Requirements, Properties, Production and Conformity; European Committee for Standardization: Brussels, Belgium, 2016. [Google Scholar]
- Tanigawa, Y.; Baba, K.; Mori, H. Estimation of concrete strength by combined non-destructive testing method. Mater. Sci. 1984, 82, 57–76. [Google Scholar]
- Giaccio, G.; Giovambattista, A. Bleeding: Evaluation of its effects on concrete behavior. Mater. Constr. 1986, 19, 265–271. [Google Scholar] [CrossRef]
- Khatib, J.M.; Mangat, P.S. Porosity of cement paste cured at 45 °C as a function of location relative to casting position. Cem. Concr. Comp. 2003, 25, 97–108. [Google Scholar] [CrossRef]
- Loh, C.K.; Tan, T.S.; Yong, T.S.; Wee, T.H. An experimental study on bleeding and channelling of cement paste and mortar. Adv. Cem. Res. 1998, 10, 1–16. [Google Scholar] [CrossRef]
- Larish, M.D. Fundamental Mechanisms of Concrete Bleeding in Bored Piles. In Proceedings of the Concrete 2019 Conference, Sydney, Australia, 8–11 September 2019. [Google Scholar]
- Kog, Y.C. Integrity Problem of Large-Diameter Bored Piles. J. Geotech. Geoenviron. Eng. 2009, 135, 237–245. [Google Scholar] [CrossRef]
- Vanhove, Y.; Khayat, K.H. Forced Bleeding Test to Assess Stability of Flowable Concrete. ACI Mater. J. 2016, 113, 753–758. [Google Scholar] [CrossRef]
- Powers, T.C. The Properties of Fresh Concrete; John Wiley & Sons, Inc.: New York, NY, USA, 1968. [Google Scholar]
- ACI 302.1R-80 Guide for Concrete Floor and Slab Construction; American Concrete Institute: Detroit, MI, USA, 2015.
- Jasinski, R.; Drobiec, Ł.; Mazur, W. Validation of Selected Non-Destructive Methods for Determining the Compressive Strength of Masonry Units Made of Autoclaved Aerated Concrete. Materials 2019, 12, 389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, R.; Orlowicz, R.; Rutkowski, R. Use of TLS (LiDAR) for Building Diagnostics with the Example of a Historic Building in Karlino. Buildings 2020, 10, 24. [Google Scholar] [CrossRef] [Green Version]
- Nowak, T.; Karolak, A.; Sobótka, M.; Wyjadłowski, M. Assessment of the Condition of Wharf Timber Sheet Wall Material by Means of Selected Non-Destructive Methods. Materials 2019, 12, 1532. [Google Scholar] [CrossRef] [Green Version]
- Schabowicz, K.; Gorzelańczyk, T.; Szymków, M. Identification of the Degree of Degradation of Fibre-Cement Boards Exposed to Fire by Means of the Acoustic Emission Method and Artificial Neural Networks. Materials 2019, 12, 656. [Google Scholar] [CrossRef] [Green Version]
- Stawiski, B.; Kania, T. Determination of the influence of cylindrical samples dimensions on the evaluation of concrete and wall mortar strength using ultrasound method. Procedia Eng. 2013, 57, 1078. [Google Scholar]
- Stawiski, B.; Kania, T. Examining the distribution of strength across the thickness of reinforced concrete elements subject to sulphate corrosion using the ultrasonic method. Materials 2019, 12, 2519. [Google Scholar] [CrossRef] [Green Version]
- Bogas, J.A.; Gomes, M.G.; Gomes, A. Compressive strength evaluation of structural lightweight concrete by non-destructive ultrasonic pulse velocity method. Ultrasonics 2013, 53, 962–972. [Google Scholar] [CrossRef]
- Brunarski, L. Estimation of concrete strength in construction. Build. Res. Inst. Quat. 1998, 2–3, 28–45. [Google Scholar]
- Anugonda, P.; Wiehn, J.S.; Turner, J.A. Diffusion of ultrasound in concrete. Ultrasonics 2001, 39, 429–435. [Google Scholar] [CrossRef]
- Sansalone, M.; Streett, W.B. Impact-Echo Nondestructive Evaluation of Concrete and Masonry; Bullbrier Press: Ithaca, NY, USA, 1997. [Google Scholar]
- Breysse, D. Nondestructive evaluation of concrete strength: An historical review and a new perspective by combining NDT methods. Constr. Build. Mater. 2012, 33, 139–163. [Google Scholar] [CrossRef]
- Facaoaru, I. Contribution à i’étude de la relation entre la résistance du béton à la compression et de la vitesse de propagation longitudinale des ultrasons. RILEM 1961, 22, 125–154. [Google Scholar]
- Leshchinsky, A. Non-destructive methods instead of specimens and cores, quality control of concrete structures. In Proceedings of the International Symposium, RILEM, Ghent, Belgium, 12–14 June 1991; E&FN SPON: London, UK, 1991; pp. 377–386. [Google Scholar]
- Bungey, J.H. The validity of ultrasonic pulse velocity testing of in-place concrete for strength. NDT Int. 1980, 13, 296–300. [Google Scholar] [CrossRef]
- Szpetulski, J. Testing of compressive strength of concrete in construction. Constr. Rev. 2016, 3, 21–24. (In Polish) [Google Scholar]
- Gudra, T.; Stawiski, B. Non-destructive strength characterization of concrete using surface waves. NDT E Int. 2000, 33, 1–6. [Google Scholar] [CrossRef]
- Komlos, K.; Popovics, S.; Nurnbergerova, T.; Babal, B.; Popovics, J.S. Ultrasonic Pulse Velocity Test of Concrete Properties as Specified in Various Standards. Cem. Concr. Compos. 1996, 18, 357–364. [Google Scholar] [CrossRef]
- PN-B-06261. Non-Destructive Testing of Structures; Ultrasound Method of Testing Compressive Strength of Concrete; Polish Committee for Standardization: Warsaw, Poland, 1974. [Google Scholar]
- EN 12504-4. Testing Concrete-Part 4: Determination of Ultrasonic Pulse Velocity; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Stawiski, B.; Stawiski, M. Testing characteristics of directional ultrasound probes with geometrically defined waveguides. NDT Bull. 2000, 10, 17–19. [Google Scholar]
- Stawiski, B. Ultrasonic Testing of Concrete and Mortar Using Point Probes; Monograph; Wrocław University of Technology Printing House: Wrocław, Poland, 2009; ISSN 0324-9875. [Google Scholar]







| Ordinal Number | Ultrasound Longitudinal Wave Velocity CL (km/s) | Compression Strength (MPa) | Difference fc from Equation (3)—fc, Ø10/10 (MPa) | |
|---|---|---|---|---|
| Destructive Test | fc from Equation (3) (0.1983∙CL4.3081) | |||
| fc, Ø10/10 | ||||
| 1 | 3.460 | 40.24 | 41.66 | 1.42 |
| 2 | 3.459 | 43.22 | 41.61 | −1.61 |
| 3 | 3.404 | 39.60 | 38.83 | −0.77 |
| 4 | 3.372 | 38.11 | 37.28 | −0.83 |
| 5 | 3.362 | 37.55 | 36.81 | −0.74 |
| 6 | 3.288 | 32.88 | 33.44 | 0.56 |
| 7 | 3.282 | 34.02 | 33.18 | −0.84 |
| 8 | 3.191 | 30.99 | 29.40 | −1.59 |
| 9 | 3.190 | 31.77 | 29.36 | −2.41 |
| 10 | 3.172 | 28.17 | 28.65 | 0.48 |
| 11 | 3.168 | 28.42 | 28.49 | 0.07 |
| 12 | 3.167 | 28.64 | 28.46 | −0.18 |
| 13 | 3.108 | 27.12 | 26.24 | −0.88 |
| 14 | 3.092 | 25.16 | 25.66 | 0.50 |
| 15 | 3.078 | 25.21 | 25.17 | −0.04 |
| 16 | 3.07 | 25.22 | 24.89 | −0.33 |
| 17 | 3.02 | 23.38 | 23.19 | −0.19 |
| 18 | 2.838 | 17.22 | 17.74 | 0.52 |
| 19 | 2.742 | 14.62 | 15.30 | 0.68 |
| Mean value | 3.182 | 30.081 | 29.755 | −0.33 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (μs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (μs) | Mean Ultrasound Netto Passing Time tn (μs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
| 1 | 21.5 | 35.3 | 36.2 | 35.75 | 2.615 | 12.47 |
| 2 | 21.0 | 29.8 | 32.0 | 30.90 | 3.026 | 23.39 |
| 3 | 20.5 | 29.4 | 29.3 | 29.35 | 3.186 | 29.20 |
| 4 | 20.0 | 30.2 | 30.2 | 30.20 | 3.096 | 25.81 |
| 5 | 19.5 | 30.5 | 30.9 | 30.70 | 3.046 | 24.06 |
| 6 | 19.0 | 30.1 | 30.6 | 30.35 | 3.081 | 25.27 |
| 7 | 18.5 | 28.6 | 29.8 | 29.20 | 3.202 | 29.84 |
| 8 | 18.0 | 29.5 | 29.7 | 29.60 | 3.159 | 28.15 |
| 9 | 17.0 | 29.4 | 29.2 | 29.30 | 3.191 | 29.40 |
| 10 | 16.0 | 28.5 | 28.4 | 28.45 | 3.286 | 33.36 |
| 11 | 15.0 | 28.4 | 29.9 | 29.15 | 3.208 | 30.08 |
| 12 | 14.0 | 28.8 | 29.8 | 29.30 | 3.191 | 29.40 |
| 13 | 13.0 | 29.1 | 28.7 | 28.90 | 3.235 | 31.18 |
| 14 | 12.0 | 29.4 | 29.4 | 29.40 | 3.180 | 28.96 |
| 15 | 11.0 | 29.2 | 29.9 | 29.55 | 3.164 | 28.34 |
| 16 | 10.0 | 28.5 | 29.7 | 29.10 | 3.213 | 30.28 |
| 17 | 9.0 | 28.5 | 28.8 | 28.65 | 3.264 | 32.40 |
| 18 | 8.0 | 28.3 | 29.4 | 28.85 | 3.241 | 31.43 |
| 19 | 7.0 | 29.2 | 29.5 | 29.35 | 3.186 | 29.20 |
| 20 | 6.0 | 28.3 | 30.2 | 29.25 | 3.197 | 29.63 |
| 21 | 5.0 | 28.8 | 29.3 | 29.05 | 3.219 | 30.52 |
| 22 | 4.0 | 29.0 | 29.2 | 29.10 | 3.213 | 30.28 |
| 23 | 3.0 | 29.7 | 29.8 | 29.75 | 3.143 | 27.54 |
| 24 | 2.0 | 29.2 | 28.6 | 28.90 | 3.235 | 31.18 |
| 25 | 1.0 | 29.5 | 29.2 | 29.35 | 3.186 | 29.20 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (μs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (μs) | Mean Ultrasound Netto Passing Time tn (μs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
| 1 | 20.5 | 31.3 | 30.5 | 30.90 | 3.040 | 24.24 |
| 2 | 20.0 | 31.1 | 30.1 | 30.60 | 3.070 | 25.28 |
| 3 | 19.5 | 30.4 | 30.3 | 30.35 | 3.096 | 26.19 |
| 4 | 19.0 | 29.6 | 30.7 | 30.15 | 3.116 | 26.95 |
| 5 | 18.5 | 29.7 | 30.1 | 29.90 | 3.142 | 27.94 |
| 6 | 18.0 | 28.4 | 28.8 | 28.60 | 3.285 | 33.83 |
| 7 | 17.0 | 28.4 | 28.9 | 28.65 | 3.279 | 33.58 |
| 8 | 16.0 | 28.4 | 28.3 | 28.35 | 3.314 | 35.14 |
| 9 | 15.0 | 27.6 | 28.4 | 28.00 | 3.355 | 37.07 |
| 10 | 14.0 | 27.6 | 28.1 | 27.85 | 3.373 | 37.94 |
| 11 | 13.0 | 28.0 | 28.3 | 28.15 | 3.337 | 36.22 |
| 12 | 12.0 | 27.8 | 28.0 | 27.90 | 3.367 | 37.64 |
| 13 | 11.0 | 28.0 | 28.0 | 28.00 | 3.355 | 37.07 |
| 14 | 10.0 | 28.6 | 28.5 | 28.55 | 3.291 | 34.09 |
| 15 | 9.0 | 27.6 | 28.5 | 28.05 | 3.349 | 36.78 |
| 16 | 8.0 | 27.4 | 28.3 | 27.85 | 3.373 | 37.94 |
| 17 | 7.0 | 27.6 | 27.6 | 27.60 | 3.404 | 39.44 |
| 18 | 6.0 | 27.7 | 27.9 | 27.80 | 3.379 | 38.23 |
| 19 | 5.0 | 27.4 | 27.8 | 27.60 | 3.404 | 39.44 |
| 20 | 4.0 | 27.7 | 27.9 | 27.80 | 3.379 | 38.23 |
| 21 | 3.0 | 27.6 | 27.5 | 27.55 | 3.410 | 39.75 |
| 22 | 2.0 | 28.1 | 28.6 | 28.35 | 3.314 | 35.14 |
| 23 | 1.0 | 27.4 | 26.6 | 27.00 | 3.480 | 43.35 |
| 24 | 0.2 | 27.4 | 26.0 | 26.70 | 3.519 | 45.49 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (µs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (µs) | Mean Ultrasound Netto Passing Time tn (µs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
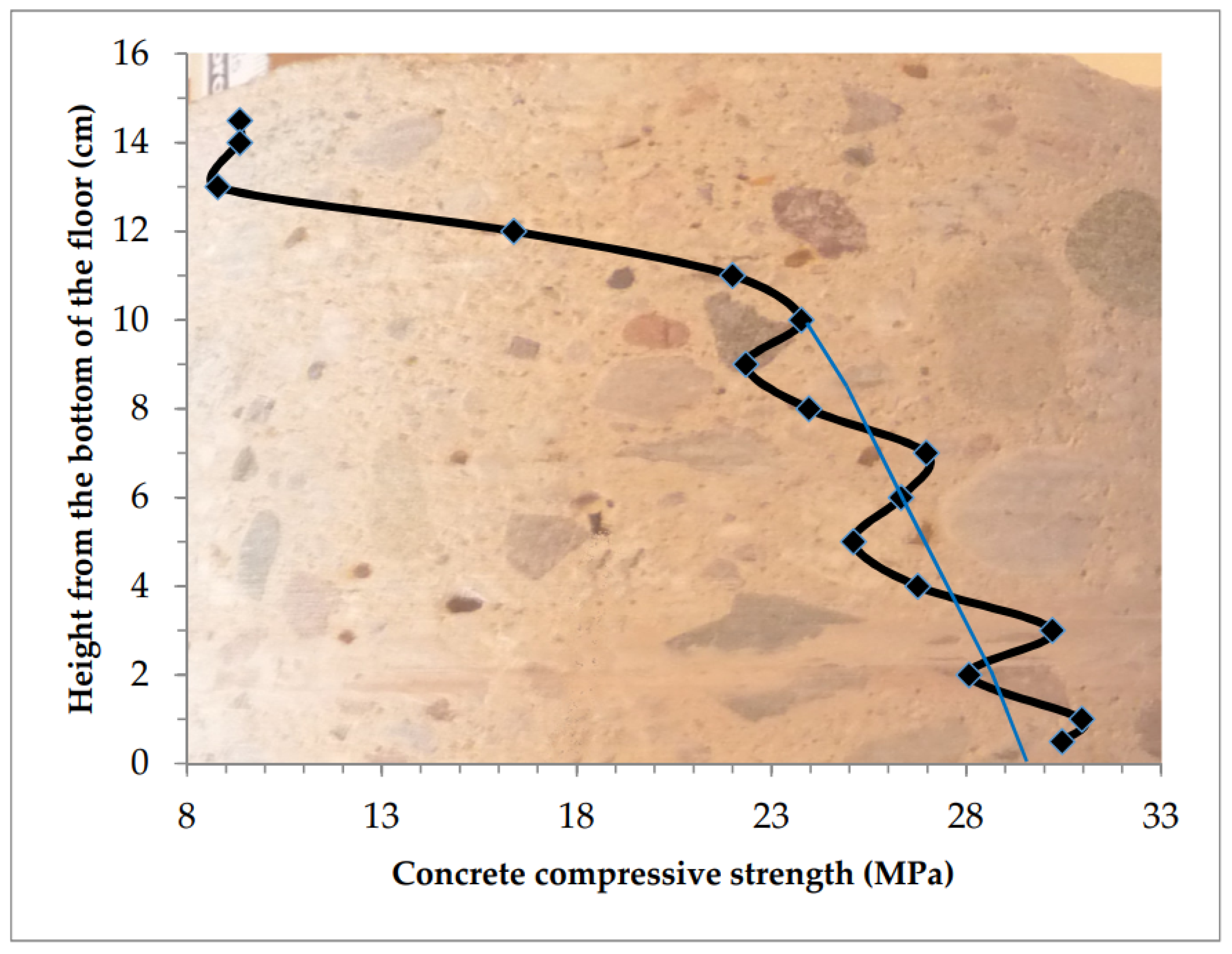
| 1 | 14.5 | 34.2 | 34.6 | 34.40 | 2.733 | 9.35 |
| 2 | 14.0 | 34.4 | 34.4 | 34.40 | 2.733 | 9.35 |
| 3 | 13.0 | 34.0 | 35.8 | 34.90 | 2.693 | 8.78 |
| 4 | 12.0 | 29.7 | 30.7 | 30.20 | 3.113 | 16.38 |
| 5 | 11.0 | 28.2 | 28.2 | 28.20 | 3.333 | 22.00 |
| 6 | 10.0 | 26.9 | 28.5 | 27.70 | 3.394 | 23.77 |
| 7 | 9.0 | 29.2 | 27.0 | 28.10 | 3.345 | 22.34 |
| 8 | 8.0 | 28.6 | 26.7 | 27.65 | 3.400 | 23.95 |
| 9 | 7.0 | 27.2 | 26.6 | 26.90 | 3.494 | 26.97 |
| 10 | 6.0 | 26.9 | 27.2 | 27.05 | 3.475 | 26.33 |
| 11 | 5.0 | 27.5 | 27.2 | 27.35 | 3.437 | 25.11 |
| 12 | 4.0 | 27.8 | 26.1 | 26.95 | 3.488 | 26.75 |
| 13 | 3.0 | 25.9 | 26.5 | 26.20 | 3.588 | 30.21 |
| 14 | 2.0 | 26.4 | 26.9 | 26.65 | 3.527 | 28.07 |
| 15 | 1.0 | 25.8 | 26.3 | 26.05 | 3.608 | 30.97 |
| 16 | 0.5 | 25.7 | 26.6 | 26.15 | 3.595 | 30.46 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (µs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (µs) | Mean Ultrasound Netto Passing Time tn (µs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
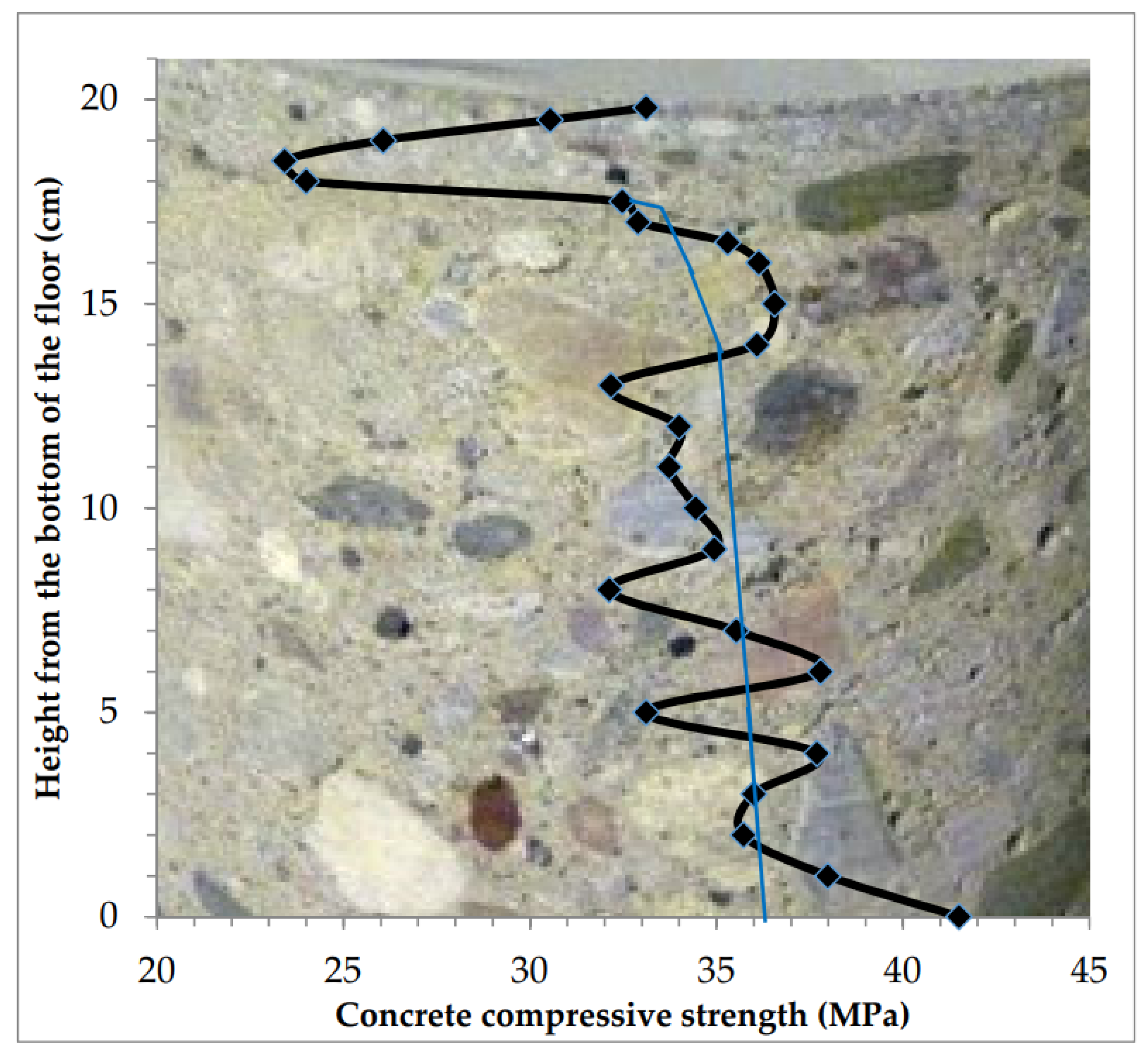
| 1 | 19.8 | 28.5 | 28.8 | 28.65 | 3.274 | 32.83 |
| 2 | 19.5 | 28.7 | 29.7 | 29.20 | 3.213 | 30.28 |
| 3 | 19.0 | 29.6 | 31.0 | 30.30 | 3.097 | 25.84 |
| 4 | 18.5 | 29.8 | 32.4 | 31.10 | 3.021 | 23.22 |
| 5 | 18.0 | 29.4 | 32.5 | 30.95 | 3.038 | 23.79 |
| 6 | 17.5 | 28.0 | 29.6 | 28.80 | 3.259 | 32.19 |
| 7 | 17.0 | 28.2 | 29.2 | 28.70 | 3.269 | 32.62 |
| 8 | 16.5 | 27.5 | 29.0 | 28.25 | 3.323 | 35.00 |
| 9 | 16.0 | 27.3 | 28.9 | 28.10 | 3.341 | 35.83 |
| 10 | 15.0 | 27.8 | 28.2 | 28.00 | 3.350 | 36.25 |
| 11 | 14.0 | 27.4 | 28.8 | 28.10 | 3.340 | 35.78 |
| 12 | 13.0 | 28.5 | 29.2 | 28.85 | 3.252 | 31.89 |
| 13 | 12.0 | 27.7 | 29.3 | 28.50 | 3.294 | 33.71 |
| 14 | 11.0 | 27.7 | 29.4 | 28.55 | 3.288 | 33.44 |
| 15 | 10.0 | 27.9 | 28.9 | 28.40 | 3.304 | 34.15 |
| 16 | 9.0 | 28.0 | 28.6 | 28.30 | 3.315 | 34.64 |
| 17 | 8.0 | 28.9 | 28.8 | 28.85 | 3.251 | 31.85 |
| 18 | 7.0 | 28.8 | 27.6 | 28.20 | 3.328 | 35.23 |
| 19 | 6.0 | 28.4 | 27.2 | 27.80 | 3.376 | 37.47 |
| 20 | 5.0 | 29.0 | 28.3 | 28.65 | 3.274 | 32.83 |
| 21 | 4.0 | 27.8 | 27.8 | 27.80 | 3.374 | 37.38 |
| 22 | 3.0 | 28.0 | 28.2 | 28.10 | 3.338 | 35.69 |
| 23 | 2.0 | 28.0 | 28.3 | 28.15 | 3.332 | 35.42 |
| 24 | 1.0 | 27.7 | 27.8 | 27.75 | 3.380 | 37.67 |
| 25 | 0.2 | 26.6 | 27.8 | 27.20 | 3.450 | 41.14 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (µs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (µs) | Mean Ultrasound Netto Passing Time tn (µs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
| 1 | 16.2 | 30.3 | 28.3 | 29.30 | 3.3560 | 19.03 |
| 2 | 16.0 | 30.0 | 28.8 | 29.40 | 3.3450 | 18.78 |
| 3 | 15.8 | 30.4 | 29.2 | 29.80 | 3.3000 | 17.76 |
| 4 | 15.6 | 31.0 | 29.0 | 30.00 | 3.2780 | 17.27 |
| 5 | 15.4 | 30.9 | 29.2 | 30.05 | 3.2730 | 17.16 |
| 6 | 15.2 | 30.9 | 29.6 | 30.25 | 3.2510 | 16.68 |
| 7 | 15.0 | 31.1 | 29.7 | 30.40 | 3.2350 | 16.33 |
| 8 | 14.8 | 30.6 | 29.8 | 30.20 | 3.2560 | 16.79 |
| 9 | 14.6 | 30.8 | 29.4 | 30.10 | 3.2670 | 17.03 |
| 10 | 14.4 | 30.2 | 29.8 | 30.00 | 3.2780 | 17.27 |
| 11 | 14.2 | 29.0 | 28.3 | 28.65 | 3.4320 | 20.82 |
| 12 | 14.0 | 28.6 | 28.0 | 28.30 | 3.4750 | 21.87 |
| 13 | 13.0 | 27.2 | 27.5 | 27.35 | 3.5960 | 24.93 |
| 14 | 12.0 | 27.0 | 27.0 | 27.00 | 3.6420 | 26.14 |
| 15 | 11.0 | 26.6 | 26.8 | 26.70 | 3.6830 | 27.24 |
| 16 | 10.0 | 26.9 | 26.6 | 26.75 | 3.6760 | 27.05 |
| 17 | 9.0 | 26.7 | 27.2 | 26.95 | 3.6490 | 26.32 |
| 18 | 8.0 | 26.4 | 26.6 | 26.50 | 3.7110 | 28.00 |
| 19 | 7.0 | 26.6 | 25.8 | 26.20 | 3.7530 | 29.17 |
| 20 | 6.0 | 26.1 | 26.6 | 26.35 | 3.7320 | 28.58 |
| 21 | 5.0 | 26.6 | 26.5 | 26.55 | 3.7040 | 27.81 |
| 22 | 4.0 | 25.8 | 25.3 | 25.55 | 3.8490 | 31.91 |
| 23 | 3.0 | 26.6 | 26.4 | 26.50 | 3.7110 | 28.00 |
| 24 | 2.0 | 26.6 | 26.9 | 26.75 | 3.6760 | 27.05 |
| 25 | 1.0 | 26.3 | 26.6 | 26.45 | 3.7180 | 28.20 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (μs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (μs) | Mean Ultrasound Netto Passing Time tn (μs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
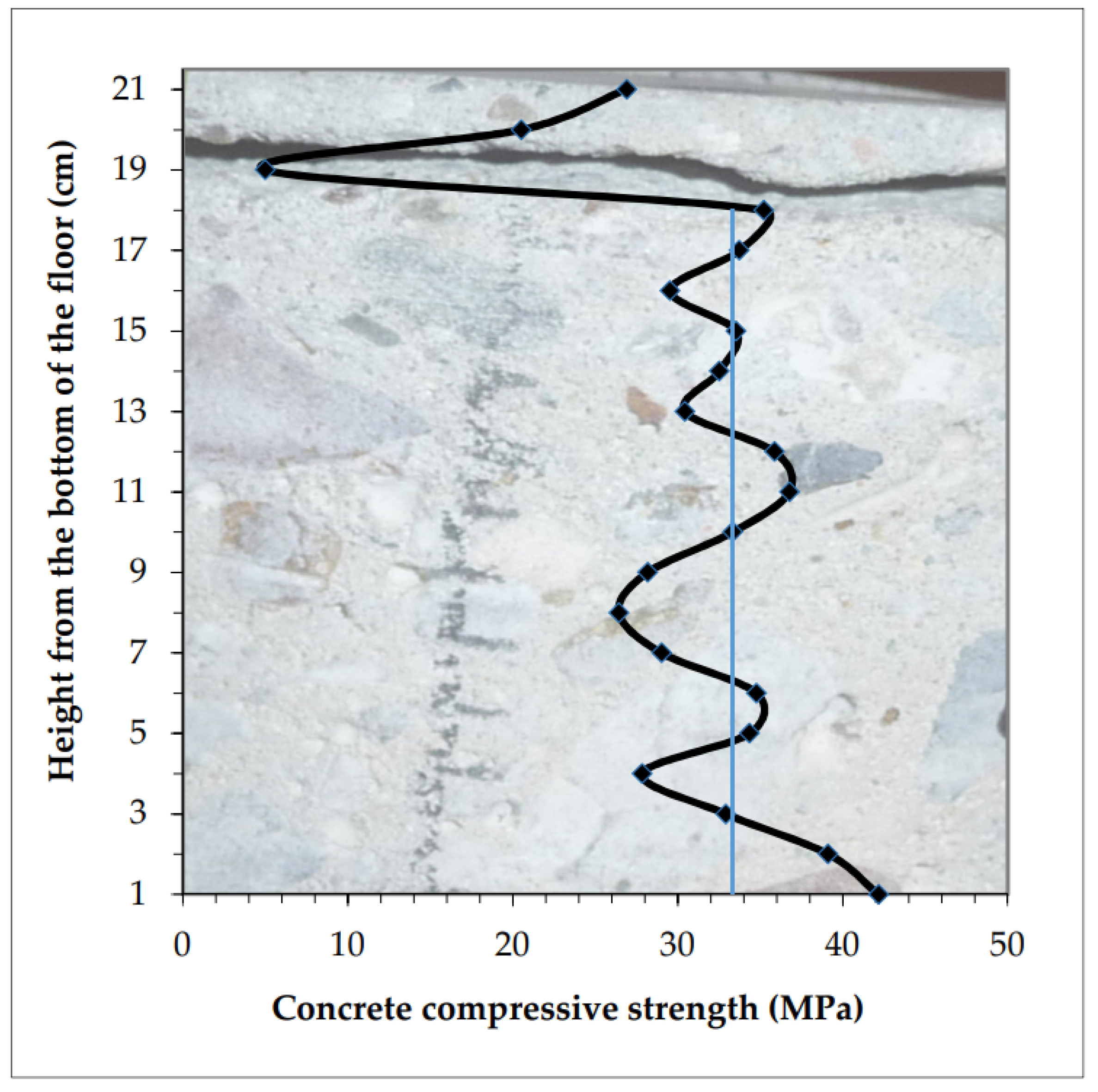
| 1 | 21.0 | 47.5 | 49.5 | 48.54 | 2.122 | 26.90 |
| 2 | 20.0 | 49.4 | 51.0 | 50.20 | 2.051 | 20.50 |
| 3 | 19.0 | 60.4 | 62.0 | 61.21 | 1.682 | 5.14 |
| 4 | 18.0 | 46.7 | 47.0 | 46.84 | 2.199 | 35.20 |
| 5 | 17.0 | 46.7 | 47.6 | 47.12 | 2.185 | 33.70 |
| 6 | 16.0 | 47.4 | 48.5 | 47.96 | 2.147 | 29.52 |
| 7 | 15.0 | 46.7 | 47.7 | 47.16 | 2.184 | 33.49 |
| 8 | 14.0 | 47.6 | 47.1 | 47.35 | 2.175 | 32.50 |
| 9 | 13.0 | 48.1 | 47.4 | 47.77 | 2.156 | 30.42 |
| 10 | 12.0 | 46.7 | 46.7 | 46.71 | 2.205 | 35.92 |
| 11 | 11.0 | 46.8 | 46.3 | 46.55 | 2.212 | 36.82 |
| 12 | 10.0 | 47.9 | 46.5 | 47.20 | 2.182 | 33.28 |
| 13 | 9.0 | 48.9 | 47.6 | 48.25 | 2.134 | 28.18 |
| 14 | 8.0 | 49.6 | 47.7 | 48.66 | 2.116 | 26.38 |
| 15 | 7.0 | 48.4 | 47.7 | 48.07 | 2.142 | 29.00 |
| 16 | 6.0 | 46.2 | 47.6 | 46.91 | 2.195 | 34.82 |
| 17 | 5.0 | 48.8 | 45.2 | 46.99 | 2.192 | 34.39 |
| 18 | 4.0 | 50.4 | 46.2 | 48.34 | 2.130 | 27.78 |
| 19 | 3.0 | 47.4 | 47.2 | 47.27 | 2.179 | 32.92 |
| 20 | 2.0 | 45.7 | 46.6 | 46.16 | 2.231 | 39.09 |
| 21 | 1.0 | 45.7 | 45.7 | 45.66 | 2.255 | 42.18 |
| Ordinal Number | Height from the Bottom of the Floor (cm) | Ultrasound Netto Passing Time in Direction I-I tn I-I (µs) | Ultrasound Netto Passing Time in Direction II-II tn II-II (µs) | Mean Ultrasound Netto Passing Time tn (µs) | Ultrasound Wave Velocity CL (km/s) | Concrete Compression Strength fc (MPa) |
|---|---|---|---|---|---|---|
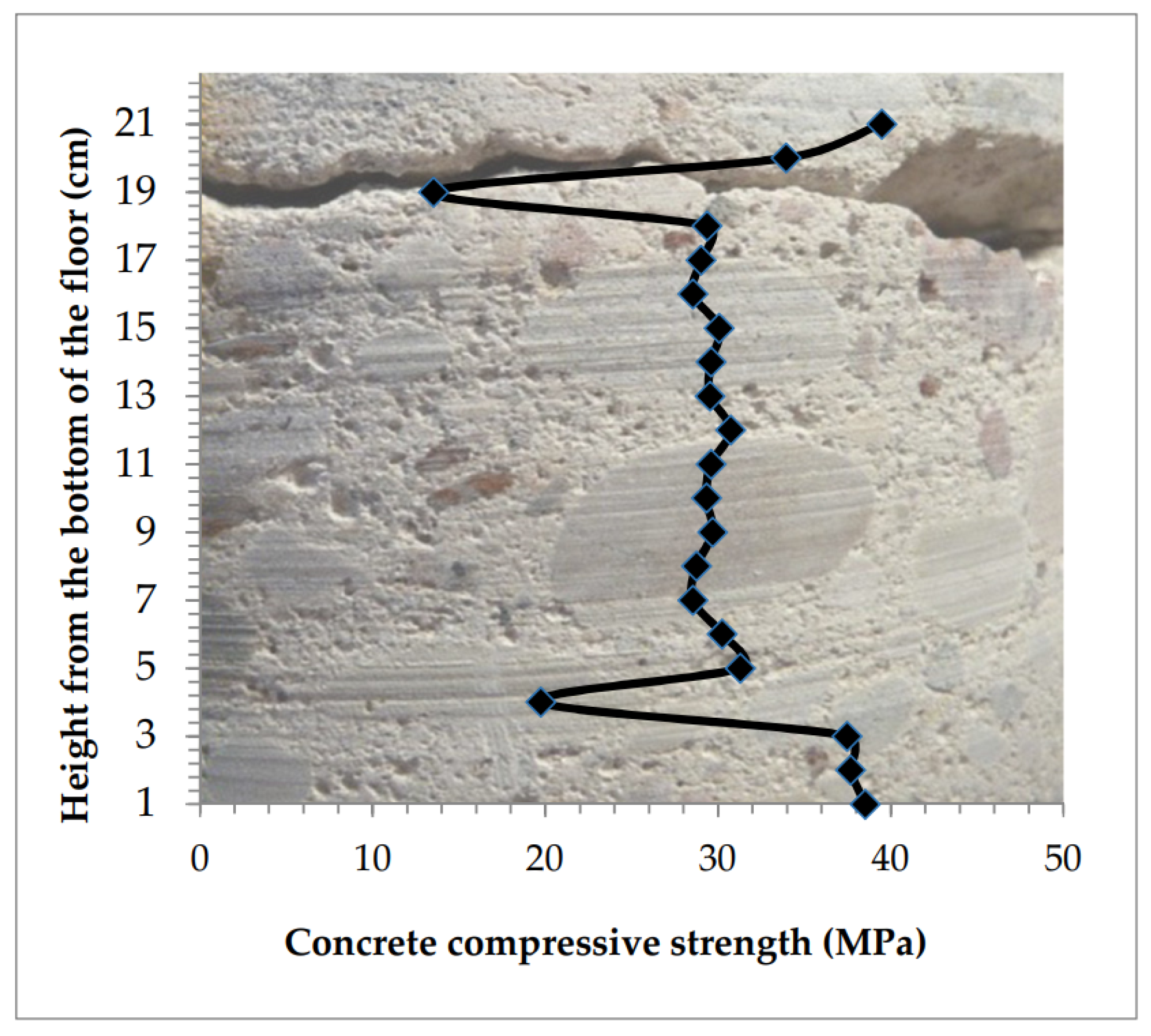
| 1 | 21.0 | 47.0 | 55.0 | 51.00 | 2.950 | 39.50 |
| 2 | 20.0 | 55.5 | 54.9 | 55.20 | 2.726 | 33.94 |
| 3 | 19.0 | 79.0 | 79.2 | 79.10 | 1.902 | 13.53 |
| 4 | 18.0 | 59.0 | 59.4 | 59.20 | 2.541 | 29.38 |
| 5 | 17.0 | 59.9 | 59.2 | 59.55 | 2.526 | 29.01 |
| 6 | 16.0 | 60.6 | 59.4 | 60.00 | 2.508 | 28.54 |
| 7 | 15.0 | 58.5 | 58.6 | 58.55 | 2.570 | 30.07 |
| 8 | 14.0 | 59.2 | 58.8 | 59.00 | 2.550 | 29.59 |
| 9 | 13.0 | 60.0 | 58.1 | 59.05 | 2.548 | 29.54 |
| 10 | 12.0 | 57.9 | 58.0 | 57.95 | 2.596 | 30.73 |
| 11 | 11.0 | 58.6 | 59.4 | 59.00 | 2.550 | 29.59 |
| 12 | 10.0 | 59.9 | 58.6 | 59.25 | 2.539 | 29.32 |
| 13 | 9.0 | 58.8 | 59.0 | 58.90 | 2.554 | 29.70 |
| 14 | 8.0 | 61.3 | 58.3 | 59.80 | 2.516 | 28.74 |
| 15 | 7.0 | 61.0 | 59.0 | 60.00 | 2.508 | 28.54 |
| 16 | 6.0 | 58.0 | 58.8 | 58.40 | 2.576 | 30.24 |
| 17 | 5.0 | 56.6 | 58.3 | 57.45 | 2.619 | 31.29 |
| 18 | 4.0 | 75.8 | 64.0 | 69.90 | 2.152 | 19.74 |
| 19 | 3.0 | 60.9 | 44.0 | 52.45 | 2.868 | 37.48 |
| 20 | 2.0 | 52.3 | 52.3 | 52.30 | 2.877 | 37.68 |
| 21 | 1.0 | 52.0 | 51.4 | 51.70 | 2.910 | 38.51 |
| Ordinal Number | Characteristics of Floor Strength Distribution | Gradient of Strength Decrease in Near Surface Zone (MPa/cm) | Gradient of Strength Increase in Hardening Zone (MPa/cm) | Compressive Strength in the Entire Cross-Section (MPa) | |||
|---|---|---|---|---|---|---|---|
| ∇fc,min | ∇fc min,10 mm | ∇fc,max | Max fc,max | Min fc,min | Average fc,av | ||
| 1 | Homogeneous with weakening of 10 mm of the top layer, (Table 2, Figure 8) | −16.7 | −16.7 | - * | 33.38 | 12.48 | 28.42 |
| 2 | Homogeneous with weakening of 35 mm of the top layer (Table 3, Figure 9) | −3.8 | −6.9 | - * | 45.49 | 24.24 | 35.29 |
| 3 | Variable across the entire cross-section with quick weakening of 50 mm of the top layer (Table 4, Figure 10 and Figure 15) | −2.8 | −7.6 | - * | 30.97 | 8.78 | 22.55 |
| 4 | Surface strengthened to the designed value of 30 MPa from 22 MPa (Table 5, Figure 11) | −9.0 | −9.0 | 7.1 | 41.14 | 23.22 | 33.45 |
| 5 | Poorly hardened surface with low strength (Table 6, Figure 12) | −4.3 | −5.1 | 2.4 | 31.91 | 16.33 | 23.09 |
| 6 | Hardened surface with too low strength (Table 7, Figure 13) | −30.1 | −30.1 | 10.9 | 42.18 | 5.14 | 30.86 |
| 7 | Excessively hardened surface with low strength (Table 8, Figure 14) | −15.8 | −15.8 | 13.0 | 39.5 | 13.53 | 30.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stawiski, B.; Kania, T. Tests of Concrete Strength across the Thickness of Industrial Floor Using the Ultrasonic Method with Exponential Spot Heads. Materials 2020, 13, 2118. https://doi.org/10.3390/ma13092118
Stawiski B, Kania T. Tests of Concrete Strength across the Thickness of Industrial Floor Using the Ultrasonic Method with Exponential Spot Heads. Materials. 2020; 13(9):2118. https://doi.org/10.3390/ma13092118
Chicago/Turabian StyleStawiski, Bohdan, and Tomasz Kania. 2020. "Tests of Concrete Strength across the Thickness of Industrial Floor Using the Ultrasonic Method with Exponential Spot Heads" Materials 13, no. 9: 2118. https://doi.org/10.3390/ma13092118
APA StyleStawiski, B., & Kania, T. (2020). Tests of Concrete Strength across the Thickness of Industrial Floor Using the Ultrasonic Method with Exponential Spot Heads. Materials, 13(9), 2118. https://doi.org/10.3390/ma13092118






